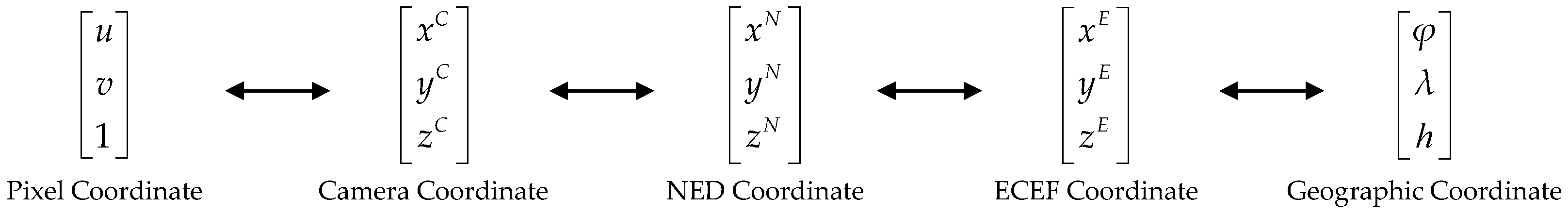Abstract
Target geolocation in long-range oblique photography (LOROP) is a challenging study due to the fact that measurement errors become more evident with increasing shooting distance, significantly affecting the calculation results. This paper introduces a novel high-accuracy target geolocation method based on multi-view observations. Unlike the usual target geolocation methods, which heavily depend on the accuracy of GNSS (Global Navigation Satellite System) and INS (Inertial Navigation System), the proposed method overcomes these limitations and demonstrates an enhanced effectiveness by utilizing multiple aerial images captured at different locations without any additional supplementary information. In order to achieve this goal, camera optimization is performed to minimize the errors measured by GNSS and INS sensors. We first use feature matching between the images to acquire the matched keypoints, which determines the pixel coordinates of the landmarks in different images. A map-building process is then performed to obtain the spatial positions of these landmarks. With the initial guesses of landmarks, bundle adjustment is used to optimize the camera parameters and the spatial positions of the landmarks. After the camera optimization, a geolocation method based on line-of-sight (LOS) is used to calculate the target geolocation based on the optimized camera parameters. The proposed method is validated through simulation and an experiment utilizing unmanned aerial vehicle (UAV) images, demonstrating its efficiency, robustness, and ability to achieve high-accuracy target geolocation.
1. Introduction
In recent years, achieving long-range, high-accuracy target geolocation is of great practical significance and has applications in many fields, such as military reconnaissance, disaster monitoring, surveying, and mapping [1,2,3]. Target geolocation primarily refers to the calculation of the geographical position of a target in an aerial remote sensing image captured through airborne camera. This is achieved by determining the target’s geographic coordinates based on its pixel coordinates in the image. Numerous scholars have extensively researched target geolocation algorithms to attain accurate target position. Barber et al. [4] introduced a method for determining the location of ground targets observed by a fixed-wing miniature air vehicle. This approach demonstrates effective localization for low-altitude and short-range targets. However, due to the typical limitations of UAVs, the flight altitude is about 20 km; this implies that for long-range imaging, the oblique angle of the camera could be significantly large, which makes it unsuitable as this method does not account for the curvature of the Earth.
In order to achieve long-range aerial image target geolocation, researchers [5,6] have calculated the intersection of the line-of-sight (LOS) vector and the target on the surface of the Earth with the Earth model, usually the World Geodetic System 1984 (WGS-84) ellipsoid. This method is sufficiently simple and robust, widely used in long-range target geolocation at present. However, when geolocating a target with only one single image, the measurement accuracy of GNSS and INS sensors, along with the altitude error of the target, can significantly influence the accuracy of the geolocation. An analysis of the factors influencing the accuracy of target geolocation was previously conducted [7]. In essence, achieving an accurate geolocation outcome relies on the precise measurement of UAVs’ navigation state and the accurate determination of the target’s altitude. Consequently, obtaining an accurate geolocation result for non-cooperative targets proves challenging, particularly when relying on onboard navigation state sensors of lower quality.
Although the LOS-based method has many limitations that make it difficult to achieve high-accuracy geolocation, it forms the basis of most geolocation algorithms. To improve the accuracy of target geolocation, researchers explored diverse approaches, such as integrating supplementary information and incorporating multiple observations into the algorithms. To reduce geolocation error caused by the uncertainty in target altitude, the methods [8,9] based on laser range finder (LRF) are proposed. Unlike the LOS-based method, which requires the altitude of the target to determine the closest intersection with the Earth model, the LRF device can directly measure the distance between the target and the aircraft, thereby enhancing the accuracy of the geolocation results. Without considering the error of GNSS and INS sensors, simulation results demonstrate that the target geolocation accuracy could be less than 8 m when the image matching slant range is about 10 km [9]. However, the effective working range of most LRFs is within 20 km, and ensuring measurement accuracy beyond this range becomes challenging. Moreover, to acquire remote sensing images over long distances, the capturing distance for long-range oblique aerial remote sensing is typically set to be greater than 30 km in practical projects [10]. To address this problem, Qiao et al. [2] introduced an improved method of LOS based on iteratively estimating the altitude of the target with a digital elevation model (DEM). The simulation and flight experiment results indicate that at an off-nadir looking angle of 80 degrees and a target ground elevation of 100 m, the geolocation accuracy improves from 600 m to 180 m with the DEM-based method. Although this method is simple and robust, it has some obvious limitations. Large-scale, high-precision DEM maps are often relatively expensive, and for some artificial targets, DEM cannot accurately provide the altitude of the target.
The cross-view target geolocation has emerged as a research hotspot in recent years [11,12,13,14,15,16]. These methods primarily involve registering and aligning images by matching UAV images with satellite map data. Subsequently, the geographical coordinates of target points are determined by locating corresponding positions within the satellite map data. Results are determined by the precision of satellite imagery and the pixel error of image matching. Fundamentally, this poses a challenge which is referred as a multi-modal image registration problem. With the development of deep learning technologies, the accuracy of registering images captured from different perspectives, times, seasons, and sensors has been steadily increasing. Compared to DEM maps, satellite imagery is more obtainable, and the accuracy of satellite imagery geolocation often reaches the level of a few meters. However, the UAV images used in these methods are typically captured at close range, exhibiting a favorable signal-to-noise ratio (SNR). Aerial images captured at long-range with a large oblique angle typically exhibit lower SNR. Atmospheric refraction and scattering significantly impact the imaging quality. The image quality may also be degraded by factors such as motion blur due to the camera shaking and obstruction caused by clouds and fog. Moreover, the spatial resolution of these images is typically not as high as satellite imagery, and the target occupies only a small region on the image. Those reasons lead to the result that cross-view-based methods are challenging to apply in practical long-range photography programs.
In addition to the methods discussed above, utilizing observations from multiple views can further reduce geolocation error. Hosseinpoor et al. [17,18] improved the accuracy of geolocation with an extended Kalman filter (EKF), which is well adapted for long-range oblique UAV images. However, this method requires the use of a considerable number of images to achieve convergent results. This study aims to achieve high-accuracy target geolocation in the context of long-range and large-oblique aerial remote sensing. We propose a novel method to achieve this with a reasonable number of images. The remainder of this paper is organized as follows. Section 2 introduces the processes of our method. We first briefly review the LOS-based method, then introduce our improvement based on camera position and attitude optimization. Section 3 provides a detailed presentation of the simulation and experimental conditions, as well as the results and analysis. Section 4 discusses the reason that our results can achieve better outcomes compared to previous methods. Finally, Section 5 summarizes this study.
2. Methods
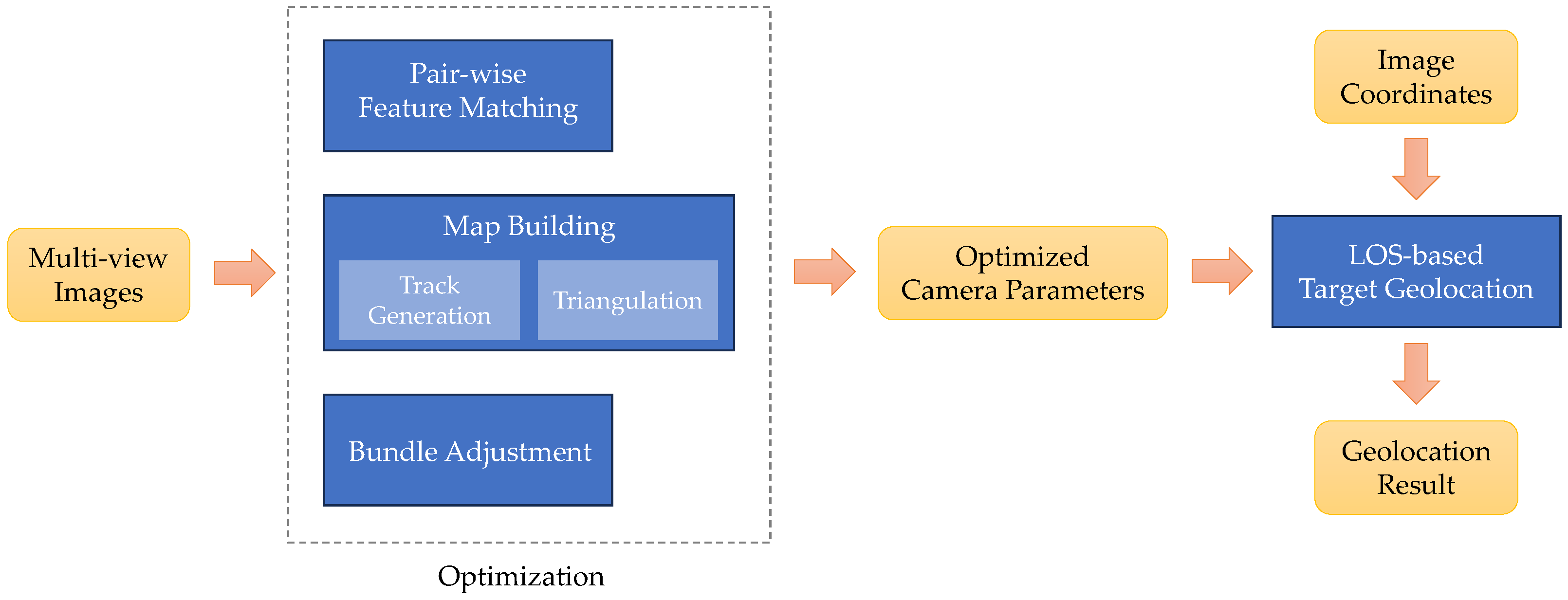
Figure 1 shows the framework of the proposed method. The proposed method can be regarded as an improved and optimized refinement of traditional approaches. We first present a brief overview of the LOS-based geolocation method, since the subsequent cost function of Equation (13) is derived from it. Then, we introduce the camera optimization, which improves the accuracy of the camera parameters through multiple-view observations. Finally, the target achieves high-accuracy geographic localization results by utilizing optimized camera parameters and an estimated target altitude.
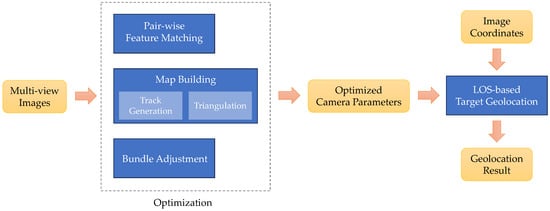
Figure 1.
Framework of the proposed method.
2.1. LOS-Based Method
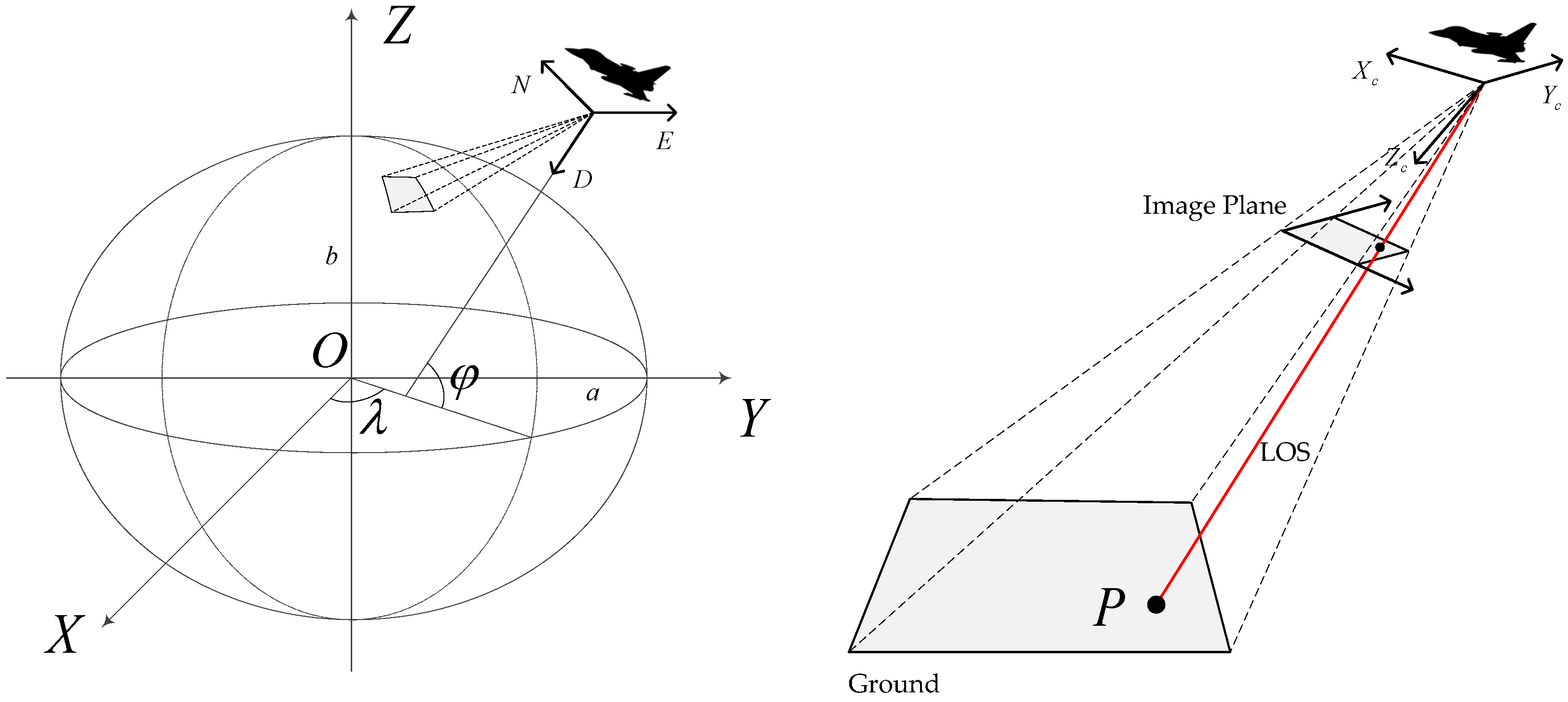
The geolocation method based on LOS was originally developed for imaging systems utilizing precision mechanical gimbals with high-performance servo systems and high-resolution inertial sensors or gyroscopes, such as the frame locator algorithm [5] and the LOS pointing algorithm [6]. Essentially, the LOS-based method utilizes coordinate transformation to convert the target point from pixel coordinates to geographic coordinates. The LOS vector is defined as the vector from the camera center to the target point. The LOS vector is calculated by the camera parameters and pixel coordinates. Then, we can obtain the geographic coordinates of the target point by calculating the intersection of the LOS vector and the WGS-84 ellipsoid, as shown in Figure 2. The WGS-84 ellipsoid is a reference ellipsoid that approximates the geoid, which is the shape that the Earth would take if the oceans were in equilibrium, at mean sea level, and extended through the continents. The WGS-84 ellipsoid is defined by the semi-major axis a and the semi-minor axis b. The semi-major axis is the equatorial radius of the ellipsoid, and the semi-minor axis is the polar radius of the ellipsoid.
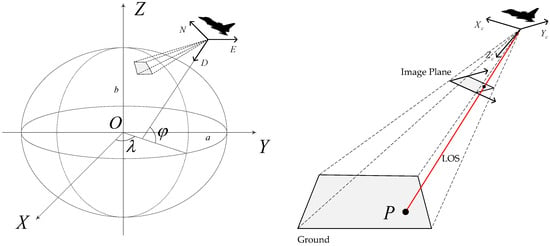
Figure 2.
Intersection of LOS vector and ellipsoidal Earth model.
To obtain the geographic coordinates of the target point, we need to transform the coordinates of the target point in the image to the geographic coordinates. In the imaging model during capturing, a total of five coordinate frames are defined, which are pixel coordinate frame, camera coordinate frame, north–east–down (NED) coordinate frame, Earth-centered-Earth-fixed (ECEF) coordinate frame, and geographic coordinate frame. Figure 3 shows symbols and transform relations between coordinate frames.

Figure 3.
Coordinate transformation.
It becomes two-dimensional after projecting a point from the 3D space to the pixel coordinate frame. We could use homogeneous coordinates to represent any point in that direction. The projection from the camera coordinate frame to the pixel coordinate frame can be expressed by the intrinsic matrix of the camera, which contains parameters such as the focal length and the principal point coordinates. The projection in the camera coordinate frame can be described as follows:
where u and v are the pixel coordinates of the target point; and are the lengths of the focal length scaled in the horizontal and vertical directions, respectively. and are the principal point coordinates of the camera. This matrix is the intrinsic matrix of the camera. , , and are the coordinates of the target point in the camera coordinate frame. Here, we analyze the impact of image distortion in LOS-based localization methods. Aerial images typically exhibit radial and tangential distortions, which can be corrected using coefficients from calibration. However, in LOS-based method, the primary factor affecting the geolocation accuracy is sensor measurement errors, and the influence of pixel displacement caused by distortion on the results is relatively minor. The camera coordinates can be transformed from NED coordinates, which can be expressed as follows:
where , , and are the coordinates of the target point in the NED coordinate frame, and is the rotation matrix of the camera (i.e., the attitude of the camera can be obtained through the INS). The NED coordinates can be transformed from the ECEF coordinates by setting the geographic coordinates of the reference point (i.e., the position of the camera can be obtained by GNSS), as shown in the following equation:
where and are the latitude and longitude of the reference point; , , and are the coordinates of the target point; and , , and are the coordinates of the reference point. To transform the ECEF coordinates to the geographic coordinates, we need some parameters of the Earth model, and its description is as follows:
where is the prime vertical radius, a is the semi-major axis of the Earth, e is the eccentricity of the Earth, h is the altitude of the target point, and and are the latitude and longitude of the target point.
Distance from target to the camera is required to calculate the geographic coordinates of the target point using the above coordinate transformations. A laser rangefinder can measure the distance at a relatively short slant range. However, in the case of shooting at long range, the accuracy of distance measurement will be significantly affected. In this case, we can use the LOS vector to calculate the intersection of the LOS and the Earth’s surface, and then determine the geographic coordinates of the target point.
The reprojection of the target point from the image to the space can be represented as follows:
where are the ECEF coordinates of the target point, s is the scale factor, is the transformation matrix from the ECEF coordinate frame to the NED coordinate frame as described in Equation (3), is the rotation matrix of the camera, and is the intrinsic matrix of the camera as described in Equation (1). are the pixel coordinates of the target point (homogeneous coordinates), and are the coordinates of the camera center in the ECEF coordinate frame. Thus, we can obtain the LOS vector as follows:
Furthermore, the point on the Earth’s surface needs to satisfy the constraints of the Earth model, for which the calculation can be approximated as [5]
where h is the altitude of the target on the surface of the Earth; a and b are the semi-major axis and the semi-minor axis of the WGS-84 ellipsoid, respectively. By solving Equations (6) and (7), we can obtain the ECEF coordinates of the target point. The geographic coordinates of the target can be obtained through an iterative algorithm based on the ECEF coordinates [19], summarized as
where i is the i-th iteration of the algorithm, is the prime vertical radius, is the altitude of the target point, is the latitude of the target point, and is the longitude of the target point. The result of Equation (8) is the final result of the LOS-based geolocation.
2.2. Camera Optimization
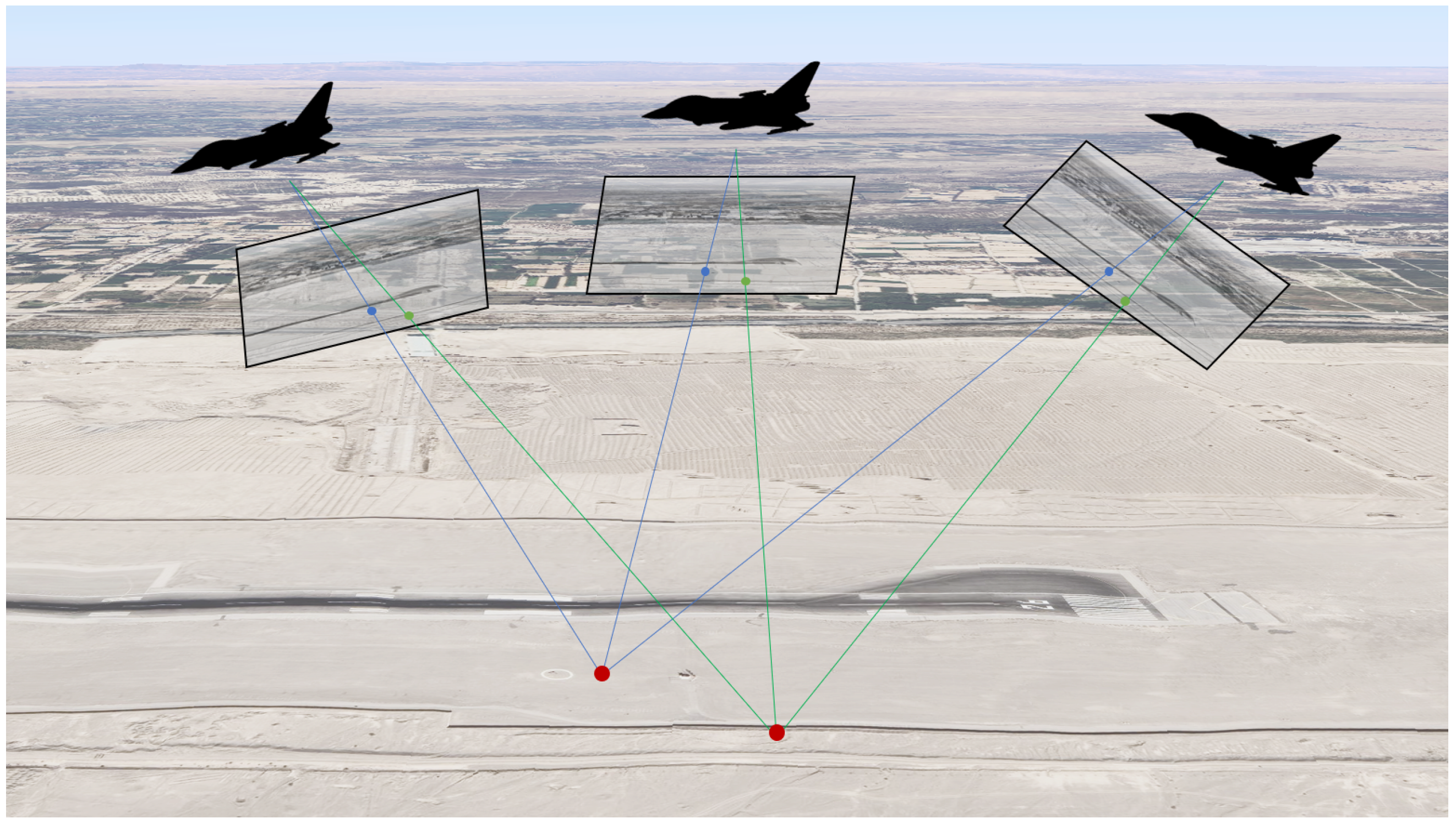
Usually, the error source in the LOS-based method is attributed to inaccuracies in the camera parameters. These errors may arise from inaccurate calibration, representing a systematic error, or from the sensors themselves during measurement. To reduce the influence of these errors, we need to optimize the camera parameters. As illustrated in Figure 4, the optimization is to observe the same target point multiple times, use the projection equations of the target point under different views to construct the error equations, and optimize the camera parameters. The optimization process can be delineated into three key steps: feature matching, map building, and bundle adjustment.
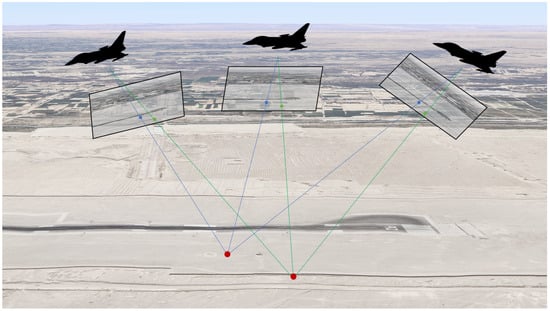
Figure 4.
Illustration of multiple-view camera optimization.
2.2.1. Feature Matching
The first step in camera optimization is feature matching between all of images. Through feature matching, the same target points under different views can be corresponded, that is, the projection positions of the target points in different views can be found. Feature matching is mainly based on feature extraction and matching. Typical feature extraction algorithms include SIFT [20], ORB [21], BRISK [22], AKAZE [23], etc. For the same optical system and CCD detector, although captured at different positions, the changes in ground objects are minimal, and there is little variation in the capturing distance and perspective. Therefore, the aforementioned feature matching algorithms can effectively accomplish the feature matching process. In our tests, we observed that SIFT achieves the highest matching accuracy, while ORB exhibits the minimum time consumption. When capturing UAV images at relatively close distances (less than 100 km), we suggest using ORB features, as it strikes a favorable balance between speed and accuracy. However, for long-range captures, we recommend utilizing SIFT features, considering that image quality is often significantly compromised in such scenarios, which presents a substantial challenge to the precision of image matching.
2.2.2. Map Building
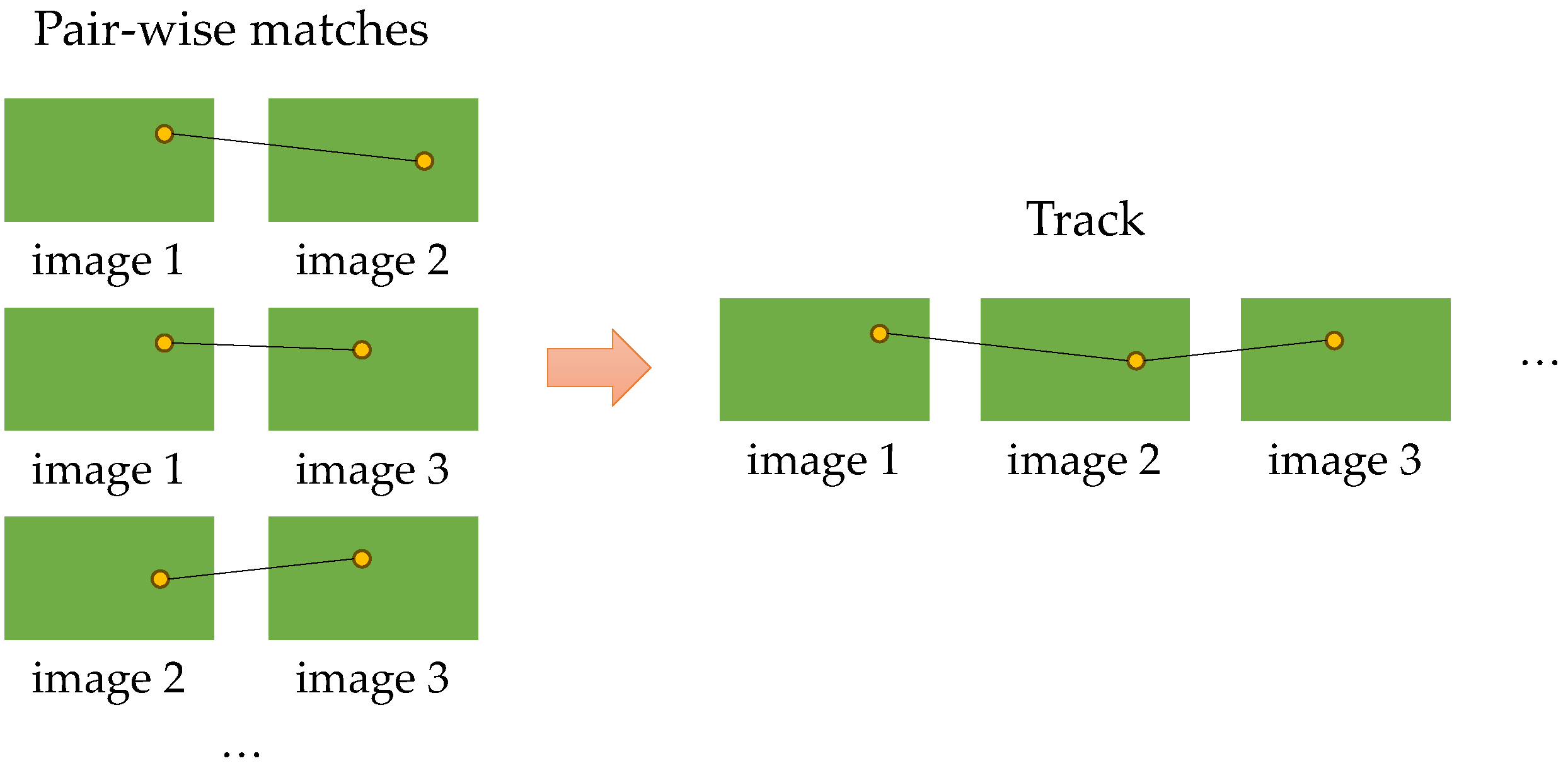
Map building is to construct a map using all the feature matching results. The map contains the spatial coordinates of all feature points. Since feature matching is performed between each pair of images, only the corresponding points of these two images can be obtained. We need to know the projection position of this point in all views so that we can use the multi-view triangulation method to initialize its spatial coordinates. This process is named as track generation [24], which simply groups the matched feature points, and each group contains the pixel coordinates of the point in the specified image. For example, some feature points have large changes in position in the image, or the contrast in the image is low, and the matching results of these feature points are unreliable. To ensure the effect of map building, these feature points need to be filtered. The filtering method is used to calculate the homography matrix between the matching images, obtain the projection position of the feature points in the other image and then use the random sample consensus (RANSAC) algorithm [25] to remove outliers.
After obtaining the filtered feature points, we can perform the track generation process as described above. As illustrated in Figure 5, the problem of track generation is to find the positions of the same feature point across a set of images. Moulon and Monasse [26] proposed an approach relying on the Union–Find algorithm to solve this problem. Initially, a singleton is created for each matched feature. Pairwise matches then involve merging the two sets containing them, with each resulting set corresponding to a track. The key aspect lies in the integration of the join function, which utilizes the Union–Find algorithm to merge corresponding subsets. It is simple and efficient, and to ensure the stability of subsequent triangulation, we set that a track must consist of points that have matching correspondences in at least five different images.
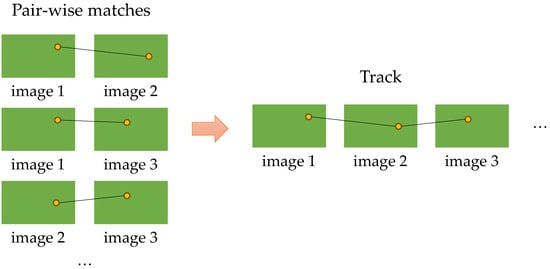
Figure 5.
Illustration of track generation.
After track generation, we can use the multi-view triangulation method to calculate the 3D coordinates of these feature points, which are also called landmarks in some structure from motion (SFM) works. More accurate triangulation results can set more accurate initial values for subsequent optimization steps. However, since our subsequent optimization is based on bundle adjustment, minor differences in triangulation have a minimal impact on the final results. Multiple-view middle point (MVMP) [27] is a direct triangulation method that can be used to calculate the 3D coordinates of feature points.
As shown in Figure 6, is a point in space, is a pointing vector in the set, and is the staring position of the vector. In the context of the target geolocation task in this paper, can be derived based on the rotation of the camera and the position of the target point in the image, while represents the origin of the camera. The goal of the triangulation is to find the optimal estimation of the 3D point coordinates with their projections in two or more images.

Figure 6.
Illustration of multiple-view midpoint method.
The midpoint method involves solving a least squares problem using the linear equations by letting , where and are already known. This approach is considered optimal under the Gaussian noise model. Equation (9) can be formulated as
where is a matrix, and is a vector. As long as not all the pointing vectors are parallel, is full-rank, and therefore, a unique solution can easily be obtained. This method can give a rough triangulation result, and then the triangulation result can be optimized using the bundle adjustment method. To simplify the calculation, the triangulation method used in this paper is the ECEF coordinate system, which is then converted into the geographic coordinate system if needed.
After all the above steps, the map-building process is completed, and the 3D coordinates of all feature points are obtained.
2.2.3. Bundle Adjustment
In aerial remote sensing, the ground scene can be captured from different views. The spatial positions of scene points can be constrained by constructing projection equations from different views. However, due to the errors of the camera parameters, the projection equations from different views are inconsistent. These errors may come from inaccurate calibration, which is a form of systematic error, or from the sensors themselves during measurement. To reduce the impact of these errors, optimizing the camera parameters becomes essential. This optimization involves adjusting both the camera parameters and scene points based on the corresponding points in images, a process commonly referred to as bundle adjustment (BA) [28].
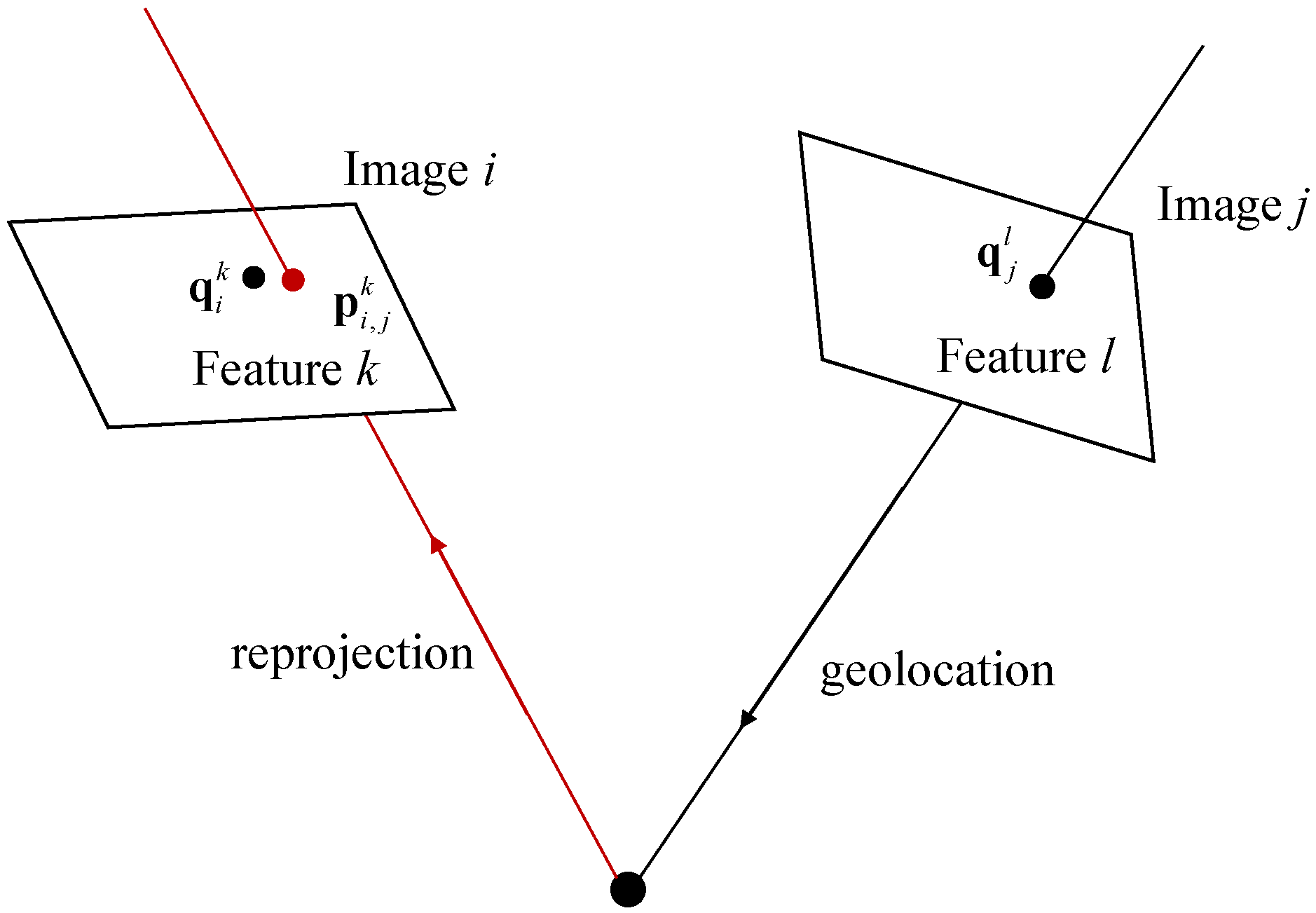
As illustrated in Figure 7, given a correspondence of , ( donates the position of the k-th feature in image i), the residual can be formulated as follows:
where is the reprojection from image j to image i of the point corresponding to . To obtain the reprojection result , the geolocation result of the target is obtained using the LOS-based method from Section 2.1, and then the projection is obtained using Equation (11). is also known as the reprojection error in some other computer vision works.
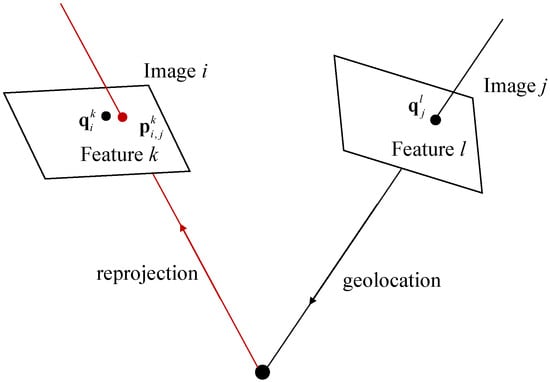
Figure 7.
Illustration of reprojection error. The red ray represents the path of reprojected to another matched image. The error between the matched point pairs is the reprojection error.
The cost function is the summation of robustified residual errors across all images:
where n represents the number of used images, denotes the set of images matching image i, and represents the set of feature matches between images i and j. The Huber loss is used to robustify the cost function, which is defined as [29]
The cost function combines the fast convergence properties of an norm optimization scheme for inliers (distance less than ), with the robustness of an norm scheme for outliers (distance greater than ) [30].
This is a non-linear least squares problem which can be solved by using the Levenberg–Marquardt algorithm. However, the LOS-based geolocation method needs to solve the intersection of the LOS and the Earth’s surface, which will make the Jacobian matrix very complex. Fortunately, we can use the ceres solver [31] to solve this. The ceres solver is an open source non-linear optimization library that can solve various types of non-linear optimization problems. By constructing the residual block based on Equation (13), the ceres solver can rapidly minimize the error equations, thereby yielding optimized results. After optimization, more accurate intrinsic and extrinsic camera parameters can be obtained, as well as the optimized 3D coordinates of landmarks.
2.3. Target Geolocation
Through the above steps, the optimized 3D coordinates of the target can be obtained directly, if the target is added as a landmark in map building. However, our primary objective is typically to acquire the optimized intrinsic and extrinsic parameters of the camera and subsequently to calculate the geographical coordinates of the target utilizing the LOS-based method. Since there may be multiple targets in the image or repeated target geolocation within the same images, performing camera optimization for each instance would significantly increase time consumption.
By saving the optimized camera parameters to the historical data, the optimized camera parameters can be used directly for geolocation in the subsequent work. The altitude of the target can be obtained by triangulation as discussed in Section 2.2.2. This sequential approach enhances the speed of our method and aligns with the core objectives of our research.
3. Results
3.1. Simulation Results
We use the real flight parameters of the UAV to generate simulation data for a static target. We can generate continuous camera parameters of the same target by adjusting the attitude of the camera. The UAV’s optical imaging system is fixed on a two-axis gimbal, at the center of which defines the origin for both the camera coordinate frame and the aircraft coordinate frame. In this right-handed coordinate system, the aircraft frame’s X-axis points towards the nose, the Y-axis points right, and the Z-axis points down. The camera’s attitude is described by the inner gimbal angles and outer gimbal angles.
In this study, simulation is performed based on the Monte Carlo method. When generating simulation data, some errors are added to the generated data. We categorize the introduced errors into two types: systematic errors and random errors. Usually, we believe that systematic errors (device installation errors, instrumentation errors, operator bias, etc.) can be eliminated by calibration. However, aerial photography is not necessarily performed every time; the systematic errors can be perfectly calibrated and eliminated, so we need to add systematic errors to the simulation data, as shown in Table 1. Random errors are randomly generated during measurement and cannot be eliminated. We assume that the random error follows a Gaussian distribution with a mean of 0 and a standard deviation of , as shown in Table 2.

Table 1.
Systematic error of the simulation data.

Table 2.
Random error of the simulation data.
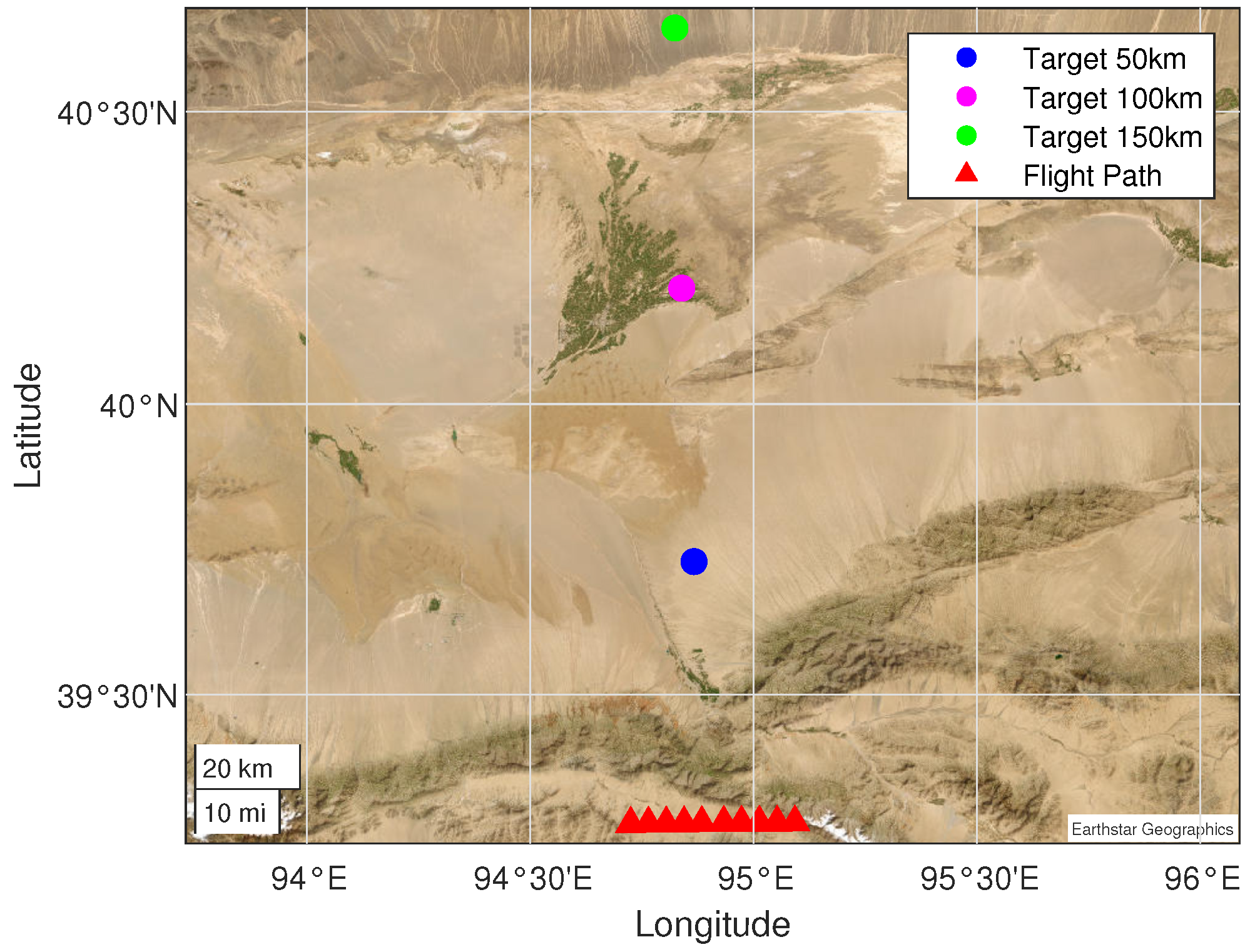
As shown in Figure 8, the red triangles represent the geographic coordinates of the aircraft when capturing images. At each position, we performed simulations 100 times, and each simulation datum was added with random errors and systematic errors based on the real data. Here, the real data refer to the real flight parameters, and then the camera gimbal angles are adjusted to center the target in the image. To measure the influence of the slant range between the target and the aircraft (different slant ranges imply varying oblique angles) on the geolocation result, we simulate three targets at different slant ranges. The blue circle represents the target, which is about 50 km away from the UAVs, while the magenta one and the green one are about 100 km and 150 km away, respectively.
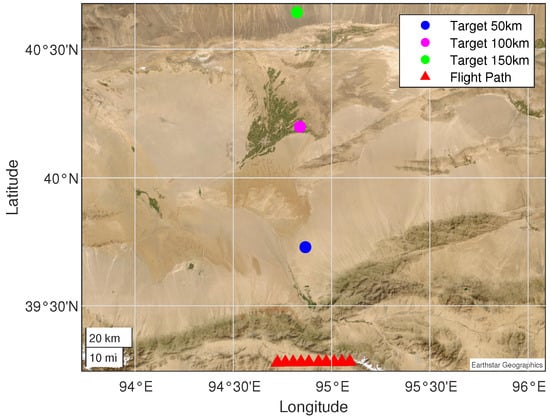
Figure 8.
Flight path in the geographic map. The red triangles represents the positions of the UAVs and the circles represent the positions of the targets when capturing images. The blue circle represents the target, which is about 50 km away from the UAVs, while the magenta one and the green one are about 100 km and 150 km away, respectively.
From the geolocation error obtained by the simulation analysis, various evaluation criteria can be used for the geolocation accuracy, such as the distance root mean square (DRMS) and circle probability error (CEP). DRMS refers to the square root of the mean squared distance error, which could be obtained simply by averaging the distance errors. Originally a measure of precision for weapon systems in military science, CEP is defined as the radius of a circle centered on the target, expected to contain 50% of rounds fired. The concept has also been adopted in target detection and geolocation applications. We believe that CEP is a more reasonable evaluation criterion, because it reflects the stability of the algorithm from a statistical point of view. However, the original CEP threshold is 50%. For more accurate positioning tasks, we believe the threshold should be adjusted to a more convincing value, such as 95%, and we call it CEP95.
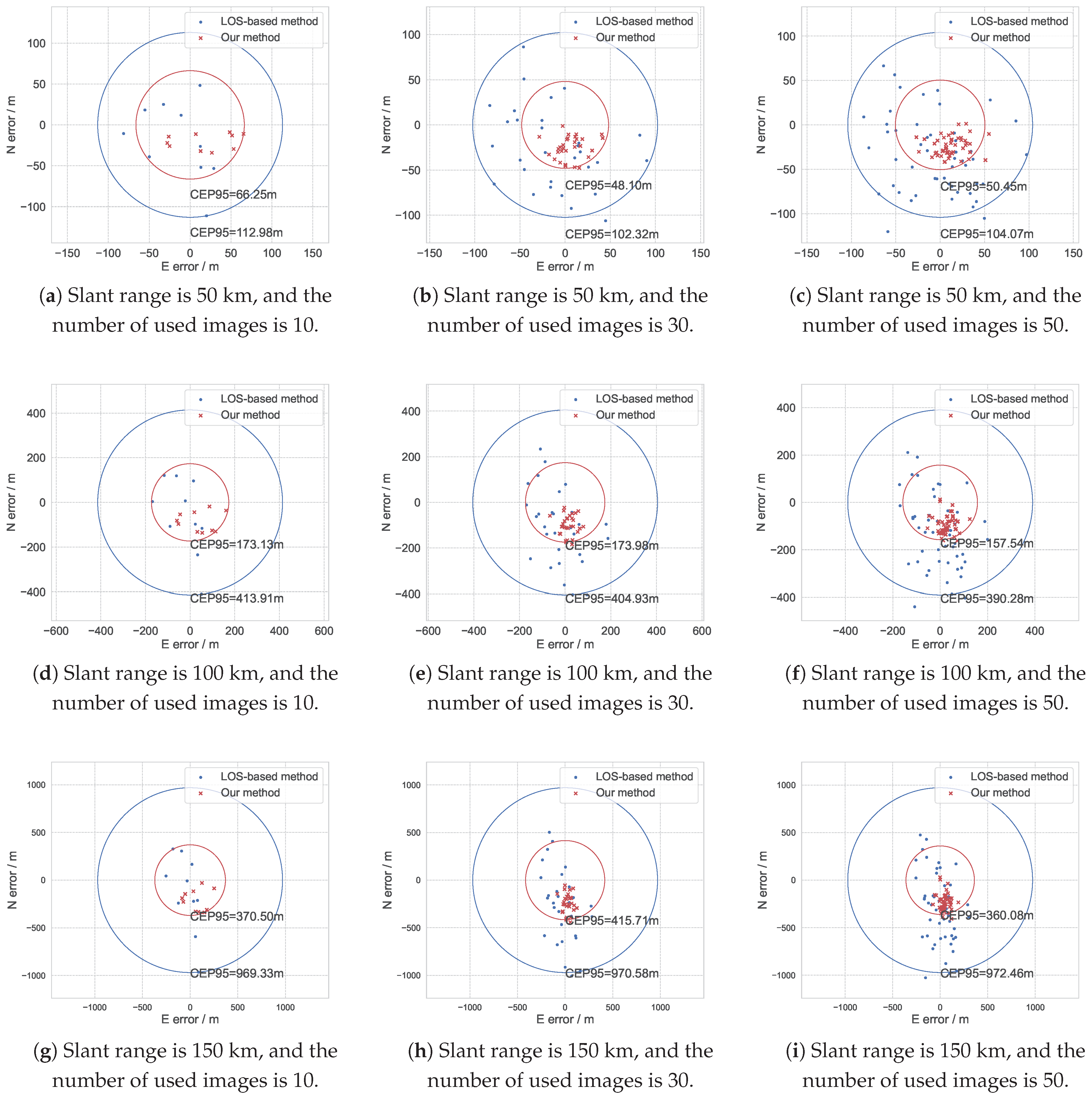
We simulate targets with slant ranges of 50 km, 100 km, and 150 km, and using 10, 30, and 50 images to perform our geolocation algorithm. The simulation is repeated 100 times for each condition, and one of the simulation results evaluated in CEP95 is shown in Figure as an illustrated example. From the figure, we can obtain a clearer view of the distribution of geolocation results, aiding in the analysis of bias introduced by systematic errors. Additionally, compared to DRMS, CEP95 is less influenced by mean regression, which proves particularly crucial in practical geolocation tasks.
We analyzed a large number of CEP95 geolocation results and can draw the conclusion that the geolocation results have been significantly improved. At the same time, since the systematic error is added during the simulation, the geolocation results have a bias, which is a certain offset toward the south of the local coordinate system. Figure 9 can representatively demonstrate this characteristic.
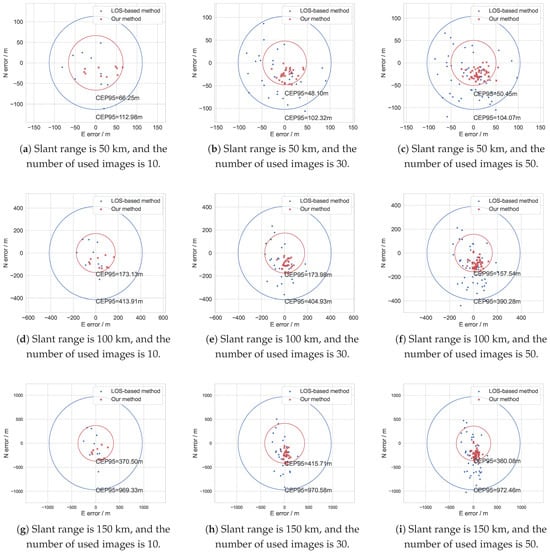
Figure 9.
One simulation result evaluated in CEP95 of using different numbers of images with slant ranges of 50 km, 100 km, and 150 km. The blue dots represent the LOS-based geolocation results, and the red crosses represent the optimized geolocation results.
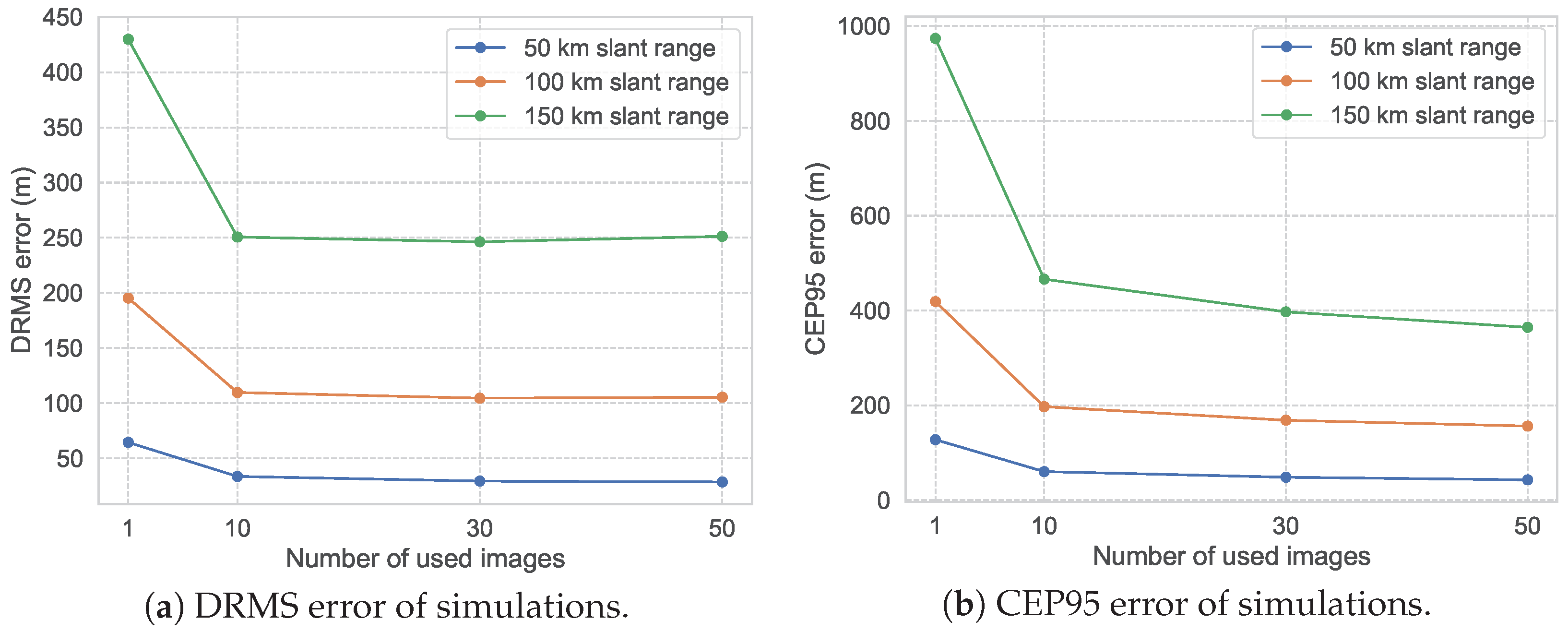
Figure 10 shows the simulation results of different numbers of images. We set different numbers of images, then perform 100 simulations for each number of images, and obtain the average result of the geolocation error (average DRMS and average CEP95). From Figure 10 and Table 3, an interesting phenomenon can be observed. When the number of used images increases from 30 to 50, the geolocation accuracy is close, and even decreases when using DRMS as the evaluation criterion. However, when using CEP95, the geolocation accuracy increases with the number of used images. This also indicates that CEP95 is a more reasonable evaluation criterion. It is also noticeable that, beyond a certain threshold of the number of used images, the enhancement in geolocation accuracy within CEP95 becomes less pronounced. This is attributed to the fact that, as the quantity of images attains a certain threshold, the diminishing effect on random errors becomes less apparent, whereas the manifestation of systematic errors becomes more pronounced. Since the algorithm is unable to eliminate systematic errors, the observable enhancement in geolocation accuracy becomes less evident beyond a specific number of images. From Figure 10 and Table 4, it can be seen that when the number of used images is 10, compared with the LOS geolocation, the effect is obvious, and the improvement of CEP95 is above 50%. However, when the number of used images reaches 30, compared with the LOS geolocation, the effect is improved by about 20%. When the number of used images reaches 50, there is almost no obvious improvement compared to when the number of used images is 30. This indicates that upon reaching a specific threshold in the number of utilized images, further increasing this count does not yield a substantial improvement in geolocation accuracy.
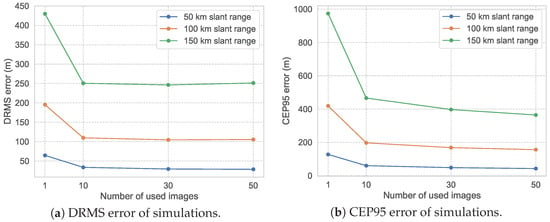
Figure 10.
Simulation results of using different numbers of images with slant ranges of 50 km, 100 km, and 150 km. Note that when the number of used images equals to one, it indicates the original LOS-based geolocation result.

Table 3.
Average DRMS of the simulation results.

Table 4.
Average CEP95 of the simulation results.
Table 5 shows the quantitative comparison of the simulation results, which are obtained from the LOS-based method, EKF-based method, and our method. For the LOS-based method, i.e., the original one-shot method, the geolocation error is very large when the slant range is 100 km and 150 km. This is mainly because when the target is far from the aircraft, the error of the oblique angle is large, which leads to a large geolocation error. The EKF-based method is based on the extended Kalman filter, which can continuously optimize the camera parameters through an iterative process. From the table, it can be seen that the filtering of the EKF-based method is effective. Compared to the LOS-based method, the EKF-based method improves the geolocation accuracy by about 47%, 50%, and 51% at 50 km, 100 km, and 150 km, respectively. Among these three methods, our method performs the best. The geolocation accuracy is improved by about 62%, 60%, and 59% at 50 km, 100 km, and 150 km, respectively. Compared with the EKF-based method, our method improves the geolocation accuracy by about 10% on average. This indicates that our method is a more effective geolocation method.

Table 5.
Quantitative comparison of the simulation results in an average CEP95.
3.2. UAV Image Results
To validate the efficiency of the proposed method, we used UAV images in a real flight experiment to evaluate the geolocation method. The airborne camera is composed of platform, inner gimbal, outer gimbal, and the imaging system, mounted on the UAV, as shown in Figure 11. It is equipped with long-focus lens, where an equivalent focal length of the camera is greater than 1.5 m, as well as an image size of 8 K × 5 K with a pixel size smaller than 10 μm. During flight, the flying altitude is between 10 km and 15 km.

Figure 11.
Airborne camera.
As shown in Figure 12, the target was observed multiple times in different views using the airborne camera during the whole flight. The upper part of the image is captured by the camera, while the red window is the area containing the target cropped from the original image. To validate the efficiency of our method, the number of used images is set to 10. This choice is deliberate, aiming to align with practical usage scenarios, where a substantial number of images may not always be available as input for the algorithm.

Figure 12.
Example of UAV images. Multiple-view of images with the same target.
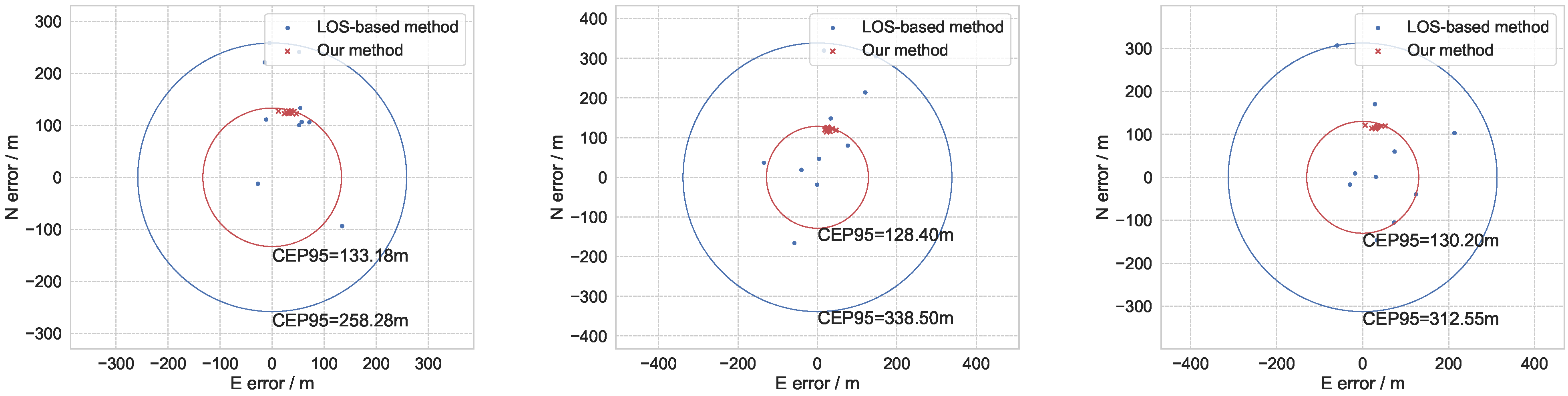
The ground-truth geographic coordinates of targets are measured on the ground by the CHC I70, which is a geodetic GNSS receiver. The measurement error of the observed point was less than 0.1 m, making it acceptable as the standard value. In this paper, we conducted experiments on three targets. The slant ranges between the targets and the UAVs are about 48 km, 52 km, and 49 km. The coordinates measuring on the ground of corresponding targets are presented from left to right in Figure 13.

Figure 13.
Ground measuring for the targets.
Figure 14 shows the comparison of the LOS-based method and our method in CEP95 using the UAV images, the optimized results of the three targets are presented from left to right. Table 6 shows the CEP95 result comparison of the LOS-based method, EKF-based method, and the proposed method. It can be seen from the figure and the table that our method has a significant advantage over the LOS-based method and EKF-based method. The average on the bottom line of Table 6 means the average result of the three targets. Compared to the LOS-based method, the EKF-based method improves the geolocation accuracy by about 37%, while our method improves by about 58%. This indicates that our method is a more effective geolocation method. From the figure, we can see that there is a certain bias in the geolocation results, which is mainly caused by the systematic error. We believe the main issue lies in the fact that we did not completely address systematic errors during the camera calibration phase.

Figure 14.
CEP95 results of UAV image experiment. From left to right are the results of the three targets.

Table 6.
Quantitative comparison of the simulation results in CEP95.
4. Discussion
The framework of our method can be summarized as feature matching, map building, camera optimization, and geolocation. In simulation and the UAV image experiment, comparisons were made between the LOS-based method, the EKF-based method, and our method. The LOS-based method is the one-shot geolocation approach known for its simplicity and efficiency, while the EKF-based method is a multi-view method that can improve geolocation accuracy and has been widely used in many fields. From the simulation results in Figure 10, we can see that our method significantly improves the geolocation accuracy. Figure 5 shows that, compared with the EKF-based method, our approach incurs a higher computational cost, but achieves superior geolocation accuracy. This is attributed to our equation based on the imaging model, which possesses a more accurate physical interpretation. In contrast, the EKF-based method employs an iterative approach and can be viewed as a form of error regression method. As for the UAV image experiment, it can be seen from Figure 12 that our experimental results show some similarity to the simulation outcomes, affirming the validity of the established theoretical model and further validating the effectiveness of the proposed method.
The proposed method enhances geolocation accuracy through multiple observations of the same target. Theoretically, this method is not only suitable for long-range targets but can also improve the geolocation accuracy of targets at shorter distances. However, when observing nearby targets, the advantages of our proposed method may not be as evident. Other approaches, such as the method based on laser range finder or the EKF-based method, can provide similarly accurate results at a faster pace. Another advantage of our approach is the ability to incorporate ground control point information when constructing error equations (if the real coordinates of the point are known), which proves highly beneficial when historical data are available. We have validated that, upon integrating control points, the accuracy of target geolocation can achieve a level within a few meters. This further confirms the correctness of our model and methodology. However, such applications are rare in practical programs, so this paper does not extensively explore this aspect.
The simulations and experiments in this paper are conducted based on a single static target. In theory, our proposed method is applicable to moving targets and multiple targets. The choice of a single static target is made to better evaluate the quantified impact of camera parameter optimization on target geolocation.
In this paper, we categorize the errors of target geolocation into systematic errors and random errors. Assuming a sufficient number of flight images, we believe that our method can effectively reduce the influence of random errors on geolocation results. Therefore, the limitation of our method lies in the systematic errors of the camera during image capture. Currently, to eliminate the influence of systematic errors, camera calibration or introducing ground control points, as mentioned above, is required. We are also exploring a more practical method for further refinement.
5. Conclusions
This paper introduces a novel method for target geolocation in long-range oblique UAV images. By using the overlapping part of the images from different views, we can obtain a large number of matching points. These matching points can be used for triangulation and as the initial values of map building. Then, we can optimize the camera parameters through bundle adjustment, reducing the influence of random errors of the camera. Finally, we use the LOS-based method and the optimized camera parameters to perform the target geolocation. The results from simulations and the experiment on UAV images demonstrate the effectiveness of our approach. Compared to the classical EKF-based method, our method exhibits significant improvements in both CEP95 and DRMS evaluation metrics.
While our method effectively reduces errors in target geolocation, a noticeable bias is evident in the CEP95 plot, which is mainly caused by systematic errors. Therefore, in future work, we will explore an effective way to mitigate the impact of systematic errors, further enhancing the accuracy of target geolocation in long-range oblique aerial photography.
Author Contributions
Conceptualization, C.L. and Y.D. methodology, C.L.; software, C.L. and J.X.; validation, H.Z. and H.K.; writing—original draft preparation, C.L.; project administration, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Science and Technology Major Project of China (No. 30-H32A01-9005-13/15).
Data Availability Statement
The data presented in this study are available on request from the corresponding author and the first author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, Y.; Zhang, W.; Li, P.; Ning, Y.; Suo, C. A Method for Autonomous Navigation and Positioning of UAV Based on Electric Field Array Detection. Sensors 2021, 21, 1146. [Google Scholar] [CrossRef] [PubMed]
- Qiao, C.; Ding, Y.; Xu, Y.; Xiu, J. Ground Target Geolocation Based on Digital Elevation Model for Airborne Wide-Area Reconnaissance System. J. Appl. Remote Sens. 2018, 12, 016004. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Zhou, Q. Real-Time Multi-Target Localization from Unmanned Aerial Vehicles. Sensors 2017, 17, 33. [Google Scholar] [CrossRef]
- Barber, D.B.; Redding, J.D.; McLain, T.W.; Beard, R.W.; Taylor, C.N. Vision-Based Target Geo-Location Using a Fixed-Wing Miniature Air Vehicle. J. Intell. Robot. Syst. 2006, 47, 361–382. [Google Scholar] [CrossRef]
- Held, K.; Robinson, B. TIER II Plus Airborne EO Sensor LOS Control and Image Geolocation. In Proceedings of the 1997 IEEE Aerospace Conference, Snowmass, CO, USA, 13 February 1997; Volume 2, pp. 377–405. [Google Scholar] [CrossRef]
- Stich, E.J. Geo-Pointing and Threat Location Techniques for Airborne Border Surveillance. In Proceedings of the 2013 IEEE International Conference on Technologies for Homeland Security (HST), Waltham, MA, USA, 12–14 November 2013; pp. 136–140. [Google Scholar]
- Fabian, A.J.; Klenke, R.; Truslow, P. Improving UAV-Based Target Geolocation Accuracy through Automatic Camera Parameter Discovery. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 2201. [Google Scholar]
- Amann, M.C.; Bosch, T.M.; Lescure, M.; Myllylae, R.A.; Rioux, M. Laser Ranging: A Critical Review of Unusual Techniques for Distance Measurement. Opt. Eng. 2001, 40, 10–19. [Google Scholar]
- Zhang, H.; Qiao, C.; Kuang, H.p. Target Geo-Location Based on Laser Range Finder for Airborne Electro-Optical Imaging Systems. Opt. Precis. Eng. 2019, 27, 8–16. [Google Scholar] [CrossRef]
- Cai, Y.; Ding, Y.; Zhang, H.; Xiu, J.; Liu, Z. Geo-Location Algorithm for Building Targets in Oblique Remote Sensing Images Based on Deep Learning and Height Estimation. Remote. Sens. 2020, 12, 2427. [Google Scholar] [CrossRef]
- Dai, M.; Hu, J.; Zhuang, J.; Zheng, E. A Transformer-Based Feature Segmentation and Region Alignment Method For UAV-View Geo-Localization. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 4376–4389. [Google Scholar] [CrossRef]
- Tian, X.; Shao, J.; Ouyang, D.; Shen, H.T. UAV-Satellite View Synthesis for Cross-view Geo-Localization. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 4804–4815. [Google Scholar] [CrossRef]
- Wang, T.; Zheng, Z.; Yan, C.; Zhang, J.; Sun, Y.; Zheng, B.; Yang, Y. Each Part Matters: Local Patterns Facilitate Cross-View Geo-Localization. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 867–879. [Google Scholar] [CrossRef]
- Wu, S.; Du, C.; Chen, H.; Jing, N. Coarse-to-Fine UAV Image Geo-Localization Using Multi-Stage Lucas-Kanade Networks. In Proceedings of the 2021 2nd Information Communication Technologies Conference (ICTC), Nanjing, China, 7–9 May 2021; pp. 220–224. [Google Scholar] [CrossRef]
- Zheng, Z.; Wei, Y.; Yang, Y. University-1652: A Multi-view Multi-source Benchmark for Drone-based Geo-localization. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 1395–1403. [Google Scholar] [CrossRef]
- Ding, L.; Zhou, J.; Meng, L.; Long, Z. A Practical Cross-View Image Matching Method between UAV and Satellite for UAV-Based Geo-Localization. Remote. Sens. 2020, 13, 47. [Google Scholar] [CrossRef]
- Hosseinpoor, H.R.; Samadzadegan, F.; Javan, F.D. Pricise Target Geolocation Based on Integeration of Thermal Video Imagery and RTK GPS in Uavs. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 333. [Google Scholar] [CrossRef]
- Hosseinpoor, H.R.; Samadzadegan, F.; DadrasJavan, F. Pricise Target Geolocation and Tracking Based on UAV Video Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 243. [Google Scholar] [CrossRef]
- Jekeli, C. Inertial Navigation Systems with Geodetic Applications; De Gruyter: Berlin, Germany; Boston, MA, USA, 2001. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An Efficient Alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust Invariant Scalable Keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar] [CrossRef]
- Alcantarilla, P.; Nuevo, J.; Bartoli, A. Fast Explicit Diffusion for Accelerated Features in Nonlinear Scale Spaces. In Proceedings of the British Machine Vision Conference 2013, Bristol, UK, 9–13 September 2013; pp. 13.1–13.11. [Google Scholar] [CrossRef]
- Agarwal, S.; Furukawa, Y.; Snavely, N.; Simon, I.; Curless, B.; Seitz, S.M.; Szeliski, R. Building Rome in a Day. Commun. ACM 2011, 54, 105–112. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Moulon, P.; Monasse, P. Unordered Feature Tracking Made Fast and Easy. In Proceedings of the CVMP 2012, London, UK, 5–6 December 2012; p. 1. [Google Scholar]
- Yang, K.; Fang, W.; Zhao, Y.; Deng, N. Iteratively Reweighted Midpoint Method for Fast Multiple View Triangulation. IEEE Robot. Autom. Lett. 2019, 4, 708–715. [Google Scholar] [CrossRef]
- Ramamurthy, K.N.; Lin, C.C.; Aravkin, A.; Pankanti, S.; Viguier, R. Distributed Bundle Adjustment. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 2146–2154. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 523. [Google Scholar]
- Brown, M.; Lowe, D.G. Automatic Panoramic Image Stitching Using Invariant Features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Agarwal, S.; Mierle, K.; Team, T.C.S. Ceres Solver. 2023. Available online: https://github.com/ceres-solver/ceres-solver (accessed on 22 February 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).