Attitude Control of Small Fixed−Wing UAV Based on Sliding Mode and Linear Active Disturbance Rejection Control
Abstract
:1. Introduction
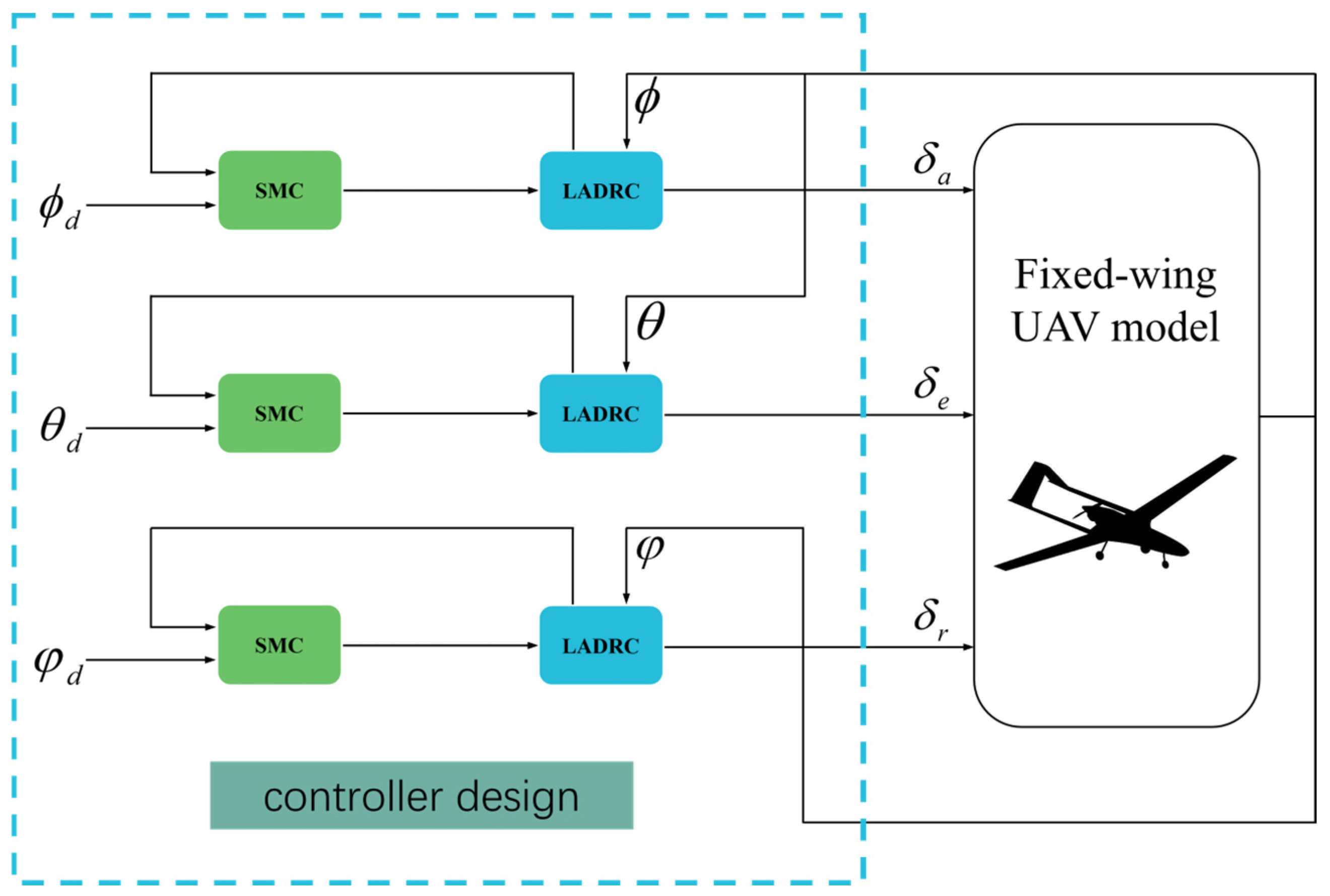
- An attitude control method based on SMC−LADRC is proposed, effectively addressing the effects of external disturbances and model uncertainty on attitude control. The control framework is shown in Figure 1.
- To estimate external disturbances and the model uncertainty, a LESO in LADRC is designed to obtain the estimated values of the attitude angle, attitude angular velocity, and total disturbance of the fixed−wing UAV. This observer compensates for the total disturbance within the controller.
- Traditional LADRC generally uses a linear combination for the error feedback law. When the system is affected by strong wind, the controller’s effectiveness is significantly reduced, thereby impacting the anti−interference and robustness of the UAV system. Unlike Reference [21], which used LADRC for attitude control and backstepping SMC for position control, and Reference [22], which employed a series control consisting of SMC and LADRC, this paper substitutes SMC for the error feedback law in LADRC. This approach leverages SMC’s insensitivity to system parameter variations, enhancing the control system’s anti−interference performance and meeting the need for a fast response.
- The Trace Differentiator (TD) is introduced to track the desired input, aiming to minimize overshoot and enhance the controller’s robustness. By incorporating the TD, the system output can achieve the more stable tracking of the desired input, leading to an improved overall performance.
2. Dynamics Model of Fixed−Wing UAV
- The Earth’s rotation is stagnant and the curvature of the Earth is zero.
- The fuselage of the UAV, centered on a central axis plane, is perfectly symmetrical.
- The acceleration of gravity remains constant, independent of position in space.
- The airframe of a fixed−wing UAV is considered rigid and does not deform or vibrate due to changes in force.
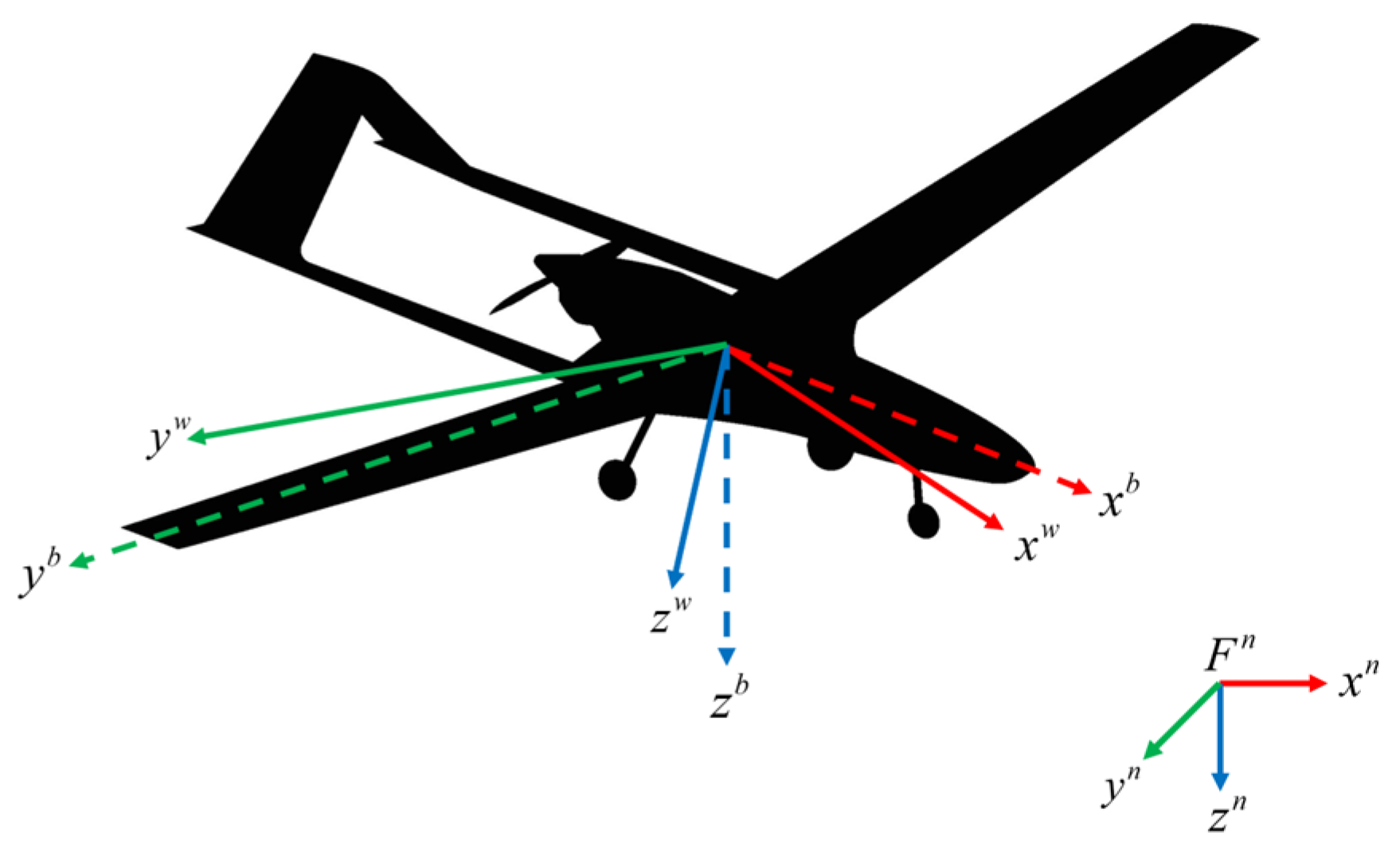
- Terrestrial inertial coordinate system (): using the starting position of the UAV as the coordinate origin, points in a northerly direction, points in an easterly direction, and points to the core.
- Coordinate system of airframe (): the origin is at the center of mass of the UAV, points towards the head along the longitudinal axis of the UAV structure, is perpendicular to the pointing in the direction of the right flank, and is in the plane of symmetry of the body, vertically downwards.
- Air coordinate system (): the origin is at the center of mass of the UAV, points in the direction of the UAV’s speed, is in the plane of symmetry of the airplane, perpendicular to the , and is perpendicular to the , rightwards. The relationship between these three coordinate systems is shown in Figure 2.
3. UAV Attitude Controller Design
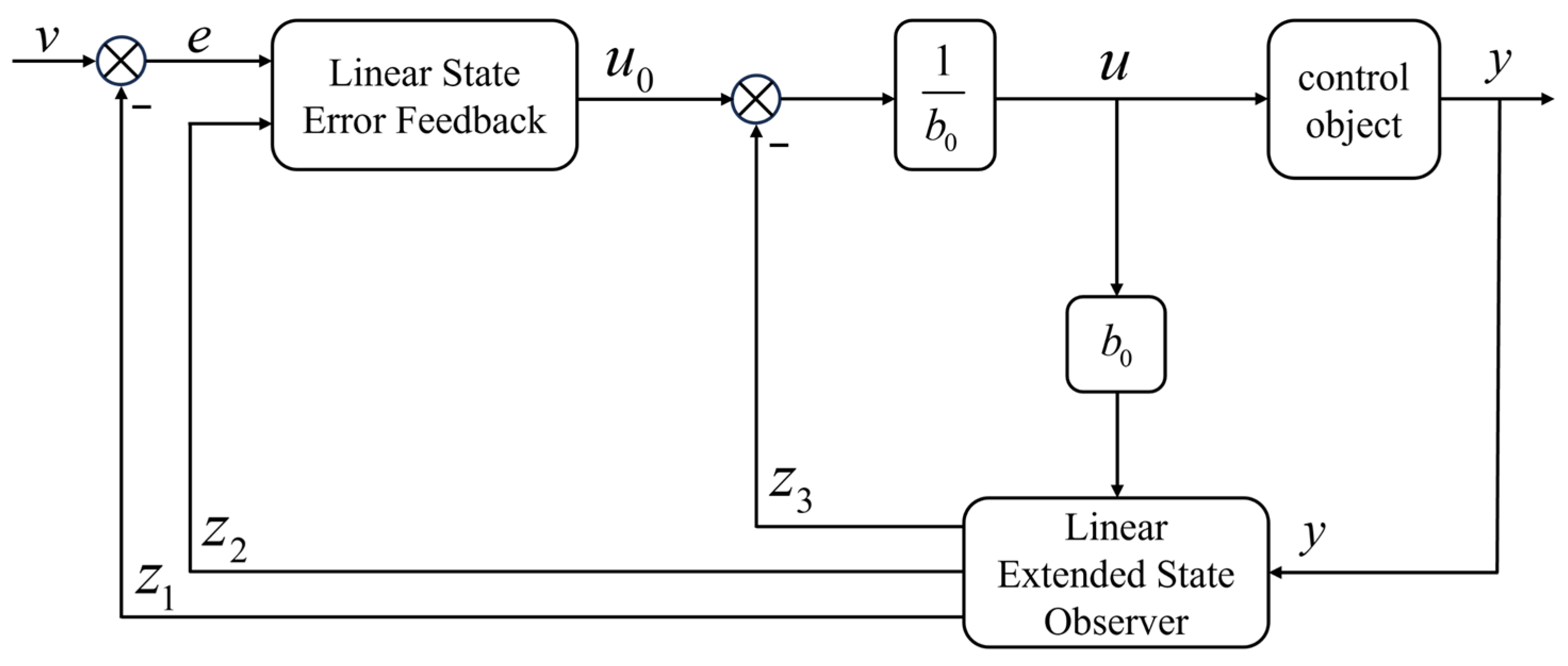
3.1. Linear Active Disturbance Rejection Control Design
3.2. SMC−LADRC Controller Design
3.3. Stability Analysis
4. Simulation and Discussion
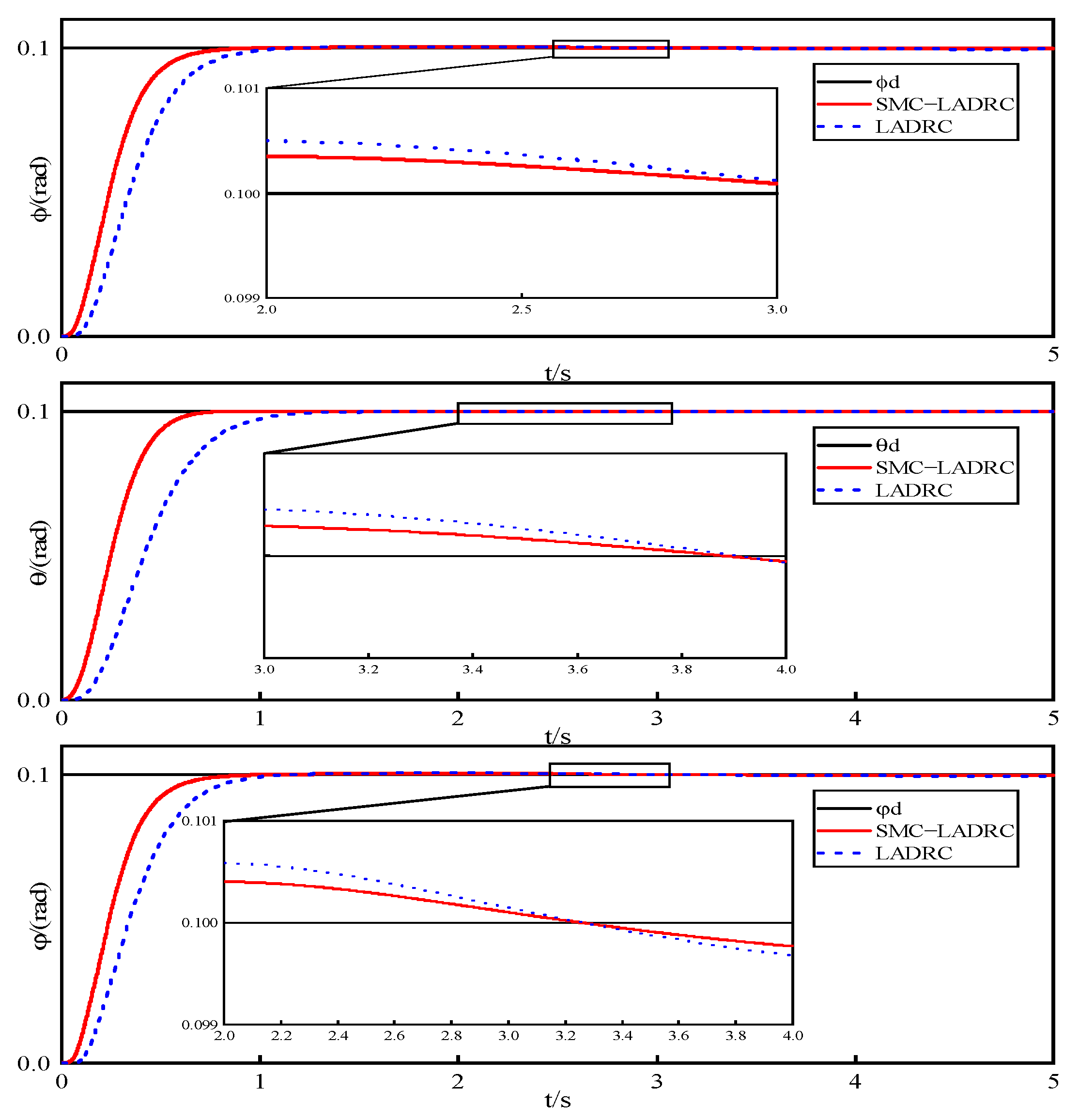
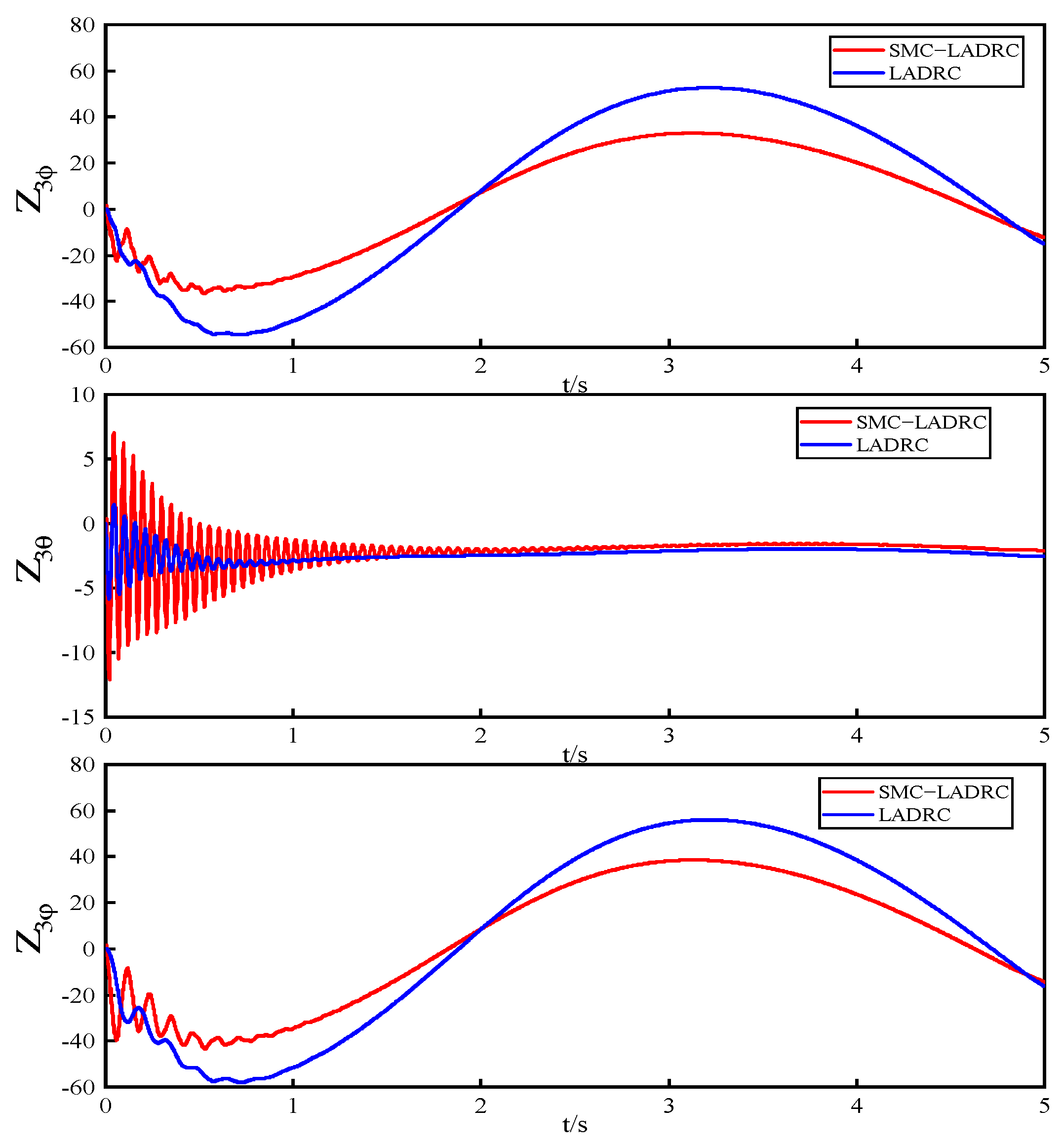
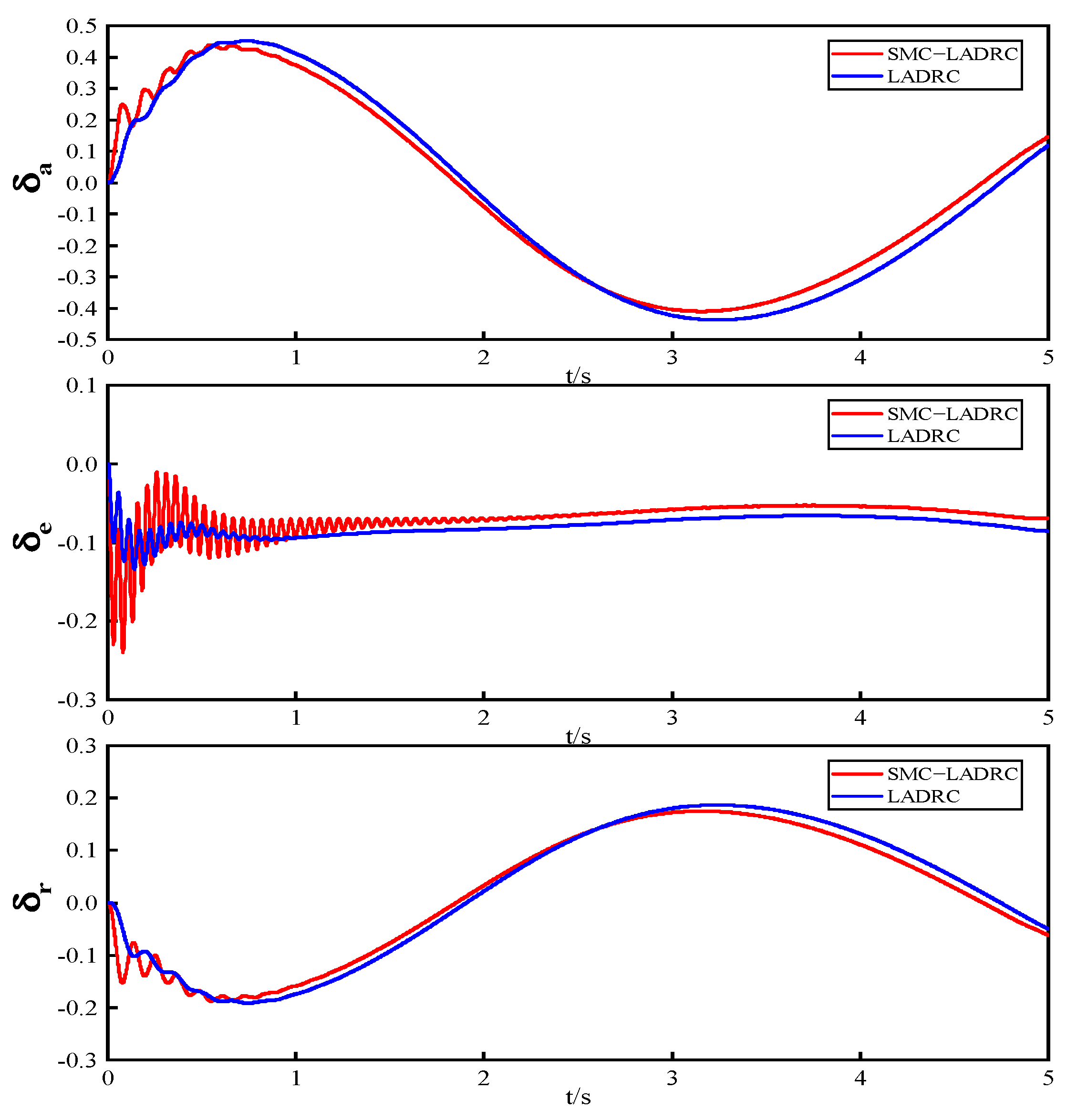
4.1. Disturbance Experiment
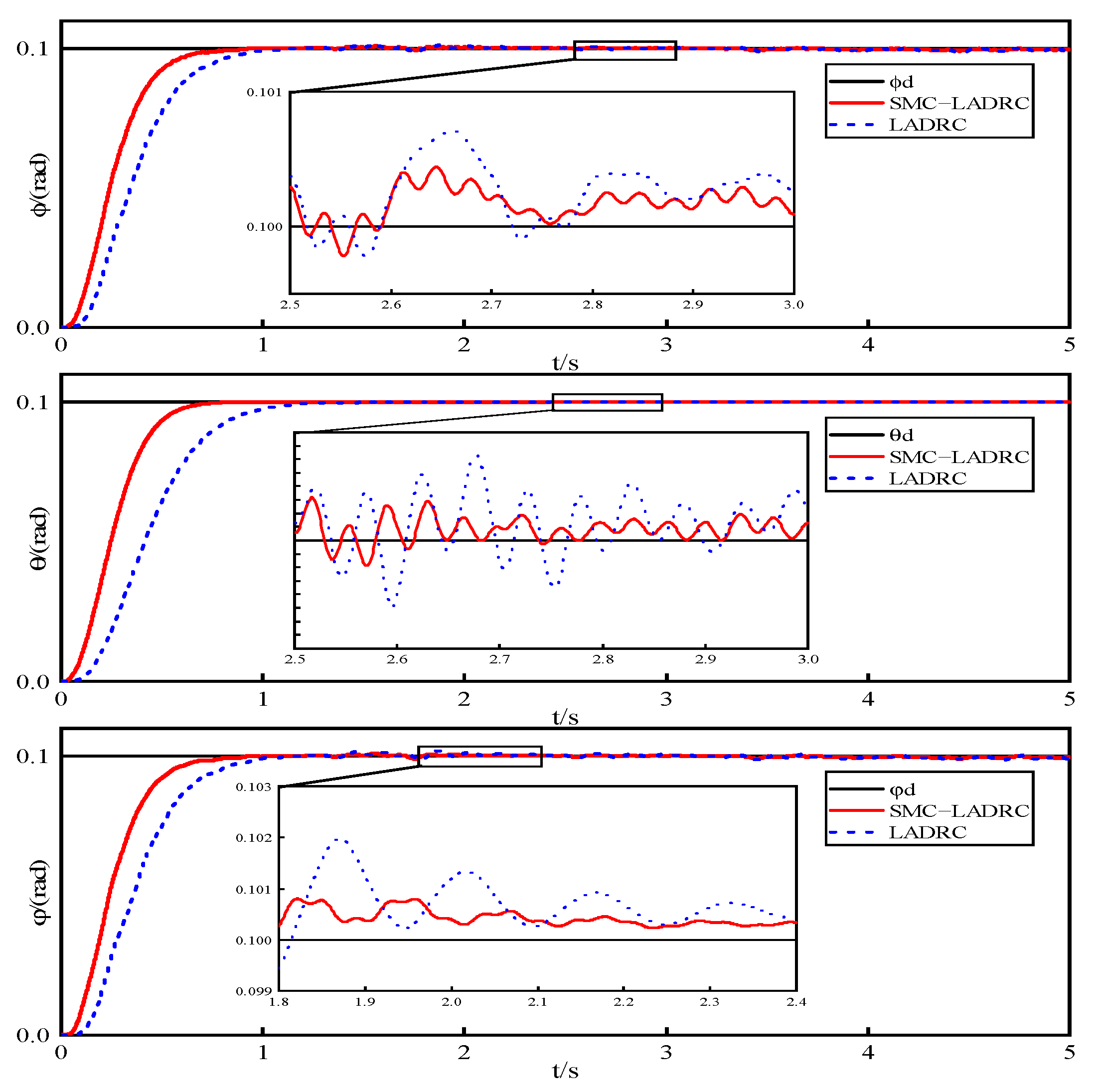
4.2. Experiments on the Effect of Sensor Noise on the System
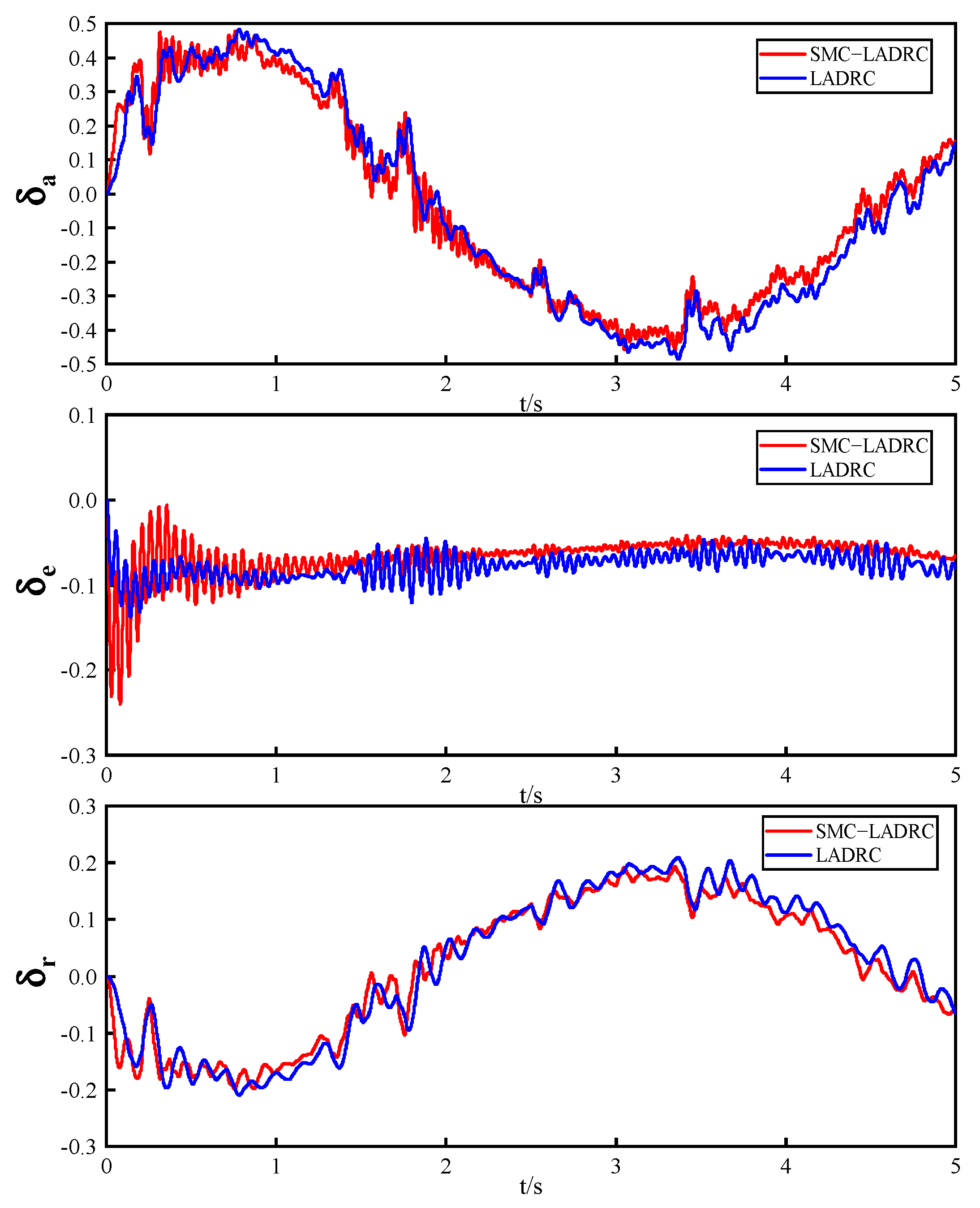
4.3. Experiments on the Effect of Changes in Mass and Moment of Inertia on Systems
5. Conclusions
- LESO in LADRC is designed to estimate external disturbances and model uncertainties, providing estimated values for the attitude angle, attitude angular velocity, and total disturbance of the fixed−wing UAV. These estimates are used to compensate for system disturbances within the controller.
- By replacing the error feedback law in LADRC with SMC, the insensitivity of SMC to system parameter variations is leveraged to enhance the anti−interference capabilities of the control system and improve the response speed.
- The Trace Differentiator (TD) is introduced to track the desired inputs, aiming to minimize overshoot and enhance controller robustness. Incorporating TD helps the system achieve more stable tracking of the desired inputs, thereby enhancing the overall performance.
- The experimental results demonstrate that compared to LADRC, SMC−LADRC exhibits faster response speeds and effectively suppresses model uncertainties, external disturbances, and internal disturbances impacting the UAV.
- The controller proposed in this paper is based on LADRC and lacks experimental comparisons with other mainstream control methods. Moreover, it is solely applied to the attitude control of fixed−wing UAVs. To address these limitations, our future research will apply the SMC−LADRC controller to the position control of fixed−wing UAVs and include comparative experiments with other control methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, A.; Xu, H.; Bi, W.; Xu, S. Adaptive mutant particle swarm optimization based precise cargo airdrop of unmanned aerial vehicles. Appl. Soft Comput. 2022, 130, 109657. [Google Scholar] [CrossRef]
- Chamuah, A.; Singh, R. Responsible governance of civilian unmanned aerial vehicle (UAV) innovations for Indian crop insurance applications. J. Responsible Technol. 2022, 9, 100025. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, X.; Dedman, S.; Rosso, M.; Zhu, J.; Yang, J.; Xia, Y.; Tian, Y.; Zhang, G.; Wang, J. UAV remote sensing applications in marine monitoring: Knowledge visualization and review. Sci. Total Environ. 2022, 838, 155939. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F. Fault−tolerant cooperative navigation of networked UAV swarms for forest fire monitoring. Aerosp. Sci. Technol. 2022, 123, 107494. [Google Scholar] [CrossRef]
- Valente, J.; Hiremath, S.; Ariza−Sentís, M.; Doldersum, M.; Kooistra, L. Mapping of Rumex obtusifolius in nature conservation areas using very high resolution UAV imagery and deep learning. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102864. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, L.; Wang, Z.; Chen, Z. PID pitch attitude control for unstable flight vehicle in the presence of actuator delay: Tuning and analysis. J. Frankl. Inst. 2014, 351, 5523–5547. [Google Scholar] [CrossRef]
- Anjali, B.; Vivek, A.; Nandagopal, J. Simulation and analysis of integral LQR controller for inner control loop design of a fixed wing micro aerial vehicle (MAV). Procedia Technol. 2016, 25, 76–83. [Google Scholar] [CrossRef]
- Matthew, J.S.; Knoebel, N.B.; Osborne, S.R.; Beard, R.W.; Eldredge, A. Adaptive backstepping control for miniature air vehicles. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar]
- Islam, S.; Liu, P.; El Saddik, A. Nonlinear adaptive control for quadrotor flying vehicle. Nonlinear Dyn. 2014, 78, 117–133. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Berlin/Heidelberg, Germany, 2014; Volume 10. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth−parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Pan, Y.; Li, N.; Zou, W.; Wang, B.; Wang, K.; Tang, X.; Bu, S.; Qin, L. An Augmented Sliding Mode Control for Fixed−Wing UAVs with External Disturbances and Model Uncertainties. Drones 2023, 7, 440. [Google Scholar] [CrossRef]
- Song, J.; Hu, Y.; Su, J.; Zhao, M.; Ai, S. Fractional−order linear active disturbance rejection control design and optimization based improved sparrow search algorithm for quadrotor uav with system uncertainties and external disturbance. Drones 2022, 6, 229. [Google Scholar] [CrossRef]
- Zheng, J.; Neusypin, K.A.; Selezneva, M.S. Auto−Landing of Moving−Mass Actuated Unmanned Aerial Vehicles Based on Linear Active Disturbance Rejection Control. Drones 2023, 7, 539. [Google Scholar] [CrossRef]
- Sun, C.; Liu, M.; Liu, C.a.; Feng, X.; Wu, H. An industrial quadrotor uav control method based on fuzzy adaptive linear active disturbance rejection control. Electronics 2021, 10, 376. [Google Scholar] [CrossRef]
- Suhail, S.A.; Bazaz, M.A.; Hussain, S. Adaptive sliding mode−based active disturbance rejection control for a quadcopter. Trans. Inst. Meas. Control 2022, 44, 3176–3190. [Google Scholar] [CrossRef]
- Zheng, J.; Selezneva, M.S.; Yi, J.; Zhu, L. Attitude control of a moving mass−actuated fixed−wing UAV based on LADRC. Proc. J. Phys. Conf. Ser. 2023, 2472, 012045. [Google Scholar] [CrossRef]
- Kikkawa, H.; Uchiyama, K. Nonlinear flight control with an extended state observer for a fixed−wing UAV. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1625–1630. [Google Scholar]
- Xu, L.; Ma, H.; Guo, D.; Xie, A.; Song, D. Backstepping Sliding−Mode and Cascade Active Disturbance Rejection Control for a Quadrotor UAV. IEEE/ASME Trans. Mechatron. 2020, 25, 2743–2753. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, T. Based on robust sliding mode and linear active disturbance rejection control for attitude of quadrotor load UAV. Nonlinear Dyn. 2022, 108, 3485–3503. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]


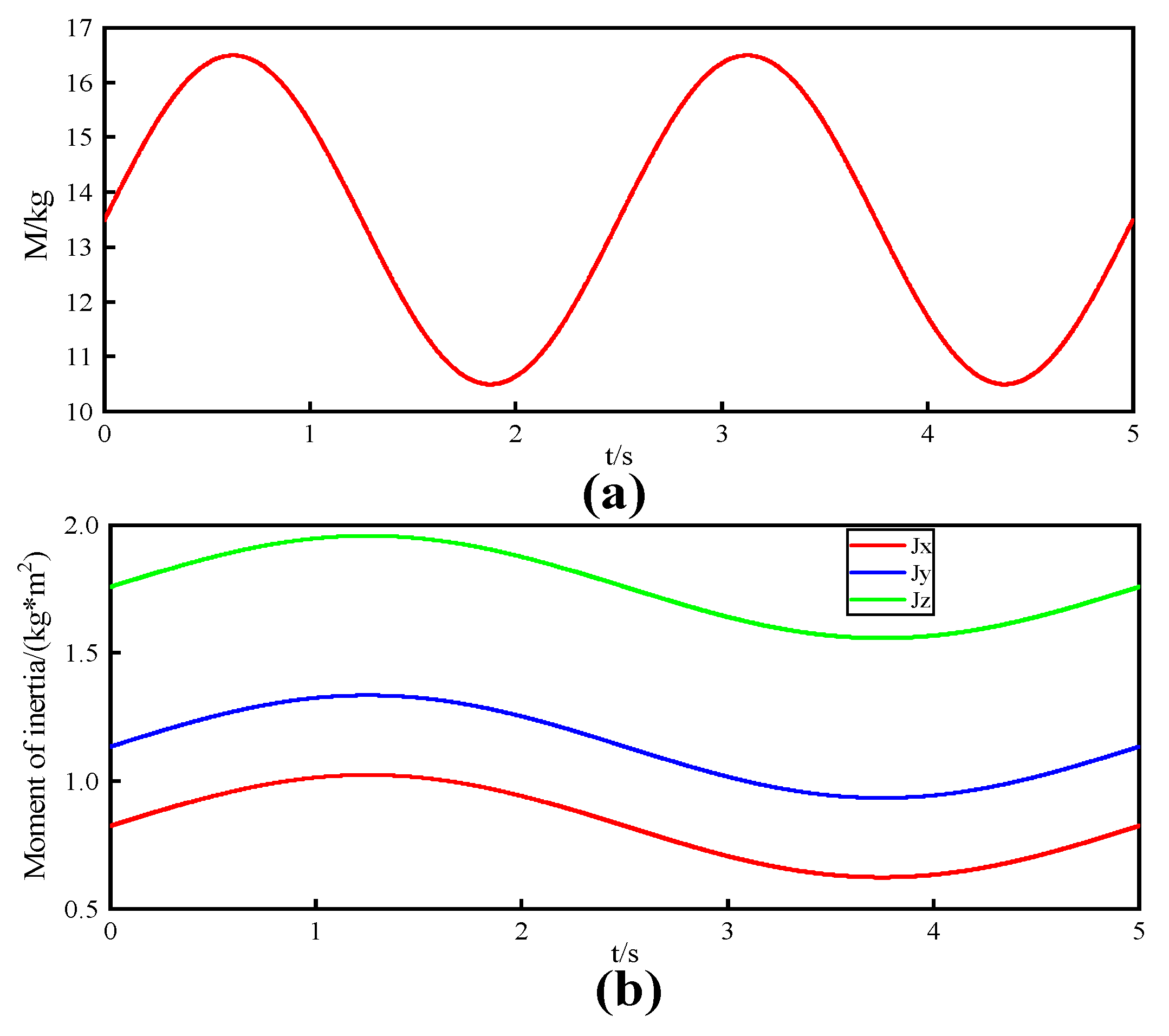
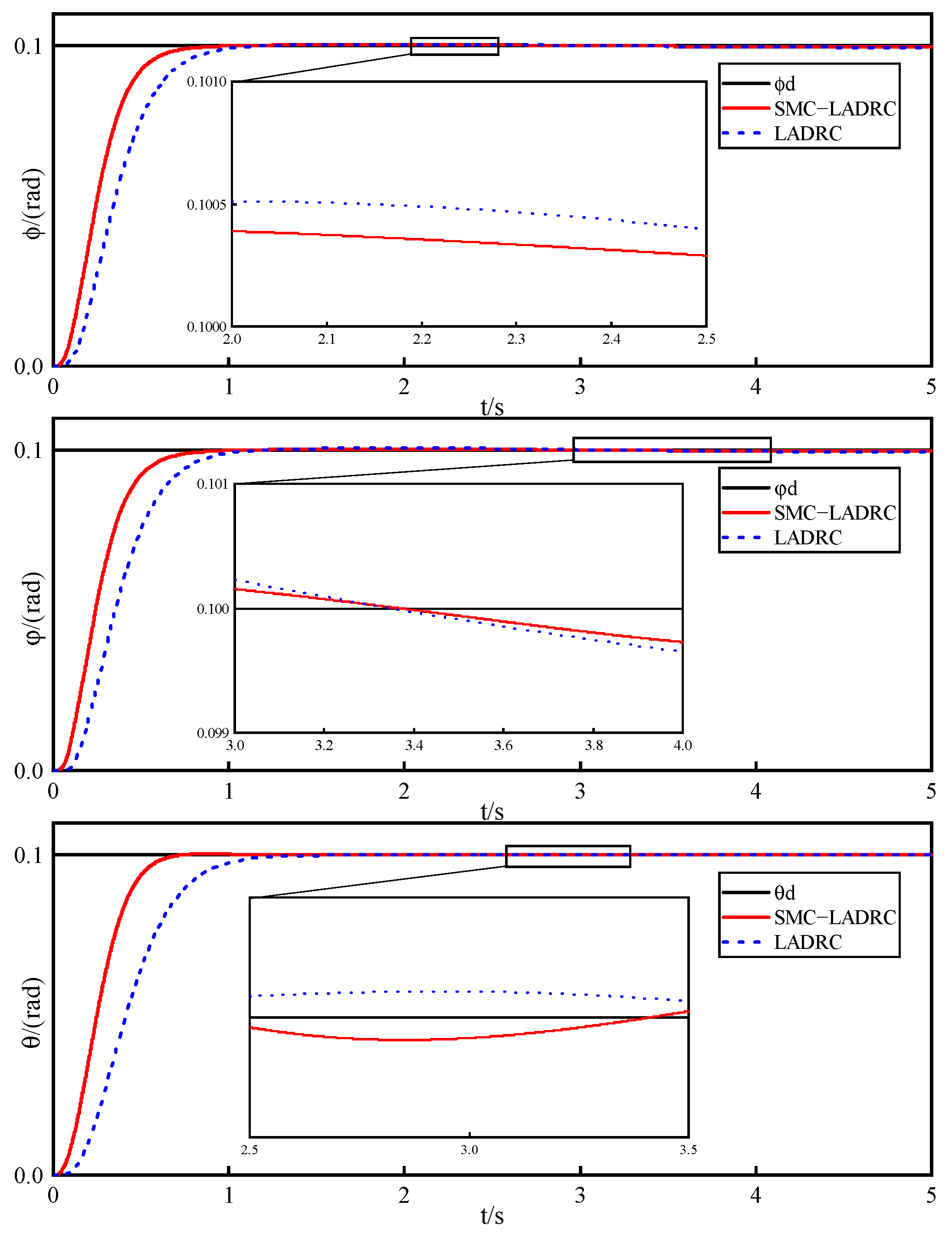
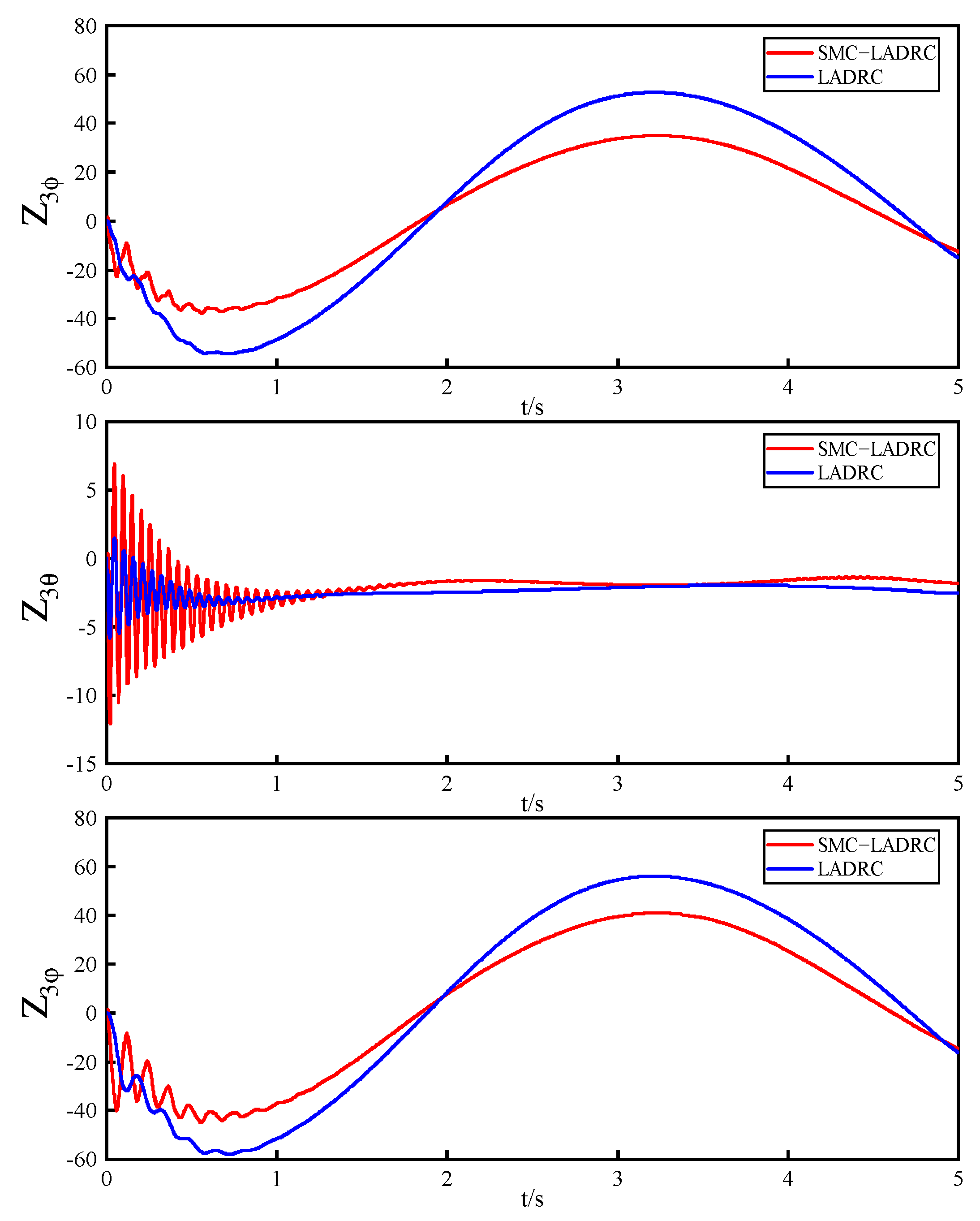
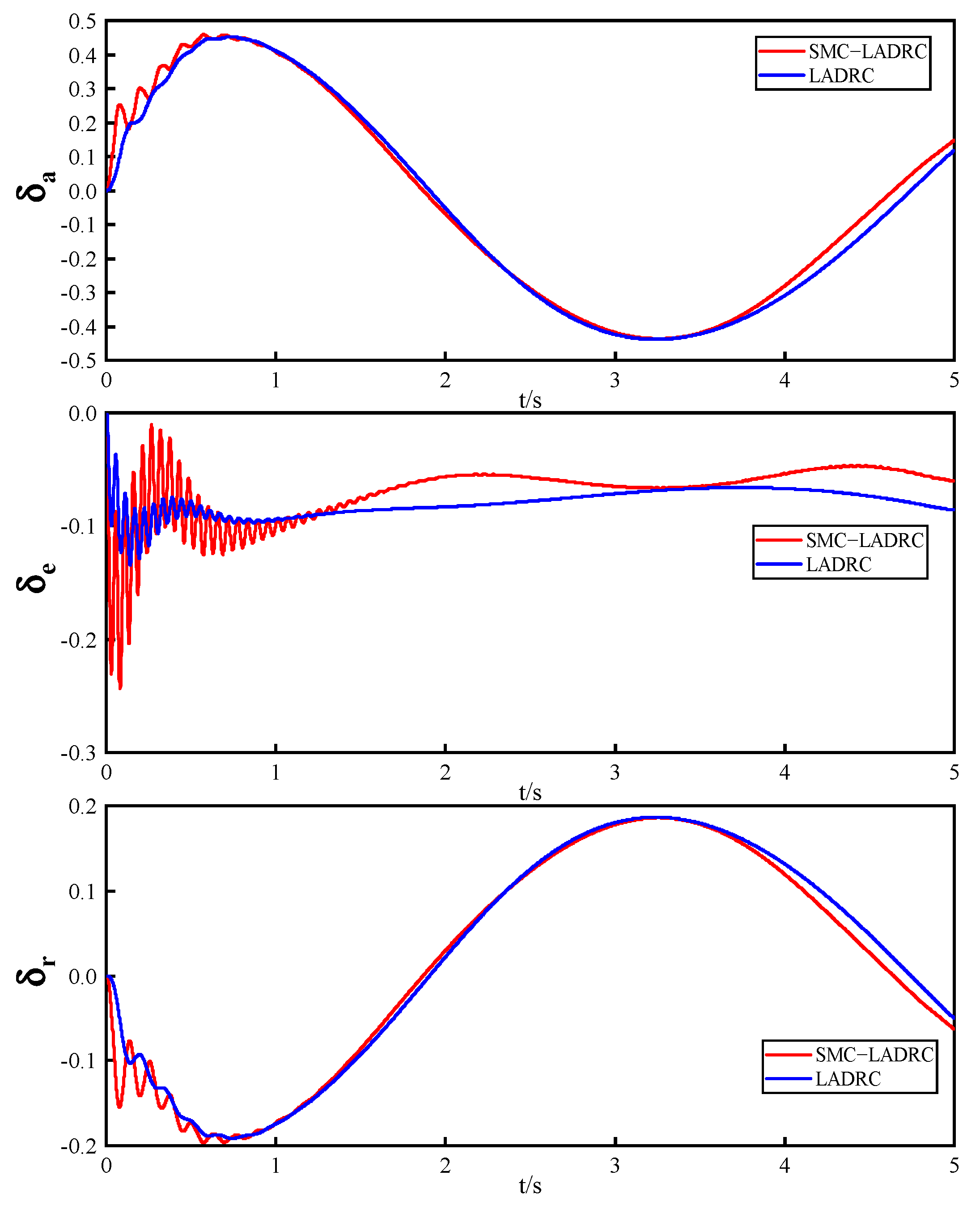
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0 | |||
| −0.9 | |||
| −0.49497 | |||
| 0.3971 | |||
| 0.1 | |||
| −0.15 | |||
| 0 | |||
| −0.12 | |||
| −0.26 | |||
| 0.14 | |||
| 80 | 0.08 | ||
| 1 | 0.105 | ||
| 0.21 | 0 | ||
| 0 | −1 | ||
| 0 | −3.6 | ||
| −0.36 | −0.58 | ||
| 0.0164 | 0 | ||
| 0.2 | 0.25 | ||
| 0 | 0.022 | ||
| 0 | −0.35 | ||
| 0.06 | −0.032 |
| Parameter | |||
|---|---|---|---|
| 8 | 8 | 8 | |
| 0.001 | 0.001 | 0.001 | |
| 80 | −30 | −240 | |
| 1600 | 1622 | 1600 | |
| 14 | 13 | 14 | |
| 16 | 11 | 16 | |
| 0.001 | 0.001 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Yan, Y.; Xiong, X.; Han, Q.; Li, Z. Attitude Control of Small Fixed−Wing UAV Based on Sliding Mode and Linear Active Disturbance Rejection Control. Drones 2024, 8, 318. https://doi.org/10.3390/drones8070318
Wang B, Yan Y, Xiong X, Han Q, Li Z. Attitude Control of Small Fixed−Wing UAV Based on Sliding Mode and Linear Active Disturbance Rejection Control. Drones. 2024; 8(7):318. https://doi.org/10.3390/drones8070318
Chicago/Turabian StyleWang, Bohao, Yuehao Yan, Xingzhong Xiong, Qiang Han, and Zhouguan Li. 2024. "Attitude Control of Small Fixed−Wing UAV Based on Sliding Mode and Linear Active Disturbance Rejection Control" Drones 8, no. 7: 318. https://doi.org/10.3390/drones8070318
APA StyleWang, B., Yan, Y., Xiong, X., Han, Q., & Li, Z. (2024). Attitude Control of Small Fixed−Wing UAV Based on Sliding Mode and Linear Active Disturbance Rejection Control. Drones, 8(7), 318. https://doi.org/10.3390/drones8070318





