Multiple Unmanned Aerial Vehicle (multi-UAV) Reconnaissance and Search with Limited Communication Range Using Semantic Episodic Memory in Reinforcement Learning
Abstract
1. Introduction
- A communication and information fusion model for the MCRS-LCR problem based on belief maps is proposed. Each UAV maintains a belief map for all UAVs and uses a max-plus-sum approach for information fusion, enabling effective communication.
- Episodic memory is introduced into the MCRS-LCR problem. Using the value factorization centralized training with a decentralized execution (CTDE) framework, episodic memory leverages the highest state values stored in memory to generate better Temporal Difference targets, enhancing MADRL performance.
- A new MADRL method called CNN-Semantic Episodic Memory Utilization (CNN-SEMU) is proposed. CNN-SEMU employs an encoder–decoder structure with a CNN to extract semantic features with the highest returns from high-dimensional map state spaces, enhancing the effectiveness of episodic memory.
2. Related Work
2.1. UAV Communication and Search Strategies
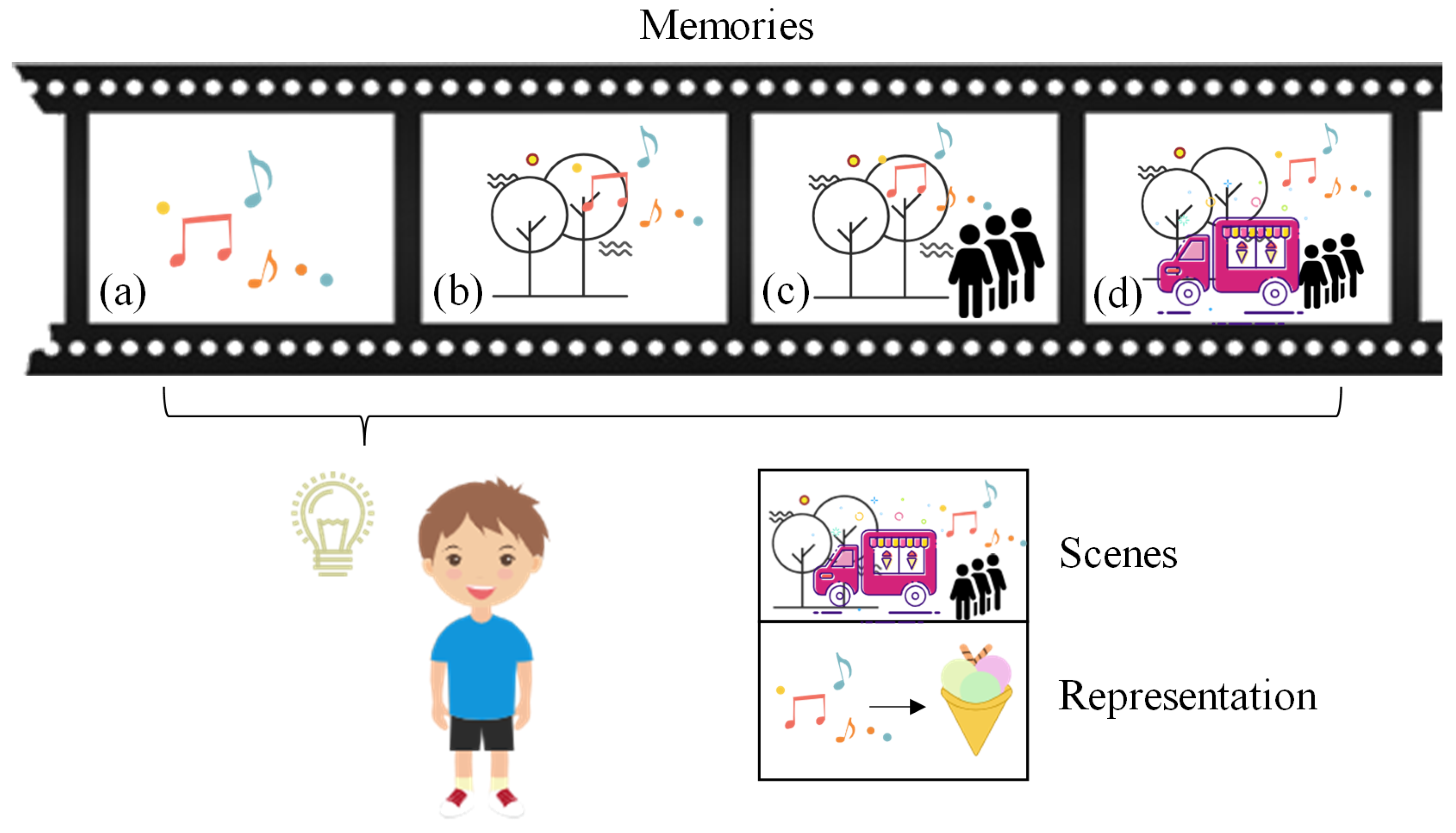
2.2. Episodic Memory in Reinforcement Learning
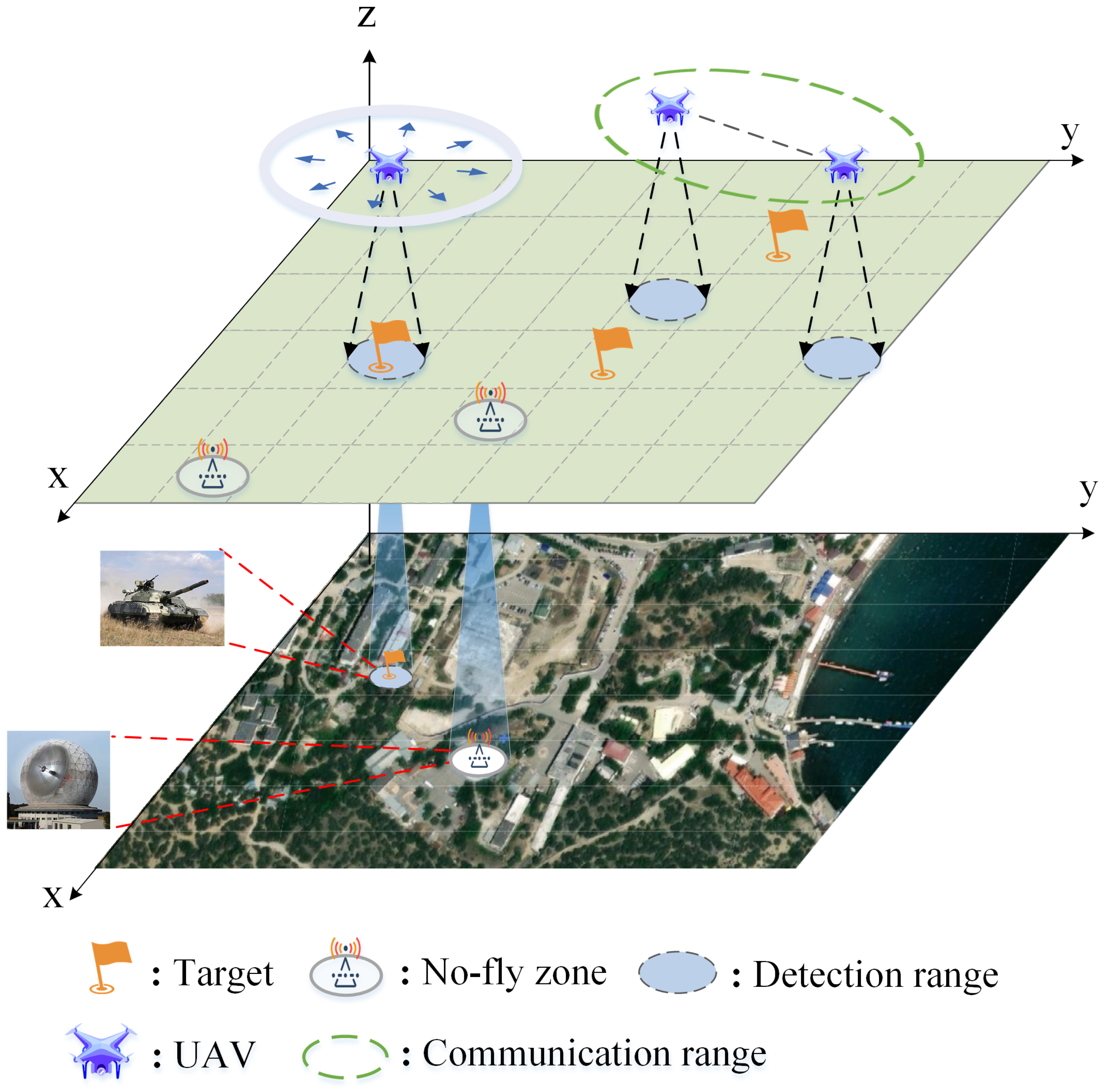
3. System Description and Problem Formulation
3.1. Reconnaissance Environment Model
3.2. UAV Model
3.3. Belief Probability Maps
3.4. UAV Communication and Information Fusion Model
3.5. Problem Formulation
4. Reformulation
4.1. Dec-POMDP
4.2. Observation, State, and Action Spaces
4.3. Reward Functions
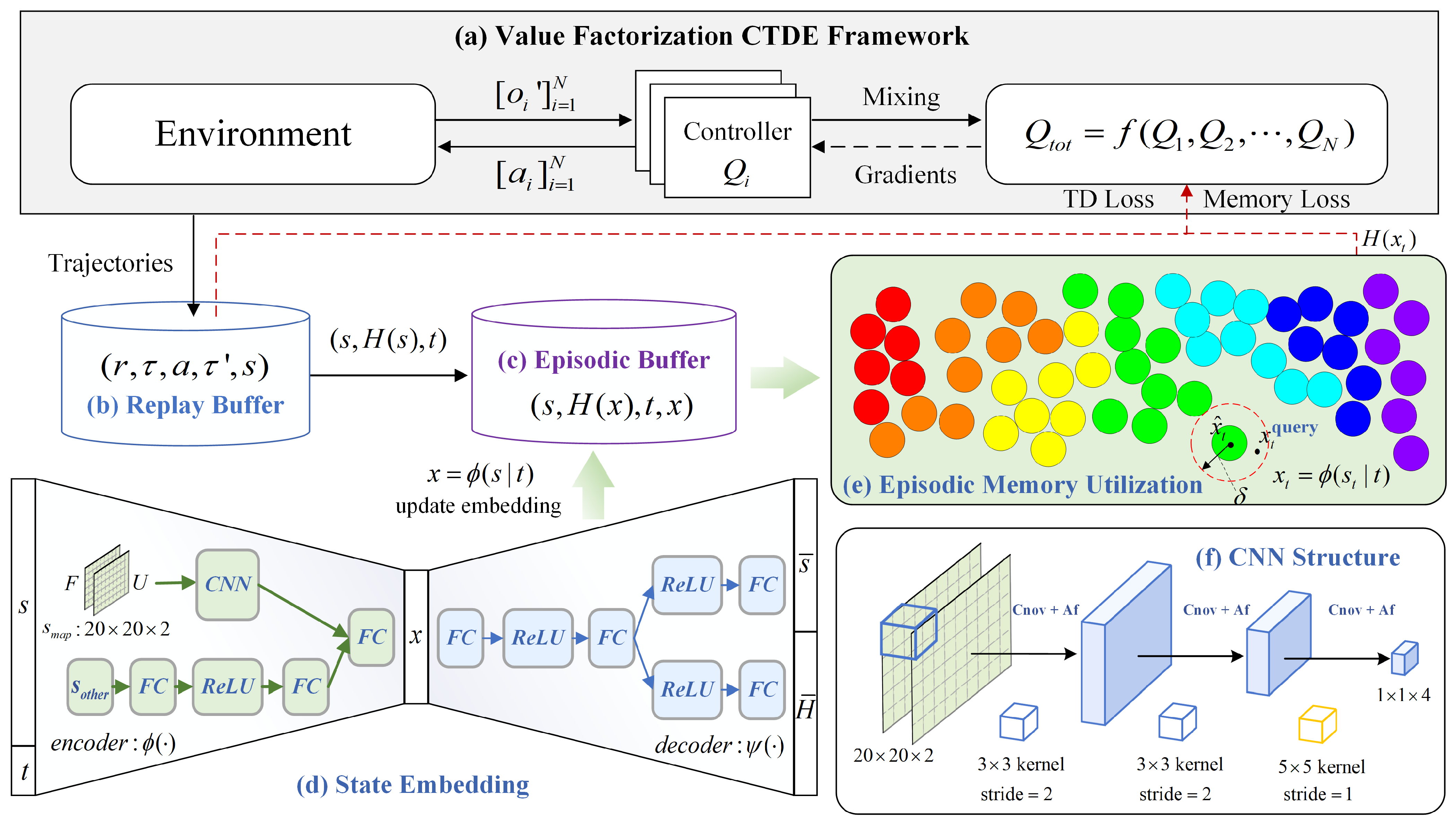
5. Methodology
5.1. Value Factorization CTDE Framework
5.2. Episodic Memory
| Algorithm 1 Construction and Update of Episodic Buffer |
|
5.3. Model Training
| Algorithm 2 CNN-SEMU |
|
6. Experiments
6.1. Experimental Environment Setup
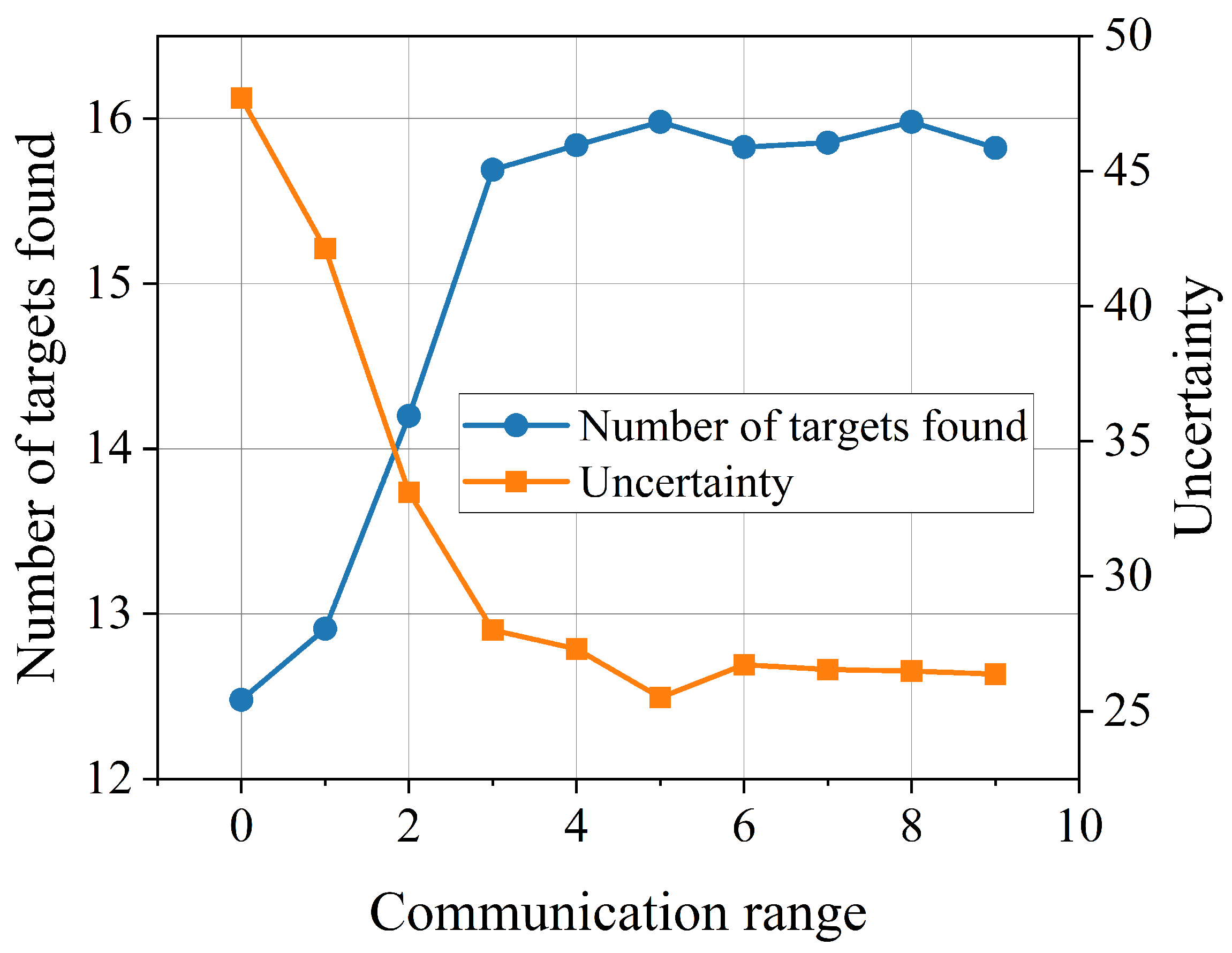
6.2. Communication Model Analysis
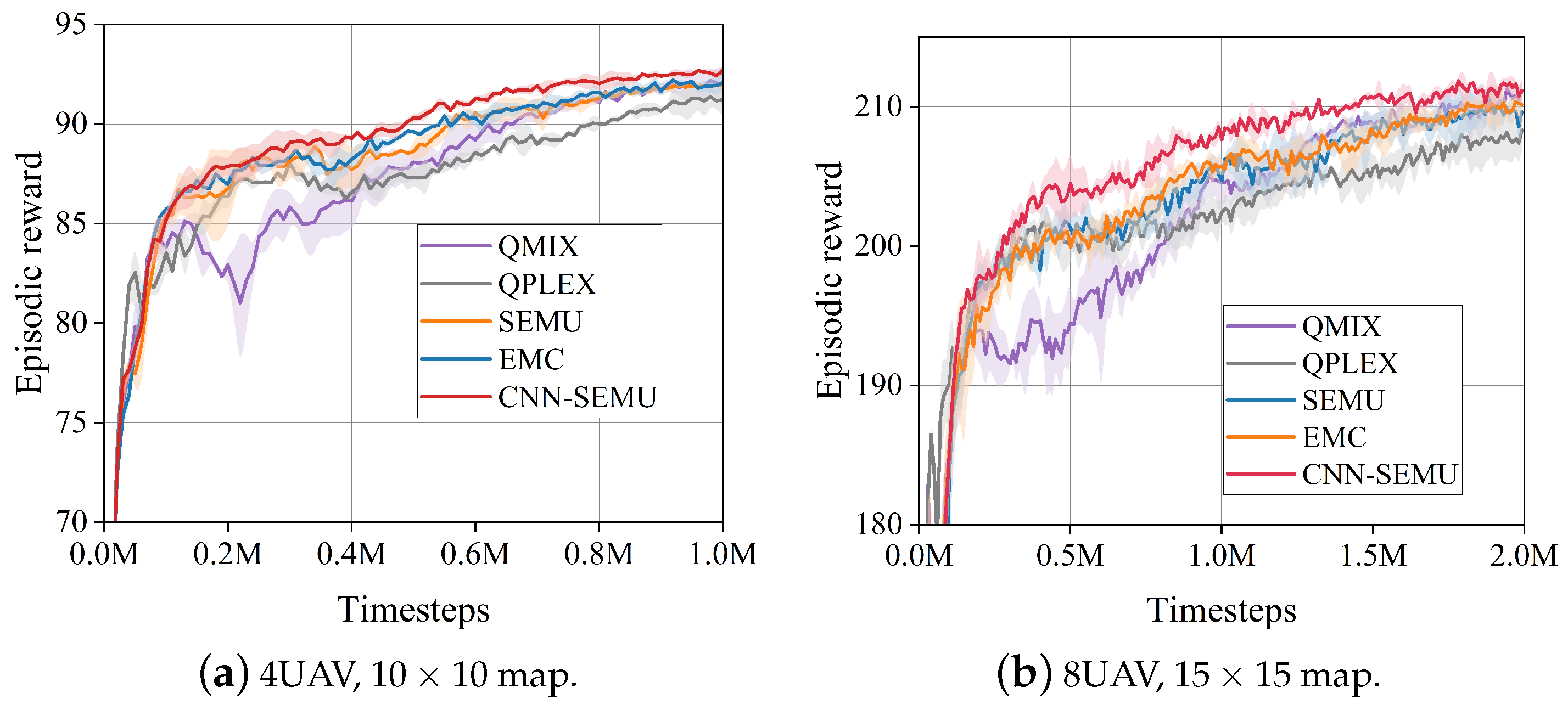
6.3. Baseline Experiment Analysis
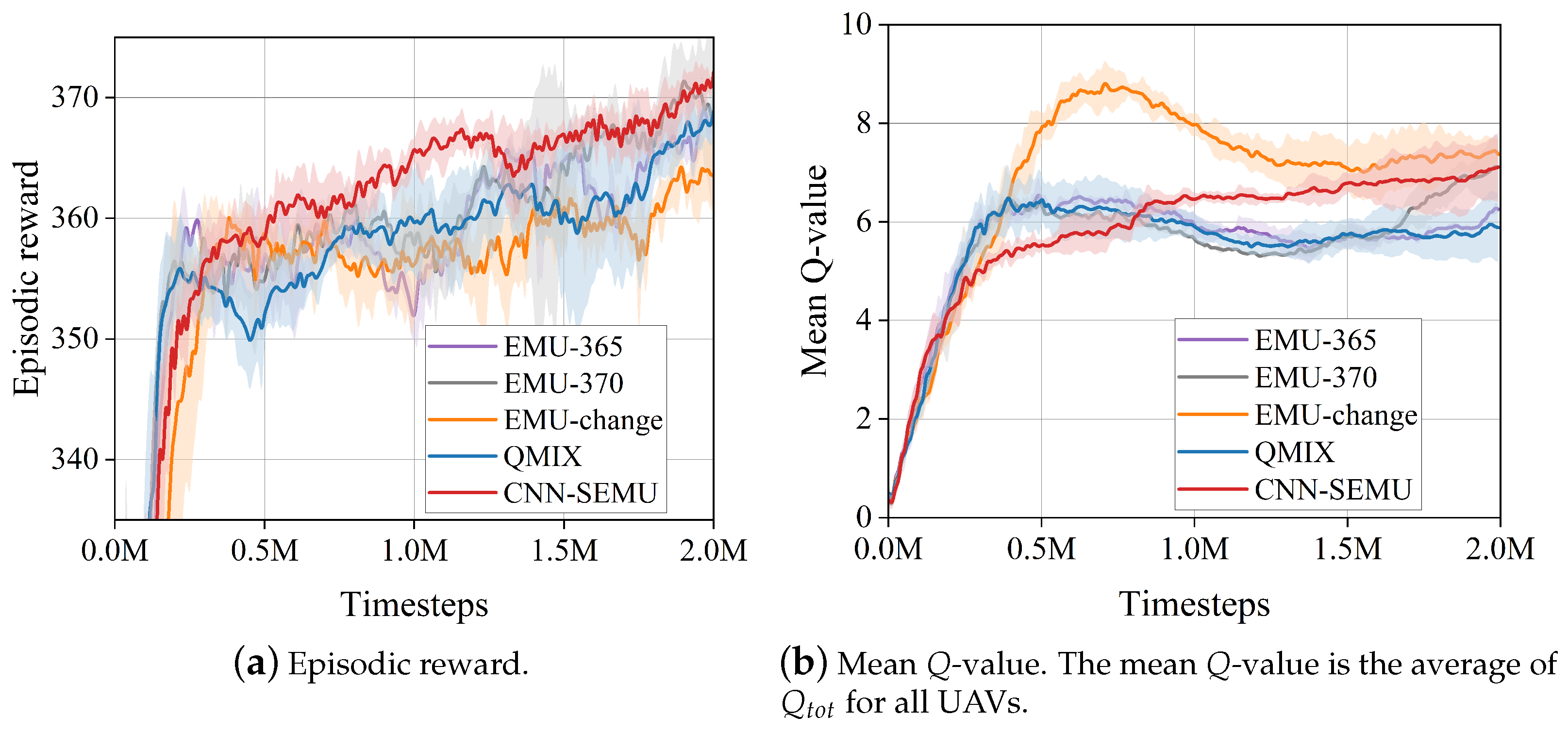
Comparison with EMU
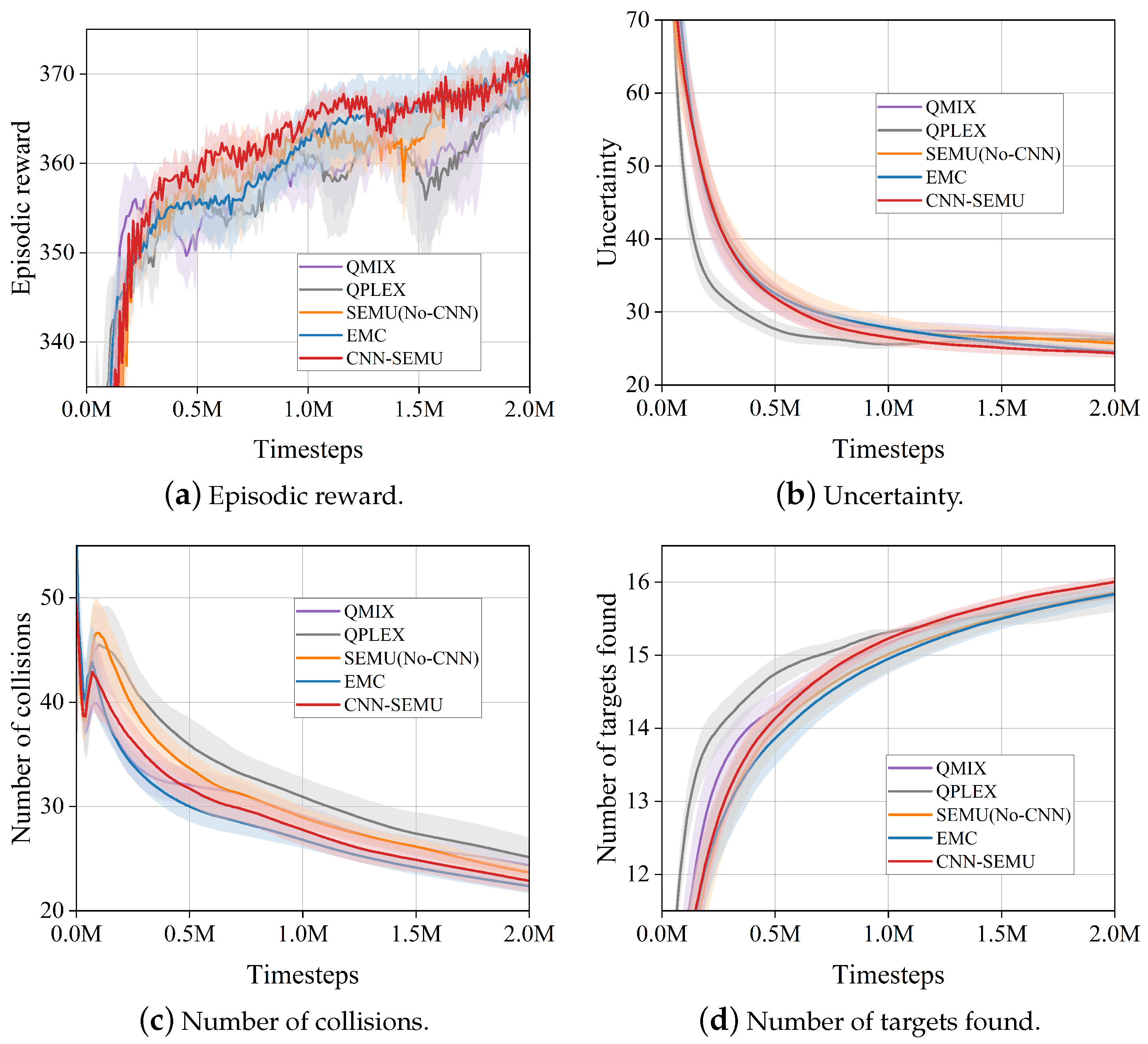
6.4. State Embedding Analysis
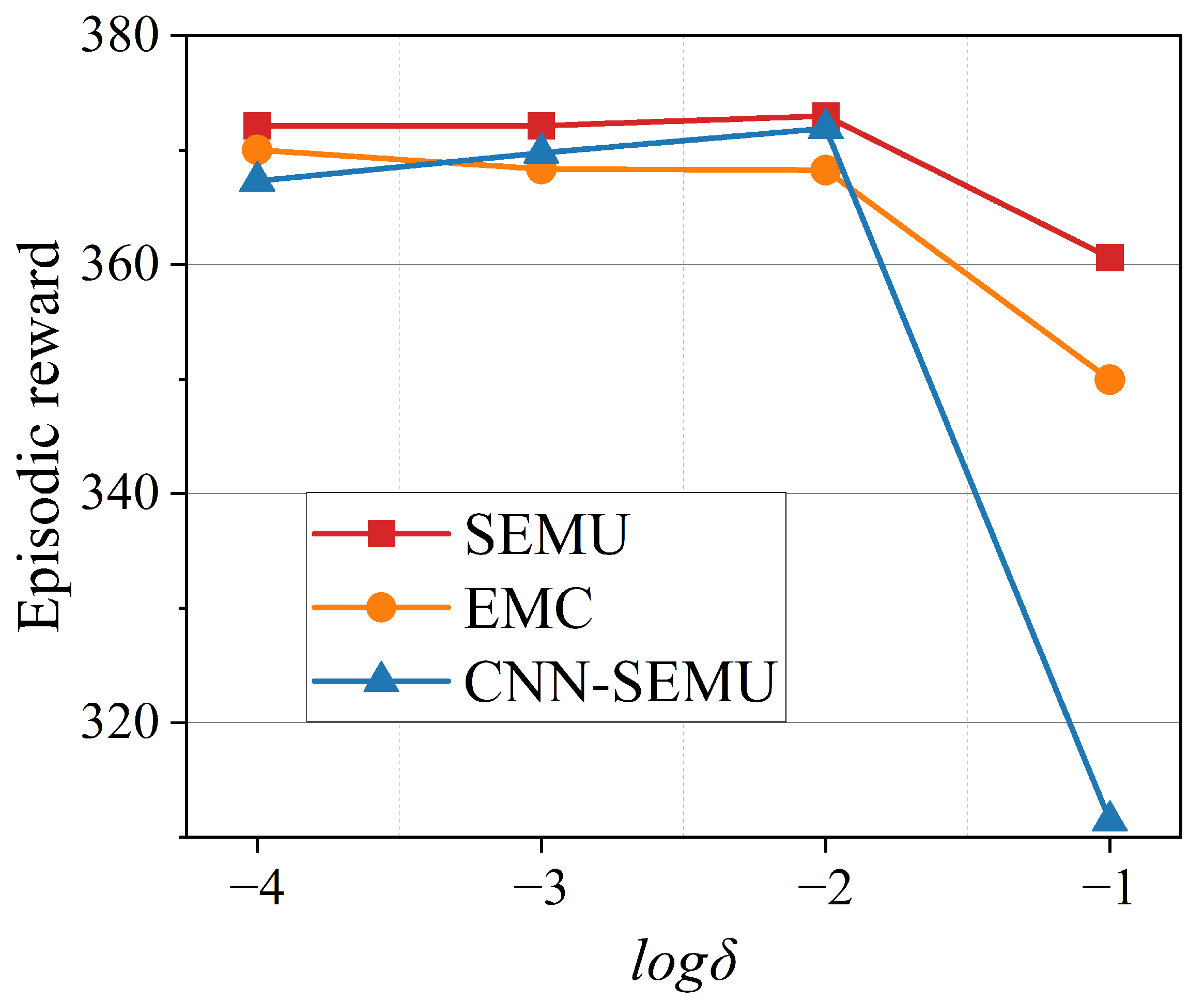
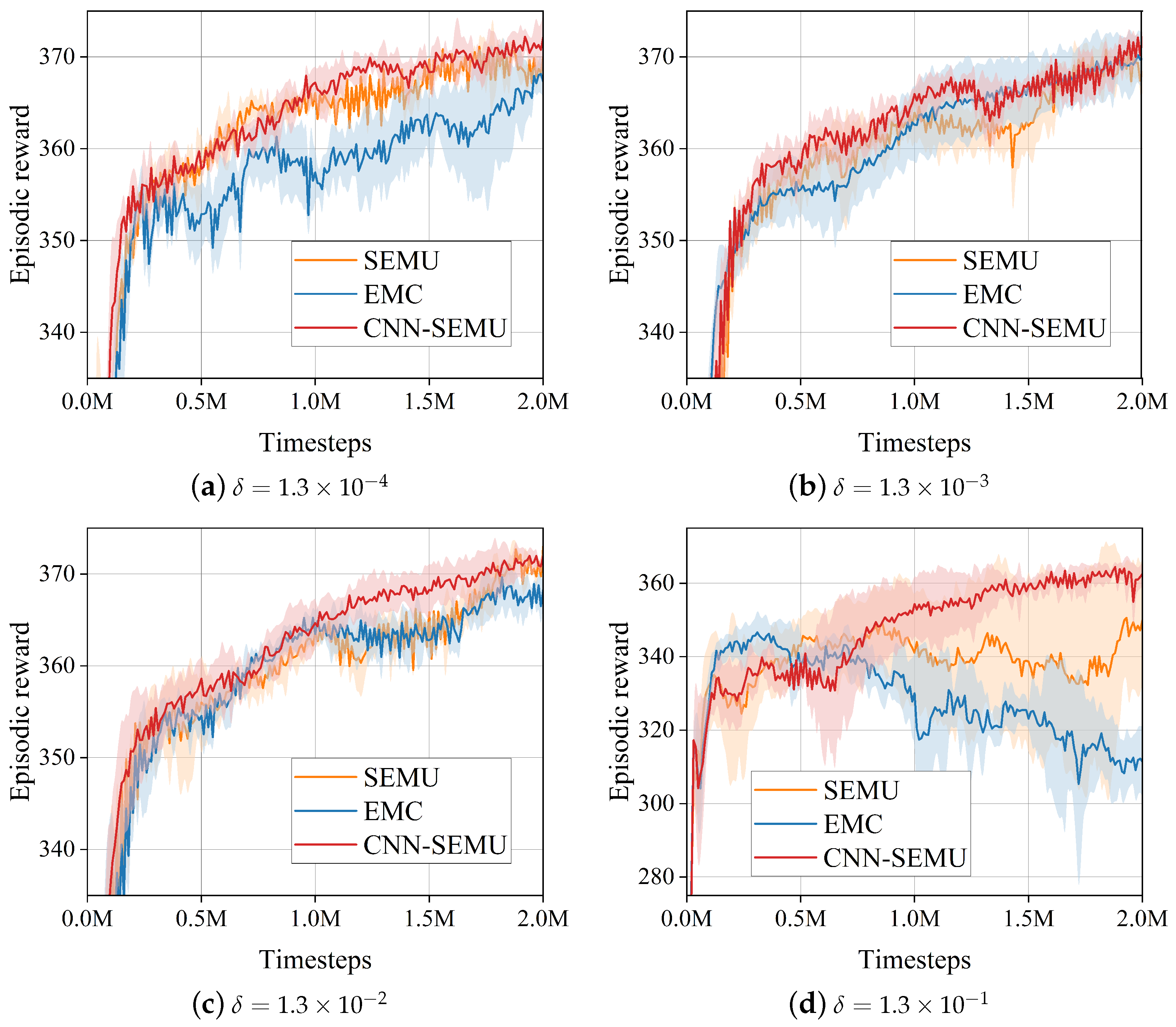
6.5. Hyperparametric Analysis
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Sun, Y.; Li, D.; Shi, J.; Li, X.; Gao, L.; Yu, L.; Han, G.; Wu, J. An Adaptive Conversion Speed Q-Learning Algorithm for Search and Rescue UAV Path Planning in Unknown Environments. IEEE Trans. Veh. Technol. 2023, 72, 15391–15404. [Google Scholar] [CrossRef]
- Li, X.; Lu, X.; Chen, W.; Ge, D.; Zhu, J. Research on UAVs Reconnaissance Task Allocation Method Based on Communication Preservation. IEEE Trans. Consum. Electron. 2024, 70, 684–695. [Google Scholar] [CrossRef]
- Liu, K.; Zheng, J. UAV Trajectory Optimization for Time-Constrained Data Collection in UAV-Enabled Environmental Monitoring Systems. IEEE Internet Things J. 2022, 9, 24300–24314. [Google Scholar] [CrossRef]
- Senthilnath, J.; Harikumar, K.; Sundaram, S. Metacognitive Decision-Making Framework for Multi-UAV Target Search without Communication. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3195–3206. [Google Scholar] [CrossRef]
- Xia, J.; Zhou, Z. The Modeling and Control of a Distributed-Vector-Propulsion UAV with Aero-Propulsion Coupling Effect. Aerospace 2024, 11, 284. [Google Scholar] [CrossRef]
- Oliehoek, F.A.; Amato, C. A Concise Introduction to Decentralized POMDPs; SpringerBriefs in Intelligent Systems, Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Zhang, B.; Lin, X.; Zhu, Y.; Tian, J.; Zhu, Z. Enhancing Multi-UAV Reconnaissance and Search Through Double Critic DDPG with Belief Probability Maps. IEEE Trans. Intell. Veh. 2024, 9, 3827–3842. [Google Scholar] [CrossRef]
- Shen, G.; Lei, L.; Zhang, X.; Li, Z.; Cai, S.; Zhang, L. Multi-UAV Cooperative Search Based on Reinforcement Learning with a Digital Twin Driven Training Framework. IEEE Trans. Veh. Technol. 2023, 72, 8354–8368. [Google Scholar] [CrossRef]
- Yan, K.; Xiang, L.; Yang, K. Cooperative Target Search Algorithm for UAV Swarms with Limited Communication and Energy Capacity. IEEE Commun. Lett. 2024, 28, 1102–1106. [Google Scholar] [CrossRef]
- Chung, T.H.; Burdick, J.W. Analysis of Search Decision Making Using Probabilistic Search Strategies. IEEE Trans. Rob. 2012, 28, 132–144. [Google Scholar] [CrossRef]
- Yang, Y.; Polycarpou, M.M.; Minai, A.A. Multi-UAV Cooperative Search Using an Opportunistic Learning Method. J. Dyn. Syst. Meas. Contr. 2007, 129, 716–728. [Google Scholar] [CrossRef]
- Liu, S.; Yao, W.; Zhu, X.; Zuo, Y.; Zhou, B. Emergent Search of UAV Swarm Guided by the Target Probability Map. Appl. Sci. 2022, 12, 5086. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, W.; Qin, W.; Tang, W. A novel UAV path planning approach: Heuristic crossing search and rescue optimization algorithm. Expert Syst. Appl. 2023, 215, 119243. [Google Scholar] [CrossRef]
- Yue, W.; Xi, Y.; Guan, X. A New Searching Approach Using Improved Multi-Ant Colony Scheme for Multi-UAVs in Unknown Environments. IEEE Access 2019, 7, 161094–161102. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, W. An Efficient UAV Localization Technique Based on Particle Swarm Optimization. IEEE Trans. Veh. Technol. 2022, 71, 9544–9557. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Samvelyan, M.; Rashid, T.; De Witt, C.S.; Farquhar, G.; Nardelli, N.; Rudner, T.G.J.; Hung, C.M.; Torr, P.H.S.; Foerster, J.; Whiteson, S. The StarCraft multi-agent challenge. In Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS, Montreal, Canada, 13–17 May 2019; Volume 4, pp. 2186–2188. [Google Scholar]
- Wang, Y.; Zhang, J.; Chen, Y.; Yuan, H.; Wu, C. An Automated Learning Method of Semantic Segmentation for Train Autonomous Driving Environment Understanding. IEEE Trans. Ind. Inf. 2024, 20, 6913–6922. [Google Scholar] [CrossRef]
- Li, J.; Liu, Q.; Chi, G. Distributed deep reinforcement learning based on bi-objective framework for multi-robot formation. Neural Netw. 2024, 171, 61–72. [Google Scholar] [CrossRef] [PubMed]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The Arcade Learning Environment: An evaluation platform for general agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Squire, L.R. Memory systems of the brain: A brief history and current perspective. Neurobiol. Learn. Mem. 2004, 82, 171–177. [Google Scholar] [CrossRef]
- Biane, J.S.; Ladow, M.A.; Stefanini, F.; Boddu, S.P.; Fan, A.; Hassan, S.; Dundar, N.; Apodaca-Montano, D.L.; Zhou, L.Z.; Fayner, V.; et al. Neural dynamics underlying associative learning in the dorsal and ventral hippocampus. Nat. Neurosci. 2023, 26, 798–809. [Google Scholar] [CrossRef]
- Turner, V.S.; O’Sullivan, R.O.; Kheirbek, M.A. Linking external stimuli with internal drives: A role for the ventral hippocampus. Curr. Opin. Neurobiol. 2022, 76, 102590. [Google Scholar] [CrossRef]
- Eichenbaum, H. Prefrontal–hippocampal interactions in episodic memory. Nat. Rev. Neurosci. 2017, 18, 547–558. [Google Scholar] [CrossRef] [PubMed]
- Blundell, C.; Uria, B.; Pritzel, A.; Li, Y.; Ruderman, A.; Leibo, J.Z.; Rae, J.; Wierstra, D.; Hassabis, D. Model-free episodic control. arXiv 2016, arXiv:1606.04460. [Google Scholar]
- Zheng, L.; Chen, J.; Wang, J.; He, J.; Hu, Y.; Chen, Y.; Fan, C.; Gao, Y.; Zhang, C. Episodic Multi-agent Reinforcement Learning with Curiosity-driven Exploration. Adv. Neural Inf. Process. Syst. 2021, 5, 3757–3769. [Google Scholar]
- Na, H.; Seo, Y.; Moon, I.C. Efficient episodic memory utilization of cooperative multi-agent reinforcement learning. arXiv 2024, arXiv:2403.01112. [Google Scholar]
- Ma, X.; Li, W.J. State-based episodic memory for multi-agent reinforcement learning. Mach. Learn. 2023, 112, 5163–5190. [Google Scholar] [CrossRef]
- Lin, Z.; Zhao, T.; Yang, G.; Zhang, L. Episodic memory deep q-networks. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI, Stockholm, Sweden, 13–19 July 2018; Volume 2018-July, pp. 2433–2439. [Google Scholar] [CrossRef]
- Johnson, W.B.; Lindenstrauss, J.; Schechtman, G. Extensions of Lipschitz maps into Banach spaces. Isr. J. Math. 1986, 54, 129–138. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; De Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. QMIX: Monotonic value function factorisation for deep multi-agent reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML 2018), Stockholm, Sweden, 10–15 July 2018; Volume 10, pp. 6846–6859. [Google Scholar]
- Wang, J.; Ren, Z.; Liu, T.; Yu, Y.; Zhang, C. QPLEX: Duplex Dueling Multi-Agent Q-Learning. arXiv 2020, arXiv:2008.01062. [Google Scholar]
- Azzam, R.; Boiko, I.; Zweiri, Y. Swarm Cooperative Navigation Using Centralized Training and Decentralized Execution. Drones 2023, 7, 193. [Google Scholar] [CrossRef]
- Khan, A.A.; Adve, R.S. Centralized and distributed deep reinforcement learning methods for downlink sum-rate optimization. IEEE Trans. Wireless Commun. 2020, 19, 8410–8426. [Google Scholar] [CrossRef]
- Son, K.; Kim, D.; Kang, W.J.; Hostallero, D.; Yi, Y. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 2019-June, pp. 10329–10346. [Google Scholar]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-decomposition networks for cooperative multi-agent learning based on team reward. In Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS, Stockholm, Sweden, 10–15 July 2018; Volume 3, pp. 2085–2087. [Google Scholar]
- Wang, M.; Xu, X.; Yue, Q.; Wang, Y. A comprehensive survey and experimental comparison of graph-based approximate nearest neighbor search. Proc. VLDB Endow. 2021, 14, 1964–1978. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, S. LightFusion: Lightweight CNN Architecture for Enabling Efficient Sensor Fusion in Free Road Segmentation of Autonomous Driving. IEEE Trans. Circuits Syst. II Express Briefs 2024. early access. [Google Scholar] [CrossRef]
- Zhang, Y.; Wilker, K. Visual-and-Language Multimodal Fusion for Sweeping Robot Navigation Based on CNN and GRU. J. Organ. End User Comput. 2024, 36, 1–21. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]



| Notation | Description |
|---|---|
| Cell at row x and column y in the map. | |
| The position of UAV i at time step t. | |
| The position of the no-fly zone k. | |
| N | Number of UAVs. |
| Number of no-fly zones. | |
| Sensor data from UAV i at time step t for . | |
| Basic probability assignments for the uncertainty and target maps at time step t for . | |
| Sensors’ basic probability assignments for the uncertainty and target maps. | |
| At time step t, the positive and negative detection times of UAV i for . | |
| The belief that the sensor both identified and failed to identify the target. | |
| The communication range of the UAV. | |
| Neighbors of UAV i at time step t. | |
| The threshold at which the target is deemed to exist. | |
| No-fly zone safety distances. | |
| Safe distance for UAVs to avoid collisions. |
| Map Size | Number of UAVs | Number of Targets | Number of No-Fly Zones | Dimension of State Space | Dimension of Observation Space | Dimension of Action Space | Episodic Length |
|---|---|---|---|---|---|---|---|
| 4 | 6 | 3 | 226 | 36 | 8 | 50 | |
| 8 | 12 | 6 | 502 | 57 | 8 | 70 | |
| 10 | 20 | 10 | 880 | 75 | 8 | 100 |
| Description | Value |
|---|---|
| UAV communication range () | 5 |
| FOV radius () | 4 |
| No-fly zone safety distances () | 1 |
| Collision safety distance between UAVs () | 1 |
| 0.8 | |
| 0.8 | |
| 1 | |
| 1 | |
| 1 | |
| 1 | |
| Episodic latent dimension () | 4 |
| Episodic buffer capacity | 1 M |
| Target discovery threshold () | 0.95 |
| Reconstruction loss scale factor () | 0.1 |
| Regularized scale factor () | 0.1 |
| State-embedding difference threshold () | 0.0013 |
| Timesteps (M) | 0.67 | 1.33 | 2.00 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EMC | SEMU | CNN-SEMU | EMC | SEMU | CNN-SEMU | EMC | SEMU | CNN-SEMU | |
| 355.69 | 363.22 | 359.17 | 360.20 | 365.63 | 369.16 | 367.30 | 370.01 | 372.11 | |
| 356.03 | 358.62 | 361.91 | 365.62 | 360.33 | 363.02 | 369.75 | 368.35 | 372.34 | |
| 359.43 | 358.84 | 359.77 | 361.68 | 361.30 | 368.24 | 366.49 | 369.74 | 371.91 | |
| 339.95 | 343.10 | 337.03 | 321.97 | 342.96 | 358.17 | 311.41 | 349.96 | 362.51 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Wang, T.; Li, M.; Cui, Y.; Lin, X.; Zhu, Z. Multiple Unmanned Aerial Vehicle (multi-UAV) Reconnaissance and Search with Limited Communication Range Using Semantic Episodic Memory in Reinforcement Learning. Drones 2024, 8, 393. https://doi.org/10.3390/drones8080393
Zhang B, Wang T, Li M, Cui Y, Lin X, Zhu Z. Multiple Unmanned Aerial Vehicle (multi-UAV) Reconnaissance and Search with Limited Communication Range Using Semantic Episodic Memory in Reinforcement Learning. Drones. 2024; 8(8):393. https://doi.org/10.3390/drones8080393
Chicago/Turabian StyleZhang, Boquan, Tao Wang, Mingxuan Li, Yanru Cui, Xiang Lin, and Zhi Zhu. 2024. "Multiple Unmanned Aerial Vehicle (multi-UAV) Reconnaissance and Search with Limited Communication Range Using Semantic Episodic Memory in Reinforcement Learning" Drones 8, no. 8: 393. https://doi.org/10.3390/drones8080393
APA StyleZhang, B., Wang, T., Li, M., Cui, Y., Lin, X., & Zhu, Z. (2024). Multiple Unmanned Aerial Vehicle (multi-UAV) Reconnaissance and Search with Limited Communication Range Using Semantic Episodic Memory in Reinforcement Learning. Drones, 8(8), 393. https://doi.org/10.3390/drones8080393







