Multi-UAV Assisted Air–Ground Collaborative MEC System: DRL-Based Joint Task Offloading and Resource Allocation and 3D UAV Trajectory Optimization
Abstract
1. Introduction
1.1. Related Work
- Task Offloading and Trajectory Optimization: As research on UAV edge computing deepens, more scholars are focusing on GD task offloading and UAV flight trajectories. With pending tasks, GDs now have more decision-making options: they can either execute tasks locally or offload them to other servers to enhance overall system performance [14]. Specifically, the decision of which server to offload a task to, what offloading method to use, and the amount of offloading tasks are the focus of current research. He et al. [15] designed a 3D dynamic multi-UAV assisted MEC system, theoretically derived, and mathematically proved the optimal unloading and flight strategies for GD to achieve fairness among UAVs. While ensuring the optimal unloading and flight strategies, in order to discover the best solution, the authors opted to solve the problem using the multi-agent deep deterministic policy gradient (MADDPG) algorithm, modeling the UAV trajectories as a series of positional updates for each UAV, which effectively reduces the energy consumption of the system and achieves high efficiency in the model processing task. Xue et al. [16] jointly optimized the task offloading decision, sub-channel allocation, and computational resource allocation in a non-orthogonal multiple access (NOMA) scenario. The energy consumption and task processing latency of the UAV are minimized. The authors considered the issue as an integer and non-integer nonlinear programming problem, solved the resource allocation problem by matching algorithm and Lagrange duality method, and subsequently designed an algorithm for multi-objective task offloading to change the offloading choice according to the resource allocation scenario, which significantly reduces the energy consumption and latency of the system. Tang et al. [17] studied a MEC system assisted by multiple access points (APs) and a UAV. The computational task of the Internet of Things on the GDs is divided into three parts: local computation, offloading to the UAV for processing, and completion on the AP via relay. The authors optimize the offloading decision and the UAV trajectory jointly to minimize the energy consumption of the system in a finite time. Minimizing the energy consumption of the system, due to the non-convex structure of the problem, the authors decouple the problem into two parts using block coordinate descent (BCD) method and solve it iteratively by using the Lagrange duality method and succession convex approximation (SCA) methodology.
- Computational Resource Allocation: Through effective resource allocation, the utilization of computing resources can be maximized and waste of resources can be avoided. Ho et al. [18] considered a UAV-assisted cloud robotics network that can perform emergency tasks such as rescue, disaster, etc., in which the tasks can be transferred to an MEC server or a distant cloud via UAVs; the authors described the problem as a joint scheme of offloading decisions and computational resource allocation and solved the non-convex problem via KKT conditions, Lagrange’s duality method, and so on. Zhang et al. [19] suggested a scenario wherein UAVs serve as relays to offload tasks to LEO satellite edge servers during natural disaster emergencies and investigated the allocation of computational resources in UAV-assisted multi-layer LEO satellite networks, which, in order to optimize the weighted sums of energy consumption and delay in the system, was converted into a Markov decision problem (MDP). To address the issue, the authors suggest a resource allocation method based on deep deterministic policy gradient and long short-term memory (DDPG-LSTM). Liu et al. [20] proposed a novel cloud edge framework to jointly optimize EUAV deployment and computational resource allocation, and the authors proposed a sequential convex programming (SCP) and sequential quadratic programming (SQP) algorithms based on deep Q-learning (SS-DQN) to obtain the EUAV deployment scheme and resource allocation scheme, respectively.
1.2. Motivation and Contributions
- We construct a model of an air–ground collaborative MEC system consisting of multi-UAV with multi-GD. A 3D dynamics model is used to model the UAVs and GDs that move randomly in 3D space and the fixed GBS. Specifically, there are three computational strategies for GD tasks: local computation, offloading to a UAV, and offloading to the GBS for computation. Each UAV flies and updates its position based on the tasks it needs to perform for the GDs. We also consider the stochastic nature of task generation and the safe distances between multi-UAV, which are highly dynamic features of the problem.
- We propose a cooperative resource optimization (CRO) problem with the intention of minimizing the energy consumption of the system. Specifically, we construct the communication, computation, and flight models of the UAVs of the system, and jointly optimize the offloading decision of the GDs, the flight trajectories of the UAVs, and the computational resource allocation of the side ends. Since there are too many variables to optimize and design the optimization problem, we decouple the optimization problem into two sub-problems by firstly letting the GDs and the UAV act as agents and design the MATD3 algorithm that performs the unloading decision and flight trajectory. On the other hand, we perform the convex optimization solution and derive the optimal solution for the side-end computational resource allocation using the KKT condition.
- Through the interaction of the two sub-problems, the joint action of task offloading, flight trajectory, and computational resource allocation is utilized to train through the designed reward function until the MATD3 algorithm converges. After theoretical analyses, our algorithm has good convergence and achieves lower energy consumption in 3D realistic scenarios.
2. System Model and Problem Construction
2.1. Network Model
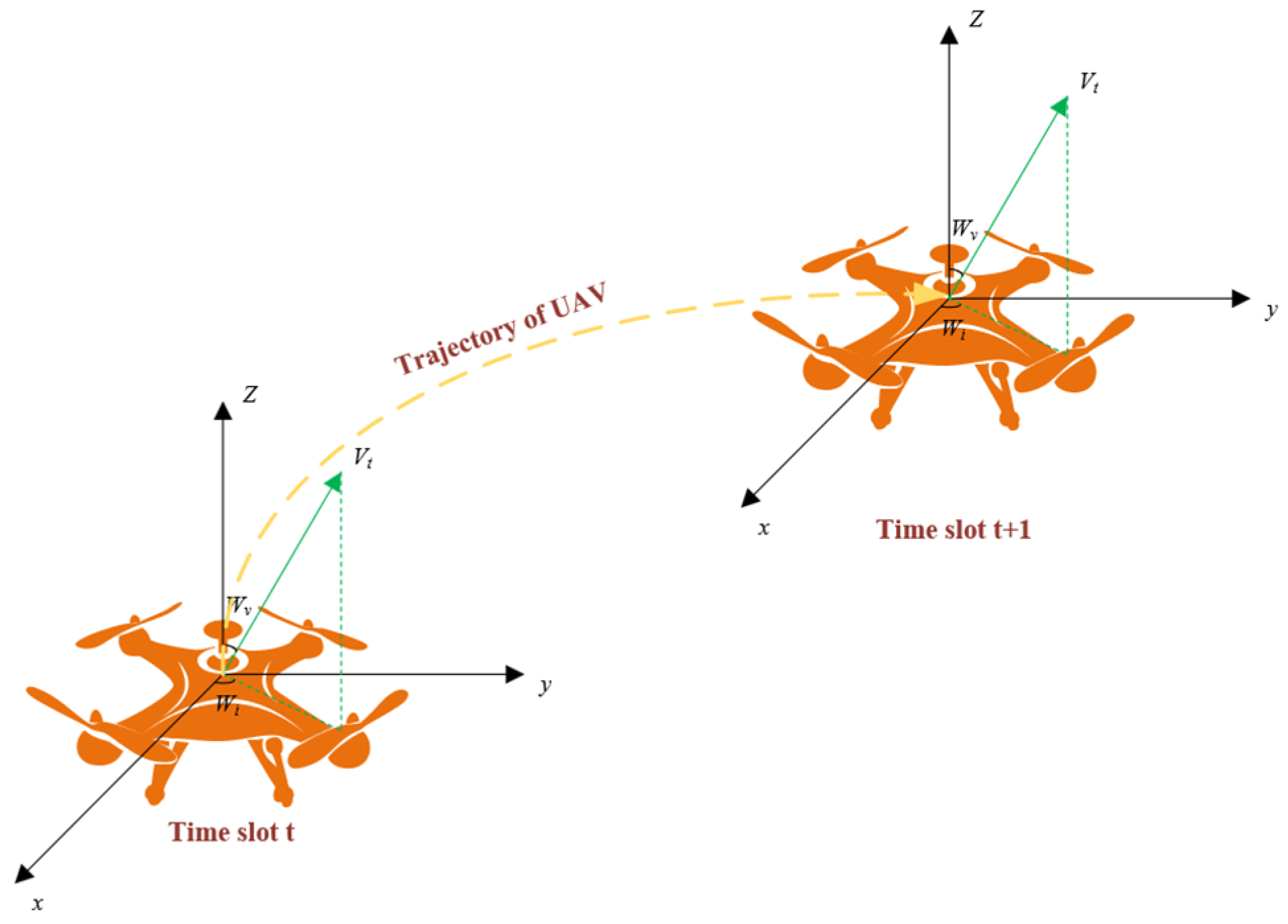
2.2. GD and UAV Mobile Model
2.3. Communication Models
2.4. Computational Model
2.4.1. Local Computation Model
2.4.2. Offloading to GBS Computation Model
2.4.3. Offloading to UAV Computational Model
2.5. Flight Model
2.6. Problem Construction
3. Problem Solution
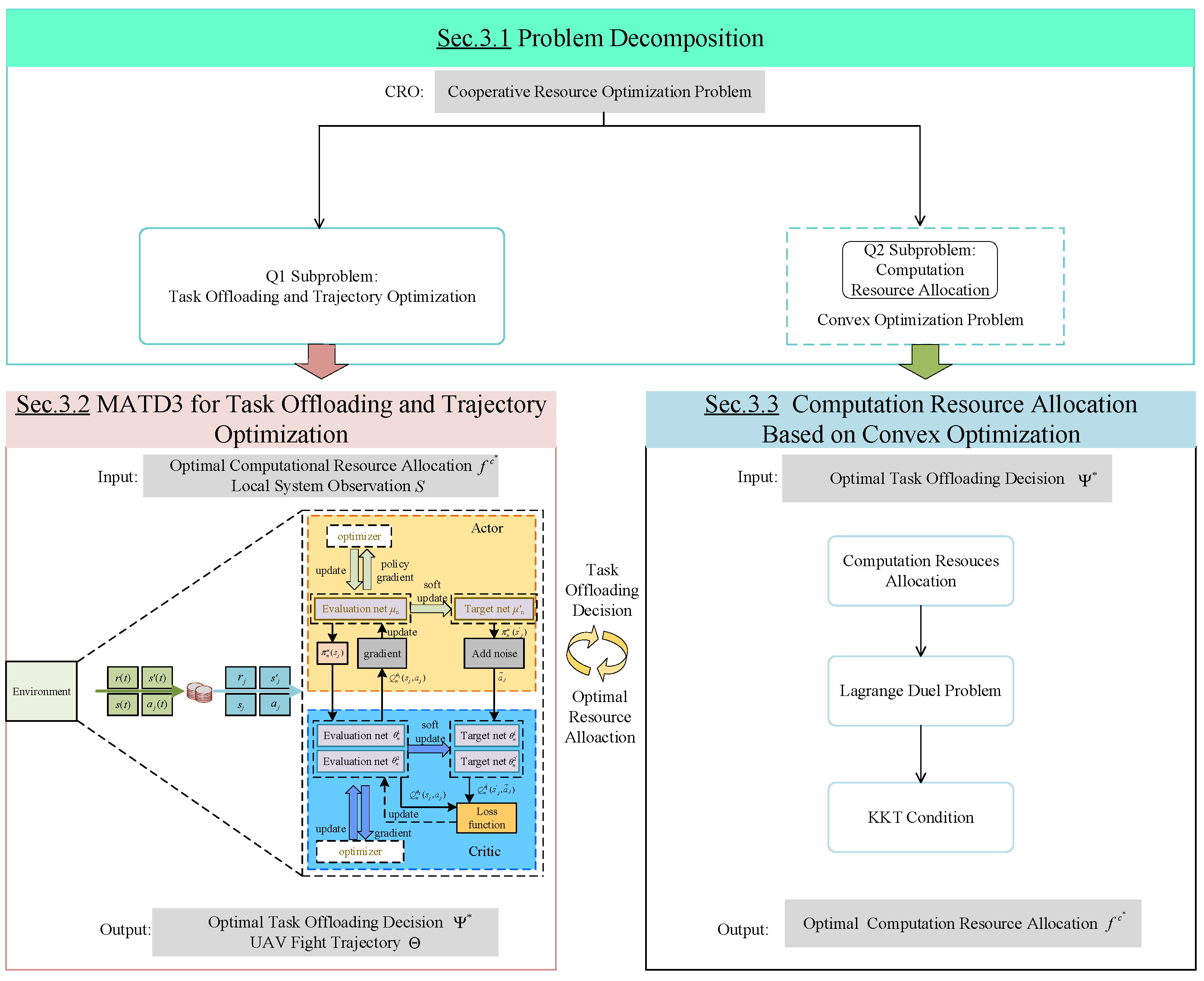
3.1. Problem Decomposition
3.1.1. Sub-Problem Q1: Task Offloading and Trajectory Optimization
3.1.2. Sub-Problem Q2: Computational Resource Allocation
3.2. MATD3 Algorithm for Task Offloading and Trajectory Optimization
- States .
- Actions .
- Reward .
| Algorithm 1: MATD3-Based GD Task Offloading and UAV Trajectory Optimization | |
| |
3.3. Computational Resource Allocation Based on Convex Optimization
4. Simulation Parameter Design and Simulation Result Analysis
4.1. Simulation Parameter Design
4.2. Analysis of Simulation Results
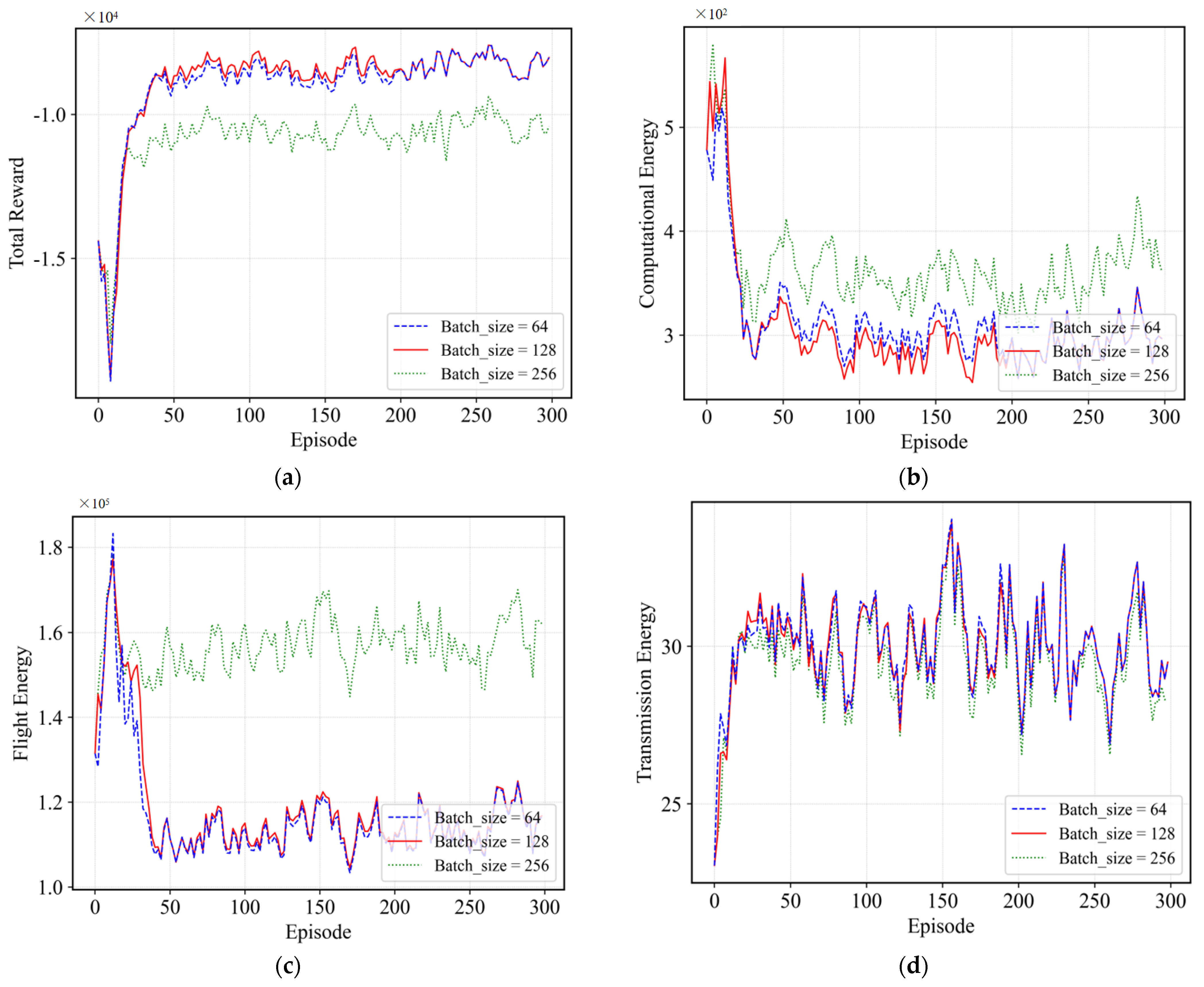
4.2.1. Effect of Different Batch_Sizes
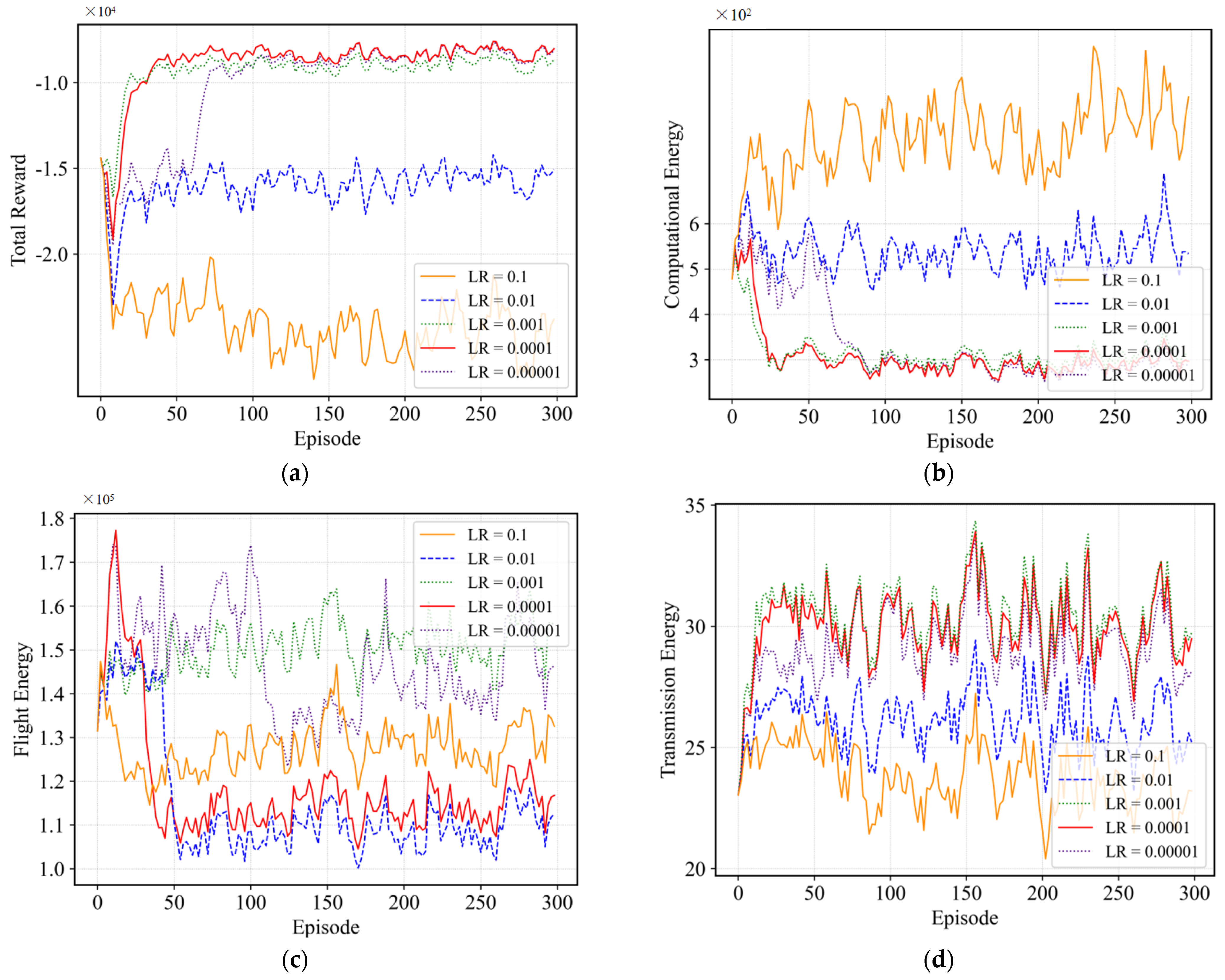
4.2.2. Effect of Different Learning Rates
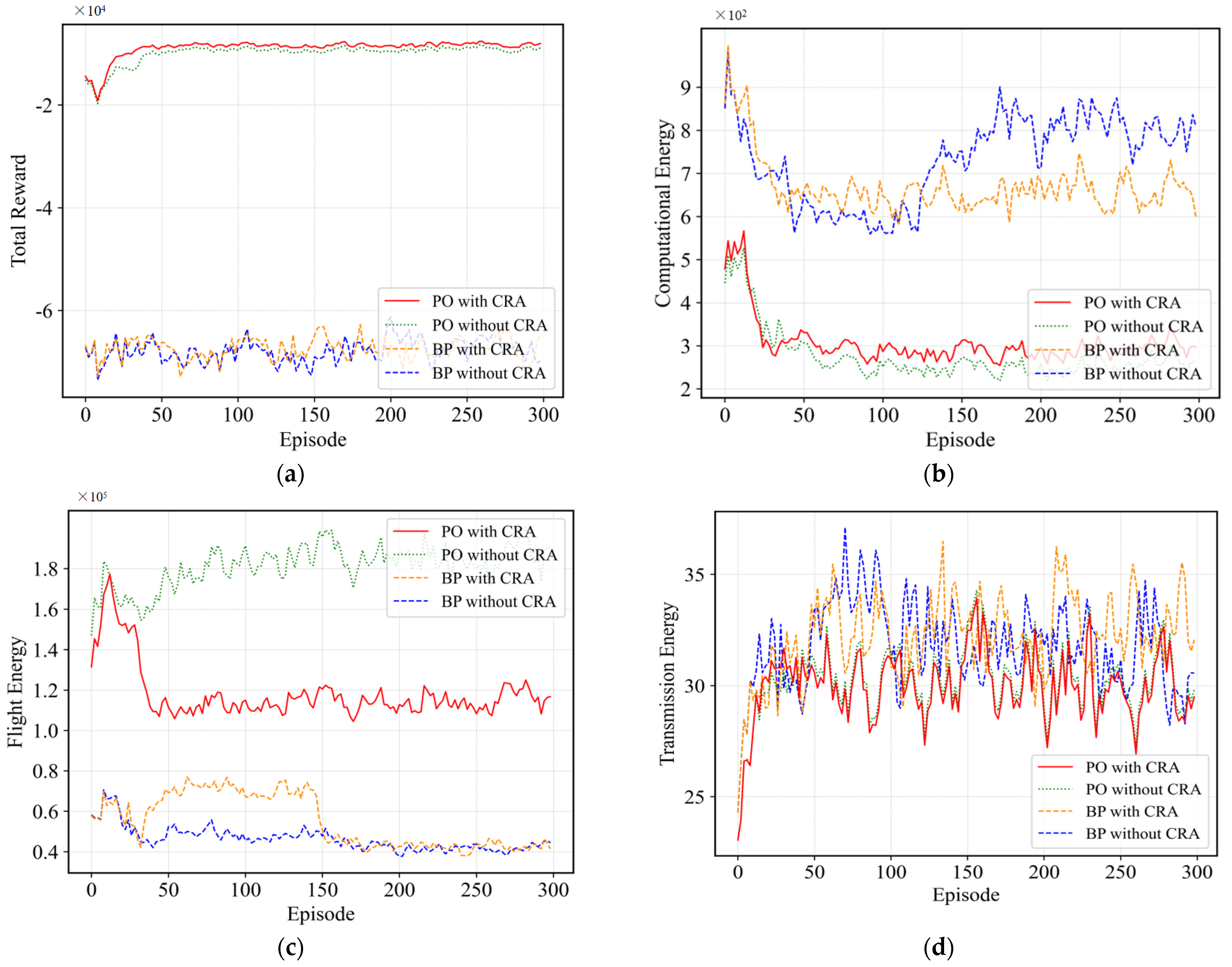
4.2.3. Effect of Computational Resource Allocation and Partial Offloading
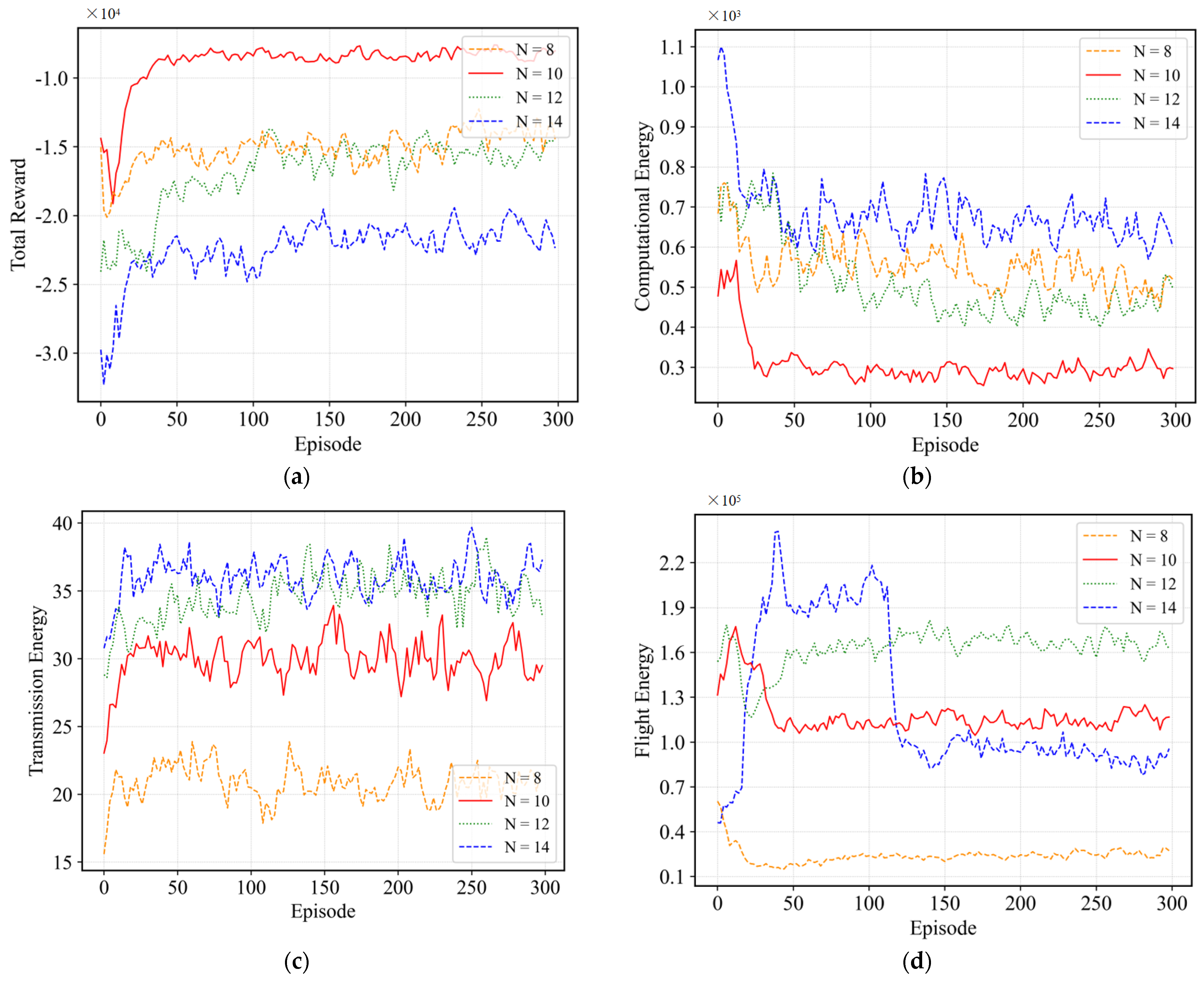
4.2.4. Effect of the Number of GDs
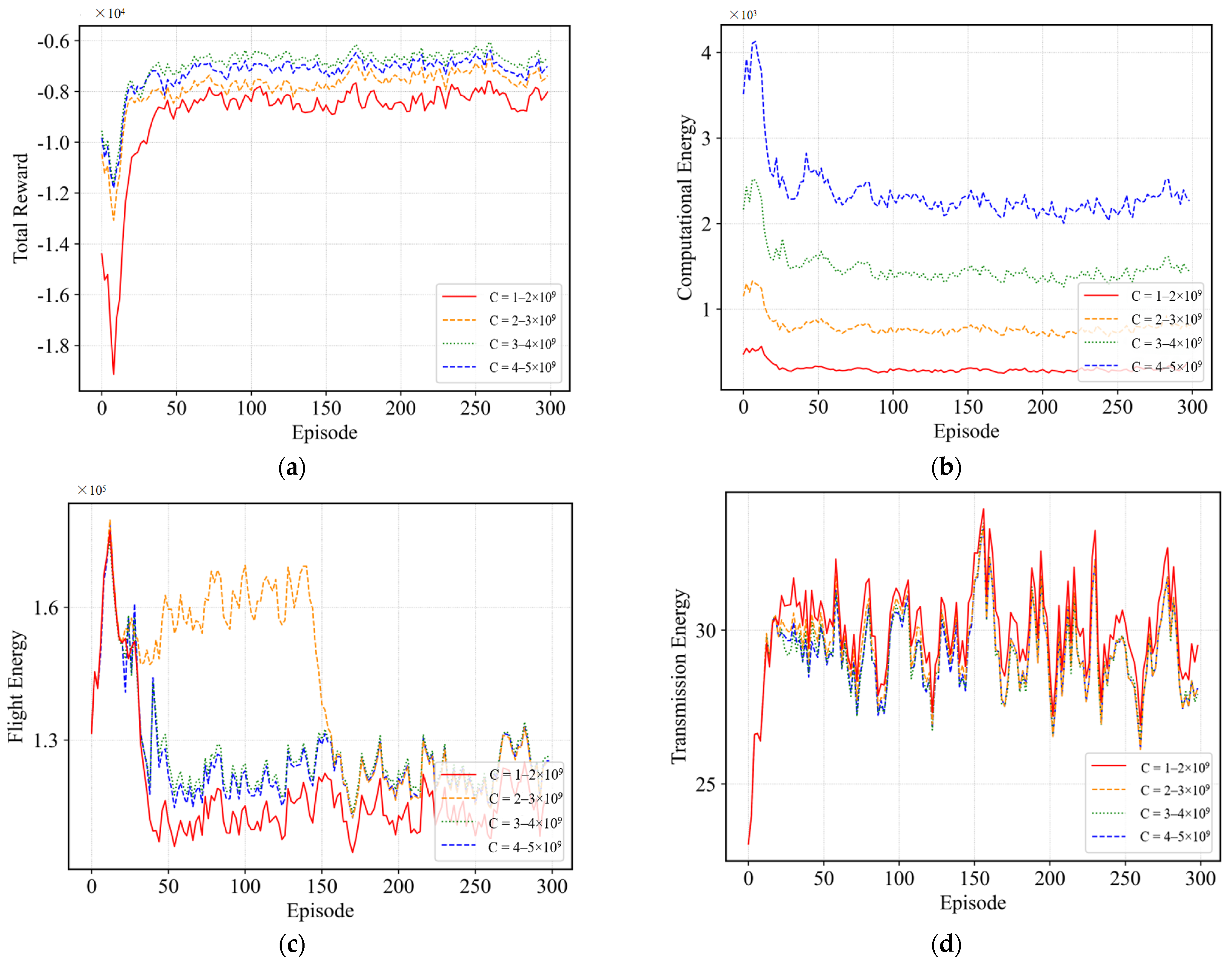
4.2.5. Effect of GDs Computing Power
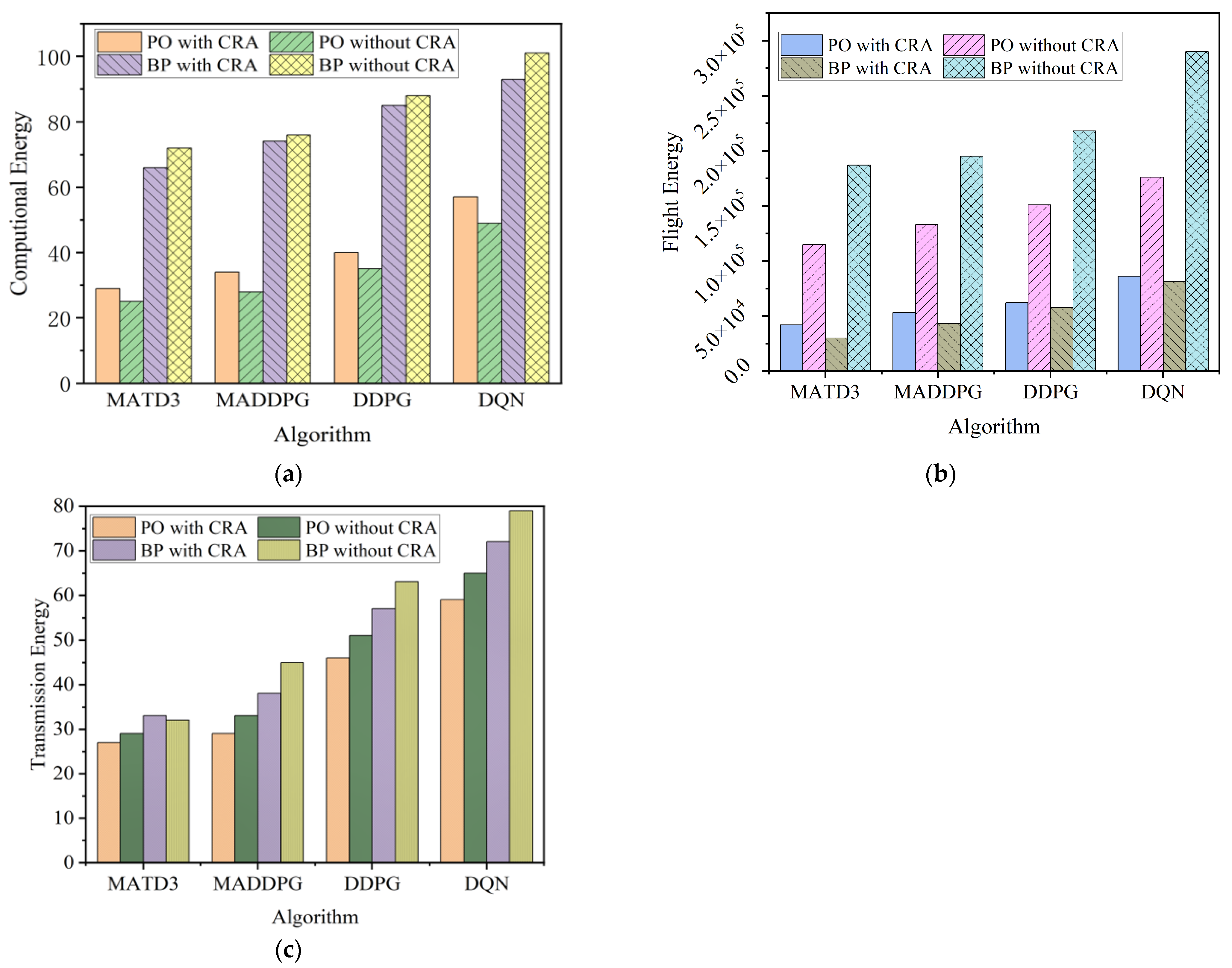
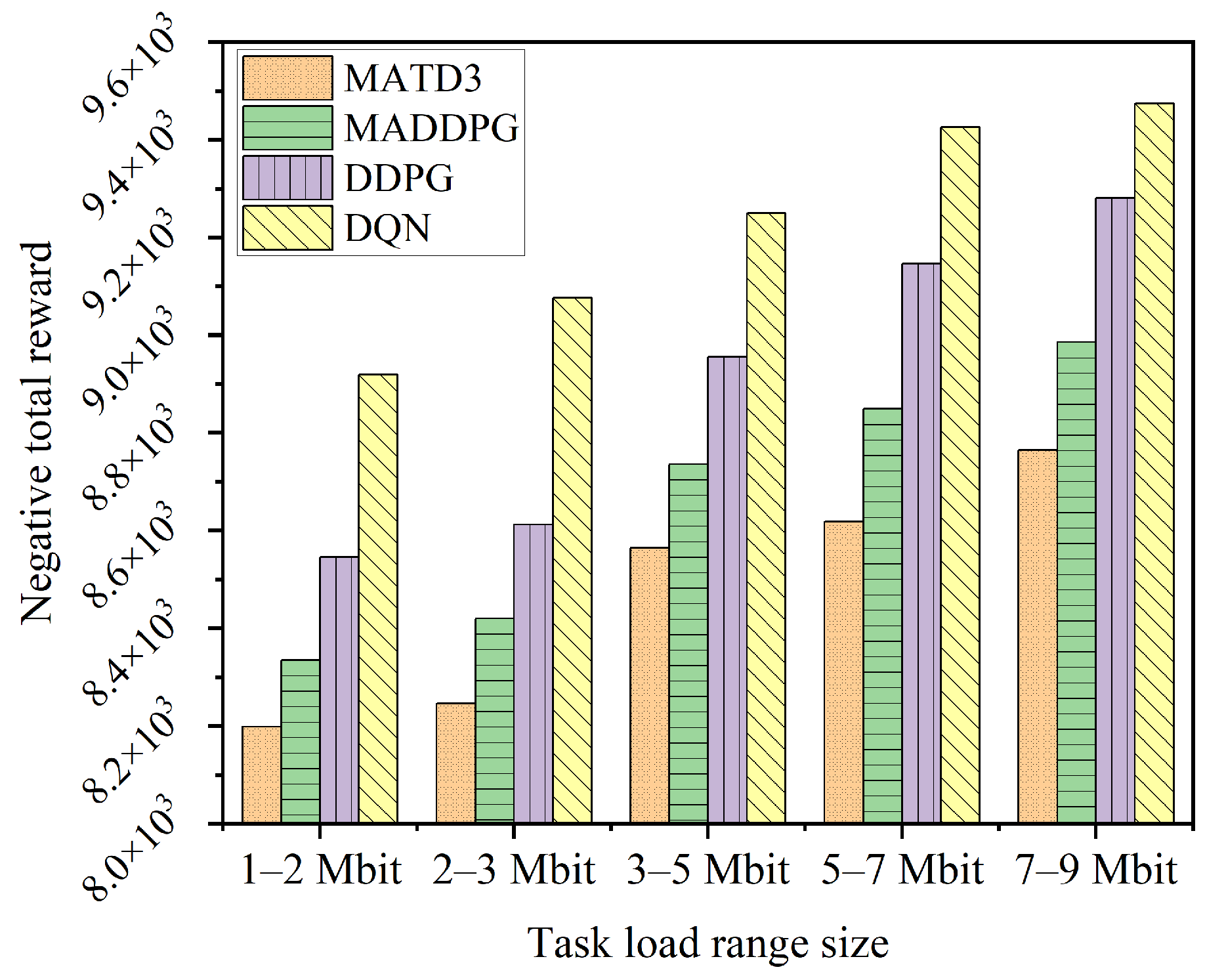
4.2.6. Comparison of This Paper’s Algorithm with the Benchmark Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, Y.J.; Chen, Q.Z.; Ling, H.F.; Xue, J.Y. Rescue Wings: Mobile Computing and Active Services Support for Disaster Rescue. IEEE Trans. Serv. Comput. 2016, 9, 594–607. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Z.; Zhang, N.; Fang, D. Disaster Relief Wireless Networks: Challenges and Solutions. IEEE Wirel. Commun. 2021, 28, 148–155. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, R.Q.; Li, Z.; Wang, Y. Mobile Edge Computing in Unmanned Aerial Vehicle Networks. IEEE Wirel. Commun. 2020, 27, 140–146. [Google Scholar] [CrossRef]
- Dai, Z.; Xu, G.; Liu, Z.; Ge, J.; Wang, W. Energy Saving Strategy of UAV in MEC Based on Deep Reinforcement Learning. Future Int. 2022, 14, 226. [Google Scholar] [CrossRef]
- Liu, L.; Wang, A.; Sun, G.; Li, J. Multiobjective Optimization for Improving Throughput and Energy Efficiency in UAV-Enabled IoT. IEEE Internet Things J. 2022, 9, 20763–20777. [Google Scholar] [CrossRef]
- Bai, T.; Wang, J.; Ren, Y.; Hanzo, L. Energy-Efficient Computation Offloading for Secure UAV-Edge-Computing Systems. IEEE Trans. Veh. Technol. 2019, 68, 6074–6087. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Shvetsov, A.V.; Kumar, S.; Shvetsova, S.V.; Alhartomi, M.A.; Hawbani, A.; Rajput, N.S.; Srivastava, S.; Saif, A.; Nyangaresi, V.O. UAV Computing-Assisted Search and Rescue Mission Framework for Disaster and Harsh Environment Mitigation. Drones 2022, 6, 154. [Google Scholar] [CrossRef]
- Munoz, O.; Pascual-Iserte, A.; Vidal, J. Optimization of Radio and Computational Resources for Energy Efficiency in Latency-Constrained Application Offloading. IEEE Trans. Veh. Technol. 2015, 64, 4738–4755. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Clerckx, B. Dynamic Air-Ground Collaboration for Multi-Access Edge Computing. In Proceedings of the ICC 2022—IEEE International Conference on Communications, Seoul, Republic of Korea, 10–20 May 2022; pp. 5365–5371. [Google Scholar]
- Lu, Y.; Huang, Y.; Hu, T. Robust Resource Scheduling for Air-Ground Cooperative Mobile Edge Computing. In Proceedings of the 2021 IEEE/CIC International Conference on Communications in China (ICCC), Xiamen, China, 28–30 July 2021; pp. 764–769. [Google Scholar]
- Seid, A.M.; Boateng, G.O.; Anokye, S.; Kwantwi, T.; Sun, G.; Liu, G. Collaborative Computation Offloading and Resource Allocation in Multi-UAV-Assisted IoT Networks: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2021, 8, 12203–12218. [Google Scholar] [CrossRef]
- Nie, Y.; Zhao, J.; Gao, F.; Yu, F.R. Semi-Distributed Resource Management in UAV-Aided MEC Systems: A Multi-Agent Federated Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2021, 70, 13162–13173. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Y.; Qi, F.; Zhou, F.; Xie, W.; He, H.; Zheng, H. Federated Deep Reinforcement Learning for Joint AeBSs Deployment and Computation Offloading in Aerial Edge Computing Network. Electronics 2022, 11, 3641. [Google Scholar] [CrossRef]
- Hu, Z.; Zeng, F.; Xiao, Z.; Fu, B.; Jiang, H.; Xiong, H.; Zhu, Y.; Alazab, M. Joint Resources Allocation and 3D Trajectory Optimization for UAV-Enabled Space-Air-Ground Integrated Networks. IEEE Trans. Veh. Technol. 2023, 72, 14214–14229. [Google Scholar] [CrossRef]
- He, Y.; Gan, Y.; Cui, H.; Guizani, M. Fairness-Based 3-D Multi-UAV Trajectory Optimization in Multi-UAV-Assisted MEC System. IEEE Internet Things J. 2023, 10, 11383–11395. [Google Scholar] [CrossRef]
- Xue, J.; Ma, Y.; Tian, G.; Dou, J.; Guan, X. Resource Allocation and Offloading Decision of UAV Based on NOMA-MEC. Wirel. Pers. Commun. 2023, 133, 259–288. [Google Scholar] [CrossRef]
- Tang, Q.; Liu, L.; Jin, C.; Wang, J.; Liao, Z.; Luo, Y. An UAV-assisted mobile edge computing offloading strategy for minimizing energy consumption. Comput. Netw. 2022, 207, 108857. [Google Scholar] [CrossRef]
- Ho, T.M.; Nguyen, K.K.; Cheriet, M. Optimized Task Offloading in UAV-Assisted Cloud Robotics. In Proceedings of the ICC 2023—IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 4773–4779. [Google Scholar]
- Zhang, H.; Xi, S.; Jiang, H.; Shen, Q.; Shang, B.; Wang, J. Resource Allocation and Offloading Strategy for UAV-Assisted LEO Satellite Edge Computing. Drones 2023, 7, 383. [Google Scholar] [CrossRef]
- Liu, B.; Liu, C.; Peng, M. Computation Offloading and Resource Allocation in Unmanned Aerial Vehicle Networks. IEEE Trans. Veh. Technol. 2023, 72, 4981–4995. [Google Scholar] [CrossRef]
- Hao, H.; Xu, C.; Zhang, W.; Yang, S.; Muntean, G.-M. Joint Task Offloading, Resource Allocation, and Trajectory Design for Multi-UAV Cooperative Edge Computing with Task Priority. IEEE Trans. Mob. Comput. 2024, 23, 8649–8663. [Google Scholar] [CrossRef]
- Gao, Y.; Yuan, X.; Yang, D.; Hu, Y.; Cao, Y.; Schmeink, A. UAV-Assisted MEC System with Mobile Ground Terminals: DRL-Based Joint Terminal Scheduling and UAV 3D Trajectory Design. IEEE Trans. Veh. Technol. 2024, 73, 10164–10180. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, C.; Wei, Z.; Pan, C.; Zhang, H.; Ren, Y. Joint UAV Hovering Altitude and Power Control for Space-Air-Ground IoT Networks. IEEE Internet Things J. 2019, 6, 1741–1753. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, H.; Shu, L.; Liu, Y. UAV-Assisted Sleep Scheduling Algorithm for Energy-Efficient Data Collection in Agricultural Internet of Things. IEEE Internet Things J. 2022, 9, 11043–11056. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Z.; Zhang, J.; Cao, X.; Zheng, D.; Gao, Y.; Kwan Ng, D.W.; Di Renzo, M. Trajectory Design for UAV-Based Internet of Things Data Collection: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2022, 9, 3899–3912. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, H.; Feng, Z.; Gao, H.; Li, W. Data-Aided Doppler Frequency Shift Estimation and Compensation for UAVs. IEEE Internet Things J. 2020, 7, 400–415. [Google Scholar] [CrossRef]
- Ding, R.; Gao, F.; Shen, X.S. 3D UAV Trajectory Design and Frequency Band Allocation for Energy-Efficient and Fair Communication: A Deep Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2020, 19, 7796–7809. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wang, L.; Wang, K.; Pan, C.; Xu, W.; Aslam, N.; Hanzo, L. Multi-Agent Deep Reinforcement Learning-Based Trajectory Planning for Multi-UAV Assisted Mobile Edge Computing. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 73–84. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Z.; Fan, M.; Wu, K. Joint Task Offloading and Resource Allocation in Multi-UAV Multi-Server Systems: An Attention-Based Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2024, 73, 11964–11978. [Google Scholar] [CrossRef]
- Ding, Y.; Han, H.; Lu, W.; Wang, Y.; Zhao, N.; Wang, X.; Yang, X. DDQN-Based Trajectory and Resource Optimization for UAV-Aided MEC Secure Communications. IEEE Trans. Veh. Technol. 2024, 73, 6006–6011. [Google Scholar] [CrossRef]


| Parametric | Description |
|---|---|
| The number of GDs K | 10 |
| The number of UAVs N | 2 |
| The number of GBS | 1 |
| The number of time slots | 50 |
| The computing resources per GD | 1 × 109–2 × 109 HZ |
| The computing resources per UAV | 5 × 109–6 × 109 HZ |
| The computing resources GBS | 1010 HZ |
| The task data size per GD | 3 Mbit–5 Mbit |
| Required CPU cycles per bit per GD | 500 cycles/bite-800 cycles/bite |
| The number of rotors per UAV | 4 |
| The weight per UAV | 2.0 Kg |
| The air density | 1.225 Kg/m3 |
| The equivalent plane area of fuselage per UAV | 0.01 m2 |
| The gravitational acceleration vector | 9.8 m/s2 |
| The local blade section drag coefficient | 0.012 |
| The thrust coefficient based on disc area | 0.302 |
| The rotor solidity | 0.0955 |
| The rotor disc area | 0.0314 m2 |
| The induced power increment correction factor | 0.131 |
| The fuselage drag ratio | 0.834 |
| The weight of per fight energy | 10−4 |
| Parametric | Description |
|---|---|
| Learning rate | 0.0001 |
| Sampling batch size | 128 |
| Discount factor | 0.95 |
| Playback experience pool size | 100,000 |
| Number of training Episodes | 300 |
| Activation function | Tanh |
| Optimizer | Adam |
| Frequency of target network updates | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Li, R.; Jing, F.; Gao, M. Multi-UAV Assisted Air–Ground Collaborative MEC System: DRL-Based Joint Task Offloading and Resource Allocation and 3D UAV Trajectory Optimization. Drones 2024, 8, 510. https://doi.org/10.3390/drones8090510
Wang M, Li R, Jing F, Gao M. Multi-UAV Assisted Air–Ground Collaborative MEC System: DRL-Based Joint Task Offloading and Resource Allocation and 3D UAV Trajectory Optimization. Drones. 2024; 8(9):510. https://doi.org/10.3390/drones8090510
Chicago/Turabian StyleWang, Mingjun, Ruishan Li, Feng Jing, and Mei Gao. 2024. "Multi-UAV Assisted Air–Ground Collaborative MEC System: DRL-Based Joint Task Offloading and Resource Allocation and 3D UAV Trajectory Optimization" Drones 8, no. 9: 510. https://doi.org/10.3390/drones8090510
APA StyleWang, M., Li, R., Jing, F., & Gao, M. (2024). Multi-UAV Assisted Air–Ground Collaborative MEC System: DRL-Based Joint Task Offloading and Resource Allocation and 3D UAV Trajectory Optimization. Drones, 8(9), 510. https://doi.org/10.3390/drones8090510





