Air Route Network Planning Method of Urban Low-Altitude Logistics UAV with Double-Layer Structure
Abstract
1. Introduction
2. Literature Review
2.1. Location Problem
2.2. Single-Route Planning
2.3. Route Network Planning
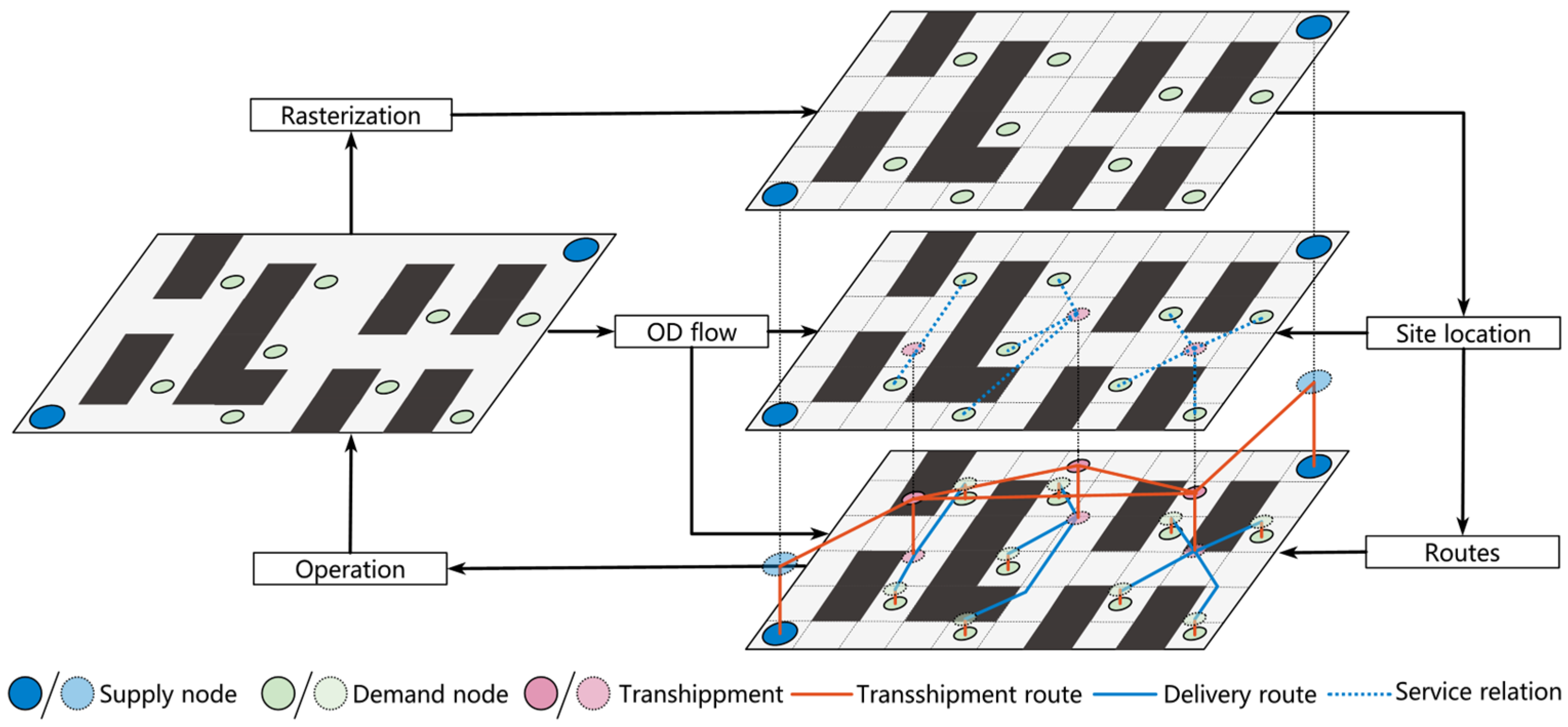
3. Problem Description and Formulation
3.1. Problem Analysis
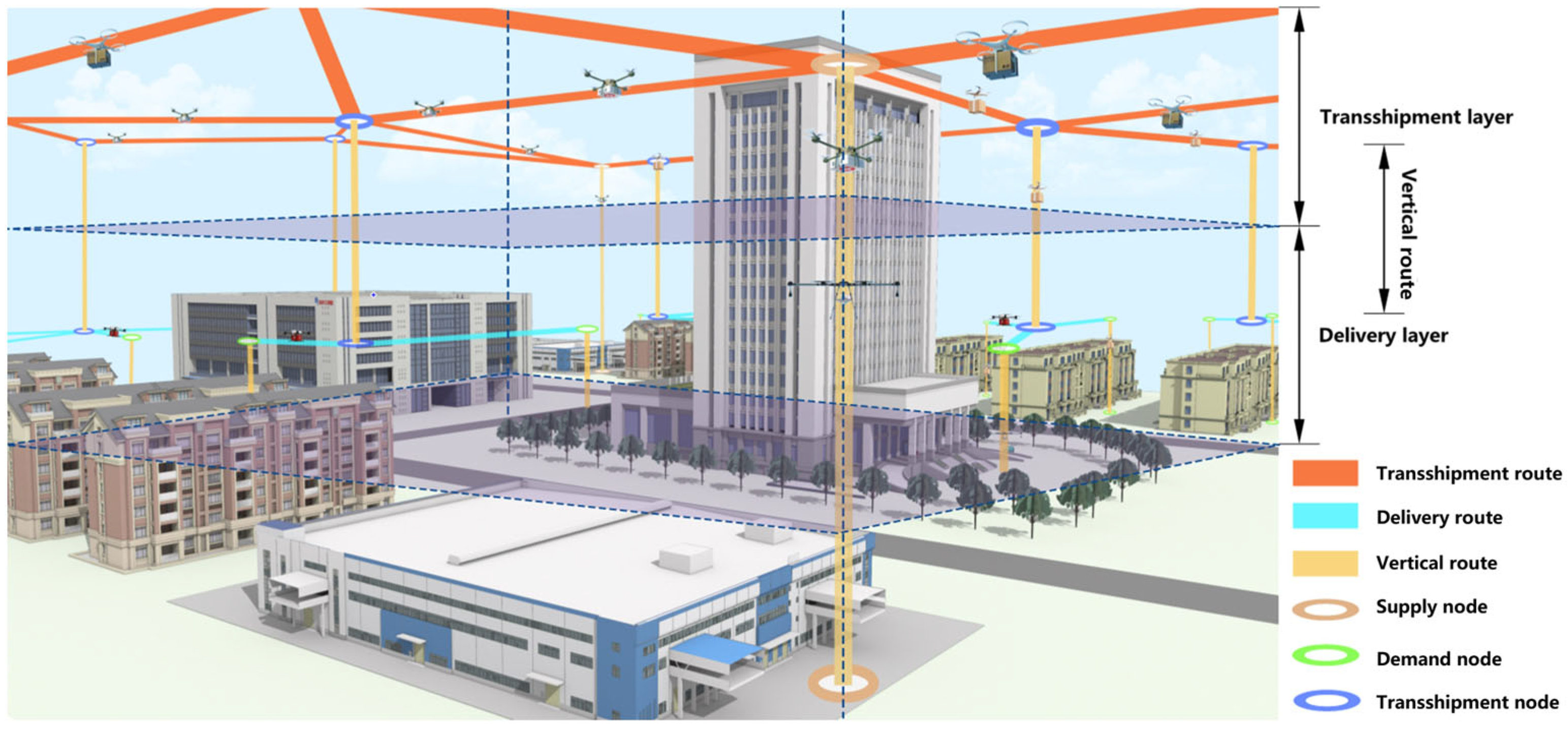
3.1.1. Scenario Analysis
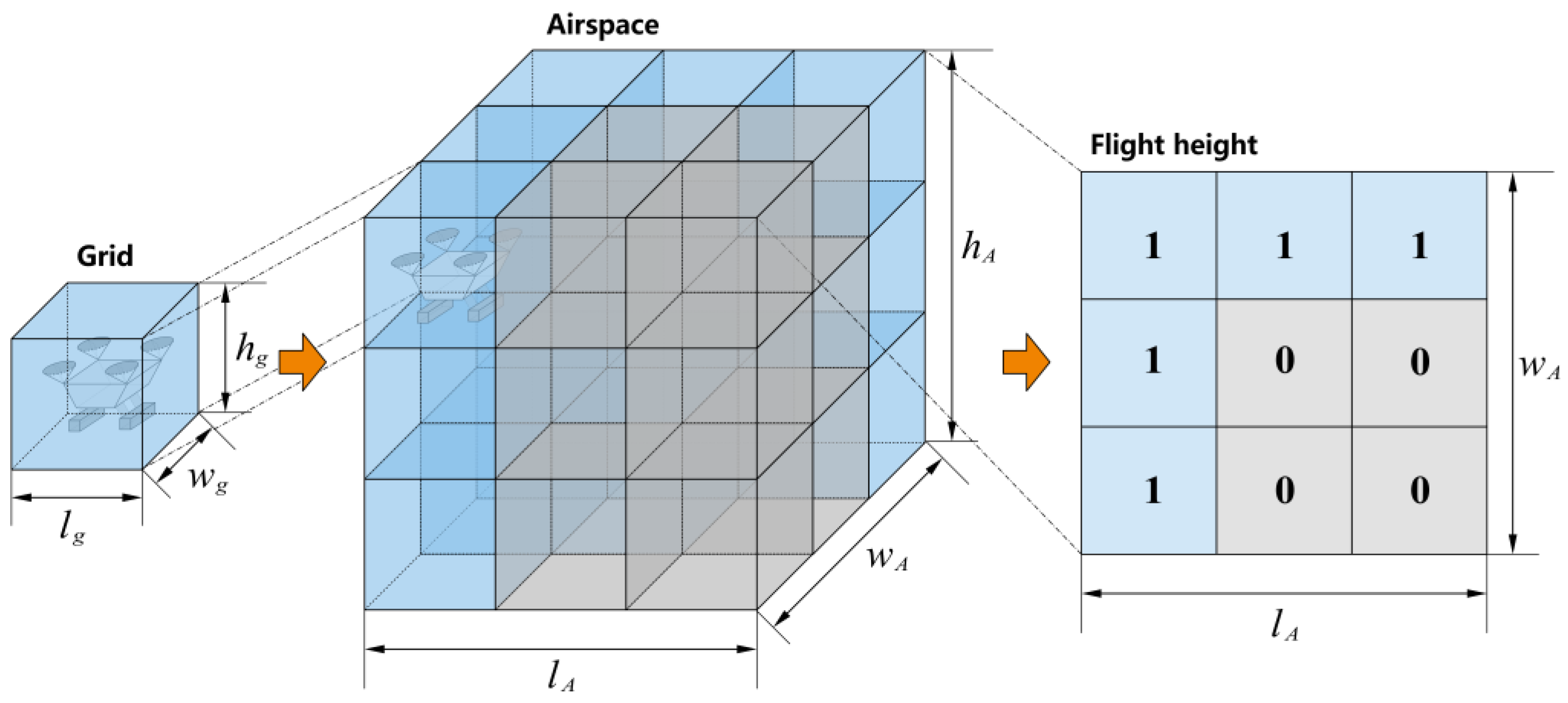
3.1.2. Rasterization of Airspace
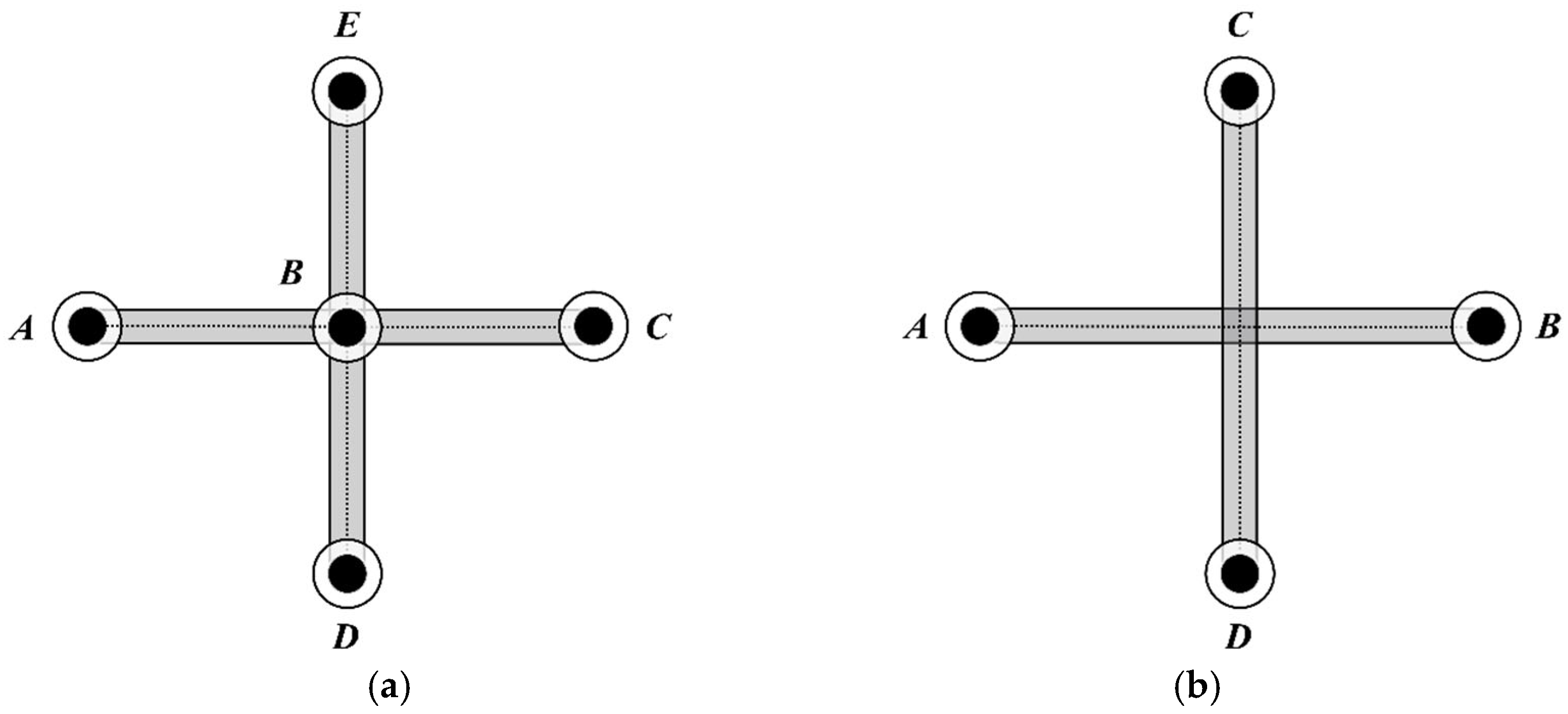
3.1.3. Route Structure
3.2. Transshipment Node Service Location Model
3.2.1. Basic Definitions and Constraints
- (1)
- Basic definitions
- (2)
- Constraint conditions
3.2.2. Optimization Objectives and Modeling
- (1)
- Minimum total service distance
- (2)
- Minimum transshipment node number
- (3)
- Minimum average service pressure
3.3. Air Route Network Planning Model
3.3.1. Basic Definitions and Constraints
- (1)
- Basic definitions
- (2)
- Constraint conditions
3.3.2. Optimization Objectives and Modeling
- (1)
- Minimum route betweenness standard deviation
- (2)
- Minimum total network distance
- (3)
- Minimum average non-linear coefficient
3.4. Indicators for Assessing the Operation of the Route Network
- (1)
- Route intersection situation
- (2)
- Route utilization situation
- (3)
- Flight duration situation
4. Double-Layer Optimization Algorithm Design
4.1. Upper-Layer Algorithm Design
4.1.1. Coding Strategy
4.1.2. Individual Update
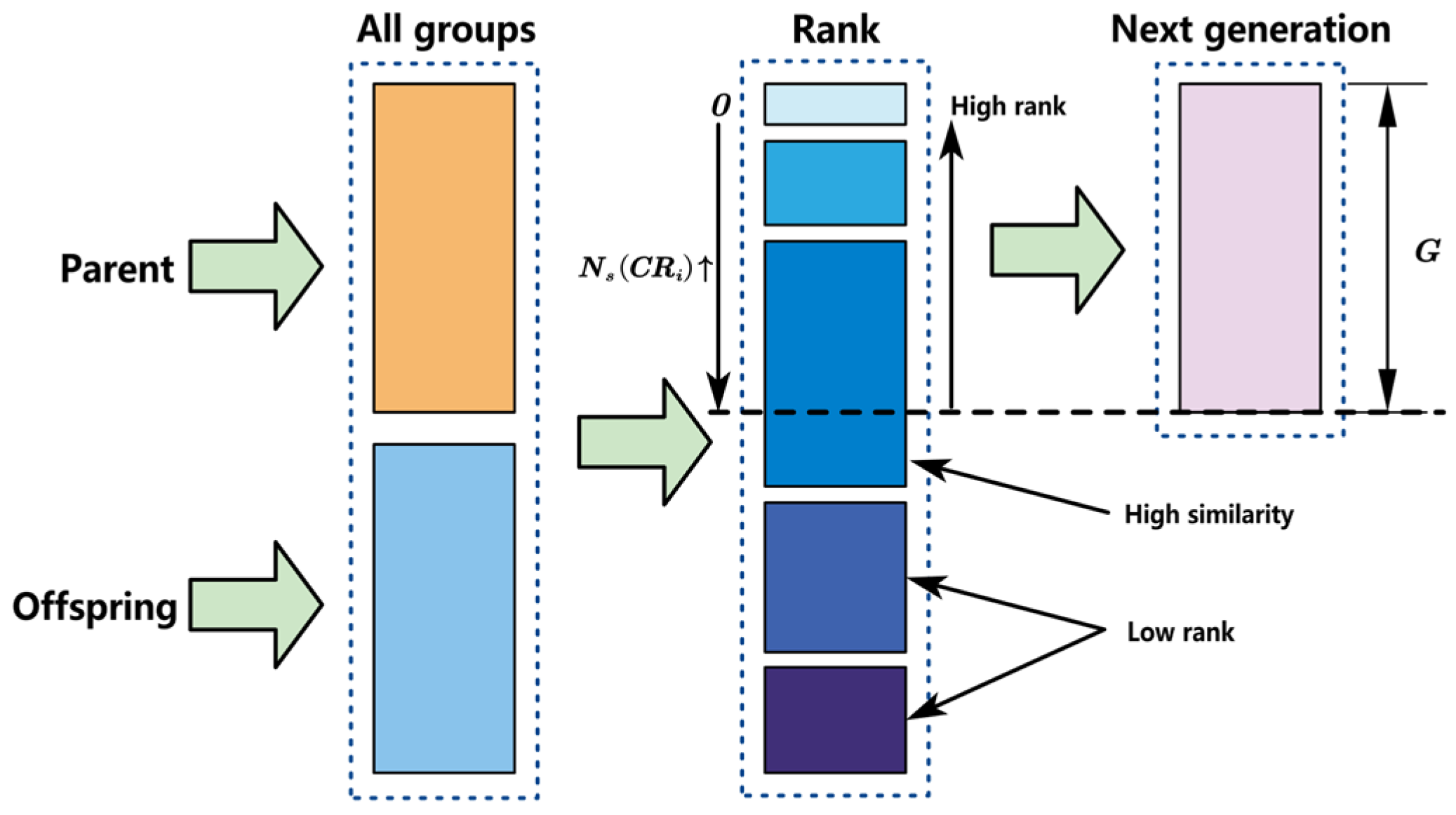
4.1.3. Metropolis Criteria
4.1.4. Algorithm Iteration
4.1.5. Algorithm Flow
| Algorithm 1: MOSA | |
| Require: | |
| 1. | The location of demand node. |
| 2. | The grid information. |
| Set: | |
| 1. | Set T0 as T, input TL and decay factor . |
| Ensure: | |
| 1. | Generate a primary solution as old individual (OI) follow the Equation (40). |
| 2. | Calculate the targets of OI. |
| 3. | Generate the domination relationship list (DRL) and solution set (ST). |
| 4. | While T > TL |
| 5. | for iterating in the inner loop. |
| 6. | Generate a new individual (NI) based on OI follow the rule in Section 4.1.2. |
| 7. | Calculate the targets of NI. |
| 8. | If NI does not satisfy Equation (12), repeat to row 6. Otherwise, move on. |
| 9. | Update ST and calculate the target of NI. |
| 10. | Compare domination relationship between NI and OI by Equation (41). |
| 11. | Update the DRL and calculate the pacc by Equation (44). |
| 12. | If rand(1) < pacc |
| 13. | NI replaces OI as the current solution. |
| 14. | end if |
| 15. | end for |
| 16. | Update T based on Equation (45). |
| 17. | end while |
| 18. | Filter the pareto solution from DRL and ST based on Equation (46). |
| 19. | Calculate the score of pareto solution based on Equation (47). |
| 20. | The solution with the highest score will be the final solution. |
4.2. Lower-Layer Algorithm Design
4.2.1. Coding Strategy
4.2.2. Genetic Operations
- (1)
- Roulette selection
- (2)
- Crossover and mutation
4.2.3. Metropolis Criteria
4.2.4. Population Renewal
5. Simulation Experiment
5.1. Scene Setting
5.2. Experimental Results
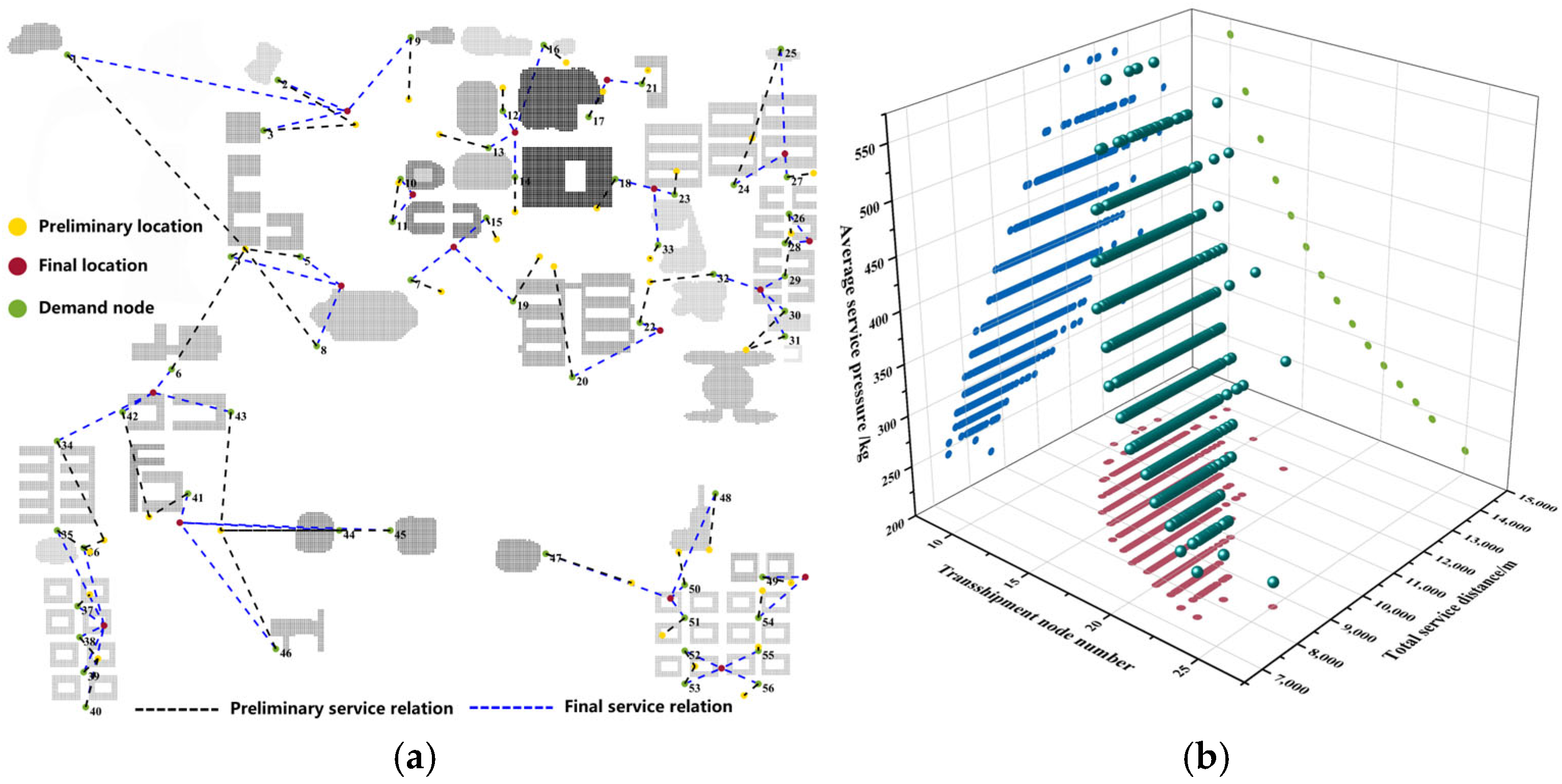
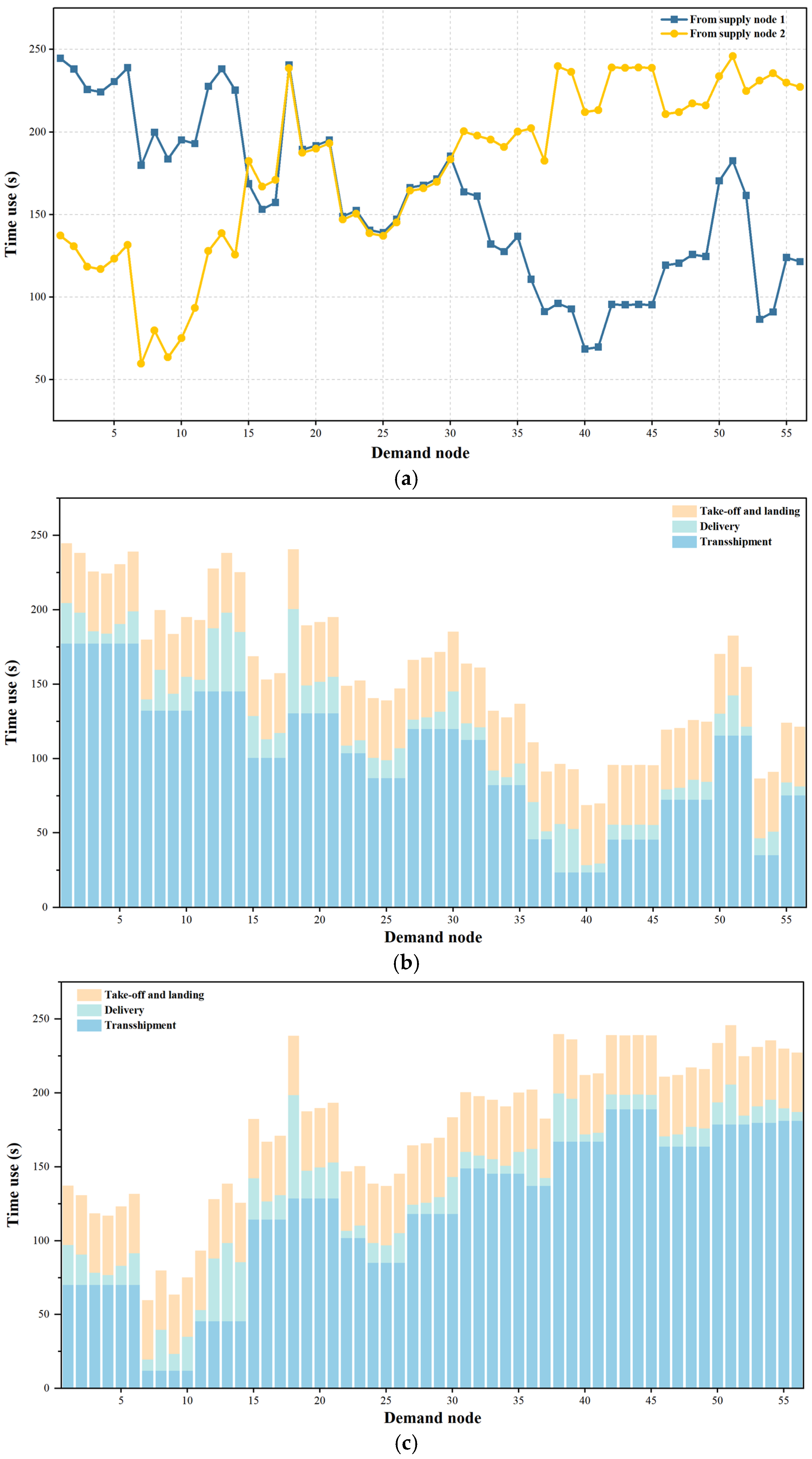
5.3. Numerical Analysis
- (1)
- Transshipment node location analysis
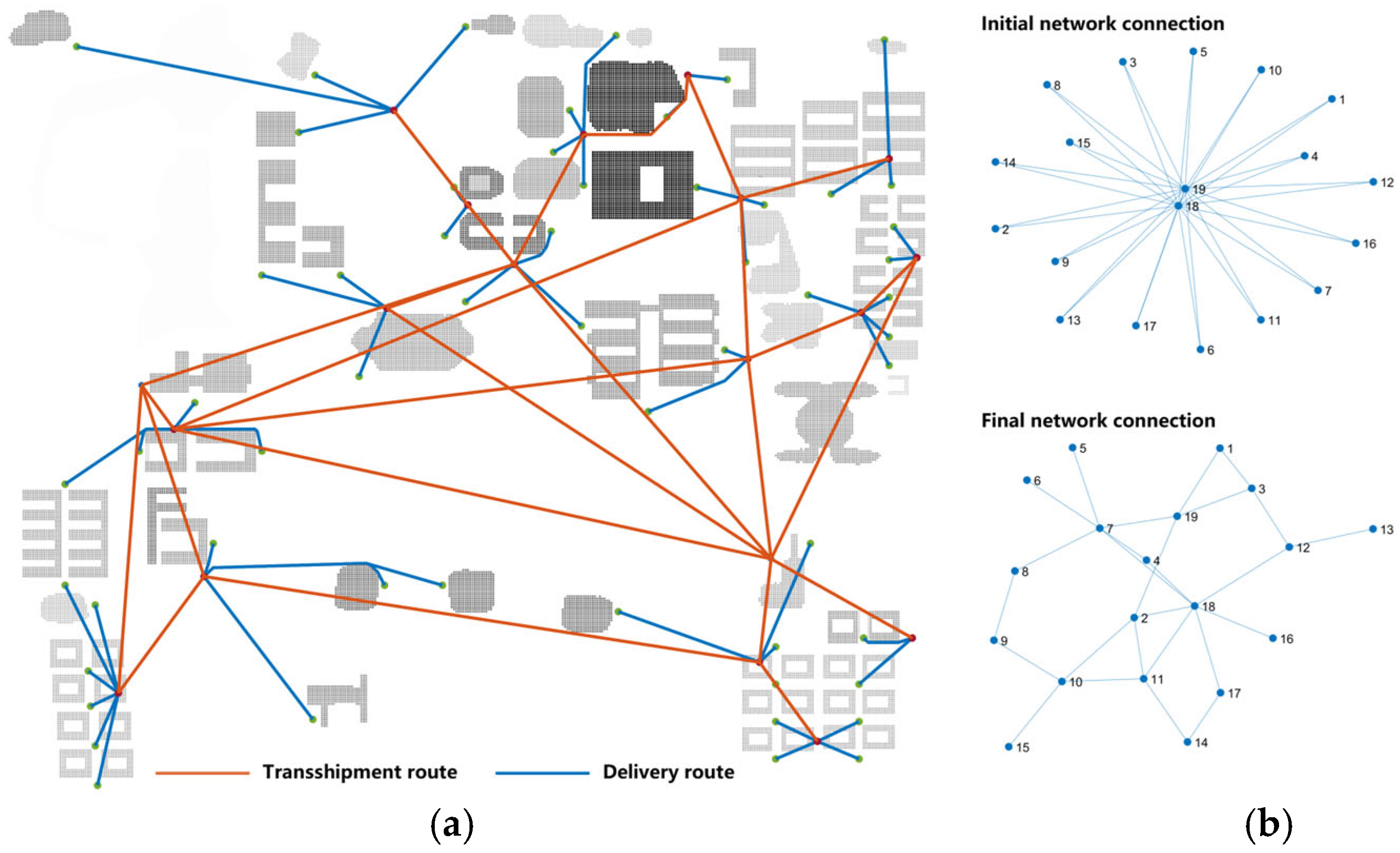
- (2)
- Route network structure analysis
- (3)
- Operational evaluation of network
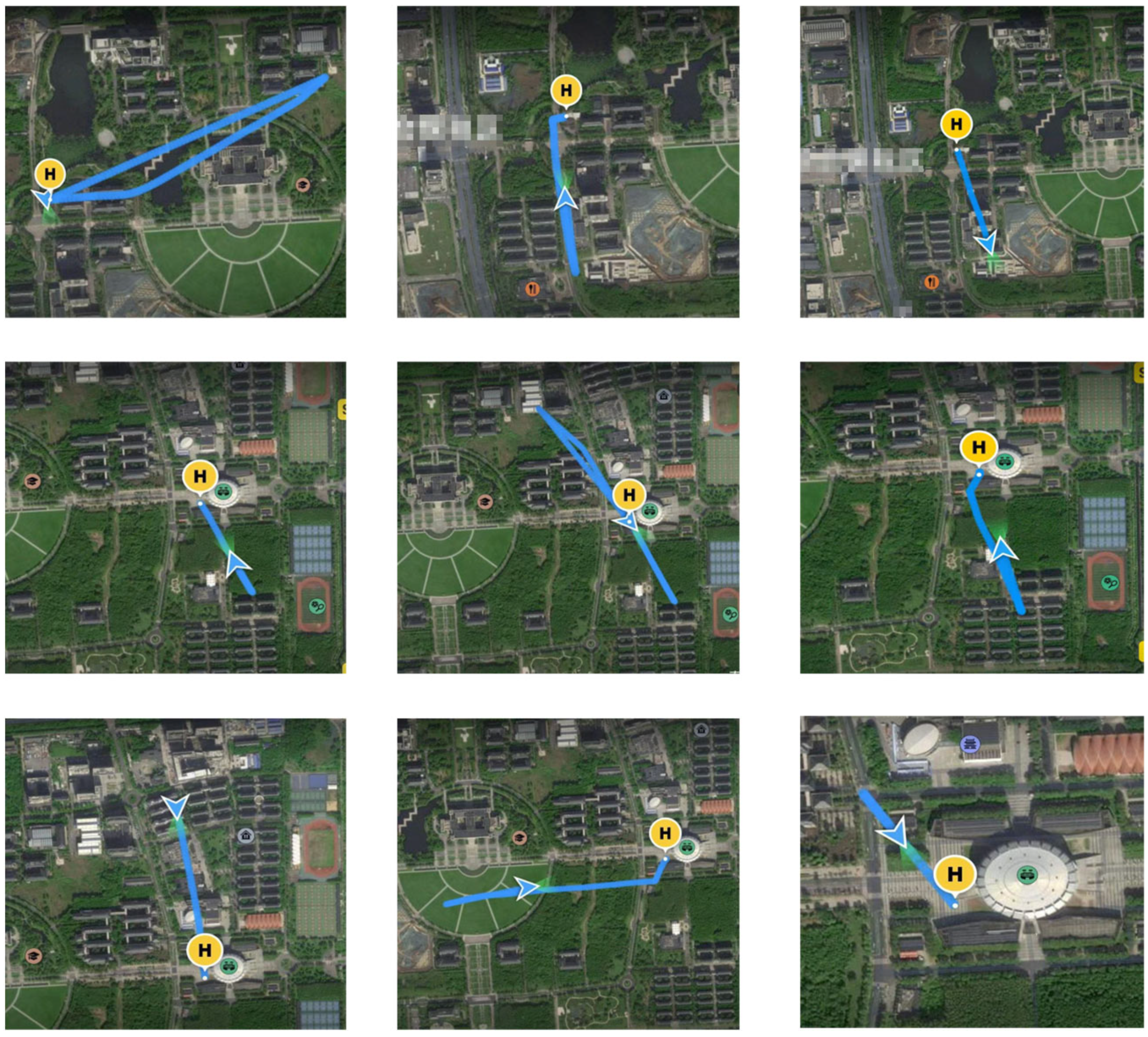
5.4. Route Flight Test
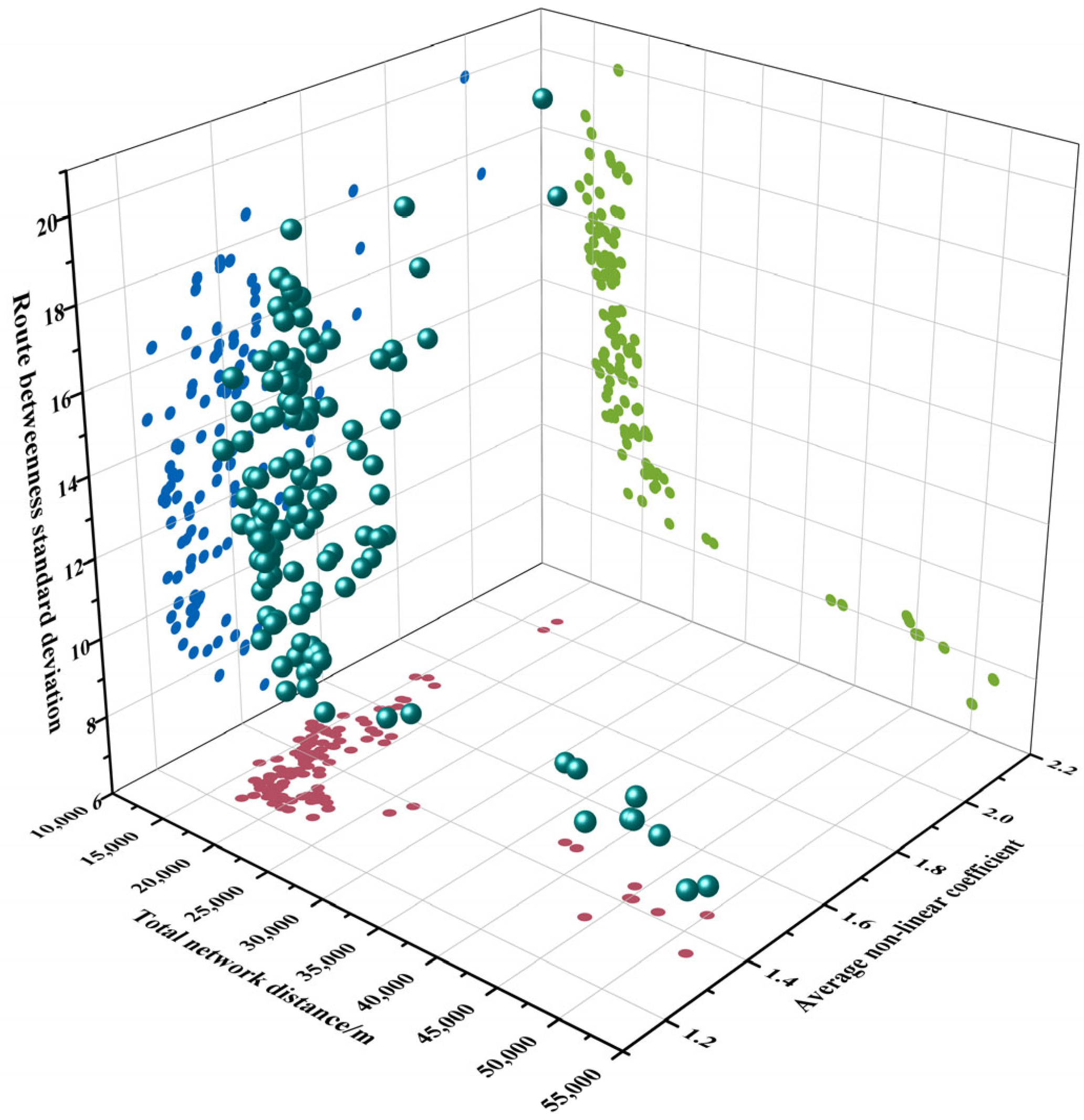
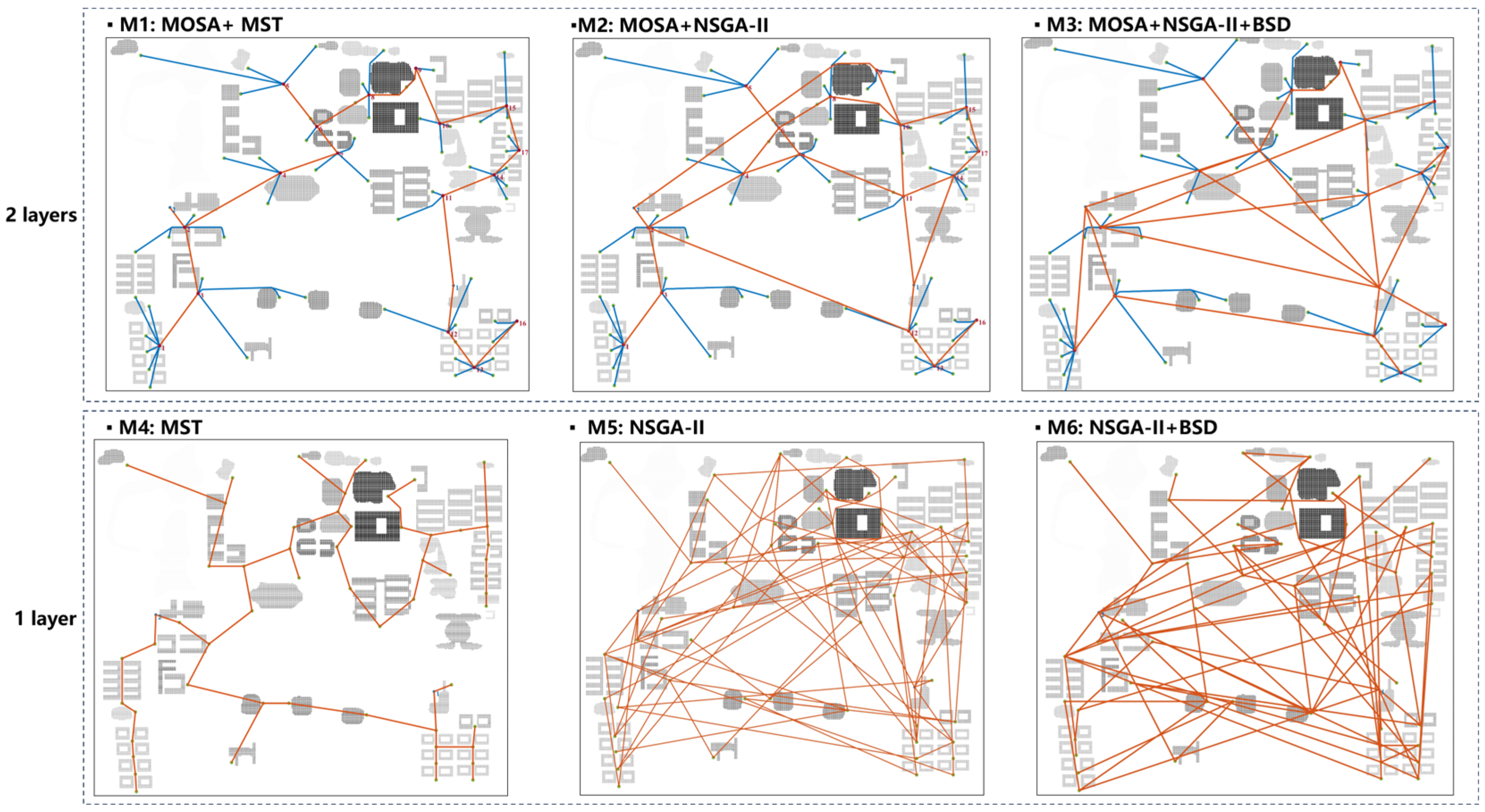
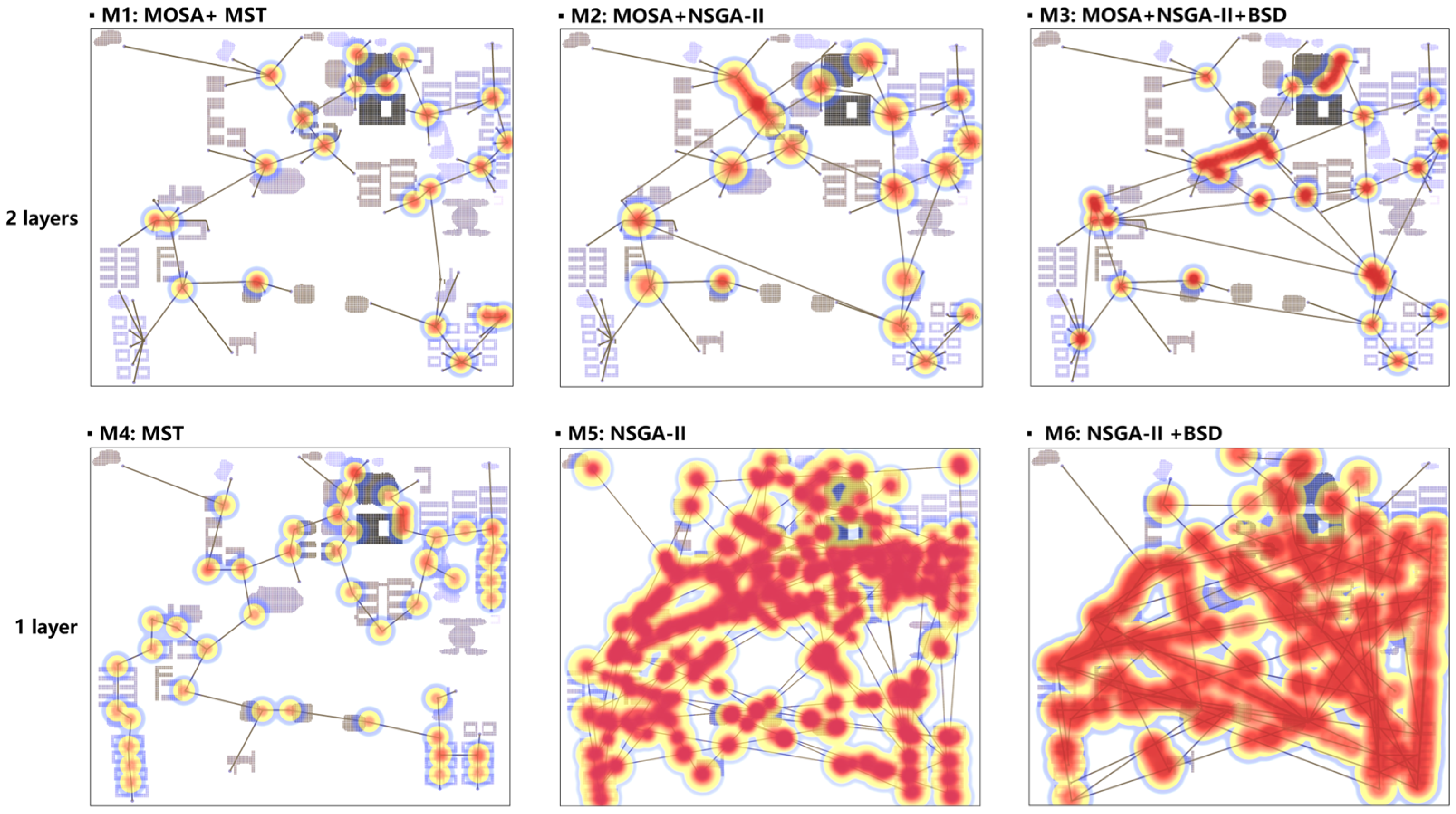
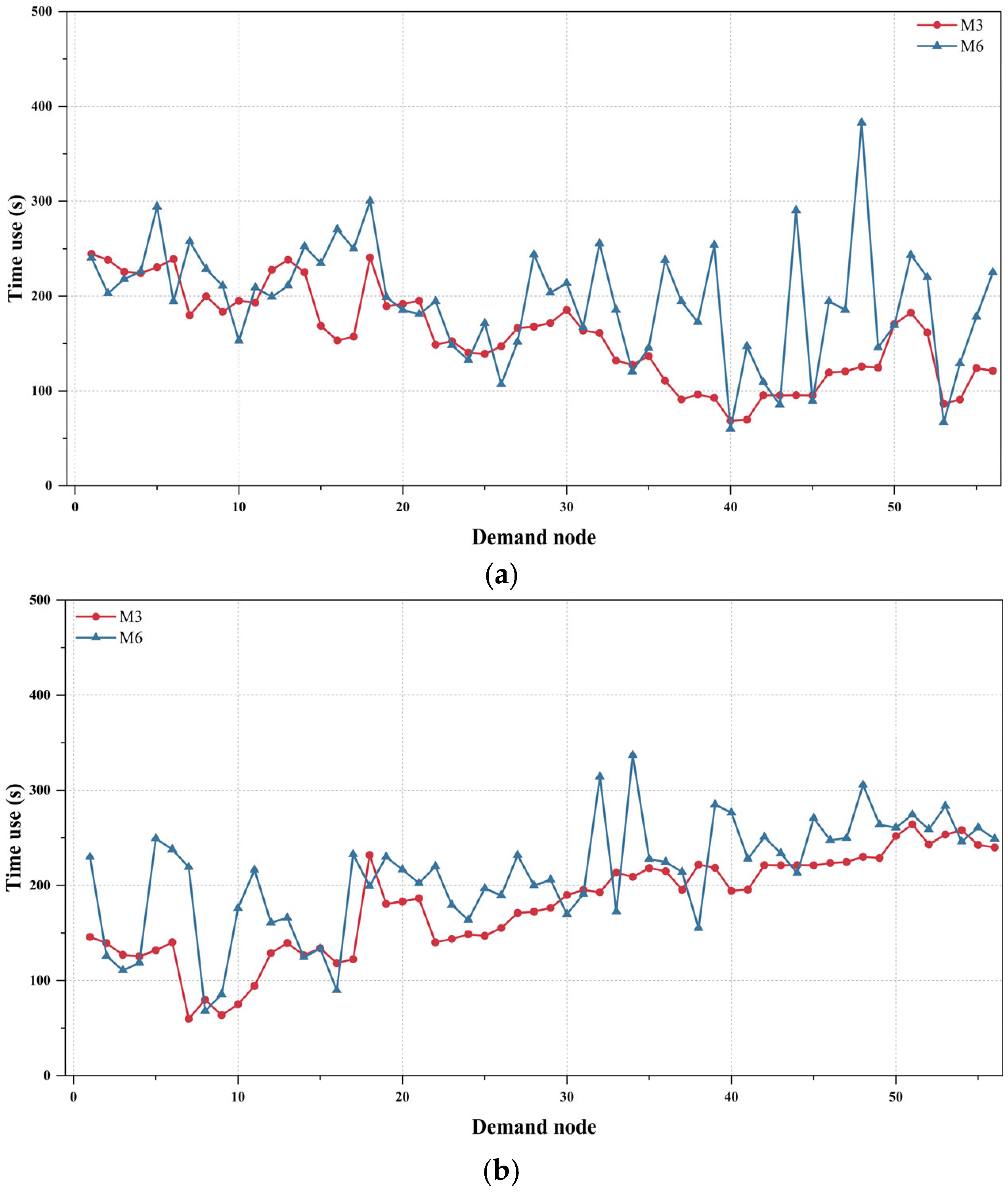
5.5. Comparison Tests
- (1)
- Route network structure.
- (2)
- Route selection method and flight performance.
- (3)
- Route betweenness standard deviation effectiveness.
- (4)
- Sensitivity analysis.
5.5.1. Analysis of Route Network Structure
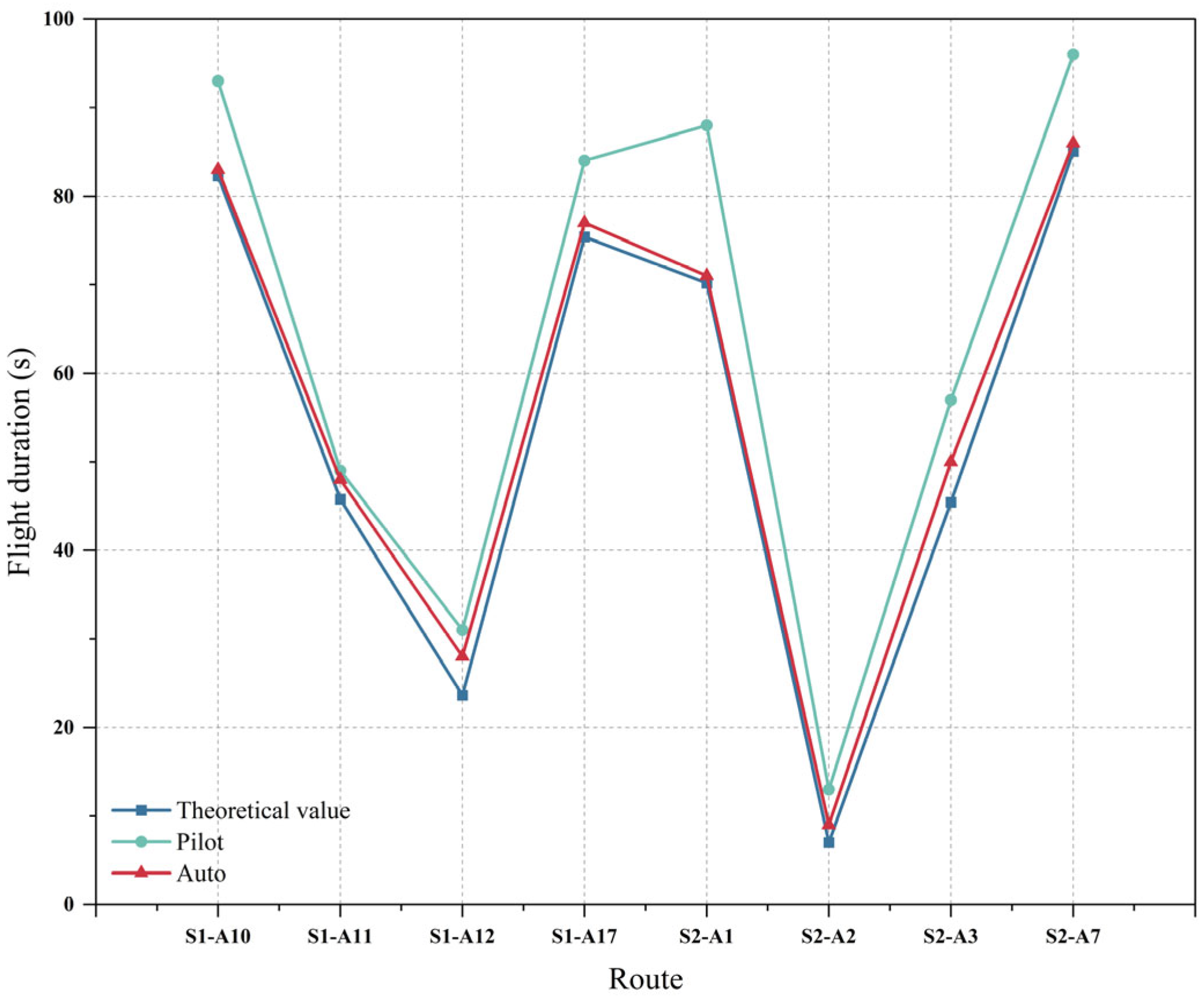
5.5.2. Analysis of Route Selection Method and Flight Performance
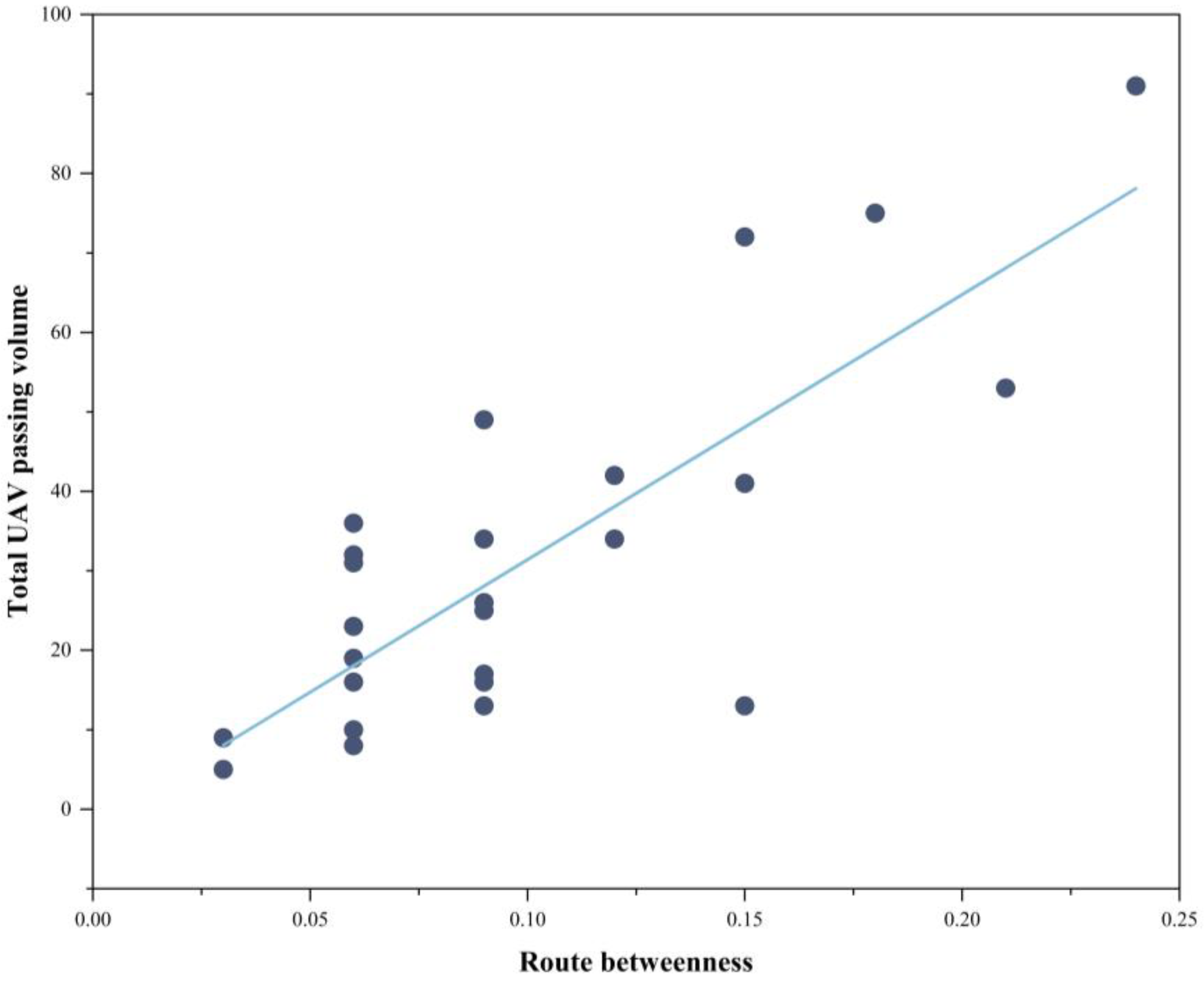
5.5.3. Analysis of Route BSD Effectiveness
5.5.4. Analysis of Sensitivity Effectiveness
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Zou, Y.; Zhang, Q.; Liu, H. Future urban air mobility management: Review. Acta Aeronauti. Astronaut. Sin. 2021, 42, 82–106. [Google Scholar]
- Chung, S.H. Applications of smart technologies in logistics and transport: A review. Transp. Res. Part E Logist. Transp. Rev. 2021, 153, 102455. [Google Scholar] [CrossRef]
- NASA. Urban Air Mobility (UAM) Market Study. 2018. Available online: https://ntrs.nasa.gov/api/citations/20190001472/downloads/20190001472.pdf (accessed on 10 September 2024).
- Liao, X.; Qu, W.; Xu, C.; He, H.; Wang, J.; Shi, W. A review of urban air mobility and its new infrastructure low-altitude public routes. Acta Aeronauti. Astronaut. Sin. 2023, 44, 6–34. [Google Scholar]
- Li, C.; Qu, W.; Li, Y.; Huang, L.; Wei, P. Overview of traffic management of urban air mobility (UAM) with eVTOL aircraft. J. Traffic Transp. Eng. 2020, 20, 35–54. [Google Scholar]
- Gharibi, M.; Boutaba, R.; Waslander, S.L. Internet of drones. IEEE Access 2016, 4, 1148–1162. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, H.; Lyons, E.; Solak, S.; Zink, M. Towards sustainable UAV operations: Balancing economic optimization with environmental and social considerations in path planning. Transp. Res. Part E Logist. Transp. Rev. 2024, 181, 103314. [Google Scholar] [CrossRef]
- Gugan, G.; Haque, A. Path planning for autonomous drones: Challenges and future directions. Drones 2023, 7, 169. [Google Scholar] [CrossRef]
- ICAO. Innovation Driving Sustainable Aviation. 2021. Available online: https://chinaerospace.oss-cn-beijing.aliyuncs.com/uploads/2021/11/26/x13XY_Innovation%20Driving%20Sustainable%20Aviation%20-%20November%202021.pdf (accessed on 20 October 2024).
- Holden, J.; Goel, N. Fast-Forwarding to a Future of on Demand Urban Air Transportation; Uber Elevate: San Francisco, CA, USA, 2016. [Google Scholar]
- Rothfeld, R.; Balac, M.; Ploetner, K.O.; Antoniou, C. Agent-based simulation of urban air mobility. In Proceedings of the Modeling and Simulation Technologies Conference, Kissimmee, FL, USA, 8–12 January 2018; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Darshan, C.; Avinash, U.; Miguel, F. Maximum coverage capacitated facility location problem with range constrained drones. Transp. Res. Part C Emerg. Technol. 2019, 99, 1–18. [Google Scholar]
- Vascik, P.D.; Hansman, R.J. Development of vertiport capacity envelopes and analysis of their sensitivity to topological and operational factors. In Proceedings of the AIAA SciTech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; AIAA: Reston, VA, USA, 2019. [Google Scholar]
- Fu, M.; Rothfeld, R.; Antoniou, C. Exploring preferences for transportation modes in an urban air mobility environment: Munich case study. Transp. Res. Rec. 2019, 2673, 427–442. [Google Scholar] [CrossRef]
- Qian, X. Research on Optimization Model of Coordinated Location and Layout of Urban Logistics UAV Landing and Landing Sites. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2021. [Google Scholar]
- Zhang, H.; Feng, D.; Zhang, X.; Liu, H.; Zhong, G.; Zhang, L. Urban logistics unmanned aerial vehicle vertiports layout planning. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 207–214. [Google Scholar]
- Fadhil, D.N. A GIS-Based Analysis for Selecting Ground Infrastructure Locations for Urban Air Mobility. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2018. [Google Scholar]
- Salama, M.R.; Srinivas, S. Collaborative truck multi-drone routing and scheduling problem: Package delivery with flexible launch and recovery sites. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102788. [Google Scholar] [CrossRef]
- Gao, J.; Zhen, L.; Laporte, G.; He, X. Scheduling trucks and drones for cooperative deliveries. Transp. Res. Part E Logist. Transp. Rev. 2023, 178, 103267. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, H. Research on truck and drone joint distribution scheduling based on cluster. Comput. Eng. Appl. 2022, 58, 287–294. [Google Scholar]
- Kuo, R.J.; Lu, S.H.; Lai, P.Y.; Mara, S.T.W. Vehicle routing problem with drones considering time windows. Expert Syst. Appl. 2022, 191, 116264. [Google Scholar] [CrossRef]
- Zhou, Y.; Su, Y.; Xie, A.; Kong, L. A newly bio-inspired path planning algorithm for autonomous obstacle avoidance of UAV. Chin. J. Aeronaut. 2021, 34, 199–209. [Google Scholar] [CrossRef]
- Niu, Y.; Yan, X.; Wang, Y.; Niu, Y. 3D real-time dynamic path planning for UAV based on improved interfered fluid dynamical system and artificial neural network. Adv. Eng. Inform. 2024, 59, 102306. [Google Scholar] [CrossRef]
- Hu, X.; Wu, Y. Risk-based discrete multi-path planning method for UAVs in urban environments. Chin. J. Aeronaut. 2021, 42, 463–474. [Google Scholar]
- Rojas Viloria, D.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned aerial vehicles/drones in vehicle routing problems: A literature review. Int. Trans. Oper. Res. 2021, 28, 1626–1657. [Google Scholar] [CrossRef]
- Zhao, Q.; Lu, F.; Wang, L.; Wang, S. Research on drones and riders joint take-out delivery routing problem. Comput. Eng. Appl. 2022, 58, 269–278. [Google Scholar]
- Lu, F.; Jiang, R.; Bi, H.; Gao, Z. Order distribution and routing optimization for takeout delivery under drone-rider joint delivery mode. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 774–796. [Google Scholar] [CrossRef]
- Shao, Q.; Li, J.; Li, R.; Zhang, J.; Gao, X. Study of urban logistics drone path planning model incorporating service benefit and risk cost. Drones 2022, 6, 418. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Lavalle, S.M.; Kuffner, J.J. Rapidly-exploring random trees: Progress and prospects. Algorithm. Comput. Robot. New Dir. 2001, 5, 293–308. [Google Scholar]
- Li, J.; Liu, H.; Lai, K.K.; Ram, B. Vehicle and UAV collaborative delivery path optimization model. Mathematics 2022, 10, 3744. [Google Scholar] [CrossRef]
- Shen, L.; Hou, Y.; Yang, Q.; Lv, M.; Dong, J.; Yang, Z.; Li, D. Synergistic path planning for ship-deployed multiple UAVs to monitor vessel pollution in ports. Transp. Res. Part D Transp. Environ. 2022, 110, 103415. [Google Scholar] [CrossRef]
- Gong, Y. Research on Air Route Network Planning Technology. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. [Google Scholar]
- Mohammed Salleh, M.F.B.; Chi, W.; Wang, Z.; Huang, S.; Tan, D.; Huang, T. Preliminary concept of adaptive urban airspace management for unmanned aircraft operations. In Proceedings of the 2018 AIAA SciTech Forum, Kissimmee, FL, USA, 8–12 January 2018; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Xu, C.; Liao, X.; Yue, H.; Lu, M.; Chen, X. Construction of a UAV low-altitude public air route based on an improved ant colony algorithm. J. Geo-Inf. Sci. 2019, 21, 570–579. [Google Scholar]
- Cohen, A.P.; Shaheen, S.A.; Farrar, E.M. Urban air mobility: History, ecosystem, market potential, and challenges. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6074–6087. [Google Scholar] [CrossRef]
- Xu, C.; Liao, X.; Ye, H.; Yue, H. Iterative construction of low-altitude UAV air route network in urban areas: Case planning and assessment. J. Geogr. Sci. 2020, 30, 1534–1552. [Google Scholar] [CrossRef]
- Hu, X.; Yang, C.; Zhou, J. Route network modeling for unmanned aerial vehicle in complex urban environment. J. Transp. Syst. Eng. Inf. Technol. 2023, 23, 251–261. [Google Scholar]
- He, X.; He, F.; Li, L.; Zhang, L.; Xiao, G. A route network planning method for urban air delivery. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102872. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Yi, J.; Liu, H. A bi-level planning approach of logistics unmanned aerial vehicle route network. Aerosp. Sci. Technol. 2023, 141, 108572. [Google Scholar] [CrossRef]
- D’Urso, F.; Santoro, C.; Santoro, F.F. Integrating Heterogeneous Tools for Physical Simulation of Multi-Unmanned Aerial Vehicles; WOA: Genova, Italy, 2018. [Google Scholar]
- Li, S.; Zhang, H.; Liu, H. Route planning for logistics unmanned aerial vehicle based on improved cellular automata algorithm. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2023, 51, 14–19. [Google Scholar]
- Li, S.; Zhang, H.; Li, Z.; Liu, H. An air route network planning model of logistics UAV terminal distribution in urban low altitude airspace. Sustainability 2021, 13, 13079. [Google Scholar] [CrossRef]










| Demand Node | Distribution Demand (kg) | Demand Node | Distribution Demand (kg) | ||
|---|---|---|---|---|---|
| Supply Node 1 | Supply Node 2 | Supply Node 1 | Supply Node 2 | ||
| 1 | 60 | 80 | 29 | 120 | 120 |
| 2 | 80 | 80 | 30 | 120 | 80 |
| 3 | 40 | 60 | 31 | 120 | 100 |
| 4 | 100 | 60 | 32 | 80 | 60 |
| 5 | 100 | 60 | 33 | 120 | 80 |
| 6 | 120 | 100 | 34 | 180 | 140 |
| 7 | 100 | 100 | 35 | 80 | 40 |
| 8 | 120 | 80 | 36 | 100 | 60 |
| 9 | 60 | 60 | 37 | 80 | 40 |
| 10 | 80 | 80 | 38 | 80 | 80 |
| 11 | 60 | 40 | 39 | 60 | 80 |
| 12 | 40 | 40 | 40 | 60 | 80 |
| 13 | 80 | 60 | 41 | 80 | 80 |
| 14 | 40 | 40 | 42 | 60 | 40 |
| 15 | 60 | 40 | 43 | 100 | 80 |
| 16 | 60 | 40 | 44 | 40 | 60 |
| 17 | 80 | 60 | 45 | 80 | 40 |
| 18 | 100 | 120 | 46 | 60 | 40 |
| 19 | 60 | 40 | 47 | 40 | 60 |
| 20 | 120 | 80 | 48 | 140 | 80 |
| 21 | 80 | 40 | 49 | 100 | 60 |
| 22 | 100 | 60 | 50 | 60 | 60 |
| 23 | 100 | 80 | 51 | 80 | 40 |
| 24 | 120 | 120 | 52 | 80 | 80 |
| 25 | 120 | 120 | 53 | 100 | 40 |
| 26 | 100 | 80 | 54 | 100 | 80 |
| 27 | 120 | 120 | 55 | 120 | 40 |
| 28 | 100 | 100 | 56 | 100 | 60 |
| Variable | Value |
|---|---|
| 1000 kg, 20 kg | |
| 5 times | |
| 200 m, 3000 m, 200 m, 90 m | |
| 10 m/s, 3 m/s |
| Transshipment Node | Service Demand Node | Delivery Cargo Volume (kg) | |
|---|---|---|---|
| From Supply Node 1 | From Supply Node 2 | ||
| A1 | B35, B36, B37, B38, B39, B40 | 460 | 380 |
| A2 | B6, B34, B42, B43 | 460 | 360 |
| A3 | B41, B44, B45, 46 | 260 | 220 |
| A4 | B4, B5, B8 | 320 | 200 |
| A5 | B1, B2, B3, B9 | 240 | 280 |
| A6 | B10, B11 | 140 | 120 |
| A7 | B7, B15, B19 | 220 | 180 |
| A8 | B12, B13, B14, B16 | 220 | 180 |
| A9 | B17, B21 | 160 | 100 |
| A10 | B18, B23, B33 | 320 | 280 |
| A11 | B20, B22 | 220 | 140 |
| A12 | B47, B48, B50, B51 | 320 | 240 |
| A13 | B52, B53, B55, B56 | 400 | 220 |
| A14 | B29, B30, B31, B32 | 440 | 360 |
| A15 | B24, B25, B27 | 360 | 360 |
| A16 | B49, B54 | 200 | 140 |
| A17 | B26, B28 | 200 | 180 |
| Supply | Transshipment | Route | Distance (m) | Supply | Transshipment | Route | Distance (m) |
|---|---|---|---|---|---|---|---|
| S1 | A1 | S1, A12, A3, A1 | 1775.25 | S2 | A1 | S2, A1 | 701.78 |
| S1 | A2 | S1, A2 | 1323.3 | S2 | A2 | S2, A2 | 122.07 |
| S1 | A3 | S1, A12, A3 | 1452.07 | S2 | A3 | S2, A3 | 455.47 |
| S1 | A4 | S1, A4 | 1006.88 | S2 | A4 | S2, A7, A4 | 1143.29 |
| S1 | A5 | S1, A7, A5 | 1306.02 | S2 | A5 | S2, A7, A5 | 1286.68 |
| S1 | A6 | S1, A7, A6 | 1038.02 | S2 | A6 | S2, A7, A6 | 1018.68 |
| S1 | A7 | S1, A7 | 870.01 | S2 | A7 | S2, A7 | 850.68 |
| S1 | A8 | S1, A7, A8 | 1200.96 | S2 | A8 | S2, A7, A8 | 1181.62 |
| S1 | A9 | S1, A11, A10, A9 | 1125.74 | S2 | A9 | S2, A7, A8, A9 | 1491.52 |
| S1 | A10 | AS1, A11, A10 | 823.05 | S2 | A10 | S2, A2, A10 | 1455.85 |
| S1 | A11 | S1, A11 | 457.74 | S2 | A11 | S2, A2, A11 | 1372.35 |
| S1 | A12 | S1, A12 | 236.33 | S2 | A12 | S2, A3, A12 | 1671.21 |
| S1 | A13 | S1, A12, A13 | 455.47 | S2 | A13 | S2, A3, A12, A13 | 1890.35 |
| S1 | A14 | S1, A11, A14 | 724.29 | S2 | A14 | S2, A2, A11, A14 | 1638.9 |
| S1 | A15 | S1, A11, A10, A15 | 1155.46 | S2 | A15 | S2, A2, A10, A15 | 1788.26 |
| S1 | A16 | S1, A16 | 354.15 | S2 | A16 | S2, A2, A18, A16 | 1799.52 |
| S1 | A17 | S1, A17 | 753.96 | S2 | A17 | S2, A2, A11, A14, A17 | 1812.17 |
| Item | Method | ||||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | ||
| Variable control | Layers | 2 | 2 | 2 | 1 | 1 | 1 |
| Method | MST | NSGA-II | NSGA-II | MST | NSGA-II | NSGA-II | |
| BSD | - | NO | YES | - | NO | YES | |
| Network structure | Size of route dataset | 227 * | 227 * | 227 * | 1653 | 1653 | 1653 |
| Total distance (m) | 22,026 | 21,527 * | 25,525 | 23,650 | 67,355 | 68,150 | |
| Transshipment (m) | 10,384 | 9884.4 * | 14,452 | 20,170 | 63,875 | 64,670 | |
| Delivery (m) | 9332 | 9332 | 9332 | - | - | - | |
| Take-off/landing (m) | 2310 * | 2310 * | 2310 * | 3480 | 3480 | 3480 | |
| Route BSD | 0.201 | 0.172 | 0.051 * | 0.365 | 0.075 | 0.054 | |
| Non-linear coefficient | 1.88 | 1.47 | 1.34 * | 2.88 | 1.78 | 1.59 | |
| Intersection number | 0 * | 1 | 4 | 0 * | 142 | 128 | |
| Logistics efficiency | Average flight duration (s) | 250.38 | 175.23 | 167.71 * | 281.96 | 199.81 | 220.09 |
| From supply node 1 (s) | 259.3 | 172.03 | 157.51 * | 329.43 | 195.28 | 212.01 | |
| From supply node 2 (s) | 241.47 | 178.43 | 177.91 * | 190.92 | 205.25 | 228.16 | |
| UAV operation | Total task flight distance (m) | 839,390 | 519,500 | 483,170 * | 955,220 | 709,560 | 737,700 |
| Total UAV passing volume | 1581 | 1110 | 800 * | 2034 | 1213 | 1101 | |
| Average route passing volume | 21.36 | 13.87 | 9.75 * | 18.01 | 28.20 | 24.3 | |
| Standard deviation of passing volume | 55.23 | 42.67 | 22.3 | 92.62 | 25.21 | 19.18 * | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, S.; Lu, J.; Wang, S. Air Route Network Planning Method of Urban Low-Altitude Logistics UAV with Double-Layer Structure. Drones 2025, 9, 193. https://doi.org/10.3390/drones9030193
Li Z, Li S, Lu J, Wang S. Air Route Network Planning Method of Urban Low-Altitude Logistics UAV with Double-Layer Structure. Drones. 2025; 9(3):193. https://doi.org/10.3390/drones9030193
Chicago/Turabian StyleLi, Zhuolun, Shan Li, Jian Lu, and Sixi Wang. 2025. "Air Route Network Planning Method of Urban Low-Altitude Logistics UAV with Double-Layer Structure" Drones 9, no. 3: 193. https://doi.org/10.3390/drones9030193
APA StyleLi, Z., Li, S., Lu, J., & Wang, S. (2025). Air Route Network Planning Method of Urban Low-Altitude Logistics UAV with Double-Layer Structure. Drones, 9(3), 193. https://doi.org/10.3390/drones9030193






