Secure Transmission for RIS-Assisted Downlink Hybrid FSO/RF SAGIN: Sum Secrecy Rate Maximization
Abstract
1. Introduction
1.1. Background
1.2. Related Works
1.3. Motivations and Contributions
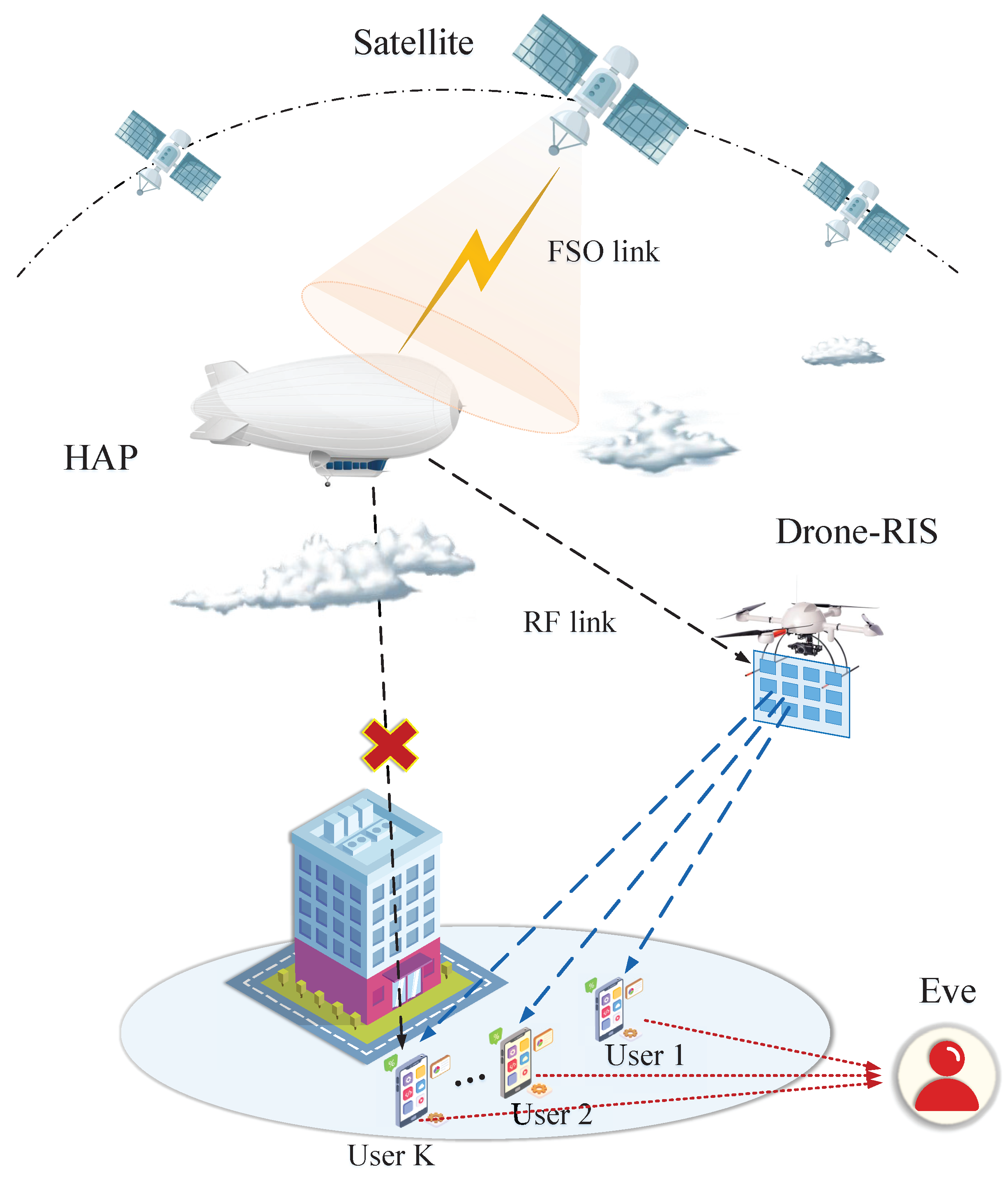
- We propose a novel architecture of RIS-assisted hybrid FSO/RF downlink SAGIN, in which drones dynamically adjust the RIS deployment positions to overcome communication issues caused by RF link blockages due to clouds or buildings. To accurately model the FSO and RF links under various weather conditions, the Málaga fading and the Nakagami-m model are employed. In addition, we adopt the RSMA strategy to achieve flexible access, thereby providing high-quality communication services for multiple users.
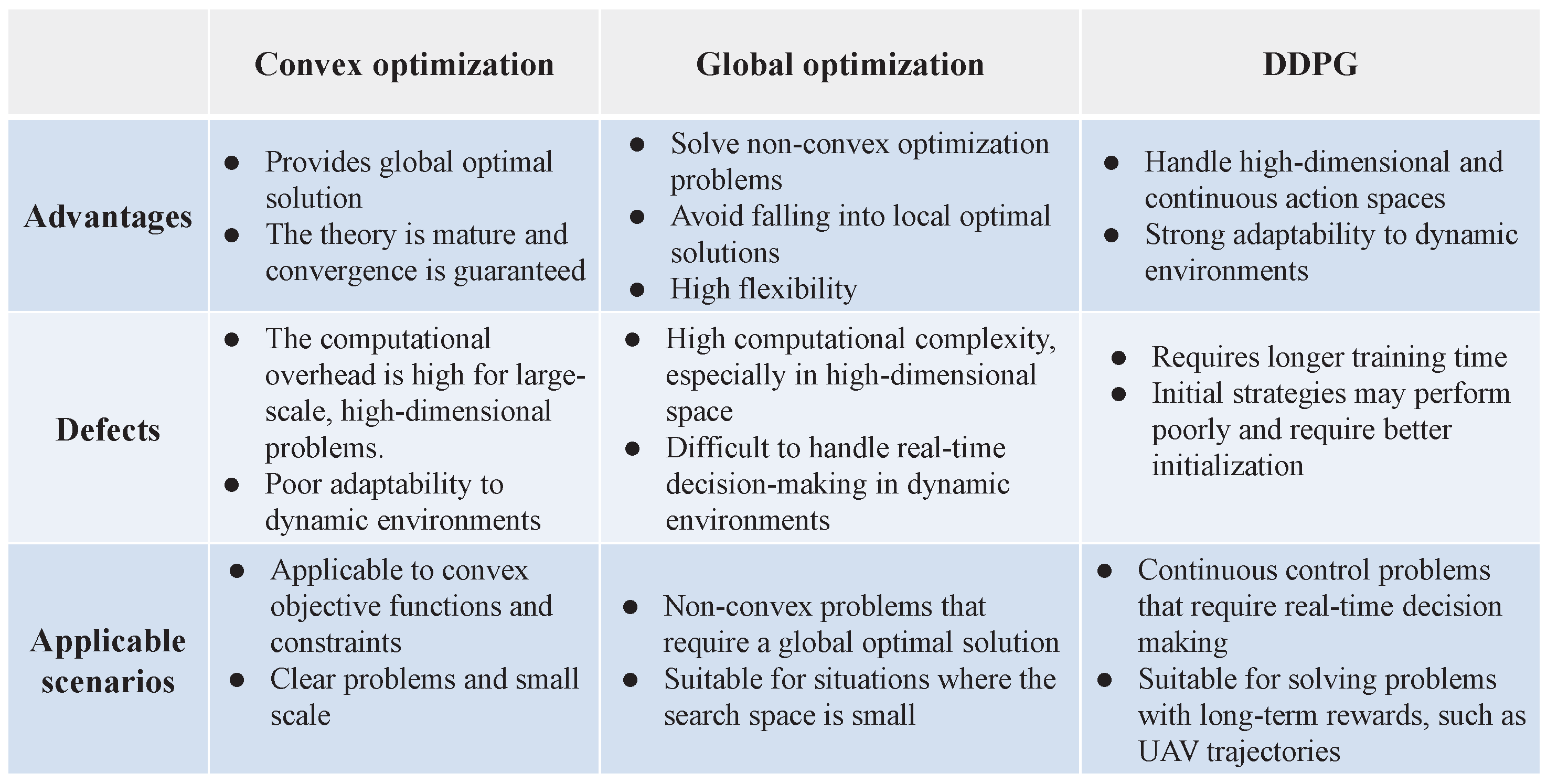
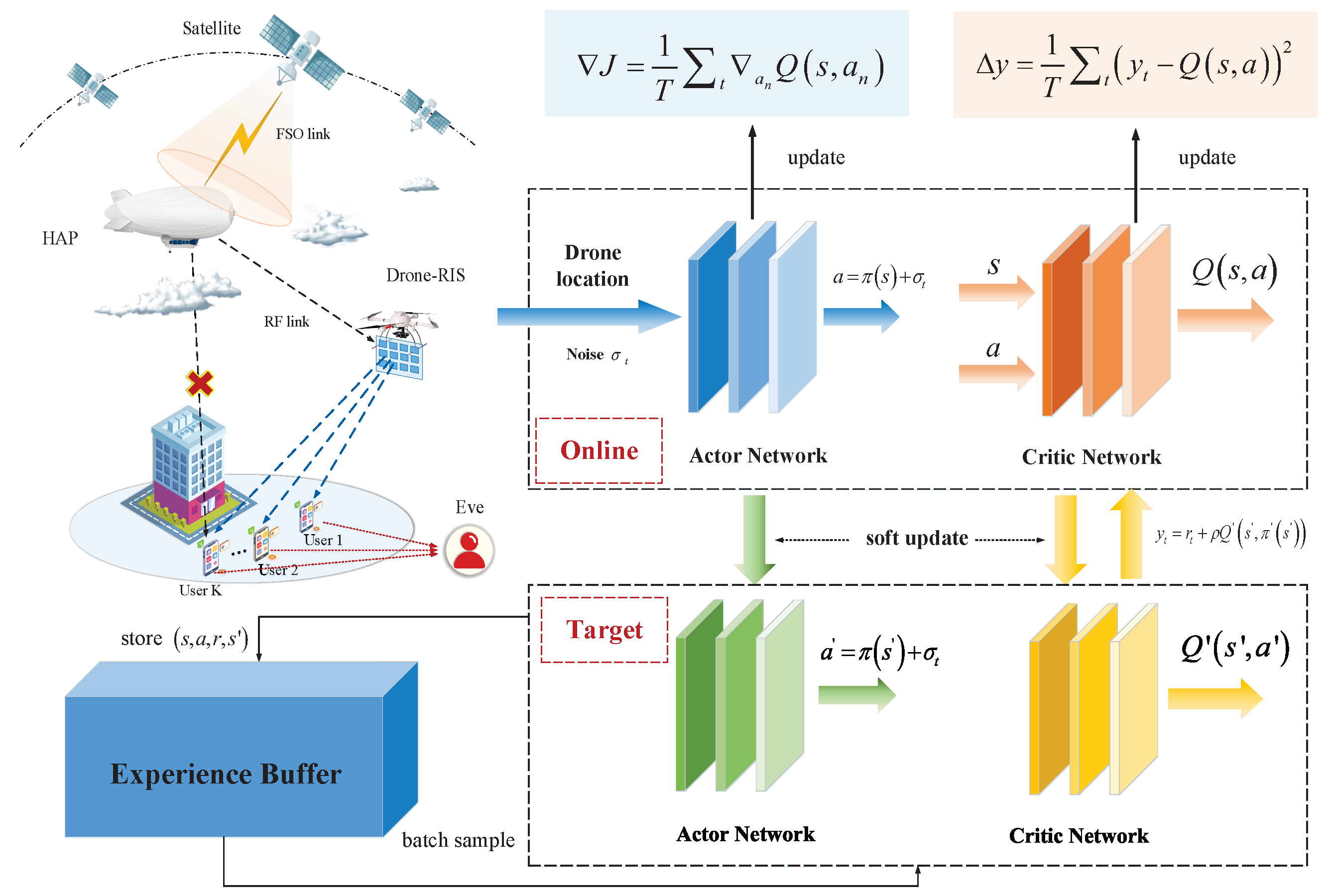
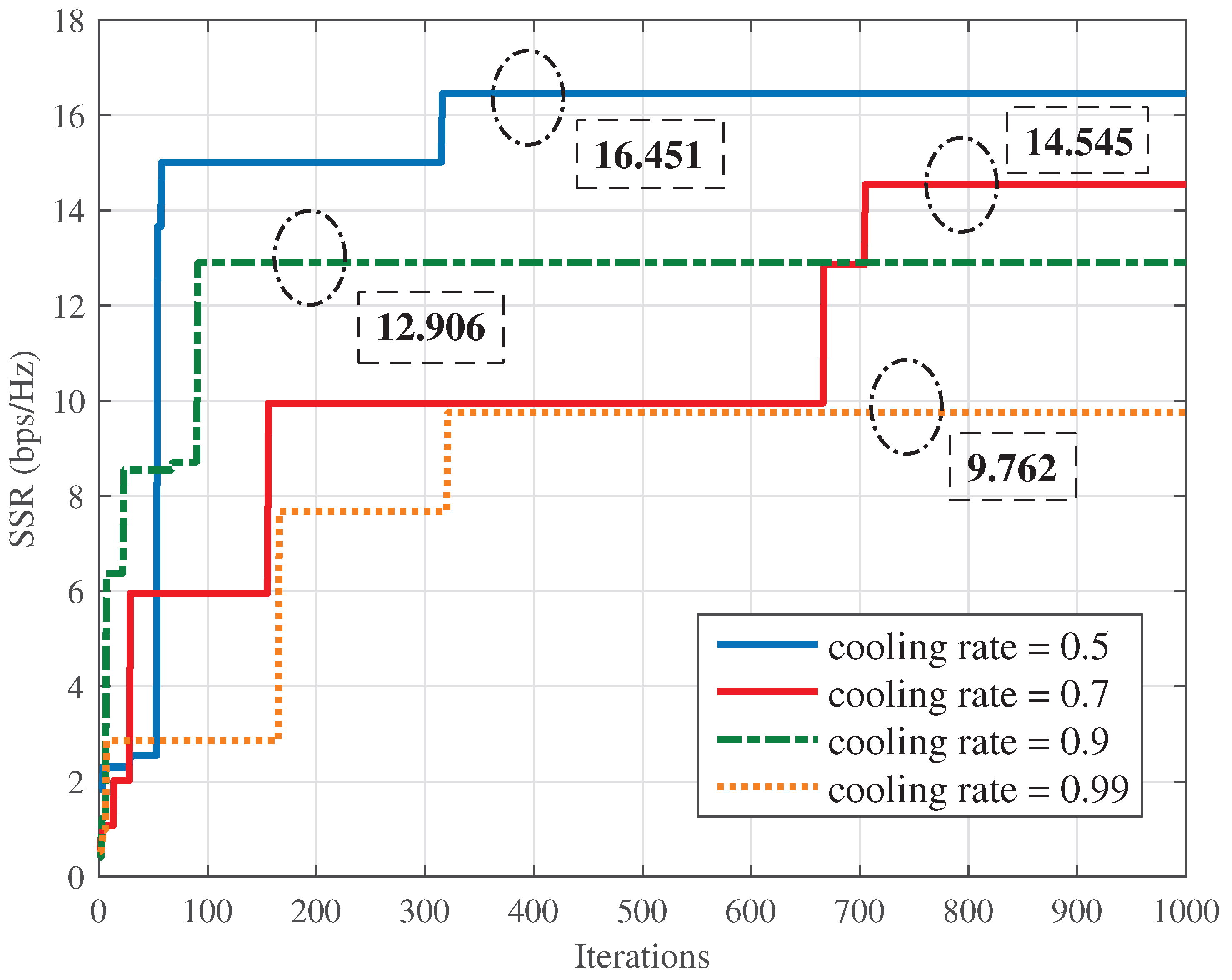
- For the SSR maximization problem, we solve it by optimizing the power allocation coefficient, RIS phase shifts, and drone trajectory. Specifically, we employ the simulated annealing (SA) algorithm to optimize power allocation and combine semi-definite programming (SDP) and penalty algorithms to obtain the optimal RIS phase shifts. Then, the designed DDPG algorithm interacts with the dynamic environment to optimize the drone’s flight trajectory. Finally, an alternating iterative framework is proposed to achieve joint optimization.
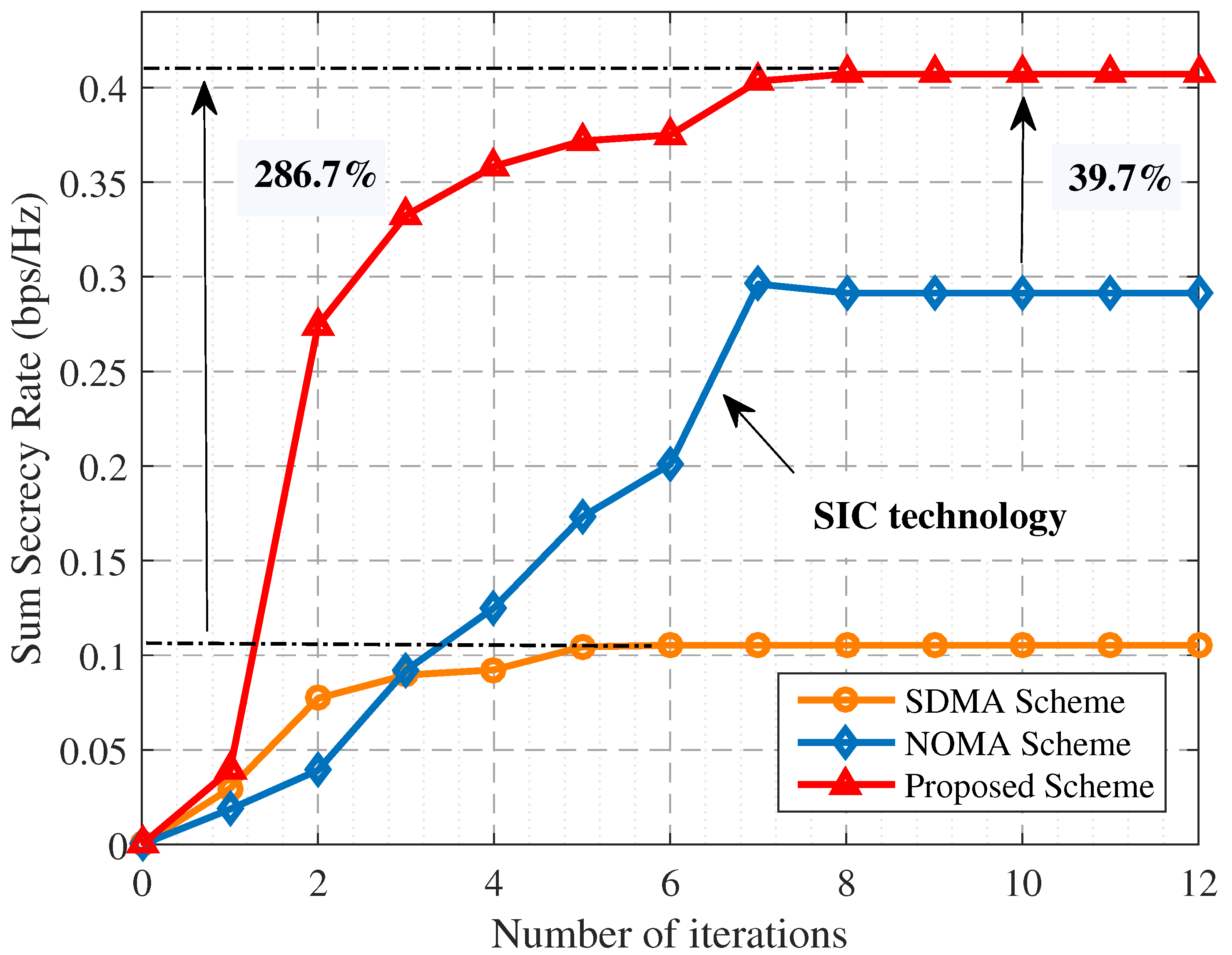
- Finally, extensive simulations are conducted to validate the superiority of the proposed scheme. The simulation results demonstrate that the proposed scheme effectively improves the SAGIN’s security performance. Compared with the NOMA and SDMA schemes, the SSR of the proposed scheme increases by 39.7% and 286.7%, respectively.
2. System Model and Problem Formulation
2.1. FSO Model
2.2. RF Model
2.3. Communication Model and Problem Formulation
3. Sum Secrecy Rate Maximization Scheme
3.1. Power Allocation
- Case 1: The public information rate of user k is less than the specified threshold, and the rate at which all users receive private information is greater than the eavesdropping rate. The objective function is set aswhere , is the penalty weight. is the balance penalty, where A is the balance error weight and is the variance of the power allocation coefficient.
- Case 2: The rate at which user k receives private information is less than the eavesdropping rate, and the public information rate of all users is greater than the specified threshold. The objective function iswhere .
- Case 3: The rate at which user k receives private information is less than the eavesdropping rate, and the rate at which user k receives public information is greater than the specified threshold. The objective function iswhere .
- Case 4: The rate at which all users receive private information is greater than the eavesdropping rate, and the rate of public information exceeds the specified threshold. The objective function is defined as
| Algorithm 1 Power allocation based on SA algorithm |
|
3.2. RIS Phase Shift Optimization
| Algorithm 2 Overall algorithm framework |
|
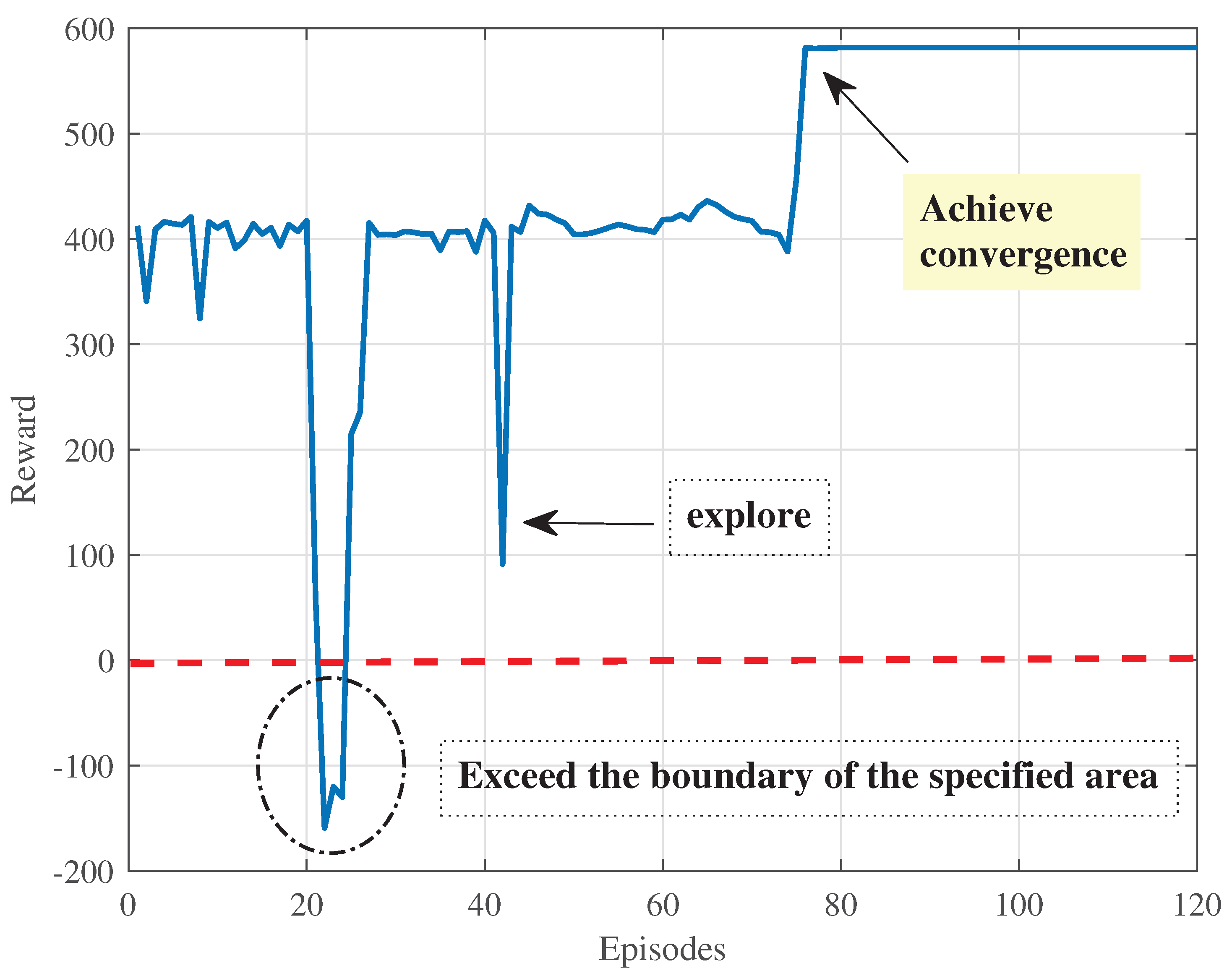
3.3. Trajectory Optimization
3.4. Overall Algorithm
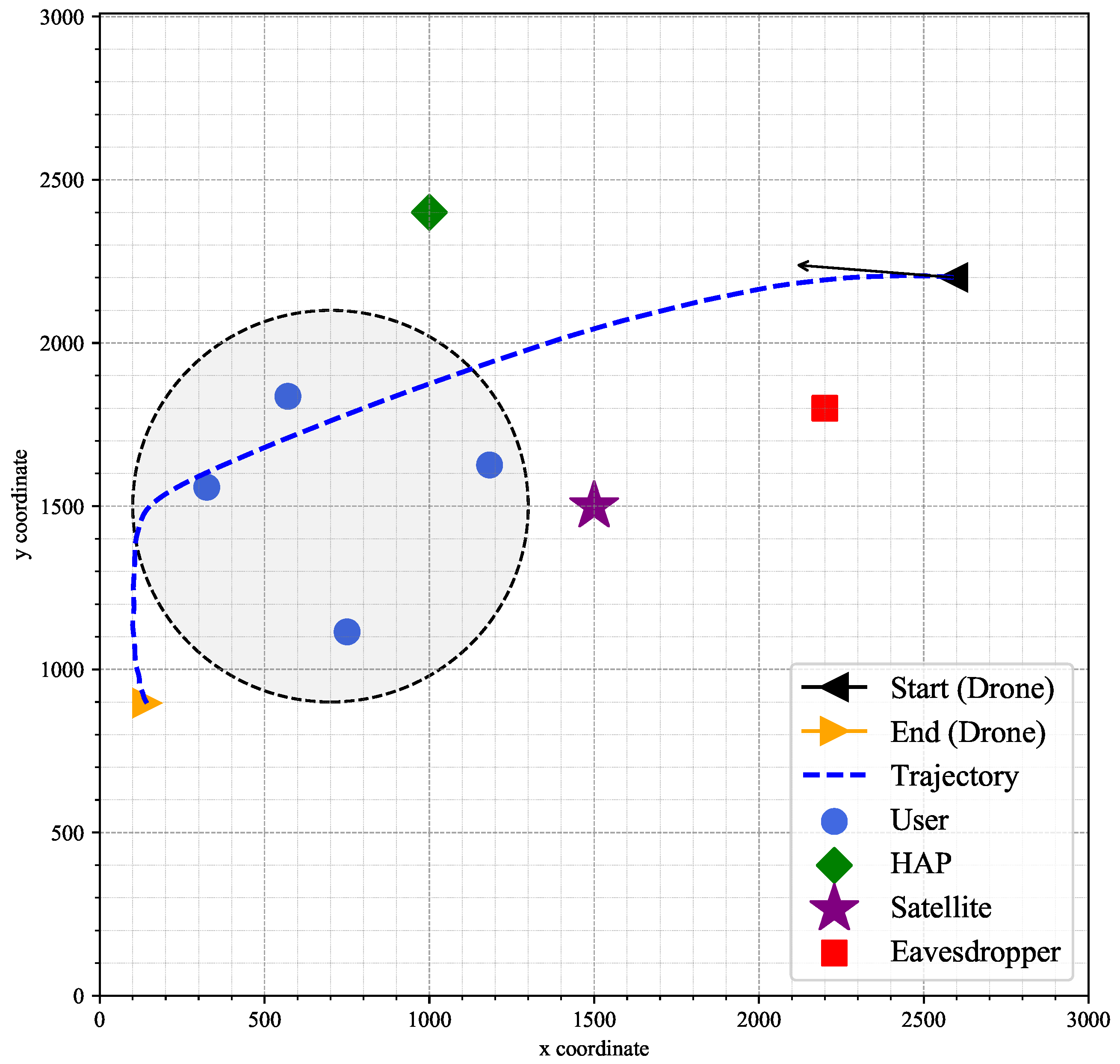
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mao, W.; Lu, Y.; Pan, G.; Ai, B. UAV-Assisted Communications in SAGIN-ISAC: Mobile User Tracking and Robust Beamforming. IEEE J. Sel. Areas Commun. 2025, 43, 186–200. [Google Scholar] [CrossRef]
- Cao, X.; Yang, B.; Yuen, C.; Han, Z. HAP-Reserved Communications in Space-Air-Ground Integrated Networks. IEEE Trans. Veh. Technol. 2021, 70, 8286–8291. [Google Scholar] [CrossRef]
- Kawamoto, Y.; Matsushita, A.; Verma, S.; Kato, N.; Kaneko, K.; Sata, A.; Hangai, M. HAPS-Based Interference Suppression Through Null Broadening with Directivity Control in Space-Air-Ground Integrated Networks. IEEE Trans. Veh. Technol. 2023, 72, 16098–16107. [Google Scholar] [CrossRef]
- Qu, L.; Xu, G.; Zeng, Z.; Zhang, N.; Zhang, Q. UAV-Assisted RF/FSO Relay System for Space-Air-Ground Integrated Network: A Performance Analysis. IEEE Trans. Wirel. Commun. 2022, 21, 6211–6225. [Google Scholar] [CrossRef]
- Lei, H.; Luo, H.; Park, K.H.; Ansari, I.S.; Lei, W.; Pan, G.; Alouini, M.S. On Secure Mixed RF-FSO Systems with TAS and Imperfect CSI. IEEE Trans. Commun. 2020, 68, 4461–4475. [Google Scholar] [CrossRef]
- Li, M.; Hong, Y.; Zeng, C.; Song, Y.; Zhang, X. Investigation on the UAV-To-Satellite Optical Communication Systems. IEEE J. Sel. Areas Commun. 2018, 36, 2128–2138. [Google Scholar] [CrossRef]
- Balti, E.; Guizani, M.; Hamdaoui, B.; Khalfi, B. Aggregate Hardware Impairments Over Mixed RF/FSO Relaying Systems with Outdated CSI. IEEE Trans. Commun. 2018, 66, 1110–1123. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Z.; Zhao, H.; Zhou, F.; Alfarraj, O.; Yang, W.; Mumtaz, S.; Leung, V.C.M. Secure Energy Efficiency for ARIS Networks with Deep Learning: Active Beamforming and Position Optimization. IEEE Trans. Wirel. Commun. 2025; to be published. [Google Scholar]
- Samy, R.; Yang, H.-C.; Rakia, T.; Alouini, M.-S. Hybrid SAG-FSO/SH-FSO/RF Transmission for Next-Generation Satellite Communication Systems. IEEE Trans. Veh. Technol. 2023, 72, 14255–14267. [Google Scholar] [CrossRef]
- Nguyen, K.-T.; Vu, T.-H.; Shin, H.; Kim, S. Performance Analysis of Active RIS and Passive RIS-Aided MISO Systems Over Nakagami-m Fading Channel With Imperfect CSI. IEEE Trans. Veh. Technol. 2024, 74, 4334–4348. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; Wei, Z.; Yu, K.; Min, L.; Mumtaz, S. Uplink Secrecy Performance of RIS-Based RF/FSO Three-Dimension Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2024, 23, 1798–1809. [Google Scholar] [CrossRef]
- Tang, X.; Jiang, T.; Liu, J.; Li, B.; Zhai, D.; Yu, F.R.; Han, Z. Secure Communication with UAV-Enabled Aerial RIS: Learning Trajectory with Reflection Optimization. IEEE Trans. Intell. Veh. 2023; to be published. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Wang, D.; Zhang, R.; Gu, X.; Pan, J. NOMA-enhanced cooperative relaying systems in drone-enabled IoV: Capacity analysis and height optimization. IEEE Trans. Veh. Technol. 2024, 73, 19065–19079. [Google Scholar] [CrossRef]
- Sun, Q.; Hu, Q.; Chen, X.; Yang, Y.; Dang, S.; Zhang, J. Performance Analysis of RIS-Aided FSO/RF Hybrid Satellite-Terrestrial Network with Imperfect CSI. IEEE Trans. Veh. Technol. 2024, 74, 2958–2972. [Google Scholar] [CrossRef]
- Wu, M.; Guo, K.; Li, X.; Lin, Z.; Wu, Y.; Tsiftsis, T.A.; Song, H. Deep Reinforcement Learning-Based Energy Efficiency Optimization for RIS-Aided Integrated Satellite-Aerial-Terrestrial Relay Networks. IEEE Trans. Commun. 2024, 72, 4163–4178. [Google Scholar] [CrossRef]
- Guo, K.; Wu, M.; Li, X.; Lin, Z.; Tsiftsis, T.A. Joint Trajectory and Beamforming Optimization for Federated DRL-Aided Space-Aerial-Terrestrial Relay Networks with RIS and RSMA. IEEE Trans. Wirel. Commun. 2024, 23, 18456–18471. [Google Scholar] [CrossRef]
- Huang, Q.; Lin, M.; Zhu, W.-P.; Cheng, J.; Alouini, M.-S. Uplink Massive Access in Mixed RF/FSO Satellite-Aerial-Terrestrial Networks. IEEE Trans. Commun. 2021, 69, 2413–2426. [Google Scholar] [CrossRef]
- Li, J.; Yang, L.; Wu, Q.; Lei, X.; Zhou, F.; Shu, F.; Mu, X.; Liu, Y.; Fan, P. Active RIS-Aided NOMA-Enabled Space- Air-Ground Integrated Networks with Cognitive Radio. IEEE J. Sel. Areas Commun. 2025, 43, 314–333. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.; Kuo, Y.; Zhou, Y. Artificial-Noise-Aided Optimal Beamforming in Layered Physical Layer Security. IEEE Commun. Lett. 2019, 23, 72–75. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Z.; Yu, K.; Wei, Z.; Zhao, H.; Al-Dhahir, N.; Guizani, M.; Leung, V.C. Active Aerial Reconfigurable Intelligent Surface Assisted Secure Communications: Integrating Sensing and Positioning. IEEE J. Sel. Areas Commun. 2024, 42, 2769–2785. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Wang, D.; Yang, L.; Zhang, R. Delay minimization for NOMA-MEC offloading in ABS-aided maritime communication networks. IEEE Trans. Veh. Technol. 2025; early access. [Google Scholar] [CrossRef]
- Li, X.; Lu, Z.; Yuan, M.; Liu, W.; Wang, F.; Yu, Y.; Liu, P. Tradeoff of Code Estimation Error Rate and Terminal Gain in SCER Attack. IEEE Trans. Instrum. Meas. 2024, 73, 8504512. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Cen, Q.; Wu, S. Deep learning–based resource allocation for secure transmission in a non-orthogonal multiple access network. Int. J. Distrib. Sens. Netw. 2022, 18, 15501329221104330. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Liu, L.; Han, Z.; Poor, H.V.; Di, B. Target Detection and Positioning Aided by Reconfigurable Surfaces: Reflective or Holographic? IEEE Trans. Wirel. Commun. 2024, 23, 19215–19230. [Google Scholar] [CrossRef]
- Sun, G.; Sheng, L.; Luo, L.; Yu, H. Game Theoretic Approach for Multipriority Data Transmission in 5G Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24672–24685. [Google Scholar] [CrossRef]
- Wang, D.; Li, J.; Lv, Q.; He, Y.; Li, L.; Hua, Q.; Alfarraj, O.; Zhang, J. Integrating Reconfigurable Intelligent Surface and UAV for Enhanced Secure Transmissions in IoT-Enabled RSMA Networks. IEEE Internet Things J. 2024; to be published. [Google Scholar] [CrossRef]
- Wang, D.; Yuan, L.; Zhao, H.; Min, L.; He, Y. Secure transmission of IRS-UAV buffer-aided relaying system with delay constraint. Chin. J. Aeronaut. 2024; in press. [Google Scholar] [CrossRef]
- Lin, Z.; Xiao, Y.; Lu, X.; Wu, C.; Wu, W. RSMA-Assisted Distributed Computation Offloading in Vehicular Networks based on Stochastic Geometry. IEEE Trans. Veh. Technol. 2025; to be published. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Le, H.D.; Pham, A.T. On the Design of RIS–UAV Relay-Assisted Hybrid FSO/RF Satellite–Aerial–Ground Integrated Network. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 757–771. [Google Scholar] [CrossRef]

| Satellite | HAP | UAV | RIS | Hybrid FSO/RF | |
|---|---|---|---|---|---|
| [1] | × | × | |||
| [2,3] | × | × | × | ||
| [4] | × | × | × | ||
| [5,6,7] | × | × | × | × | |
| [8] | × | × | |||
| [9,10] | × | × | × | ||
| [11] | × | ||||
| [12,13] | × | × | × | ||
| This paper | ✓ | ✓ | ✓ | ✓ | ✓ |
| Parameter | Value |
|---|---|
| Number of ground users, K | 4 |
| Channel gain, | −30 dBm |
| Frequency, | 2.4 GHz |
| Satellite’s transmit power, | 10 dB |
| Transmit antenna gain, | 38.5 dB |
| Receiving antenna gain, | 42.7 dB |
| Path loss, | 111.26 dB |
| Pointing error, | 1 |
| Altitude of drone, | 1000 m |
| Drone’s flight speed, | 10 m/s |
| Initial position of drone, | [2600, 2200] |
| Satellite’s location, | [1500, 1500, 600,000] |
| HAP’s location, | [1000, 2400, 14,000] |
| Eavesdropper’s location, | [2200, 1800, 0] |
| The flight area of drone, | m |
| Total time slots, T | 500 |
| Learning rate of actor network | 0.001 |
| Learning rate of critic network | 0.002 |
| Experience replay buffer capacity | 10,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yang, W.; Liu, T.; Li, L.; Jin, Y.; He, Y.; Wang, D. Secure Transmission for RIS-Assisted Downlink Hybrid FSO/RF SAGIN: Sum Secrecy Rate Maximization. Drones 2025, 9, 198. https://doi.org/10.3390/drones9030198
Li J, Yang W, Liu T, Li L, Jin Y, He Y, Wang D. Secure Transmission for RIS-Assisted Downlink Hybrid FSO/RF SAGIN: Sum Secrecy Rate Maximization. Drones. 2025; 9(3):198. https://doi.org/10.3390/drones9030198
Chicago/Turabian StyleLi, Jiawei, Weichao Yang, Tong Liu, Li Li, Yi Jin, Yixin He, and Dawei Wang. 2025. "Secure Transmission for RIS-Assisted Downlink Hybrid FSO/RF SAGIN: Sum Secrecy Rate Maximization" Drones 9, no. 3: 198. https://doi.org/10.3390/drones9030198
APA StyleLi, J., Yang, W., Liu, T., Li, L., Jin, Y., He, Y., & Wang, D. (2025). Secure Transmission for RIS-Assisted Downlink Hybrid FSO/RF SAGIN: Sum Secrecy Rate Maximization. Drones, 9(3), 198. https://doi.org/10.3390/drones9030198








