Analysis of Unmanned Surface Vehicles Heading KF-Based PI-(1+PI) Controller Using Improved Spider Wasp Optimizer
Abstract
:1. Introduction
- This paper introduces an Improved Spider Wasp Optimization (ISWO) algorithm, enhancing the original SWO by integrating a dynamic adaptive grouping strategy, perturbation dimension-symmetric distance optimization and nonlinear time-varying weights. The improved algorithm is subsequently applied to practical problems and its performance is evaluated to verify its effectiveness. The improved algorithm was applied to both transfer function parameter identification and controller tuning and demonstrated the best optimization performance compared to the selected algorithm.
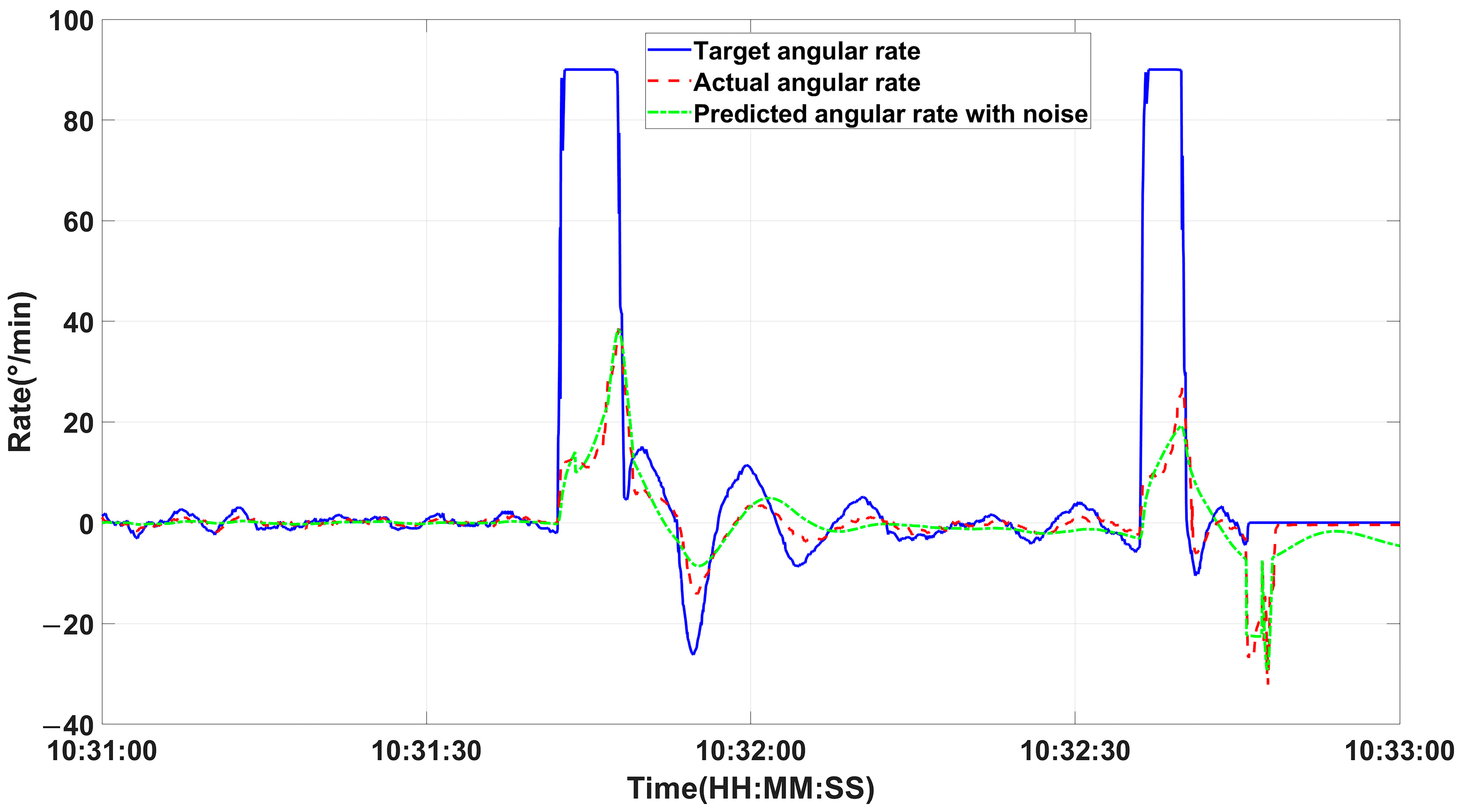
- In this paper, an accurate transfer function model of an USV can be established using only the target angular rate and the actual angular rate from voyage logs, greatly reducing the cost and complexity. The ISWO algorithm is employed to fine-tune the model parameters, resulting in a highly accurate vessel model. Subsequently, a Kalman filter-based cascaded PI-(1+PI) controller was proposed to regulate the previously identified transfer function model. Compared to the traditional PID controller with an N-filter, the proposed controller exhibits superior performance and robustness.
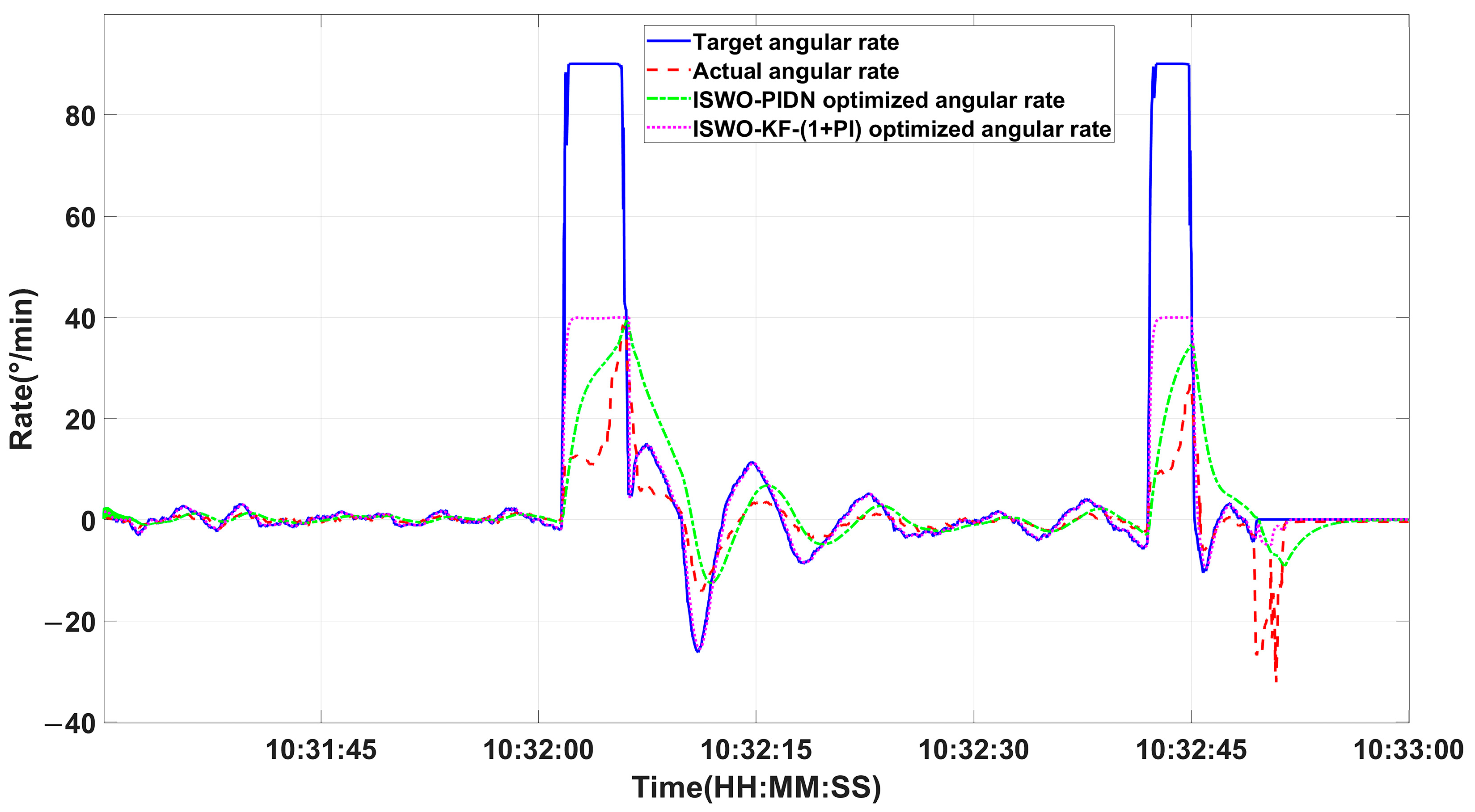
- In this paper, the performance of the proposed Kalman filter-based cascaded PI-(1+PI) controller was validated through hardware-in-the-loop simulation. Under identical navigation planning tasks, the proposed controller outperformed the traditional PID controller in terms of tracking accuracy and overall control performance.
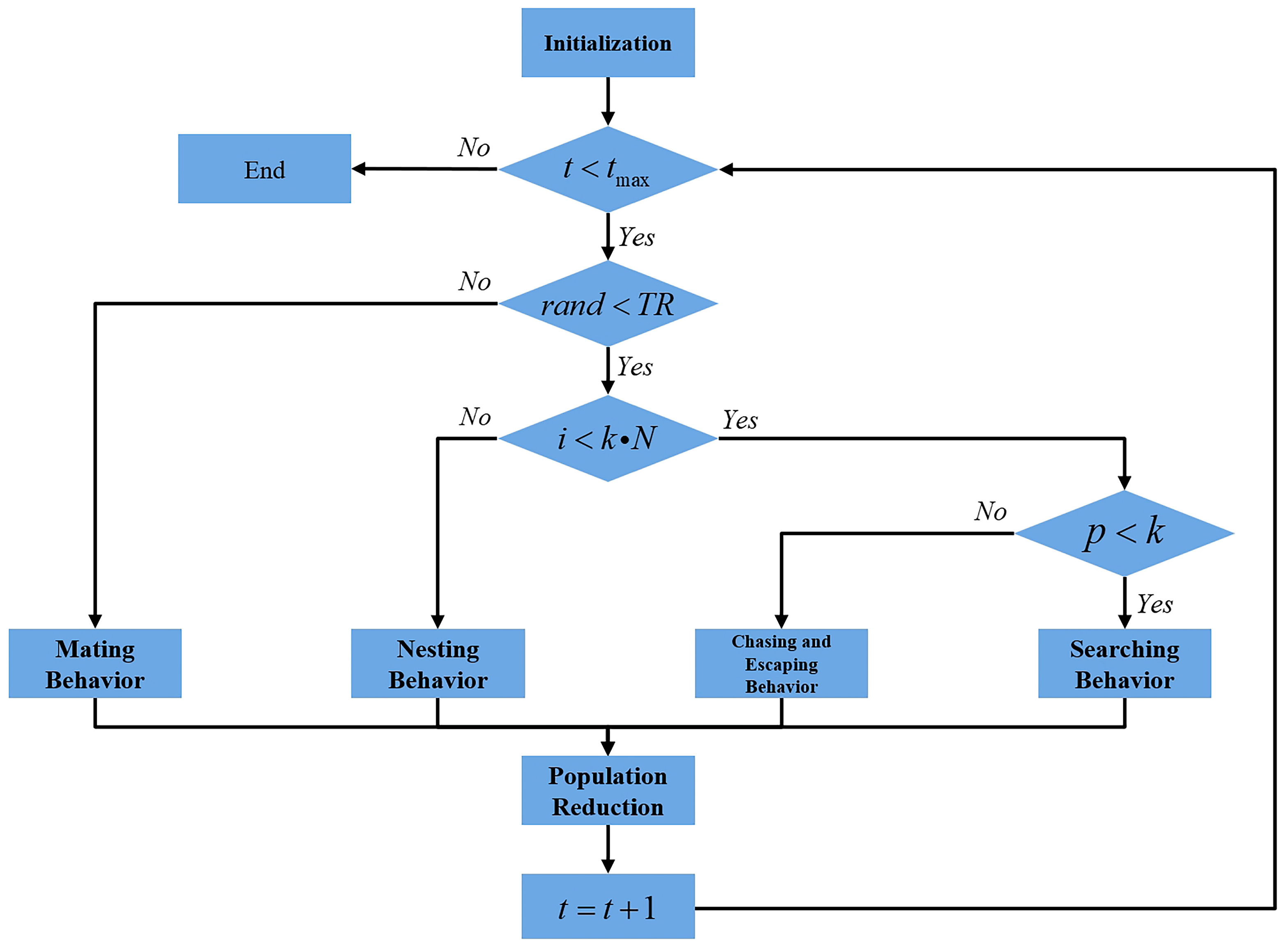
2. Spider Wasp Optimizer
2.1. Initialization
2.2. Searching Behavior
2.3. Chasing and Escaping Behavior
2.4. Nesting Behavior
2.5. Mating Behavior
2.6. Population Reduction
3. Proposed Improved Spider Wasp Optimizer
3.1. Dynamic Adaptive Grouping Strategy
3.2. Perturbation Dimension-Symmetric Distance Optimization
3.3. Nonlinear Time-Varying Weights
4. The System Transfer Function Model for USVs
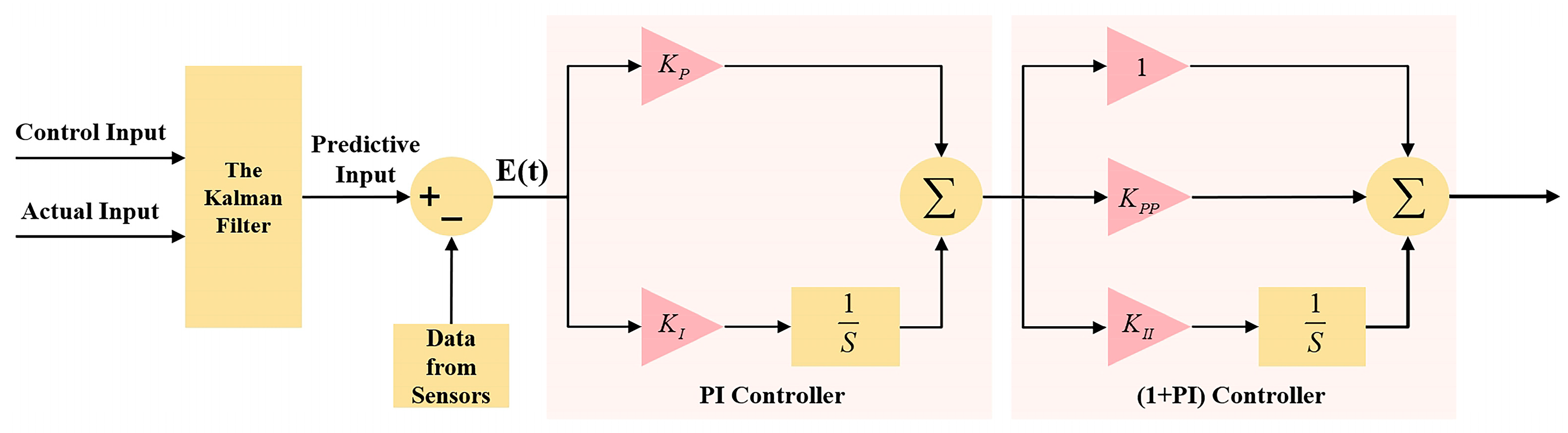
5. USV Heading Control System Applying KF-PI(1+PI) Controller
- State Equation
- 2.
- Measurement Equation
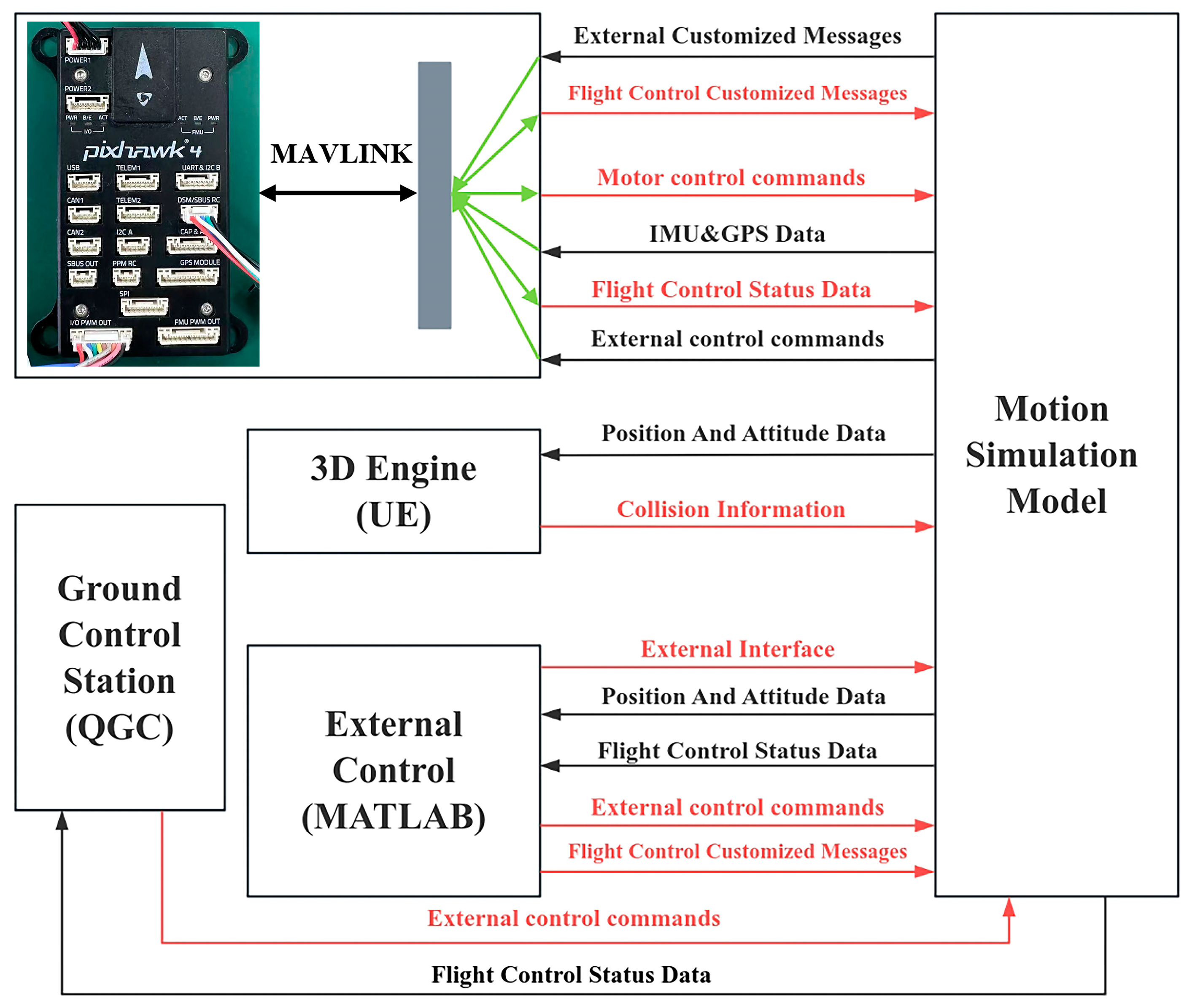
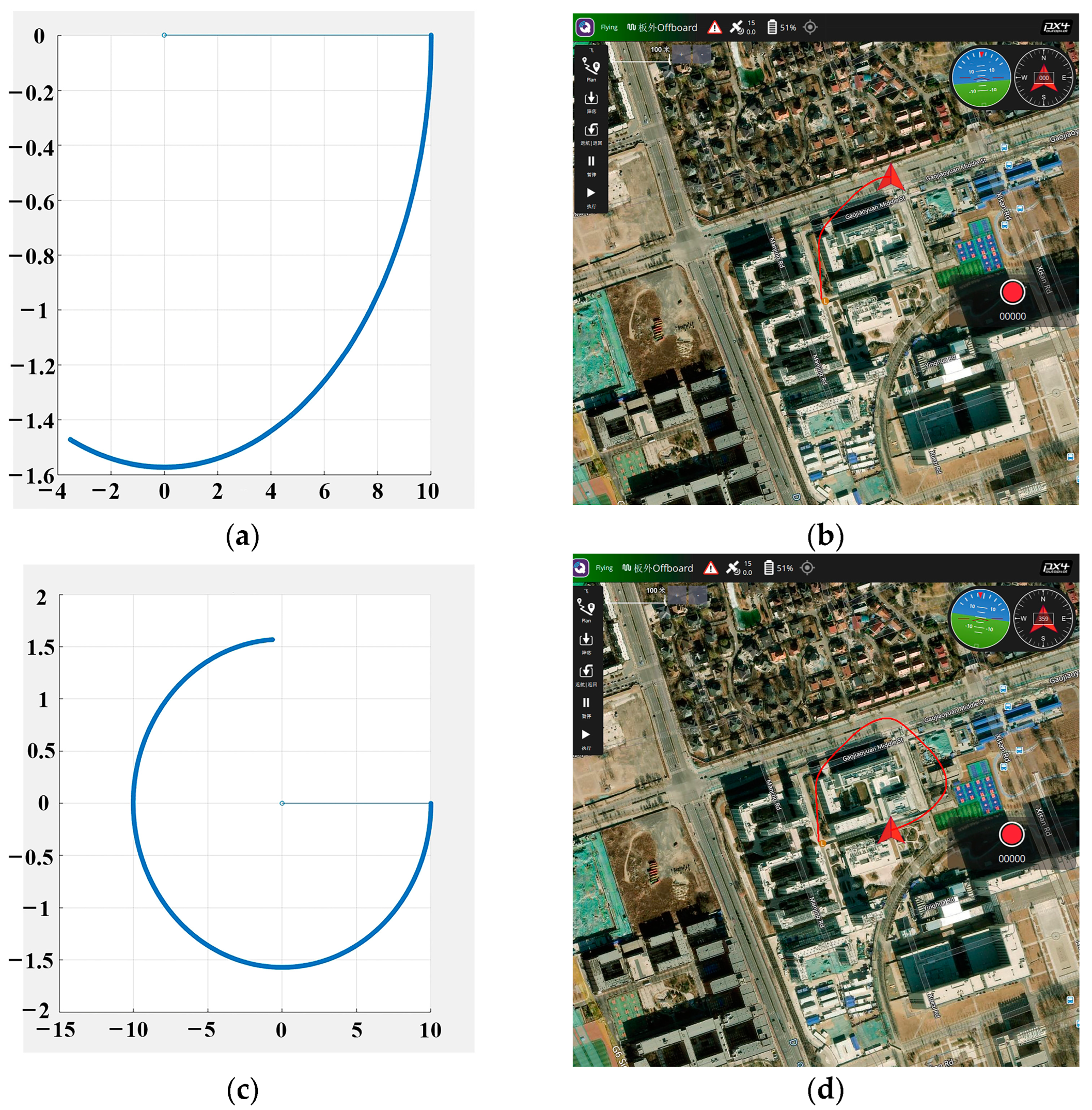
6. Hardware-in-the-Loop Simulation Verification
7. Conclusions and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lewicka, O.; Specht, M.; Stateczny, A.; Specht, C.; Dardanelli, G.; Brčić, D.; Szostak, B.; Halicki, A.; Stateczny, M.; Widźgowski, S. Integration data model of the bathymetric monitoring system for shallow waterbodies using UAV and USV platforms. Remote Sens. 2022, 14, 4075. [Google Scholar] [CrossRef]
- Kassuba, Z.; Goldenbogen, M.; Jannetta, C.; Vicent, X.; Sarda, E.I. Development of a Water Quality Monitoring System on a USV. In Proceedings of the OCEANS 2024-Halifax, Halifax, NS, Canada, 23–26 September 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Jiang, C.; Zhang, W. A survey of maritime unmanned search system: Theory, applications and future directions. Ocean. Eng. 2023, 285, 115359. [Google Scholar] [CrossRef]
- Wang, X.; Yin, Y.; Jing, Q. Maritime search path planning method of an unmanned surface vehicle based on an improved bug algorithm. J. Mar. Sci. Eng. 2023, 11, 2320. [Google Scholar] [CrossRef]
- Zhang, G.; Yin, S.; Huang, C.; Zhang, W.; Li, J. Structure synchronized dynamic event-triggered control for marine ranching AMVs via the multi-task switching guidance. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20295–20308. [Google Scholar] [CrossRef]
- Du, Z.; Li, W.; Shi, G. Multi-USV collaborative obstacle avoidance based on improved velocity obstacle method. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2024, 10, 04023049. [Google Scholar] [CrossRef]
- Cao, J.; Dou, J.; Liu, J.; Wei, X.; Guo, Z. Multi-agent deep reinforcement learning framework strategized by unmanned aerial vehicles for multi-vessel full communication connection. Remote Sens. 2023, 15, 4059. [Google Scholar] [CrossRef]
- Fan, Y.; Sun, Z.; Wang, G. A novel intelligent collision avoidance algorithm based on deep reinforcement learning approach for USV. Ocean. Eng. 2023, 287, 115649. [Google Scholar] [CrossRef]
- Zhao, Y.; Han, F.; Han, D.; Peng, X.; Zhao, W. Decision-making for the autonomous navigation of USVs based on deep reinforcement learning under IALA maritime buoyage system. Ocean. Eng. 2022, 266, 112557. [Google Scholar] [CrossRef]
- Sathish, K.; Venkata, R.C.; Anbazhagan, R.; Pau, G. Review of localization and clustering in USV and AUV for underwater wireless sensor networks. Telecom 2023, 4, 43–64. [Google Scholar] [CrossRef]
- Er, M.J.; Ma, C.; Liu, T.; Gong, H. Intelligent motion control of unmanned surface vehicles: A critical review. Ocean. Eng. 2023, 280, 114562. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Bucknall, R. Filtering based multi-sensor data fusion algorithm for a reliable unmanned surface vehicle navigation. J. Mar. Eng. Technol. 2023, 22, 67–83. [Google Scholar] [CrossRef]
- Cahyadi, M.N.; Asfihani, T.; Mardiyanto, R.; Erfianti, R. Performance of GPS and IMU sensor fusion using unscented Kalman filter for precise i-Boat navigation in infinite wide waters. Geod. Geodyn. 2023, 14, 265–274. [Google Scholar] [CrossRef]
- Shamsuzzoha, M.; Lee, M. Design of advanced PID controller for enhanced disturbance rejection of second-order processes with time delay. AIChE J. 2008, 54, 1526–1536. [Google Scholar] [CrossRef]
- Miao, R.; Dong, Z.; Wan, L.; Zeng, J. Heading control system design for a micro-USV based on an adaptive expert S-PID algorithm. Pol. Marit. Res. 2018, 25, 6–13. [Google Scholar] [CrossRef]
- Wang, H.L.; Yin, C.Y.; Lu, L.; Wang, D.; Peng, Z. Cooperative path following control of UAV and USV cluster for maritime search and rescue. Chin. J. Ship Res. 2022, 17, 157–165. [Google Scholar] [CrossRef]
- Peng, L.; Bai, W.; Zhang, W. Course Tracking Control of USV Based on Optimal Backstepping Method Via Reinforcement Learning. In Proceedings of the 2024 International Annual Conference on Complex Systems and Intelligent Science (CSIS-IAC), Guangzhou, China, 20–22 September 2024; pp. 234–239. [Google Scholar] [CrossRef]
- Dong, Z.; Qi, S.; Yu, M.; Zhang, Z.; Zhang, H.; Li, J.; Liu, Y. An improved dynamic surface sliding mode method for autonomous cooperative formation control of underactuated USVs with complex marine environment disturbances. Pol. Marit. Res. 2022, 29, 47–60. [Google Scholar] [CrossRef]
- Karnani, C.; Raza, S.A.; Asif, M.; Ilyas, M. Adaptive control algorithm for trajectory tracking of underactuated unmanned surface vehicle (UUSV). J. Robot. 2023, 2023, 4820479. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Shan, Q.; Zhang, W. A novel cooperative design for USV–UAV systems: 3-D mapping guidance and adaptive fuzzy control. IEEE Trans. Control. Netw. Syst. 2022, 10, 564–574. [Google Scholar] [CrossRef]
- Fossen, T.I. A survey on nonlinear ship control: From theory to practice. In Proceedings of the 5th IFAC Conference on Manoeuvring and Control of Marine Craft, Aalborg, Denmark, 23–25 August 2000; Volume 5, pp. 1–16. [Google Scholar] [CrossRef]
- Amerongen, J.V.; Udink Cate, A.L. Model reference adaptive autopilots for ships. Automatica 1975, 11, 441–450. [Google Scholar] [CrossRef]
- Kallstrom, C.G.; Astrom, K.J. Adaptive autopilots for tanker. Automatica 1979, 15, 241–254. [Google Scholar] [CrossRef]
- Goud, H.; Sharma, P.C.; Nisar, K.; Brahim, A.A.A.; Haque, M.R.; Yadav, N.S.; Swarnkar, P.; Gupta, M.; Chand, L. PSO Based Multi-Objective Approach for Controlling PID Controller. Comput. Mater. Contin. 2022, 71, 4409–4423. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Al-Wahaibi, S.S.S.; Lu, Q. Entropy-maximizing TD3-based reinforcement learning for adaptive PID control of dynamical systems. Comput. Chem. Eng. 2023, 178, 108393. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Q. Fractional Order PID Control Based on Improved Whale Optimization Algorithm. In Proceedings of the 2024 IEEE 6th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 24 May 2024; Volume 6, pp. 1676–1682. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Elaziz, M.A.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Jia, H.; Rao, H.; Wen, C.; Mirjalili, S. Crayfish optimization algorithm. Artif. Intell. Rev. 2023, 56 (Suppl. 2), 1919–1979. [Google Scholar] [CrossRef]
- Zou, X.; Li, J. Marine Predators Algorithm Based on Trigonometric Function. In Proceedings of the 2022 IEEE 5th International Conference on Computer and Communication Engineering Technology (CCET), Beijing, China, 19–21 August 2022; pp. 13–17. [Google Scholar] [CrossRef]
- Barua, S.; Merabet, A.; Al-Durra, A.; El-Fouly, T.; El-Saadany, E.F. Lévy arithmetic optimization for energy management of solar wind microgrid with multiple diesel generators for off-grid communities. Appl. Energy 2024, 371, 123736. [Google Scholar] [CrossRef]
- Shikoun, N.H.; Al-Eraqi, A.S.; Fathi, I.S. BinCOA: An efficient binary crayfish optimization algorithm for feature selection. IEEE Access 2024, 12, 28621–28635. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Z.; Wei, Y.; Liu, Y.; Wu, W. A Self-Tuning Variable Universe Fuzzy PID Control Framework with Hybrid BAS-PSO-SA Optimization for Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2025, 13, 558. [Google Scholar] [CrossRef]
- Long, Y.; Liu, S.; Qiu, D.; Li, C.; Guo, X.; Shi, B.; AbouOmar, M.S. Local path planning with multiple constraints for USV based on improved bacterial foraging optimization algorithm. J. Mar. Sci. Eng. 2023, 11, 489. [Google Scholar] [CrossRef]
- Bai, X.; Li, B.; Xu, X.; Xiao, Y. USV path planning algorithm based on plant growth. Ocean. Eng. 2023, 273, 113965. [Google Scholar] [CrossRef]
- Sahal, M.; Gamayanti, N.; Cendikiarani, M.T. Surge Speed and Yaw Angle Control System Design on Unmanned Surface Vehicle (USV) Using PID-Fuzzy-Genetic Algorithm. In Proceedings of the 2024 International Seminar on Intelligent Technology and Its Applications (ISITIA), Mataram, Indonesia, 10–12 July 2024; pp. 571–576. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Spider wasp optimizer: A novel meta-heuristic optimization algorithm. Artif. Intell. Rev. 2023, 56, 11675–11738. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Braik, M.S.; Al-Betar, M.A.; Awadallah, M.A. Boosted spider wasp optimizer for high-dimensional feature selection. J. Bionic Eng. 2024, 21, 2424–2459. [Google Scholar] [CrossRef]
- Sui, J.; Tian, Z.; Wang, Z. Multiple strategies improved spider wasp optimization for engineering optimization problem solving. Sci. Rep. 2024, 14, 29048. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Li, Z.; Wang, H.; Hu, Y.; Jiang, H.; Jiang, X.; Chen, D. An Improved Spider-Wasp Optimizer for Obstacle Avoidance Path Planning in Mobile Robots. Mathematics 2024, 12, 2604. [Google Scholar] [CrossRef]
- Hong, Z.; Wang, X.; Li, M.; Gu, Y.; Zhao, J.; Cao, X. Identification of USV Maneuvering Model Based on Multi-Output Gaussian Process Regression. In Proceedings of the 2023 China Automation Congress (CAC), Chongqing, China, 17–19 November 2023; pp. 6300–6305. [Google Scholar] [CrossRef]
- Cheng, M.; Yao, J.; Ren, Q. A Model Predictive Control Approach for USV Autonomous Cruising via Disturbance Learning. In Proceedings of the 2024 IEEE 18th International Conference on Control & Automation (ICCA), Reykjavík, Iceland, 18–21 June 2024; pp. 988–993. [Google Scholar] [CrossRef]
- Song, R.; Gao, S.; Li, Y. Sim-to-Real in Unmanned Surface Vehicle Control: A System Identification-Based Approach for Enhanced Training Environments. In Proceedings of the 2024 9th International Conference on Electronic Technology and Information Science (ICETIS), Hangzhou, China, 17–19 May 2024; pp. 563–570. [Google Scholar] [CrossRef]



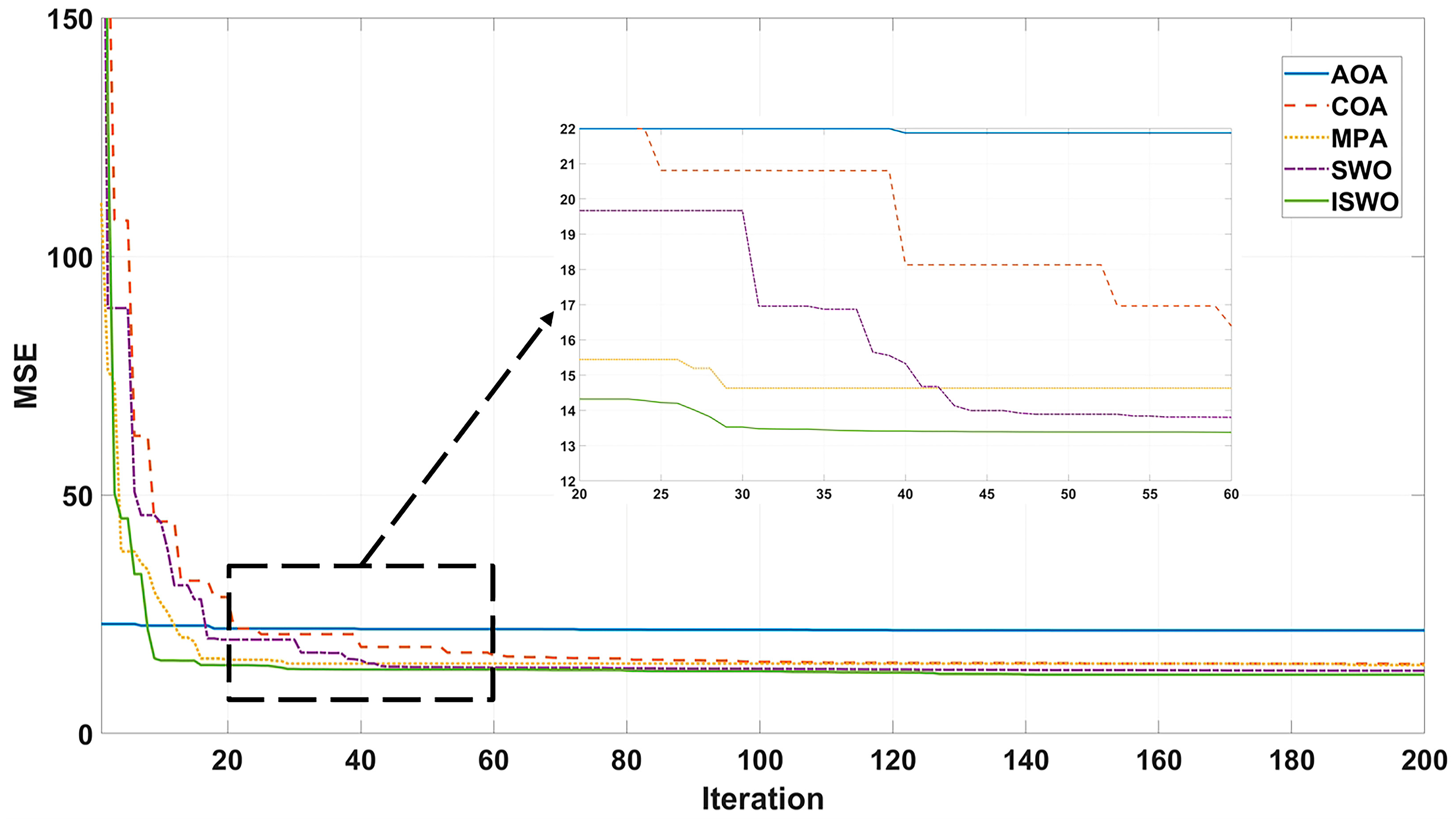



| Algorithms | A | B | C | D | E | F | G | H | I | MSE |
|---|---|---|---|---|---|---|---|---|---|---|
| AOA | 0.3653 | −0.0534 | −0.1298 | 0.0551 | 3.2900 | 0.0948 | −0.0636 | 0.0040 | 0.0506 | 21.6096 |
| COA | 0.3471 | 14.9063 | 5.6802 | −4.9923 | 0.0593 | 4.3985 | 18.0961 | 42.1631 | −17.0022 | 13.9872 |
| MPA | 29.1350 | −18.3403 | 48.8925 | −2.3084 | 6.4603 | 33.6848 | 25.4213 | 41.9222 | 49.9997 | 13.2185 |
| SWO | 21.1367 | −22.4140 | 38.3144 | 0.3674 | 4.7251 | 22.6607 | 7.9922 | 20.0445 | 49.5938 | 13.0824 |
| ISWO | 0.3889 | 3.5385 | 19.3807 | −5.6865 | 0.0337 | 1.8889 | 5.6983 | 42.3748 | −2.0363 | 12.3403 |
| Algorithms | KP | KI | KD | N | ITAE |
|---|---|---|---|---|---|
| AOA | 83.1465 | 500 | 500 | 0 | 244.0278 |
| COA | 83.1403 | 500 | 35.4979 | 0 | 244.0278 |
| MPA | 83.1404 | 500 | 249.9738 | 0 | 244.0278 |
| SWO | 76.8290 | 499.9972 | 219.9980 | 0.0028 | 244.0285 |
| ISWO | 82.8684 | 500 | 0 | 494.2768 | 244.8782 |
| Gains | KP | KI | KD | KPP | KII | N | Q | R |
|---|---|---|---|---|---|---|---|---|
| Min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Max | 500 | 500 | 500 | 500 | 500 | 500 | 5 | 5 |
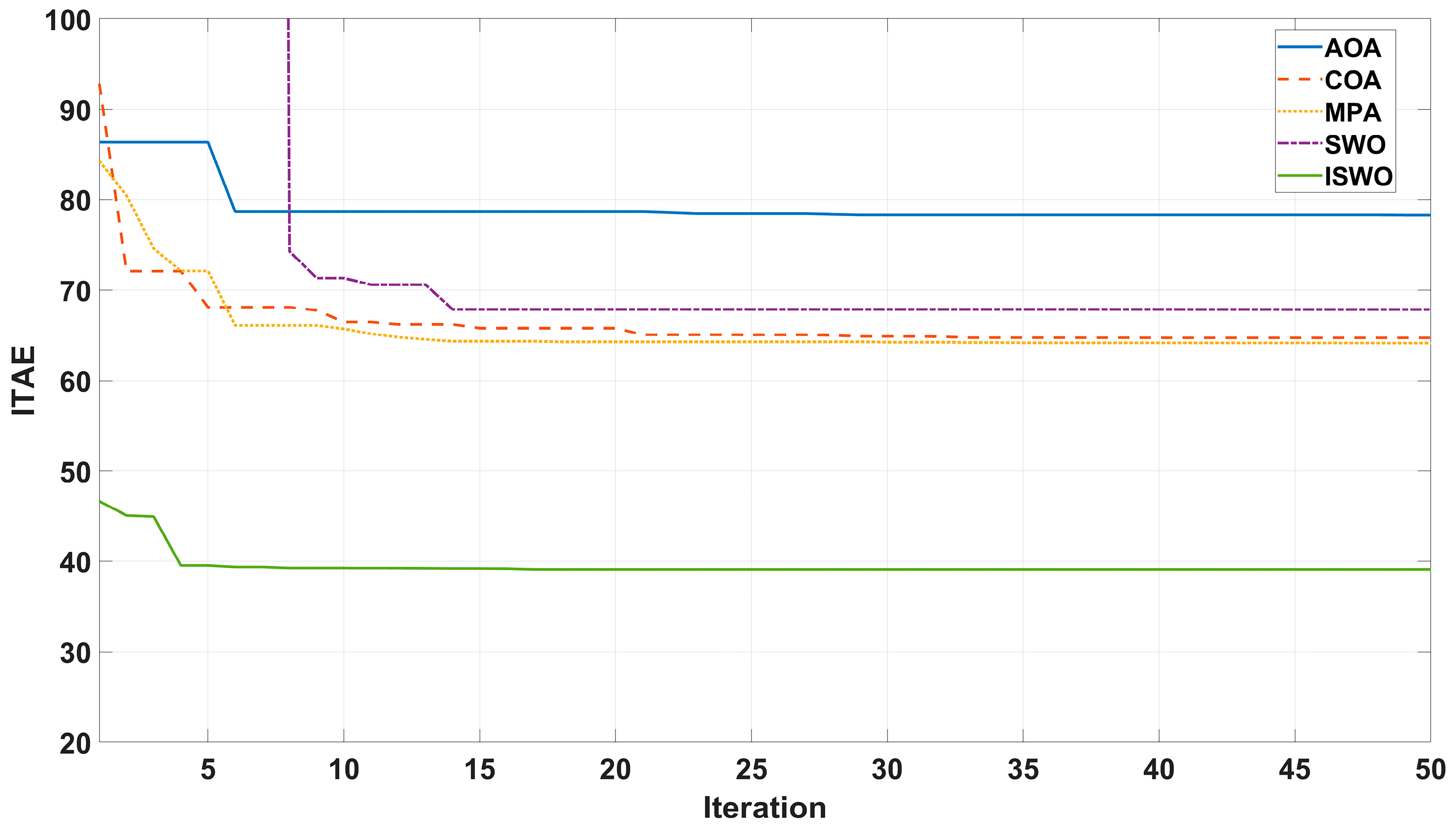
| Algorithms | KP | KI | KPP | KII | Q | R | ITAE |
|---|---|---|---|---|---|---|---|
| AOA | 54.4844 | 500 | 0 | 72.4791 | 0.1157 | 4.7644 | 78.2803 |
| COA | 0.6537 | 51.4096 | 134.4796 | 0.8306 | 4.5011 | 0.7270 | 64.7241 |
| MPA | 29.2631 | 0.0038 | 20,118 | 242.0166 | 0.6365 | 0.100 | 64.1399 |
| SWO | 37.9674 | 79.0734 | 1.3544 | 197.3003 | 4.2045 | 2.3757 | 67.8528 |
| ISWO | 8.7167 | 499.9980 | 6.1584 | 495.8548 | 0.0848 | 0.0085 | 39.1001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zeng, X.; Wang, J.; Li, Q.; Fan, B.; Zeng, Q. Analysis of Unmanned Surface Vehicles Heading KF-Based PI-(1+PI) Controller Using Improved Spider Wasp Optimizer. Drones 2025, 9, 326. https://doi.org/10.3390/drones9050326
Li X, Zeng X, Wang J, Li Q, Fan B, Zeng Q. Analysis of Unmanned Surface Vehicles Heading KF-Based PI-(1+PI) Controller Using Improved Spider Wasp Optimizer. Drones. 2025; 9(5):326. https://doi.org/10.3390/drones9050326
Chicago/Turabian StyleLi, Xiaoyu, Xiangye Zeng, Jingyi Wang, Qi Li, Baoshuo Fan, and Qi Zeng. 2025. "Analysis of Unmanned Surface Vehicles Heading KF-Based PI-(1+PI) Controller Using Improved Spider Wasp Optimizer" Drones 9, no. 5: 326. https://doi.org/10.3390/drones9050326
APA StyleLi, X., Zeng, X., Wang, J., Li, Q., Fan, B., & Zeng, Q. (2025). Analysis of Unmanned Surface Vehicles Heading KF-Based PI-(1+PI) Controller Using Improved Spider Wasp Optimizer. Drones, 9(5), 326. https://doi.org/10.3390/drones9050326





