Process Stability during Laser Beam Welding with Beam Oscillation and Wire Feed
Abstract
:1. Introduction
- full penetration through the sheet material;
- the melt pool must be wider than the sheet thickness;
- oversized melt pool widths lead to buttonhole destabilization and the risk of pinholes;
- radii conditions of front and rear buttonhole determine the movement, elongation and constriction [30].
2. Modelling
3. Setup and Methods
4. Experimental Results
5. Discussion
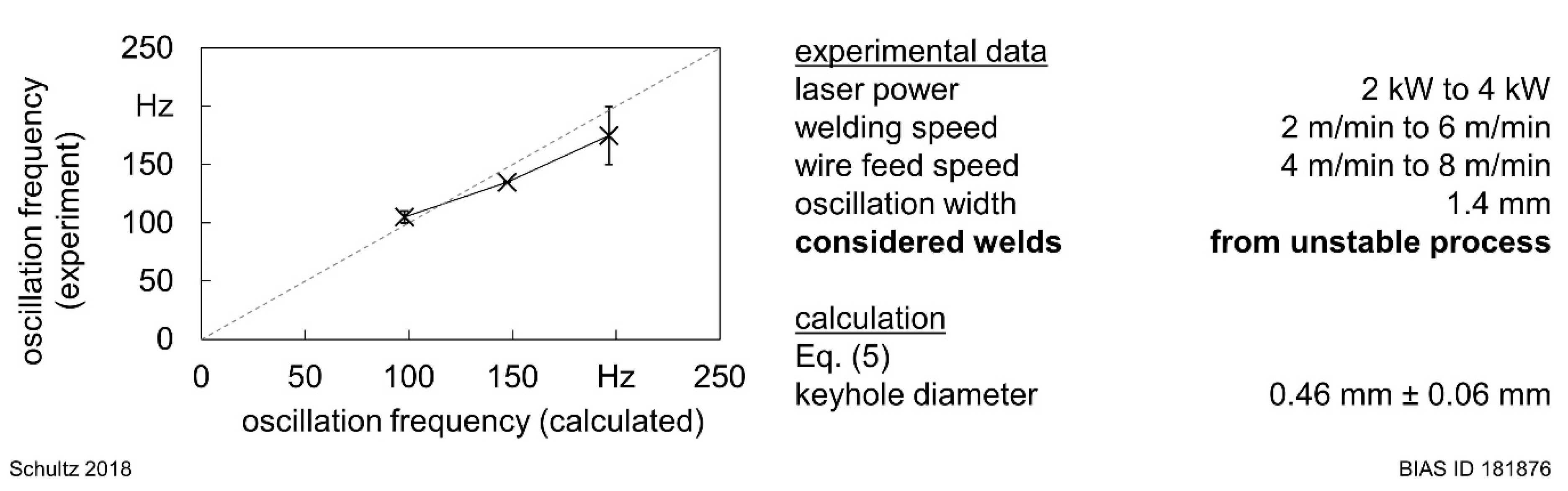
5.1. Model Validity and Sensitivity
5.2. Instabilities during Laser Welding with Beam Oscillation
6. Conclusions
- solid wire segments can overtake the oscillating laser beam at e.g., low oscillation frequencies and prevent a buttonhole from growing to a self-sustaining size;
- for buttonhole welding, an even melt of the wire tip is required.
- buttonhole welding has an influence on solidification behavior (height to width ratio results near a value of 1);
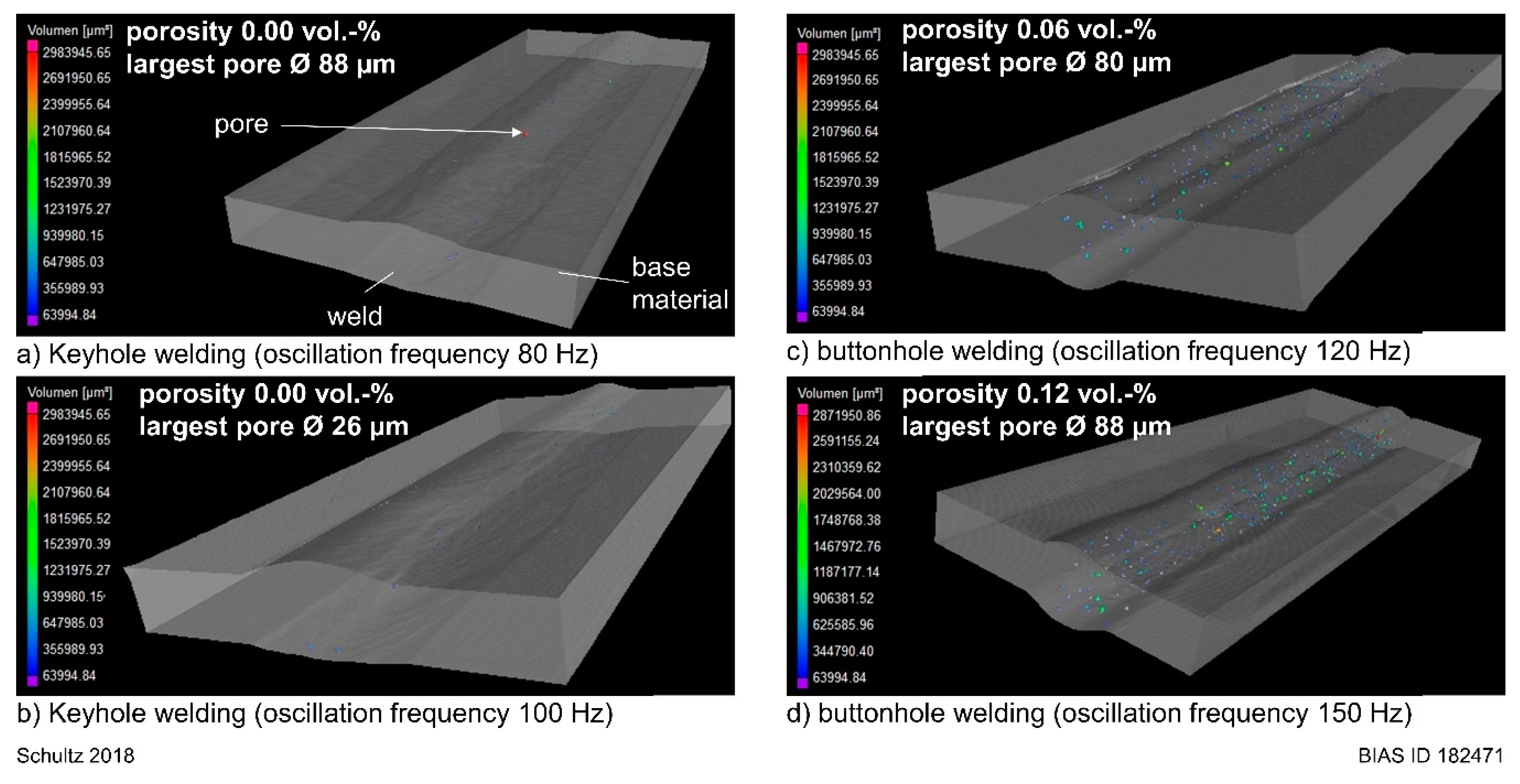
- buttonhole welding can lead to a fine porosity of the seam.
Funding
Acknowledgments
Conflicts of Interest
References
- EAA—European Aluminium Association. Aluminium in Cars—Unlock the Light-Weighting Potentials; European Aluminium Association: Brussels, Belgium, 2015; pp. 5–11. [Google Scholar]
- Reisgen, U.; Olschok, S.; Wagner, N.; Zäh, M.; Oefele, F.; Ruhstorfer, M. Aktuelle Fügeverfahren für Aluminiumwerkstoffe. DVS Bericht Strahlschweißen von Aluminium 2010, 266, 22–27. [Google Scholar]
- Dilthey, U. Schweißtechnische Fertigungsverfahren 2; Springer-Verlag: Berlin, Germany, 2005; Volume 229. [Google Scholar]
- Matthes, J. Schweißtechnik: Schweißen von metallischen Konstruktionswerkstoffen; Fachbuchverlag Leipzig im Carl Hanser Verlag: Leipzig, Germany, 2006. [Google Scholar]
- Wu, S.C.; Yu, X.; Zuo, R.Z.; Zhang, W.H.; Xie, H.L.; Jiang, J.Z. Porosity, Element Loss, and Strength Model on Softening Behavior of Hybrid Laser Arc Welded Al-Zn-Mg-Cu Alloy with Synchrotron Radiation Analysis. Weld. J. 2013, 92, 64–71. [Google Scholar]
- Seefeld, T.; Schultz, V. New developments in filler wire assisted laser joining of Aluminium. In Proceedings of the LAMP2013—6th International Congress on Laser Advanced Materials Processing, Niigata, Japan, 23–26 July 2013. [Google Scholar]
- Salminen, A. The filler wire—Laser beam interaction during laser welding with low alloyed steel filler wire. Mechanika 2010, 84, 67–74. [Google Scholar]
- Hatwig, J.; Reinhart, G.; Zaeh, M.F. Automated task planning for industrial robots and laser scanners for remote laser beam welding and cutting. Prod. Eng. Res. Deve 2010, 4, 327–332. [Google Scholar] [CrossRef]
- Vollertsen, F. Properties and Prospects of High Brightness Solid State Lasers. Laser Tech. J. 2009, 6, 27–31. [Google Scholar] [CrossRef]
- Cho, W.-I.; Na, S.-J.; Thomy, C.; Vollertsen, F. Numerical simulation of molten pool dynamics in high power disk laser welding. J. Mater. Process. Technol. 2012, 212, 262–275. [Google Scholar] [CrossRef]
- Calleja, A.; Tabernero, I.; Fernández, A.; Celaya, A.; Lamikiz, A.; López de Lacalle, L.N. Improvement of strategies and parameters for multi-axis laser cladding operations. Opt. Lasers Eng. 2014, 56, 113–120. [Google Scholar] [CrossRef]
- Aalderink, B.J.; Pathiraj, B.; Aarts, R.G.K.M. Seam gap bridging of laser based processes for the welding of aluminium sheets for industrial applications. Int. J. Adv. Manuf. Technol. 2010, 48, 143–154. [Google Scholar] [CrossRef]
- Liu, Q.S.; Mahdavian, S.M.; Aswin, D.; Ding, S. Experimental study of temperature and clamping force during Nd: YAG laser butt welding. Opt. Laser Technol. 2009, 41, 794–799. [Google Scholar] [CrossRef]
- Sun, Z.; Kuo, M. Bridging the joint gap with wire feed laser welding. J. Mater. Process. Technol. 1999, 87, 213–222. [Google Scholar] [CrossRef]
- Binroth, C. Beitrag zur Prozeßstabilität beim CO2-Laserstrahlschweißen von Aluminium mit Zusatzwerkstoff. Ph.D. Thesis, University Bremen Strahltechnik Band 1, BIAS Verlag, Bremen, Germany, 1995. [Google Scholar]
- Albert, F.; Starcevic, D. Möglichkeiten zur Beeinflussung der Nahtrauheit beim Laserstrahlschweißen von Türen und Klappen aus Aluminium. In Proceedings of the 10th conference on Laser-Anwenderforum (LAF’16), Bremen, Germany, 23–24 November 2016. [Google Scholar]
- Schweier, M.; Haubold, M.W.; Zaeh, M.F. Analysis of spatters in laser welding with beam oscillation. CIRP J. Manuf. Sci. Technol. 2016, 14, 35–42. [Google Scholar] [CrossRef]
- Berend, O.; Haverkamp, H.; Meier, O.; Engelbrecht, L. High-frequency beam oscillating to increase the process stability during laser welding with high melt pool dynamics. In Proceedings of the 24th ICALEO Conference, Miami, FL, USA, 31 October–3 November 2005; pp. 1032–1041. [Google Scholar]
- Kraetzsch, M.; Standfuss, J.; Klotzbach, A.; Kaspar, J.; Brenner, B.; Beyer, E. Laser Beam Welding with High-Frequency Beam Oscillation: Welding of Dissimilar Materials with Brilliant Fiber Lasers. Laser Manuf. Phys. Procedia 2011, 12, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Göbel, G.; Brenner, B.; Beyer, E. New Application Possibilities for Fiber Laser Welding. In Proceedings of the 26th International Congress on Application of Lasers & Electro-Optics, ICALEO 2007, Orlando, FL, USA, 29 October–1 November 2007; pp. 102–108. [Google Scholar]
- Dittrich, D.; Schedewy, R.; Brenner, B.; Standfuß, J. Laser-multi-pass-narrow-gap-welding of hot crack sensitive thick Aluminium plates. Laser Manuf. Phys. Procardia 2013, 41, 225–233. [Google Scholar]
- Schultz, V.; Seefeld, T.; Vollertsen, F. Gap Bridging Ability in Laser Beam Welding of Thin Aluminum Sheets. In Proceedings of the 8th International Conference on Photonic Technologies (LANE 2014), Physics Procedia, Munich, Germany, 8–11 September 2014; Schmidt, M., Vollertsen, F., Merklein, M., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2014; Volume 56, pp. 545–553. [Google Scholar]
- Schultz, V.; Seefeld, T.; Vollertsen, F. Spaltüberbrückbarkeit beim Laserstrahl-schweißen mit Strahloszillation. Schweißen und Schneiden 2015, 67, 518–522. (In Germany) [Google Scholar]
- Ericsson, I.; Powell, J.; Kaplan, A. Surface tension generated defects in full penetration laser keyhole welding. J. Laser Appl. 2014, 26, 012006. [Google Scholar] [CrossRef]
- Haglund, P.; Eriksson, I.; Powell, P.; Kaplan, A. Surface tension stabilized laser welding (donut laser welding)—A new laser welding Technique. J. Laser Appl. 2013, 25, 031501. [Google Scholar] [CrossRef]
- Aalderink, B.J.; de Lange, D.F.; Aarts, R.G.K.M.; Meijer, J. Keyhole shapes during laser welding of thin metal sheets. J. Phys. D Appl. Phys. 2007, 40, 5388–5393. [Google Scholar] [CrossRef]
- Vollertsen, F. Loopless Production: Definition and Examples from Joining. In Proceedings of the 69th IIW Annual Assembly and International Conference, Melbourne Convention Exhibition Centre, Melbourne, Australia, 10–15 July 2016. [Google Scholar]
- Cho, W.-I.; Schultz, V.; Woizeschke, P. Numerical study of the effect of the oscillation frequency in buttonhole welding. J. Mater. Process. Technol. 2018, 261, 202–212. [Google Scholar] [CrossRef]
- Cho, W.-I.; Schultz, V.; Vollertsen, F. Simulation of the buttonhole formation during laser welding with wire feeding and beam oscillation. In Proceedings of the Lasers in Manufacturing (LIM17), Munich, Germany, 26–29 June 2017. [Google Scholar]
- Schultz, V.; Woizeschke, P. High Seam Surface Quality in Keyhole Laser Welding: Buttonhole Welding. J. Manuf. Mater. Process. 2018, 2, 78. [Google Scholar] [CrossRef]
- Schultz, V.; Cho, W.-I.; Woizeschke, P.; Vollertsen, F. Laser deep penetration weld seams with high surface quality. In Proceedings of the Lasers in Manufacturing (LIM17), Munich, Germany, 26–29 June 2017. [Google Scholar]
- Tang, Z.; Seefeld, T.; Vollertsen, F. Laser Brazing of Aluminum with a new filler wire AlZn13Si10Cu4. Phys. Procedia 2013, 41, 128–136. [Google Scholar] [CrossRef]
- Engelbrecht, L. Umstieg von YAG auf Diode: Mehr Prozessstabilität, weniger Kosten beim Laserlöten der Dachnullfuge mit angepassten Strahleigenschaften. In Proceedings of the European Automotive Laser Applications (EALA), Bad Neuheim, Germany, 2 February 2009. [Google Scholar]


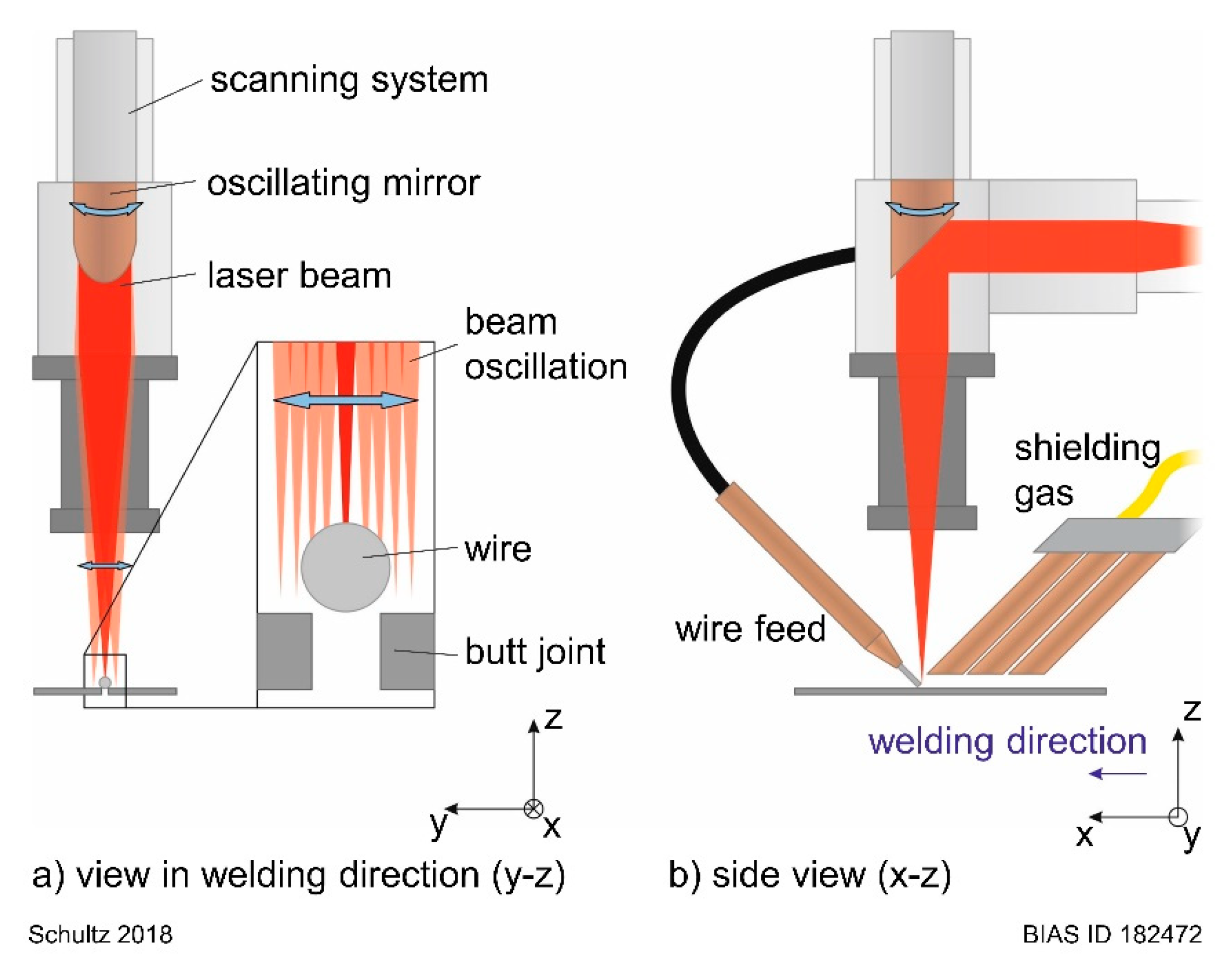

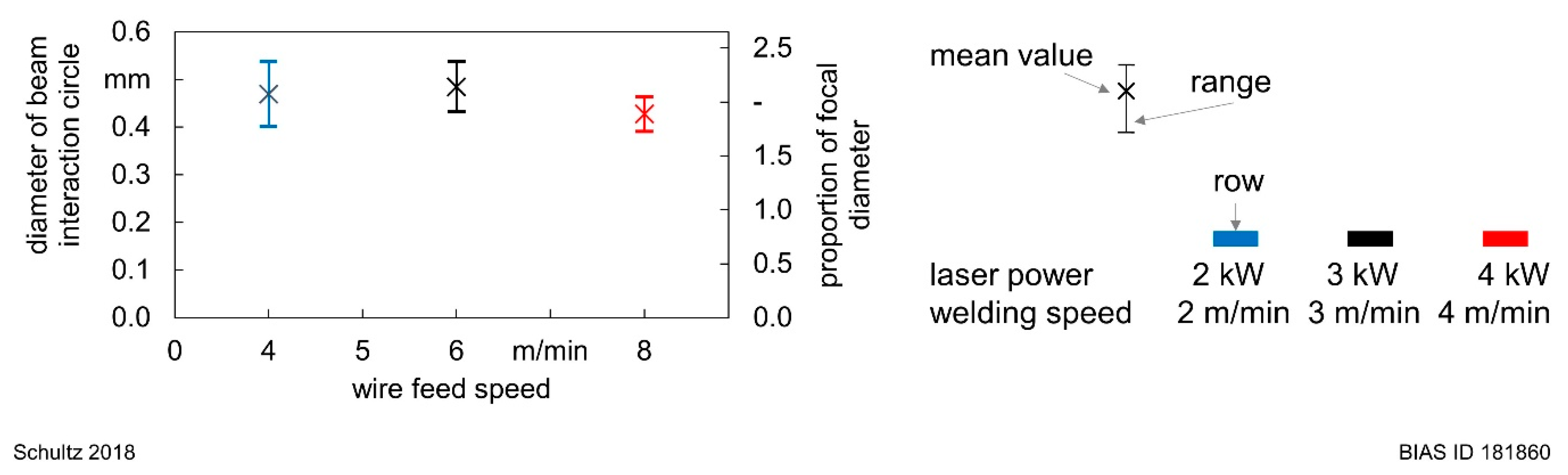
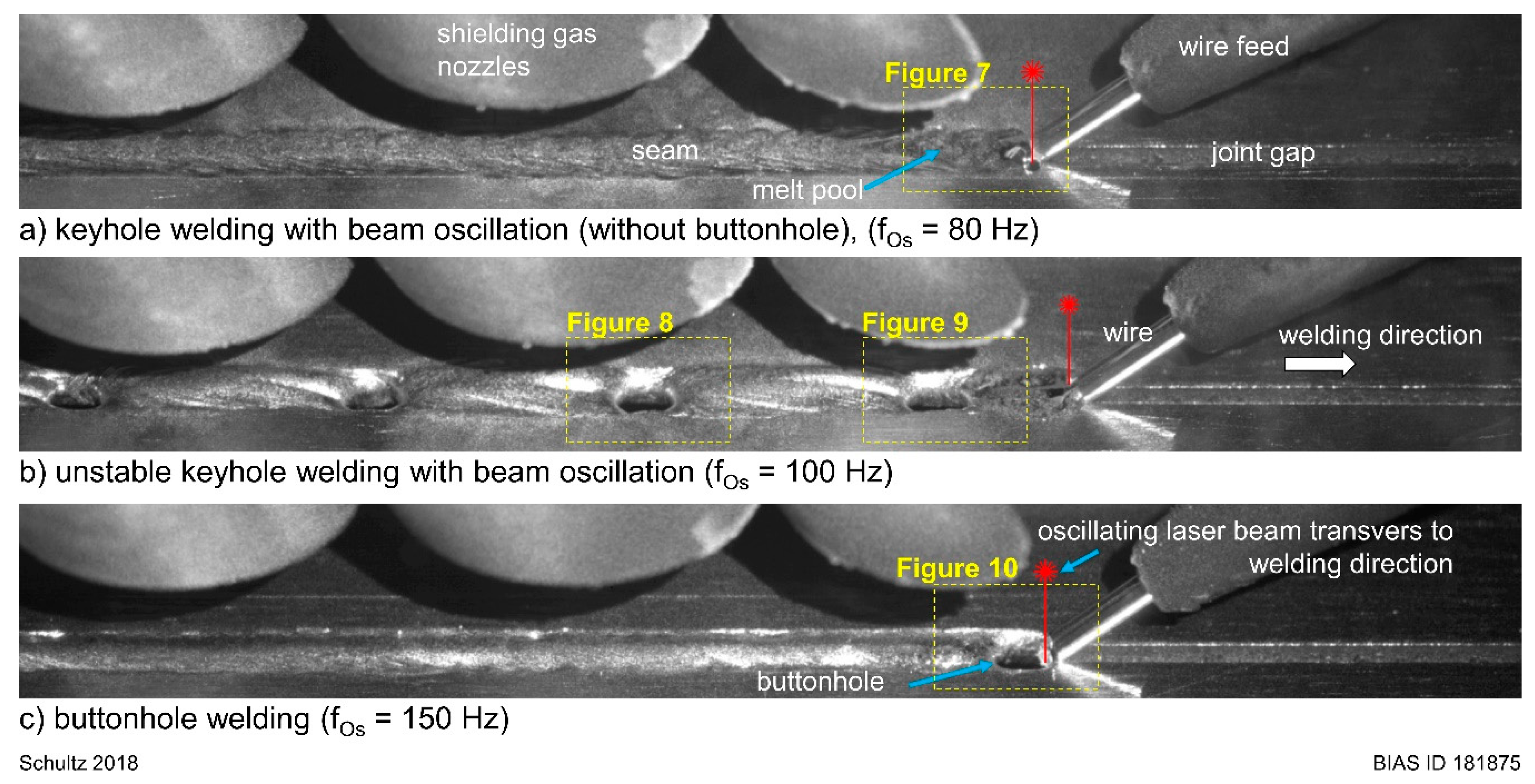







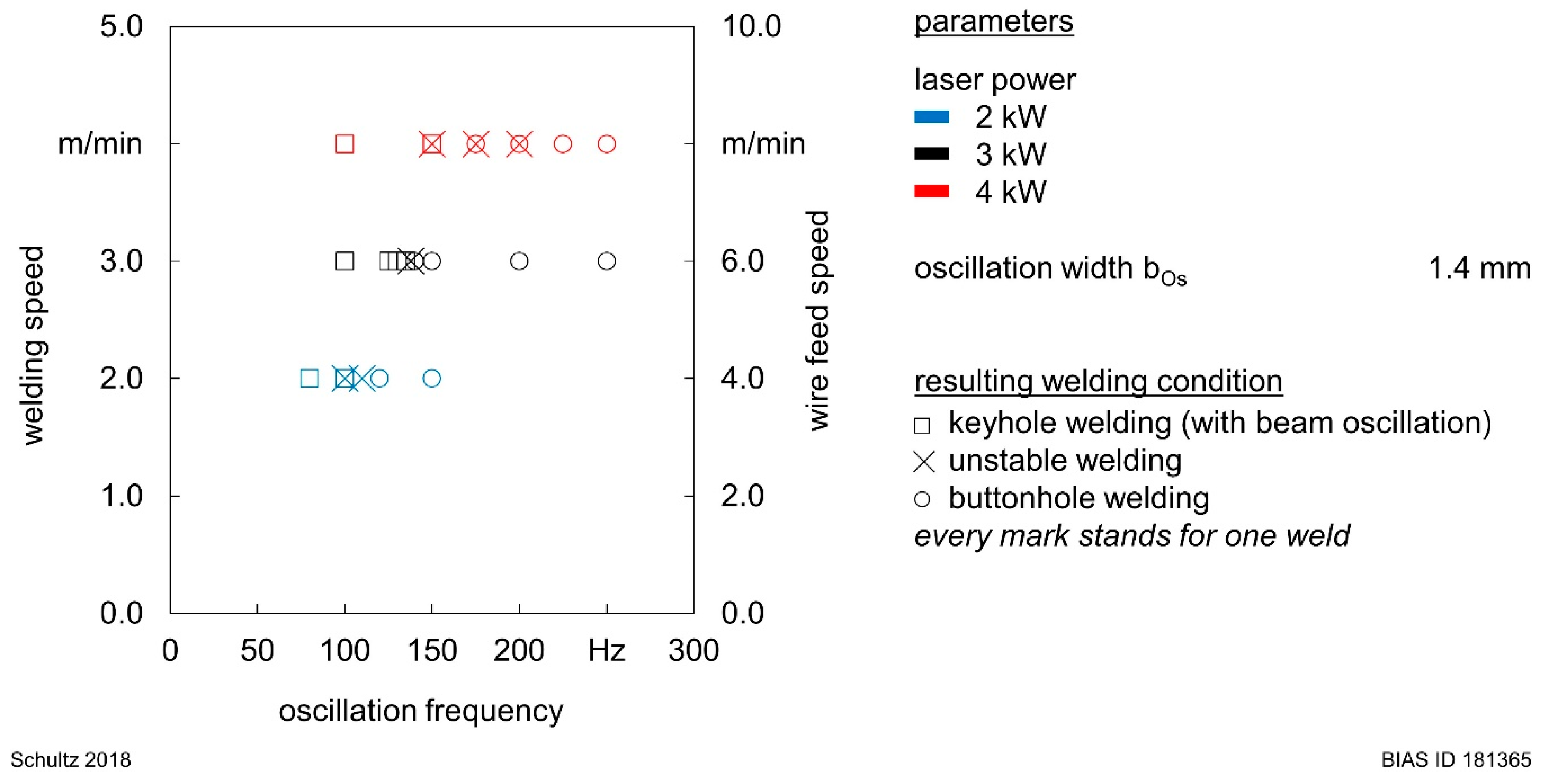


| Row | [mm] | ||||||
|---|---|---|---|---|---|---|---|
| r1 | 2 | 2 | 4 | 35 | 1.4 | 80 to 150 | 1 |
| r2 | 3 | 3 | 6 | 35 | 1.4 | 100 to 250 | 1 |
| r3 | 4 | 4 | 8 | 35 | 1.4 | 100 to 250 | 1 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schultz, V. Process Stability during Laser Beam Welding with Beam Oscillation and Wire Feed. J. Manuf. Mater. Process. 2019, 3, 17. https://doi.org/10.3390/jmmp3010017
Schultz V. Process Stability during Laser Beam Welding with Beam Oscillation and Wire Feed. Journal of Manufacturing and Materials Processing. 2019; 3(1):17. https://doi.org/10.3390/jmmp3010017
Chicago/Turabian StyleSchultz, Villads. 2019. "Process Stability during Laser Beam Welding with Beam Oscillation and Wire Feed" Journal of Manufacturing and Materials Processing 3, no. 1: 17. https://doi.org/10.3390/jmmp3010017
APA StyleSchultz, V. (2019). Process Stability during Laser Beam Welding with Beam Oscillation and Wire Feed. Journal of Manufacturing and Materials Processing, 3(1), 17. https://doi.org/10.3390/jmmp3010017





