A Unique Methodology for Tool Life Prediction in Machining
Abstract
1. Introduction
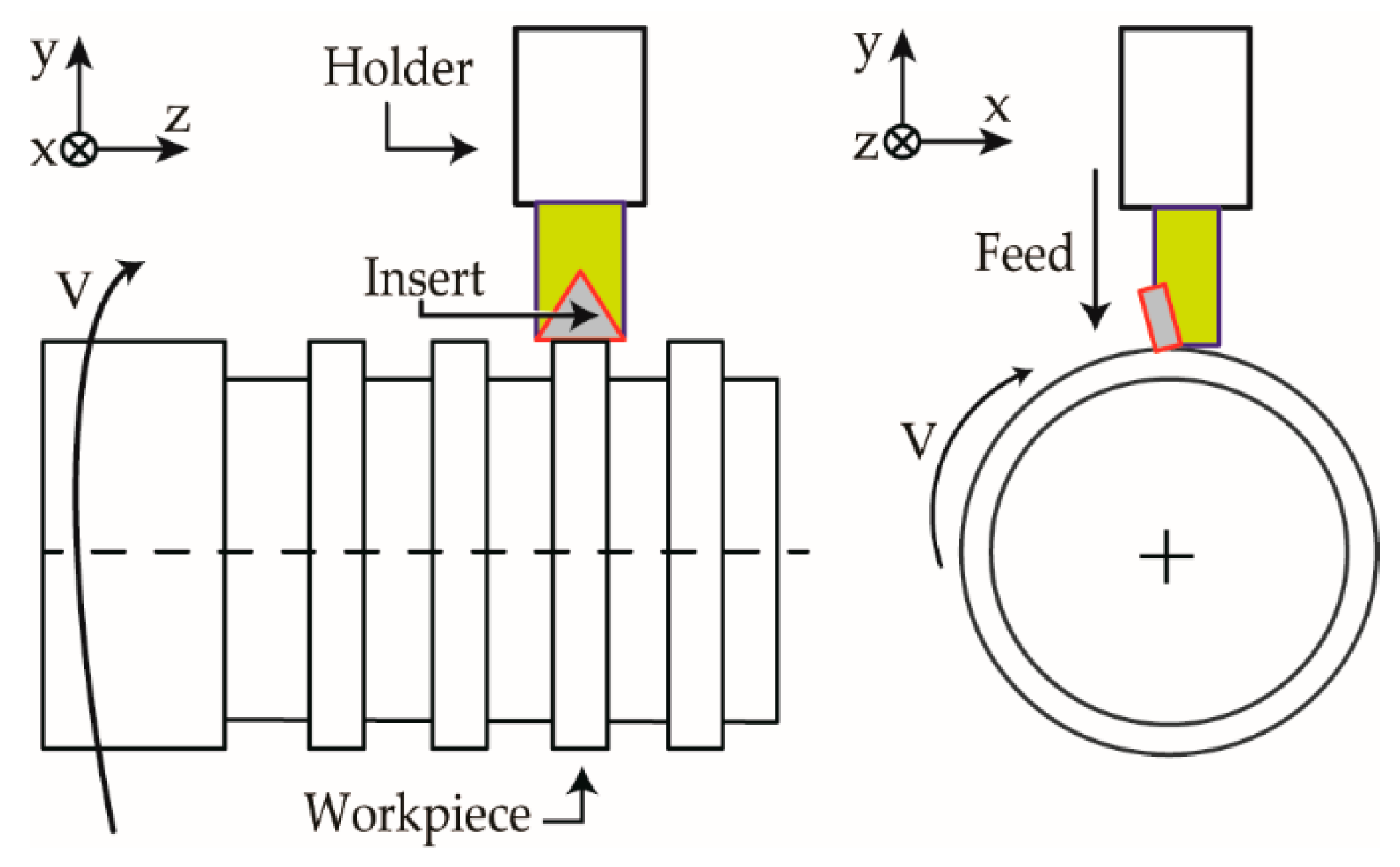
2. Experimental Work
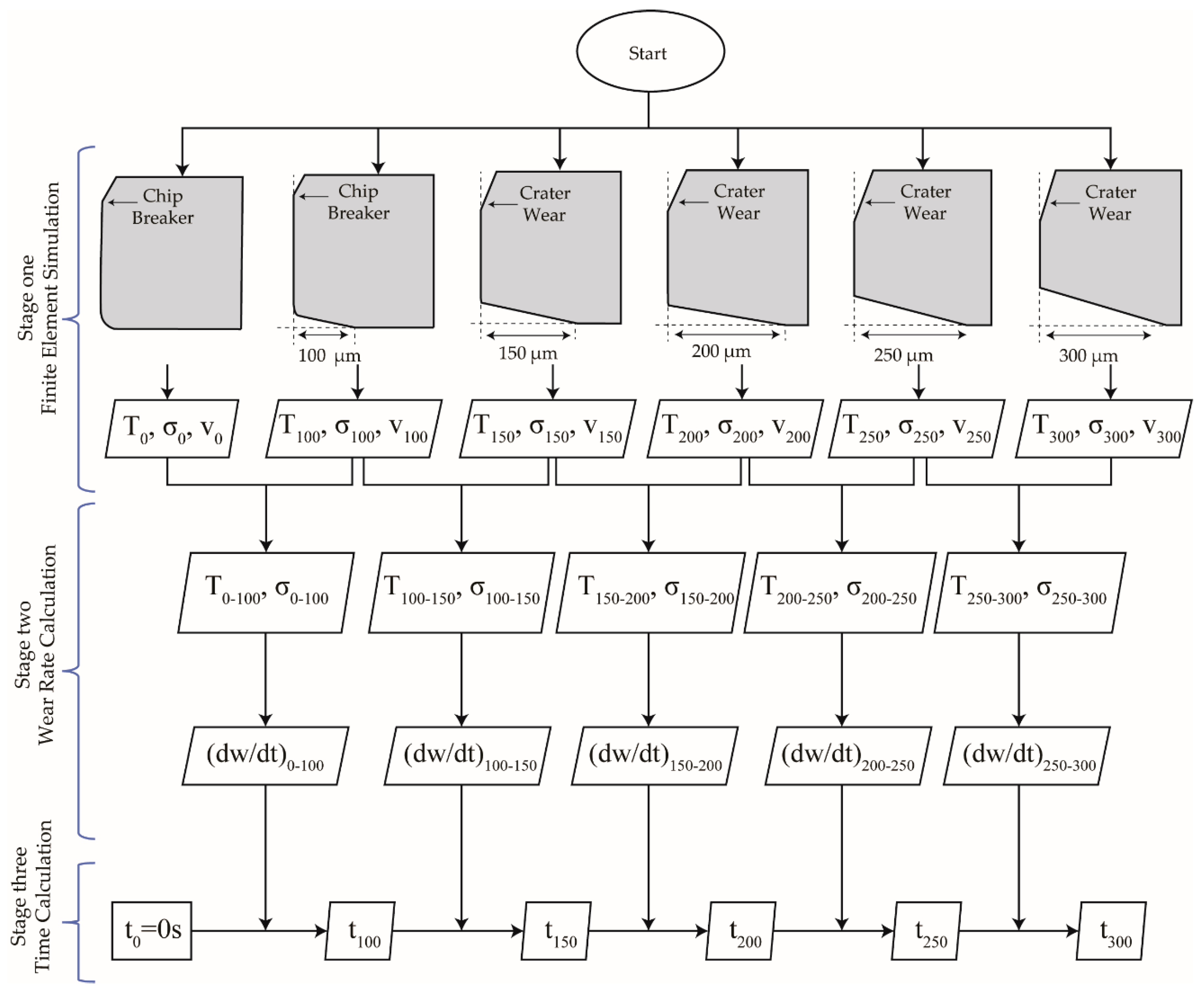
3. Tool Life Prediction Approach
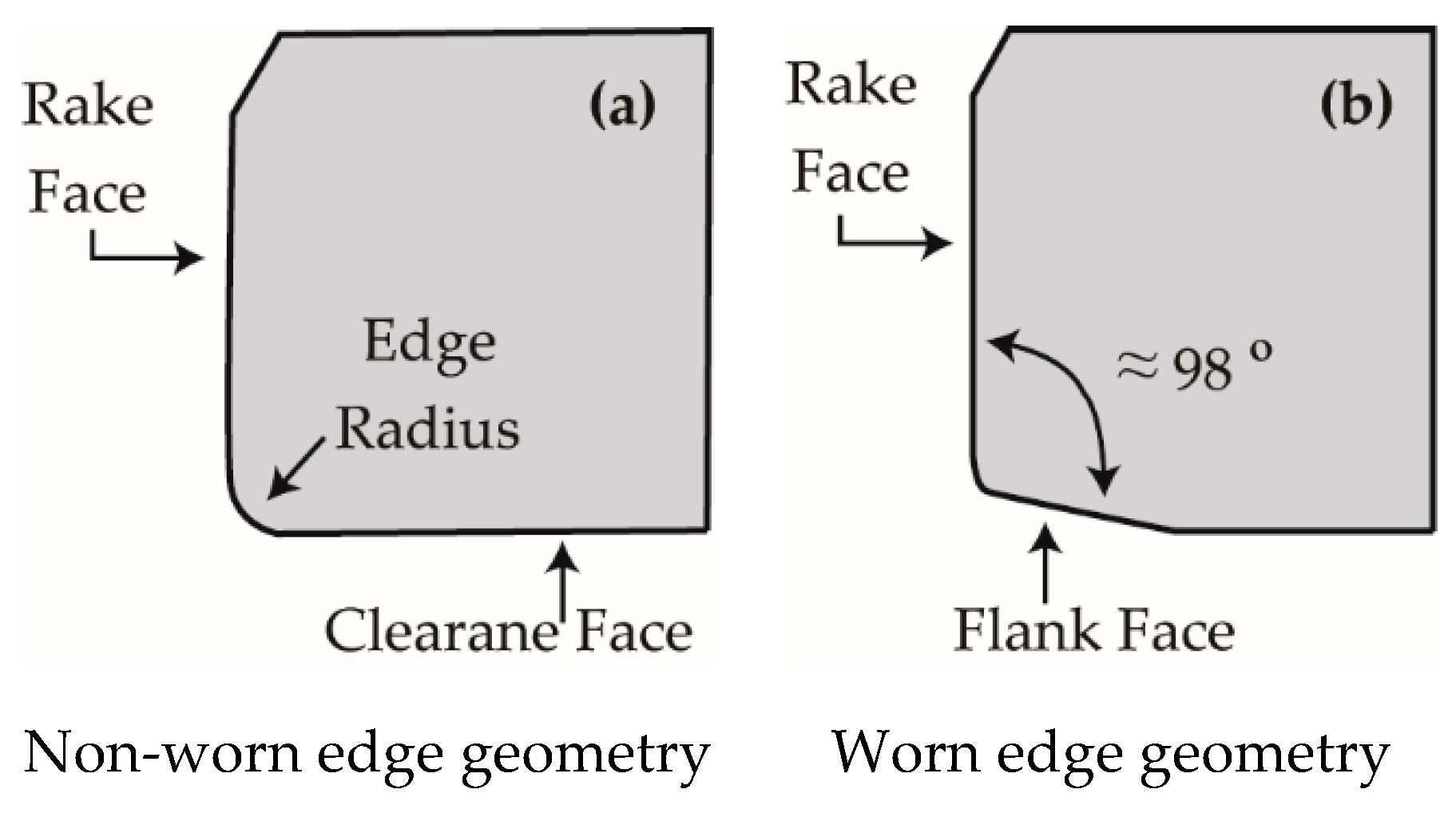
3.1. Finite Element Simulation
3.2. Wear Rate Calculation
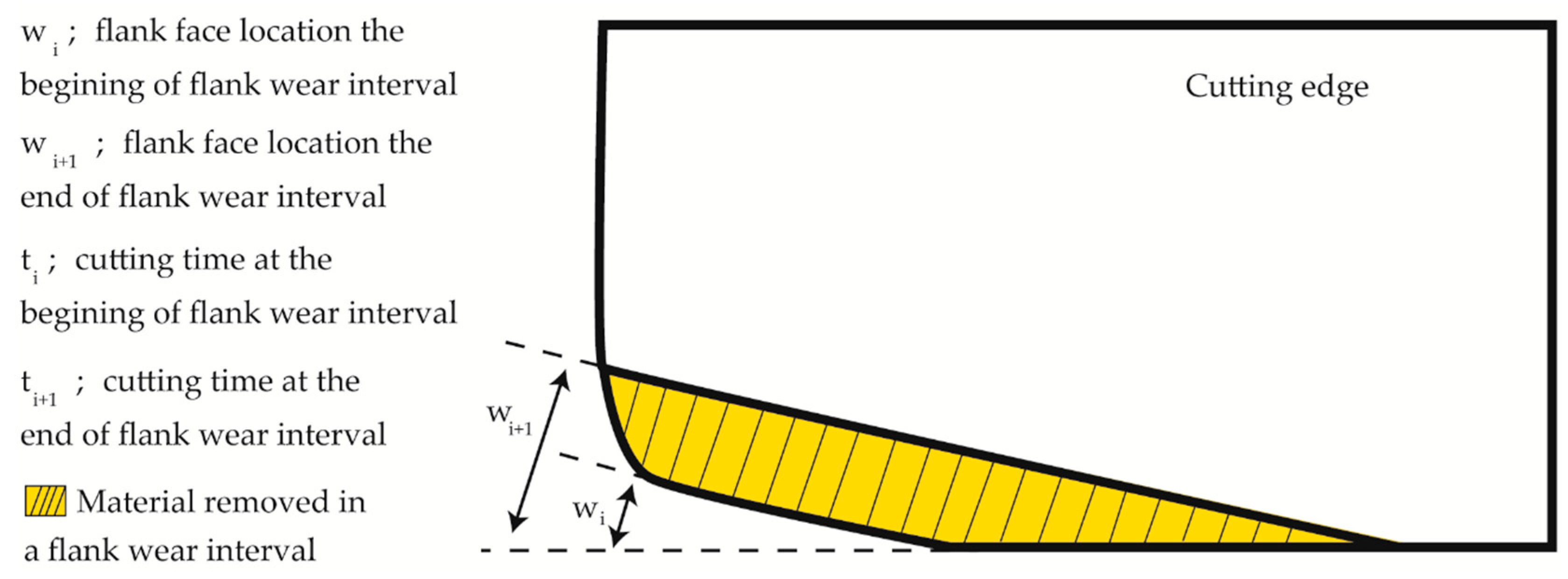
3.3. Cutting Time Calculation
4. Wear Rate Model Calibration
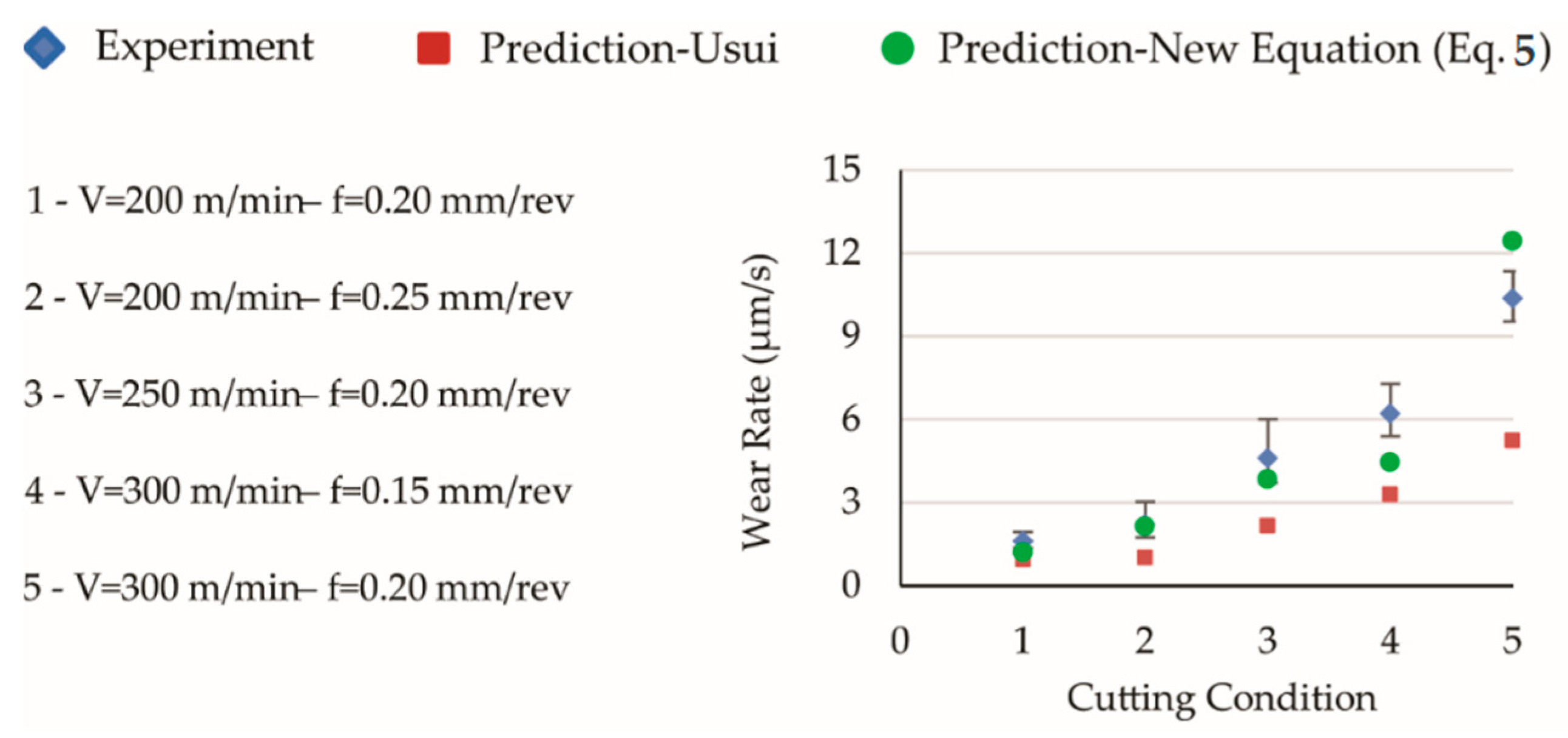
5. Results and Discussions
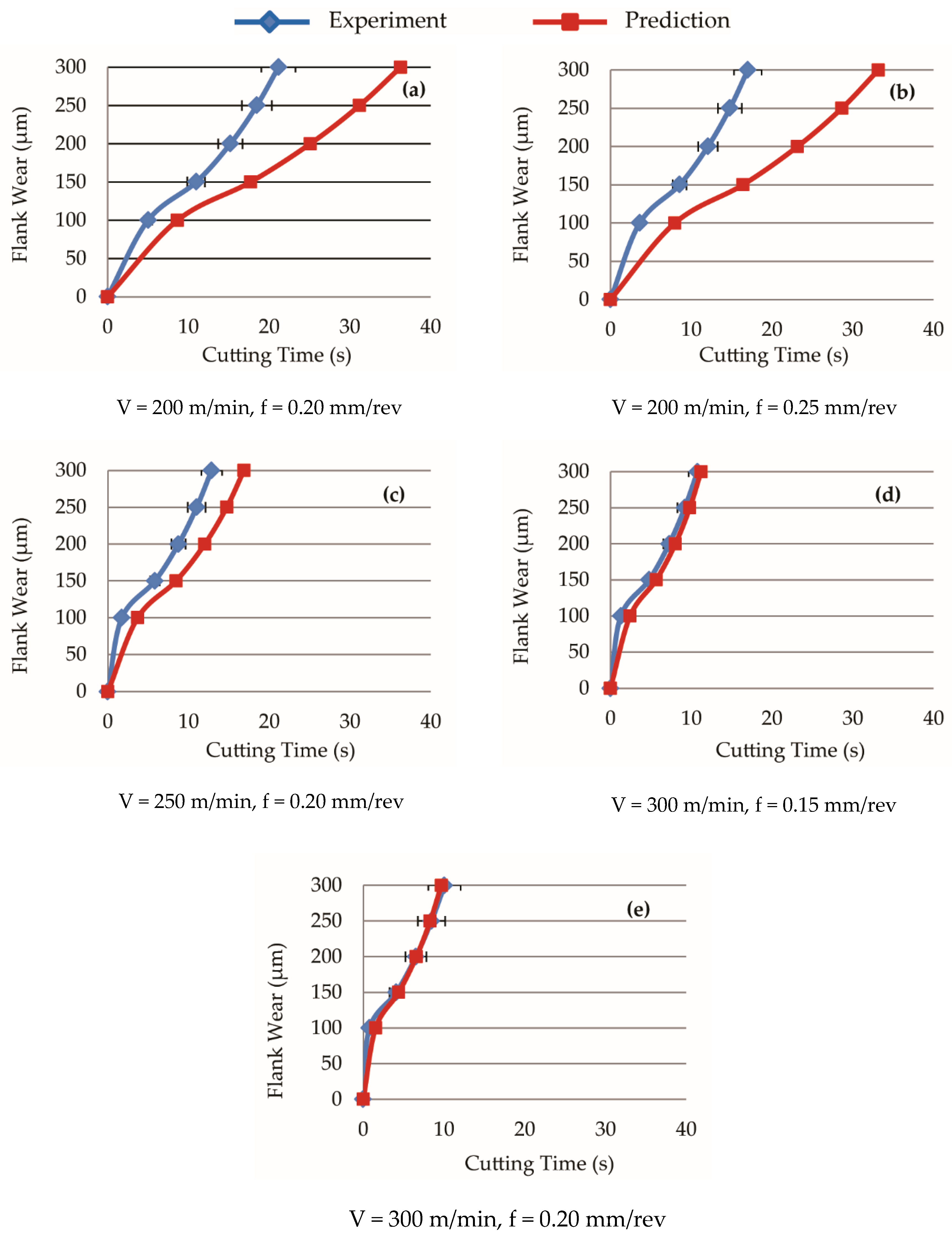
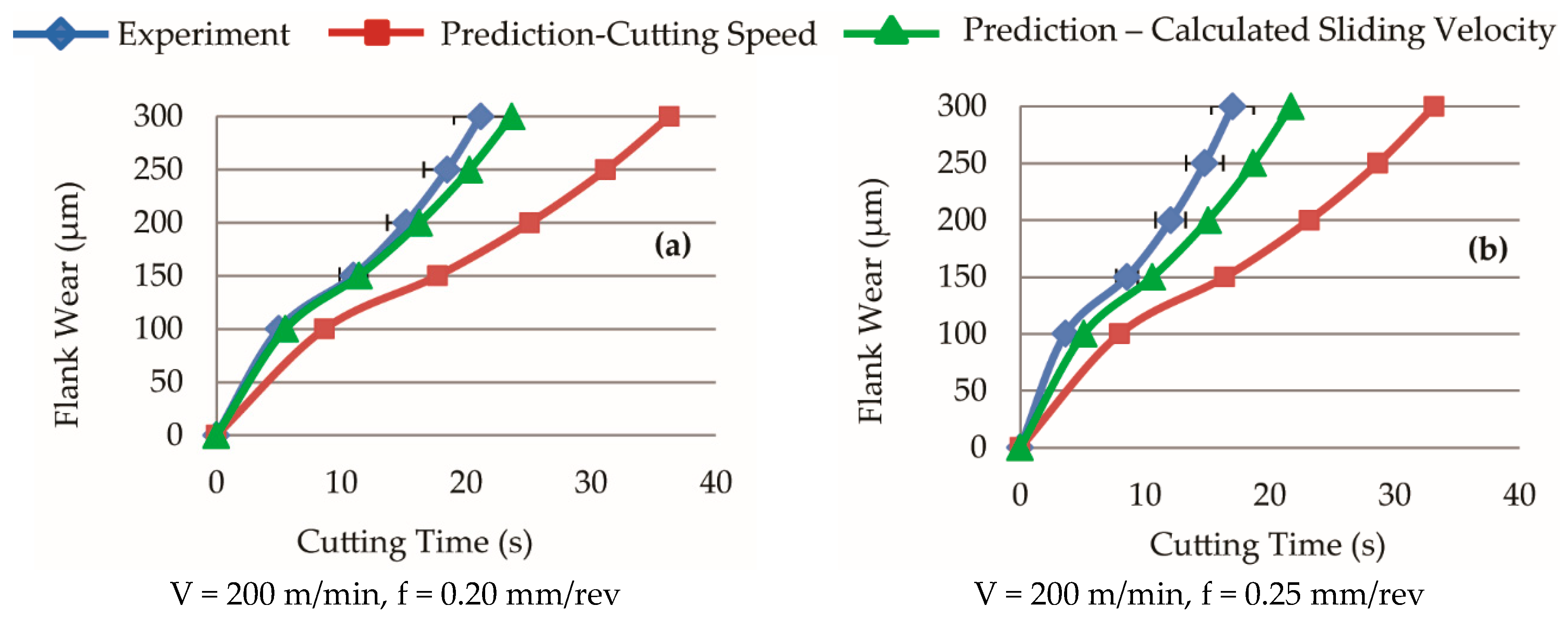
5.1. Tool Life
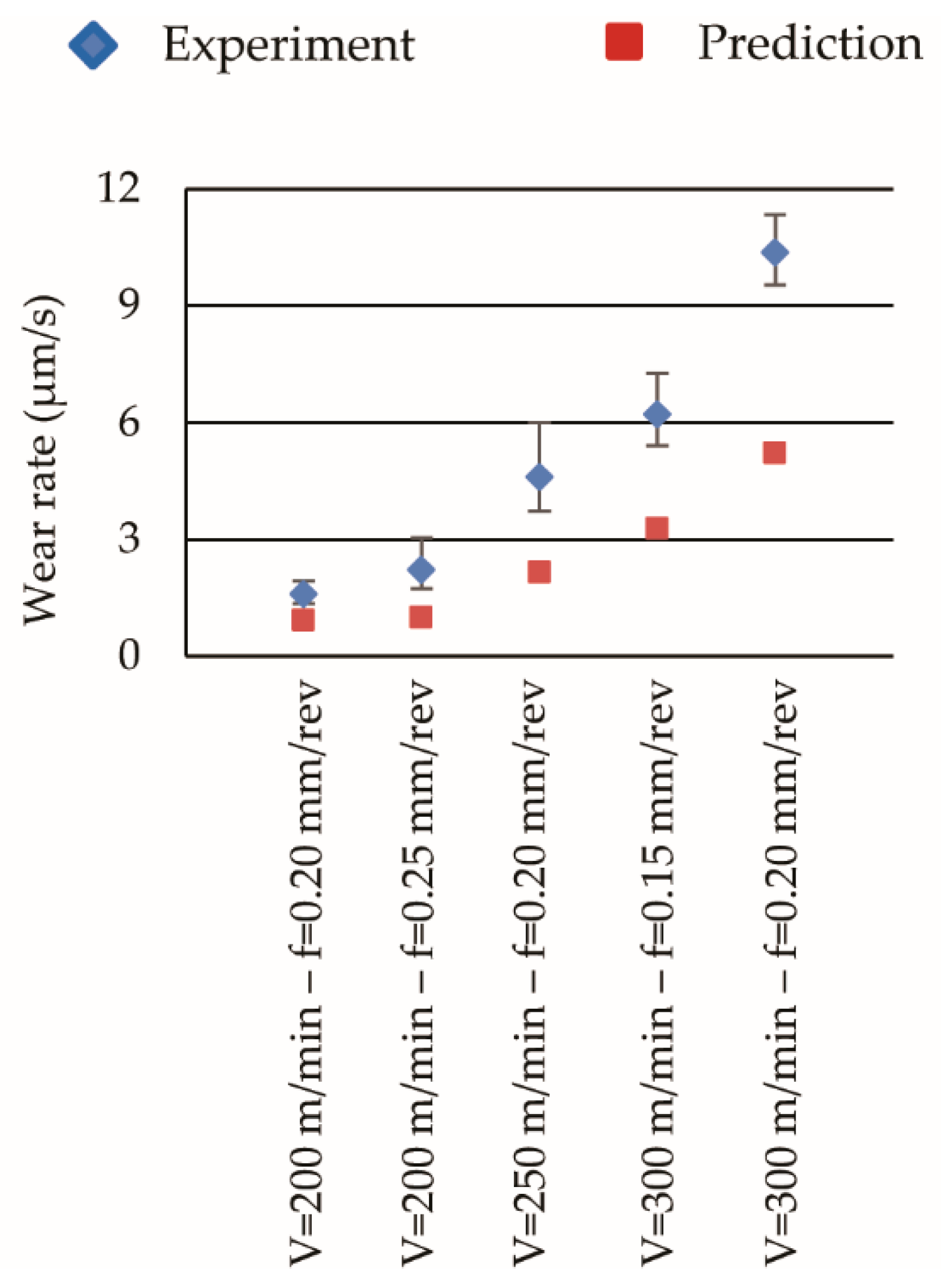
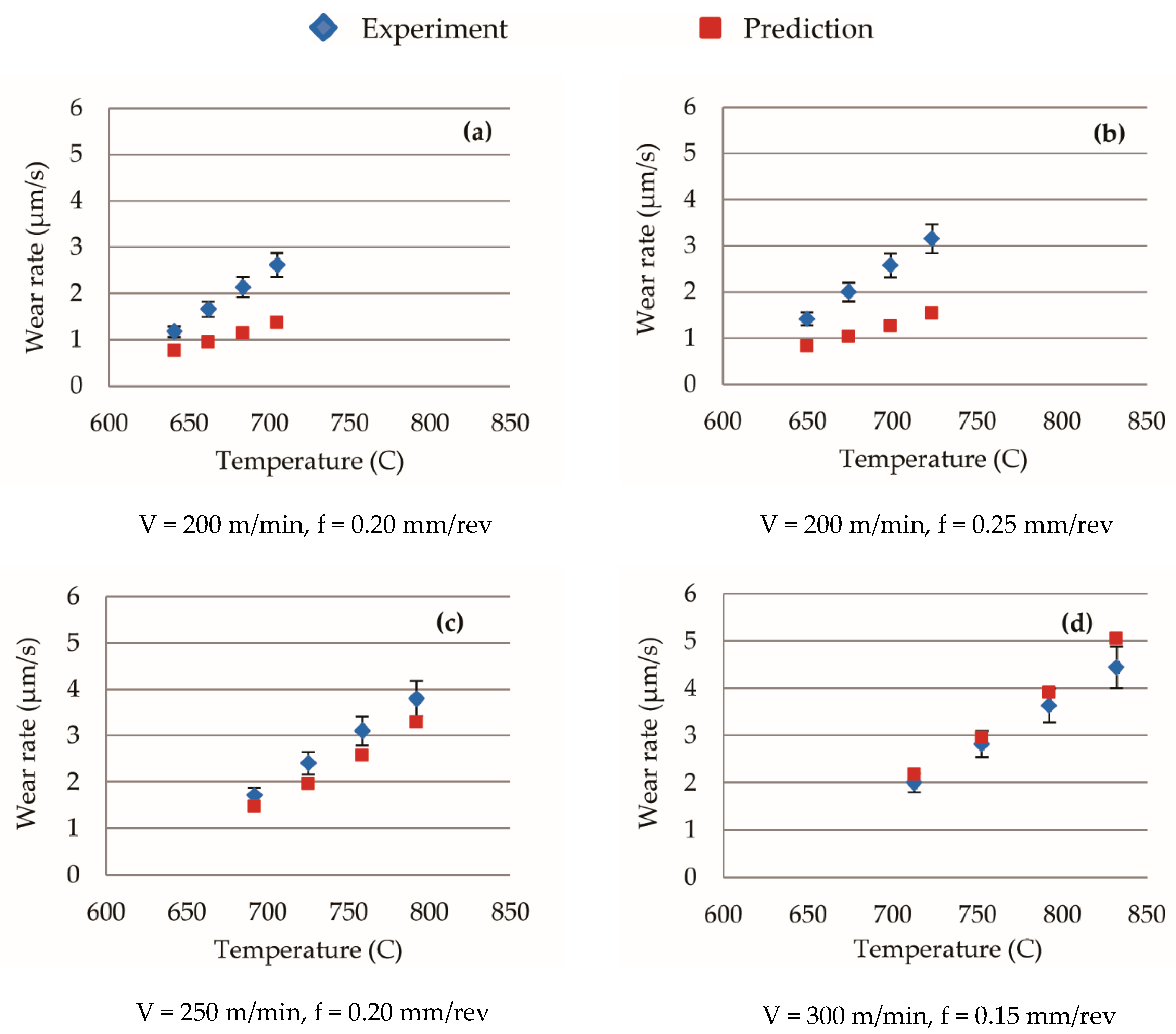
5.2. Wear Rate Predictions in the Initial Cutting Period
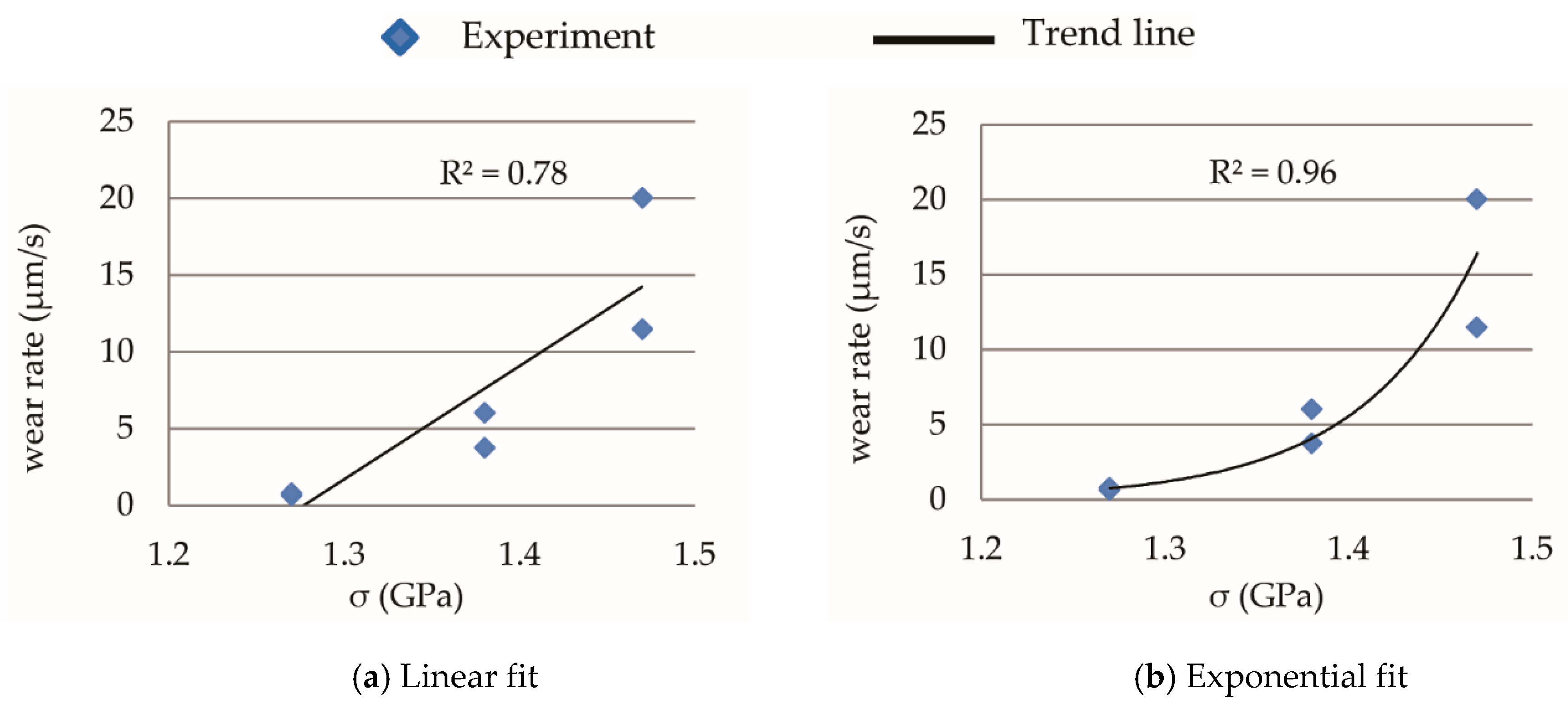
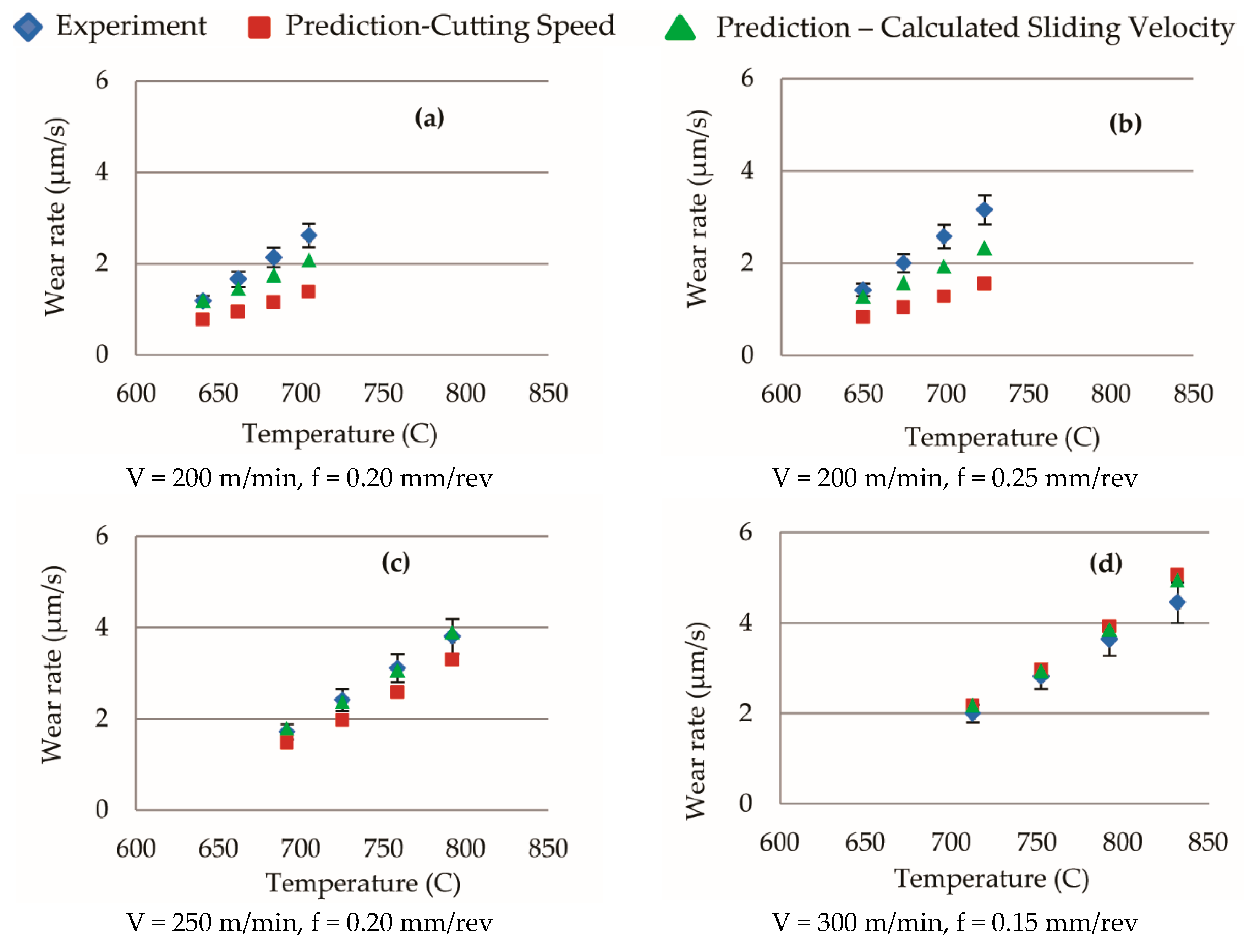
5.3. Recommendation for Improvement in Wear Rate Estimation During Initial Period
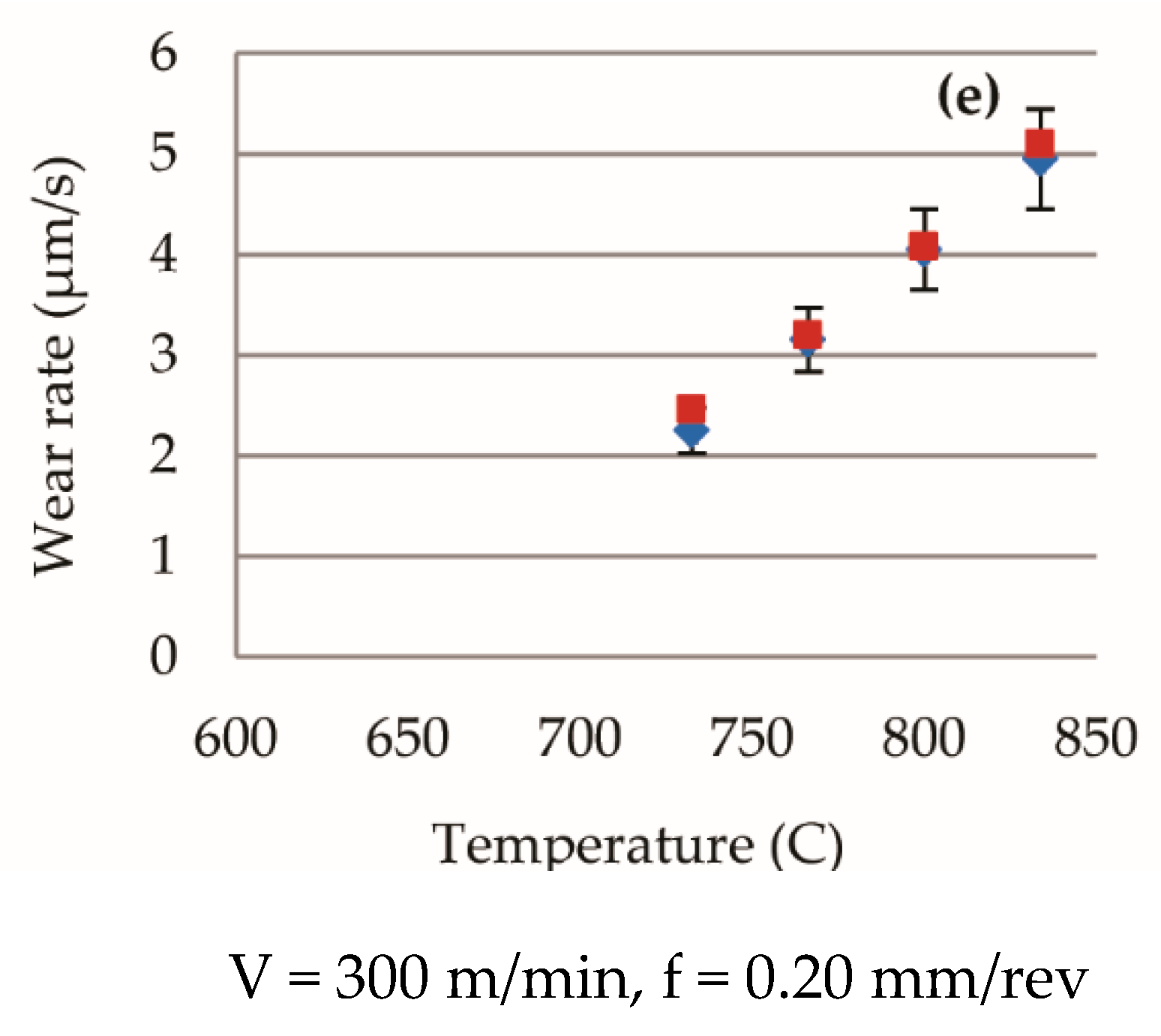
5.4. Wear Rate Predictions in the Secondary and Tertiary Cutting Periods
5.5. Strain and Velocity Distributions Beneath the Newly Generated Surface
5.6. Computational Time Improvement
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Taylor, F.W. On the art of cutting metals. Trans. Am. Soc. Mech. Eng. 1907, 28, 31–58. [Google Scholar]
- Li, B. A review of tool wear estimation using theoretical analysis and numerical simulation technologies. Int. J. Refract. Met. Hard Mater. 2012, 35, 143–151. [Google Scholar] [CrossRef]
- Shaw, M.C.; Dirke, S.O. On the wear of cutting tools. Microtecnic 1956, 10, 187–193. [Google Scholar]
- Trigger, K.J.; Chao, B.T. The mechanism of crater wear of cemented carbide tools. Trans. ASME 1956, 78, 1119. [Google Scholar]
- Usui, E.; Shirakashi, T.; Kitagawa, T. Analytical prediction of cutting tool wear. Int. J. Wear 1984, 100, 129–151. [Google Scholar] [CrossRef]
- Kitagawa, T.; Maekawa, K.; Shirakashi, T.; Usui, E. Analytical prediction of flank wear of carbide tools in turning plain carbon steels, part 1: Characteristic equation of flank wear. Bull. Japan Soc. Prec. Eng. 1988, 22, 263–269. [Google Scholar]
- Maekawa, K.; Kitagawa, T.; Shirakashi, T.; Usui, E. Analytical prediction of flank wear of carbide tools in turning plain carbon steels, part 2: Prediction of flank wear. Bull. Japan Soc. Prec. Eng. 1989, 23, 126–133. [Google Scholar]
- Denkena, B.; Köhler, J.; Mengesha, M.S. Influence of the cutting edge rounding on the chip formation process: Part 1. Investigation of material flow, process forces, and cutting temperature. Prod. Eng. 2012, 6, 329–338. [Google Scholar] [CrossRef]
- Sanchez, A.M.; Canteli, J.A.; Cantero, J.L.; Miguelez, M.H. Numerical analysis of tool wear effect in machining induced residual stresses. Simul. Model. Pract. Theory 2011, 19, 872–886. [Google Scholar] [CrossRef]
- Yen, Y.C.; Söhner, J.; Lilly, B.; Altan, T. Estimation of tool wear in orthogonal cutting using the finite element analysis. J. Mater. Process. Technol. 2004, 146, 82–91. [Google Scholar] [CrossRef]
- Xie, L.-J.; Schmidt, J.; Schmidt, C.; Biesinger, F. 2D FEM estimate of tool wear in turning operation. Int. J. Wear 2005, 258, 1479–1490. [Google Scholar] [CrossRef]
- Filice, L.; Micari, F.; Settineri, L.; Umbrello, D. Wear modelling in mild steel orthogonal cutting when using uncoated carbide tools. Int. J. Wear 2007, 262, 545–554. [Google Scholar] [CrossRef]
- Zanger, F.; Schulze, V. Investigation on Mechanisms of Tool Wear in Machining of Ti-6Al-4V using FEM Simulation. Procedia CIRP 2013, 8, 158–163. [Google Scholar] [CrossRef]
- Attanasio, A.; Ceretti, E.; Fiorentino, A.; Cappellini, C.; Giardini, C. Investigation and FEM-based simulation of tool wear in turning operations with uncoated carbide tools. Int. J. Wear 2010, 269, 344–350. [Google Scholar] [CrossRef]
- Attanasio, A.; Ceretti, E.; Giardini, C. 3D FEM Simulation of Flank Wear in Turning. In Proceedings of the 14th International ESAFORM Conference on Material Forming, Belfast, UK, 27–29 April 2011; pp. 561–566. [Google Scholar]
- Malakizadi, A.; Gruber, H.; Sadik, I.; Nyborg, L. An FEM-based approach for tool wear estimation in machining. Int. J. Wear 2016, 368–369, 10–24. [Google Scholar] [CrossRef]
- Malakizadi, A.; Cedergren, S.; Surreddi, K.B.; Nyborg, L. A methodology to evaluate the machinability of Alloy 718 by means of FE simulation. In Proceedings of Advanced Manufacturing Engineering and Technologies; NEWTECH: Stockholm, Sweden, 2013; pp. 95–106. [Google Scholar]
- Hosseinkhani, K.; Ng, E. A Combined Empirical and Numerical Approach for Tool Wear Prediction in Machining. Procedia CIRP 2015, 31, 304–309. [Google Scholar] [CrossRef]
- Lane, B.M.; Dow, T.A.; Scattergood, R. Thermo-chemical wear model and worn shapes for single-crystal diamond tools cutting steel. Int. J. Wear 2013, 300, 216–224. [Google Scholar] [CrossRef]
- Hosseinkhani, K.; Ng, E. Analysis of the cutting mechanics under the influence of worn tool geometry. Procedia CIRP 2013, 8, 117–122. [Google Scholar] [CrossRef]
- Hosseinkhani, K.; Ng, E. A hybrid experimental and simulation approach to evaluate the calibration of tool wear rate models in machining. Int. J. Adv. Manuf. Technol. 2018, 96, 2709–2724. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles, 2nd ed.; Oxford University Press Inc.: Oxford, UK, 2005. [Google Scholar]
- Binder, M.; Klocke, F.; Doebbeler, B. An advanced numerical approach on tool wear simulation for tool and process design in metal cutting. Simul. Model. Pract. Theory 2017, 70, 65–82. [Google Scholar] [CrossRef]
- Palmai, Z. Proposal for a new theoretical model of the cutting tool’s flank wear. Int. J. Wear 2013, 303, 437–445. [Google Scholar] [CrossRef]
- Filice, L.; Umbrello, D.; Beccasri, S.; Micari, F. On the FE Codes Capability for Tool Temperature Calculation in Machining Processes. J. Mater. Process. Technol. 2006, 174, 286–292. [Google Scholar] [CrossRef]
- Han, S.; Melkote, S.N.; Haluska, M.S.; Watkinsc, T.R. White Layer Formation Due to Phase Transformation in Orthogonal Machining of AISI 1045 Annealed Steel. Mater. Sci. Eng. 2008, 488, 195–204. [Google Scholar] [CrossRef]

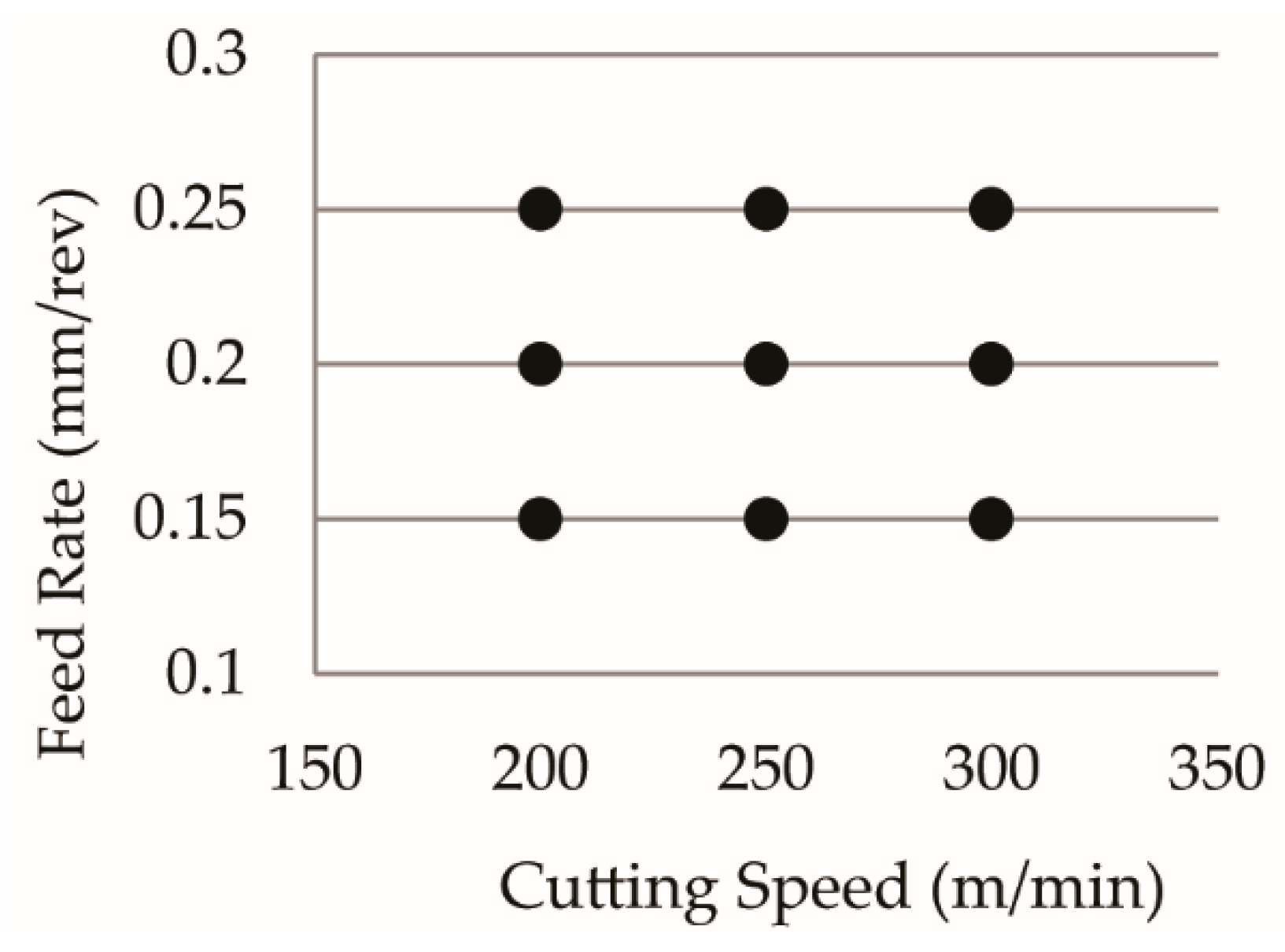







| Cutting Speed (m/min) | 200 to 300 |
| Feed Rate (mm/rev) | 0.15 to 0.25 |
| Depth of Cut (mm) | 3 |
| Rake Angle (°) | −6 |
| Flank Wear Intervals | Average Temperature and Pressure |
|---|---|
| 0–100 | |
| 100–150 | |
| 150–200 | |
| 200–250 | |
| 250–300 |
| Period | B1 (m2/MN) | B2 (°C) |
|---|---|---|
| Initial Period | 1.89 × 10−6 | 7141 |
| Secondary/Tertiary Periods | 1.95× 10−8 | 3266 |
| Region | B1 (m2/MN) | B2 (°C) |
|---|---|---|
| Initial Period | 9.14 × 10−5 | 7005 |
| Secondary/Tertiary Periods | 9.42 × 10−8 | 3135 |
| Computational Time in Series Approach, Equation (7) | Computational Time in Parallel Approach, Equation (8) | |||||
|---|---|---|---|---|---|---|
| (s) | 30 | 300 | 3000 | 30 | 300 | 3000 |
| (s) | 0.5 | 0.5 | 0.5 | |||
| (s) | 5 × 10−8 | 5 × 10−8 | 5 × 10−8 | 5 × 10−8 | 5 × 10−8 | 5 × 10−8 |
| 250,000 | 250,000 | 250,000 | 250,000 | 250,000 | 250,000 | |
| (s) | 120 | 120 | 120 | 120 | 120 | 120 |
| - | - | - | 6 | 6 | 6 | |
| Actual computational time | 0.28 × 106 s 4800 min | 2.88 × 106 s 48,000 min | 28.8 × 106 s 480,000 min | 28.8 × 103 s 480 min | 28.8 × 103 s 480 min | 28.8 × 103 s 480 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseinkhani, K.; Ng, E.-G. A Unique Methodology for Tool Life Prediction in Machining. J. Manuf. Mater. Process. 2020, 4, 16. https://doi.org/10.3390/jmmp4010016
Hosseinkhani K, Ng E-G. A Unique Methodology for Tool Life Prediction in Machining. Journal of Manufacturing and Materials Processing. 2020; 4(1):16. https://doi.org/10.3390/jmmp4010016
Chicago/Turabian StyleHosseinkhani, Keyvan, and Eu-Gene Ng. 2020. "A Unique Methodology for Tool Life Prediction in Machining" Journal of Manufacturing and Materials Processing 4, no. 1: 16. https://doi.org/10.3390/jmmp4010016
APA StyleHosseinkhani, K., & Ng, E.-G. (2020). A Unique Methodology for Tool Life Prediction in Machining. Journal of Manufacturing and Materials Processing, 4(1), 16. https://doi.org/10.3390/jmmp4010016




