Response Surface Methodology and Artificial Neural Network-Based Models for Predicting Performance of Wire Electrical Discharge Machining of Inconel 718 Alloy
Abstract
:1. Introduction
2. Experimentation
2.1. Workpiece Material
2.2. Experimental Setup
2.3. Response Surface Methodology (RSM)
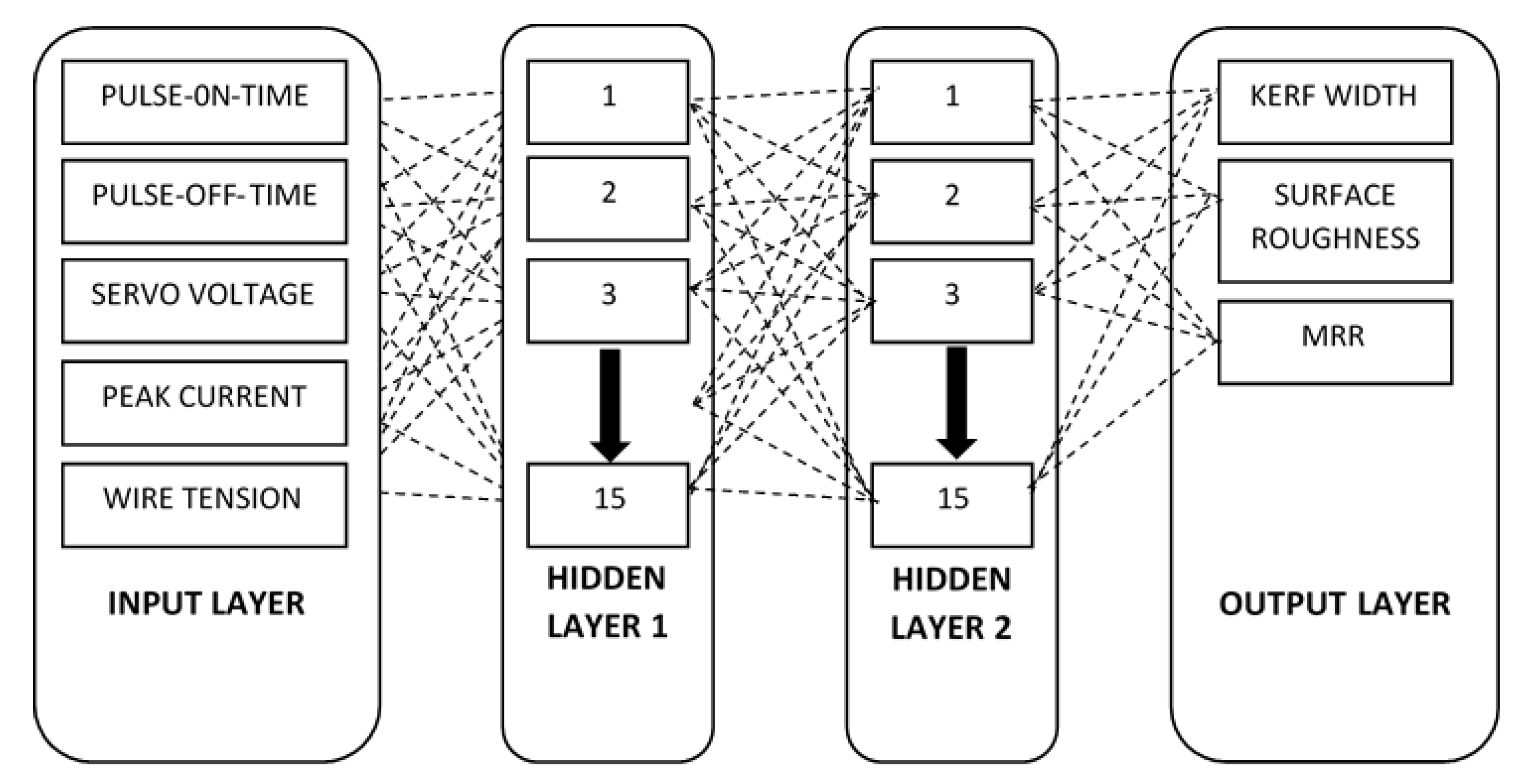
2.4. Artificial Neural Network (ANN)
2.5. Non-Dominated Sorting Genetic Algorithm (NSGA-II)
3. Results and Discussion
3.1. ANOVA Simulation
3.2. Regression Equations
3.3. ANN Performance
3.4. Validation Experiments
3.5. Parametric Study Using the Developed ANN Model
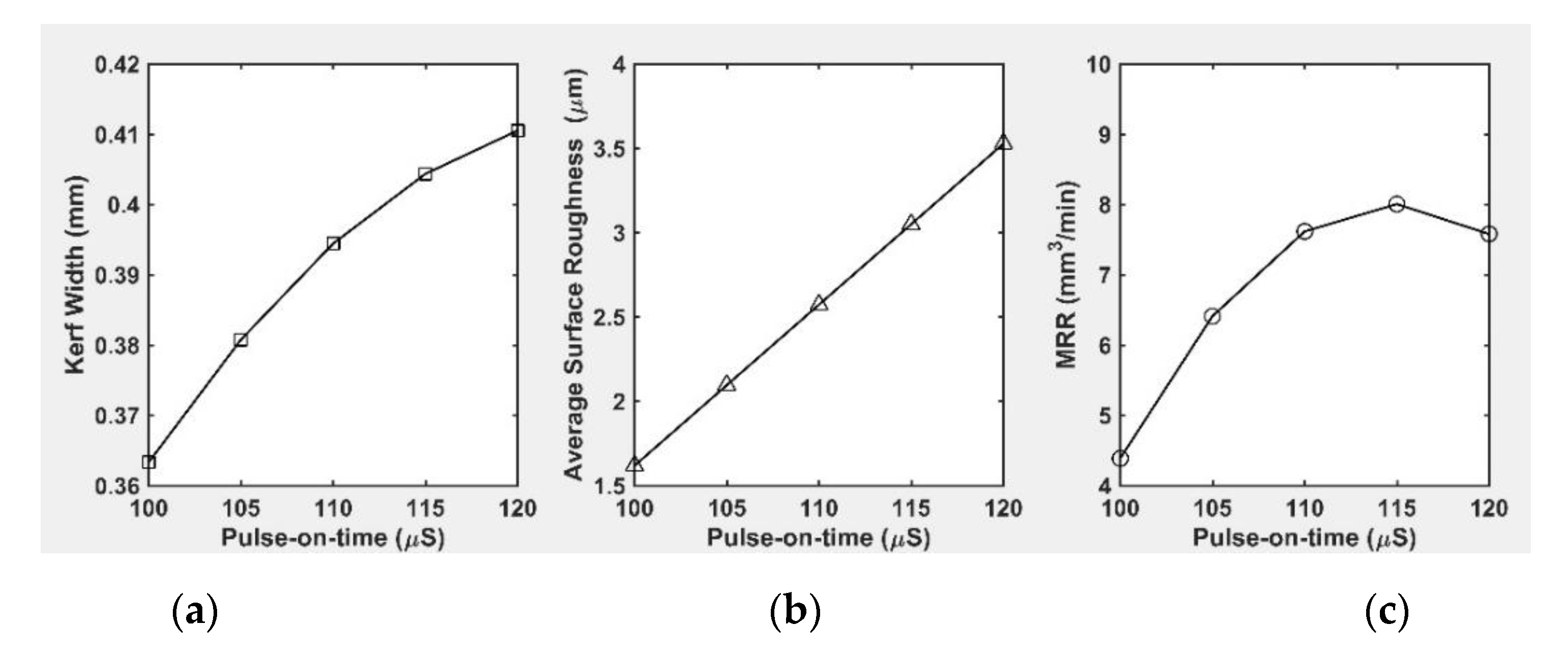
3.5.1. Effect of Pulse-On-Time
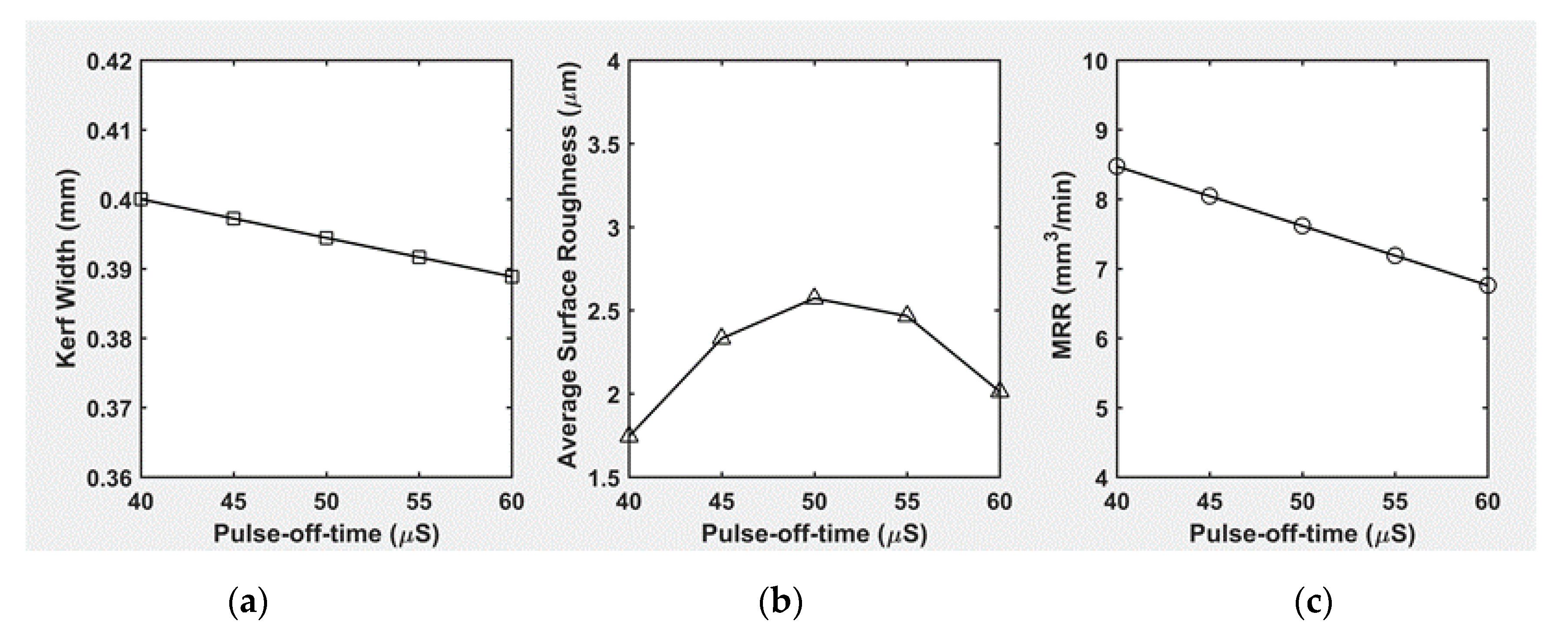
3.5.2. Effect of Pulse-Off-Time
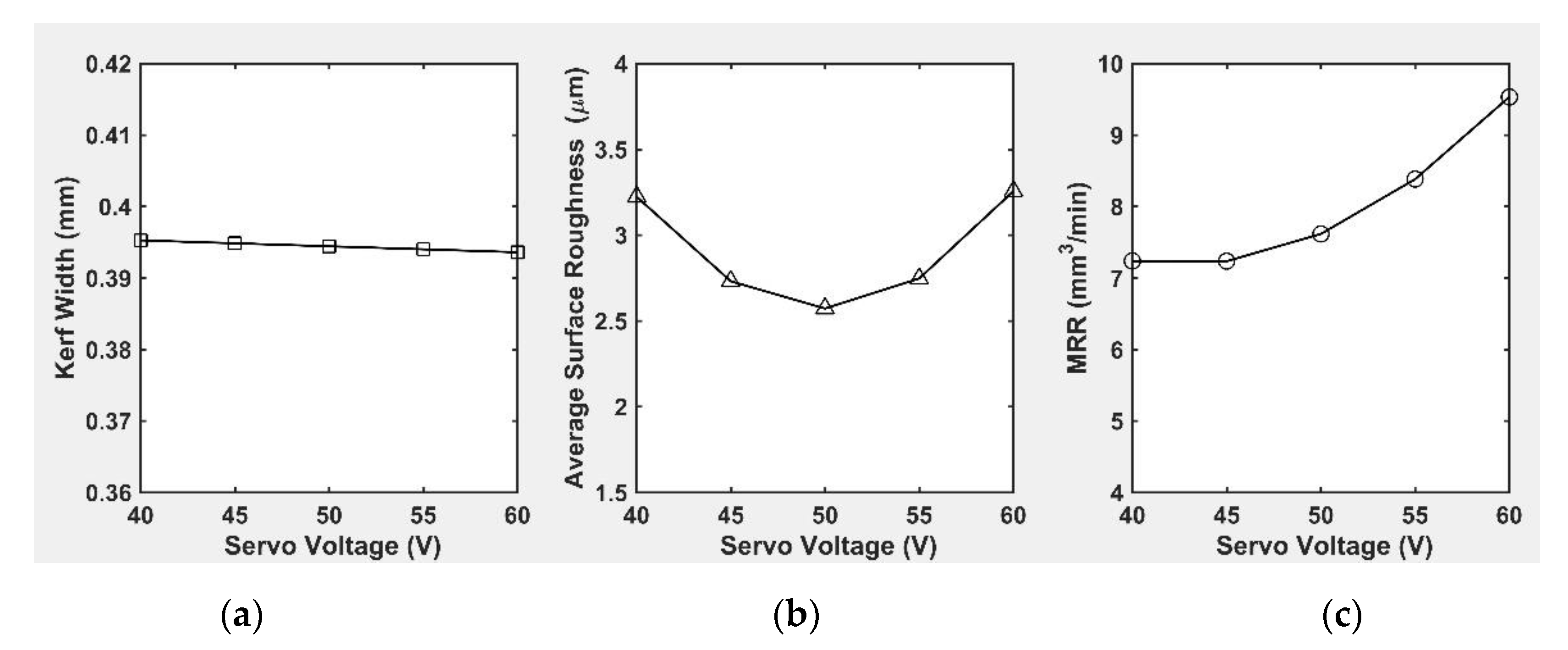
3.5.3. Effect of Servo-Voltage
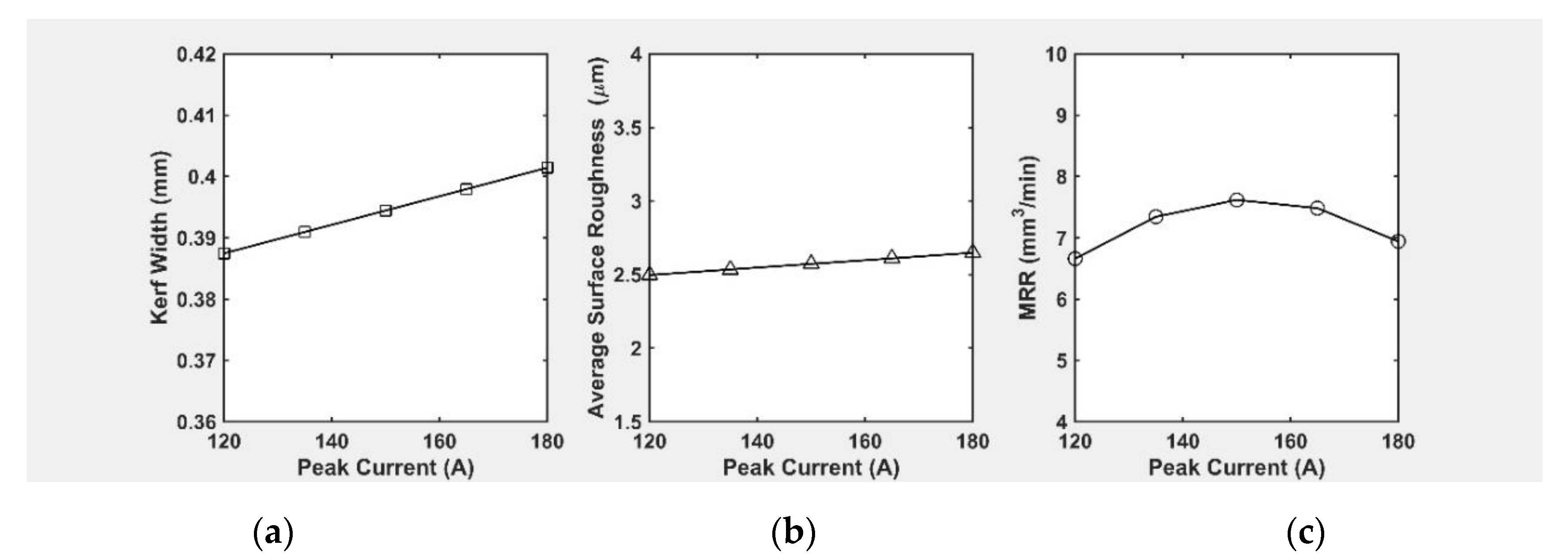
3.5.4. Effect of Peak Current
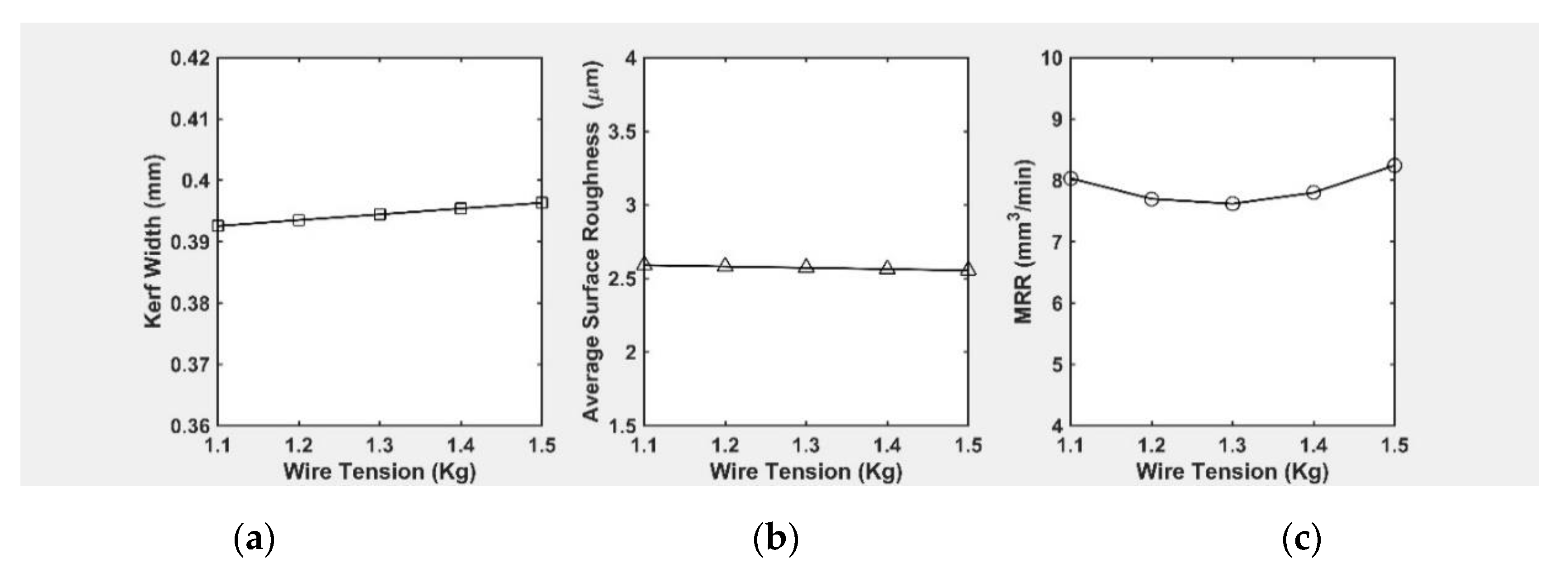
3.5.5. Effect of Wire Tension
3.6. Surface Morphology of the Wed Machined Specimens
3.7. NSGA-II Optimisation
4. Conclusions
- ANOVA results indicate that TON has the highest impact on the machining of Inconel 718 by the WEDM process. Here, the percentage contributions of TON on Kf, Ra, and MRR were found to be 73.07%, 90.31%, and 46.99%, respectively. With an incrase in TON, the Kf, Ra, and MRR were found to increase due to the increase of discharge energy.
- The results of ANOVA and analysis of experimental data indicate that the RSM models for Kf, Ra, and MRR are well fitted with the experimental values having a prediction error less than ±12%.
- A robust process model was developed on the basis of a feed-forward back propagation neural network structure with 5-13-15-3 structure with minimum prediction MSE.
- The confirmation experiments performed for the validation of both RSM and ANN models show that ANN, owing to its better modelling ability, is superior in giving appropriate and reliable predictions of Kf, Ra, and MRR compared to that of RSM models. The lower value of MSE for ANN (1.49%) than MSE for RSM (5.71%) further validates the better fitting of the neural network.
- The surface morphology of WEDM machined samples shows the presence of a larger size of globules of debris, bigger pockmarks and voids, and further uneven deposition of layers for high discharge energy settings.
Author Contributions
Funding
Conflicts of Interest
References
- Venkatesan, K. The study on force, surface integrity, tool life and chip on laser assisted machining of inconel 718 using Nd:YAG laser source. J. Adv. Res. 2017, 8, 407–423. [Google Scholar] [CrossRef] [PubMed]
- Nalbant, M.; Altın, A.; Gökkaya, H. The effect of cutting speed and cutting tool geometry on machinability properties of nickel-base Inconel 718 super alloys. Mater. Des. 2007, 28, 1334–1338. [Google Scholar] [CrossRef]
- Chalisgaonkar, R.; Kumar, J. Multi-response optimization and modeling of trim cut WEDM operation of commercially pure titanium (CPTi) considering multiple user’s preferences. Eng. Sci. Technol. Int. J. 2015, 18, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Sharma, N.; Khanna, R.; Gupta, R.D. WEDM process variables investigation for HSLA by response surface methodology and genetic algorithm. Eng. Sci. Technol. Int. J. 2015, 18, 171–177. [Google Scholar] [CrossRef] [Green Version]
- Najafi, F.T. The computer in the construction industry. Comput. Struct. 1991, 41, 1125–1132. [Google Scholar] [CrossRef]
- Tilekar, S.; Das, S.S.; Patowari, P.K. Process Parameter Optimization of Wire EDM on Aluminum and Mild Steel by Using Taguchi Method. Procedia Mater. Sci. 2014, 5, 2577–2584. [Google Scholar] [CrossRef]
- Tosun, N.; Cogun, C.; Tosun, G. A study on kerf and material removal rate in wire electrical discharge machining based on Taguchi method. J. Mater. Process. Technol. 2004, 152, 316–322. [Google Scholar] [CrossRef]
- Hewidy, M.S.; El-Taweel, T.A.; El-Safty, M.F. Modelling the machining parameters of wire electrical discharge machining of Inconel 601 using RSM. J. Mater. Process. Technol. 2005, 169, 328–336. [Google Scholar] [CrossRef]
- Mahapatra, S.S.; Patnaik, A. Optimization of wire electrical discharge machining (WEDM) process parameters using Taguchi method. Int. J. Adv. Manuf. Technol. 2006, 34, 911–925. [Google Scholar] [CrossRef]
- Kumar, K.; Agarwal, S. Multi-objective parametric optimization on machining with wire electric discharge machining. Int. J. Adv. Manuf. Technol. 2011, 62, 617–633. [Google Scholar] [CrossRef]
- Sarkar, S.; Mitra, S.; Bhattacharyya, B. Parametric analysis and optimization of wire electrical discharge machining of γ-titanium aluminide alloy. J. Mater. Process. Technol. 2005, 159, 286–294. [Google Scholar] [CrossRef]
- Kuriakose, S.; Mohan, K.; Shunmugam, M.S. Data mining applied to wire-EDM process. J. Mater. Process. Technol. 2003, 142, 182–189. [Google Scholar] [CrossRef]
- Manna, A.; Bhattacharyya, B. Taguchi and Gauss elimination method: A dual response approach for parametric optimization of CNC wire cut EDM of PRAlSiCMMC. Int. J. Adv. Manuf. Technol. 2005, 28, 67–75. [Google Scholar] [CrossRef]
- Bobbili, R.; Madhu, V.; Gogia, A.K. Modelling and analysis of material removal rate and surface roughness in wire-cut EDM of armour materials. Eng. Sci. Technol. Int. J. 2015, 18, 664–668. [Google Scholar] [CrossRef] [Green Version]
- Patil, N.G.; Brahmankar, P.K. Some studies into wire electro-discharge machining of alumina particulate-reinforced aluminum matrix composites. Int. J. Adv. Manuf. Technol. 2009, 48, 537–555. [Google Scholar] [CrossRef]
- Yadav, R.N.; Yadava, V. Multiobjective optimization of slotted electrical discharge abrasive grinding of metal matrix composite using artificial neural network and nondominated sorting genetic algorithm. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2013, 227, 1442–1452. [Google Scholar] [CrossRef]
- Samanta, B.; Erevelles, W.; Omurtag, Y. Prediction of workpiece surface roughness using soft computing. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2008, 222, 1221–1232. [Google Scholar] [CrossRef]
- Biswas, R.; Kuar, A.S.; Biswas, S.K.; Mitra, S. Artificial neural network modelling of Nd:YAG laser microdrilling on titanium nitride—Alumina composite. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2009, 224, 473–482. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Karunamoorthy, L. Modeling and multi-response optimization of Inconel 718 on machining of CNC WEDM process. J. Mater. Process. Technol. 2008, 207, 343–349. [Google Scholar] [CrossRef]
- Saha, P.; Singha, A.; Pal, S.K.; Saha, P. Soft computing models based prediction of cutting speed and surface roughness in wire electro-discharge machining of tungsten carbide cobalt composite. Int. J. Adv. Manuf. Technol. 2007, 39, 74–84. [Google Scholar] [CrossRef]
- Khan, I.A.; Rajput, T.S. Modeling of wire electrical discharge machining of alloy steel (HCHCr). Int. J. Precis. Eng. Manuf. 2012, 13, 1989–1995. [Google Scholar] [CrossRef]
- Shandilya, P.; Jain, P.K.; Jain, N.K. Prediction of surface roughness during wire electrical discharge machining of SiCp/6061 Al metal matrix composite. Int. J. Ind. Syst. Eng. 2012, 12. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Z.; Guo, J.; Ming, W.; Li, M.; Huang, Y. Modeling and Optimization of Medium-Speed WEDM Process Parameters for Machining SKD11. Mater. Manuf. Process. 2013, 28, 1124–1132. [Google Scholar] [CrossRef]
- Ugrasen, G.; Ravindra, H.V.; Prakash, G.V.N.; Keshavamurthy, R. Process Optimization and Estimation of Machining Performances Using Artificial Neural Network in Wire EDM. Procedia Mater. Sci. 2014, 6, 1752–1760. [Google Scholar] [CrossRef] [Green Version]
- Vates, U.K.; Singh, N.K.; Singh, R.V. Modelling of Process Parameters on D2 Steel using Wire Electrical Discharge Machining with combined approach of RSM and ANN. Int. J. Sci. Eng. Res. 2014, 8, 2026–2035. [Google Scholar]
- Shakeri, S.; Ghassemi, A.; Hassani, M.; Hajian, A. Investigation of material removal rate and surface roughness in wire electrical discharge machining process for cementation alloy steel using artificial neural network. Int. J. Adv. Manuf. Technol. 2015, 82, 549–557. [Google Scholar] [CrossRef]
- Jafari, R.; Kahya, M.; Oliaei, S.N.B.; Ünver, H.Ö.; Özyurt, T.O. Modeling and analysis of surface roughness of microchannels produced by μ-WEDM using an ANN and Taguchi method. J. Mech. Sci. Technol. 2017, 31, 5447–5457. [Google Scholar] [CrossRef]
- Singh, B.; Misra, J.P. Surface finish analysis of wire electric discharge machined specimens by RSM and ANN modeling. Measurement 2019, 137, 225–237. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Barman, T.; Sahoo, P.; Davim, J. Modeling and Optimization of Fractal Dimension in Wire Electrical Discharge Machining of EN 31 Steel Using the ANN-GA Approach. Materials 2019, 12, 454. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.R.; Rahman, M.M.; Kadirgama, K. An experimental investigation on surface finish in die-sinking EDM of Ti-5Al-2.5Sn. Int. J. Adv. Manuf. Technol. 2015, 77, 1727–1740. [Google Scholar] [CrossRef]
- Chaudhary, T.; Siddiquee, A.N.; Chanda, A.K. Effect of wire tension on different output responses during wire electric discharge machining on AISI 304 stainless steel. Def. Technol. 2019, 15, 541–544. [Google Scholar] [CrossRef]
- Unune, D.R.; Mali, H.S. Artificial neural network–based and response surface methodology–based predictive models for material removal rate and surface roughness during electro-discharge diamond grinding of Inconel 718. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2016, 230, 2082–2091. [Google Scholar] [CrossRef]
- Mazaheri, H.; Ghaedi, M.; Ahmadi Azqhandi, M.H.; Asfaram, A. Application of machine/statistical learning, artificial intelligence and statistical experimental design for the modeling and optimization of methylene blue and Cd(ii) removal from a binary aqueous solution by natural walnut carbon. Phys. Chem. Chem. Phys. 2017, 19, 11299–11317. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, S.; Senthilvelan, T.; Sriram, G. Evaluation of Machining Parameters of Hot Turning of Stainless Steel (Type 316) by Applying ANN and RSM. Mater. Manuf. Process. 2010, 25, 1131–1141. [Google Scholar] [CrossRef]
- Zopf, C.; Kaliske, M. Numerical characterisation of uncured elastomers by a neural network based approach. Comput. Struct. 2017, 182, 504–525. [Google Scholar] [CrossRef]
- Pradhan, B.B.; Bhattacharyya, B. Modelling of micro-electrodischarge machining during machining of titanium alloy Ti-6Al-4V using response surface methodology and artificial neural network algorithm. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2009, 223, 683–693. [Google Scholar] [CrossRef]
- Chokshi, P.; Dashwood, R.; Hughes, D.J. Artificial Neural Network (ANN) based microstructural prediction model for 22MnB5 boron steel during tailored hot stamping. Comput. Struct. 2017, 190, 162–172. [Google Scholar] [CrossRef] [Green Version]
- Unune, D.R.; Nirala, C.K.; Mali, H.S. ANN-NSGA-II dual approach for modeling and optimization in abrasive mixed electro discharge diamond grinding of Monel K-500. Eng. Sci. Technol. Int. J. 2018, 21, 322–329. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. Ieee Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Wang, H.; Hu, S.; Yang, C.; Wang, Y. Multi-objective online optimization of a marine diesel engine using NSGA-II coupled with enhancing trained support vector machine. Appl. Therm. Eng. 2018, 137, 218–227. [Google Scholar] [CrossRef]
- Unune, D.R.; Mali, H.S. Parametric modeling and optimization for abrasive mixed surface electro discharge diamond grinding of Inconel 718 using response surface methodology. Int. J. Adv. Manuf. Technol. 2017, 93, 3859–3872. [Google Scholar] [CrossRef]
- Dabade, U.A.; Karidkar, S.S. Analysis of Response Variables in WEDM of Inconel 718 Using Taguchi Technique. Procedia Cirp 2016, 41, 886–891. [Google Scholar] [CrossRef] [Green Version]
- Youssefi, S.; Emam-Djomeh, Z.; Mousavi, S.M. Comparison of Artificial Neural Network (ANN) and Response Surface Methodology (RSM) in the Prediction of Quality Parameters of Spray-Dried Pomegranate Juice. Dry. Technol. 2009, 27, 910–917. [Google Scholar] [CrossRef]
- Singh, V.; Bhandari, R.; Yadav, V.K. An experimental investigation on machining parameters of AISI D2 steel using WEDM. Int. J. Adv. Manuf. Technol. 2017, 93, 203–214. [Google Scholar] [CrossRef]
- Raju, P.; Sarcar, M.M.M.; Satyanarayana, B. Optimization of Wire Electric Discharge Machining Parameters for Surface Roughness on 316 L Stainless Steel Using Full Factorial Experimental Design. Procedia Mater. Sci. 2014, 5, 1670–1676. [Google Scholar] [CrossRef] [Green Version]
- Vijayabhaskar, S.; Rajmohan, T. Experimental Investigation and Optimization of Machining Parameters in WEDM of Nano-SiC Particles Reinforced Magnesium Matrix Composites. Silicon 2018. [Google Scholar] [CrossRef]
- Kumar, H.; Manna, A.; Kumar, R. Modeling of Process Parameters for Surface Roughness and Analysis of Machined Surface in WEDM of Al/SiC-MMC. Trans. Indian Inst. Met. 2018, 71, 231–244. [Google Scholar] [CrossRef]
- Kung, K.-Y.; Chiang, K.-T. Modeling and Analysis of Machinability Evaluation in the Wire Electrical Discharge Machining (WEDM) Process of Aluminum Oxide-Based Ceramic. Mater. Manuf. Process. 2008, 23, 241–250. [Google Scholar] [CrossRef]
- Sreenivasa Rao, M.; Venkaiah, N. Experimental investigations on surface integrity issues of Inconel-690 during wire-cut electrical discharge machining process. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2016, 232, 731–741. [Google Scholar] [CrossRef]
- Unune, D.R.; Mali, H.S. Experimental investigation on low-frequency vibration-assisted µ-ED milling of Inconel 718. Mater. Manuf. Process. 2018, 33, 964–976. [Google Scholar] [CrossRef]
- Torres, A.; Puertas, I.; Luis, C.J. Modelling of surface finish, electrode wear and material removal rate in electrical discharge machining of hard-to-machine alloys. Precis. Eng. 2015, 40, 33–45. [Google Scholar] [CrossRef]




| Author(s) | Prediction Model | Training Method | Work Piece | Machining Parameters | Response Variables | Summary |
|---|---|---|---|---|---|---|
| Ramakrishnan and Karunamoorthy [19] | feedforward neural network | - | Inconel 601 | TON, delay time, wire feed rate, ignition current | MRR, Ra | TON found to be most imfluecing factor for MRR. |
| Saha et al. [20] | feed-forward back-propagation neural network with 1-hidden layer | - | tungsten carbide-cobalt (WC-Co) composite | TON, TOFF, IP, capacitance | Cutting speed, Ra | ANN predicts MRR & Ra with 3.29% overall mean prediction error. |
| Khan and Rajput [21] | feed-forward back-propagation neural network | - | Alloy Steel (HCHCr) | TON, TOFF, IP, average gap voltage, WT, Wire feed | Cutting speed, Ra | Higher cutting speed degrades surface finish. |
| Shandilya and Jain [22] | Back-propagation neural network with 1-hidden layer | - | SiCp/6061 Al metal matrix composite | TON, TOFF, voltage, wire feed | Surface roughness | ANN model outperforms RSM model prediction. |
| Zhang et al. [23] | BPNN with 2-hidden layers | - | SKD11 steel | TON, TOFF, IP, wire speed, tracking coefficient | Cutting speed, Ra, MRR | TON, TOFF are significant factors for Ra. |
| Ugrasen et al. [24] | BPNN with 1-hidden layer | Levenberg-Marquardt | - | TON, pulse-off-time, IP, bed speed | VMRR, accuracy, Ra | ANN model with 70% training data gave best prediction as that of model with 50% or 60% training data. |
| Vates et al. [25] | ANN with 1-hidden layer | - | D2 Steel | gap voltage, flush rate, TON, TOFF, wire feed, and WT | Ra, MRR | Best surface finish achieved at lower MRR values. |
| Shakeri et al. [26] | Feedforward backpropagation neural network | Levenberg-Marquardt | cementation alloy steel | wire speed, servo speed, frequency, IP | Ra, MRR | ANN model outperformed Regression models prediction. |
| Jafari et al. [27] | ANN with 1-hidden layer | Bayesian regularization | Copper | TON, TOFF, IP, spark gap voltage, wire speed | Ra | IP had most significant effect of Ra followed by TON. |
| Singh and Mishra [28] | BPNN with 1-hidden layer | Levenberg-Marquardt | Nimonic 263 | TON, TOFF, IP, spark gap voltage | Ra, recast layer thickness | |
| Mukhopadhyay et al. [29] | feedforward neural network | Levenberg-Marquardt | EN 31 tool steel | Discharge current, SV, TON, TOFF | fractal dimension |
| Component | Ni | C | Si | Mn | P | Cr | Fe | Mo |
|---|---|---|---|---|---|---|---|---|
| Weight % | 55.40 | 00.03 | 00.08 | 00.04 | 00.01 | 23.80 | 03.70 | 13.30 |
| Component | V | Nb | W | Co | Ti | Al | Zr | |
| Weight % | 00.09 | 02.78 | 00.26 | 00.26 | 00.81 | 00.19 | 00.08 |
| Input Parameter | Symbol | Unit | Level | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| pulse-on-time | TON | µs | 100 | 110 | 120 |
| pulse-off-time | TOFF | µs | 40 | 50 | 60 |
| servo-voltage | SV | V | 40 | 50 | 60 |
| peak current | IP | A | 120 | 150 | 180 |
| wire tension | WT | kg | 1.1 | 1.3 | 1.5 |
| S. No. | Input Machining Parameters | Response Variables | ||||||
|---|---|---|---|---|---|---|---|---|
| Pulse on Time (µs) | Pulse off Time (µs) | Servo Voltage (V) | Peak current (A) | Wire Tension (kg) | Kerf Width (mm) | Average Surface Roughness (µm) | MRR (mm3/min) | |
| 1 | 120 | 40 | 60 | 120 | 1.1 | 0.402 | 3.71 | 10.53 |
| 2 | 100 | 40 | 40 | 180 | 1.1 | 0.382 | 1.71 | 05.28 |
| 3 | 100 | 60 | 40 | 120 | 1.1 | 0.350 | 1.52 | 02.39 |
| 4 | 120 | 60 | 60 | 120 | 1.1 | 0.385 | 3.77 | 09.04 |
| 5 | 110 | 40 | 50 | 150 | 1.3 | 0.399 | 1.51 | 08.34 |
| 6 | 120 | 60 | 60 | 120 | 1.5 | 0.404 | 3.58 | 08.18 |
| 7 | 120 | 50 | 50 | 150 | 1.3 | 0.416 | 3.51 | 08.19 |
| 8 | 100 | 40 | 40 | 120 | 1.1 | 0.356 | 1.75 | 04.64 |
| 9 | 120 | 60 | 40 | 180 | 1.5 | 0.404 | 3.81 | 05.85 |
| 10 | 110 | 50 | 50 | 150 | 1.5 | 0.395 | 2.86 | 07.91 |
| 11 | 100 | 40 | 60 | 120 | 1.5 | 0.369 | 1.27 | 06.53 |
| 12 | 120 | 60 | 40 | 120 | 1.5 | 0.411 | 3.38 | 05.58 |
| 13 | 120 | 60 | 40 | 120 | 1.1 | 0.391 | 3.55 | 05.38 |
| 14 | 120 | 40 | 60 | 180 | 1.1 | 0.433 | 3.09 | 10.22 |
| 15 | 100 | 60 | 60 | 180 | 1.1 | 0.361 | 1.74 | 05.14 |
| 16 | 110 | 50 | 50 | 120 | 1.3 | 0.386 | 2.27 | 06.68 |
| 17 | 100 | 50 | 50 | 150 | 1.3 | 0.365 | 1.61 | 04.19 |
| 18 | 120 | 40 | 60 | 120 | 1.5 | 0.433 | 2.87 | 10.36 |
| 19 | 120 | 40 | 40 | 120 | 1.1 | 0.397 | 3.35 | 07.38 |
| 20 | 110 | 50 | 50 | 150 | 1.3 | 0.392 | 2.60 | 07.96 |
| 21 | 110 | 50 | 50 | 150 | 1.3 | 0.378 | 2.52 | 07.54 |
| 22 | 100 | 60 | 60 | 120 | 1.1 | 0.350 | 1.70 | 04.91 |
| 23 | 100 | 60 | 60 | 120 | 1.5 | 0.337 | 1.51 | 04.78 |
| 24 | 120 | 40 | 40 | 180 | 1.5 | 0.411 | 3.51 | 07.78 |
| 25 | 100 | 40 | 40 | 120 | 1.5 | 0.366 | 1.55 | 04.94 |
| 26 | 100 | 40 | 60 | 120 | 1.1 | 0.349 | 1.48 | 06.36 |
| 27 | 120 | 40 | 60 | 180 | 1.5 | 0.426 | 3.30 | 10.80 |
| 28 | 120 | 60 | 60 | 180 | 1.5 | 0.407 | 4.00 | 08.85 |
| 29 | 100 | 60 | 40 | 180 | 1.1 | 0.368 | 1.54 | 03.47 |
| 30 | 100 | 60 | 40 | 120 | 1.5 | 0.360 | 1.32 | 02.69 |
| 31 | 110 | 50 | 50 | 150 | 1.3 | 0.392 | 2.59 | 07.35 |
| 32 | 120 | 60 | 60 | 180 | 1.1 | 0.414 | 3.80 | 08.95 |
| 33 | 110 | 50 | 50 | 180 | 1.3 | 0.402 | 2.49 | 07.33 |
| 34 | 100 | 40 | 60 | 180 | 1.1 | 0.381 | 1.53 | 05.19 |
| 35 | 100 | 60 | 60 | 180 | 1.5 | 0.359 | 1.91 | 05.64 |
| 36 | 110 | 50 | 50 | 150 | 1.3 | 0.391 | 2.59 | 07.44 |
| 37 | 110 | 50 | 50 | 150 | 1.3 | 0.385 | 2.91 | 07.96 |
| 38 | 110 | 60 | 50 | 150 | 1.3 | 0.387 | 2.28 | 06.41 |
| 39 | 110 | 50 | 50 | 150 | 1.3 | 0.392 | 2.64 | 07.41 |
| 40 | 100 | 40 | 60 | 180 | 1.5 | 0.366 | 1.91 | 06.79 |
| 41 | 100 | 40 | 40 | 180 | 1.5 | 0.370 | 1.20 | 05.38 |
| 42 | 120 | 40 | 40 | 120 | 1.5 | 0.407 | 3.14 | 07.33 |
| 43 | 110 | 50 | 50 | 150 | 1.3 | 0.402 | 2.59 | 07.16 |
| 44 | 110 | 50 | 60 | 150 | 1.3 | 0.394 | 3.00 | 08.92 |
| 45 | 120 | 40 | 40 | 180 | 1.1 | 0.419 | 3.36 | 07.18 |
| 46 | 110 | 50 | 50 | 150 | 1.3 | 0.392 | 2.56 | 07.40 |
| 47 | 120 | 60 | 40 | 180 | 1.1 | 0.410 | 3.69 | 04.82 |
| 48 | 110 | 50 | 50 | 150 | 1.1 | 0.392 | 2.15 | 08.77 |
| 49 | 100 | 60 | 40 | 180 | 1.5 | 0.378 | 1.71 | 03.83 |
| 50 | 110 | 50 | 40 | 150 | 1.3 | 0.420 | 3.51 | 08.26 |
| Source | Sum of Square | Degree of freedom | Mean Square | F Value | p-Value Prob > F | Percentage Contribution | |
|---|---|---|---|---|---|---|---|
| Model | 0.024 | 09 | 2.655 × 10−3 | 053.32 | <0.0001 | significant | |
| A-Pulse-on-time | 0.019 | 01 | 0.019 | 379.94 | <0.0001 | 73.07% | |
| B-Pulse-off-time | 1.055 × 10−4 | 01 | 1.055 × 10−3 | 021.20 | <0.0001 | 00.40% | |
| C-Servo Voltage | 2.375 × 10−5 | 01 | 2.375 × 10−5 | 000.48 | 0.4938 | 00.09% | |
| D-Peak Current | 1.657 × 10−3 | 01 | 1.657 × 10−3 | 033.28 | <0.0001 | 06.37% | |
| E-Wire Tension | 1.210 × 10−4 | 01 | 1.210 × 10−4 | 002.43 | 0.1269 | 00.46% | |
| AC | 3.890 × 10−4 | 01 | 3.890 × 10−4 | 007.81 | 0.0079 | 01.49% | |
| BC | 3.696 × 10−4 | 01 | 3.696 × 10−4 | 007.42 | 0.0095 | 01.42% | |
| DE | 7.443 × 10−4 | 01 | 7.443 × 10−4 | 014.95 | 0.0004 | 02.86% | |
| A2 | 6.137 × 10−4 | 01 | 6.137 × 10−4 | 012.33 | 0.0011 | 02.36% | |
| Residual | 1.992 × 10−3 | 40 | 4.979 × 10−5 | ||||
| Lack of Fit | 1.654 × 10−3 | 33 | 5.014 × 10−5 | 001.04 | 0.5246 | not significant | |
| Pure Error | 3.371 × 10−4 | 07 | 4.816 × 10−5 | ||||
| Cor Total | 0.026 | 49 | |||||
| 7.056 × 10−3 | R2 | 00.923 | |||||
| Mean | 0.39 | Adjusted R2 | 00.905 | ||||
| C.V. % | 1.81 | Predicted R2 | 00.884 | ||||
| PS | 2.986 × 10−3 | Adequacy Precision | 30.326 | ||||
| Source | Sum of Square | Degree of Freedom | Mean Square | F Value | p-Value Prob > F | Percentage Contribution | |
|---|---|---|---|---|---|---|---|
| Model | 34.27 | 10 | 03.43 | 090.04 | <0.0001 | Significant | |
| A-Pulse-on-time | 30.95 | 01 | 30.95 | 813.04 | <0.0001 | 90.31% | |
| B-Pulse-off-time | 00.61 | 01 | 00.61 | 016.13 | 0.0003 | 01.77% | |
| C-Servo Voltage | 8.768 × 10−3 | 01 | 8.768 × 10−3 | 000.23 | 0.6339 | 00.02% | |
| D-Peak Current | 00.19 | 01 | 00.19 | 005.08 | 0.0300 | 00.55% | |
| E-Wire Tension | 00.01 | 01 | 00.01 | 000.28 | 0.5967 | 00.03% | |
| AB | 00.23 | 01 | 00.23 | 005.94 | 0.0195 | 00.67% | |
| BC | 00.11 | 01 | 00.11 | 002.92 | 0.0954 | 00.32% | |
| DE | 00.30 | 01 | 00.30 | 007.89 | 0.0077 | 00.87% | |
| B2 | 01.75 | 01 | 01.75 | 045.97 | <0.0001 | 05.10% | |
| C2 | 01.62 | 01 | 01.62 | 042.51 | <0.0001 | 04.67% | |
| Residual | 01.48 | 39 | 00.03 | ||||
| Lack of Fit | 01.39 | 32 | 00.04 | 003.11 | 0.0613 | not significant | |
| Cor Total | 35.76 | 49 | |||||
| 0.20 | R2 | 00.958 | |||||
| Mean | 2.55 | Adjusted R2 | 00.947 | ||||
| C.V. % | 7.64 | Predicted R2 | 00.929 | ||||
| (PS) | 2.52 | Adequacy Precision | 28.842 | ||||
| Source | Sum of Square | Degree of Freedom | Mean Square | F Value | p-Value Prob > F | Percentage Contribution | |
|---|---|---|---|---|---|---|---|
| Model | 184.38 | 12 | 15.37 | 080.17 | <0.0001 | significant | |
| A-Pulse-on-time | 086.65 | 01 | 86.65 | 452.11 | <0.0001 | 46.99% | |
| B-Pulse-off-time | 024.94 | 01 | 24.94 | 130.11 | <0.0001 | 13.52% | |
| C-Servo Voltage | 044.77 | 01 | 44.77 | 233.57 | <0.0001 | 24.28% | |
| D-Peak Current | 000.68 | 01 | 00.68 | 003.54 | 0.0678 | 00.36% | |
| E-Wire Tension | 000.37 | 01 | 00.37 | 001.92 | 0.1740 | 00.20% | |
| AC | 005.20 | 01 | 05.20 | 027.13 | <0.0001 | 02.82% | |
| BC | 000.66 | 01 | 00.66 | 003.46 | 0.0707 | 00.35% | |
| DE | 000.76 | 01 | 00.76 | 003.95 | 0.0544 | 00.01% | |
| A2 | 006.98 | 01 | 06.98 | 036.41 | <0.0001 | 03.78% | |
| C2 | 001.55 | 01 | 01.55 | 008.07 | 0.0073 | 00.84% | |
| D2 | 001.75 | 01 | 01.75 | 009.13 | 0.0046 | 00.94% | |
| E2 | 000.71 | 01 | 00.71 | 003.68 | 0.0628 | 00.38% | |
| Residual | 007.09 | 37 | 00.19 | ||||
| Lack of Fit | 006.51 | 30 | 00.22 | 002.62 | 0.0939 | not significant | |
| Pure Error | 000.58 | 07 | 00.08 | ||||
| Cor Total | 191.48 | 49 | |||||
| 00.44 | R2 | 00.963 | |||||
| Mean | 06.83 | Adjusted R2 | 00.951 | ||||
| C.V. % | 06.41 | Predicted R2 | 00.914 | ||||
| PS | 16.36 | Adequacy Precision | 34.899 | ||||
| For hidden Layer = 1 | For Hidden Layer = 2 | |||
|---|---|---|---|---|
| No. of Neurons | MSE | No. of Neurons in the 1st Layer | No. of Neurons in the 2nd Layer | MSE |
| 1 | 1.103645 | 13 | 1 | 0.986389 |
| 2 | 0.337575 | 13 | 2 | 1.619909 |
| 3 | 0.219654 | 13 | 3 | 0.401487 |
| 4 | 0.146387 | 13 | 4 | 0.154014 |
| 5 | 0.124594 | 13 | 5 | 0.270056 |
| 6 | 0.150487 | 13 | 6 | 0.070328 |
| 7 | 0.145620 | 13 | 7 | 0.138533 |
| 8 | 0.077698 | 13 | 8 | 0.445419 |
| 9 | 0.049678 | 13 | 9 | 1.158510 |
| 10 | 0.088550 | 13 | 10 | 0.150517 |
| 11 | 0.090630 | 13 | 11 | 0.328056 |
| 12 | 2.448050 | 13 | 12 | 0.081355 |
| 13 | 0.047438 | 13 | 12 | 0.191720 |
| 14 | 0.155834 | 13 | 14 | 0.203620 |
| 15 | 4.100331 | 13 | 15 | 0.014916 |
| S. No. | Input Parameters | Response Variables | Predicted Values | Absolute Error | Percentage Error | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RSM | ANN | RSM | ANN | RSM | ANN | |||||||||||||||||||||
| TON | TOFF | V | IP | T | Kf | Ra | MRR | Kf | Ra | MRR | Kf | Ra | MRR | Kf | Ra | MRR | Kf | Ra | MRR | Kf | Ra | MRR | Kf | Ra | MRR | |
| 1 | 100 | 50 | 60 | 150 | 1.3 | 0.338 | 2.12 | 5.50 | 0.359 | 2.30 | 5.90 | 0.343 | 2.17 | 5.60 | 0.020 | 0.180 | 0.399 | 0.004 | 0.051 | 0.104 | 6.0 | 8.4 | 7.2 | 1.4 | 2.4 | 1.8 |
| 2 | 110 | 50 | 40 | 180 | 1.1 | 0.378 | 2.97 | 6.33 | 0.405 | 3.21 | 6.82 | 0.383 | 3.03 | 6.43 | 0.026 | 0.241 | 0.489 | 0.004 | 0.056 | 0.105 | 7.1 | 8.1 | 7.7 | 1.2 | 1.8 | 1.6 |
| 3 | 120 | 40 | 40 | 150 | 1.5 | 0.381 | 3.06 | 7.82 | 0.411 | 3.30 | 8.42 | 0.386 | 3.12 | 7.94 | 0.030 | 0.240 | 0.597 | 0.005 | 0.059 | 0.123 | 7.9 | 7.8 | 7.6 | 1.3 | 1.9 | 1.5 |
| 4 | 105 | 40 | 50 | 120 | 1.3 | 0.349 | 1.13 | 5.83 | 0.379 | 1.23 | 6.30 | 0.359 | 1.16 | 5.97 | 0.030 | 0.096 | 0.477 | 0.009 | 0.023 | 0.146 | 8.6 | 8.4 | 8.1 | 2.8 | 2.1 | 2.5 |
| 5 | 110 | 60 | 60 | 140 | 1.5 | 0.355 | 2.47 | 8.57 | 0.385 | 2.67 | 9.25 | 0.362 | 2.52 | 8.73 | 0.029 | 0.201 | 0.682 | 0.006 | 0.043 | 0.165 | 8.3 | 8.1 | 7.9 | 1.9 | 1.7 | 1.9 |
| 6 | 120 | 60 | 50 | 180 | 1.4 | 0.368 | 2.86 | 5.73 | 0.410 | 3.16 | 6.30 | 0.380 | 2.96 | 5.89 | 0.042 | 0.300 | 0.565 | 0.011 | 0.102 | 0.156 | 11.4 | 10..4 | 9.8 | 3.1 | 3.5 | 2.7 |
| S. No. | Optimum Combination of Parameters | Predicted Optimal Responses | ||||||
|---|---|---|---|---|---|---|---|---|
| Pulse on Time (µs) | Pulse off Time (µs) | Servo Voltage (V) | Peak Current (A) | Wire Tension (kg) | Kerf Width (mm) | Average Surface Roughness (µm) | MRR (mm3/min) | |
| 1 | 115.7 | 41.3479 | 58.9851 | 145.6258 | 1.5 | 0.4115 | 2.9032 | 11.0445 |
| 2 | 116.1976 | 51.0227 | 58.8759 | 140.2582 | 1.002 | 0.4007 | 3.7455 | 10.081 |
| 3 | 115.7361 | 48.609 | 58.4004 | 140.9127 | 1.1499 | 0.403 | 3.5708 | 9.9281 |
| 4 | 111.8471 | 53.369 | 57.6318 | 139.7052 | 1.1846 | 0.3912 | 3.1399 | 8.982 |
| 5 | 106.2293 | 43.3575 | 55.8224 | 138.0302 | 1.4665 | 0.3886 | 1.9739 | 8.3452 |
| 6 | 109.0756 | 51.2509 | 54.952 | 135.5442 | 1.1557 | 0.3843 | 2.6745 | 8.0852 |
| 7 | 107.6299 | 54.3343 | 56.1504 | 137.6518 | 1.1792 | 0.3789 | 2.5472 | 7.7192 |
| 8 | 103.8108 | 55.7966 | 55.6415 | 136.7205 | 1.1733 | 0.3653 | 2.0421 | 6.2681 |
| 9 | 103.509 | 58.5855 | 56.0647 | 131.1638 | 1.1326 | 0.359 | 1.8143 | 5.9988 |
| 10 | 102.5863 | 59.2397 | 56.1829 | 129.3532 | 1.1186 | 0.3541 | 1.6625 | 5.5898 |
| 11 | 100.6012 | 40.2018 | 49.5448 | 125.1871 | 1.4991 | 0.3712 | 0.7983 | 5.3027 |
| 12 | 103.6348 | 58.6548 | 53.2785 | 125.4858 | 1.245 | 0.3623 | 1.5738 | 4.9978 |
| 13 | 100.4823 | 41.0112 | 49.6387 | 126.0315 | 1.2619 | 0.3636 | 1.0146 | 4.7551 |
| 14 | 100.8304 | 58.3529 | 54.7529 | 134.7287 | 1.1789 | 0.3524 | 1.4451 | 4.5571 |
| 15 | 100.1058 | 59.7993 | 54.683 | 127.479 | 1.1017 | 0.344 | 1.2261 | 4.1407 |
| 16 | 100.1064 | 59.6998 | 53.5976 | 126.8243 | 1.116 | 0.3449 | 1.1667 | 3.9059 |
| 17 | 100.1194 | 59.7852 | 51.1414 | 127.104 | 1.2612 | 0.3511 | 0.9925 | 3.1583 |
| 18 | 100.1884 | 59.7203 | 49.7307 | 123.9073 | 1.3032 | 0.3529 | 0.9621 | 2.8823 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lalwani, V.; Sharma, P.; Pruncu, C.I.; Unune, D.R. Response Surface Methodology and Artificial Neural Network-Based Models for Predicting Performance of Wire Electrical Discharge Machining of Inconel 718 Alloy. J. Manuf. Mater. Process. 2020, 4, 44. https://doi.org/10.3390/jmmp4020044
Lalwani V, Sharma P, Pruncu CI, Unune DR. Response Surface Methodology and Artificial Neural Network-Based Models for Predicting Performance of Wire Electrical Discharge Machining of Inconel 718 Alloy. Journal of Manufacturing and Materials Processing. 2020; 4(2):44. https://doi.org/10.3390/jmmp4020044
Chicago/Turabian StyleLalwani, Vishal, Priyaranjan Sharma, Catalin Iulian Pruncu, and Deepak Rajendra Unune. 2020. "Response Surface Methodology and Artificial Neural Network-Based Models for Predicting Performance of Wire Electrical Discharge Machining of Inconel 718 Alloy" Journal of Manufacturing and Materials Processing 4, no. 2: 44. https://doi.org/10.3390/jmmp4020044
APA StyleLalwani, V., Sharma, P., Pruncu, C. I., & Unune, D. R. (2020). Response Surface Methodology and Artificial Neural Network-Based Models for Predicting Performance of Wire Electrical Discharge Machining of Inconel 718 Alloy. Journal of Manufacturing and Materials Processing, 4(2), 44. https://doi.org/10.3390/jmmp4020044






