Dexel-Based Simulation of Directed Energy Deposition Additive Manufacturing
Abstract
:1. Introduction
2. State of the Art
3. Objective and Approach
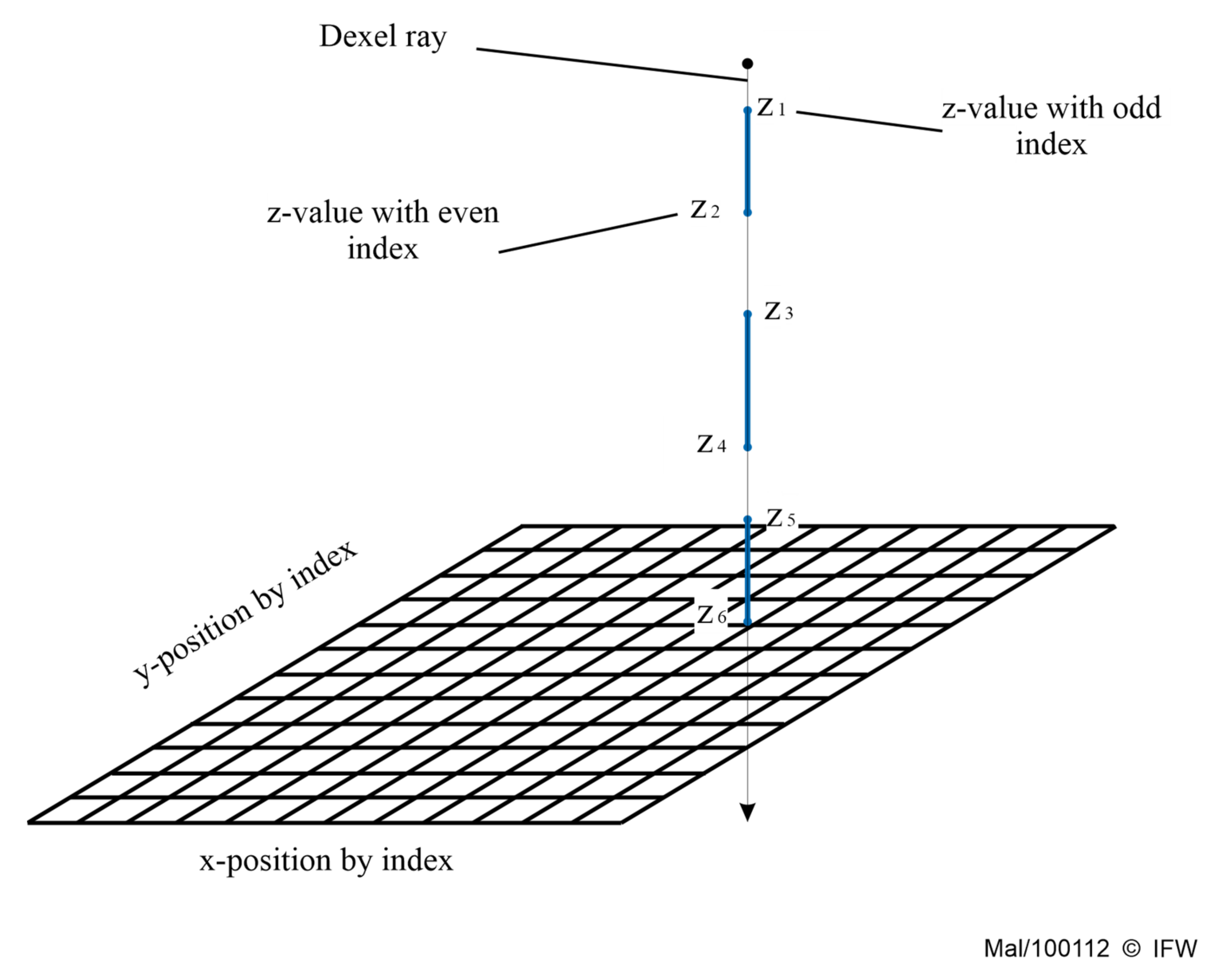
4. Tri-Dexel-Based Simulation Method
4.1. Material Deposition into Dexel Models
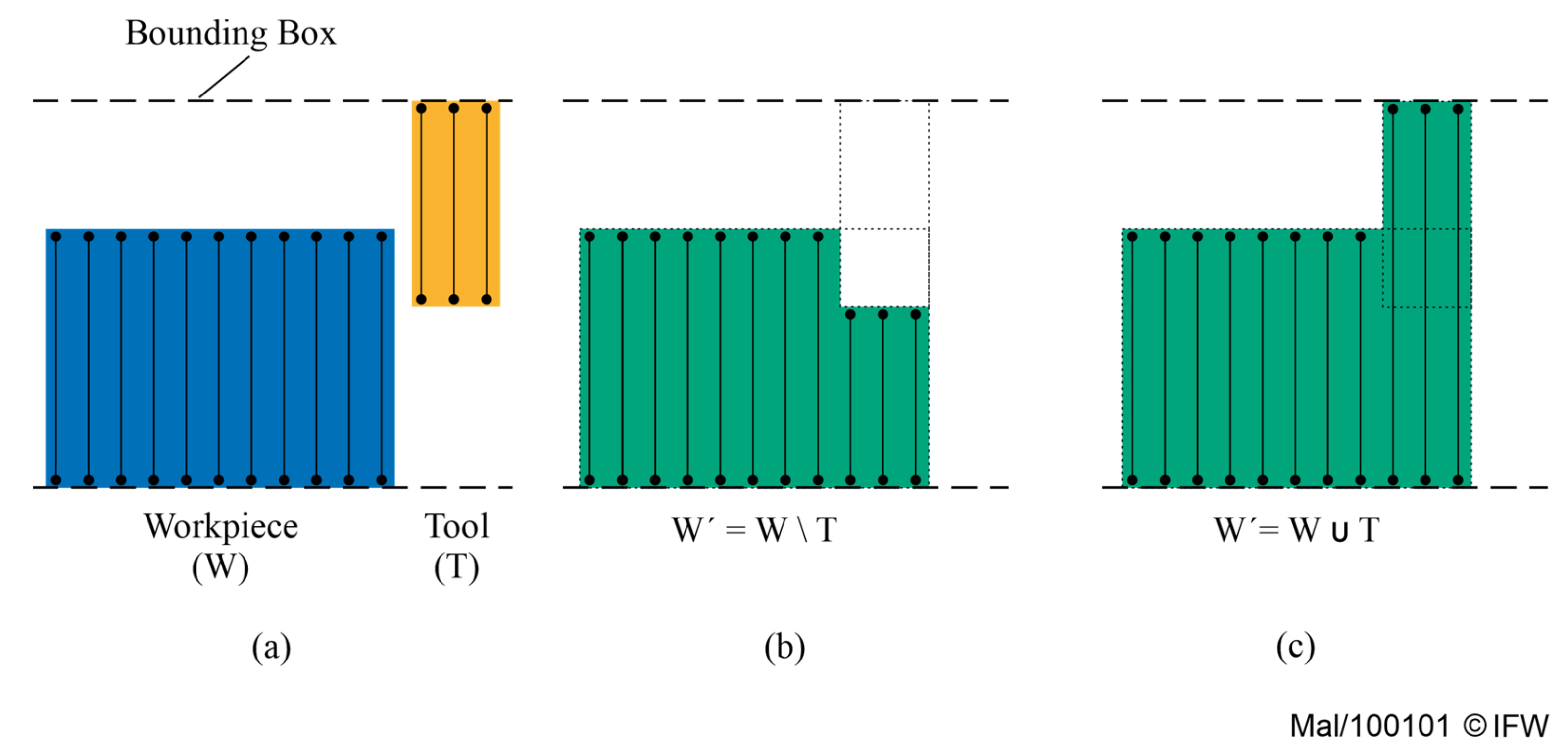
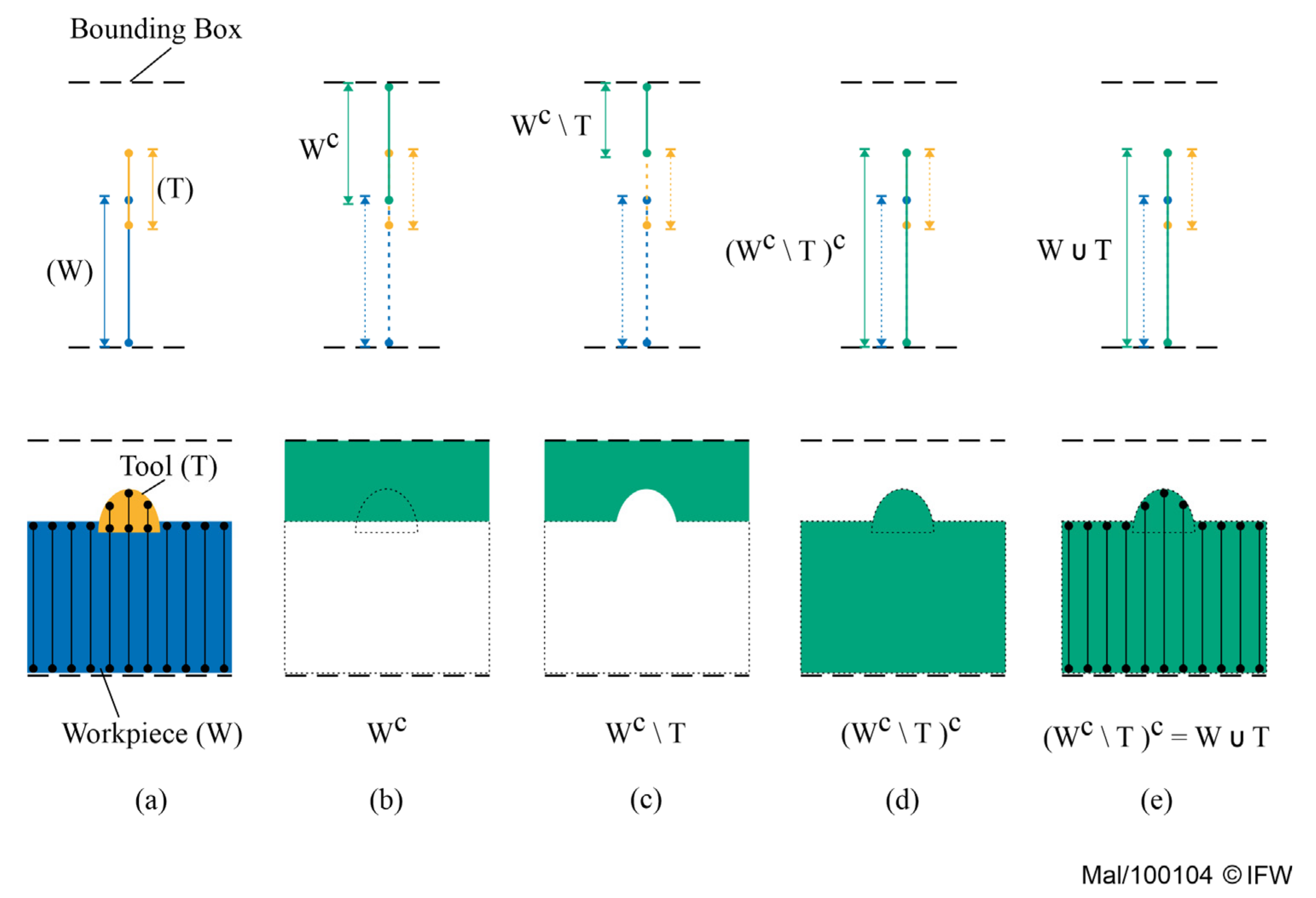
4.2. Determining the Shape of the Virtual Tool
4.3. Extension Capability
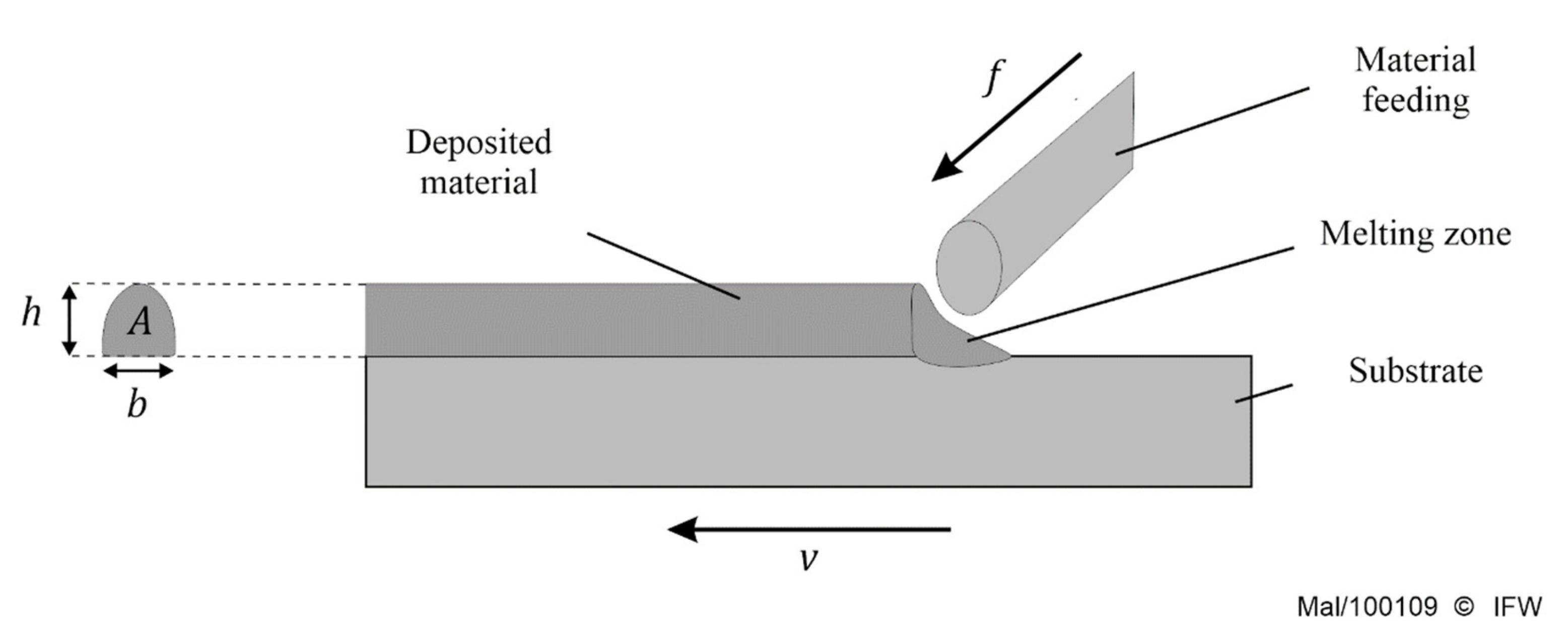
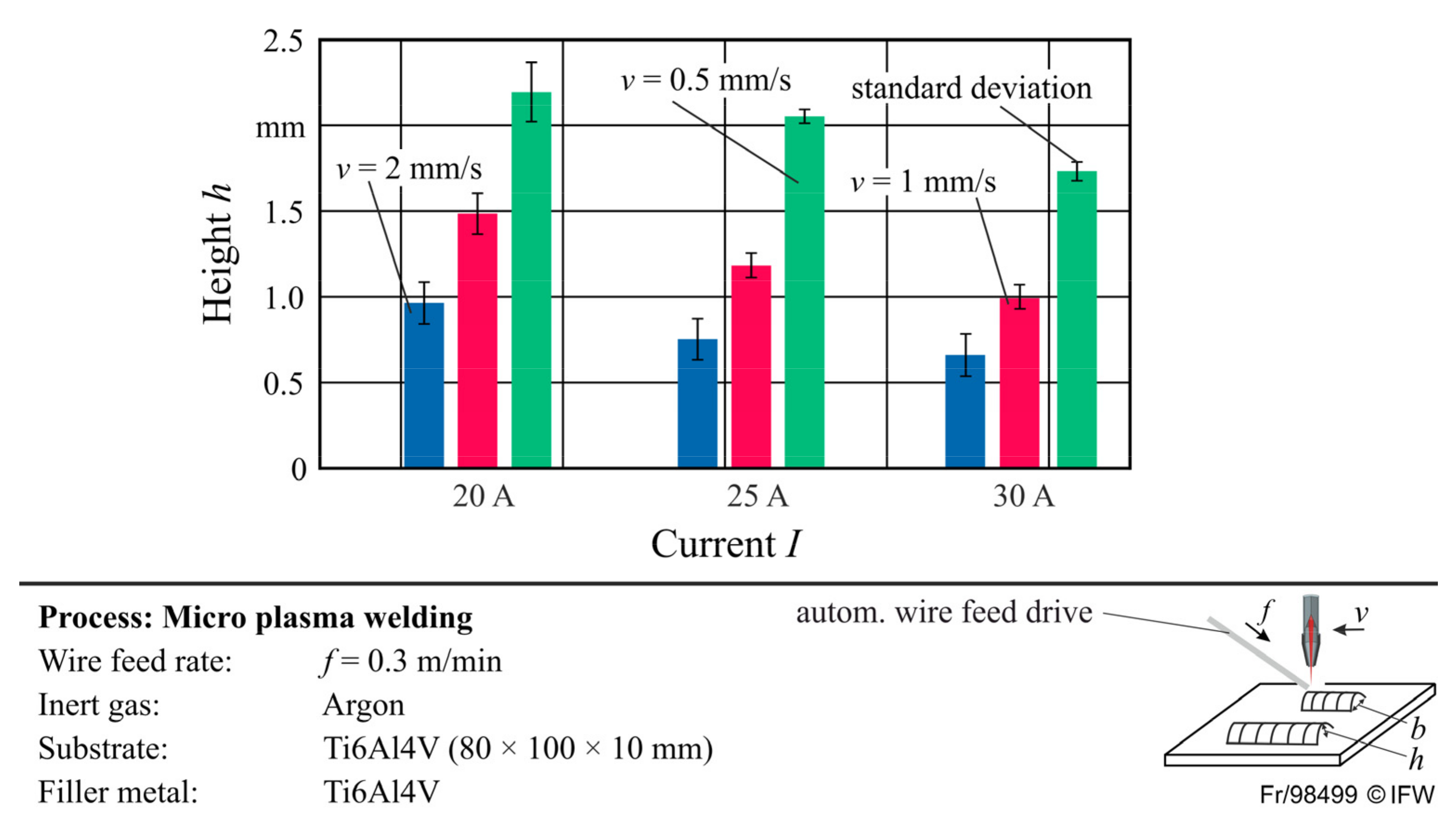
5. Application on Micro-Plasma Welding with Empirical Data
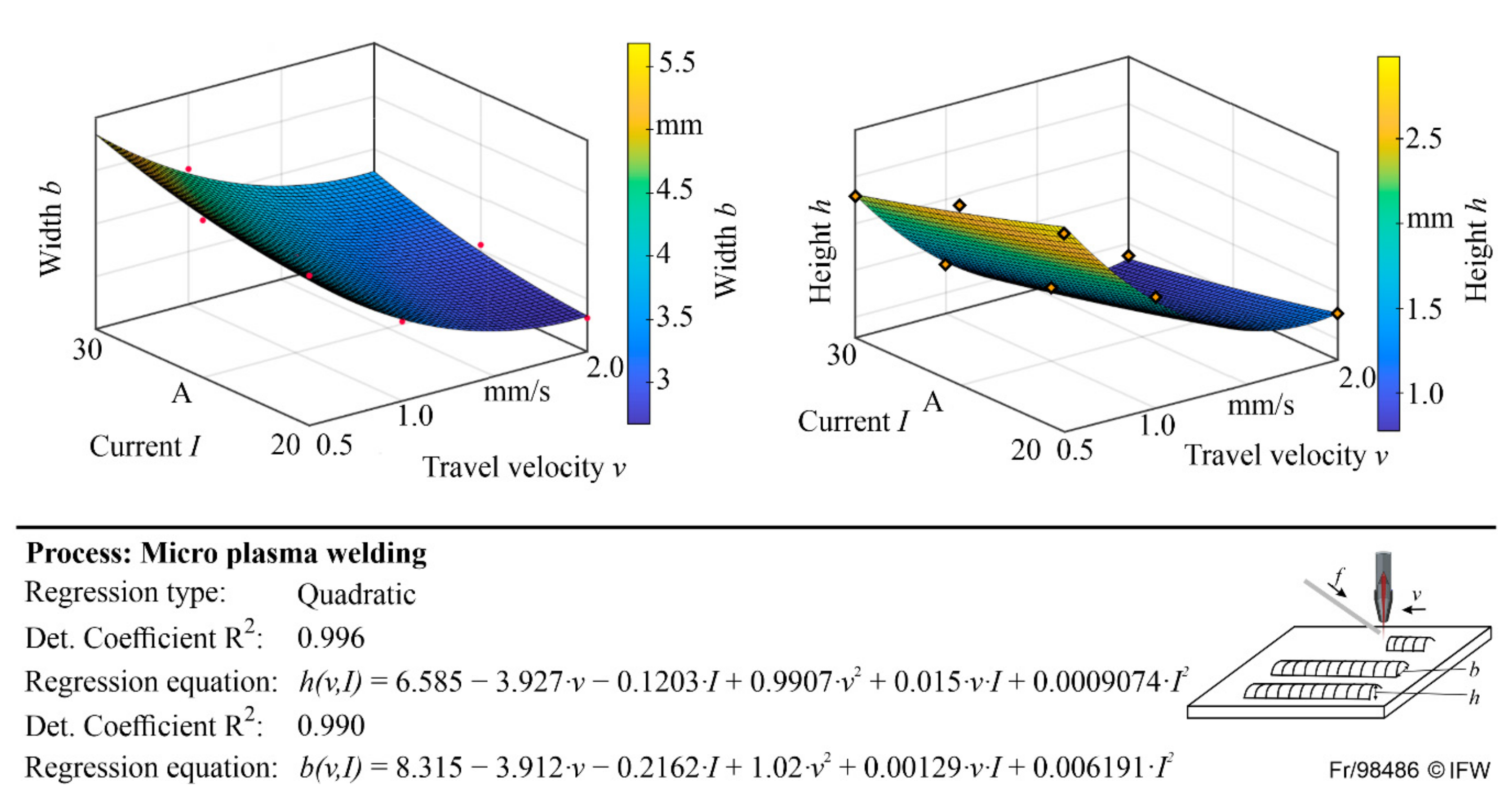
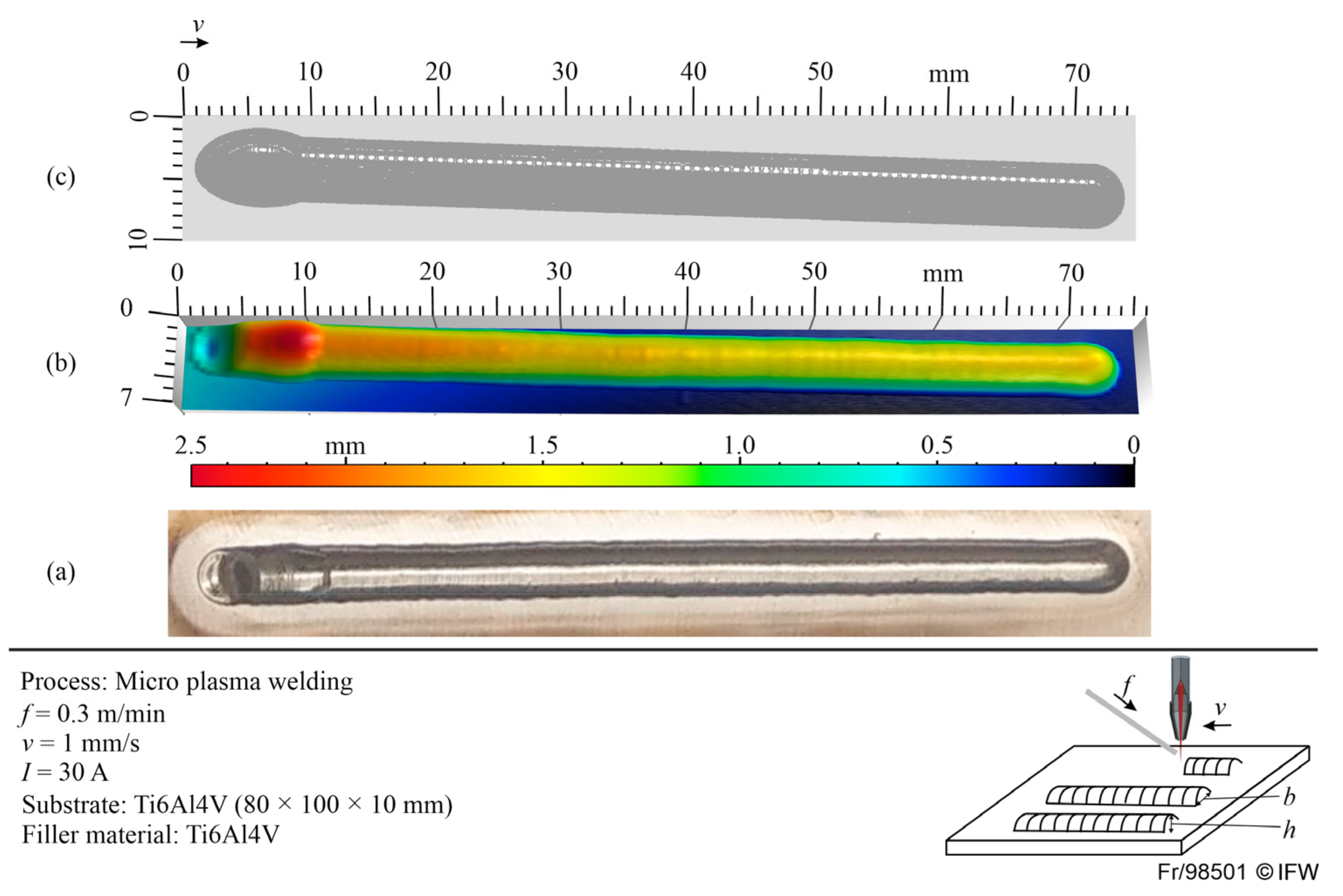
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Markl, M.; Körner, C. Multiscale Modeling of Powder Bed–Based Additive Manufacturing. Annu. Rev. Mater. Res. 2016, 46, 93–123. [Google Scholar] [CrossRef]
- Hejripour, F.; Binesh, F.; Hebel, M.; Aidun, D.K. Thermal modeling and characterization of wire arc additive manufactured duplex stainless steel. J. Mater. Process. Technol. 2019, 272, 58–71. [Google Scholar] [CrossRef]
- Li, R.; Xiong, J. Influence of interlayer dwell time on stress field of thin-walled components in WAAM via numerical simulation and experimental tests. Rapid Prototyp. J. 2019, 25, 1433–1441. [Google Scholar] [CrossRef]
- Hertel, M. Numerische Simulation des MSG-Prozesses. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2016. [Google Scholar]
- Bai, X.; Colegrove, P.; Ding, J.; Zhou, X.; Diao, C.; Bridgeman, P.; Hönnige, J.R.; Zhang, H.; Williams, S. Numerical analysis of heat transfer and fluid flow in multilayer deposition of PAW-based wire and arc additive manufacturing. Int. J. Heat Mass Transf. 2018, 124, 504–516. [Google Scholar] [CrossRef] [Green Version]
- Seidel, C.M. Finite-Elemente-Simulation des Aufbauprozesses beim Laserstrahlschmelzen. Ph.D. Thesis, Technische Universität München, München, Germany, 2016. [Google Scholar]
- Van Hook, T. Real-Time Shaded NC Milling Display. SIGGRAPH Comput. Graph. 1986, 20, 15–20. [Google Scholar] [CrossRef]
- Requicha, A.; Rossignac, J. Solid modeling and beyond. IEEE Eng. Med. Boil. Mag. 1992, 12, 31–44. [Google Scholar] [CrossRef]
- Denkena, B.; Böß, V. Technological NC Simulation for Grinding and Cutting Processes Using CutS. In Proceedings of the 12th CIRP Conference on Modelling of Machining Operations, Donostia-San Sebastian, Spain, 7–8 May 2009; pp. 563–566. [Google Scholar]
- Aremu, A.; Brennan-Craddock, J.; Panesar, A.; Ashcroft, I.; Hague, R.; Wildman, R.D.; Tuck, C.J. A voxel-based method of constructing and skinning conformal and functionally graded lattice structures suitable for additive manufacturing. Addit. Manuf. 2017, 13, 1–13. [Google Scholar] [CrossRef]
- Böß, V.; Denkena, B.; Breidenstein, B.; Dittrich, M.-A.; Nguyen, H. Improving technological machining simulation by tailored workpiece models and kinematics. Procedia CIRP 2019, 82, 224–230. [Google Scholar] [CrossRef]
- Altintas, Y.; Kersting, P.; Biermann, D.; Budak, E.; Denkena, B.; Lazoglu, I. Virtual process systems for part machining opera-tions. CIRP Annals 2014, 63, 585–605. [Google Scholar] [CrossRef]
- He, S.; Zeng, X.; Yan, C.; Gong, H.; Lee, C.-H. Tri-Dexel Model Based Geometric Simulation of Multi-axis Additive Manufac-turing. IJIRA 2017, 10464, 819–830. [Google Scholar]
- Sun, Y.-J.; Yan, C.; Wu, S.-W.; Gong, H.; Lee, C.-H. Geometric simulation of 5-axis hybrid additive-subtractive manufacturing based on Tri-dexel model. Int. J. Adv. Manuf. Technol. 2018, 99, 2597–2610. [Google Scholar] [CrossRef]
- Dal, M.; Fabbro, R. An overview of the state of art in laser welding simulation. Opt. Laser Technol. 2016, 78, 2–14. [Google Scholar] [CrossRef] [Green Version]
- Wiederkehr, P.; Bergmann, J.A. An integrated macroscopic model for simulating SLM and milling processes. Prod. Eng. 2018, 12, 465–472. [Google Scholar] [CrossRef]
- Denkena, B.; Tracht, K.; Yu, J.-H. Advanced NC-Simulation based on the Dexelmodel and the HRMC-Algorithm. Prod. Eng. Res. Dev. 2006, 13, 91–94. [Google Scholar]


| Author | Method | Process/Application | Results |
|---|---|---|---|
| He et al. (2017) [13] | Calculation of material deposit with swept volume using a constant cross-section of deposited material for 5-axis Tri-Dexel-based simulation | Laser metal deposition using an industrial robot/impeller, vane |
|
| Aremu et al. (2017) [10] |
| Variable/objects with inner lattice structure |
|
| Dal et al. (2016) [15] |
| Laser welding/various applications |
|
| Hertel (2016) [4] |
| Gas metal arc welding (GMAW) |
|
| Seidel (2016) [6] |
| Laser welding/boroscop eye and turbine blade (Inconel 718) |
|
| Wiederkehr and Bergmann (2018) [16] |
| Selective laser melting (SLM) and milling process/impeller and other applications | Simulated geometry can be used in subsequent milling simulations |
| Sun et al. (2018) [14] |
| Hybrid additive–subtractive manufacturing (SLM and 5-axis-milling)/impeller | Improvement of micro swept volume model |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Böß, V.; Denkena, B.; Dittrich, M.-A.; Malek, T.; Friebe, S. Dexel-Based Simulation of Directed Energy Deposition Additive Manufacturing. J. Manuf. Mater. Process. 2021, 5, 9. https://doi.org/10.3390/jmmp5010009
Böß V, Denkena B, Dittrich M-A, Malek T, Friebe S. Dexel-Based Simulation of Directed Energy Deposition Additive Manufacturing. Journal of Manufacturing and Materials Processing. 2021; 5(1):9. https://doi.org/10.3390/jmmp5010009
Chicago/Turabian StyleBöß, Volker, Berend Denkena, Marc-André Dittrich, Talash Malek, and Sven Friebe. 2021. "Dexel-Based Simulation of Directed Energy Deposition Additive Manufacturing" Journal of Manufacturing and Materials Processing 5, no. 1: 9. https://doi.org/10.3390/jmmp5010009
APA StyleBöß, V., Denkena, B., Dittrich, M. -A., Malek, T., & Friebe, S. (2021). Dexel-Based Simulation of Directed Energy Deposition Additive Manufacturing. Journal of Manufacturing and Materials Processing, 5(1), 9. https://doi.org/10.3390/jmmp5010009





