Validation of the Cooling Model for TMCP Processing of Steel Sheets with Oxide Scale Using Industrial Experiment Data
Abstract
:1. Introduction
2. Materials and Methods
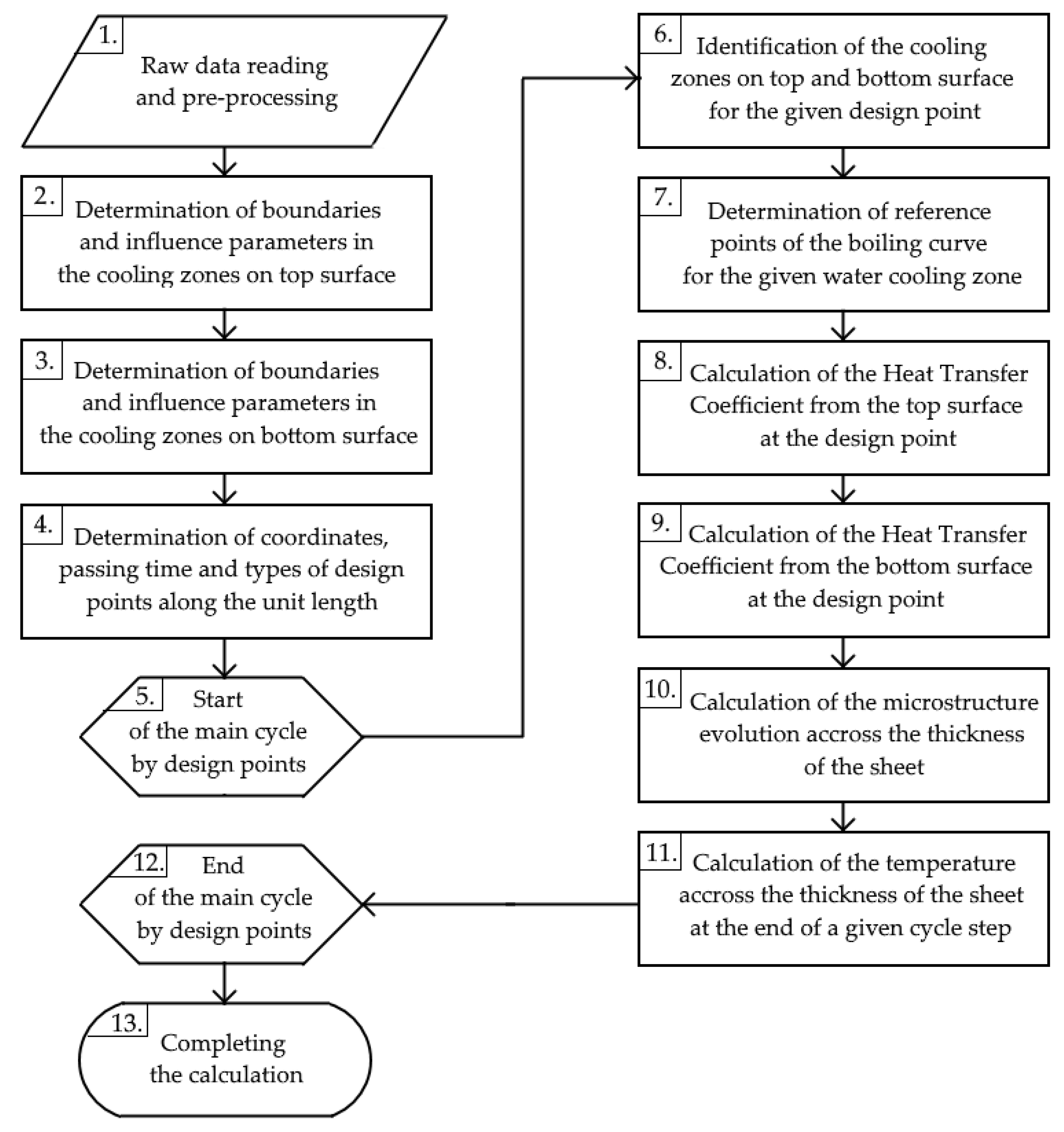
2.1. Cooling Model
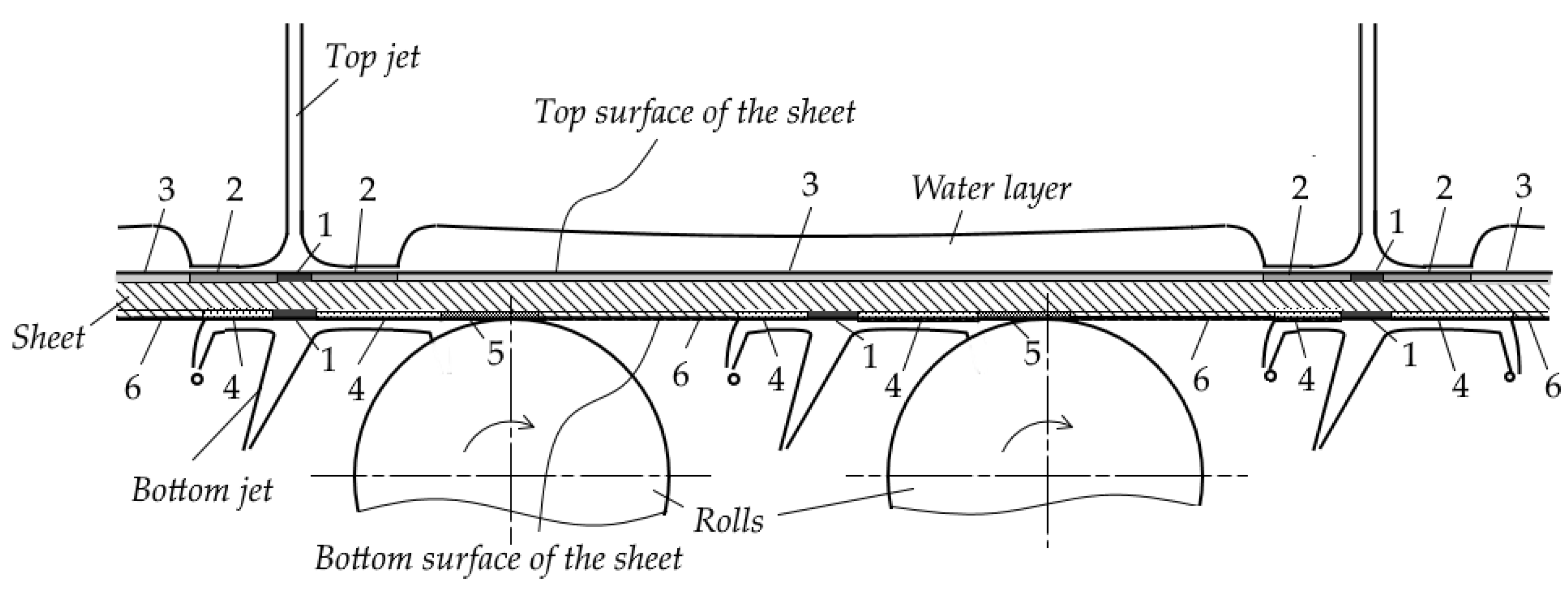
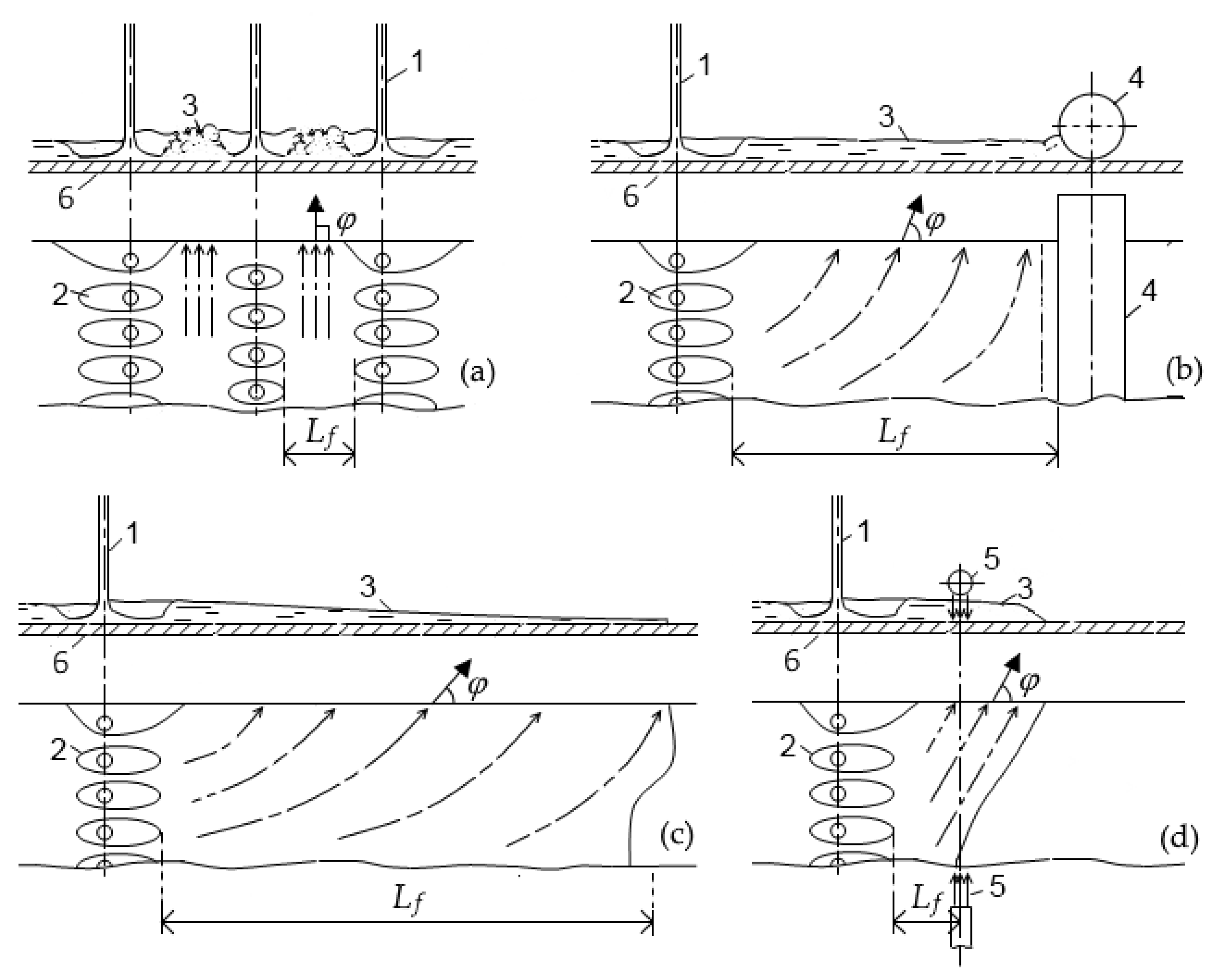
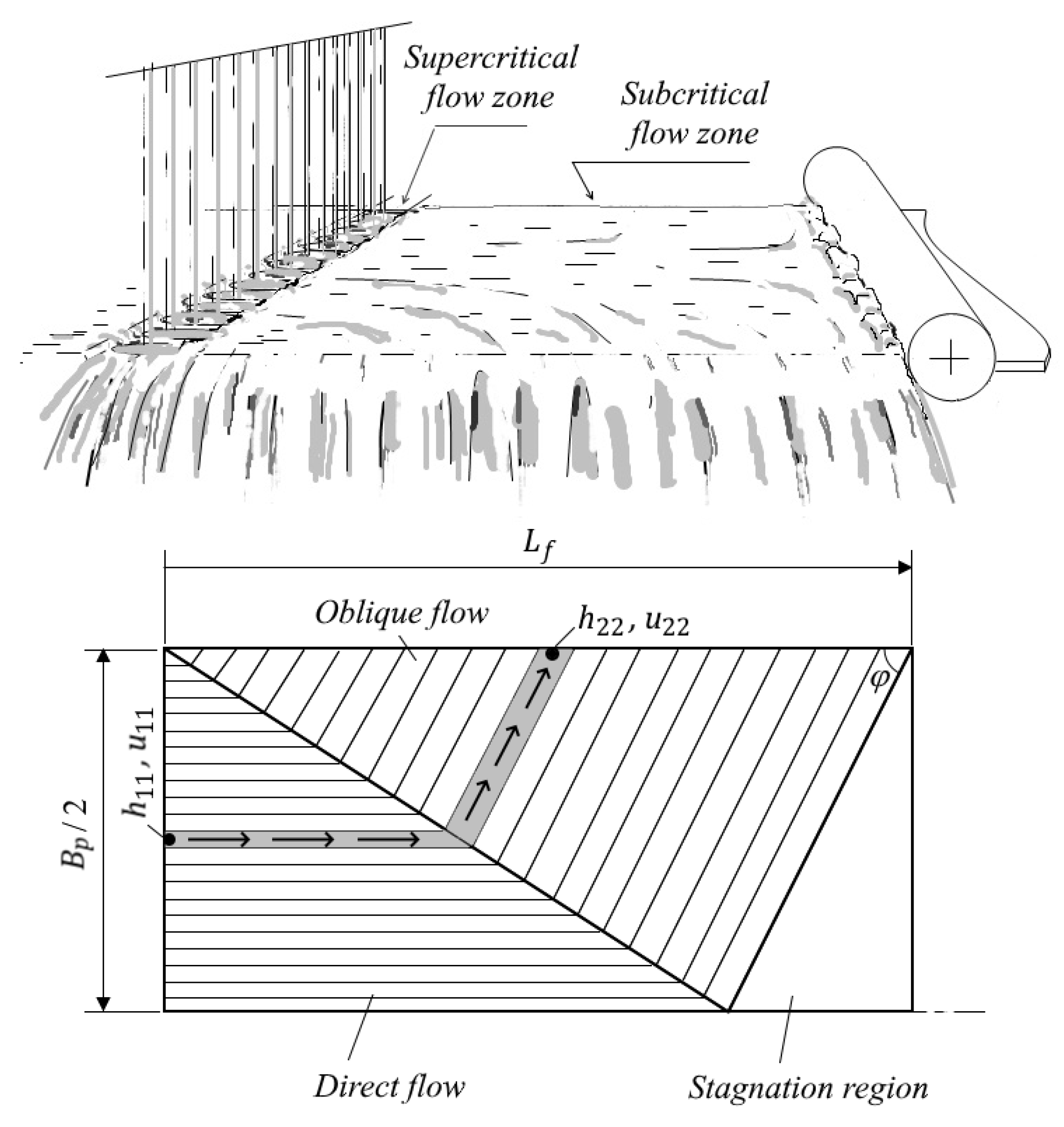
2.1.1. Boundaries of Water-Cooling Zones and Parameters of Water Flow
- −
- for the drops going downward:
- −
- for the drops going upward:
- −
- The boundary post-jump height, above which the jump becomes submerged [m]:
- −
- The boundary post-jump height, above which the jump occurs inside the inviscid flow region [m]:
- −
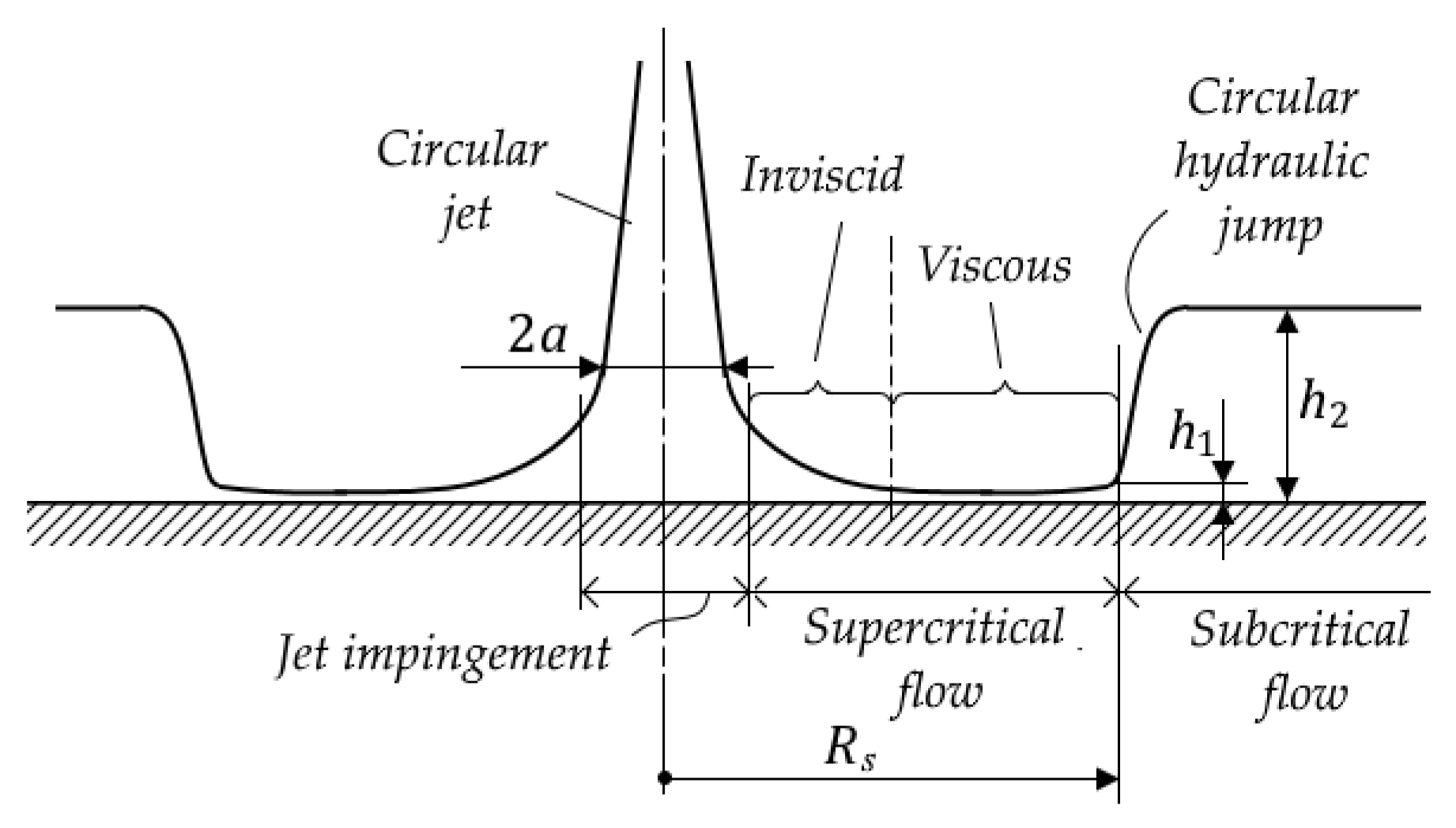
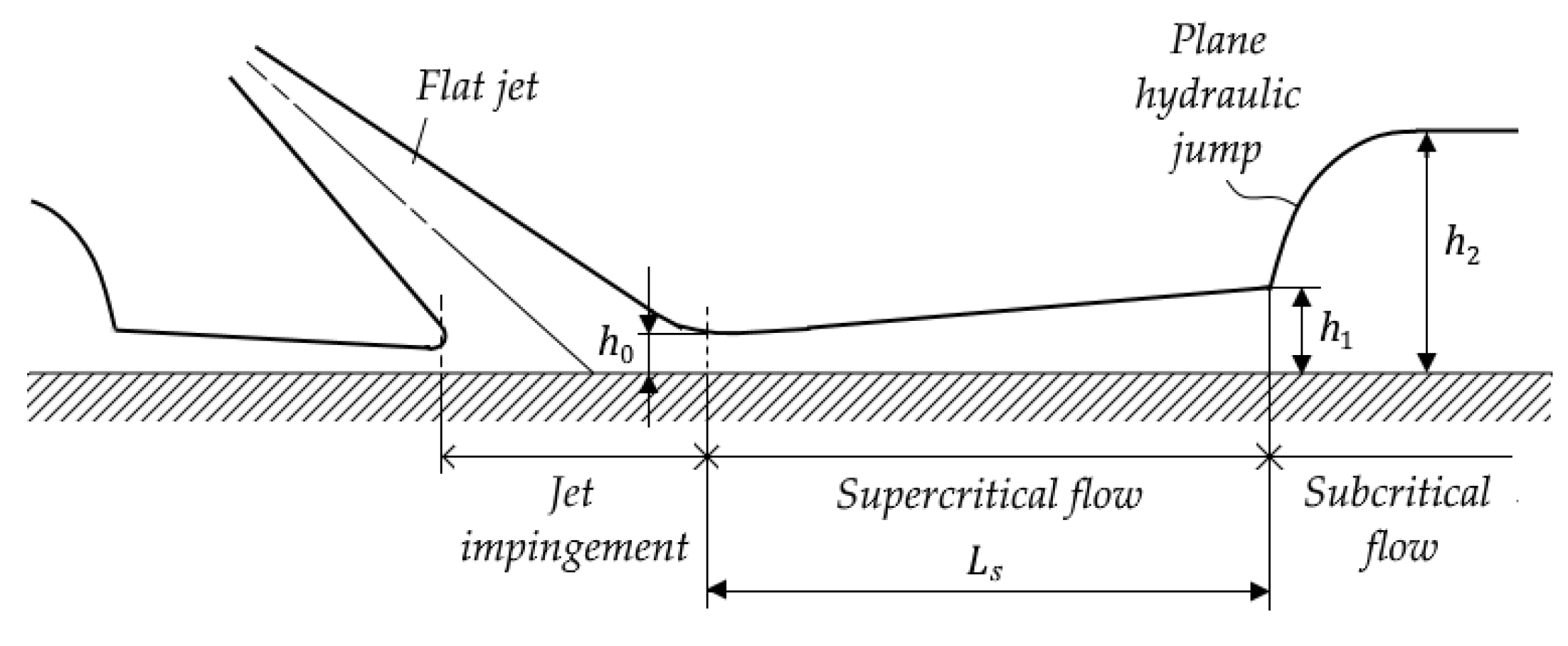
- Radius Rs of the circular hydraulic jump [m] (subscript “s” denotes “spot”):
- (a)
- if (jump occurs inside the viscous region), then
- (b)
- if (jump occurs inside the inviscid region), then (expression (13) is known as the Rayleigh formula for an ideal fluid [42]).
- (a)
- “clamped layer”—the water layer between closely spaced jets on a limited area of the surface. The height of such a layer may be so great that the jets are no longer able to overcome it (the hydraulic jump becomes submerged);
- (b)
- “bounded layer”—the water layer between adjacent rows of jets or between a row of jets and a pinch roll separated by a relatively large distance;
- (c)
- “open layer”—the water layer that spreads over the surface of the sheet without any obstruction; such a layer is formed, as a rule, before the first or after the last cooling bank in the absence of special devices for removing water from the surface;
- (d)
- “shifted layer”—the water layer which is removed from the sheet by special devices (hydro or pneumatic separators).
- −
- auxiliary parameter Φ:
- −
- Friction parameter
- −
- Shape parameter δ:
- −
- Angular runoff coefficient
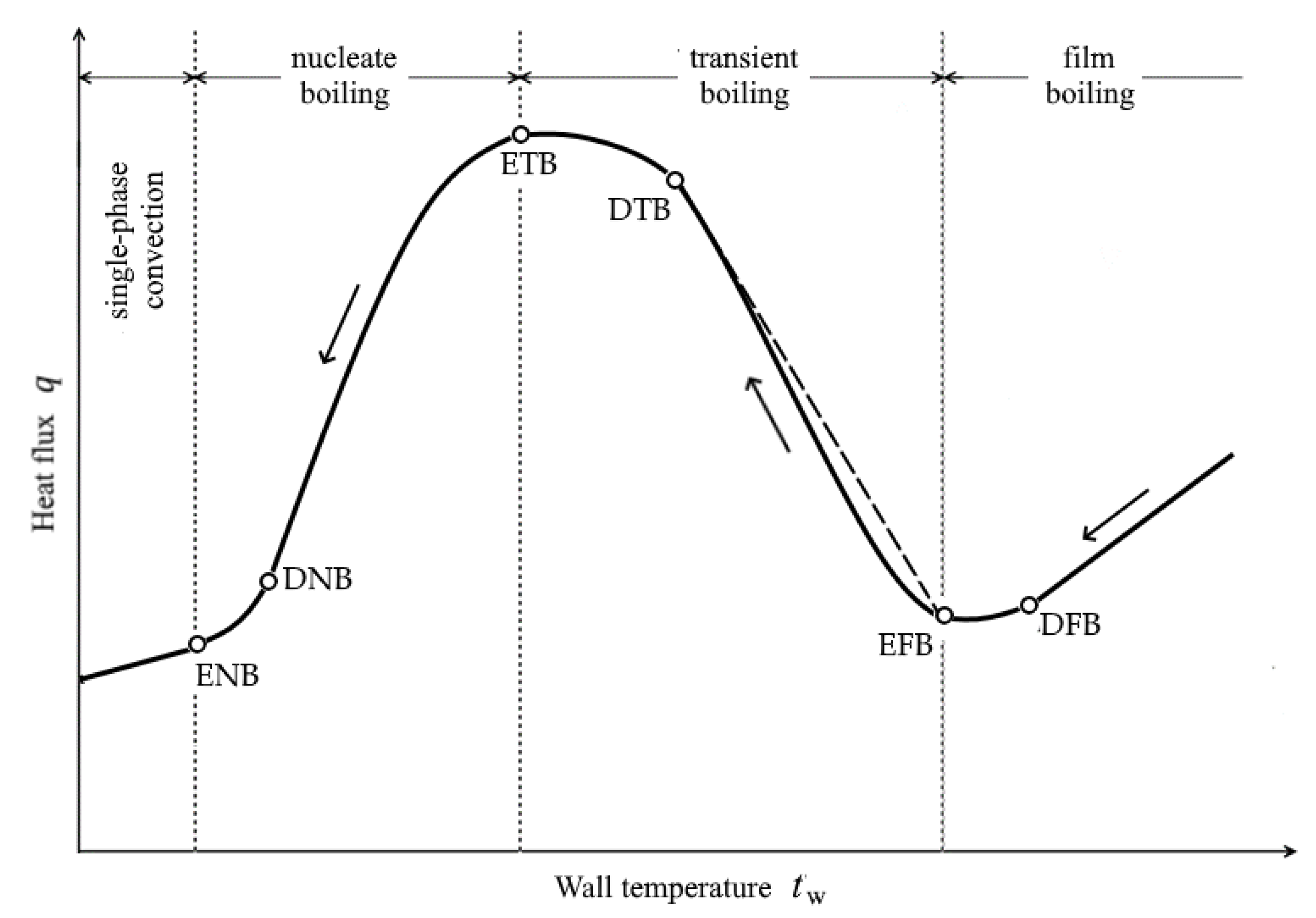
2.1.2. Heat Flux in the Water-Cooling Zones
- −
- density [kg·m−3]:
- −
- thermal conductivity [W·m−1·K−1]:
- −
- true isobaric specific-mass-heat capacity [J·kg−1K−1]:
- −
- At the End of Film Boiling (i.e., at the EFB-point), according to Wang-Shi [63]:
- −
- At the End of Transition Boiling (at the ETB point), in the Kutateladze-Leont’ev method for Critical Heat Flux [64] (p. 311):
- −
- at the End of Nucleate Boiling (at the ENB point), according to Isachenko-Kushnyrev [66] (p. 178).
2.1.3. Microstructure
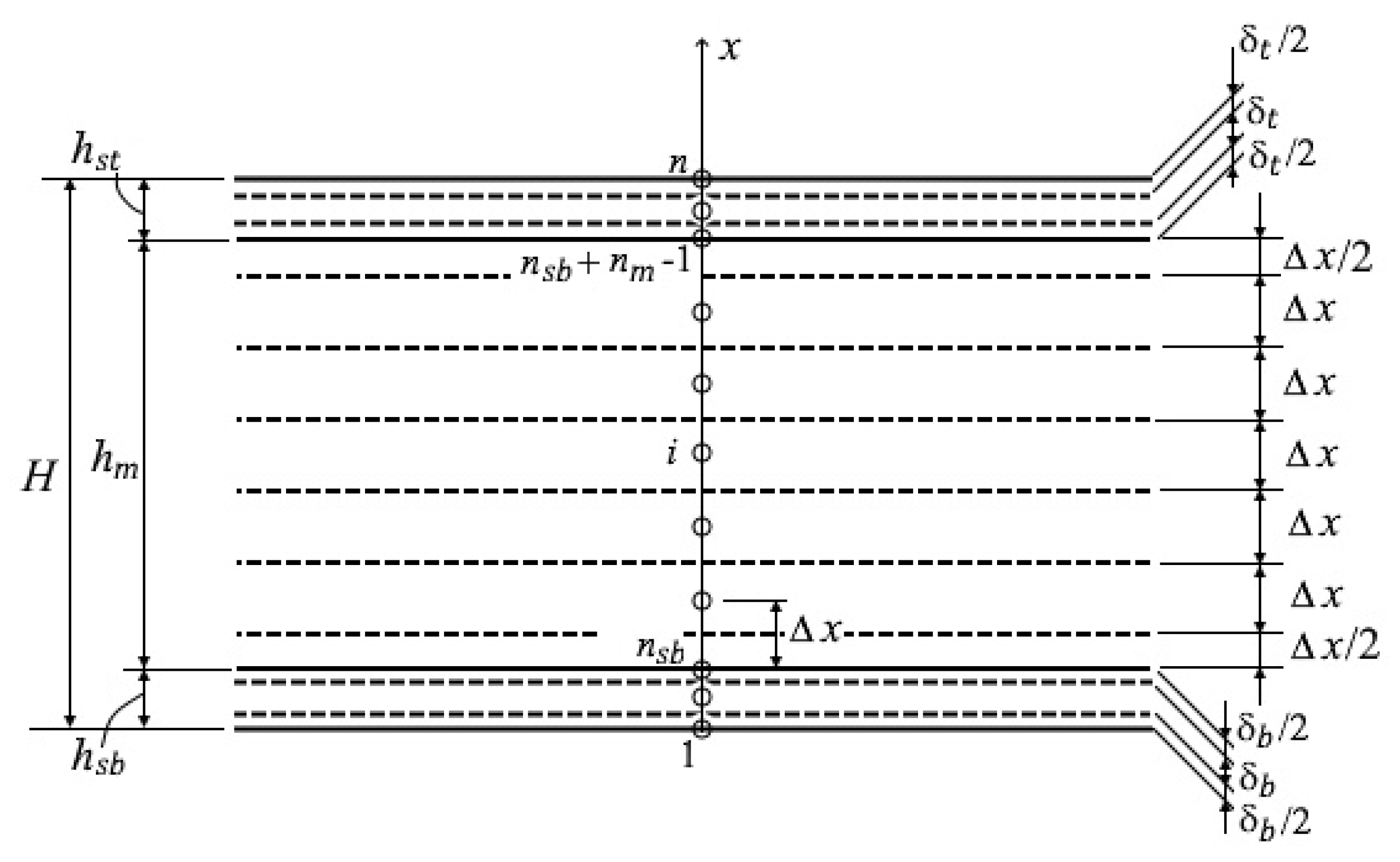
2.1.4. Temperature Distribution across the Thickness of the Sheet
- −
- Inside the metal body (:
- −
- Inside the bottom scale layer (:
- −
- Inside the top scale layer (:
- −
- Conjugation conditions between the bottom scale layer and the metal (:
- −
- Conjugation conditions between the top scale layer and the metal ():
- −
- Boundary conditions at the bottom scale surface ():
- −
- Boundary conditions at the top scale surface ():
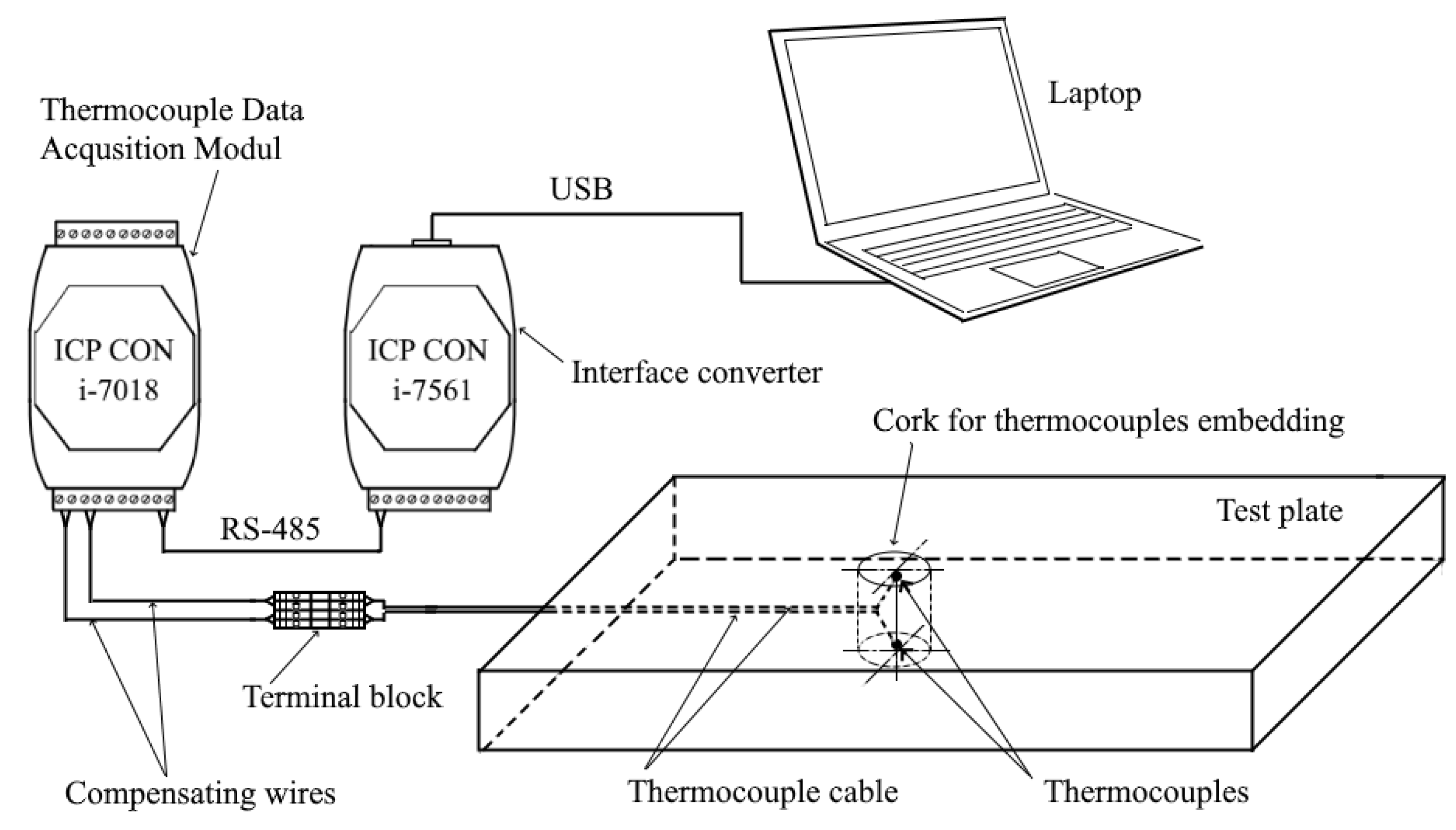
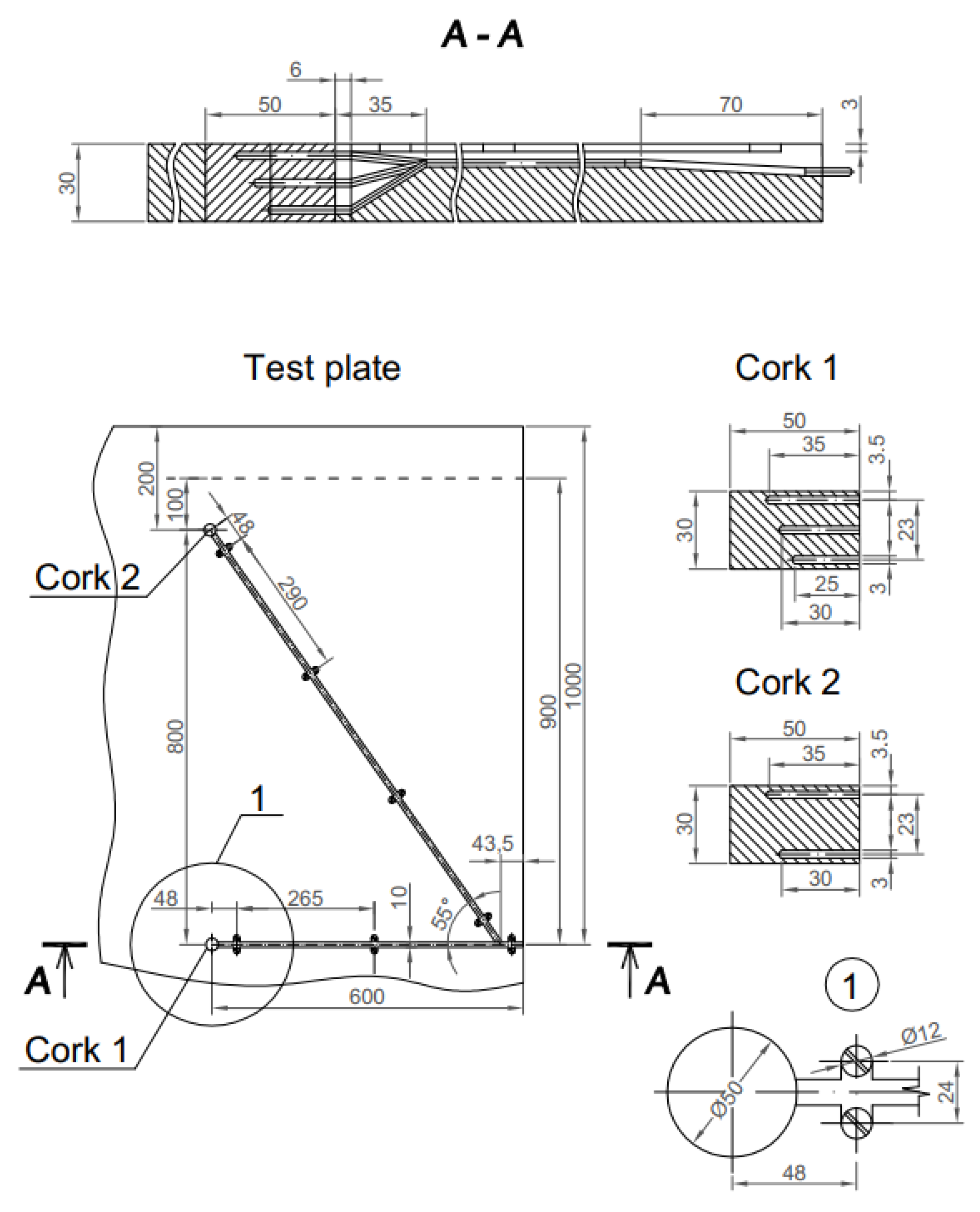
2.2. Experimental Studies
2.2.1. Experimental Procedure
2.2.2. Estimation of Oxide Scale Thickness on the Surface of the Test Plates
3. Results
- −
- −
- The thermophysical properties of the test plate as a function of temperature, according to the formulas [55] for medium-carbon steel (see Appendix B);
- −
- −
- The oxide scale thickness was assumed to be constant throughout the cooling period of each test and equal to the values given in Table 2.
- (1)
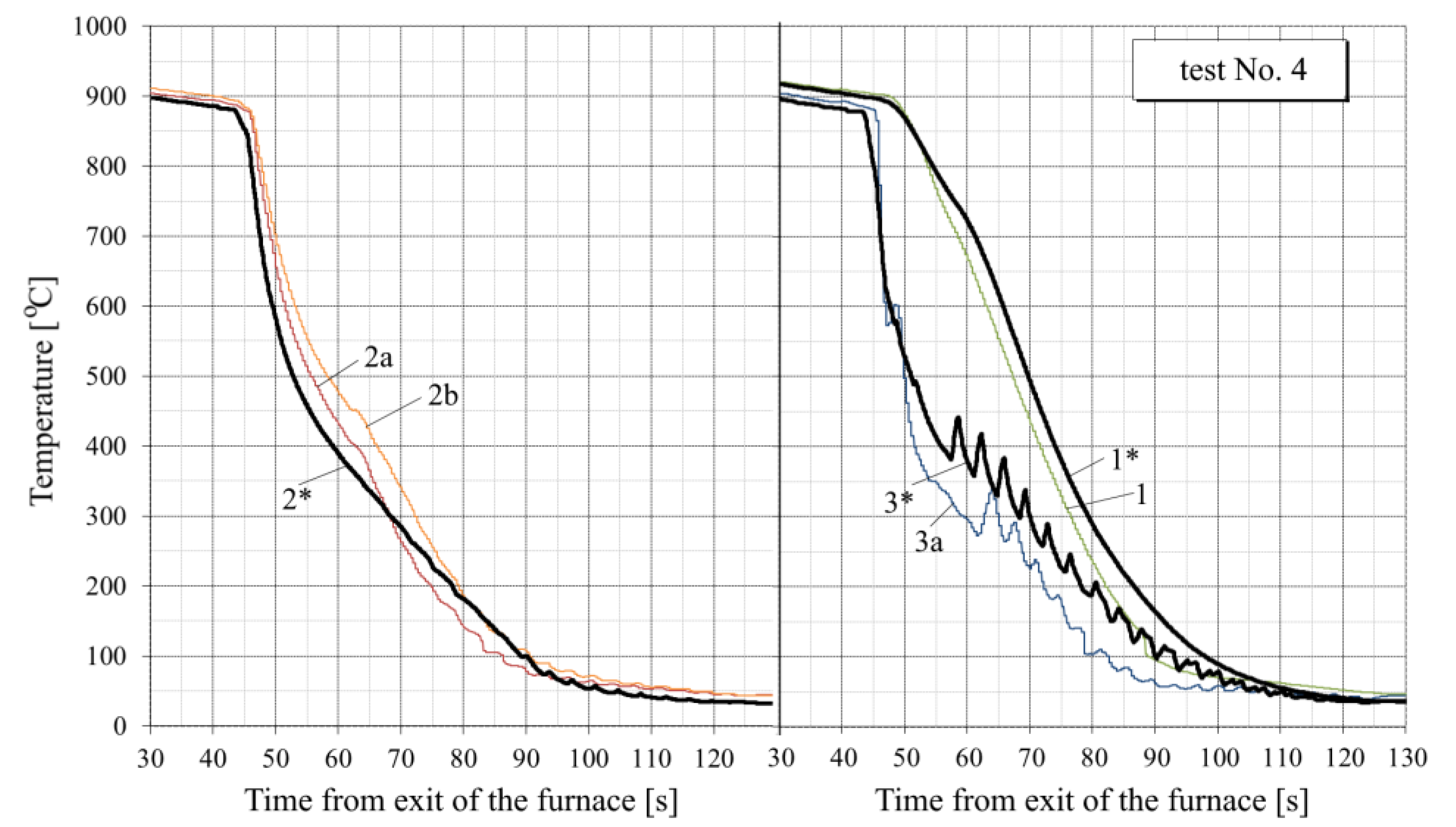
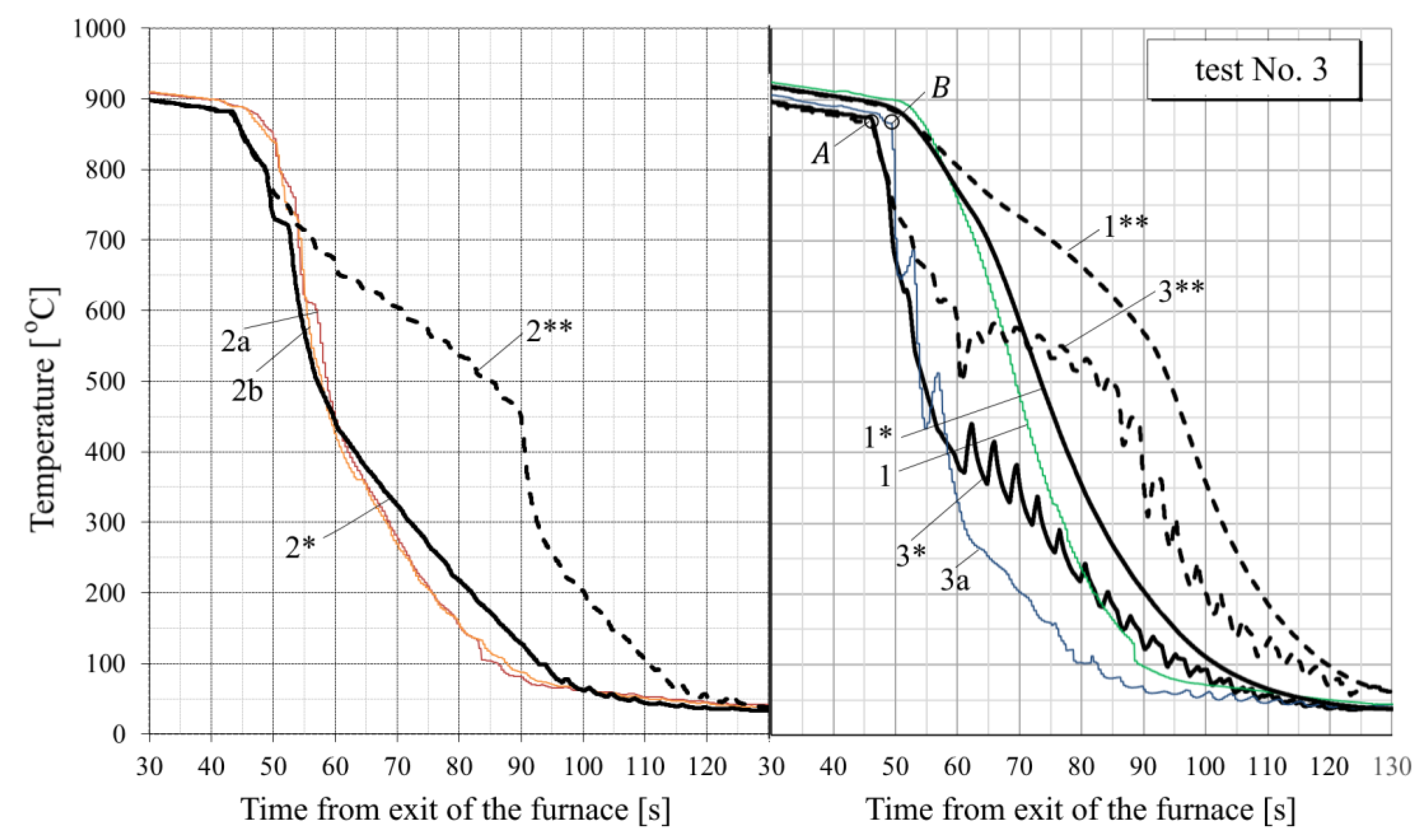
- For all tests, the calculated temperature at the RQM outlet corresponds to the measured temperature, with deviations not exceeding 10 °C. Therefore, the total heat loss of the sheet is taken into account correctly, which indirectly confirms the adequacy of the calculation of the first and second critical surface temperatures corresponding to the changes in the film, transition and nucleate boiling regimes (i.e., the EFB and ETB temperature in Figure 8).
- (2)
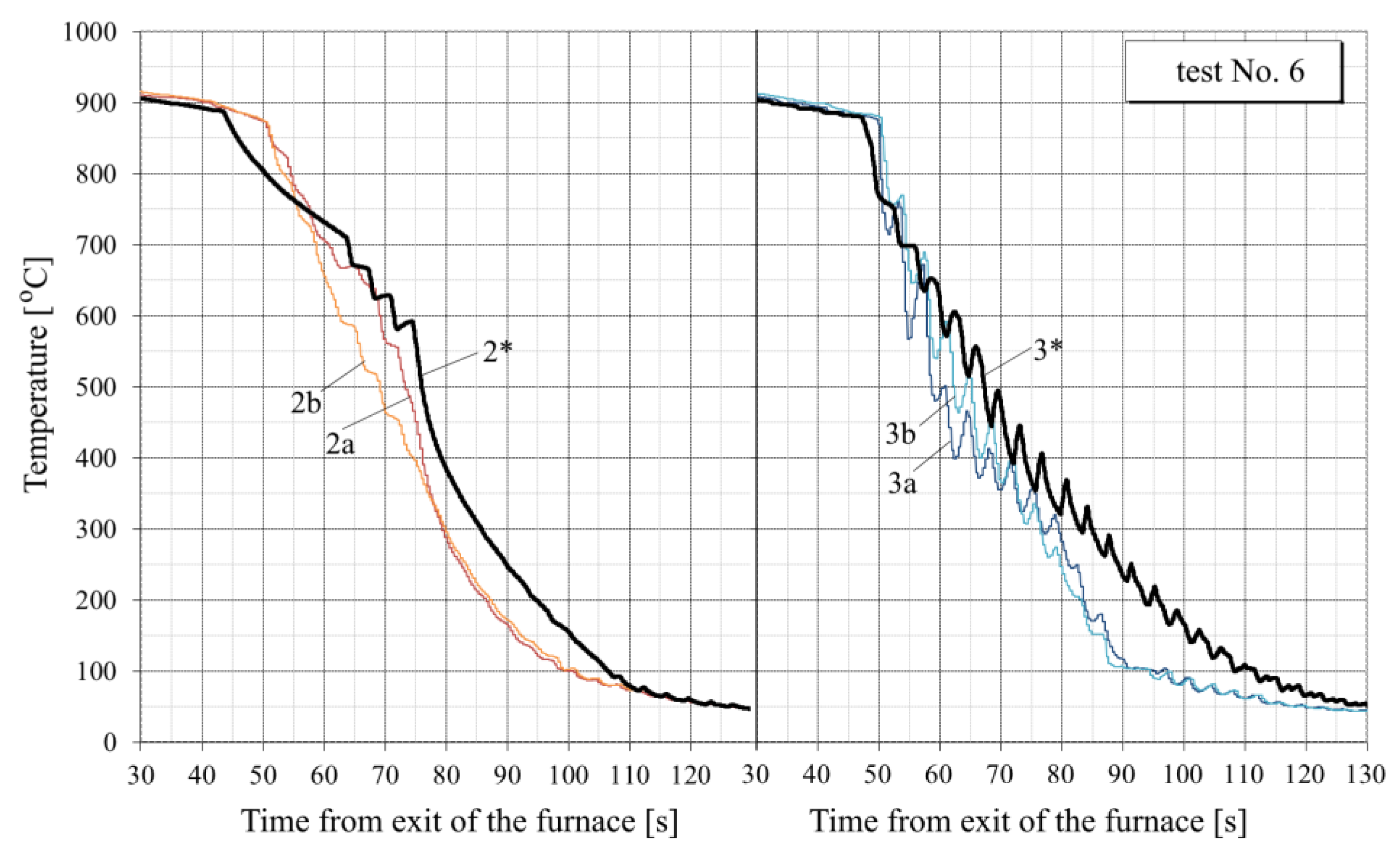
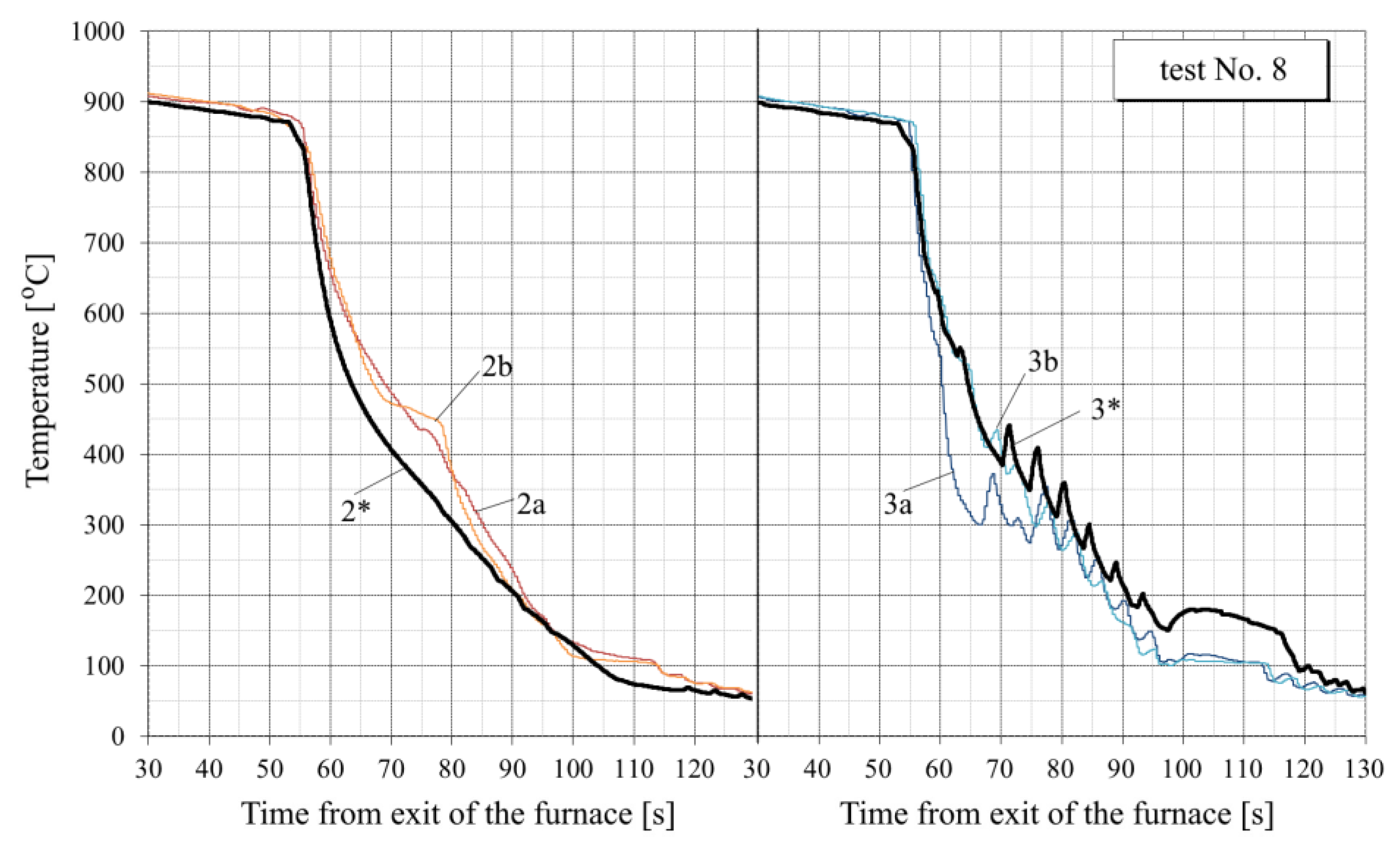
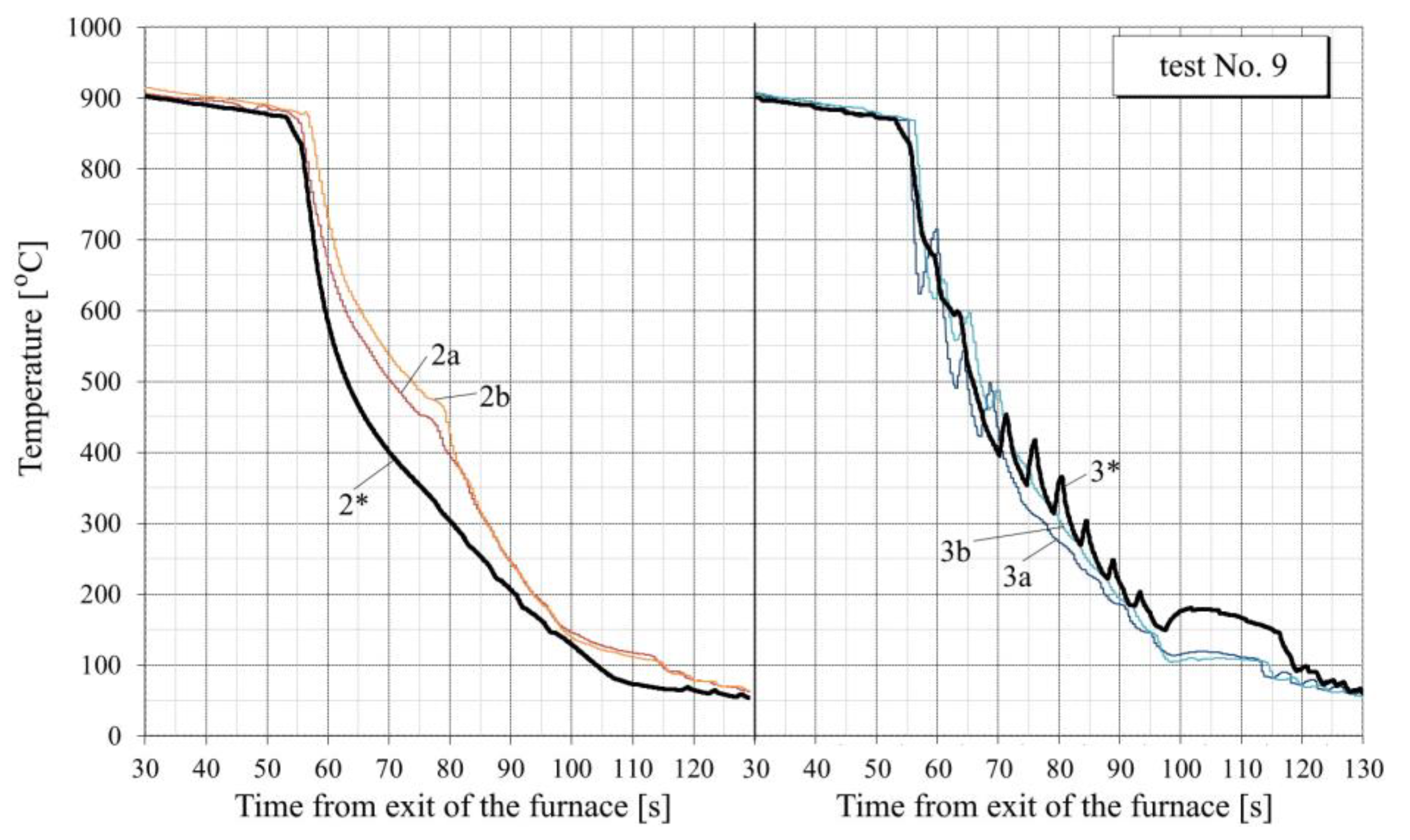
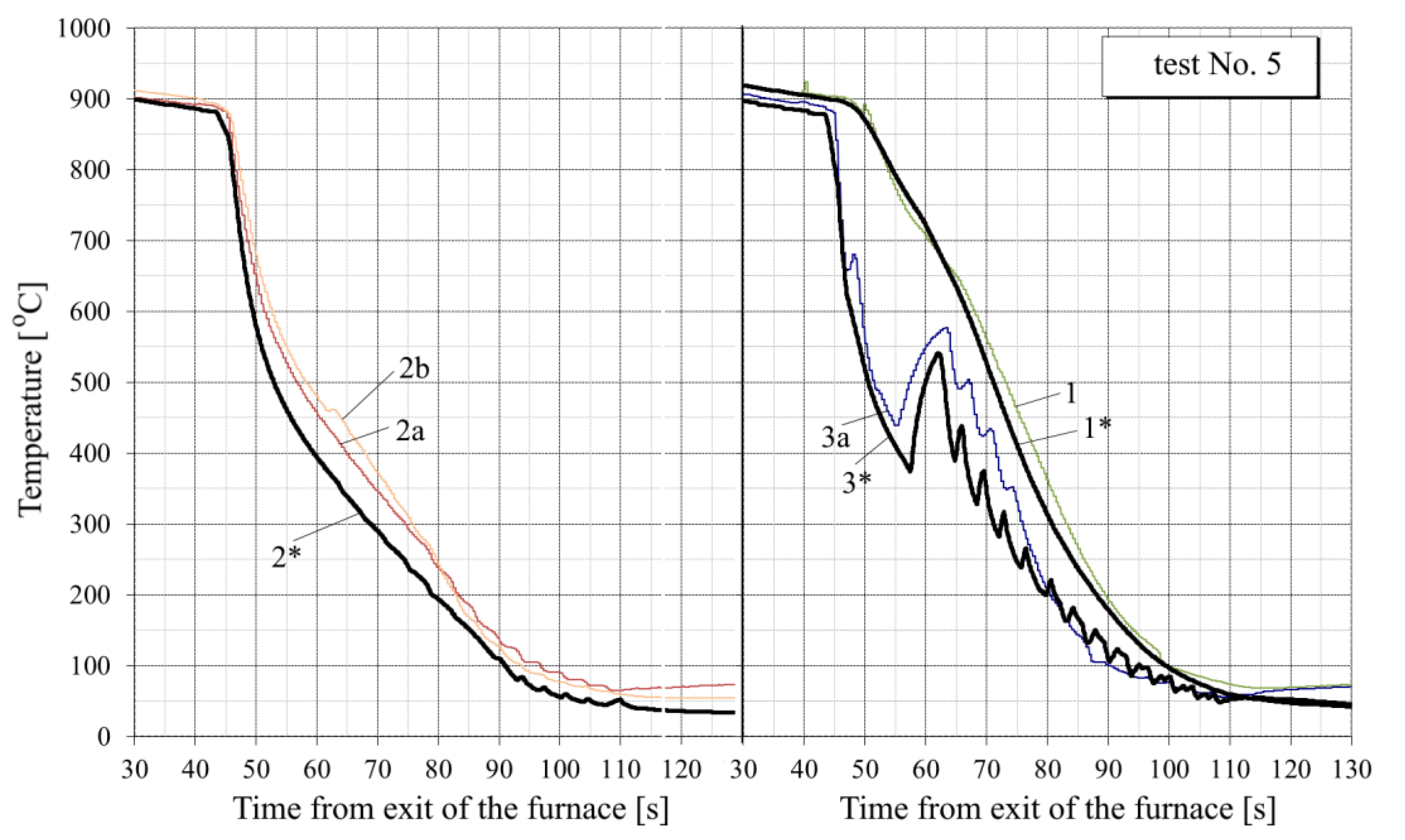
- In the tests with interrupted cooling (Nos. 5, 8, 9 and 10—see Figure 15, Figure 16, Figure A6 and Figure A7), the calculated temperature graphs repeat the characteristic changes in the course of the experimental curves. This suggests that the sizes of the characteristic zones of jet cooling, as well as the parameters of water spreading over the top and bottom surfaces of the sheet, are correctly taken into account.
- (3)
- The degree of closeness of the calculated and experimental curves remains approximately at the same level at significantly different water temperatures (from 23 °C in tests Nos. 1–5 to 32–34 °C in tests Nos. 6–10), which indicates the correctness of taking this factor into account in the model.
- (4)
- Oxide scale thickness on the plate surface is the main parameter of the model which defines its agreement with the experiment. For comparison, Figure 14 also shows the graphs for test No. 3, calculated without taking oxide scale into account (dotted curves marked by the numbers with two asterisks). It can be seen that in this case, there are very rough discrepancies between the calculated and experimental data.
- (5)
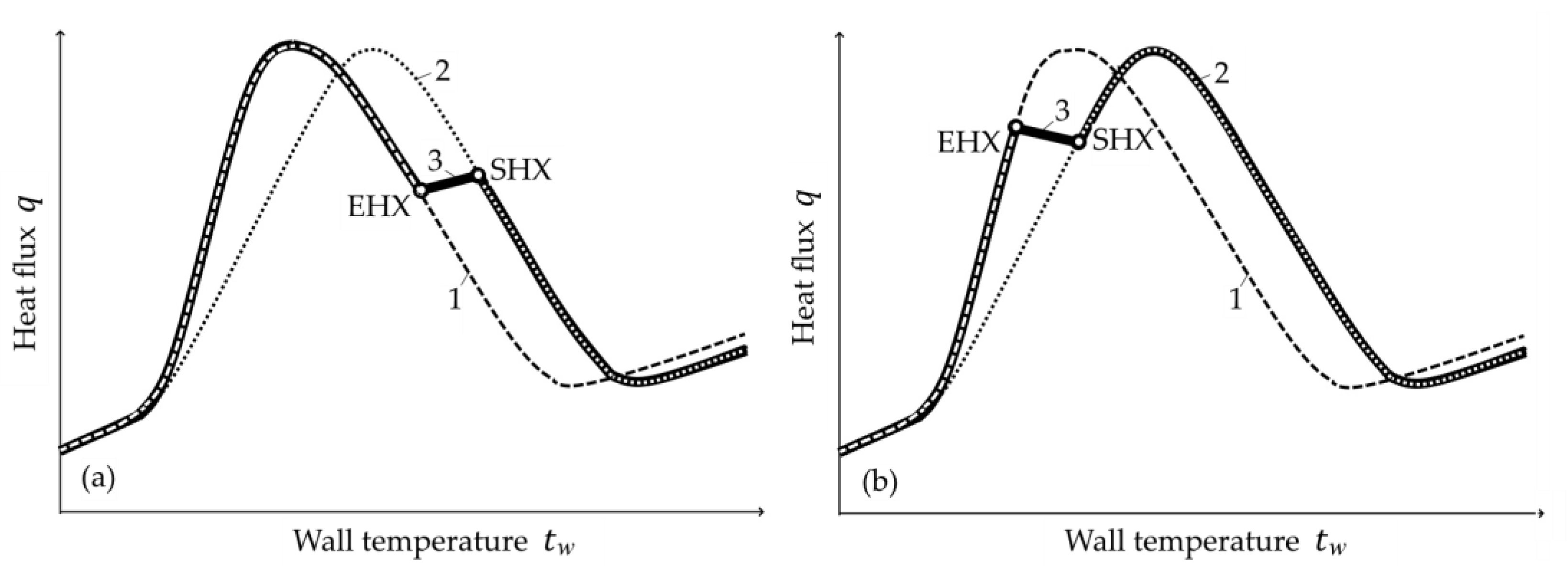
- In tests Nos. 2, 3, 6 and 7 (Figure 14, Figure A2, Figure A4 and Figure A5), in the area of surface thermocouple readings below 400–450 °C, the calculated temperature is much higher than the experimental one. In our opinion, this is due to the assumption made in the simulation of constant thickness of the scale during the entire cooling period. This assumption is generally not true, because during accelerated cooling, oxide scale can crack and be removed (partially or completely) from the sheet surface by water jets. At the same time, the influence of scale depends on the water boiling regime: at high temperatures corresponding to film and transient boiling, oxide scale, as a rule, increases the intensity of heat transfer to the surface; at stable nucleate boiling, on the contrary, reduces it [90]. Therefore, if oxide scale is removed from the sheet surface after stable nucleate boiling is achieved, it is accompanied by an increase in the intensity of cooling. In spray cooling, stable nucleate boiling of water usually begins at 200–250 °C at the surface, which, at the corresponding heat flux values, approximately corresponds to a temperature of 400–450 °C at a depth of 2.5–3 mm (for a plate 30 mm thick). This explains the above-mentioned overestimation of the calculated temperature in the noted experiments with surface thermocouple readings below 400–450 °C. This effect is also confirmed by model calculations. For example, in Figure 14, it is seen that at indications of surface thermocouples above 400–450 °C, the slope angle of the experimental plots is close to the slope angle of the design graphs with scale, and below this boundary, to the slope angle of design graphs without scale.
- (6)
- In practically all cases, there is a “lag” for 1–3 s of the experimental curves from the calculated ones at the very beginning of intensive cooling (see, for example, points A and B in Figure 14). This, most likely, can be explained by the thermal inertia of thermocouples [91], which manifests, to the greatest extent, as a sharp change in metal temperature.
- (7)
- To quantify the “proximity” of the experimental and calculated graphs, the value of the average cooling rate at a certain temperature interval was used. Table 3 summarizes the average cooling rate in the three typical temperature ranges: 800–400 °C, 400–200 °C and 200–100 °C. The value in each cell of this table is obtained by averaging over all experiments. It can be seen that calculated cooling rates are, in general, somewhat lower than experimentally determined (on average, by 12–20% at different temperature intervals). Higher cooling rates in the experiments (than in the simulation) can be explained by the factors mentioned above: the thermal inertia of thermocouples (see item 6) and scale removal from the plate surface during cooling in RQM (see item 5). In this case, if the thermal inertia of thermocouples affects only the “apparent” cooling rate, the reduction in the scale layer affects the actual intensity of heat transfer.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



Appendix B
- −
- Thermal conductivity [W·m−1·K−1]:
- −
- True isobaric specific-mass-heat capacity [J·kg−1·K−1]:
- −
- Density [kg·m−3]:
References
- Uranga, P.; Rodríguez-Ibabe, J.M. Thermomechanical Processing of Steels. Metals 2020, 10, 641. [Google Scholar] [CrossRef]
- Ohaeri, E.G.; Szpunar, J.A. An overview on pipeline steel development for cold climate applications. J. Pipeline Sci. Eng. 2022, 2, 1–17. [Google Scholar] [CrossRef]
- Schwinn, V.; Bauer, J.; Flüss, P.; Kirsch, H.-J.; Amoris, E. Recent Developments and Applications of TMCP Steel Plates. Rev. Metall. 2011, 108, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Militzer, M. Thermomechanical Processed Steels. In Comprehensive Materials Processing, 1st ed.; Hashmi, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 1, pp. 191–216. [Google Scholar] [CrossRef]
- Endo, S.; Nakata, N. Development of Thermo-Mechanical Control Process (TMCP) and High Performance Steel in JFE Steel. JFE Tech. Rep. 2015, 20, 1–6. [Google Scholar]
- Igi, S.; Miyake, M. Development of Thermo-Mechanical Control Process (TMCP) and High Performance Steels in JFE Steel. JFE Tech. Rep. 2021, 26, 86–94. [Google Scholar]
- Nishioka, K.; Ichikawa, K. Progress in thermomechanical control of steel plates and their commercialization. Sci. Technol. Adv. Mater. 2012, 13, 023001. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Zhou, S.; Chen, R.; Da, G.; Yong, Q.; Yang, Z.; Shen, J.; Shang, C.; Liu, Q. The Influence of Temperature on the Microstructure and Properties of Nb-V-Ti-Mo Complex Microalloyed High-Strength Fire-Resistant Steel. Metals 2021, 11, 1670. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Wang, B.; Tian, Y.; Zhang, T.; Yuan, G.; Liu, Z.; Wang, G. Development and Application of Thermo-mechanical Control Process Involving Ultra-fast Cooling Technology in China. ISIJ Int. 2019, 59, 2131–2141. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Zang, P.; Peng, X.; Yan, L.; Li, G. Comparison of Microstructure and Mechanical Properties of High Strength and Toughness Ship Plate Steel. Materials 2021, 14, 5886. [Google Scholar] [CrossRef]
- Nowotnik, A.; Siwecki, T. The effect of TMCP parameters on the microstructure and mechanical properties of Ti–Nb microalloyed steel. J. Microsc. 2010, 237, 258–262. [Google Scholar] [CrossRef]
- Choi, B.C.; Kim, B.; Kim, B.J.; Choi, Y.-W.; Lee, S.J.; Jeon, J.B.; Kim, Y.; Kim, H.C. Effect of Microstructure on Low-Temperature Fracture Toughness of a Submerged-Arc-Welded Low-Carbon and Low-Alloy Steel Plate. Metals 2021, 11, 1839. [Google Scholar] [CrossRef]
- Paiva, F.; Santos, A.; Buono, V.; Gandra, C. Influence of accelerated cooling conditions on microstructure and flatness of API steel heavy plates. In 56° Seminário de Laminação e Conformação de Metais, São Paulo, 2019; Blucher: Sao Paulo, Brazil, 2019; pp. 51–61. [Google Scholar] [CrossRef]
- Kirillov, P.L.; Ninokata, H. Heat transfer in nuclear thermal hydraulics. In Thermal-Hydraulics of Water Cooled Nuclear Reactors, 1st ed.; D’Auria, F., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 357–492. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of spray cooling—Part 2: High temperature boiling regimes and quenching applications. Int. J. Heat Mass Transf. 2017, 115, 1206–1222. [Google Scholar] [CrossRef]
- Kohler, C.; Jeschar, R.; Scholz, R.; Slowik, J.; Borchardt, G. Influence of oxide scales on heat transfer in secondary cooling zones in the continuous casting process. Part 1: Heat transfer through hot-oxidized steel surfaces cooled by spray-water. Steel Res. 1990, 61, 295–301. [Google Scholar]
- Slowik, J.; Borchardt, G.; Kohler, C.; Jeschar, R.; Scholz, R. Influence of oxide scales on heat transfer in secondary cooling zones in the continuous casting process. Part II: Determination of material properties of oxide scales on the steel under spray-water cooling conditions. Steel Res. 1990, 61, 302–311. [Google Scholar] [CrossRef]
- Wendelstorf, J.; Spitzer, K.-H.; Wendelstorf, R. Effect of oxide layers on spray water cooling heat transfer at high surface temperatures. Int. J. Heat Mass Transf. 2008, 51, 4892–4901. [Google Scholar] [CrossRef]
- Resl, O.; Chabičovský, M.; Hnízdil, M.; Kotrbáček, P.; Raudenský, M. Influence of Porous Oxide Layer on Water Spray Cooling. In Proceedings of the 9th International Conference of Fluid Flow, Heat and Mass Transfer (FFHMT’22), Niagara Falls, ON, Canada, 8–10 June 2022. Paper No. 125. [Google Scholar] [CrossRef]
- Horsky, J.; Hrabovsky, J.; Raudensky, M. Impact of the oxide scale on spray cooling intensity. In Proceedings of the 10th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, HEFAT2014, Orlando, FL, USA, 14–16 July 2014; pp. 1480–1485. Available online: http://hdl.handle.net/2263/44729 (accessed on 10 July 2022).
- Chabičovský, M.; Hnizdil, M.; Tseng, A.; Raudenský, M. Effects of oxide layer on Leidenfrost temperature during spray cooling of steel at high temperatures. Int. J. Heat Mass Transf. 2015, 88, 236–246. [Google Scholar] [CrossRef]
- Chabičovský, M.; Resl, O.; Raudenský, M. Impact of oxide layer on spray cooling intensity and homogeneity during continuous casting of steel. In Proceedings of the Metal’2018, Brno, Czech Republic, 23–25 May 2018; pp. 69–74. [Google Scholar]
- Hernandez-Avila, V.H. Heat Transfer Model of the Hot Rolling Runout Table-Cooling and Coil Cooling of Steel. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 1994; 133p. [Google Scholar]
- Singh, A.P.; Prasad, A.; Prakash, K.; Sengupta, D.; Murty, G.M.D.; Jha, S. Influence of thermomechanical processing and accelerated cooling on microstructures and mechanical properties of plain carbon and microalloyed steels. Mater. Sci. Technol. 1999, 15, 121–126. [Google Scholar] [CrossRef]
- Gomez, G.; Schicht, J.; Perez, T.; Goldschmit, M.; Vigliocco, A. Thermo-metallurgical model of the cooling table for a flat product hot rolling mill. In Proceedings of the Materials Science and Technology Conference, Cincinnati, OH, USA, 15–19 October 2006; pp. 1677–1687. [Google Scholar]
- Muhin, U.; Belskij, S.; Makarov, E.; Koynov, T. Simulation of accelerated strip cooling on the hot rolling mill run-out roller table. Frat. Integrità Strutt. 2016, 37, 305–311. [Google Scholar] [CrossRef] [Green Version]
- Koldin, A.; Dema, R.; Nalimova, M.; Mihailov, E.; Shapovalov, A.; Kharchenko, M. Modeling of the thermal state of the hot rolled strip in the accelerated cooling process Part 1: Heat transfer model. J. Chem. Technol. Metall. 2019, 54, 1330–1336. Available online: https://dl.uctm.edu/journal/node/j2019-6/26_19-88_p_1330-1336.pdf (accessed on 10 July 2022).
- Liu, W.-W.; Li, H.-J.; Wang, Z.-D.; Wang, G.-D. Mathematical model for cooling process and its self-learning applied in hot rolling mill. J. Shanghai Univ. 2011, 15, 548–552. [Google Scholar] [CrossRef]
- Malinowski, Z.; Cebo-Rudnicka, A.; Hadała, B.; Szajding, A.; Telejko, T. Implementation of one and three dimensional models for heat transfer coefficient identification over the plate cooled by the circular water jets. Heat Mass Transf. 2018, 54, 2195–2213. [Google Scholar] [CrossRef] [Green Version]
- Ivantsov, O.V.; Kaskin, B.K.; Vaskin, A.M.; Viventsov, A.S.; Zimakov, E.A. Stabilization of the mechanical properties of rolled products after the reconstruction of the laminar cooling system on 1700 Hot Strip Mill. Metallurg 2005, 2, 42–44. (In Russian) [Google Scholar]
- Belobrov, Y.N.; Gritsenko, S.A.; Eletskih, V.I.; Kozhevnikov, G.V.; Vakulenko, A.M.; Ostapenko, A.L.; Beygelzimer, E.E.; Kuzmin, A.V.; Egorov, N.T. Creation of a modern complex for heat treatment of heavy-plate products at the HSW HUTA STALI metallurgical plant, Poland. Chernaya Metall. Byull. 2008, 8, 36–39. (In Russian) [Google Scholar]
- Beygelzimer, E.E.; Ostapenko, A.L.; Kuzmin, A.V.; Kozlenko, D.A. Integrated software for ACS of controlled cooling of rolled sheets. Stal 2006, 8, 18–23. (In Russian) [Google Scholar]
- Ning, J.; Liang, S.Y. Evaluation of an Analytical Model in the Prediction of Machining Temperature of AISI 1045 Steel and AISI 4340 Steel. J. Manuf. Mater. Process. 2018, 2, 74. [Google Scholar] [CrossRef] [Green Version]
- Shokrani, A.; Biermann, D. Advanced Manufacturing and Machining Processes. J. Manuf. Mater. Process. 2020, 4, 102. [Google Scholar] [CrossRef]
- Beygelzimer, E.E.; Beygelzimer, Y.E. Calculation of the theoretical dimensions of the spray impact spot taking into account the inclination and rotation of the nozzle. Izv. Vuzov. Chernaya Metall. 2012, 8, 32–36. (In Russian) [Google Scholar]
- Visaria, M.; Mudawar, I. Theoretical and experimental study of the effects of spray inclination on two-phase spray cooling and critical heat flux. Int. J. Heat Mass Transf. 2008, 51, 2398–2410. [Google Scholar] [CrossRef]
- Beygelzimer, E.E.; Beygelzimer, Y.E. Engineering calculation of sprayer jet form for cooling metal sheets. Izv. Vuzov. Chernaya Metall. 2012, 55, 43–47. [Google Scholar] [CrossRef] [Green Version]
- Idelchik, I.E. Handbook of Hydraulic Resistance, 4th ed.; Begell House Inc.: Danbury, CT, USA, 2008; 861p. [Google Scholar]
- Chaudhry, M.H. Open-Channel Flow, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008; 523p. [Google Scholar]
- Munson, B.R.; Young, D.F.; Okiishi, T.H. Fundamentals of Fluid Mechanics, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; 928p. [Google Scholar]
- Beygelzimer, E.E. An engineering method for estimation of the radius of a contact-spot, formed by the round liquid jet on the upper surface of hot rolled sheet. Met. Cast. Ukr. 2011, 219, 12–19. (In Russian) [Google Scholar]
- Lord Rayleigh, O.M. On the Theory of Long Waves and Bores. In Proceedings of the Royal Society of London. Ser. A Publ. R. Soc. 1914, 619, 324–328. Available online: https://www.jstor.org/stable/93519 (accessed on 10 July 2022).
- Watson, E.J. The Spread of the Liquid Jet Over a Horizontal Plane. J. Fluid Mech. 1964, 20, 481–499. [Google Scholar] [CrossRef]
- Subramanya, K. Flow in Open Channels, 3rd ed.; Tata McGraw-Hill Publishing Co.: New York, NY, USA, 2009; 547p. [Google Scholar]
- Beygelzimer, E.E. About the calculation of the length of the intensive cooling of sheet metal by water curtains. Met. Cast. Ukr. 2011, 223, 48–54. (In Russian) [Google Scholar]
- Beygelzimer, E.E. Engineering method for evaluation of thickness and velocity of the water layer, spreading over the upper surface of the wide strip when jet cooling. Met. Cast. Ukr. 2012, 234, 21–30. (In Russian) [Google Scholar]
- Beygelzimer, E.E. Estimation of length of the water layer, unlimitedly spreading over the upper surface of strip when jet cooling. Met. Cast. Ukr. 2012, 235, 19–24. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; 615p. [Google Scholar]
- Cheong, H.-F. Discharge Coefficient of Lateral Diversion from Trapeziodal Channel. J. Irrig. Drain Eng. 1991, 117, 461–475. [Google Scholar] [CrossRef]
- Beygelzimer, E. Approach to the simulation of jet-impingement cooling based on the reference points of boiling curve. Metall. Ore Min. Ind. 2017, 5, 85–90. (In Russian) [Google Scholar]
- Nukiyama, S. The maximum and minimum values of the heat Q transmitted from metal to boiling water under atmospheric pressure. Int. J. Heat Mass Transf. 1984, 27, 959–970. [Google Scholar] [CrossRef]
- Kalinin, E.K.; Berlin, I.I.; Kostiouk, V.V. Transition Boiling Heat Transfer. In Advances in Heat Transfer; Academic Press, Inc.: Moscow, Russia, 1987; Volume 18, pp. 241–323. [Google Scholar] [CrossRef]
- Skripov, V.P.; Pavlov, P.; Sinitsyn, E.N. Heating of liquids to boiling by a pulsating heat supply: 2. Experiments with water, alcohols, n-hexane and nonane. High Temperature 1965, 3, 670–674. [Google Scholar]
- Lykov, A.V. Analytical Heat Diffusion Theory; Academic Press, Inc.: New York, NY, USA, 1968; 685p. [Google Scholar]
- Makovskiy, V.A. Empirical formulas for expressing the temperature dependence of the thermophysical properties of steel. Steel 1972, 1, 87–89. (In Russian) [Google Scholar]
- Beygelzimer, E.; Beygelzimer, Y. Generalized estimates for the density of oxide scale in the range from 0 °C to 1300 °C. arXiv 2021, arXiv:2110.09791v1. [Google Scholar]
- Beygelzimer, E.; Beygelzimer, Y. Thermal conductivity of oxide scale and its components in the range from 0 °C to 1300 °C: Generalized estimates with account for movability of phase transitions. arXiv 2021, arXiv:2110.11632v1. [Google Scholar]
- Beygelzimer, E.; Beygelzimer, Y. Generalized estimates for thermal expansion of oxide scale in the range from 0 °C to 1300 °C with account for movability of phase transitions in its components. arXiv 2021, arXiv:2110.08528v1. [Google Scholar]
- Beygelzimer, E.; Beygelzimer, Y. Heat Capacity of oxide scale in the range from 0 C to 1300 C: Generalized estimates with account for movability of phase transitions. arXiv 2021, arXiv:2110.11101v1. [Google Scholar]
- Kutateladze, S.S.; Styrikovich, M.A. Hydrodynamics of Gas-Liquid Systems; Energiya: Moscow, Russia, 1976; 296p. (In Russian) [Google Scholar]
- Johnson, H.A. Transient boiling heat transfer to water. Int. J. Heat Mass Transf. 1971, 14, 67–82. [Google Scholar] [CrossRef]
- Ershov, I.Y.; Kuvaeva, A.M. Influence of the degree of subcooling on the boiling heat transfer coefficient. Izv. Vuzov. Energ. 1962, 11, 84–87. (In Russian) [Google Scholar]
- Wang, B.-X.; Shi, D.-H. A semi-empirical theory for forced-flow turbulent film boiling of subcooled liquid along a horizontal plate. Int. J. Heat Mass Transf. 1985, 28, 1499–1505. [Google Scholar] [CrossRef]
- Kutateladze, S.S. Fundamentals of Heat Transfer; Edward Arnold: London, UK, 1963; 485p. [Google Scholar]
- Kutateladze, S.S.; Leont’ev, A.I. Heat and Mass Transfer and Friction in the Turbulent Boundary Layer; Energoatomizdat: Moscow, Russia, 1985; 320p. [Google Scholar]
- Isachenko, V.P.; Kushnyrev, V.I. Jet Cooling; Energoatomizdat: Moscow, Russia, 1984; 216p. (In Russian) [Google Scholar]
- Vander Voort, G.F. (Ed.) Atlas of Time-Temperature Diagrams for Irons and Steels; ASM Int.: West Perth, Australia, 1991; 783p. [Google Scholar]
- Popova, L.E.; Popov, A.A. Diagrams of Transformation of Austenite in Steels and of Betta Solution in Titanium Alloys. In A Handbook of Heat Treatment Specialist, 3rd ed.; Metallurgiya: Moscow, Russia, 1991; 503p. (In Russian) [Google Scholar]
- Callister, W.D., Jr.; Rethwisch, D.G. Material Science and Engineering: An Introduction, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; 1000p. [Google Scholar]
- Scheil, E. Anlaufzeit der Austenitumwandlung [Start-up time of austenite transformation]. Arch. Das Eisenhuttenwes. 1935, 12, 565–567. [Google Scholar] [CrossRef]
- Lusk, M.; Jou, H.-J. On the Rule of Additivity in Phase Transformation Kinetics. Met. Mater. Trans. A 1997, 28A, 287–291. [Google Scholar] [CrossRef]
- Carlone, G.S.; Palazzo, R.; Pasquino, R. Finite element analysis of the steel quenching process: Temperature field and solid–solid phase change. Comput. Math. Appl. 2010, 59, 585–594. [Google Scholar] [CrossRef] [Green Version]
- Lička, S.; Wozniak, J. Matematický model pro analýzu technologických podmínek válcování ocelí za tepla [Mathematical model for the analysis of technological conditions of hot rolling of steels]. Hutn. Actual 1981, 22, 1–49. [Google Scholar]
- Mazur, V.L.; Nogovitsyn, O.V. Theory and Technology of Sheet Rolling: Numerical Analysis and Applications; CRC Press: Boca Raton, FL, USA, 2018; 494p. [Google Scholar] [CrossRef]
- Pereloma, E.; Edmonds, D.V. (Eds.) Phase Transformations in Steels. Volume 1. Fundamentals and Diffusion-Controlled Transformations; Woodhead Publishing: Oxford, UK; Cambridge, UK; Philadelphia, PA, USA; New Delhi, India, 2012; 634p. [Google Scholar]
- Austin, J.B.; Rickett, R.L. Kinetics of the decomposition of austenite at constant temperature. Trans. Am. Inst. Min. Metall. Eng. 1939, 964, 1–20. [Google Scholar]
- Starink, M.J. Kinetic equations for diffusion-controlled precipitation reactions. J. Mater. Sci. 1997, 32, 4061–4070. [Google Scholar] [CrossRef]
- Koistinen, D.P.; Marburger, R.E. A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbon alloys and plain carbon steels. Acta Metall. 1959, 7, 59–60. [Google Scholar] [CrossRef]
- Ariza, E.A.; Martorano, M.A.; de Lima, N.B.; Tschiptschin, A.P. Numerical Simulation with Thorough Experimental Validation to Predict the Build-up of Residual Stresses during Quenching of Carbon and Low-Alloy Steels. ISIJ Int. 2014, 54, 1396–1405. [Google Scholar] [CrossRef] [Green Version]
- Allen III, M.B.; Isaacson, E.I. Numerical Analysis for Applied Science, 2nd ed.; John Wiley&Sons Inc.: Hoboken, NJ, USA, 2019; 583p. [Google Scholar]
- Tiunov, V.N.; Gritsenko, S.A.; Ostapenko, A.L.; Beygelzimer, E.E.; Kozlenko, D.A. PAO NKMZ roller quenching machines. Steel Transl. 2014, 44, 921–925. [Google Scholar] [CrossRef]
- Ostapenko, A.L.; Goncharov, N.V.; Kuzmin, A.V. Experimental investigations into cooling the sheets and plates in the rolling quenching machine. Chern. Metall. Bull. Sci. Tech. Econ. Inform. 2008, 8, 43–49. (In Russian) [Google Scholar]
- Ostapenko, A.L.; Beygelzimer, E.E.; Kozlenko, D.A.; Gritsenko, S.A.; Goncharov, N.V. Sheet cooling in a roller quenching machine. Steel Transl. 2016, 46, 349–355. [Google Scholar] [CrossRef]
- Birks, N.; Meier, G.H. Introduction to High Temperature Oxidation of Metals; Edward Arnold: London, UK, 1983; 198p. [Google Scholar]
- Arreola-Villa, S.A.; Vergara-Hernández, H.J.; Solorio-Diáz, G.; Pérez-Alvarado, A.; Vázquez-Gómez, O. and Chávez-Campos, G-M. Kinetic Study of Oxide Growth at High Temperature in Low Carbon Steel. Metals 2022, 12, 147. [Google Scholar] [CrossRef]
- Kubaschewski, O.; Hopkins, B.E. Oxidation of Metals and Alloys, 2nd ed.; Butterworths Scientific Publications: London, UK, 1962; 239p. [Google Scholar]
- Peretyatko, V.N.; Temlyantsev, N.V.; Temlyantsev, M.V.; Mihaylenko, Y.E. Heating of Steel Slabs; Teplotehnik: Moscow, Russia, 2008; 192p. (In Russian) [Google Scholar]
- Sun, B.; Cheng, L.; Du, C.-Y.; Zhang, J.-K.; He, Y.-Q.; Cao, G.-M. Effect of Oxide Scale Microstructure on Atmospheric Corrosion Behavior of Hot Rolled Steel Strip. Coatings 2021, 11, 517. [Google Scholar] [CrossRef]
- Sukov, G.S.; Tiunov, V.N.; Gritsenko, S.A. Improving the design of a roller quenching machine for heat treatment of sheet metal. Chernaya Metall. Byull. 2016, 4, 68–74. [Google Scholar]
- Beygelzimer, E. Effect of scale on the shape of the boiling curve during jet-impingement cooling. Metall. Ore Min. Ind. 2018, 1, 59–62. (In Russian) [Google Scholar]
- Zholkov, Y.A. Thermal inertia of thermocouples. Meas. Tech. 1961, 4, 983–985. [Google Scholar] [CrossRef]



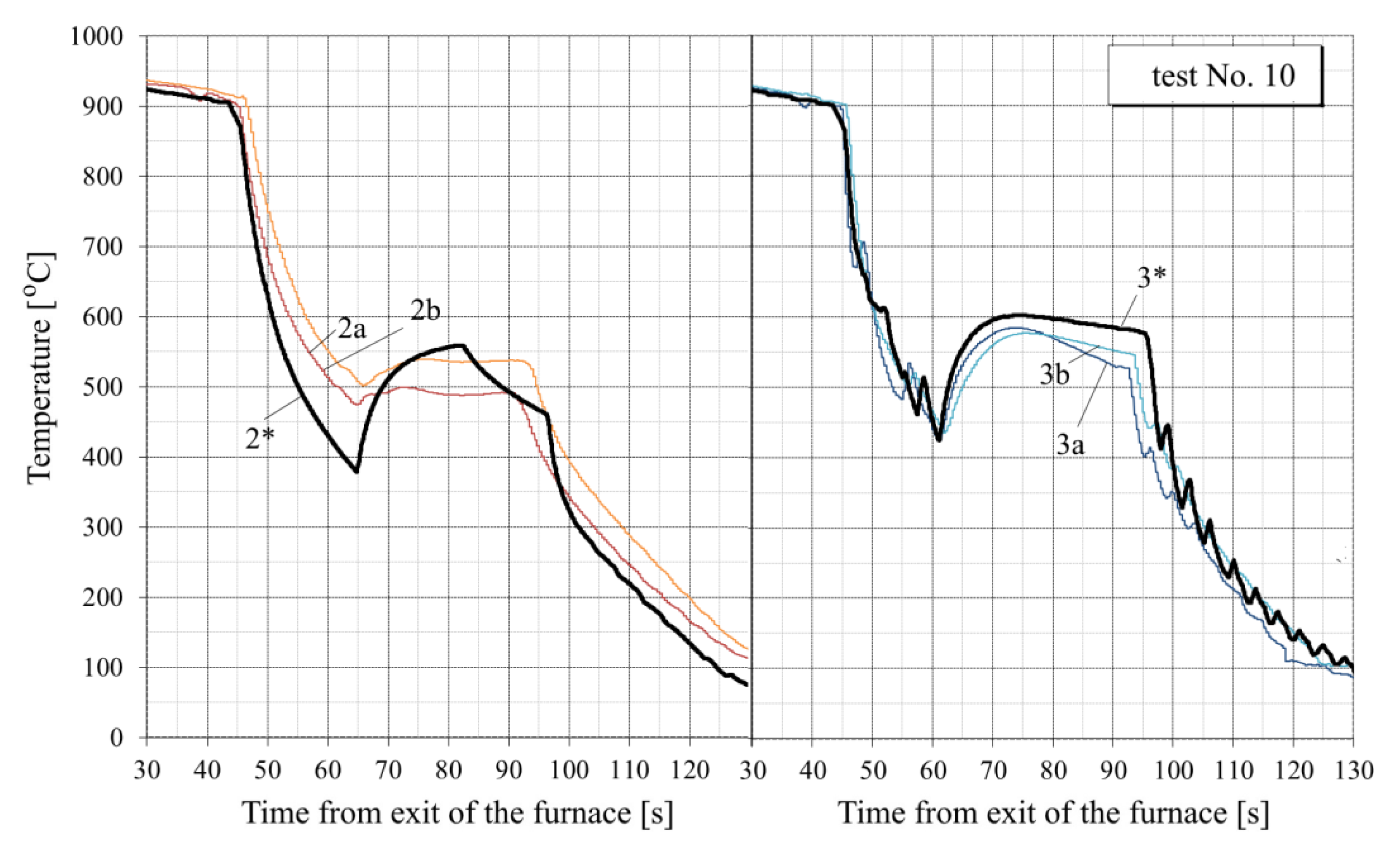
| Test No. | Heating Temperature [°C] | Plate Speed [ms−1] | Water Temperature [°C] | Water Flow Rates by RQM Zone *: Top (above the Line) and Bottom (below the Line) [m3h−1] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H1 | H2-3 | L1-2 | L3 | L4 | L5 | L6 | ||||
| 1 | 850 | 0.12 | 23 | 530 | 290 | 110 | 110 | 110 | 0 | 0 |
| 510 | 510 | 190 | 190 | 190 | 0 | 0 | ||||
| 2 | 950 | 0.11 | 23 | 310 | 290 | 110 | 110 | 110 | 0 | 0 |
| 510 | 510 | 190 | 190 | 190 | 0 | 0 | ||||
| 3 | 950 | 0.11 | 23 | 0 | 290 | 110 | 110 | 110 | 75 | 0 |
| 0 | 490 | 190 | 190 | 190 | 115 | 0 | ||||
| 4 | 950 | 0.11 | 23 | 310 | 100 | 110 | 110 | 110 | 70 | 0 |
| 510 | 180 | 190 | 190 | 190 | 115 | 0 | ||||
| 5 | 950 | 0.11 | 23 | 310 | 0 | 110 | 110 | 110 | 0 | 0 |
| 510 | 0 | 190 | 190 | 190 | 0 | 0 | ||||
| 6 | 950 | 0.11 | 34 | 0 | 120 | 130 | 130 | 90 | 130 | 130 |
| 0 | 210 | 210 | 210 | 160 | 210 | 210 | ||||
| 7 | 950 | 0.11 | 34 | 310 | 0 | 130 | 110 | 110 | 75 | 0 |
| 310 | 200 | 190 | 153 | 170 | 115 | 0 | ||||
| 8 | 950 | 0.09 | 34 | 310 | 0 | 130 | 0 | 110 | 75 | 0 |
| 310 | 200 | 190 | 0 | 170 | 115 | 0 | ||||
| 9 | 950 | 0.09 | 33 | 310 | 0 | 130 | 0 | 110 | 75 | 0 |
| 210 | 200 | 190 | 0 | 170 | 115 | 0 | ||||
| 10 | 980 | 0.11 | 32 | 310 | 100 | 0 | 0 | 90 | 110 | 75 |
| 410 | 175 | 0 | 0 | 155 | 170 | 115 | ||||
| Test No. | Total Heating Time [min-sec] | Plate Temperature [°C] | Oxide Scale Thickness [μm] |
|---|---|---|---|
| 1 | 47′10″ | 853 | 47 |
| 845 | 42 | ||
| 2 | 55′27″ | 956 | 113 |
| 948 | 103 | ||
| 3 | 46′16″ | 957 | 105 |
| 950 | 97 | ||
| 4 | 43′57″ | 956 | 105 |
| 949 | 95 | ||
| 5 | 43′30″ | 956 | 103 |
| 950 | 94 | ||
| 6 | 56′28″ | 962 | 104 |
| 958 | 98 | ||
| 7 | 52′23″ | 958 | 123 |
| 954 | 116 | ||
| 8 | 51′48″ | 957 | 123 |
| 951 | 117 | ||
| 9 | 45′29″ | 958 | 110 |
| 950 | 104 | ||
| 10 | 60′43″ | 982 | 147 |
| 976 | 138 |
| Nature of the Data | Reference Coordinate by Sheet Thickness * | Average Cooling Rate [°C/s] in Temperature Range | ||
|---|---|---|---|---|
| 800–400 °C | 400–200 °C | 200–100 °C | ||
| Experiment (thermocouples) | top | 27.5 | 14.4 | 8.0 |
| center | 23.7 | 20.3 | 11.4 | |
| bottom | 42.2 | 14.3 | 7.9 | |
| Calculation (model) | top | 29.4 | 11.0 | 8.4 |
| center | 21.2 | 16.3 | 9.0 | |
| bottom | 32.2 | 11.9 | 6.5 | |
| Deviation (calculation minus experiment) | top | 1.8 | −3.5 | 0.4 |
| center | −2.5 | −4.0 | −2.4 | |
| bottom | −10.0 | −2.4 | −1.5 | |
| averaged over three coordinates ** | −3.6 (−12%) | −3.3 (−20%) | −1.1 (−13%) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beygelzimer, E.; Beygelzimer, Y. Validation of the Cooling Model for TMCP Processing of Steel Sheets with Oxide Scale Using Industrial Experiment Data. J. Manuf. Mater. Process. 2022, 6, 78. https://doi.org/10.3390/jmmp6040078
Beygelzimer E, Beygelzimer Y. Validation of the Cooling Model for TMCP Processing of Steel Sheets with Oxide Scale Using Industrial Experiment Data. Journal of Manufacturing and Materials Processing. 2022; 6(4):78. https://doi.org/10.3390/jmmp6040078
Chicago/Turabian StyleBeygelzimer, Emmanuil, and Yan Beygelzimer. 2022. "Validation of the Cooling Model for TMCP Processing of Steel Sheets with Oxide Scale Using Industrial Experiment Data" Journal of Manufacturing and Materials Processing 6, no. 4: 78. https://doi.org/10.3390/jmmp6040078
APA StyleBeygelzimer, E., & Beygelzimer, Y. (2022). Validation of the Cooling Model for TMCP Processing of Steel Sheets with Oxide Scale Using Industrial Experiment Data. Journal of Manufacturing and Materials Processing, 6(4), 78. https://doi.org/10.3390/jmmp6040078






