2D Axisymmetric Modeling of Refill Friction Stir Spot Welding and Experimental Validation
Abstract
:1. Introduction
2. Materials and Methods
3. Simulation of RFSSW
4. Results
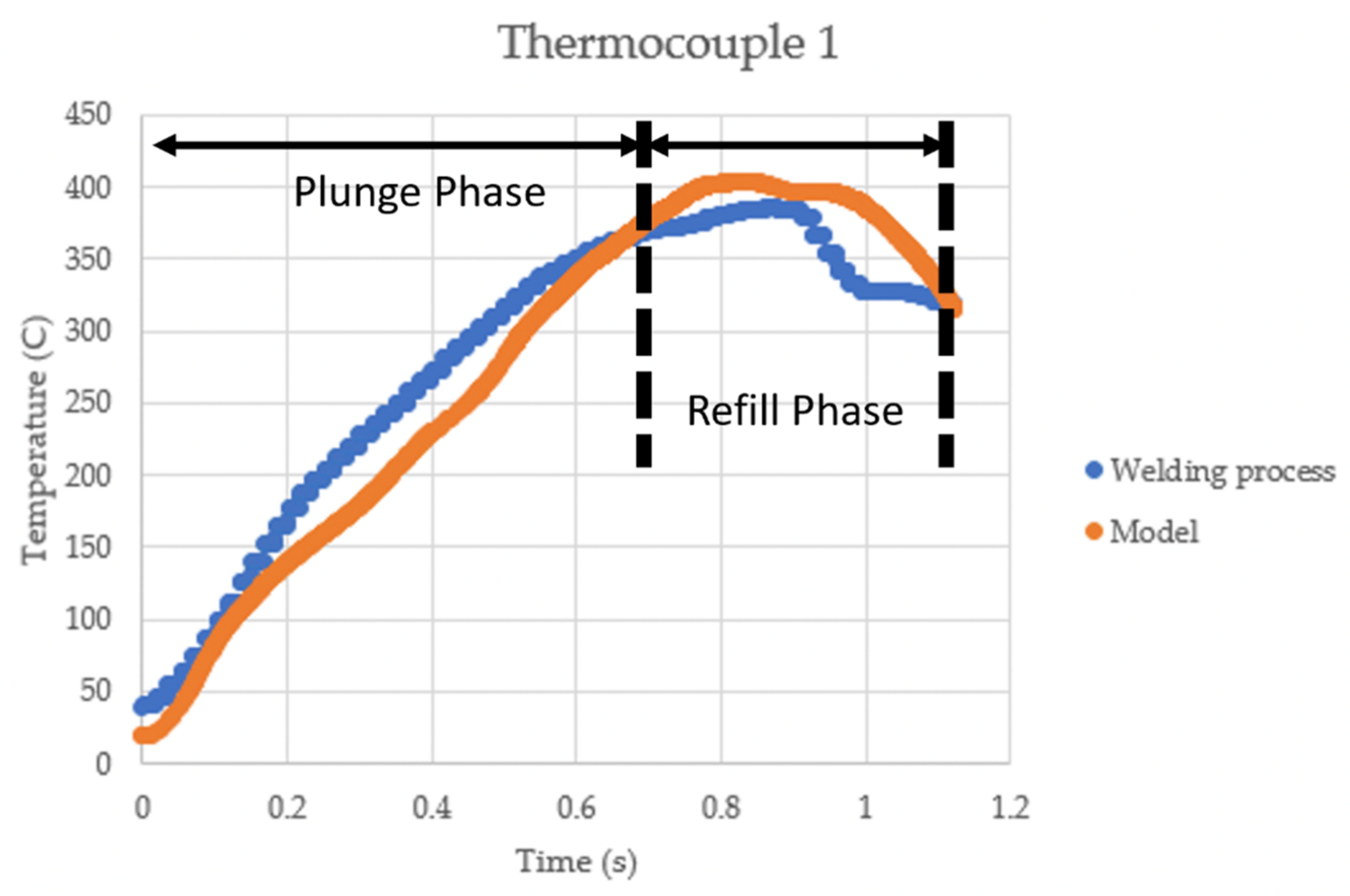
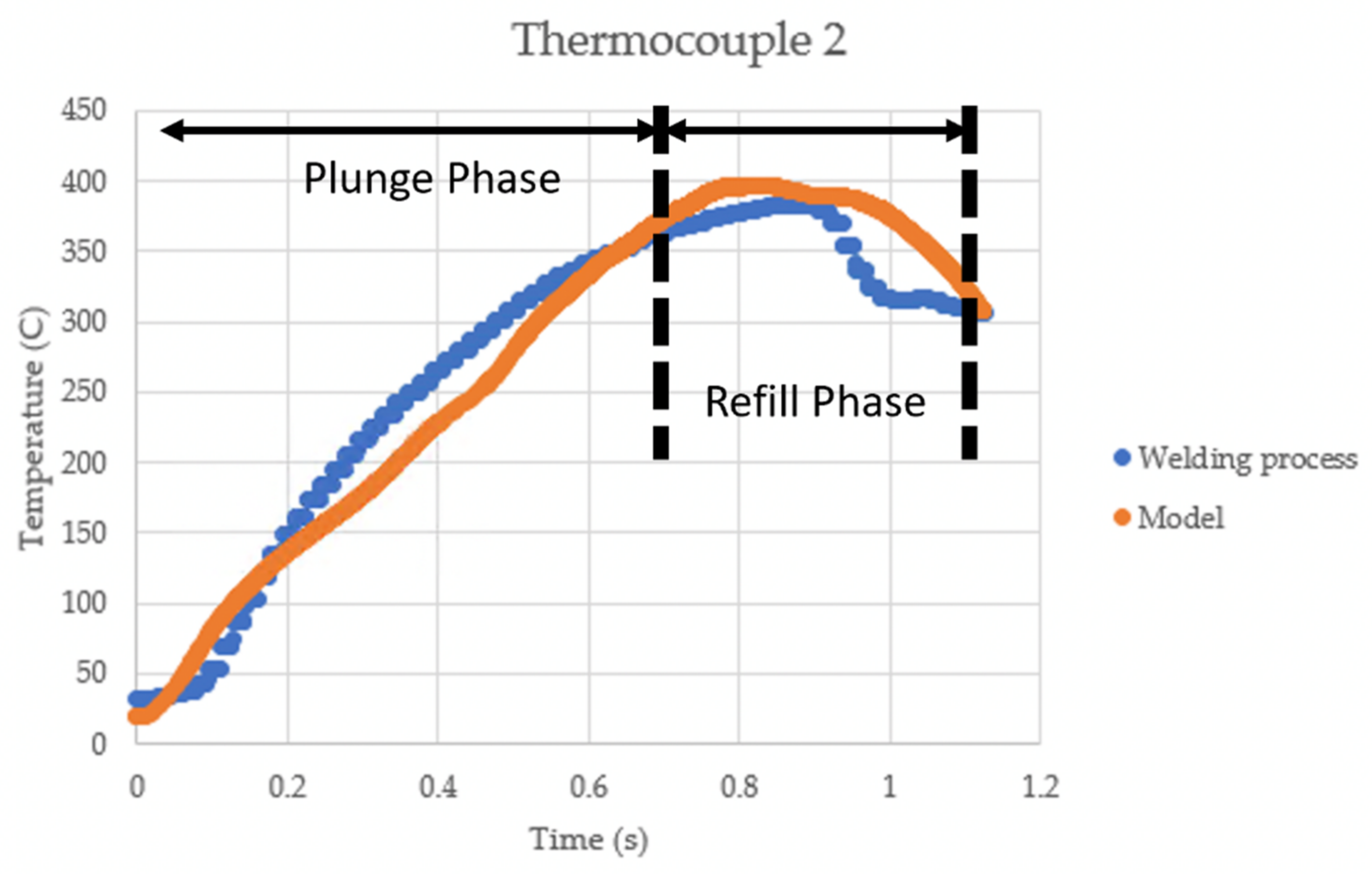
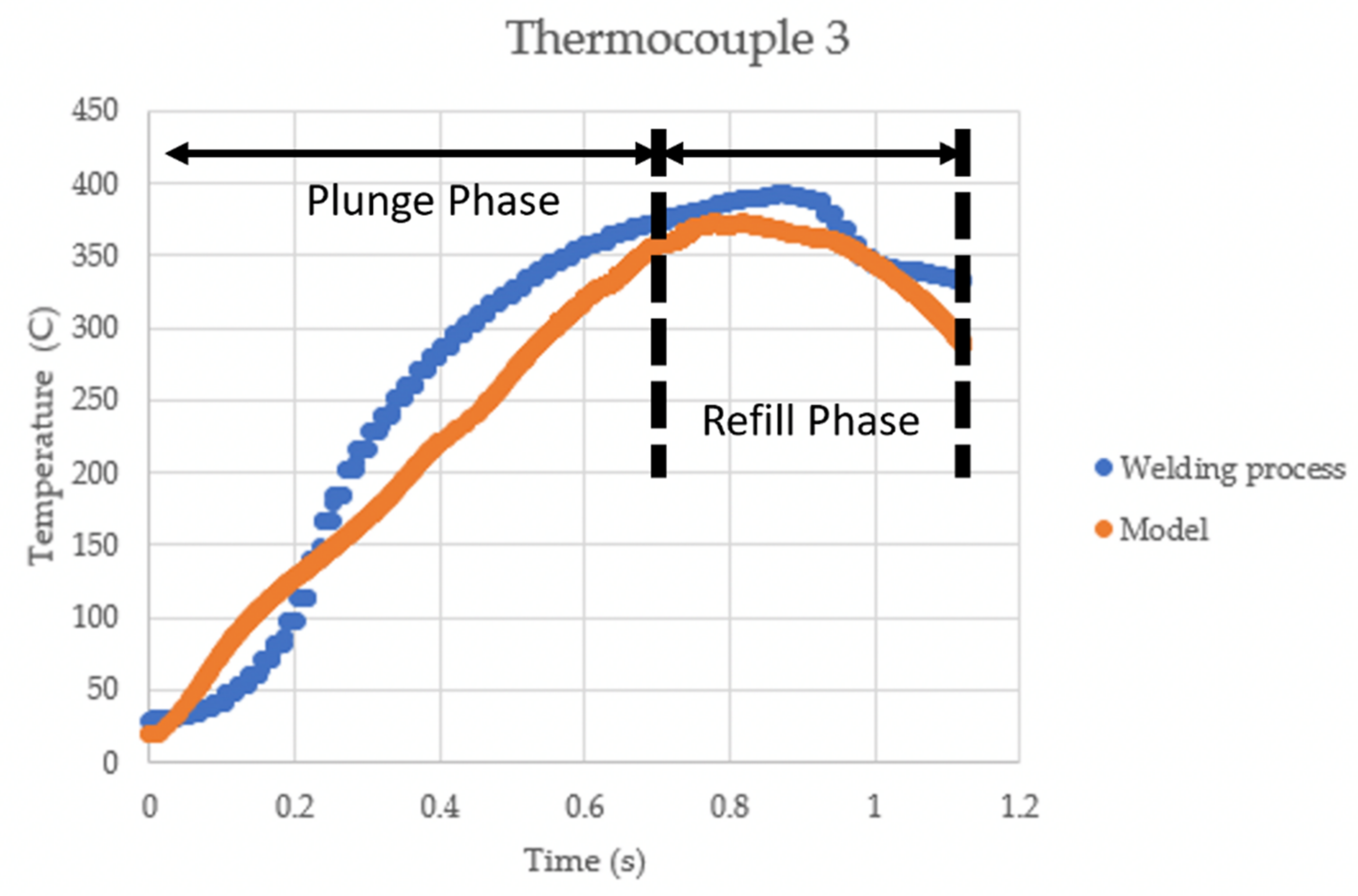
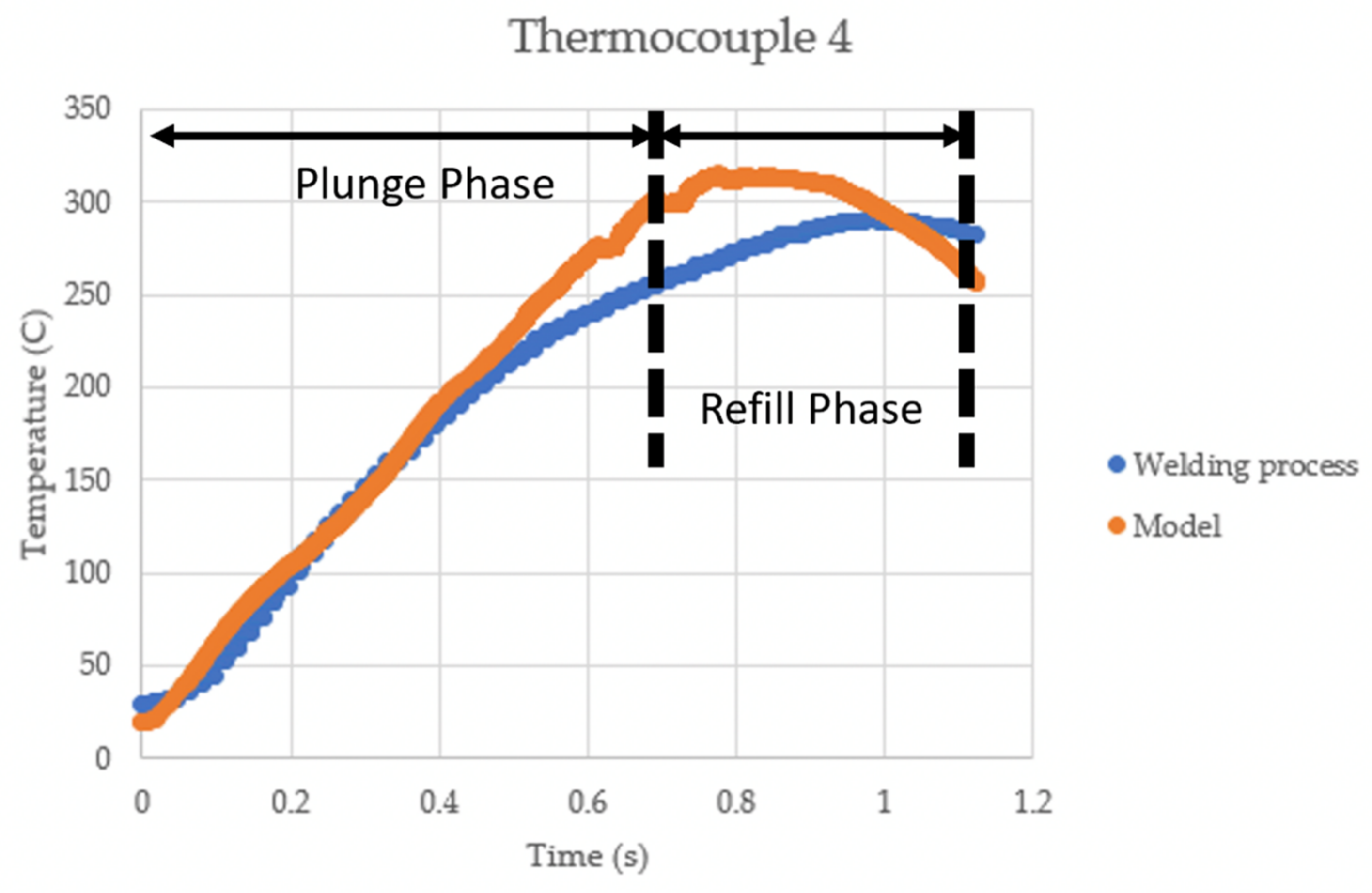
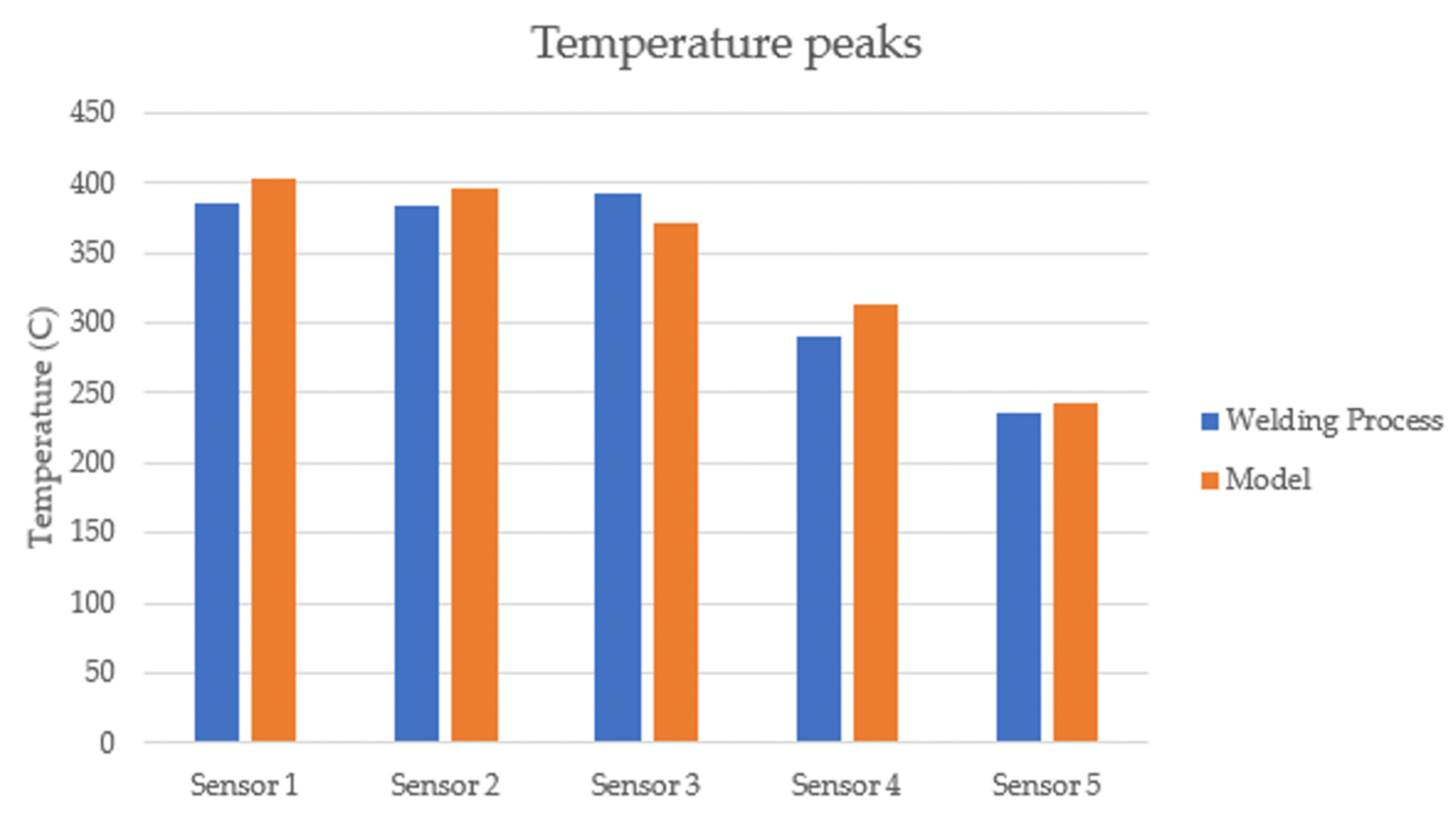
4.1. Temperature Predictions
4.2. Material Flow and Defect Formation
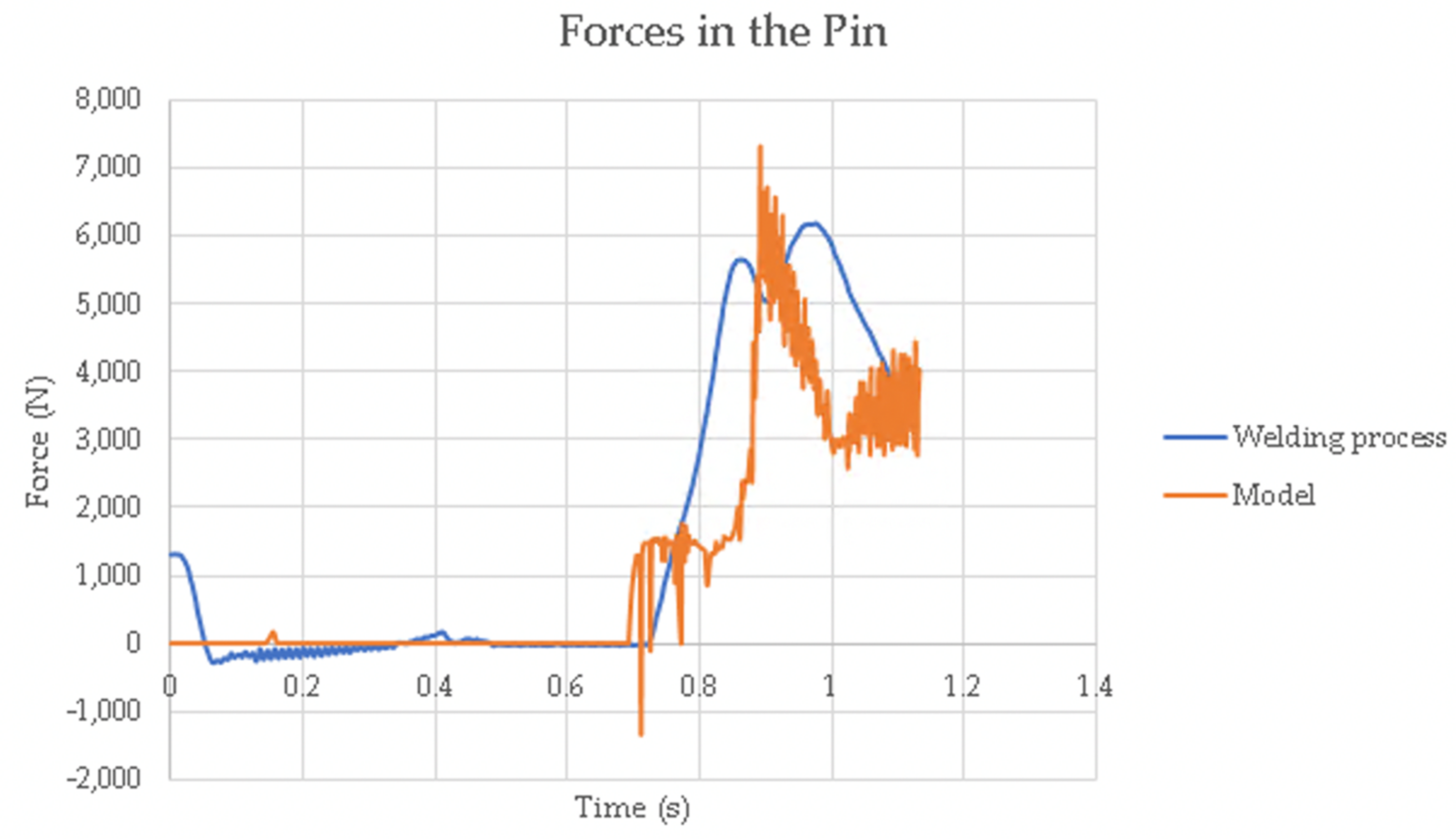
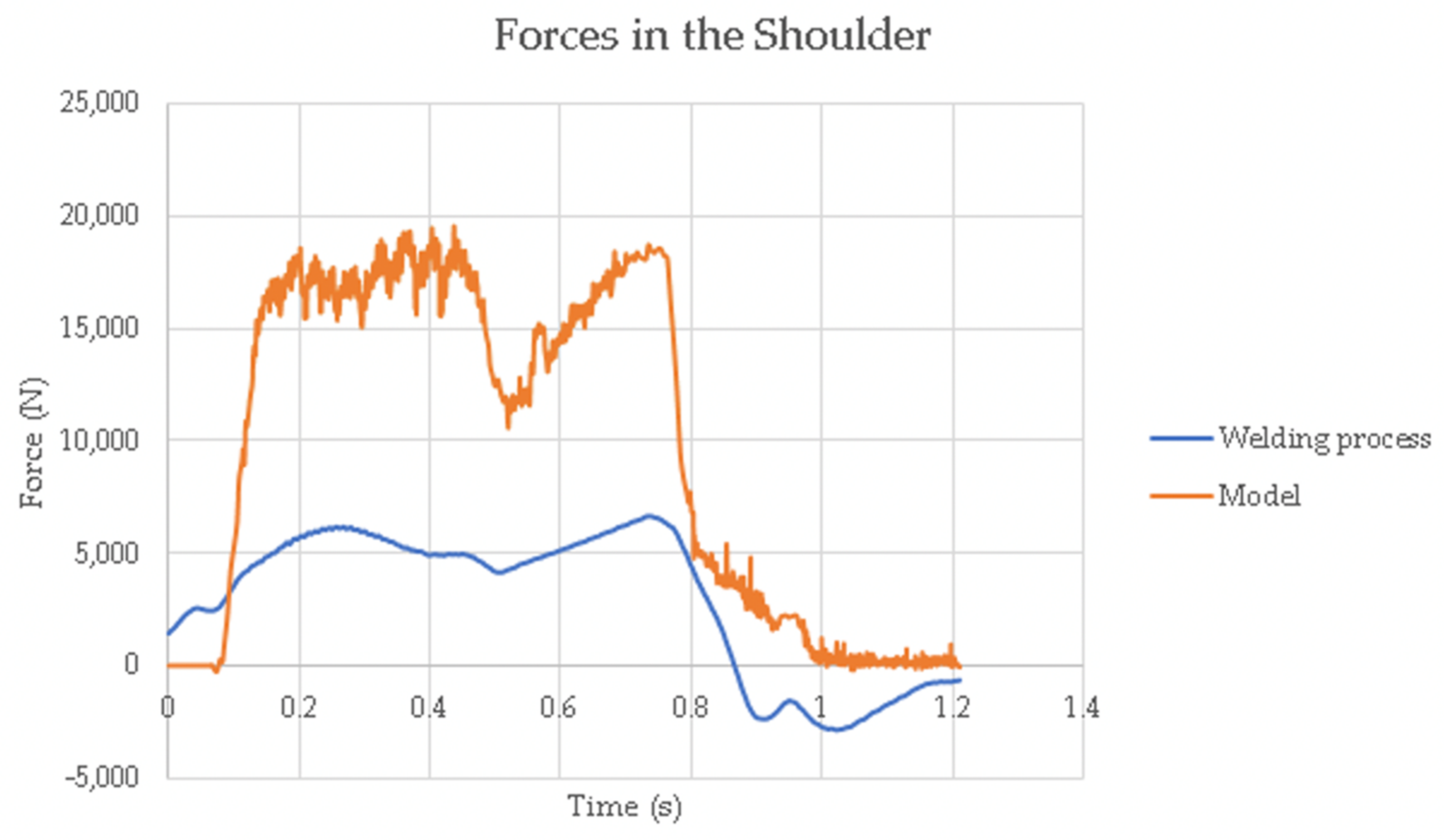
4.3. Forces
5. Conclusions
- The model predicted heat generation from the friction between the tools and the AA 7075-T6 material within 5% of the actual temperatures experienced by the thermocouples in experiments across a range of areas, both inside the weld nugget and in the material directly adjacent to the weld.
- The model demonstrated the ability to relate the kinematics of tool motion to material flow in the process by accurately replicating the patterns of defect formation within the weld material. Similarly, with the variation in tool motion, the model demonstrated an ability to predict the reduction/elimination of internal voids, in alignment with experimental observation.
- The model has successfully demonstrated its ability to predict the forces experienced by the pin, with progress to be made in its ability to predict the forces experienced by the shoulder. Discrepancies between prediction and experimental forces of the shoulder can likely be attributed to flow stresses for AA 7075-T6 that may be appropriate for the modeling of metal forming, but not for RFSSW, where intense shearing of the material, especially by the shoulder, is not accounted for.
Author Contributions
Funding
Conflicts of Interest
References
- Chupradit, S.; Bokov, D.O.; Suksatan, W.; Landowski, M.; Fydrych, D.; Abdullah, M.E.; Derazkola, H.A. Pin Angle Thermal Effects on Friction Stir Welding of AA5058 Aluminum Alloy: CFD Simulation and Experimental Validation. Materials 2021, 14, 7565. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Jia, R.; Zhang, H.; Cheng, W.; Zhai, X. EBSD Characterization of the Microstructure of 7A52 Aluminum Alloy Joints Welded by Friction Stir Welding. Materials 2021, 14, 6362. [Google Scholar] [CrossRef] [PubMed]
- Badkoobeh, F.; Mostaan, H.; Rafiei, M.; Bakhsheshi-Rad, H.R.; Berto, F. Friction Stir Welding/Processing of Mg-Based Alloys: A Critical Review on Advancements and Challenges. Materials 2021, 14, 6726. [Google Scholar] [CrossRef] [PubMed]
- Moiduddin, K.; Siddiquee, A.N.; Abidi, M.H.; Mian, S.H.; Mohammed, M.K. Friction Stir Welding of Thick Plates of 4Y3Gd Mg Alloy: An Investigation of Microstructure and Mechanical Properties. Materials 2021, 14, 6924. [Google Scholar] [CrossRef] [PubMed]
- Venukumar, S.; Muthukumaran, S.; Swaroop, Y. Microstructure and Mechanical Properties of Refilled Friction Stir Spot Welding of Commercial Pure Aluminium. Mater. Sci. Forum 2013, 765, 776–780. [Google Scholar] [CrossRef]
- Andres, J.; Wrońska, A.; Gałaszczyński, T.; Luty, G.; Burek, R. Effect of process parameters on microstructure and mechanical properties of rfssw lap joints of thin AL7075-T6 sheets. Arch. Metall. Mater. 2018, 63, 39–43. [Google Scholar] [CrossRef]
- Chai, P.; Wang, Y. Effect of Rotational Speed on Microstructure and Mechanical Properties of 2060 Aluminum Alloy RFSSW Joint. Met. Mater. Int. 2019, 25, 1574–1585. [Google Scholar] [CrossRef]
- Balasubramaniam, G.L.; Boldsaikhan, E.; Fukada, S.; Fujimoto, M.; Kamimuki, K. Effects of Refill Friction Stir Spot Weld Spacing and Edge Margin on Mechanical Properties of Multi-Spot-Welded Panels. J. Manuf. Mater. Process. 2020, 4, 55. [Google Scholar] [CrossRef]
- Balasubramaniam, G.L.; Boldsaikhan, E.; Rosario, G.F.J.; Ravichandran, S.P.; Fukada, S.; Fujimoto, M.; Kamimuki, K. Mechanical Properties and Failure Mechanisms of Refill Friction Stir Spot Welds. J. Manuf. Mater. Process. 2021, 5, 118. [Google Scholar] [CrossRef]
- Shilling, C.; dos Santos, J. Method and Device for Joining at least Two Adjoining Work Pieces by Friction Welding. U.S. Patent 6,722,556, 20 April 2004. [Google Scholar]
- Itapu, S.K.; Muci-Küchler, K.H. Visualization of Material Flow in the Refill Friction Stir Spot Welding Process; SAE International: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef]
- Kalagara, S.; Muci-Kuchler, K.H. Numerical simulation of a refill friction stir spot welding process. In Proceedings of the 4th Symposium on Friction Stir Welding and Processing, Orlando, FL, USA, 25 February–1 March 2007; pp. 369–378. [Google Scholar]
- Muci-Küchler, K.H.; Kalagara, S.; Arbegast, W.J. Simulation of a Refill Friction Stir Spot Welding Process Using a Fully Coupled Thermo-Mechanical FEM Model. J. Manuf. Sci. Eng. 2010, 132, 014503. [Google Scholar] [CrossRef]
- HongGang, Y.; HaiJun, Y.; Xing, H. Simulation on the plunge stage in refill friction stir spot welding of Aluminum Alloys. In Proceedings of the 4th International Conference on Mechatronics, Materials, Chemistry and Computer Engineering, Xi’an, China, 12–13 December 2015; pp. 521–524. [Google Scholar]
- Okada, H.; Kamimuki, K.; Fujimoto, M. Assembly Study of Refill FSSW. SAE Int. J. Aerosp. 2013, 6, 299–304. [Google Scholar] [CrossRef]
- Kubit, A.; Trzepiecinski, T. A fully coupled thermo-mechanical numerical modelling of the refill friction stir spot welding process in Alclad 7075-T6 aluminium alloy sheets. Arch. Civ. Mech. Eng. 2020, 20, 117. [Google Scholar] [CrossRef]
- Xiong, J.; Peng, X.; Shi, J.; Wang, Y.; Sun, J.; Liu, X.; Li, J. Numerical simulation of thermal cycle and void closing during friction stir spot welding of AA-2524 at different rotational speeds. Mater. Charact. 2021, 174, 110984. [Google Scholar] [CrossRef]
- Zhang, H.F.; Zhou, L.; Li, G.H.; Tang, Y.T.; Li, W.L.; Wang, R. Prediction and validation of temperature distribution and material flow during refill friction stir spot welding of AZ91D magnesium alloy. Sci. Technol. Weld. Join. 2021, 26, 153–160. [Google Scholar] [CrossRef]
- Ferguson Perforating. 7075 Aluminum Alloy. Available online: https://www.fergusonperf.com/the-perforating-process/material-information/specialized-aluminum/7075-aluminium-alloy/ (accessed on 8 August 2022).
- Hovanski, Y.; Curtis, A.; Michaelis, S.; Blackhurst, P.; Larsen, B. Advances in Refill Spot Welding Productivity; Springer: Cham, Switzerland, 2021; pp. 189–197. [Google Scholar]
- Larsen, B.; Hovanski, Y. Reducing Cycle Times of Refill Friction Stir Spot Welding in Automotive Aluminum Alloys; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Kubit, A.; Trzepiecinski, T.; Faes, K.; Drabczyk, M.; Bochnowski, W.; Korzeniowski, M. Analysis of the effect of structural defects on the fatigue strength of RFSSW joints using C-scan scanning acoustic microscopy and SEM. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1308–1321. [Google Scholar] [CrossRef]
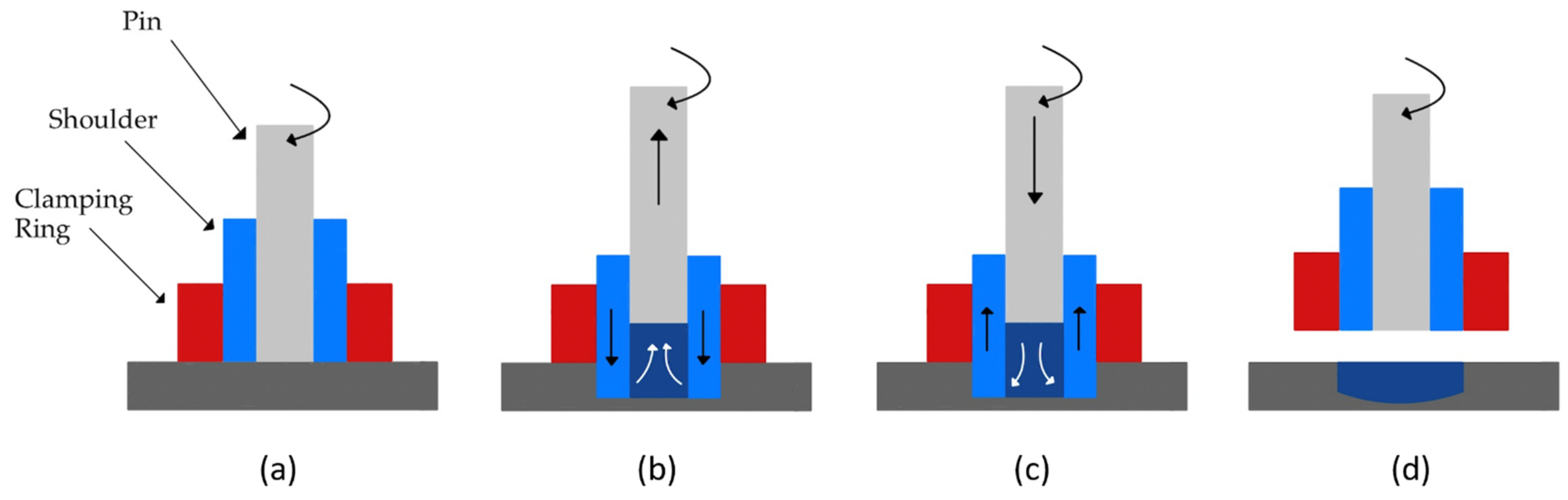


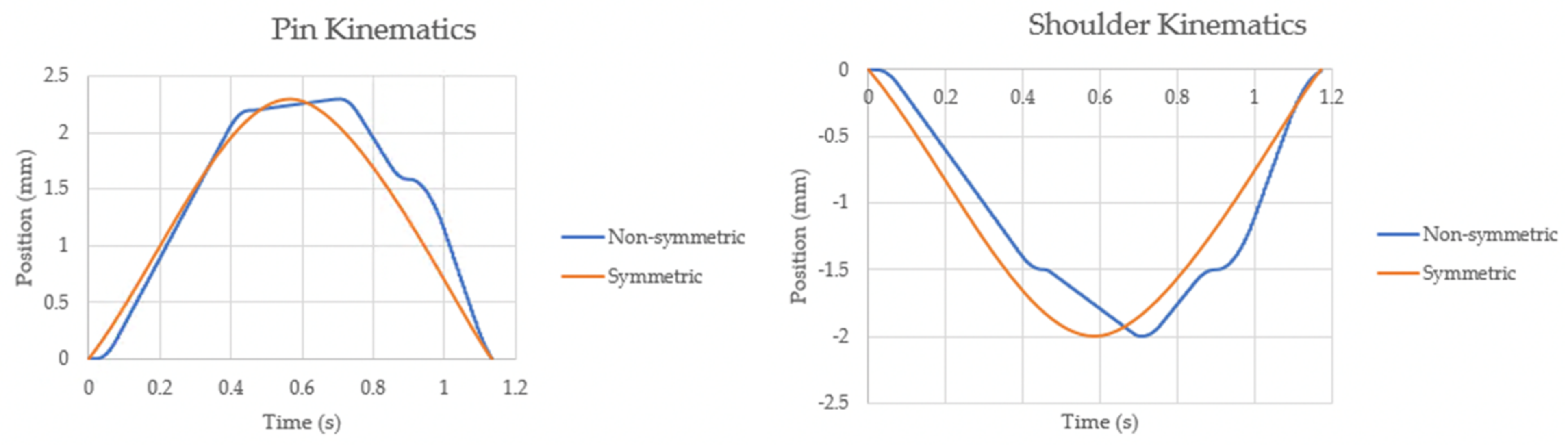
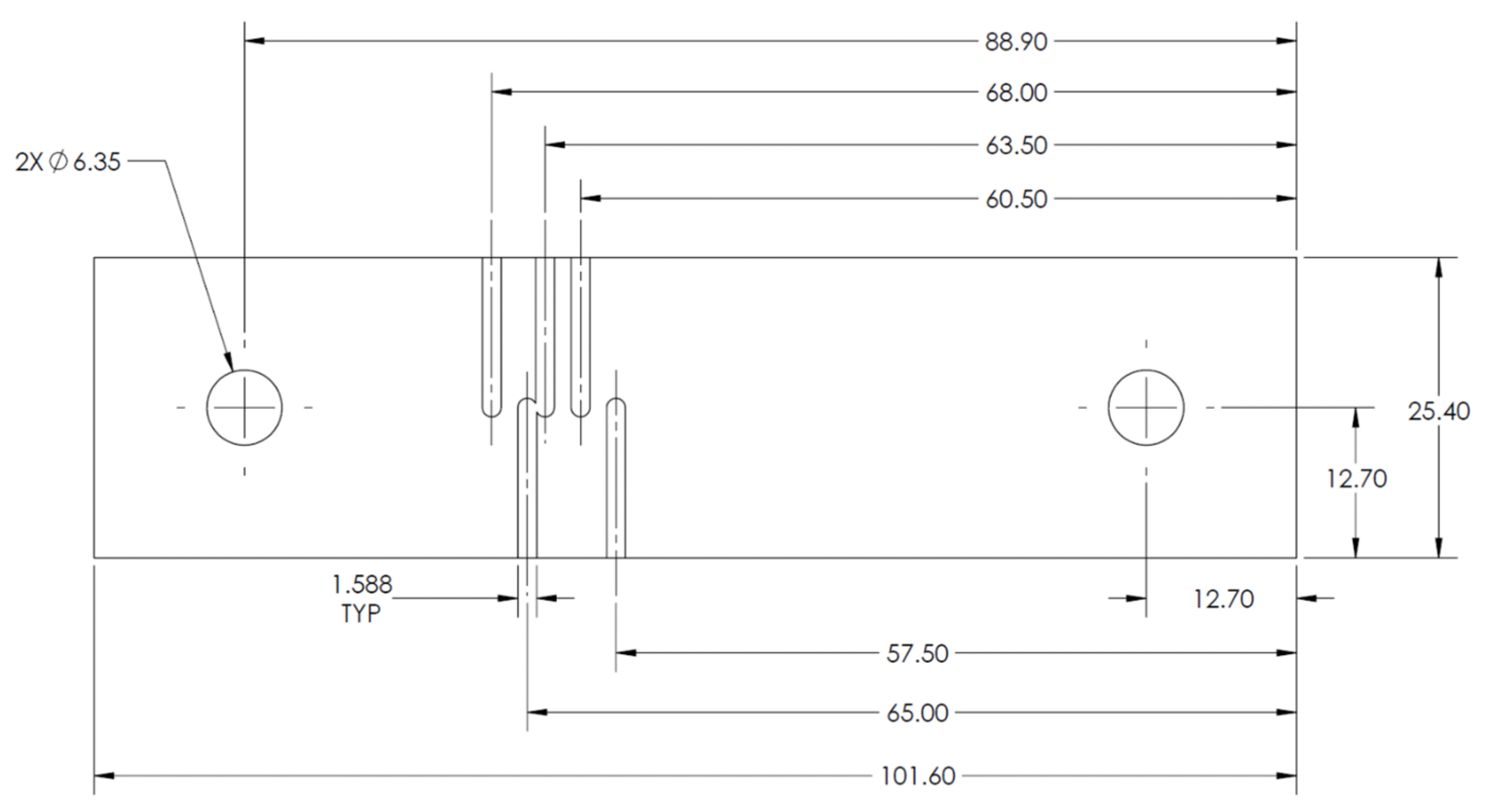
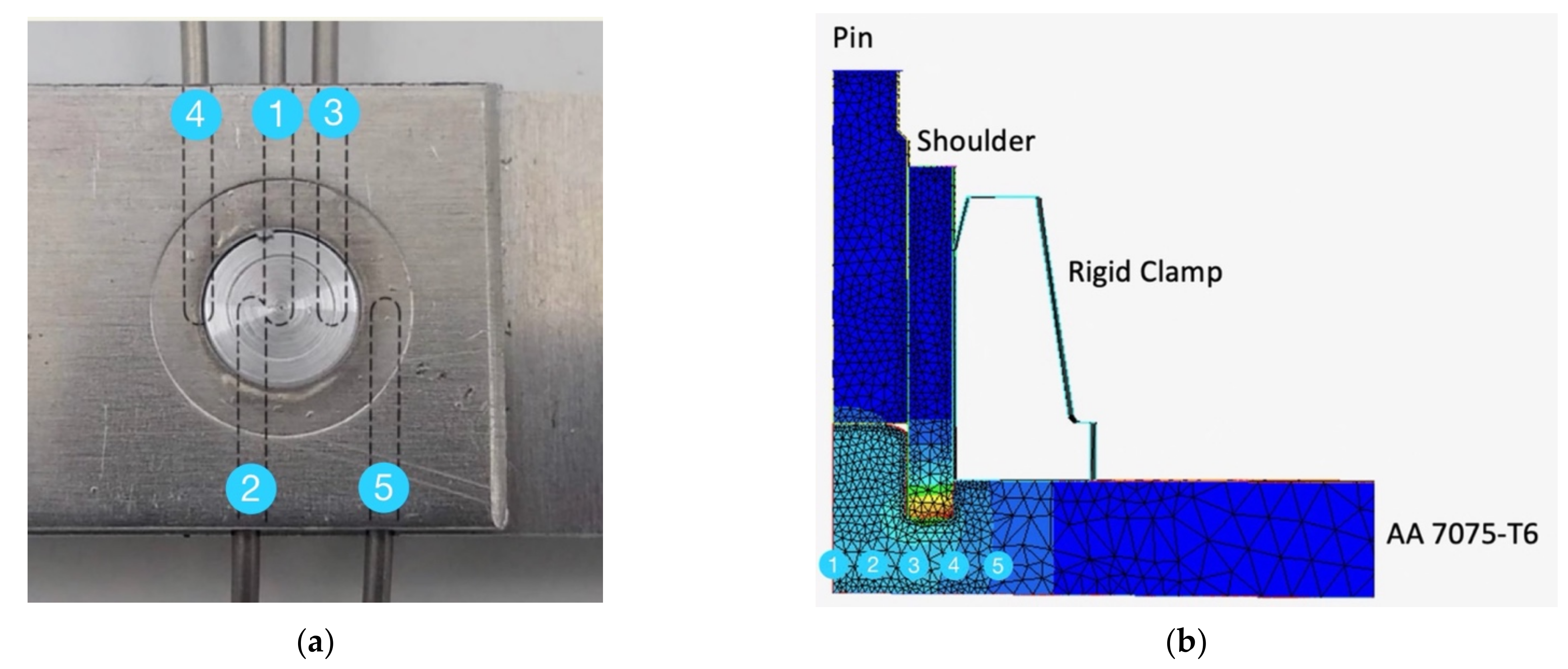
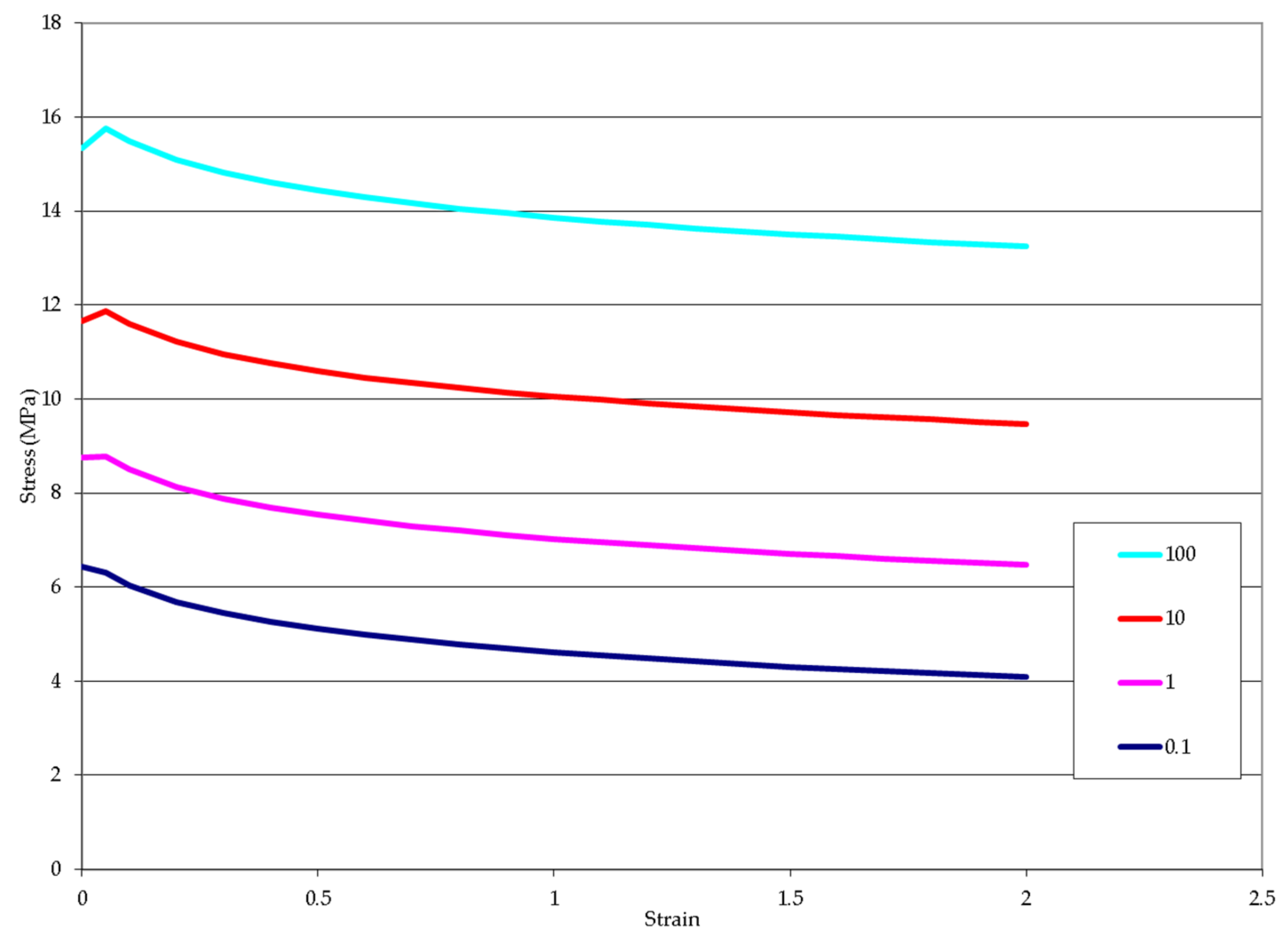




| Tool | Dimension (mm) |
|---|---|
| Pin outer diameter | 4.40 |
| Shoulder inner diameter | 4.45 |
| Shoulder outer diameter | 7.00 |
| Rigid clamp inner diameter | 7.05 |
| Rigid clamp outer diameter | 15.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berger, E.; Miles, M.; Curtis, A.; Blackhurst, P.; Hovanski, Y. 2D Axisymmetric Modeling of Refill Friction Stir Spot Welding and Experimental Validation. J. Manuf. Mater. Process. 2022, 6, 89. https://doi.org/10.3390/jmmp6040089
Berger E, Miles M, Curtis A, Blackhurst P, Hovanski Y. 2D Axisymmetric Modeling of Refill Friction Stir Spot Welding and Experimental Validation. Journal of Manufacturing and Materials Processing. 2022; 6(4):89. https://doi.org/10.3390/jmmp6040089
Chicago/Turabian StyleBerger, Evan, Michael Miles, Andrew Curtis, Paul Blackhurst, and Yuri Hovanski. 2022. "2D Axisymmetric Modeling of Refill Friction Stir Spot Welding and Experimental Validation" Journal of Manufacturing and Materials Processing 6, no. 4: 89. https://doi.org/10.3390/jmmp6040089
APA StyleBerger, E., Miles, M., Curtis, A., Blackhurst, P., & Hovanski, Y. (2022). 2D Axisymmetric Modeling of Refill Friction Stir Spot Welding and Experimental Validation. Journal of Manufacturing and Materials Processing, 6(4), 89. https://doi.org/10.3390/jmmp6040089






