Load Introduction Specimen Design for the Mechanical Characterisation of Lattice Structures under Tensile Loading
Abstract
1. Introduction
2. Materials and Methods
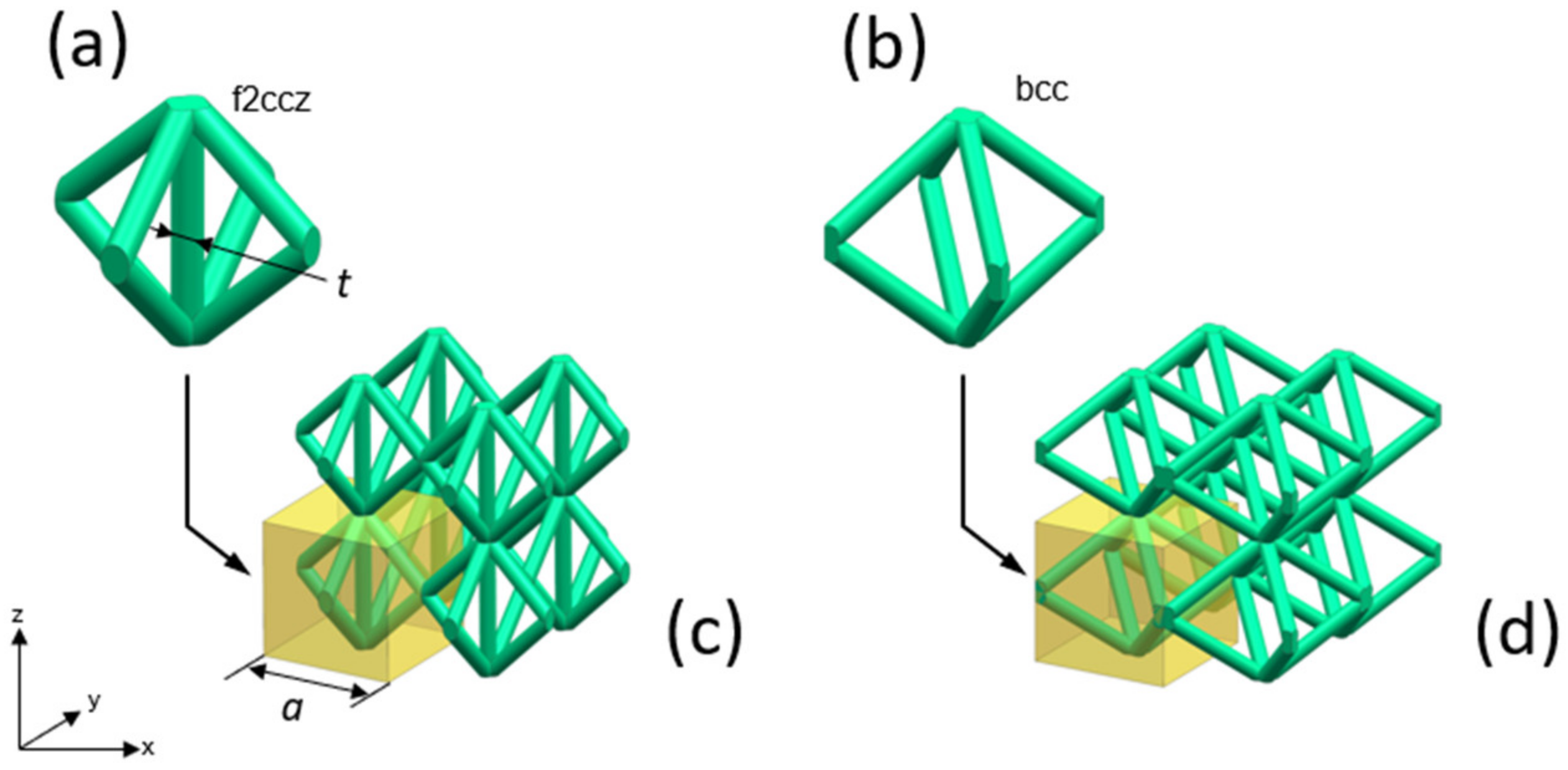
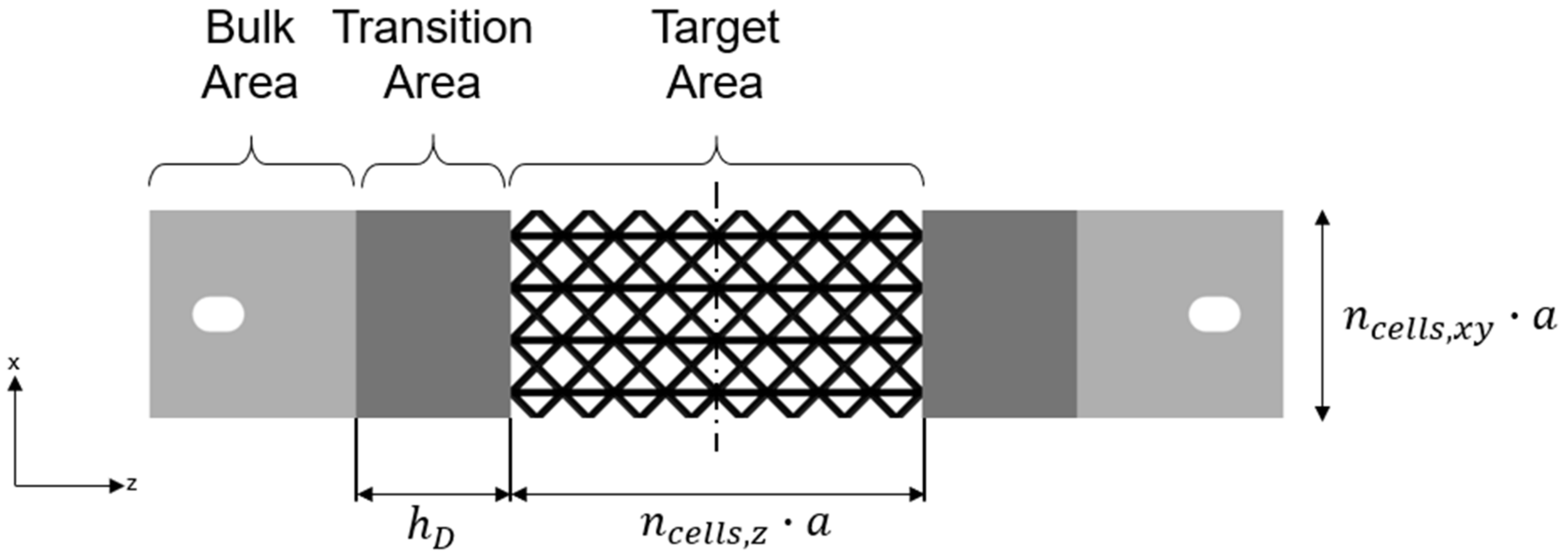
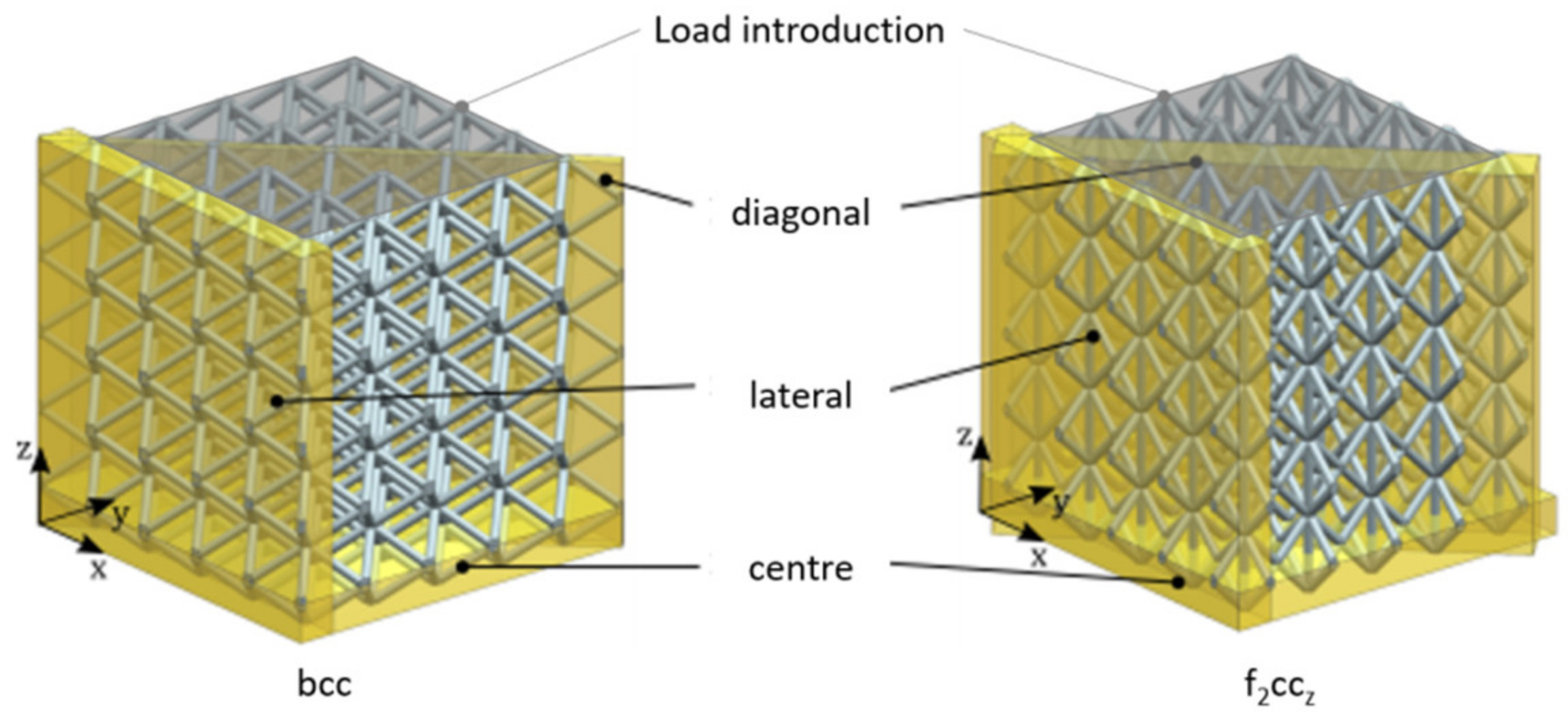
2.1. Design Setup
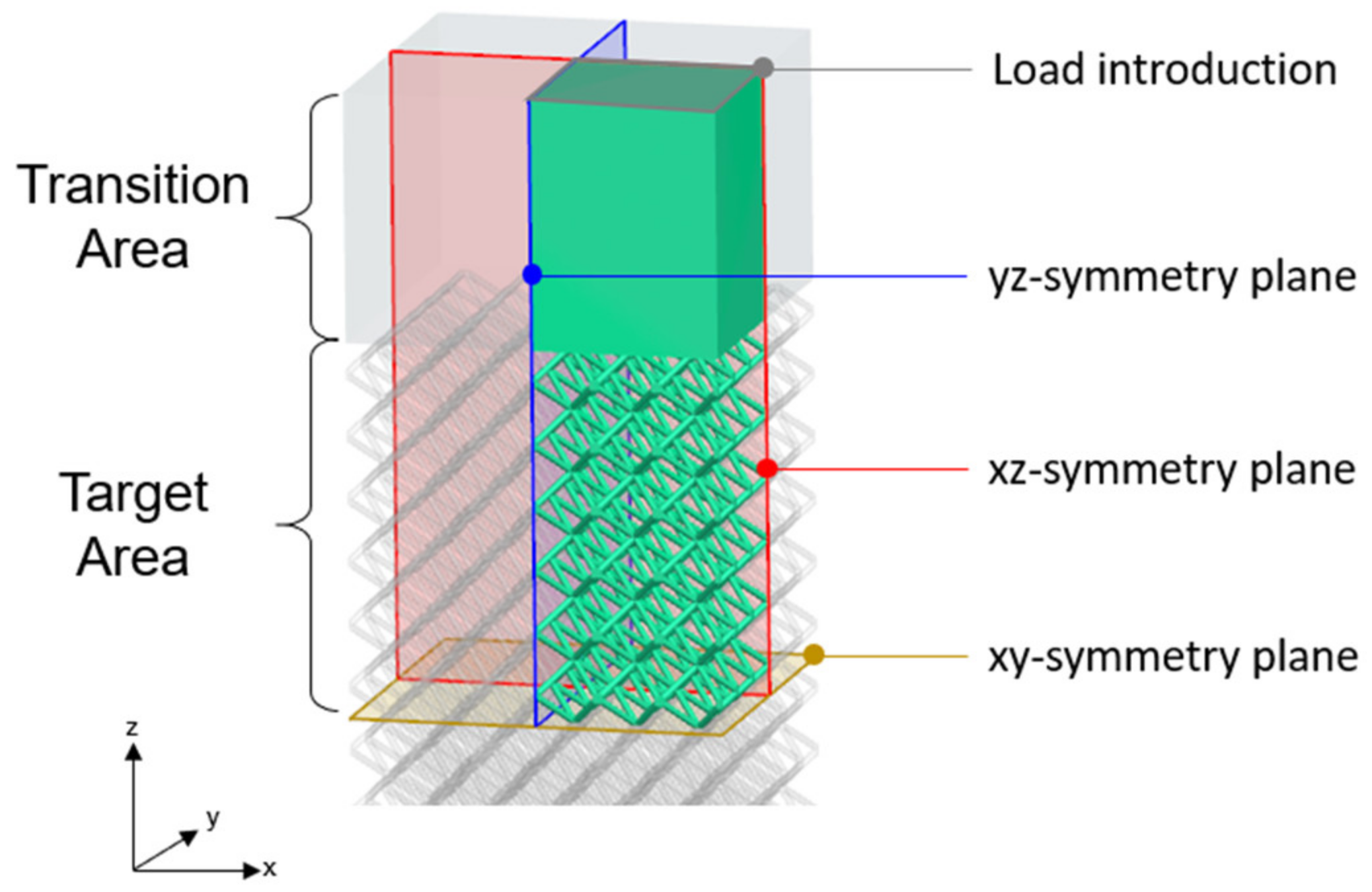
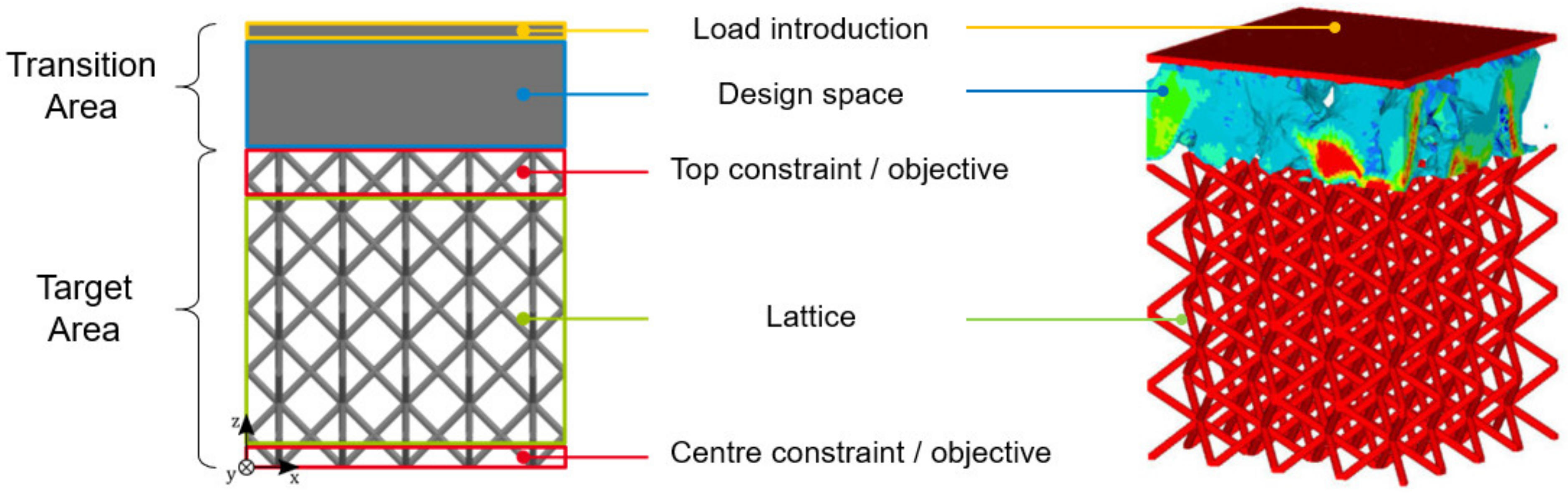
2.2. Numerical Setup
- Minimise the maximum von Mises stress in the top lattice region with the minimum von Mises stress constraint in the centre lattice region above the corresponding analytical yield stress of the considered unit cell [44].
- Maximise the minimum von Mises stress in the lattice centre region with stress constraints for uniaxiality in the top lattice region and .
- Minimise the compliance of the design space with the stress constraints for uniaxiality in the top lattice region and .
2.3. DoE Setup
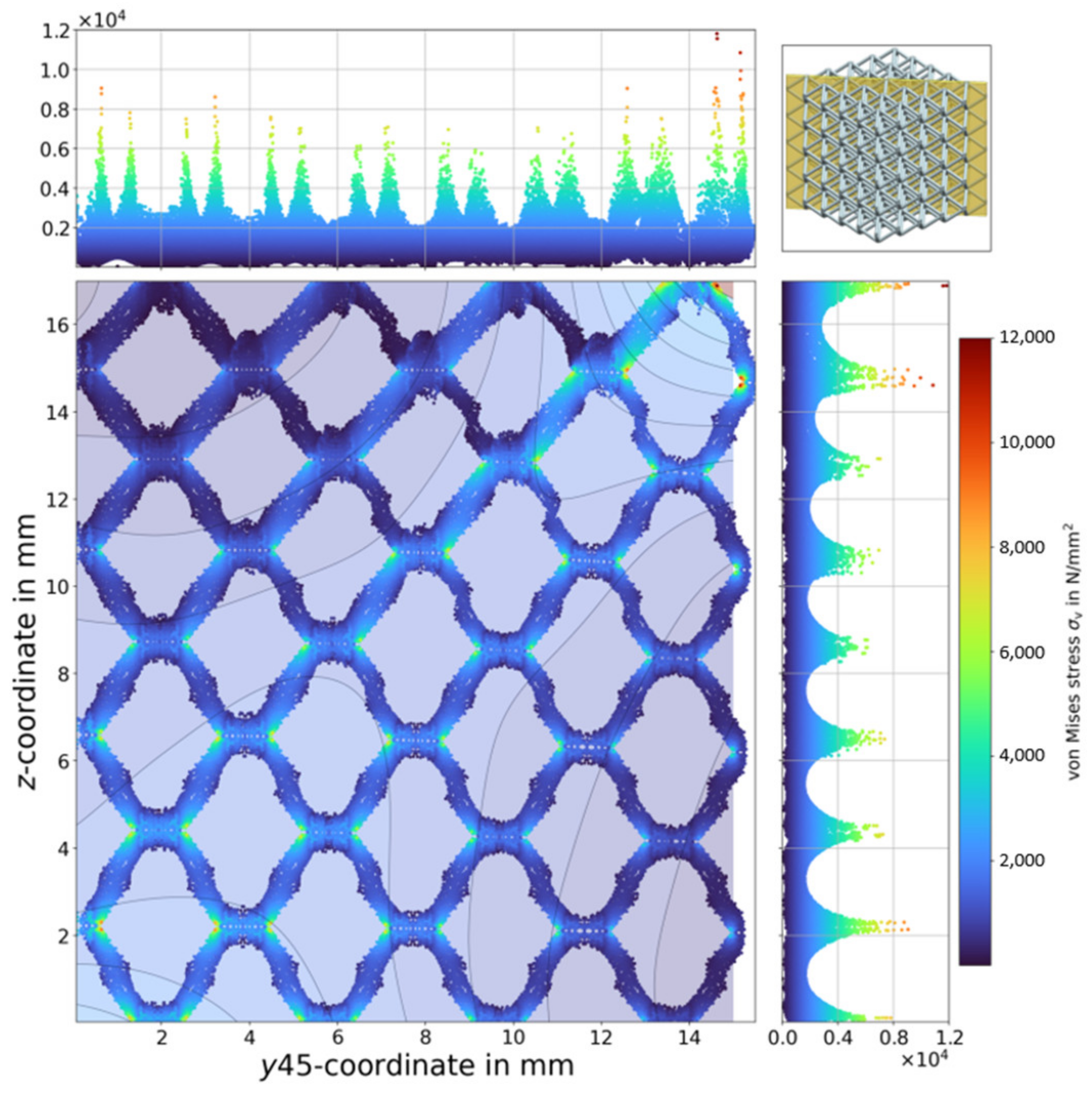
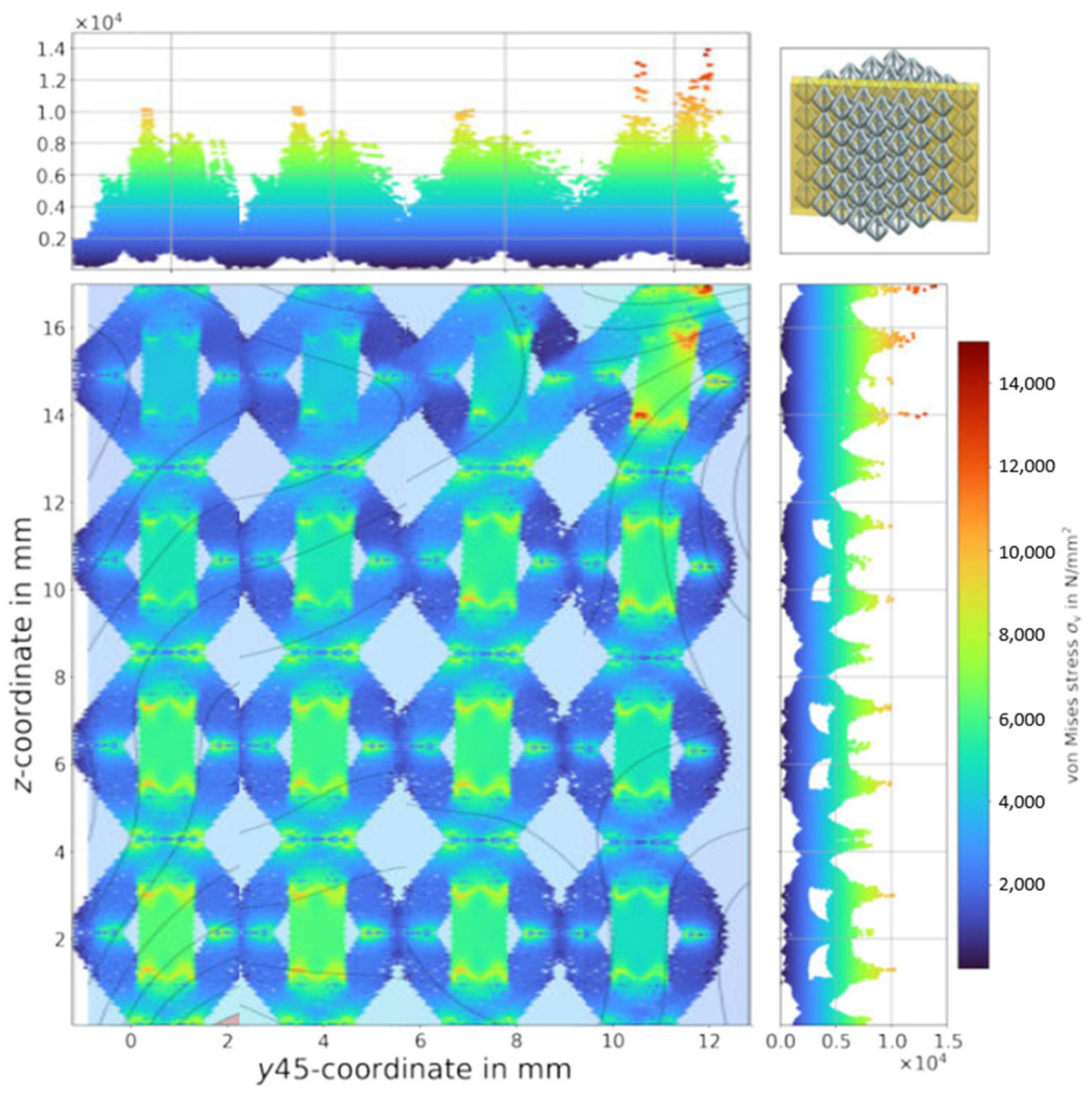
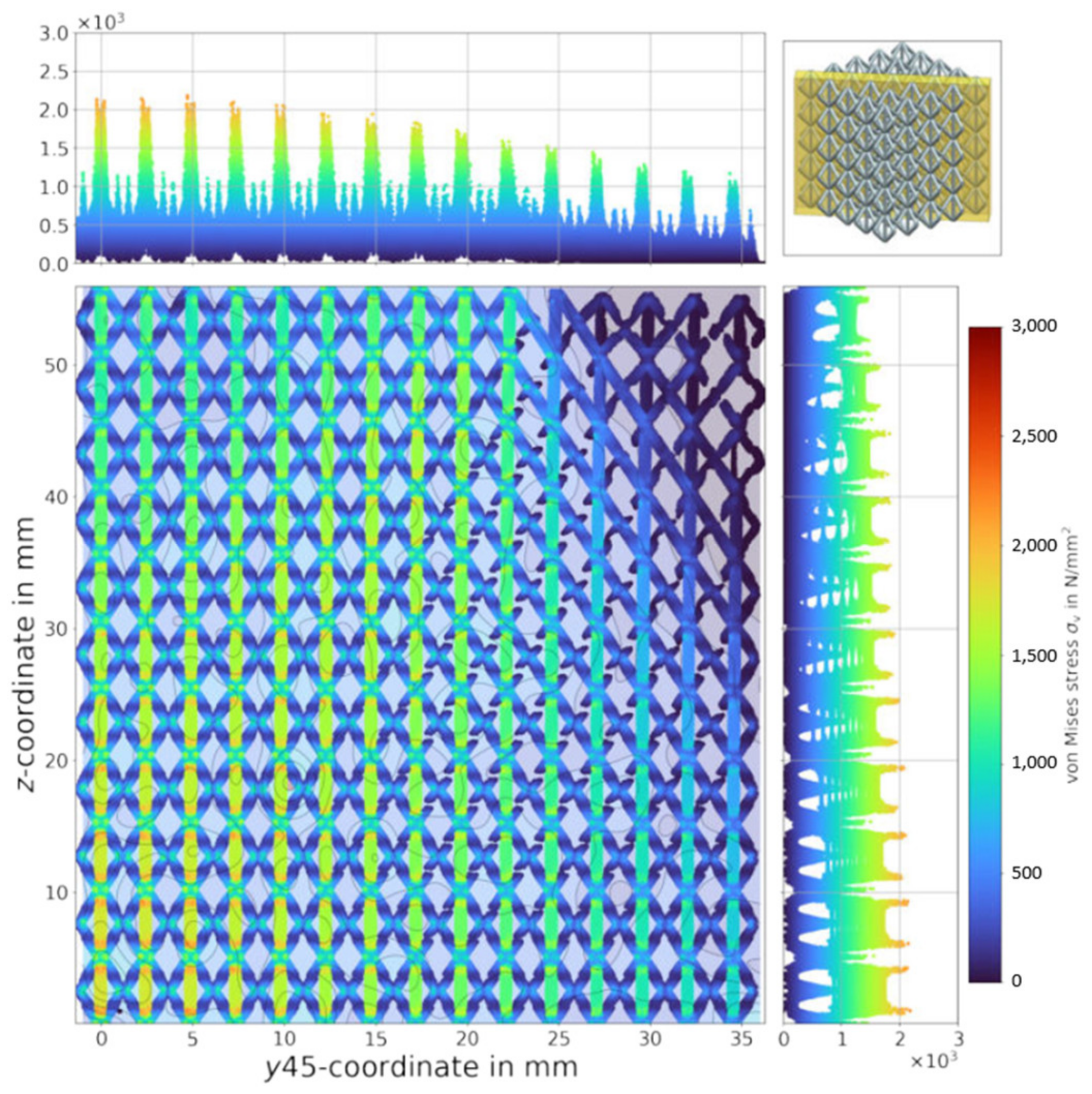
2.4. Evaluation and Visualisation of Results
3. Results and Discussion
3.1. Samples without a Transition Region
3.2. Optimisation Results
3.2.1. DoE Correlation Analysis
3.2.2. Relevant Topology-Optimised Design Features
3.3. Proposed Specimen
3.3.1. Design
3.3.2. Numerical Verification
3.3.3. Proof of Concept Validation
3.3.4. Potential towards Normalised Design Guidelines
4. Conclusions
- Small lattice structures, i.e., with few unit cells, should be avoided. This enables a three-dimensional load distribution along the main load paths that are typical of a given unit cell.
- A small transition area should be preferred, since it reduces the sample height as far as a load introduction without stress concentration is guaranteed. It is advisable to individually adjust the height of the desired transition area of a given sample to a narrow height until a deterioration of the result is observed.
- In the framework of the topology optimisation analysis of lattice structures under tensile loading, it is advisable to use the compliance objective with stress constraints and a loading modelled as negative pressure.
- The optimisation variables identified as relevant for the identification of small-scale features can be set as standard first. It is advisable to enable them only if the specific topology material appears overly localised or if no proper connection is created to the lattice.
- Compliant edges to avoid edge effects;
- Concentric cross-section at the interface with the bulk area;
- Pillar-like and/or web-like structures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Richard, H.A.; Schramm, B.; Zipsner, T. (Eds.) Additive Fertigung von Bauteilen und Strukturen; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017. [Google Scholar]
- Buchbinder, D.; Meiners, W. Generative Fertigung von Aluminiumbauteilen für die Serienproduktion; Fraunhofer Institut für Lasertechnik: Aachen, Germany, 2010. [Google Scholar]
- Walzl, A. Potentiale und Restriktionen von Gitterstrukturen für die additive Fertigung. Ph.D. Thesis, Lehrstuhl für Umformtechnik, Montanuniversität Loeben, Leoben, Austria, 2018. [Google Scholar]
- Zhu, J.; Zhou, H.; Wang, C.; Zhou, L.; Yuan, S.; Zhang, W. A review of topology optimization for additive manufacturing: Status and challenges. Chin. J. Aeronaut. 2021, 34, 91–110. [Google Scholar] [CrossRef]
- Teufelhart, S. Belastungsoptimiertes Design von Gitterstrukturen für die additive Fertigung nach dem bionischen Prinzip der kraftflussgerechten Gestaltung. Ph.D. Thesis, Fakultät für Maschinenwesen, Technische Universität München, München, Germany, 2016. [Google Scholar]
- Plocher, J.; Panesar, A. Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. Mater. Des. 2019, 183, 108164. [Google Scholar] [CrossRef]
- Rehme, O. Cellular Design for Laser Freeform Fabrication. Ph.D. Thesis, Institut für Laser- und Anlagensystemtechnik, Technische Universität Hamburg-Harburg, Hamburg, Germany, 2009. [Google Scholar]
- Chen, L.-Y.; Liang, S.-X.; Liu, Y.; Zhang, L.-C. Additive manufacturing of metallic lattice structures: Unconstrained design, accurate fabrication, fascinated performances, and challenges. Mater. Sci. Eng. R Rep. 2021, 146, 100648. [Google Scholar] [CrossRef]
- Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and Functional: A Review of Biomimetic Design in Additive Manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Sohrabian, M.; Vaseghi, M.; Khaleghi, H.; Dehrooyeh, S. Structural Investigation of Delicate-Geometry Fused Deposition Modeling Additive Manufacturing Scaffolds: Experiment and Analytics. J. Mater. Eng. Perform 2021, 30, 6529–6541. [Google Scholar] [CrossRef]
- Niu, J.; Choo, H.L.; Sun, W.; Mok, S.H. Numerical study on load-bearing capabilities of beam-like lattice structures with three different unit cells. Int. J. Mech. Mater. Des. 2018, 14, 443–460. [Google Scholar] [CrossRef]
- Bourell, D.; Kruth, J.P.; Leu, M.; Levy, G.; Rosen, D.; Beese, A.M.; Clare, A. Materials for additive manufacturing. CIRP Ann.-Manuf. Technol. 2017, 66, 659–681. [Google Scholar] [CrossRef]
- Großmann, A.; Gosmann, J.; Mittelstedt, C. Lightweight lattice structures in selective laser melting: Design, fabrication and mechanical properties. Mater. Sci. Eng. A 2019, 766, 138356. [Google Scholar] [CrossRef]
- Benedetti, M.; Plessis, A.D.; Ritchie, R.O.; Dallago, M.; Razavi, S.; Berto, F. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Mater. Sci. Eng. R Rep. 2021, 144, 100606. [Google Scholar] [CrossRef]
- Riva, L.; Ginestra, S.; Ceretti, E. Mechanical characterization and properties of laser-based powder bed–fused lattice structures: A review. Int. J. Adv. Manuf. Technol. 2021, 113, 649–671. [Google Scholar] [CrossRef]
- Lietaert, K.; Cutolo, A.; Boey, D.; van Hooreweder, B. Fatigue life of additively manufactured Ti6Al4V scaffolds under tension-tension, tension-compression and compression-compression fatigue load. Sci. Rep. 2018, 8, 4957. [Google Scholar] [CrossRef] [PubMed]
- Meyer, G.; Brenne, F.; Niendorf, T.; Mittelstedt, C. Influence of the Miniaturisation Effect on the Effective Stiffness of Lattice Structures in Additive Manufacturing. Metals 2020, 10, 1442. [Google Scholar] [CrossRef]
- Alsalla, H.; Hao, L.; Smith, C. Fracture toughness and tensile strength of 316L stainless steel cellular lattice structures manufactured using the selective laser melting technique. Mater. Sci. Eng. A 2016, 669, 1–6. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.; Karadeniz, S. Static mechanical behaviours of stainless steel micro-lattice structures under different loading conditions. Mater. Sci. Eng. A 2013, 586, 392–406. [Google Scholar] [CrossRef]
- Meyer, G.; Schelleis, K.; Weeger, O.; Mittelstedt, C. Tensile specimen design proposal for truss-based lattice structures. Mech. Adv. Mater. Struct. 2022, 1–28. [Google Scholar] [CrossRef]
- Panesar., A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for Additive Manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Daynes, S.; Feih, S.; Lu, W.F.; Wei, J. Optimisation of functionally graded lattice structures using isostatic lines. Mater. Des. 2017, 127, 215–223. [Google Scholar] [CrossRef]
- Goel, A.; Anand, S. Design of Functionally Graded Lattice Structures using B-splines for Additive Manufacturing. Procedia Manuf. 2019, 34, 655–665. [Google Scholar] [CrossRef]
- Alzahrani, M.; Choi, S.-K.; Rosen, D.W. Design of truss-like cellular structures using relative density mapping method. Mater. Des. 2015, 85, 349–360. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, P.; Biyikli, E.; Bai, J.; Robbins, J.; To, A. Efficient design optimization of variable-density cellular structures for additive manufacturing: Theory and experimental validation. Rapid Prototyp. J. 2017, 23, 660–677. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.; Aremu, A.; Tuck, C.; Ashcroft, I.; Wildman, R.; Hague, R. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Radman, A.; Huang, X.; Xie, Y.M. Topology optimization of functionally graded cellular materials. J. Mater. Sci. 2013, 48, 1503–1510. [Google Scholar] [CrossRef]
- Liu, F.; Mao, Z.; Zhang, P.; Zhang, D.Z.; Jiang, J.; Ma, Z. Functionally graded porous scaffolds in multiple patterns: New design method, physical and mechanical properties. Mater. Des. 2018, 160, 849–860. [Google Scholar] [CrossRef]
- Rankine, W.J.M. XVII. Principle of the equilibrium of polyhedral frames. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1864, 27, 92. [Google Scholar] [CrossRef]
- Maxwell, J.C.L. On the calculation of the equilibrium and stiffness of frames. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1864, 27, 294–299. [Google Scholar] [CrossRef]
- Maxwell, J.C. I.—On Reciprocal Figures, Frames, and Diagrams of Forces. Trans. R. Soc. Edinb. 1870, 26, 1–40. [Google Scholar] [CrossRef]
- Michell, A. LVIII. The limits of economy of material in frame-structures. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1904, 8, 589–597. [Google Scholar] [CrossRef]
- Mattheck, C. Design and growth rules for biological structures and their application to engineering. Fat Frac. Eng. Mat. Struct. 1990, 13, 535–550. [Google Scholar] [CrossRef]
- Wu, J.; Aage, N.; Westermann, R.; Sigmund, O. Infill Optimization for Additive Manufacturing-Approaching Bone-Like Porous Structures. IEEE Trans. Vis. Comput. Graph. 2018, 24, 1127–1140. [Google Scholar] [CrossRef]
- Cheng, L.; Bai, J.; To, A.C. Functionally graded lattice structure topology optimization for the design of additive manufactured components with stress constraints. Comput. Methods Appl. Mech. Eng. 2018, 344, 334–359. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Guest, J.K. Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Struct. Multidisc. Optim. 2016, 54, 1157–1172. [Google Scholar] [CrossRef]
- Hoffarth, M.; Gerzen, N.; Pedersen, C. ALM Overhang Constraint in Topology Optimization for Industrial Applications. In Proceedings of the 12th World Congress on Structural and Multidisciplinary Optimisation, Braunschweig, Germany, 5–9 June 2017. [Google Scholar]
- Langelaar, M. Combined optimization of part topology, support structure layout and build orientation for additive manufacturing. Struct. Multidisc. Optim. 2018, 57, 1985–2004. [Google Scholar] [CrossRef]
- Liu, J.; Yu, H. Concurrent deposition path planning and structural topology optimization for additive manufacturing. RPJ 2017, 23, 930–942. [Google Scholar] [CrossRef]
- Sigmund, O. Manufacturing tolerant topology optimization. Acta Mech. Sin. 2009, 25, 227–239. [Google Scholar] [CrossRef]
- Altair Engineering Inc. HyperWorks 14.0: OptiStruct User’s Guide; Altair Engineering, Inc.: Troy, MI, USA, 2015. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. (Eds.) Cellular Solids: Structure and Properties, 2nd ed.; Cambridge Univ. Press: Cambridge, UK, 1988. [Google Scholar]
- Souza, J.; Großmann, A.; Mittelstedt, C. Micromechanical analysis of the effective properties of lattice structures in additive manufacturing. Addit. Manuf. 2018, 23, 53–69. [Google Scholar] [CrossRef]
- Geng, X.; Lu, Y.; Liu, C.; Li, W.; Yue, Z. Fracture characteristic analysis of cellular lattice structures under tensile load. Int. J. Solids Struct. 2019, 163, 170–177. [Google Scholar] [CrossRef]
- Jin, Q.-Y.; Yu, J.-H.; Ha, K.-S.; Lee, W.-J.; Park, S.-H. Multi-dimensional lattices design for ultrahigh specific strength metallic structure in additive manufacturing. Mater. Des. 2021, 201, 109479. [Google Scholar] [CrossRef]
- Bendsøe, M.; Sigmund, O. (Eds.) Topology Optimization: Theory, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Yago, D.; Cante, J.; Lloberas-Valls, O.; Oliver, J. Topology Optimization Methods for 3D Structural Problems: A Comparative Study. Arch. Comput. Methods Eng. 2021, 29, 1525–1567. [Google Scholar] [CrossRef]
- Siebertz, K.; van Bebber, D.; Hochkirchen, T. (Eds.) Statistische Versuchsplanung: Design of Experiments (DoE), 2nd ed.; Vieweg: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Viana, F.A.C. A Tutorial on Latin Hypercube Design of Experiments. Qual. Reliab. Engng. Int. 2016, 32, 1975–1985. [Google Scholar] [CrossRef]
- Cady, F. The Data Science Handbook; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Duysinx, P.; Bendsøe, M. Topology optimization of continuum structures with local stress constraints. Int. J. Numer. Meth. Engng. 1998, 43, 1453–1478. [Google Scholar] [CrossRef]
- Holmberg, E.; Torstenfelt, B.; Klarbring, A. Stress constrained topology optimization. Struct. Multidisc. Optim. 2013, 48, 33–47. [Google Scholar] [CrossRef]
- Zhou, M.; Sigmund, O. On fully stressed design and p-norm measures in structural optimization. Struct. Multidisc. Optim. 2017, 56, 731–736. [Google Scholar] [CrossRef]
- Lee, K.; Ahn, K.; Yoo, J. A novel P-norm correction method for lightweight topology optimization under maximum stress constraints. Comput. Struct. 2016, 171, 18–30. [Google Scholar] [CrossRef]
- Le, C.; Norato, J.; Bruns, T.; Ha, C.; Tortorelli, D. Stress-based topology optimization for continua. Struct. Multidisc. Optim. 2010, 41, 605–620. [Google Scholar] [CrossRef]
- Tiernan, P.; Hannon, A. Design optimisation of biaxial tensile test specimen using finite element analysis. Int. J. Mater. Form. 2014, 7, 117–123. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, M.Y.; Chen, F. Structure-material integrated design by level sets. Struct. Multidisc. Optim. 2016, 54, 1145–1156. [Google Scholar] [CrossRef]
- Meyer, G.; Wang, H.; Mittelstedt, C. Influence of geometrical notches and form optimization on the mechanical properties of additively manufactured lattice structures. Mater. Des. 2022, 222, 111082. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, L.; Sun, L.; Li, N. Optimization of graded filleted lattice structures subject to yield and buckling constraints. Mater. Des. 2021, 206, 109746. [Google Scholar] [CrossRef]
- Savio, G.; Meneghello, R.; Concheri, G. Geometric modeling of lattice structures for additive manufacturing. Rapid Prototyp. J. 2018, 24, 351–360. [Google Scholar] [CrossRef]
- DIN 50099:2018; Tensile Testing of Metallic Cellular Materials. Beuth Verlag GmbH: Berlin, Germany, 2018.
- Bijak-Zochowski, M.; Waas, A.M.; Anderson, W.J.; Miniatt, C.E. Reduction of contact stress by use of relief notches. Exp. Mech. 1991, 31, 271–275. [Google Scholar] [CrossRef]
- Dallago, M.; Fontanari, V.; Torresani, E.; Leoni, M.; Pederzolli, C.; Potrich, C.; Benedetti, M. Fatigue and biological properties of Ti-6Al-4V cellular structures with variously arranged cubic cells made by selective laser melting. J. Mech. Behav. Biomed. Mater. 2018, 78, 381–394. [Google Scholar] [CrossRef] [PubMed]
- EOS GmbH—Electro Optical Systems. Material Data Sheet—EOS Aluminium AlSi10Mg. Available online: https://fathommfg.com/wp-content/uploads/2020/11/EOS_Aluminium_AlSi10Mg_en.pdf (accessed on 29 December 2022).





| Sample Run | Load Type | DISCRETE | TOPDISC | Constraint/Objective | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5.12 | 10 | 12 | 1.57 × a | 1 | 2 | 1 | 0.31 | 1.42 × t | 1.00 × t * | 3 |
| 2 | 7.84 | 10 | 8 | 3.78 × a | 1 | 4 | 0 | 0.18 | 0.82 × t | 0.74 × t * | 1 |
| 3 | 8.98 | 6 | 4 | 2.18 × a | 1 | 3 | 1 | 0.49 | 0.55 × t | 0.77 × t | 2 |
| 4 | 9.51 | 14 | 14 | 5.06 × a | 2 | 2 | 0 | 0.25 | 0.27 × t | 1.47 × t | 3 |
| 5 | 6.94 | 10 | 12 | 0.97 × a | 1 | 3 | 0 | 0.22 | 1.28 × t | 2.13 × t | 3 |
| 6 | 6.61 | 12 | 14 | 5.58 × a | 1 | 4 | 0 | 0.42 | 0.67 × t | 1.81 × t | 1 |
| 7 | 8.34 | 6 | 18 | 3.34 × a | 1 | 1 | 0 | 0.10 | 0.80 × t | 1.05 × t * | 1 |
| 8 | 8.49 | 14 | 20 | 3.96 × a | 2 | 3 | 0 | 0.14 | 0.95 × t | 1.50 × t * | 2 |
| 9 | 7.56 | 16 | 8 | 5.94 × a | 2 | 1 | 1 | 0.36 | 0.43 × t | 1.00 × t | 2 |
| 10 | 6.28 | 16 | 22 | 1.92 × a | 1 | 4 | 1 | 0.32 | 0.58 × t | 1.30 × t | 2 |
| 11 | 9.91 | 14 | 20 | 2.64 × a | 2 | 1 | 1 | 0.27 | 0.60 × t | 1.11 × t * | 3 |
| 12 | 4.19 | 12 | 22 | 3.14 × a | 1 | 4 | 0 | 0.40 | 1.20 × t | 2.16 × t * | 2 |
| 13 | 4.76 | 8 | 16 | 4.52 × a | 2 | 2 | 0 | 0.37 | 2.04 × t | 2.36 × t * | 1 |
| 14 | 5.44 | 8 | 18 | 4.88 × a | 2 | 1 | 1 | 0.47 | 1.68 × t | 2.40 × t * | 1 |
| 15 | 5.96 | 8 | 10 | 0.75 × a | 2 | 3 | 1 | 0.19 | 1.34 × t | 1.72 × t * | 3 |
| Lattice Specificity | Variable | Correlation Outcome | Relevant Score Criteria |
|---|---|---|---|
| f2ccz | General correlation | ||
| Negative surface pressure | General correlation | ||
| Only for the z-stress distribution score | |||
| Compliance optimisation with stress constraint | General correlation | ||
| Only for the connectivity score | |||
| Only for the connectivity score | |||
| bcc | Not high but indication through the z-stress distribution score | ||
| General correlation | |||
| General correlation, especially for the xy-stress distribution score | |||
| Negative surface pressure | Structure score and material distribution score | ||
| Only for the xy-stress distribution score | |||
| Compliance optimisation with stress constraint | General correlation | ||
| Both | Turned off | No correlation observable | |
| Standard value of 0.3 | No correlation observable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.; Meyer, G.; Greiner, M.; Mittelstedt, C. Load Introduction Specimen Design for the Mechanical Characterisation of Lattice Structures under Tensile Loading. J. Manuf. Mater. Process. 2023, 7, 37. https://doi.org/10.3390/jmmp7010037
Jung J, Meyer G, Greiner M, Mittelstedt C. Load Introduction Specimen Design for the Mechanical Characterisation of Lattice Structures under Tensile Loading. Journal of Manufacturing and Materials Processing. 2023; 7(1):37. https://doi.org/10.3390/jmmp7010037
Chicago/Turabian StyleJung, Justin, Guillaume Meyer, Matthias Greiner, and Christian Mittelstedt. 2023. "Load Introduction Specimen Design for the Mechanical Characterisation of Lattice Structures under Tensile Loading" Journal of Manufacturing and Materials Processing 7, no. 1: 37. https://doi.org/10.3390/jmmp7010037
APA StyleJung, J., Meyer, G., Greiner, M., & Mittelstedt, C. (2023). Load Introduction Specimen Design for the Mechanical Characterisation of Lattice Structures under Tensile Loading. Journal of Manufacturing and Materials Processing, 7(1), 37. https://doi.org/10.3390/jmmp7010037






