Recoater-Induced Distortions and Build Failures in Selective Laser Melting of Thin-Walled Ti6Al4V Parts
Abstract
1. Introduction
2. Experimental Campaign
3. Computational Simulation
3.1. Thermal Problem
3.2. Mechanical Analysis
3.3. Computational Modeling of SLM
3.4. Material Properties and Boundary Conditions
3.5. Modeling of the Recoater Action
4. Results and Discussion
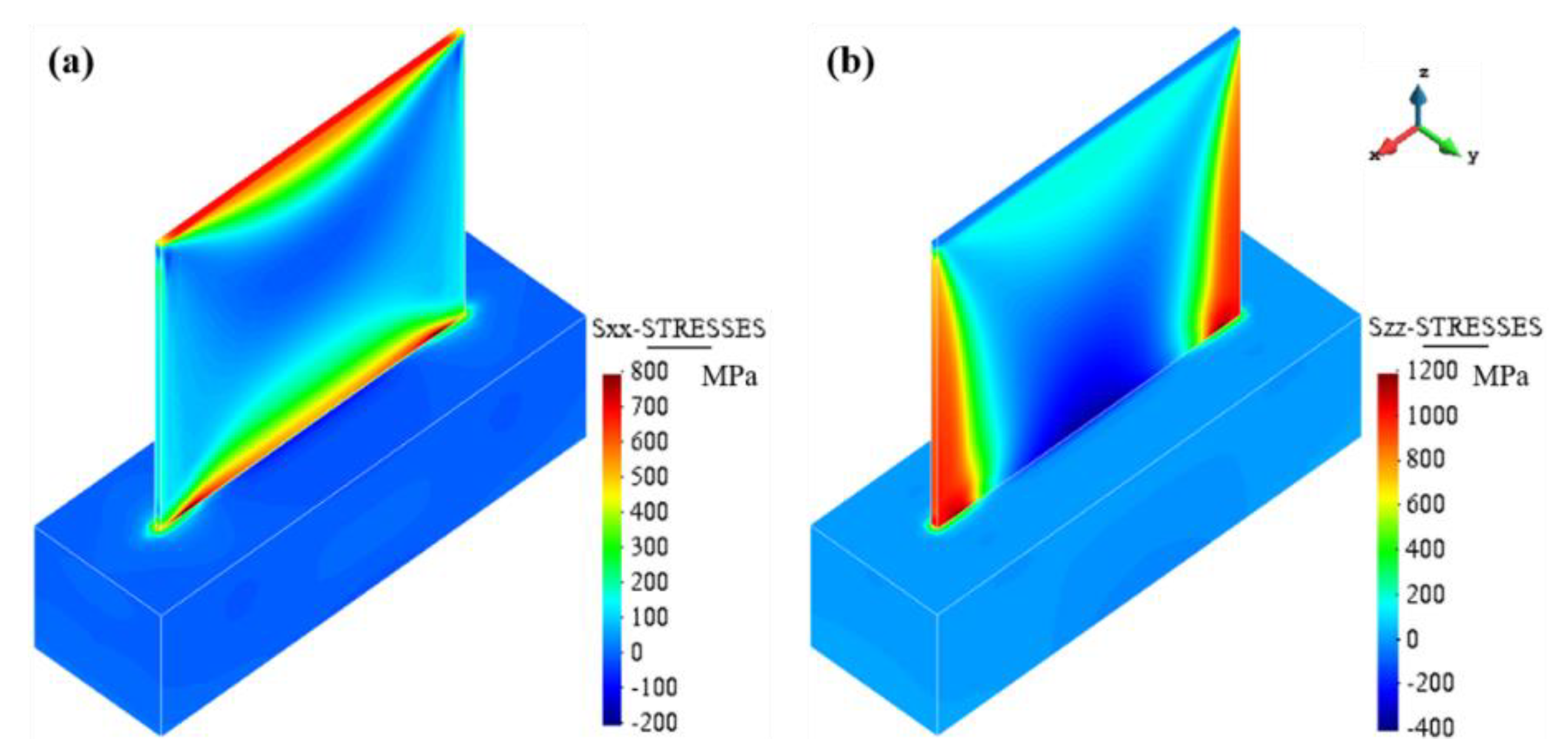
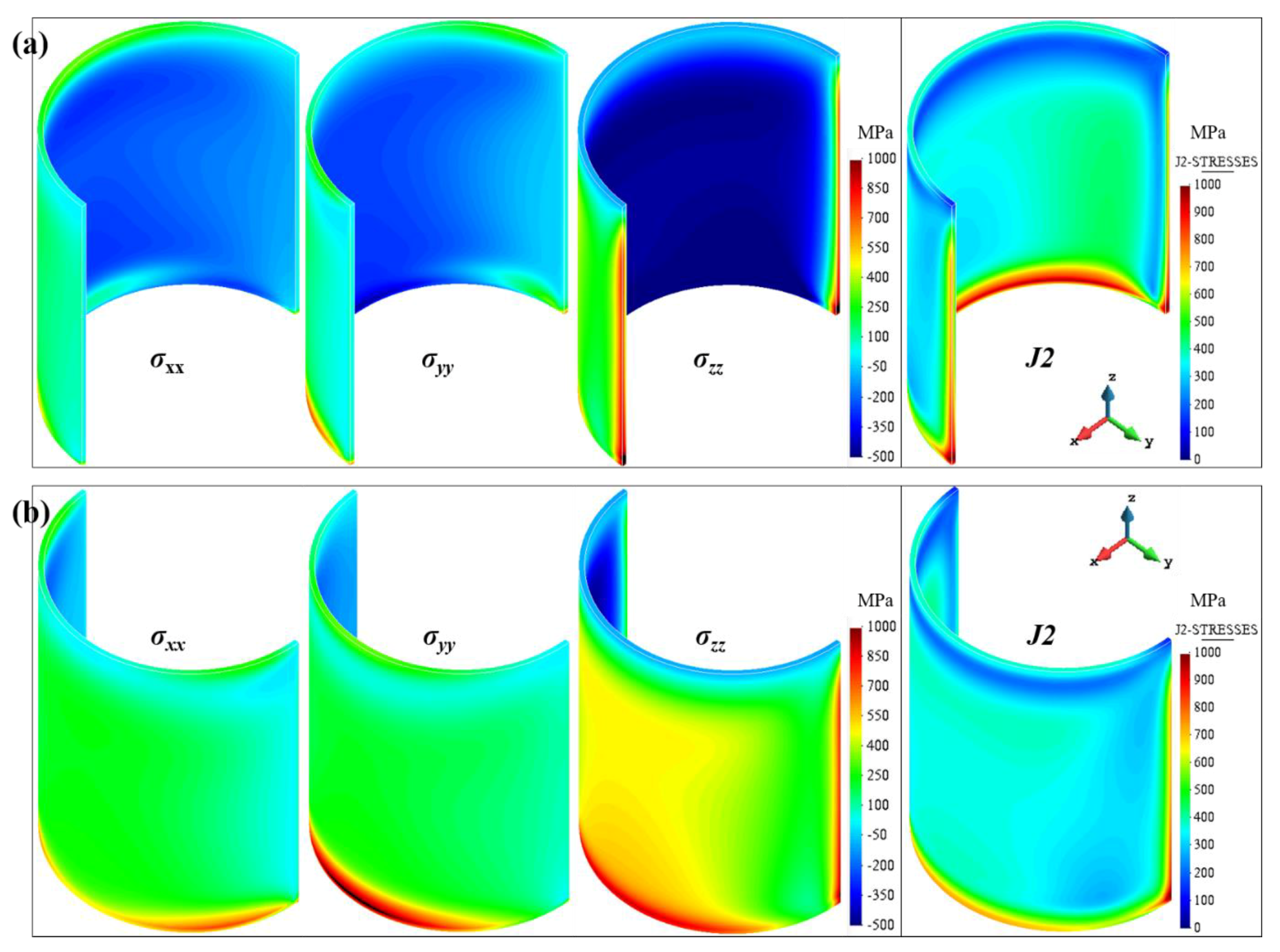
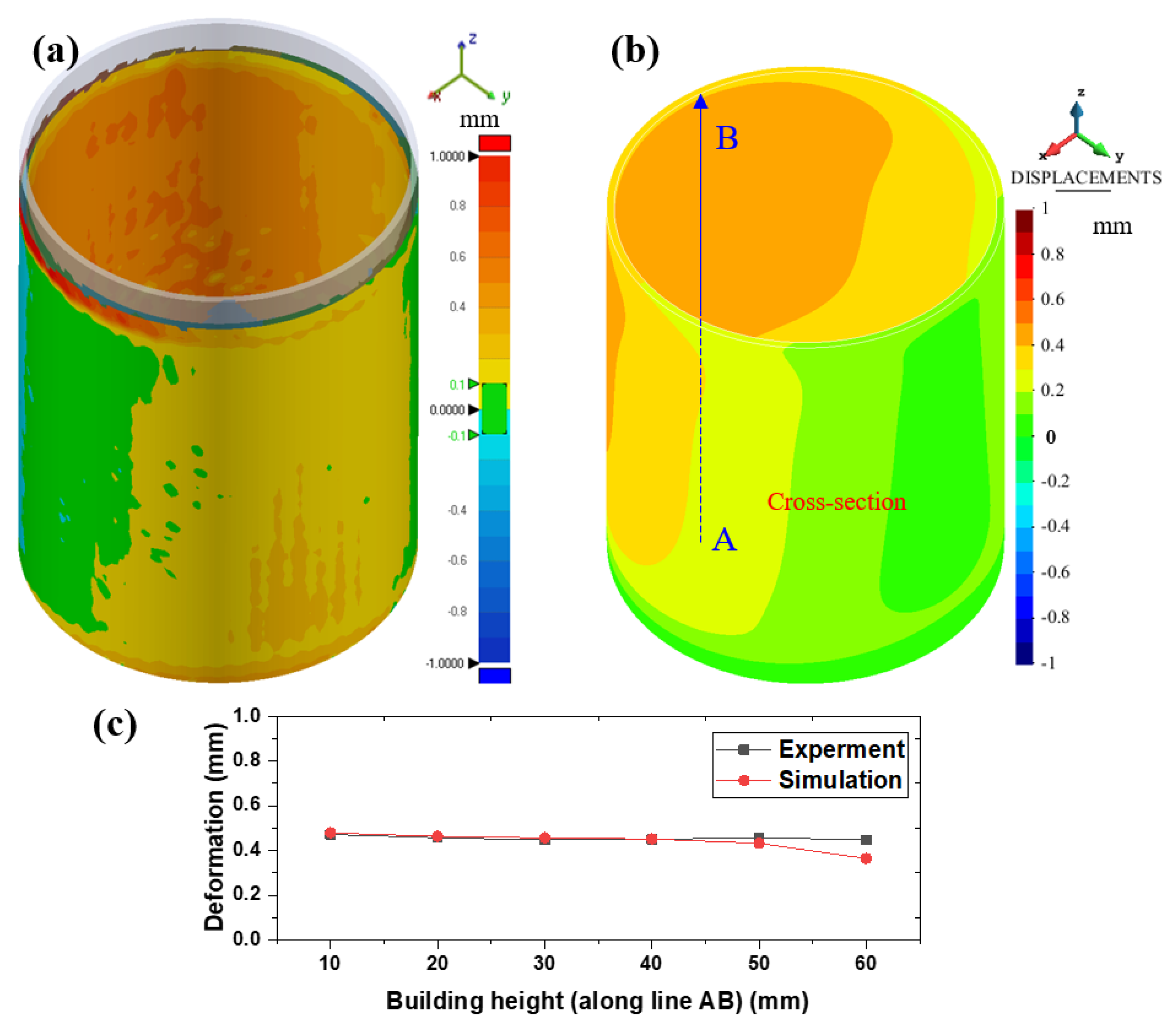
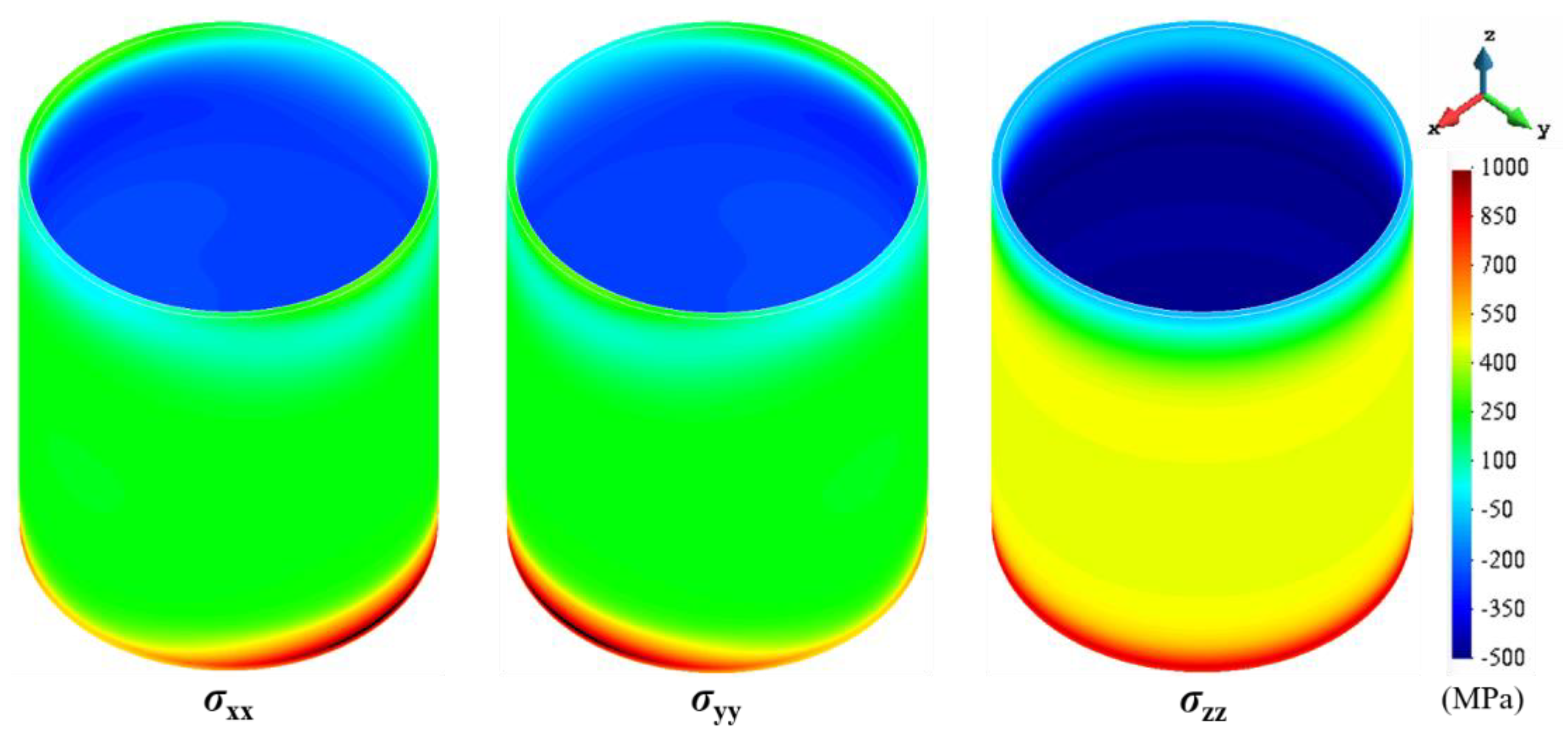
4.1. Single-Wall Structures
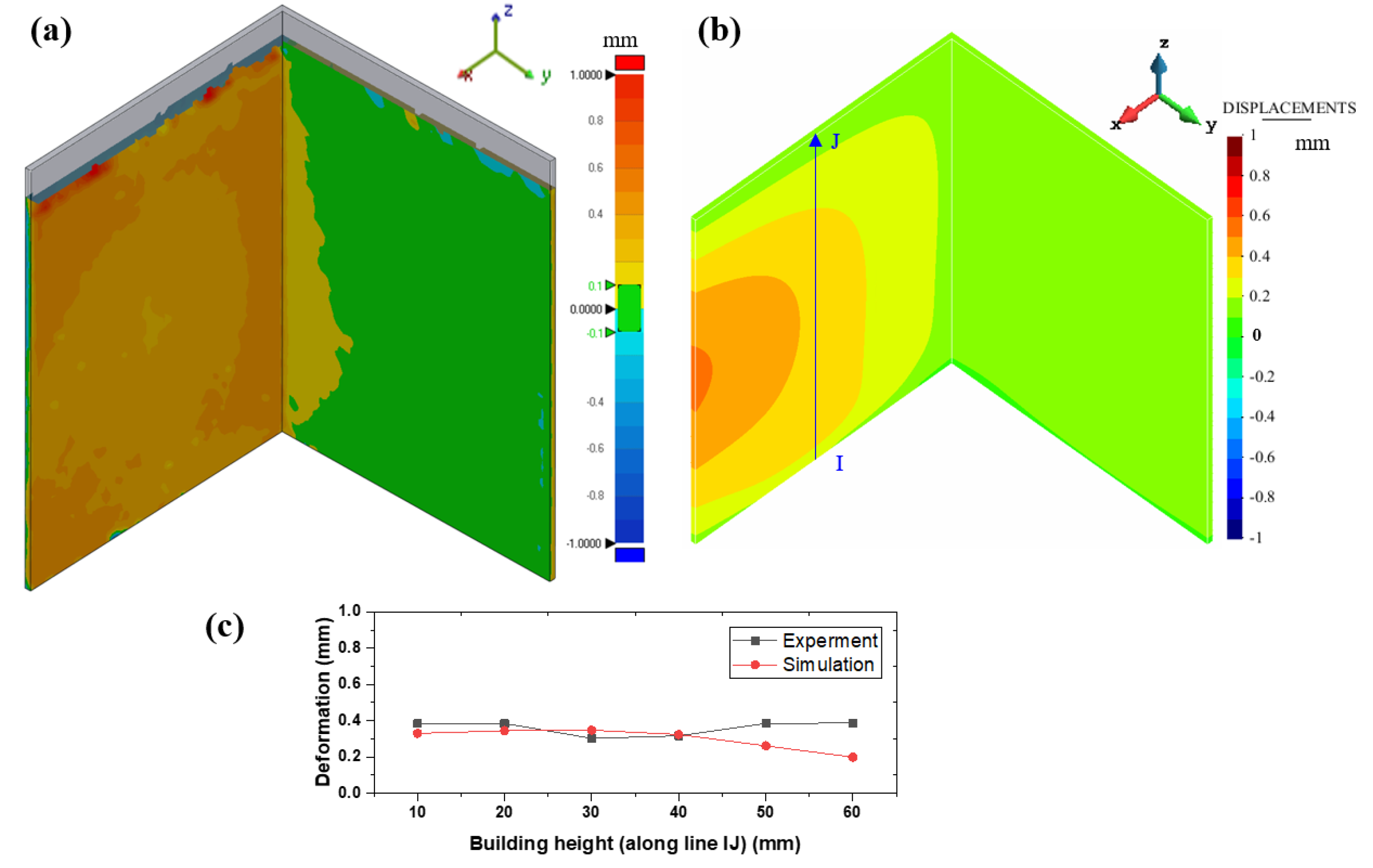
4.2. Open Thin-Walled Structures
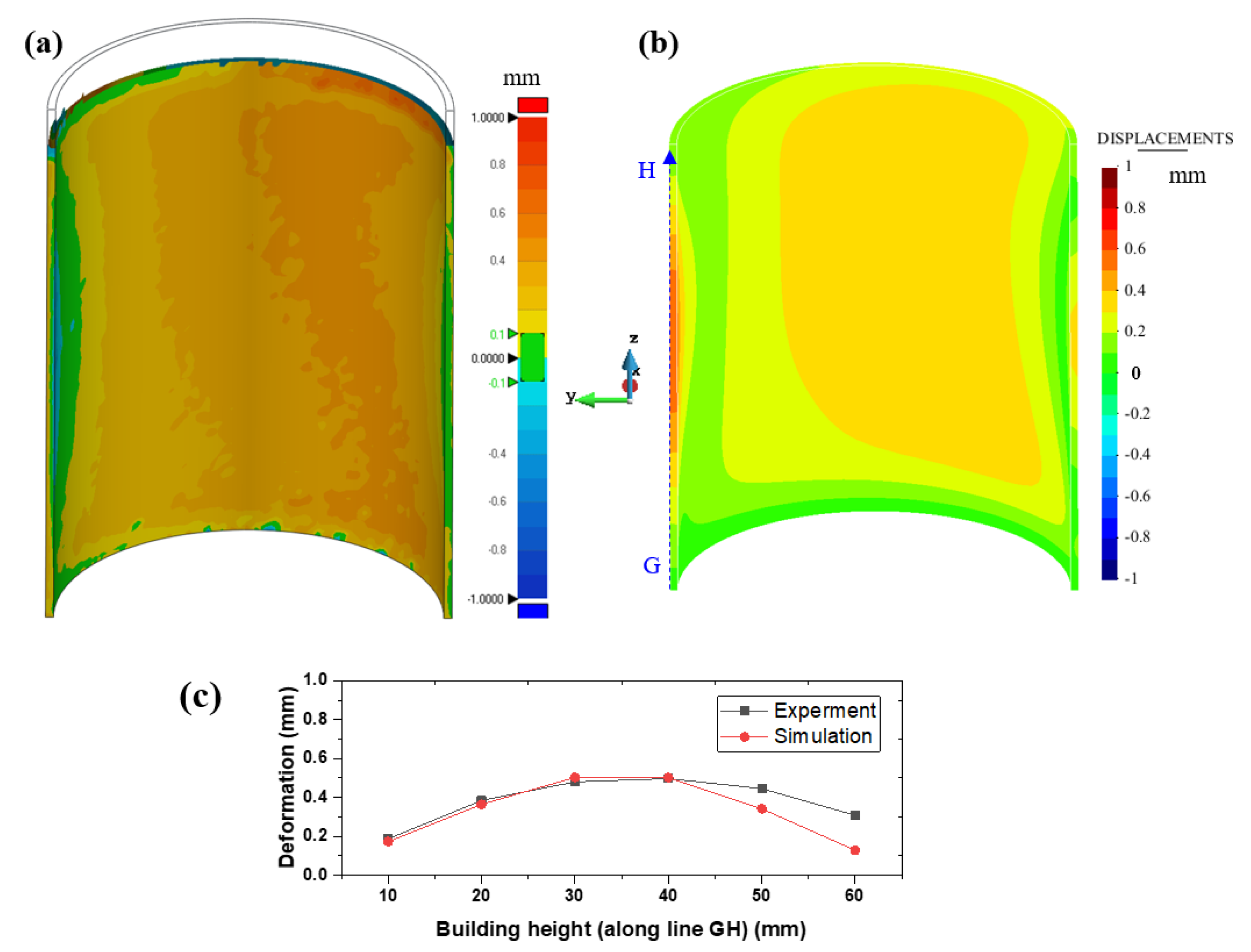
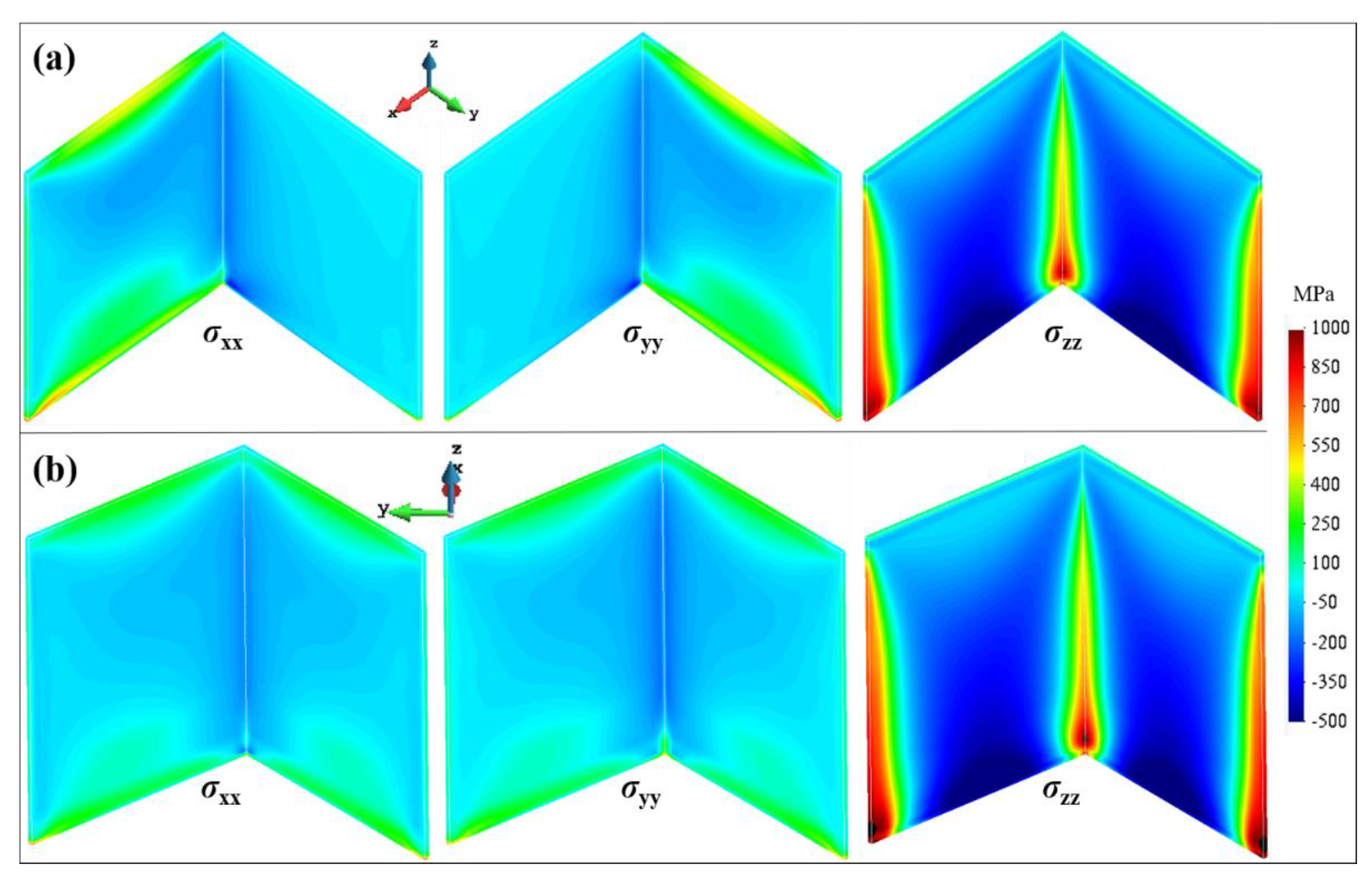
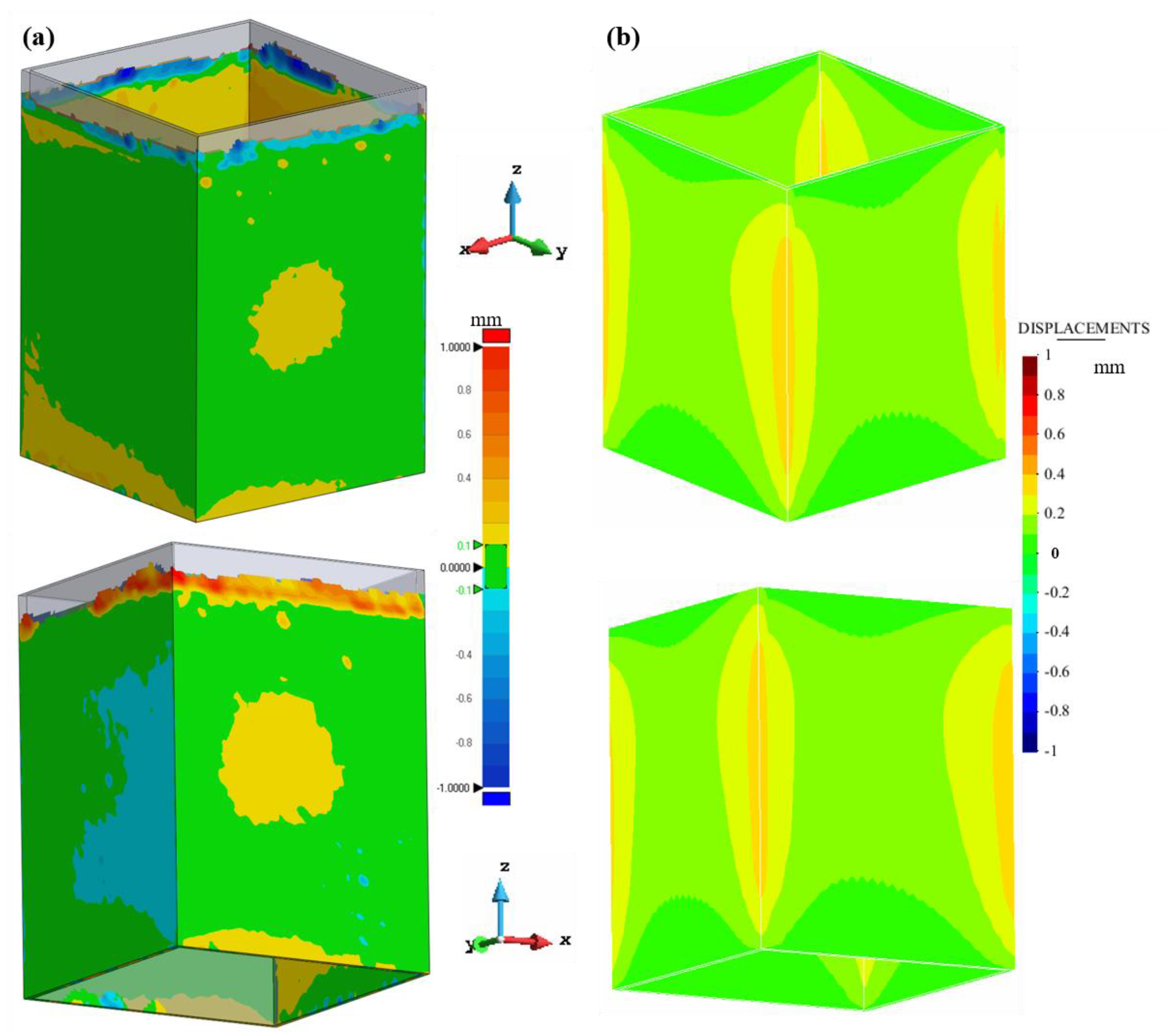
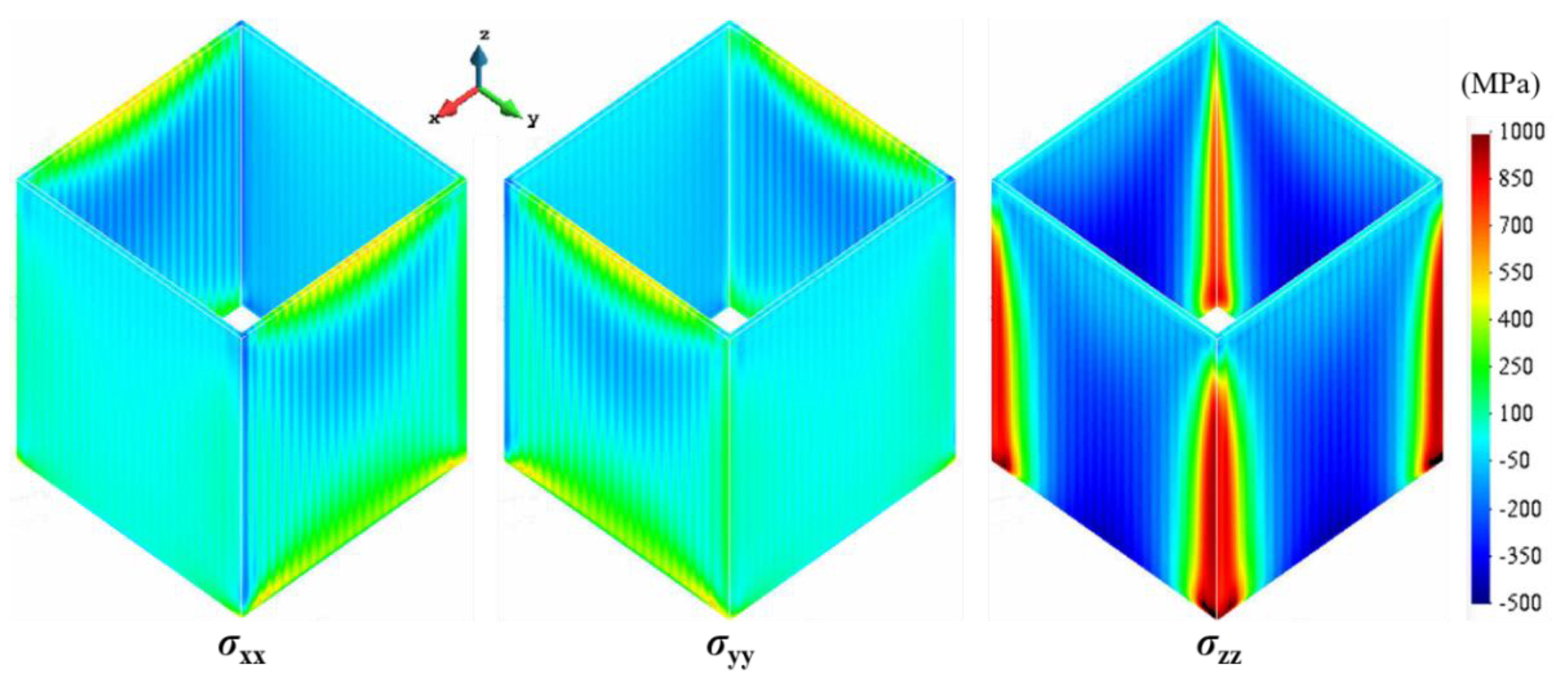
4.3. Closed Thin-Walled Structures
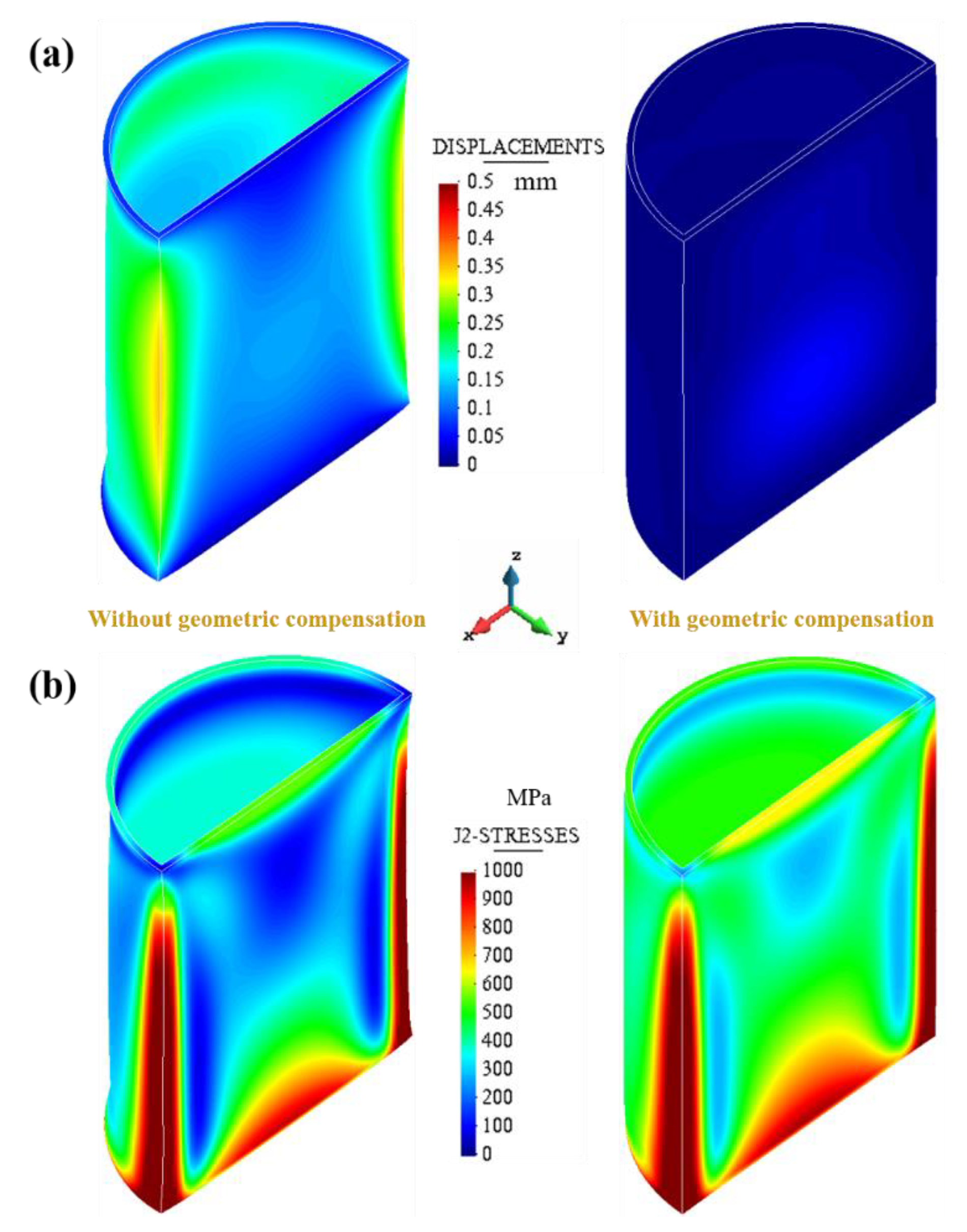
5. Proposed Strategies to Reduce the Warpage of Thin-Walled Structures
6. Conclusions
- The recoating system affects the residual warpage of the build. Thus, the orientation of the part on the build-plate with respect to the recoating direction makes a difference. This effect is more pronounced when open structures are considered. The higher structural stiffness of the closed-structures mitigates this phenomenon.
- The vertical displacements at the top surface of the build are amplified by the bulging phenomenon shown by these kinds of structures. The interference between the recoating system and the roughness generated by the non-uniform powder bed spreading generates increased loading in the direction of the recoater’s movement. The induced bending is more pronounced when these loads are orthogonal to the thin surfaces. Thus, the orientation of the lightweight structures on the base platform is relevant.
- Open lightweight structures are more prone to warpage due to their reduced structural stiffness compared to closed ones. However, higher residual stresses appear on the latter and can be relaxed through post-annealing treatment. Therefore, component integration is a possible solution to increase the overall stiffness of the build to better resist the thermal stresses induced by the fabrication process as well as generate a more uniform temperature field, thus lowering temperature gradients and stress concentrations.
- Geometry compensation is a good inverse engineering strategy to modify the original nominal geometry, accounting for the part warpage due to the AM process and ensuring optimal geometrical accuracy in SLM-parts.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, X.; Zhang, W.; Chiumenti, M.; Cervera, M.; Gillham, B.; Yu, P.; Yin, S.; Lin, X.; Babu, R.P.; Lupoi, R. Crack-free laser powder bed fusion by substrate design. Addit. Manuf. 2022, 59, 103149. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.D.; de Lacalle, L.N.L.; Urbikain, G.; Pereira, O.; Martínez, S.; Bris, J. On the relationship between cutting forces and anisotropy features in the milling of LPBF Inconel 718 for near net shape parts. Int. J. Mach. Tools Manuf. 2021, 170, 103801. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. Mater. Des. 2019, 183, 108164. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.D.; Marin, F.; Martínez, S.; Lamikiz, A.; Urbikain, G.; de Lacalle, L.N.L. Stiffening near-net-shape functional parts of Inconel 718 LPBF considering material anisotropy and subsequent machining issues. Mech. Syst. Signal Process. 2022, 168, 108675. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, T.; Ji, X.; Hu, J.; Li, T.; Lin, X.; Huang, W. 3D printing well organized porous iron-nickel/polyaniline nanocages multiscale supercapacitor. J. Alloy. Compd. 2018, 760, 78–83. [Google Scholar] [CrossRef]
- Prasad, A.; Yuan, L.; Lee, P.; Patel, M.; Qiu, D.; Easton, M.; StJohn, D. Towards understanding grain nucleation under Additive Manufacturing solidification conditions. Acta Mater. 2020, 195, 392–403. [Google Scholar] [CrossRef]
- Martin, A.A.; Calta, N.P.; Khairallah, S.A.; Wang, J.; Depond, P.J.; Fong, A.Y.; Thampy, V.; Guss, G.M.; Kiss, A.M.; Stone, K.H.; et al. Dynamics of pore formation during laser powder bed fusion additive manufacturing. Nat. Commun. 2019, 10, 1987. [Google Scholar] [CrossRef] [PubMed]
- Hooper, P.A. Melt pool temperature and cooling rates in laser powder bed fusion. Addit. Manuf. 2018, 22, 548–559. [Google Scholar] [CrossRef]
- Diegel, O.; Nordin, A.; Motte, D. A Practical Guide to Design for Additive Manufacturing; Springer: Singapore, 2019. [Google Scholar]
- Chakraborty, A.; Tangestani, R.; Batmaz, R.; Muhammad, W.; Plamondon, P.; Wessman, A.; Yuan, L.; Martin, É. In-process failure analysis of thin-wall structures made by laser powder bed fusion additive manufacturing. J. Mater. Sci. Technol. 2021, 98, 233–243. [Google Scholar] [CrossRef]
- Cheng, L.; Liang, X.; Bai, J.; Chen, Q.; Lemon, J.; To, A. On utilizing topology optimization to design support structure to prevent residual stress induced build failure in laser powder bed metal additive manufacturing. Addit. Manuf. 2019, 27, 290–304. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, G.; Li, J.; Cervera, M.; Chiumenti, M.; Chen, J.; Lin, X.; Huang, W. Simulation-assisted investigation on the formation of layer bands and the microstructural evolution in directed energy deposition of Ti6Al4V blocks. Virtual Phys. Prototyp. 2021, 16, 387–403. [Google Scholar] [CrossRef]
- Megahed, M.; Mindt, H.-W.; N’Dri, N.; Duan, H.; Desmaison, O. Metal additive-manufacturing process and residual stress modeling. Integr. Mater. Manuf. Innov. 2016, 5, 61–93. [Google Scholar] [CrossRef]
- Uhlmann, E.; Kersting, R.; Klein, T.B.; Cruz, M.F.; Borille, A.V. Additive Manufacturing of Titanium Alloy for Aircraft Components. Procedia CIRP 2015, 35, 55–60. [Google Scholar] [CrossRef]
- Wu, Z.; Narra, S.P.; Rollett, A. Exploring the fabrication limits of thin-wall structures in a laser powder bed fusion process. Int. J. Adv. Manuf. Technol. 2020, 110, 191–207. [Google Scholar] [CrossRef]
- Thompson, S.M.; Aspin, Z.S.; Shamsaei, N.; Elwany, A.; Bian, L. Additive manufacturing of heat exchangers: A case study on a multi-layered Ti–6Al–4V oscillating heat pipe. Addit. Manuf. 2015, 8, 163–174. [Google Scholar] [CrossRef]
- Kilian, M.; Hartwanger, C.; Schneider, M.; Hatzenbichler, M. Waveguide components for space applications manufactured by additive manufacturing technology. IET Microw. Antennas Propag. 2017, 11, 1949–1954. [Google Scholar] [CrossRef]
- Calleja-Ochoa, A.; Gonzalez-Barrio, H.; López de Lacalle, N.; Martínez, S.; Albizuri, J.; Lamikiz, A. A new approach in the design of microstructured ultralight components to achieve maximum functional performance. Materials 2021, 14, 1588. [Google Scholar] [CrossRef]
- Pascual, A.; Ortega, N.; Plaza, S.; de Lacalle, L.N.L.; Ukar, E. Analysis of the influence of L-PBF porosity on the mechanical behavior of AlSi10Mg by XRCT-based FEM. J. Mater. Res. Technol. 2023, 22, 958–981. [Google Scholar] [CrossRef]
- Yavari, R.; Smoqi, Z.; Riensche, A.; Bevans, B.; Kobir, H.; Mendoza, H.; Song, H.; Cole, K.; Rao, P. Part-scale thermal simulation of laser powder bed fusion using graph theory: Effect of thermal history on porosity, micro-structure evolution, and recoater crash. Mater. Des. 2021, 204, 109685. [Google Scholar] [CrossRef]
- Kayacan, M.Y.; Özsoy, K.; Duman, B.; Yilmaz, N.; Kayacan, M.C. A study on elimination of failures resulting from layering and internal stresses in Powder Bed Fusion (PBF) additive manufacturing. Mater. Manuf. Process. 2019, 34, 1467–1475. [Google Scholar] [CrossRef]
- Lu, X.; Chiumenti, M.; Cervera, M.; Li, J.; Lin, X.; Ma, L.; Zhang, G.; Liang, E. Substrate design to minimize residual stresses in Directed Energy Deposition AM processes. Mater. Des. 2021, 202, 109525. [Google Scholar] [CrossRef]
- Zhang, W.; Tong, M.; Harrison, N.M. Resolution, energy and time dependency on layer scaling in finite element modelling of laser beam powder bed fusion additive manufacturing. Addit. Manuf. 2019, 28, 610–620. [Google Scholar] [CrossRef]
- Carraturo, M.; Kollmannsberger, S.; Reali, A.; Auricchio, F.; Rank, E. An immersed boundary approach for residual stress evaluation in selective laser melting processes. Addit. Manuf. 2021, 46, 102077. [Google Scholar] [CrossRef]
- Promoppatum, P.; Onler, R.; Yao, S.-C. Numerical and experimental investigations of micro and macro characteristics of direct metal laser sintered Ti-6Al-4V products. J. Mater. Process. Technol. 2016, 240, 262–273. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Yi, Z.; Su, X. Research on the fabricating quality optimization of the overhanging surface in SLM process. Int. J. Adv. Manuf. Technol. 2012, 65, 1471–1484. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Liu, R.; Xiao, D.; Sun, J. Study on the designing rules and processability of porous structure based on selective laser melting (SLM). J. Mater. Process. Technol. 2013, 213, 1734–1742. [Google Scholar] [CrossRef]
- Yakout, M.; Cadamuro, A.; Elbestawi, M.A.; Veldhuis, S.C. The selection of process parameters in additive manufacturing for aerospace alloys. Int. J. Adv. Manuf. Technol. 2017, 92, 2081–2098. [Google Scholar] [CrossRef]
- Le, T.-P.; Wang, X.; Davidson, K.P.; Fronda, J.E.; Seita, M. Experimental analysis of powder layer quality as a function of feedstock and recoating strategies. Addit. Manuf. 2021, 39, 101890. [Google Scholar] [CrossRef]
- Weinberg, J. A Precision Blade Mechanism for Powder Recoating in Selective Laser Melting. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2018. [Google Scholar]
- Zhu, C.; Chen, X.; Wu, H.; Zhu, J.; Peng, T.; Lv, J.; Wu, Y. Multi-Objective Optimization of Selective Laser Melting Processes for Minimizing Energy Consumption and Maximizing Product Tensile Strength. Metals 2022, 12, 1782. [Google Scholar] [CrossRef]
- Chiumenti, M.; Neiva, E.; Salsi, E.; Cervera, M.; Badia, S.; Moya, J.; Chen, Z.; Lee, C.; Davies, C.; Chiumenti, M.; et al. Numerical modelling and experimental validation in Selective Laser Melting. Addit. Manuf. 2017, 18, 171–185. [Google Scholar] [CrossRef]
- Kobir, M.H.; Yavari, R.; Riensche, A.R.; Bevans, B.D.; Castro, L.; Cole, K.D.; Rao, P. Prediction of recoater crash in laser powder bed fusion additive manufacturing using graph theory thermomechanical modeling. Prog. Addit. Manuf. 2022, 1–26. [Google Scholar] [CrossRef]
- Cao, J.; Gharghouri, M.A.; Nash, P. Finite-element analysis and experimental validation of thermal residual stress and distortion in electron beam additive manufactured Ti-6Al-4V build plates. J. Mater. Process. Technol. 2016, 237, 409–419. [Google Scholar] [CrossRef]
- Vastola, G.; Sin, W.; Sun, C.-N.; Sridhar, N. Design guidelines for suppressing distortion and buckling in metallic thin-wall structures built by powder-bed fusion additive manufacturing. Mater. Des. 2022, 215, 110489. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Zhang, Z.; Kucukkoc, I. The influence of scan length on fabricating thin-walled components in selective laser melting. Int. J. Mach. Tools Manuf. 2018, 126, 1–12. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, Z.; Zhu, H.; Zeng, X. Deformation and control method of thin-walled part during laser powder bed fusion of Ti–6Al–4V alloy. Int. J. Adv. Manuf. Technol. 2020, 110, 3467–3478. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Li, J.; Ma, L.; Wei, L.; Hu, Y.L.; Huang, W. Finite element analysis and experimental validation of the thermomechanical behavior in laser solid forming of Ti-6Al-4V. Addit. Manuf. 2018, 21, 30–40. [Google Scholar] [CrossRef]
- Chiumenti, M.; Cervera, M.; Salmi, A.; de Saracibar, C.A.; Dialami, N.; Matsui, K. Finite element modeling of multi-pass welding and shaped metal deposition processes. Comput. Methods Appl. Mech. Eng. 2010, 199, 2343–2359. [Google Scholar] [CrossRef]
- Lu, X.; Chiumenti, M.; Cervera, M.; Zhang, G.; Lin, X. Mitigation of residual stresses and microstructure homogenization in directed energy deposition processes. Eng. Comput. 2022, 38, 4771–4790. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Huang, W. In situ measurements and thermo-mechanical simulation of Ti–6Al–4V laser solid forming processes. Int. J. Mech. Sci. 2019, 153, 119–130. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Michaleris, P. Effect of stress relaxation on distortion in additive manufacturing process modeling. Addit. Manuf. 2016, 12, 51–59. [Google Scholar] [CrossRef]
- Chen, Z.; Ye, H.; Xu, H. Distortion control in a wire-fed electron-beam thin-walled Ti-6Al-4V freeform. J. Mater. Process. Technol. 2018, 258, 286–295. [Google Scholar] [CrossRef]
- Chiumenti, M.; Cervera, M.; de Saracibar, C.A.; Dialami, N. Numerical modeling of friction stir welding processes. Comput. Methods Appl. Mech. Eng. 2013, 254, 353–369. [Google Scholar] [CrossRef]
- Moreira, C.A.; Caicedo, M.A.; Cervera, M.; Chiumenti, M.; Baiges, J. A multi-criteria h-adaptive finite-element framework for industrial part-scale thermal analysis in additive manufacturing processes. Eng. Comput. 2022, 38, 4791–4813. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.Y.; Fang, X.Y.; Guo, Y.B. On the Simulation Scalability of Predicting Residual Stress and Distortion in Selective Laser Melting. J. Manuf. Sci. Eng. 2018, 140, 041013. [Google Scholar] [CrossRef]
- Chiumenti, M.; Cervera, M.; Dialami, N.; Wu, B.; Jinwei, L.; de Saracibar, C.A. Numerical modeling of the electron beam welding and its experimental validation. Finite Elem. Anal. Des. 2016, 121, 118–133. [Google Scholar] [CrossRef]
- Zhang, W.; Tong, M.; Harrison, N.M. Multipart Build Effects on Temperature and Residual Stress by Laser Beam Powder Bed Fusion Additive Manufacturing. 3D Print. Addit. Manuf. 2021. [Google Scholar] [CrossRef]
- Abarca, M.J.; Darabi, R.; de Sa, J.C.; Parente, M.; Reis, A. Multi-scale modeling for prediction of residual stress and distortion in Ti–6Al–4V semi-circular thin-walled parts additively manufactured by laser powder bed fusion (LPBF). Thin-Walled Struct. 2023, 182, 110151. [Google Scholar] [CrossRef]
- Biegler, M.; Elsner, B.A.; Graf, B.; Rethmeier, M. Geometric distortion-compensation via transient numerical simulation for directed energy deposition additive manufac-turing. Sci. Technol. Weld. Join. 2020, 25, 468–475. [Google Scholar] [CrossRef]
- Hajializadeh, F.; Ince, A. Integration of artificial neural network with finite element analysis for residual stress prediction of direct metal deposition process. Mater. Today Commun. 2021, 27, 102197. [Google Scholar] [CrossRef]
- Yang, T.; Xie, D.; Yue, W.; Wang, S.; Rong, P.; Shen, L.; Zhao, J.; Wang, C. Distortion of Thin-Walled Structure Fabricated by Selective Laser Melting Based on Assumption of Constraining Force-Induced Distortion. Metals 2019, 9, 1281. [Google Scholar] [CrossRef]
- Dunbar, A.J. Analysis of the Laser Powder Bed Fusion Additive Manufacturing Process through Experimental Measurement and Finite Element Modeling; The Pennsylvania State University: State College, PA, USA, 2016. [Google Scholar]
- He, P.; Sun, C.; Wang, Y. Material distortion in laser-based additive manufacturing of fuel cell component: Three-dimensional numerical analysis. Addit. Manuf. 2021, 46, 102188. [Google Scholar] [CrossRef]
- Afazov, S.; Semerdzhieva, E.; Scrimieri, D.; Serjouei, A.; Kairoshev, B.; Derguti, F. An improved distortion compensation approach for additive manufacturing using optically scanned data. Virtual Phys. Prototyp. 2021, 16, 1–13. [Google Scholar] [CrossRef]
- Hartmann, C.; Lechner, P.; Himmel, B.; Krieger, Y.; Lueth, T.C.; Volk, W. Compensation for Geometrical Deviations in Additive Manufacturing. Technologies 2019, 7, 83. [Google Scholar] [CrossRef]

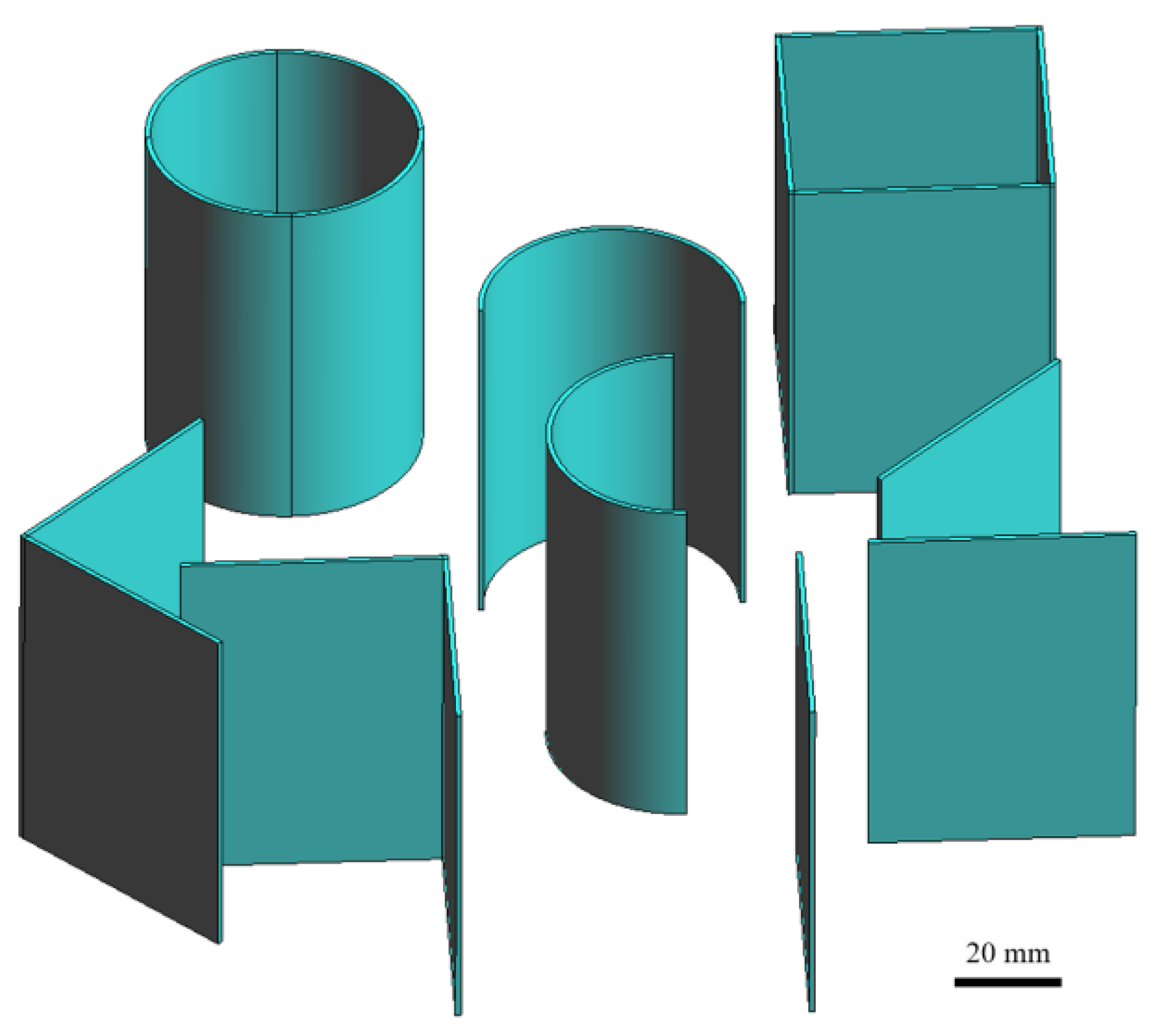
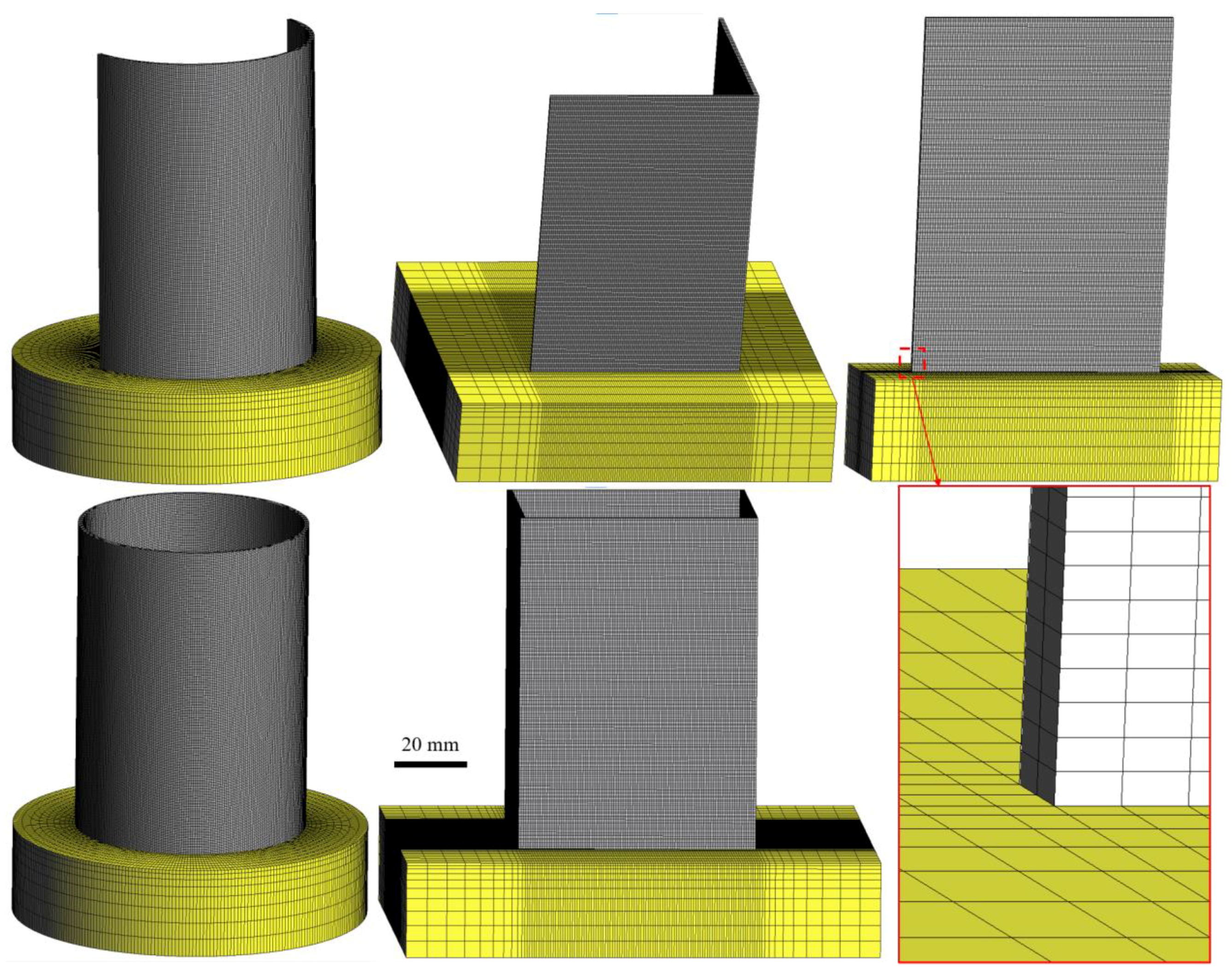




| Laser Power (W) | Layer Thickness (µm) | Scan Speed (mm/s) | Hatch Spacing (µm) | Laser Beam Diameter (µm) |
|---|---|---|---|---|
| 300 | 40 | 700 | 70 | 70 |
| Thin-Walled Structures | Number of FE Elements | Number of Nodes |
|---|---|---|
| Cylindrical part Semi-cylindrical part Square part L-shape part Single-wall part | 244,480 145,280 339,840 219,560 65,680 | 352,320 204,450 477,309 295,959 94,395 |
| Temperature (°C) | Density (kg/m3) | Specific Heat (J/(kg·°C)) | Thermal Conductivity (W/(m·°C)) | Poisson’s Ratio | Young’s Modulus (GPa) | Thermal Dilatancy (μm/m/°C) | Yield Stress (MPa) |
|---|---|---|---|---|---|---|---|
| 20 205 500 995 1100 1200 1600 1650 2000 | 4420 4395 4350 4282 4267 4252 4198 3886 3818 | 546 584 651 753 641 660 732 831 831 | 7.0 8.75 12.6 22.7 19.3 21.0 25.8 35 35 | 0.345 0.35 0.37 0.43 0.43 0.43 0.43 0.43 0.43 | 110 100 76 15 5 4 1 0.1 0.01 | 8.78 10.0 11.2 12.3 12.4 12.42 12.5 12.5 12.5 | 850 630 470 13 5 1 0.5 0.1 0.01 |
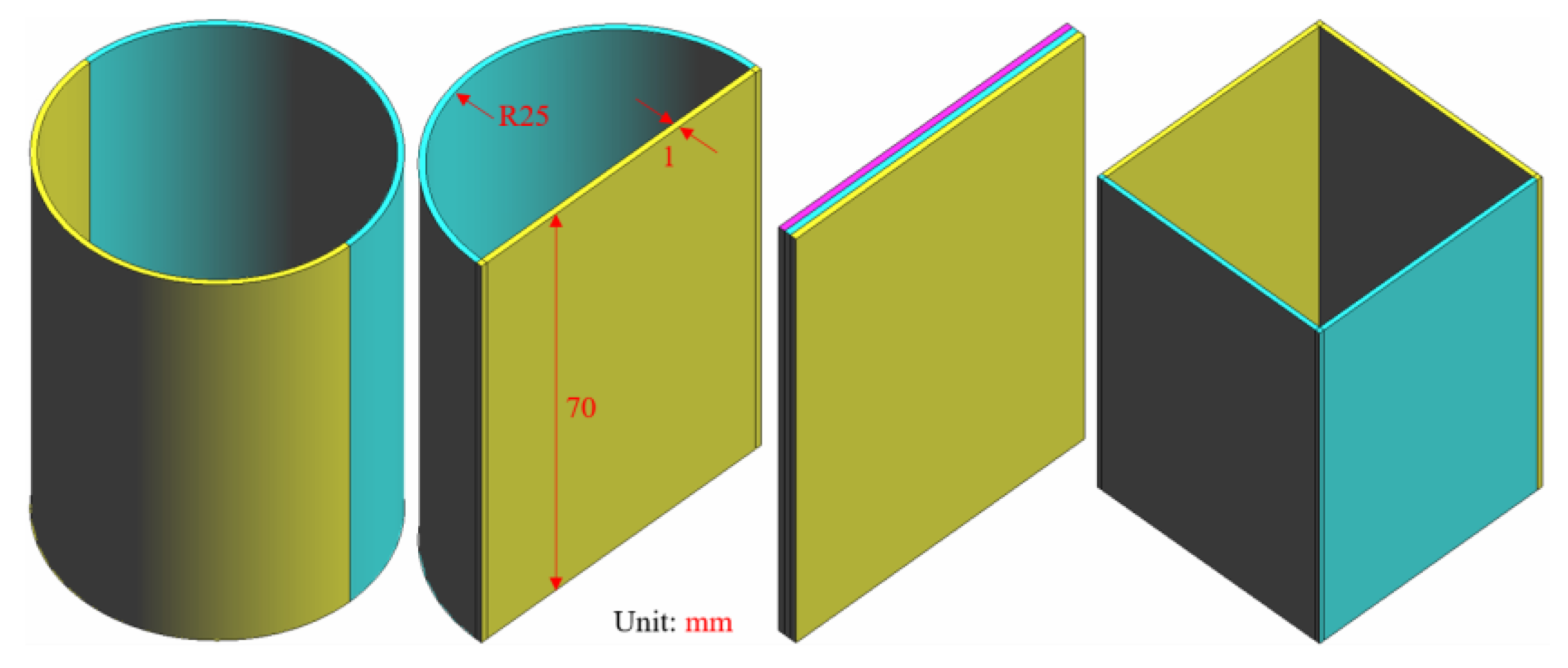
| Part Shape | Horizontal Size (mm) | Wall Thickness (mm) | Designed Building Heights (mm) | Actual Building Heights (mm) |
|---|---|---|---|---|
| Cylinder Semi-cylinder L-shape Square Single-wall | Ø50.0 Ø50.0 50.0 × 50.0 50.0 × 50.0 50.0 × 1.0 | 1.0 1.0 1.0 1.0 1.0 | 70.0 70.0 70.0 70.0 70.0 | ≈62.0 ≈62.0 ≈62.0 ≈62.0 ≈50.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Chiumenti, M.; Cervera, M.; Slimani, M.; Gonzalez, I. Recoater-Induced Distortions and Build Failures in Selective Laser Melting of Thin-Walled Ti6Al4V Parts. J. Manuf. Mater. Process. 2023, 7, 64. https://doi.org/10.3390/jmmp7020064
Lu X, Chiumenti M, Cervera M, Slimani M, Gonzalez I. Recoater-Induced Distortions and Build Failures in Selective Laser Melting of Thin-Walled Ti6Al4V Parts. Journal of Manufacturing and Materials Processing. 2023; 7(2):64. https://doi.org/10.3390/jmmp7020064
Chicago/Turabian StyleLu, Xufei, Michele Chiumenti, Miguel Cervera, Mehdi Slimani, and Iban Gonzalez. 2023. "Recoater-Induced Distortions and Build Failures in Selective Laser Melting of Thin-Walled Ti6Al4V Parts" Journal of Manufacturing and Materials Processing 7, no. 2: 64. https://doi.org/10.3390/jmmp7020064
APA StyleLu, X., Chiumenti, M., Cervera, M., Slimani, M., & Gonzalez, I. (2023). Recoater-Induced Distortions and Build Failures in Selective Laser Melting of Thin-Walled Ti6Al4V Parts. Journal of Manufacturing and Materials Processing, 7(2), 64. https://doi.org/10.3390/jmmp7020064









