Towards a Simulation-Assisted Prediction of Residual Stress-Induced Failure during Powder Bed Fusion of Metals Using a Laser Beam: Suitable Fracture Mechanics Models and Calibration Methods
Abstract
:1. Introduction
- Which type of fracture models are suitable from a physical point of view to model residual stress-induced fracture during PBF-LB/M?
- How can these models be calibrated to consider the particularities of the PBF-LB/M process and the formed material?
2. Model Selection
2.1. Examination of Material Behavior and Crack Formation
2.2. Model Description
- Be applicable to ductile materials;
- Predict a crack initiation due to residual stresses anywhere in the part;
- Describe a real crack propagation with a magnitude of millimeters;
- Be usable with an FEM process simulation yielding strains and stresses, and cause low additional computational costs.
3. Model Calibration
3.1. Overview
- Experimental approach;
- Experimental and simulative approach;
- AM-adapted approach.
3.2. Experimental Approach
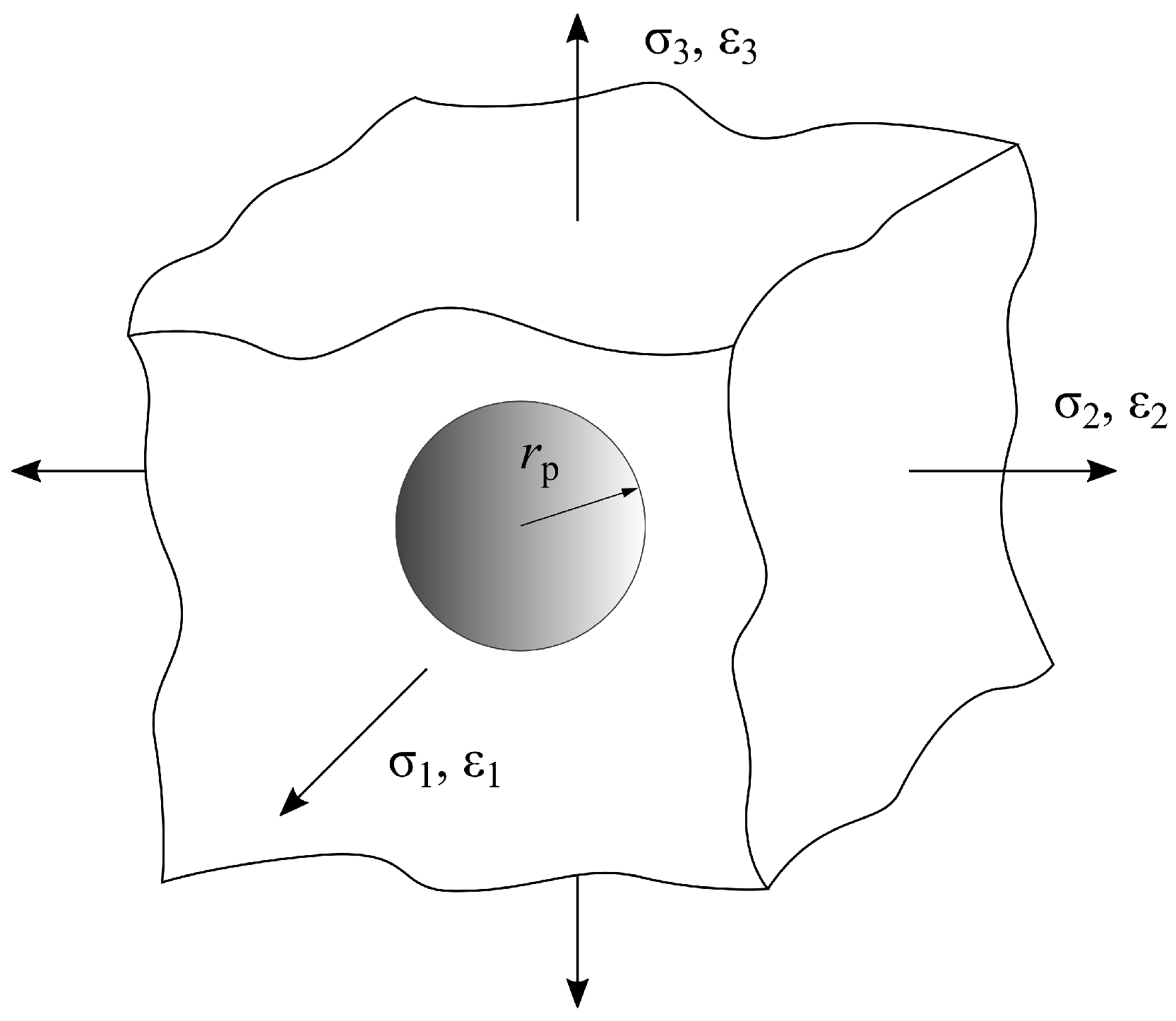
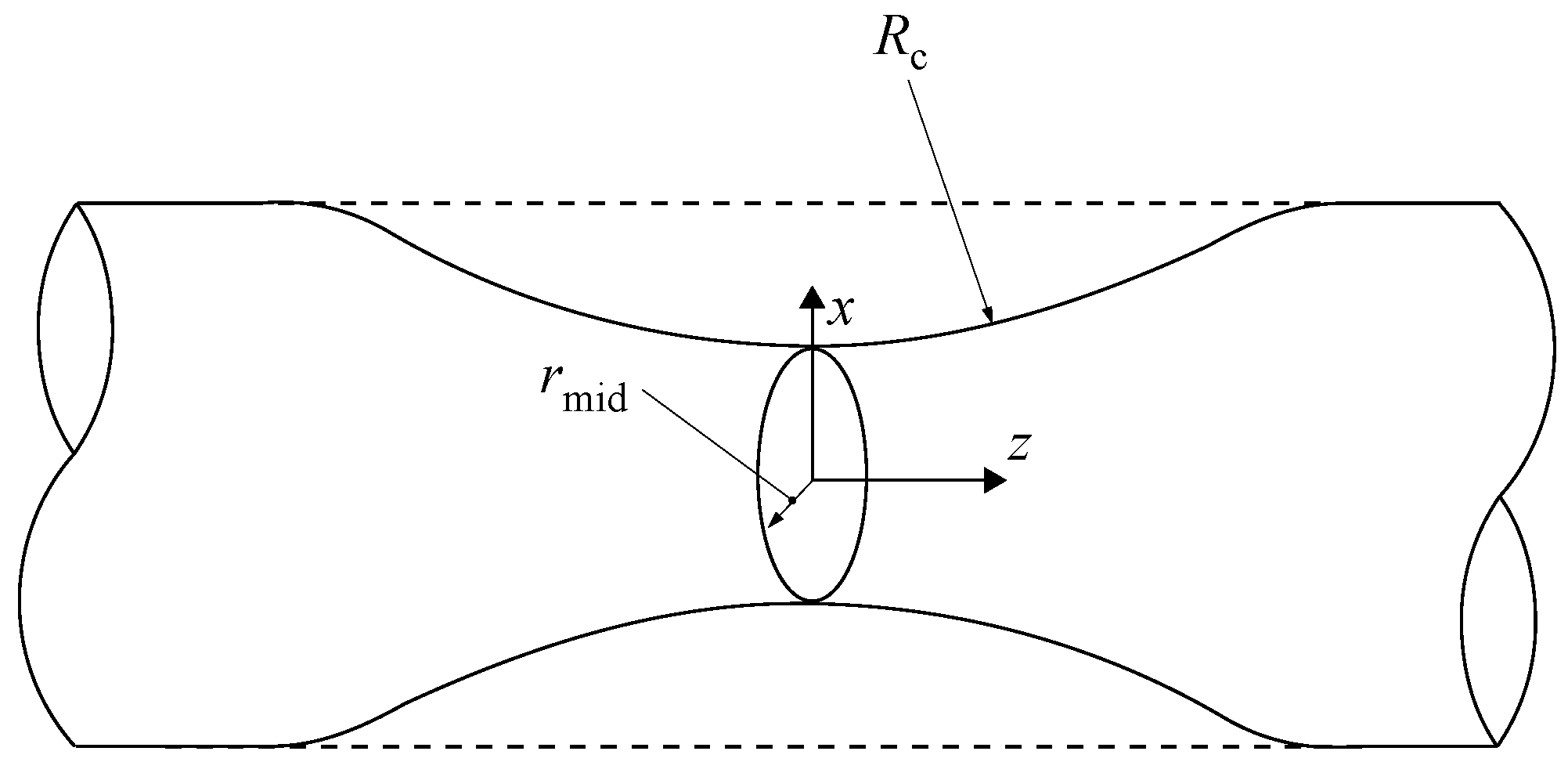
3.2.1. Determination of the Stress Triaxiality and the Equivalent Plastic Failure Strain
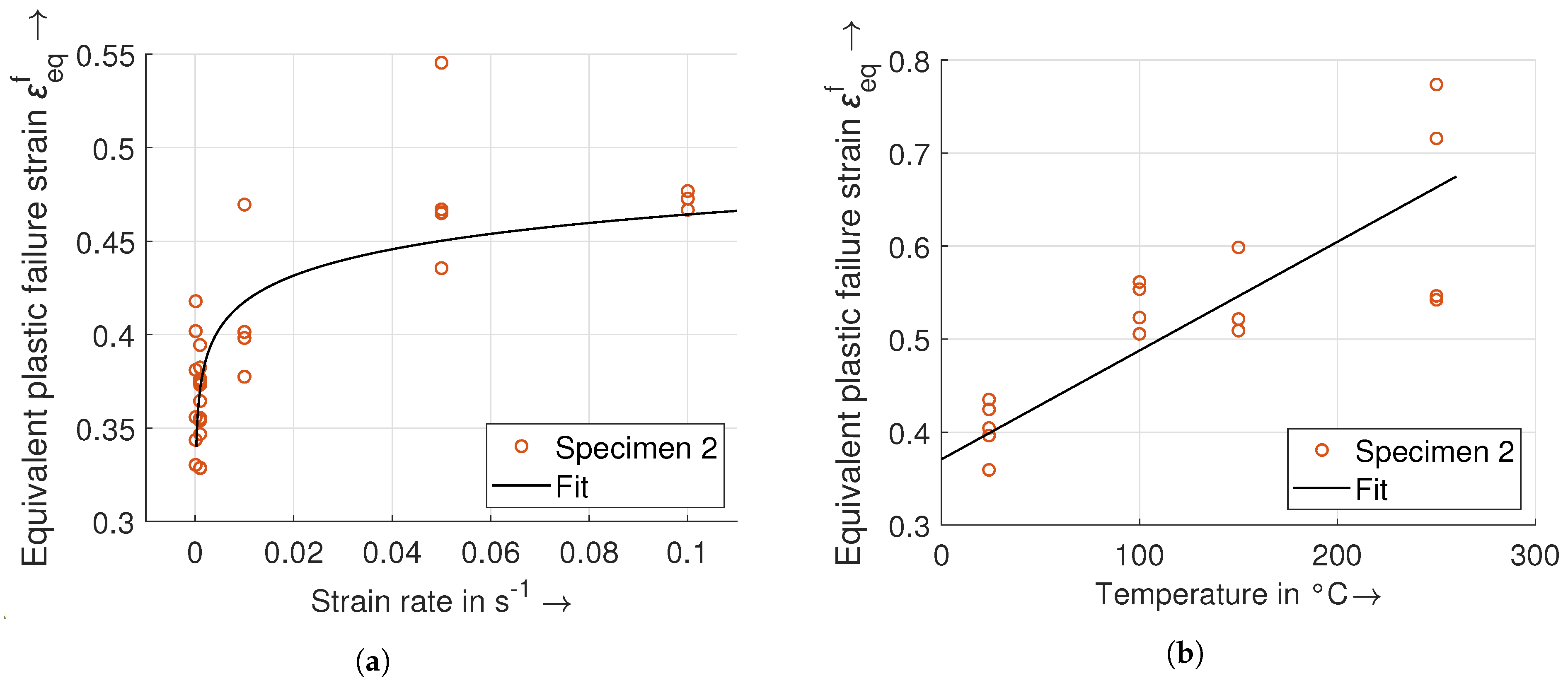
3.2.2. Determination of the Strain Rate and the Temperature-Dependent Values
3.3. Simulative and Experimental Approach
3.3.1. Meshing
3.3.2. Simulation of the Manufacturing Process
3.3.3. Simulative Tensile Tests
3.4. AM-Adapted Approach
3.4.1. AM Experiments
3.4.2. Meshing
3.4.3. Simulation of the PBF-LB/M Process
4. Results and Discussion
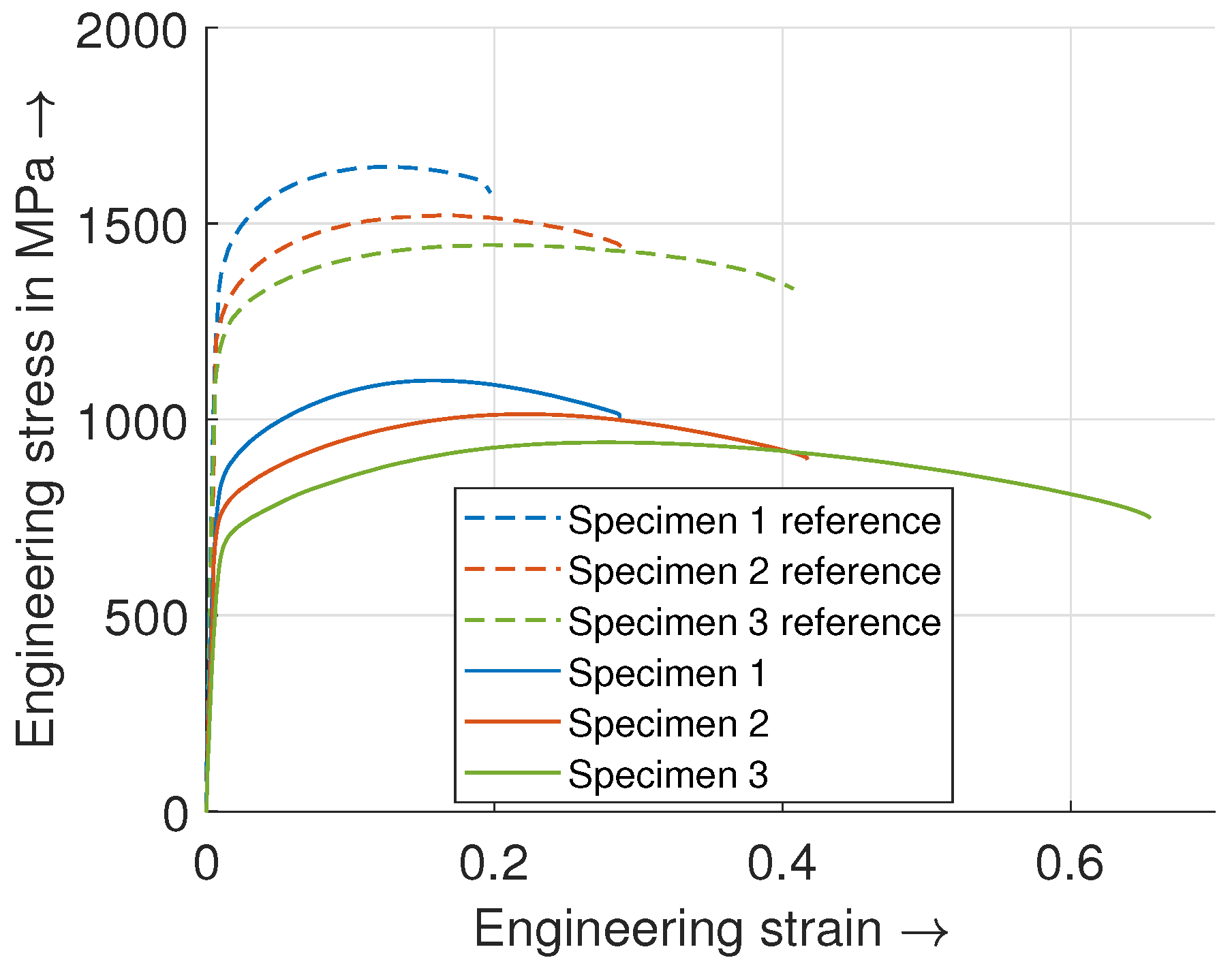
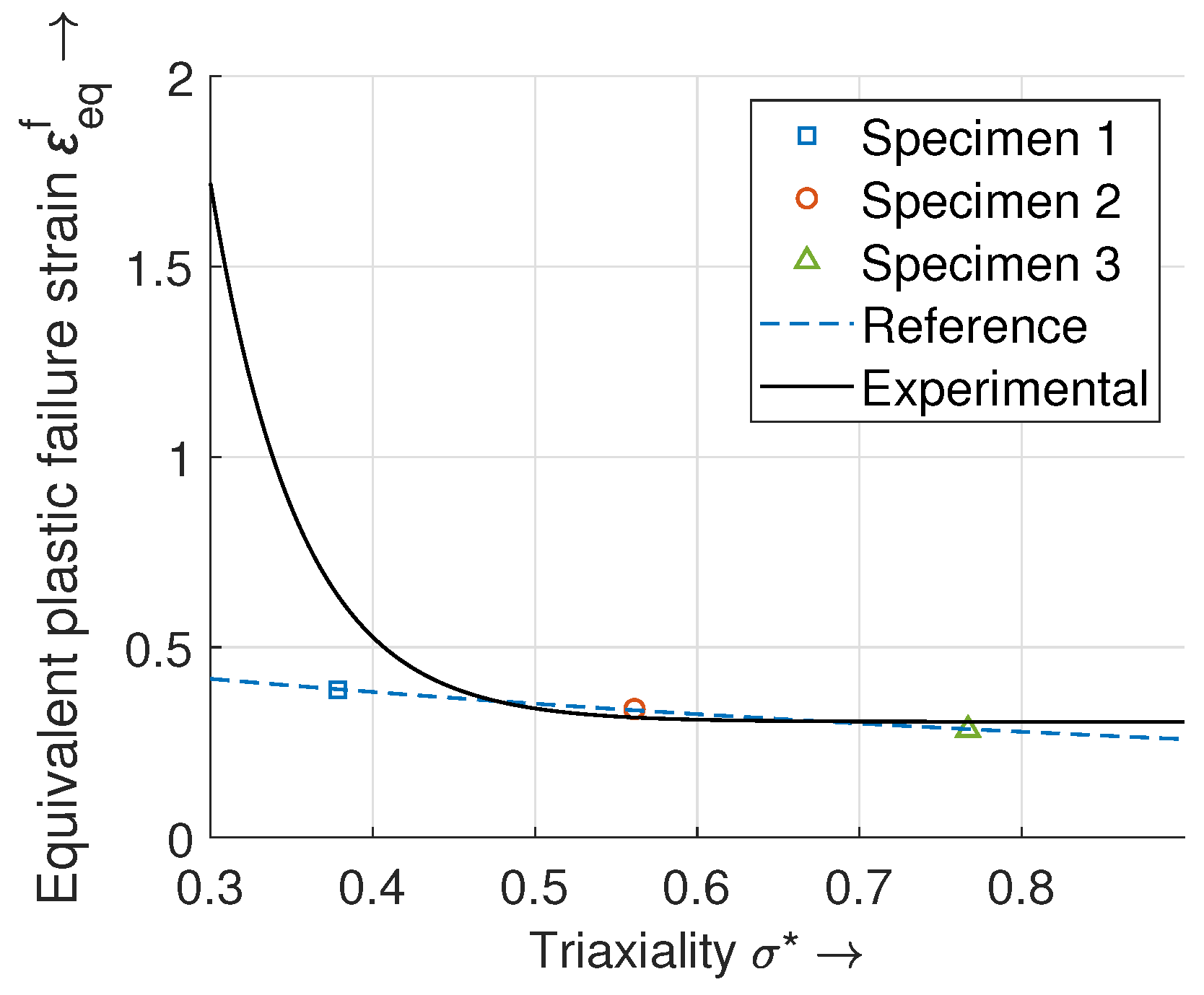
4.1. Calibration Results of the Stress Triaxiality for the RT and JC Model
4.1.1. Description and Interpretation of the Results
4.1.2. Interpretation of the Fitting Quality
4.1.3. Comparison of the Failure Models
4.2. Calibration Results of the Strain Rate and the Temperature of the JC Model
- = 0.0465 and = 4.2307.
4.3. Comparison with the Literature
4.3.1. Material Behavior
4.3.2. Calibration Results
- = 0.0988, = 0.4493, and = .
5. Conclusions and Outlook
- The ductile behavior of additively manufactured IN718 parts provides a justification for the use of strain-based failure criteria;
- Due to the simplicity of the models, no significant increase in the computational costs for the simulation of the building process is to be expected;
- The three calibration approaches show pronounced differences with regard to the fitting curves, which is especially the case for the JC model, suggesting differing predictive capabilities regarding cracking behavior;
- Significant differences of the calibration results were observed for the additively manufactured IN718 specimens compared with the conventional specimens from the literature at low triaxialities;
- The calibration process of the proposed failure models proved to require less effort compared with that of the GTN model due to a reduced number of calibration constants.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| FEM | Finite Element Method |
| GTN | Gurson-Tvergaard-Needleman |
| IN718 | Inconel 718 |
| iwb | Institute for Machine Tools and Industrial Management |
| JC | Johnson-Cook |
| PBF-LB/M | Powder Bed Fusion of Metals using a Laser Beam |
| RT | Rice-Tracey |
| TP | Tracking Point |
Appendix A. Material and Failure Characterization


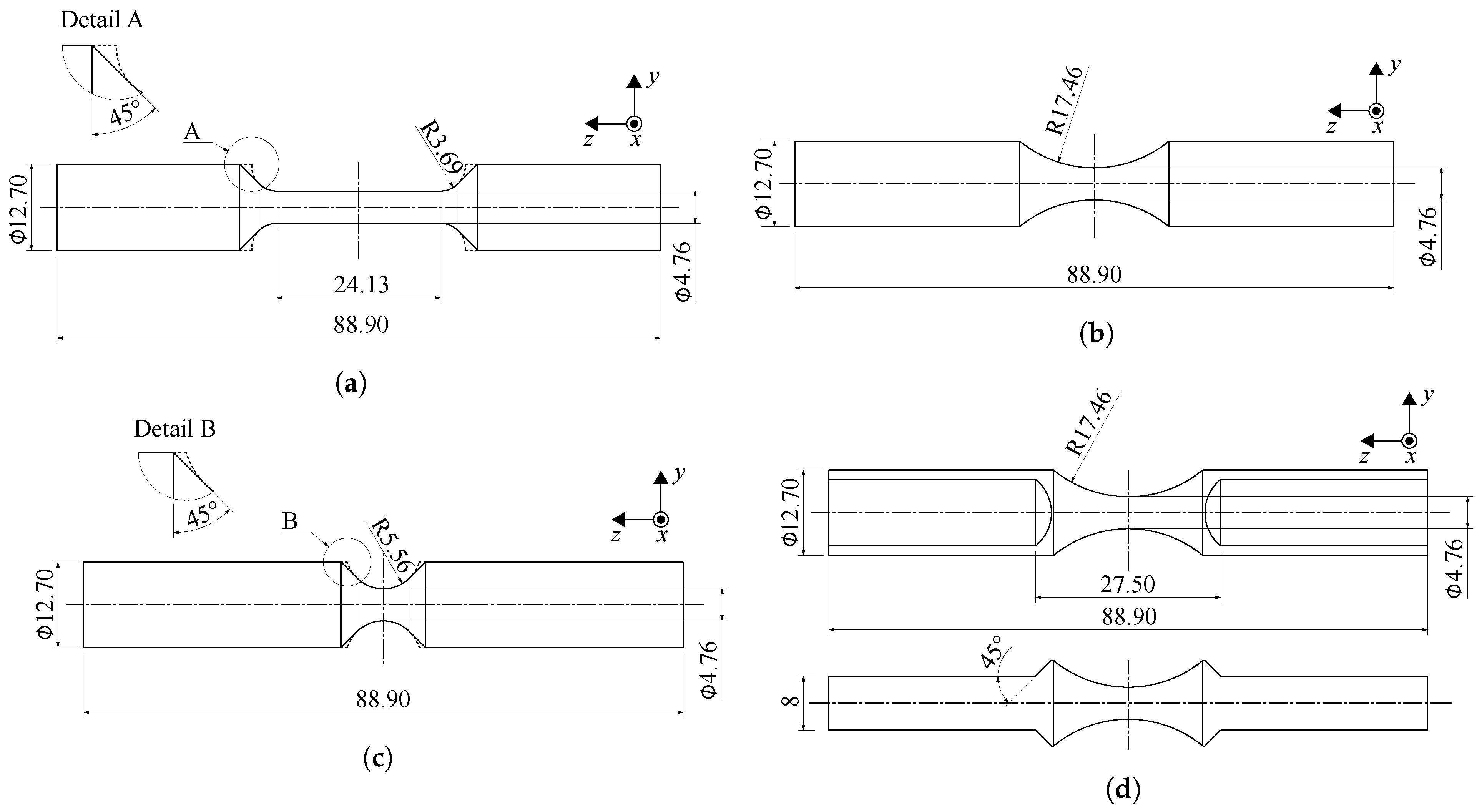
Appendix B. Tensile Test Geometries
Appendix C. Comparison of the Mechanical Properties
References
- Huang, R.; Riddle, M.; Graziano, D.; Warren, J.; Das, S.; Nimbalkar, S.; Cresko, J.; Masanet, E. Energy and emissions saving potential of additive manufacturing: The case of lightweight aircraft components. J. Clean. Prod. 2016, 135, 1559–1570. [Google Scholar] [CrossRef]
- Uhlmann, E.; Kersting, R.; Klein, T.B.; Cruz, M.F.; Borille, A.V. Additive Manufacturing of Titanium Alloy for Aircraft Components. Procedia CIRP 2015, 35, 55–60. [Google Scholar] [CrossRef]
- Kruth, J. Material Incress Manufacturing by Rapid Prototyping Techniques. CIRP Ann. 1991, 40, 603–614. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J.P. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Colegrove, P.A.; Donoghue, J.; Martina, F.; Gu, J.; Prangnell, P.; Hönnige, J. Application of bulk deformation methods for microstructural and material property improvement and residual stress and distortion control in additively manufactured components. Scr. Mater. 2017, 135, 111–118. [Google Scholar] [CrossRef]
- Wimmer, A.; Kolb, C.; Assi, M.; Favre, J.; Bachmann, A.; Fraczkiewicz, A.; Zaeh, M. Investigations on the influence of adapted metal-based alloys on the process of laser beam melting. J. Laser Appl. 2020, 32, 022029. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Zhao, Y.F. Manufacturability analysis of metal laser-based powder bed fusion additive manufacturing—A survey. Int. J. Adv. Manuf. Technol. 2020, 110, 57–78. [Google Scholar] [CrossRef]
- Carlton, H.D.; Haboub, A.; Gallegos, G.F.; Parkinson, D.Y.; MacDowell, A.A. Damage evolution and failure mechanisms in additively manufactured stainless steel. Mater. Sci. Eng. 2016, 651, 406–414. [Google Scholar] [CrossRef]
- Solberg, K.; Berto, F. Notch-defect interaction in additively manufactured Inconel 718. Int. J. Fatigue 2019, 122, 35–45. [Google Scholar] [CrossRef]
- Solberg, K.; Berto, F. A diagram for capturing and predicting failure locations in notch geometries produced by additive manufacturing. Int. J. Fatigue 2020, 134, 105428. [Google Scholar] [CrossRef]
- Rao, P.K.; Liu, J.P.; Roberson, D.; Kong, Z.J.; Williams, C. Online Real-Time Quality Monitoring in Additive Manufacturing Processes Using Heterogeneous Sensors. J. Manuf. Sci. Eng. 2015, 137, 061007. [Google Scholar] [CrossRef]
- Everton, S.K.; Hirsch, M.; Stravroulakis, P.; Leach, R.K.; Clare, A.T. Review of in-situ process monitoring and in-situ metrology for metal additive manufacturing. Mater. Des. 2016, 95, 431–445. [Google Scholar] [CrossRef]
- Lednev, V.N.; Sdvizhenskii, P.A.; Asyutin, R.D.; Tretyakov, R.S.; Grishin, M.Y.; Stavertiy, A.Y.; Fedorov, A.N.; Pershin, S.M. In situ elemental analysis and failures detection during additive manufacturing process utilizing laser induced breakdown spectroscopy. Opt. Express 2019, 27, 4612–4628. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi-Tabasi, H.; de Formanoir, C.; Van Petegem, S.; Jhabvala, J.; Hocine, S.; Boillat, E.; Sohrabi, N.; Marone, F.; Grolimund, D.; Van Swygenhoven, H.; et al. Direct observation of crack formation mechanisms with operando Laser Powder Bed Fusion X-ray imaging. Addit. Manuf. 2022, 51, 102619. [Google Scholar] [CrossRef]
- Tran, H.T.; Chen, Q.; Mohan, J.; To, A.C. A new method for predicting cracking at the interface between solid and lattice support during laser powder bed fusion additive manufacturing. Addit. Manuf. 2020, 32, 101050. [Google Scholar] [CrossRef]
- Tran, H.T.; Liang, X.; To, A.C. Efficient prediction of cracking at solid-lattice support interface during laser powder bed fusion via global-local J-integral analysis based on modified inherent strain method and lattice support homogenization. Addit. Manuf. 2020, 36, 101590. [Google Scholar] [CrossRef]
- Lee, Y.; Kirka, M.; Ferguson, J.; Paquit, V. Correlations of cracking with scan strategy and build geometry in electron beam powder bed additive manufacturing. Addit. Manuf. 2020, 32, 101031. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J. Finite element simulation and experimental validation of distortion and cracking failure phenomena in direct metal laser sintering fabricated component. Addit. Manuf. 2017, 16, 49–57. [Google Scholar] [CrossRef]
- Bresson, Y.; Tongne, A.; Selva, P.; Arnaud, L. Numerical modelling of parts distortion and beam supports breakage during selective laser melting (SLM) additive manufacturing. Int. J. Adv. Manuf. Technol. 2022, 119, 5727–5742. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I-Yield Criteria and Flow Rules for Porous Ductile Media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Tvergaard, V. Influence of void nucleation on ductile shear fracture at a free surface. J. Mech. Phys. Solids 1982, 30, 399–425. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Jiang, W.; Duan, M.; Chen, D.; Li, B. Ductile fracture prediction of additive manufactured Ti6Al4V alloy based on an extended GTN damage model. Eng. Fract. Mech. 2021, 256, 107989. [Google Scholar] [CrossRef]
- Shafaie, M.; Khademi, M.; Sarparast, M.; Zhang, H. Modified GTN parameters calibration in additive manufacturing of Ti-6Al-4 V alloy: A hybrid ANN-PSO approach. Int. J. Adv. Manuf. Technol. 2022, 123, 4385–4398. [Google Scholar] [CrossRef]
- Sarparast, M.; Shafaie, M.; Babakan, A.M.; Davoodi, M.; Zhang, H. Investigation of ANN structure on predicting the fracture behavior of additively manufactured Ti-6Al-4V alloys. arXiv 2023. [Google Scholar] [CrossRef]
- Bayerlein, F. Managing Form Deviations in Laser Beam Melting by Pre-Deformation. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2020. [Google Scholar]
- Zhang, B.; Wang, P.; Chew, Y.; Wen, Y.; Zhang, M.; Wang, P.; Bi, G.; Wei, J. Mechanical properties and microstructure evolution of selective laser melting Inconel 718 along building direction and sectional dimension. Mater. Sci. Eng. 2020, 794, 139941. [Google Scholar] [CrossRef]
- McLouth, T.D.; Witkin, D.B.; Lohser, J.R.; Sitzman, S.D.; Adams, P.M.; Lingley, Z.R.; Bean, G.E.; Yang, J.M.; Zaldivar, R.J. Temperature and strain-rate dependence of the elevated temperature ductility of Inconel 718 prepared by selective laser melting. Mater. Sci. Eng. 2021, 824, 141814. [Google Scholar] [CrossRef]
- Lee, J.; Lee, M.; Jung, I.D.; Choe, J.; Yu, J.H.; Kim, S.; Sung, H. Correlation between microstructure and tensile properties of STS 316L and Inconel 718 fabricated by selective laser melting (SLM). J. Nanosci. Nanotechnol. 2020, 20, 6807–6814. [Google Scholar] [CrossRef]
- Purtscher, P. Micromechanisms of ductile fracture and fracture toughness in a high-strength austenitic steel. In At Low Temperatures-XIII; Colorado School of Mines, Arthur Lakes Library: Boulder, CO, USA, 1990; p. 95. [Google Scholar]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- d’Escatha, Y.; Devaux, J. Numerical study of initiation, stable crack growth, and maximum load, with a ductile fracture criterion based on the growth of holes. In Elastic-Plastic Fracture; ASTM International: West Conshohocken, PA, USA, 1979. [Google Scholar]
- Hancock, J.; Mackenzie, A. On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states. J. Mech. Phys. Solids 1976, 24, 147–160. [Google Scholar] [CrossRef]
- Fischer, F.D.; Kolednik, O.; Shan, G.; Rammerstorfer, F. A note on calibration of ductile failure damage indicators. Int. J. Fract. 1995, 73, 345–357. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. In Engineering Fracture Mechanics; Elsevier: Amsterdam, The Netherlands, 1985; Volume 21, pp. 31–48. [Google Scholar]
- Bao, Y. Prediction of Ductile Crack Formation in Uncracked Bodies. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Wierzbicki, T.; Bao, Y.; Lee, Y.W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Bai, Y. Effect of Loading History on Necking and Fracture. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Murugesan, M.; Jung, D.W. Johnson cook material and failure model parameters estimation of AISI-1045 medium carbon steel for metal forming applications. Materials 2019, 12, 609. [Google Scholar] [CrossRef] [PubMed]
- Ressa, A. Plastic Deformation and Ductile Fracture Behavior of Inconel 718. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 2015. [Google Scholar]
- Liutkus, T.J. Digital Image Correlation in Dynamic Punch Testing and Plastic Deformation Behavior of Inconel 718. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 2014. [Google Scholar]
- Bridgman, P.W. Studies in Large Plastic Fracture; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- Choung, J.; Cho, S. Study on true stress correction from tensile tests. J. Mech. Sci. Technol. 2008, 22, 1039–1051. [Google Scholar] [CrossRef]
- Pottlacher, G.; Hosaeus, H.; Kaschnitz, E.; Seifter, A. Thermophysical properties of solid and liquid Inconel 718 Alloy. Scand. J. Metall. 2002, 31, 161–168. [Google Scholar] [CrossRef]
- Gebhardt, C. Praxisbuch FEM mit ANSYS Workbench; Carl Hanser Verlag: München, Germany, 2014. [Google Scholar]
- Dhondt, G. CalculiX CrunchiX USER’S MANUAL Version 2.16. 2019. Available online: http://www.dhondt.de/ccx_2.16.pdf (accessed on 22 November 2023).
- Wang, Z.; Guan, K.; Gao, M.; Li, X.; Chen, X.; Zeng, X. The microstructure and mechanical properties of deposited-IN718 by selective laser melting. J. Alloys Compd. 2012, 513, 518–523. [Google Scholar] [CrossRef]
- Strößner, J.; Terock, M.; Glatzel, U. Mechanical and microstructural investigation of nickel-based superalloy IN718 manufactured by selective laser melting (SLM). Adv. Eng. Mater. 2015, 17, 1099–1105. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]

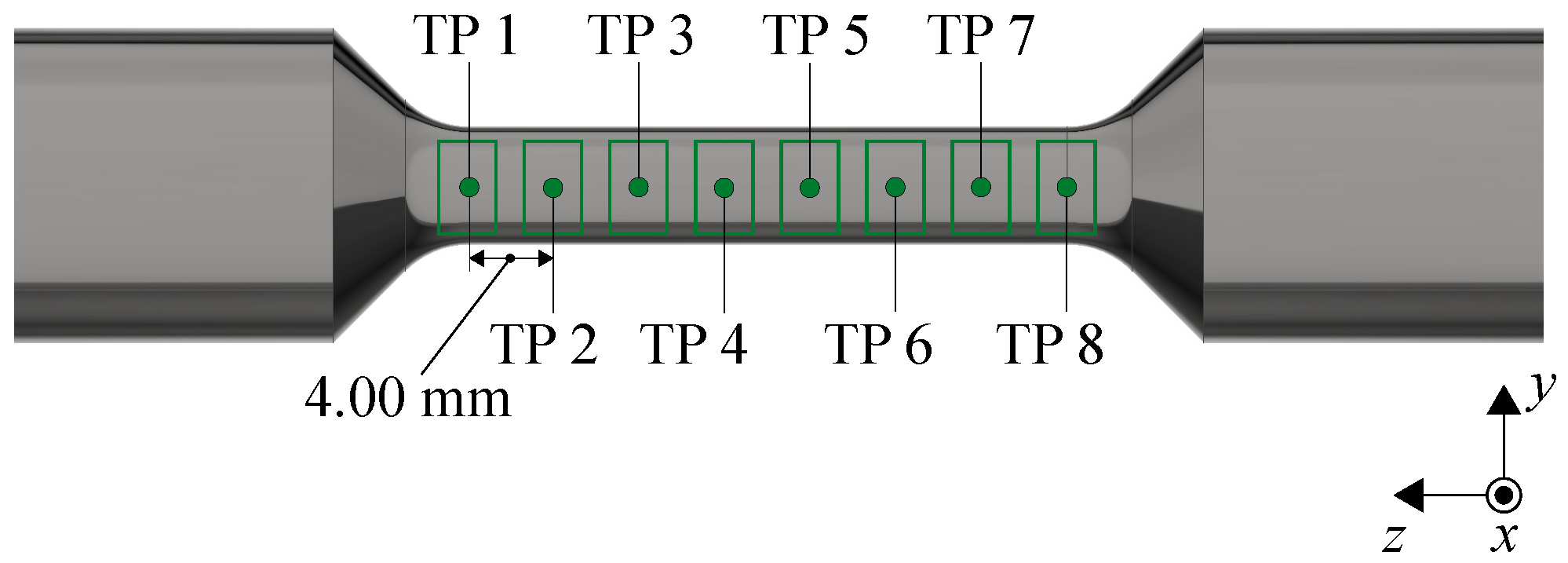
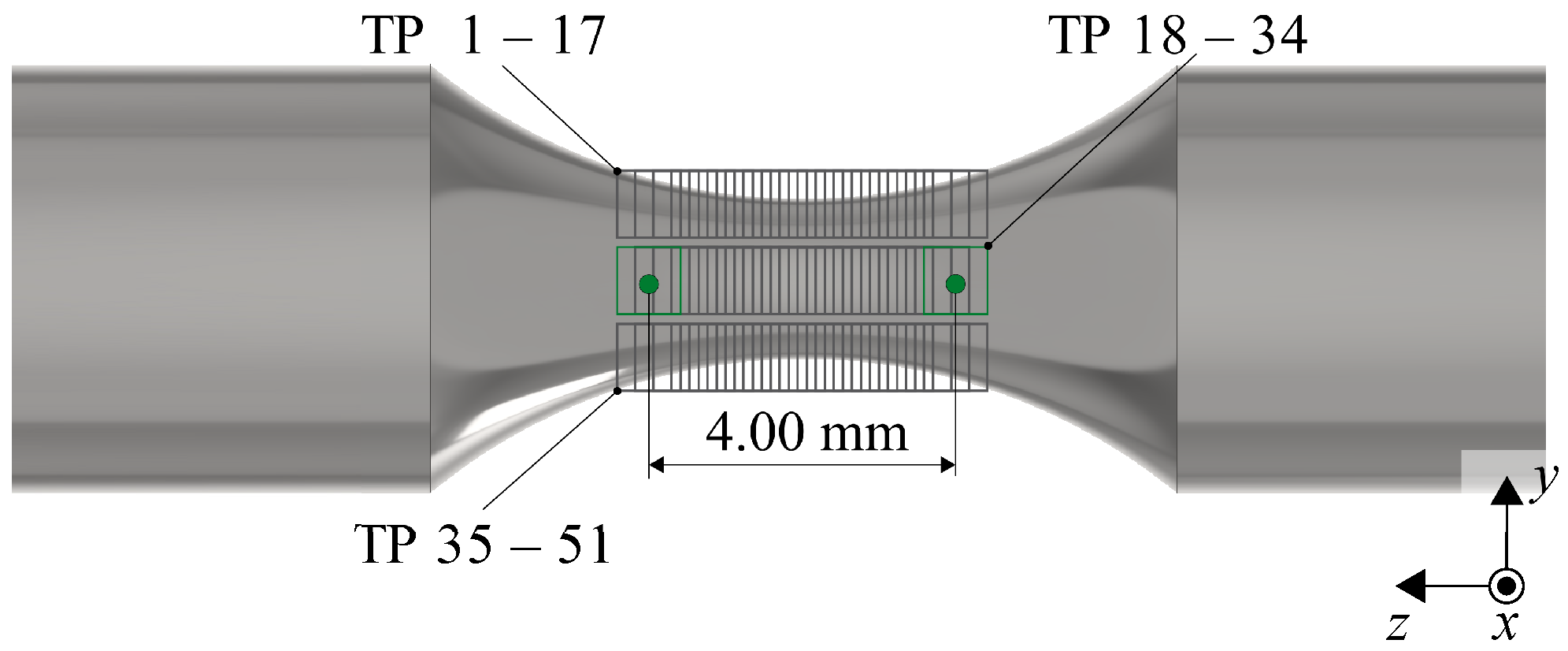
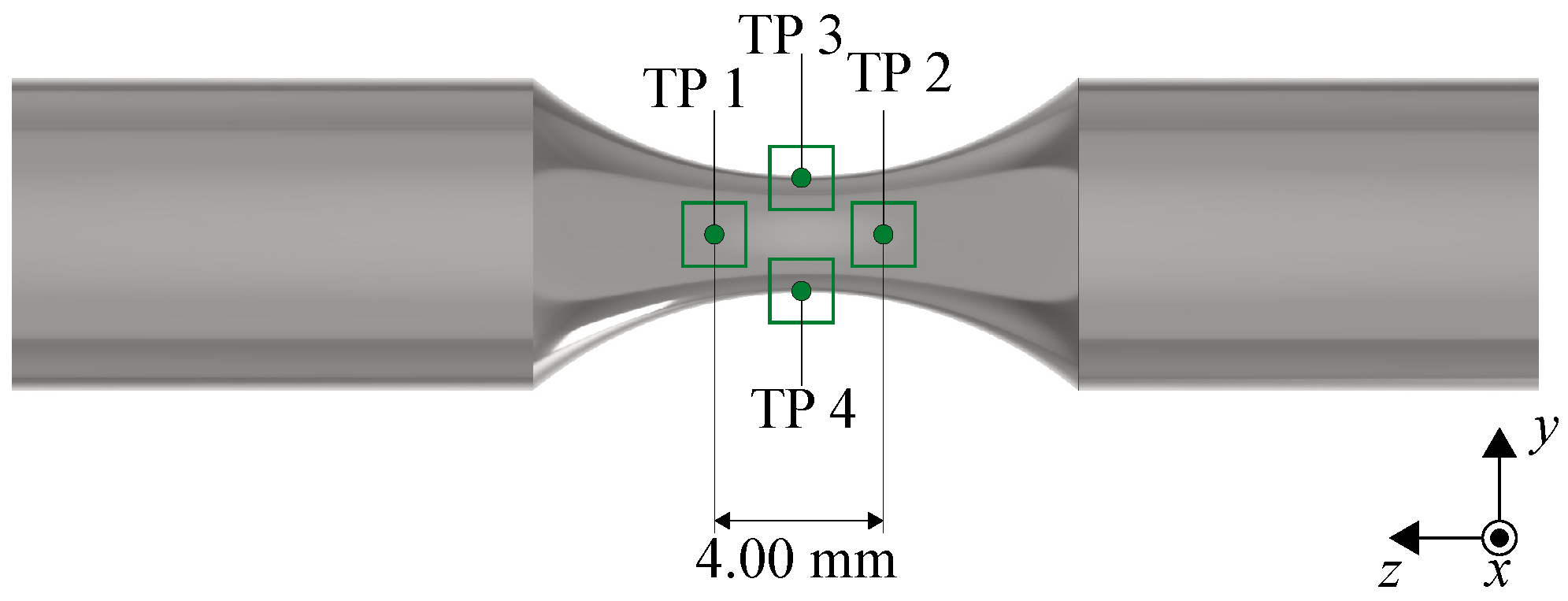
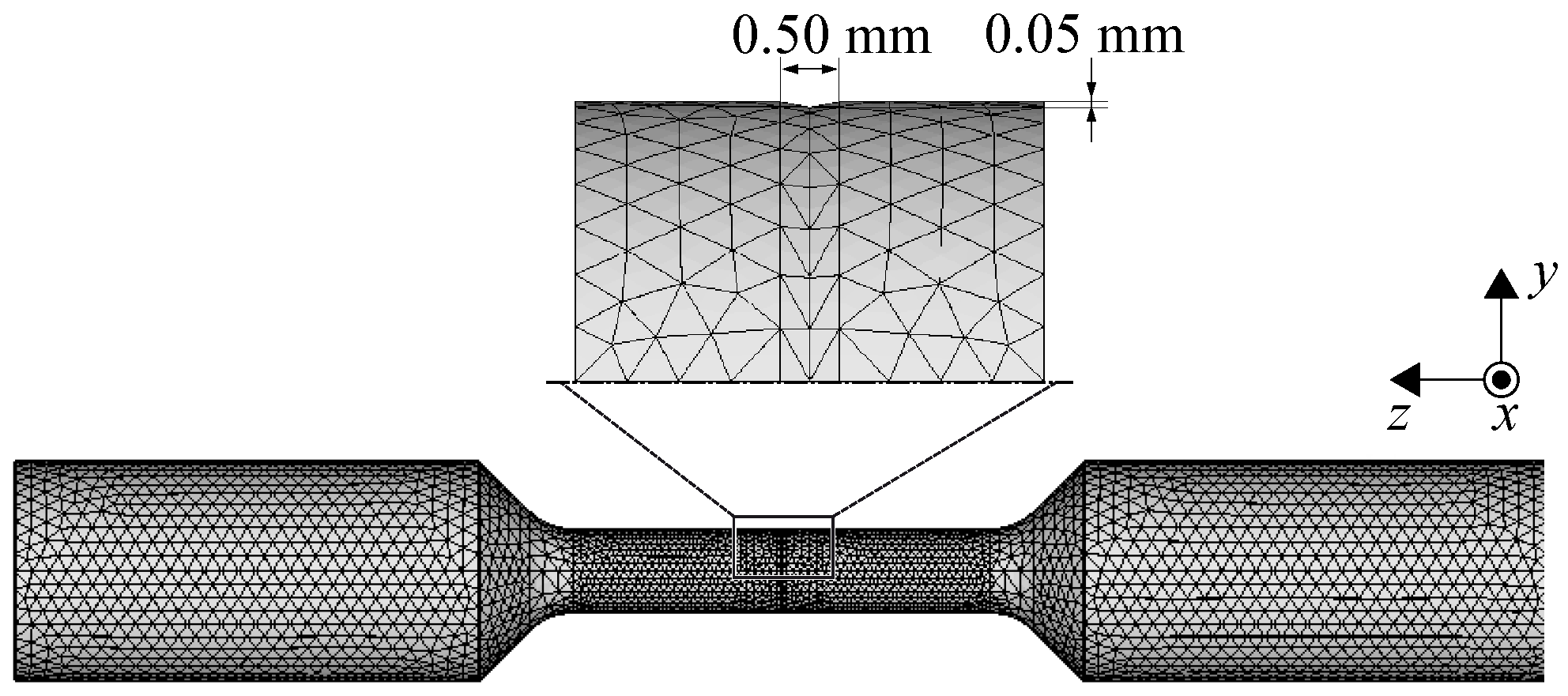
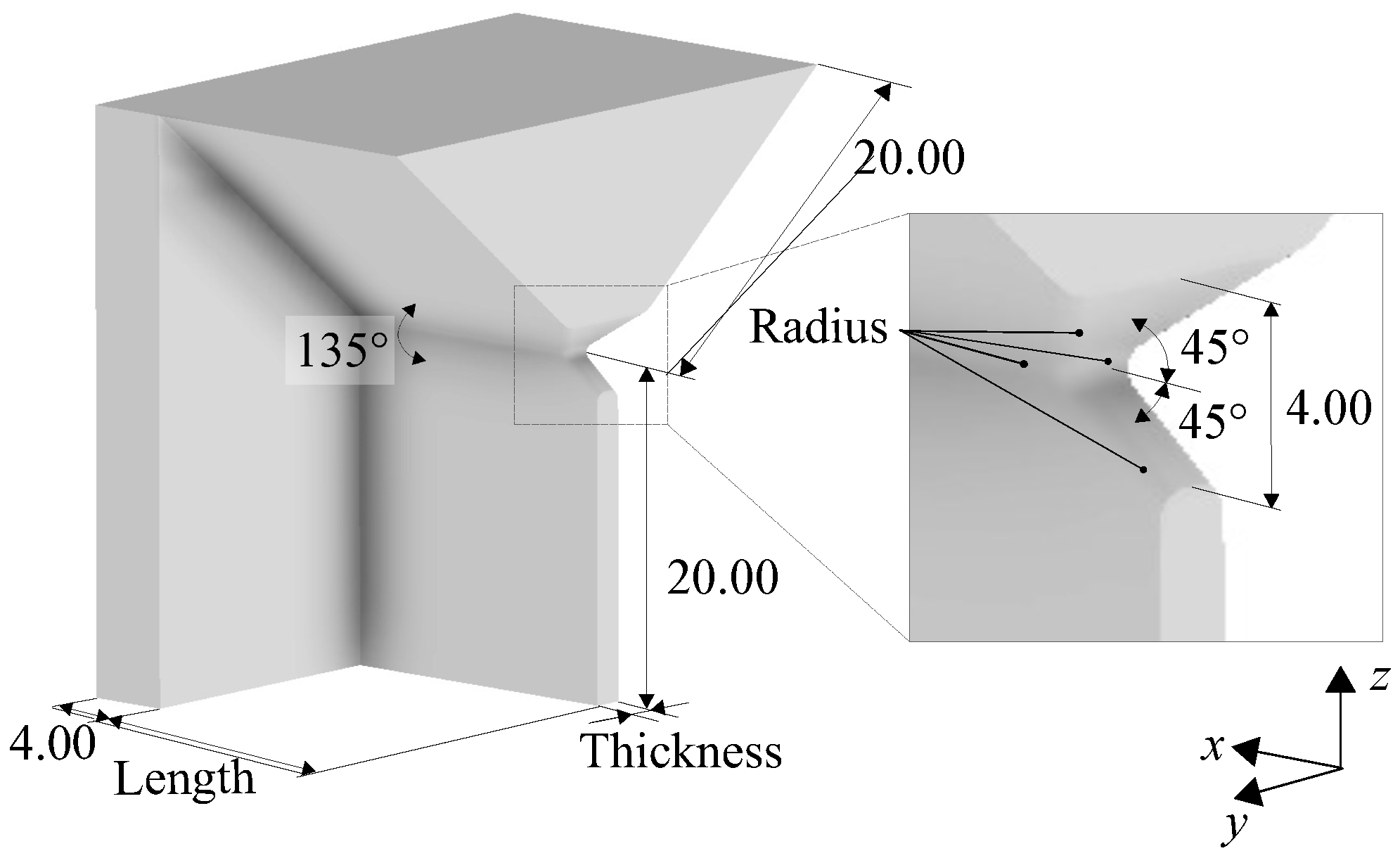



| Parameter | Laser Power | Scan Speed | Hatch Distance | Layer Height |
|---|---|---|---|---|
| Value | 285 W | 960 mm/s | 0.11 mm | 0.04 mm |
| No. | Specimen Type | Description | Reference | |
|---|---|---|---|---|
| 1 | Specimen 1 | Round, smooth (axisymmetric) | Modified based on [41,42] | 0.378 |
| 2 | Specimen 2 | Round, notched (axisymmetric) | Based on [41,42], no modifications | 0.562 |
| 3 | Specimen 3 | Round, notched (axisymmetric) | Modified based on [41,42] | 0.768 |
| 2T | Specimen 2T | Round, notched (axisymmetric) | Modified based on [41,42] | 0.562 |
| Name | Length in mm | Thickness in mm | Radius in mm |
|---|---|---|---|
| Specimen A | 20.00 | 3.00 | 0.30 |
| Specimen B | 20.00 | 2.00 | 0.50 |
| Specimen C | 15.00 | 1.50 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panzer, H.; Wolf, D.; Bachmann, A.; Zaeh, M.F. Towards a Simulation-Assisted Prediction of Residual Stress-Induced Failure during Powder Bed Fusion of Metals Using a Laser Beam: Suitable Fracture Mechanics Models and Calibration Methods. J. Manuf. Mater. Process. 2023, 7, 208. https://doi.org/10.3390/jmmp7060208
Panzer H, Wolf D, Bachmann A, Zaeh MF. Towards a Simulation-Assisted Prediction of Residual Stress-Induced Failure during Powder Bed Fusion of Metals Using a Laser Beam: Suitable Fracture Mechanics Models and Calibration Methods. Journal of Manufacturing and Materials Processing. 2023; 7(6):208. https://doi.org/10.3390/jmmp7060208
Chicago/Turabian StylePanzer, Hannes, Daniel Wolf, Andreas Bachmann, and Michael Friedrich Zaeh. 2023. "Towards a Simulation-Assisted Prediction of Residual Stress-Induced Failure during Powder Bed Fusion of Metals Using a Laser Beam: Suitable Fracture Mechanics Models and Calibration Methods" Journal of Manufacturing and Materials Processing 7, no. 6: 208. https://doi.org/10.3390/jmmp7060208
APA StylePanzer, H., Wolf, D., Bachmann, A., & Zaeh, M. F. (2023). Towards a Simulation-Assisted Prediction of Residual Stress-Induced Failure during Powder Bed Fusion of Metals Using a Laser Beam: Suitable Fracture Mechanics Models and Calibration Methods. Journal of Manufacturing and Materials Processing, 7(6), 208. https://doi.org/10.3390/jmmp7060208