Vickers Hardness Mechanical Models and Thermoplastic Polymer Injection-Molded Products’ Static Friction Coefficients
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Injection Molding
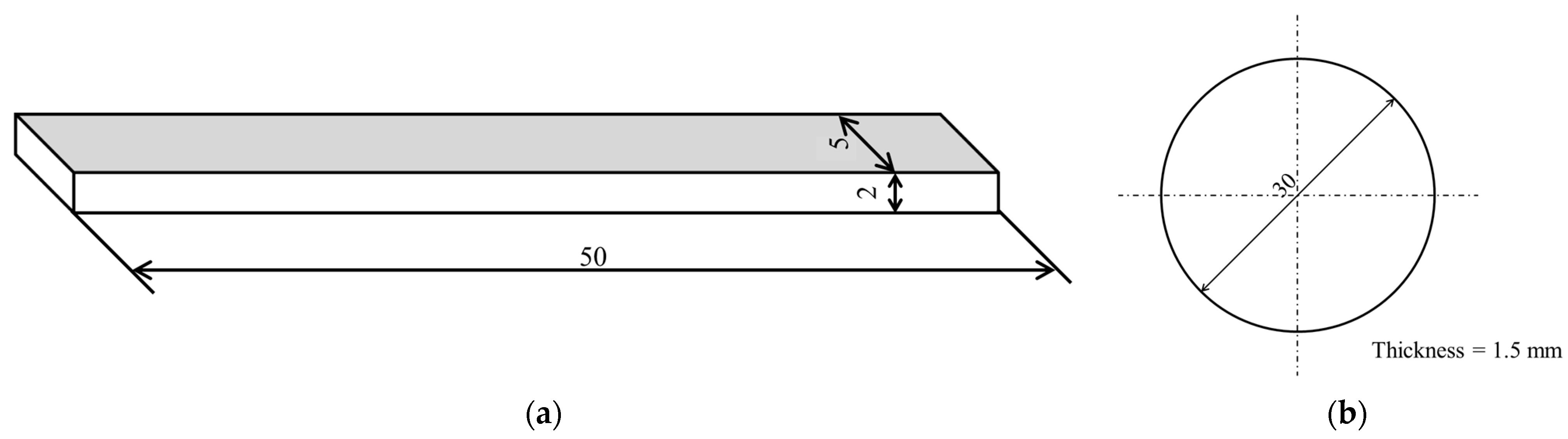
2.3. Three-Point Bending Tests
2.4. Micro Vickers Hardness Testing
2.5. Friction Coefficients at Static Loading
3. Results and Discussion
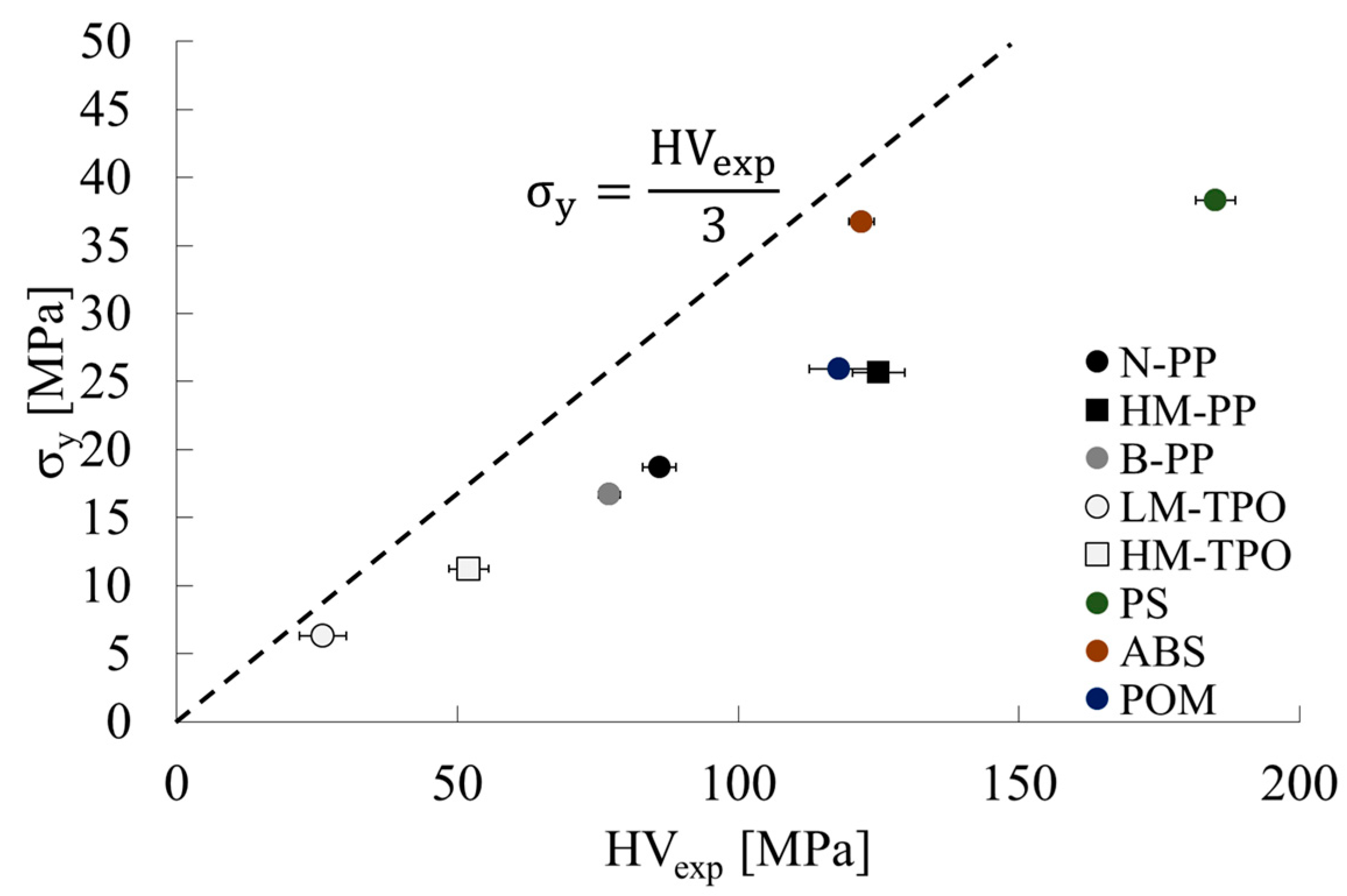
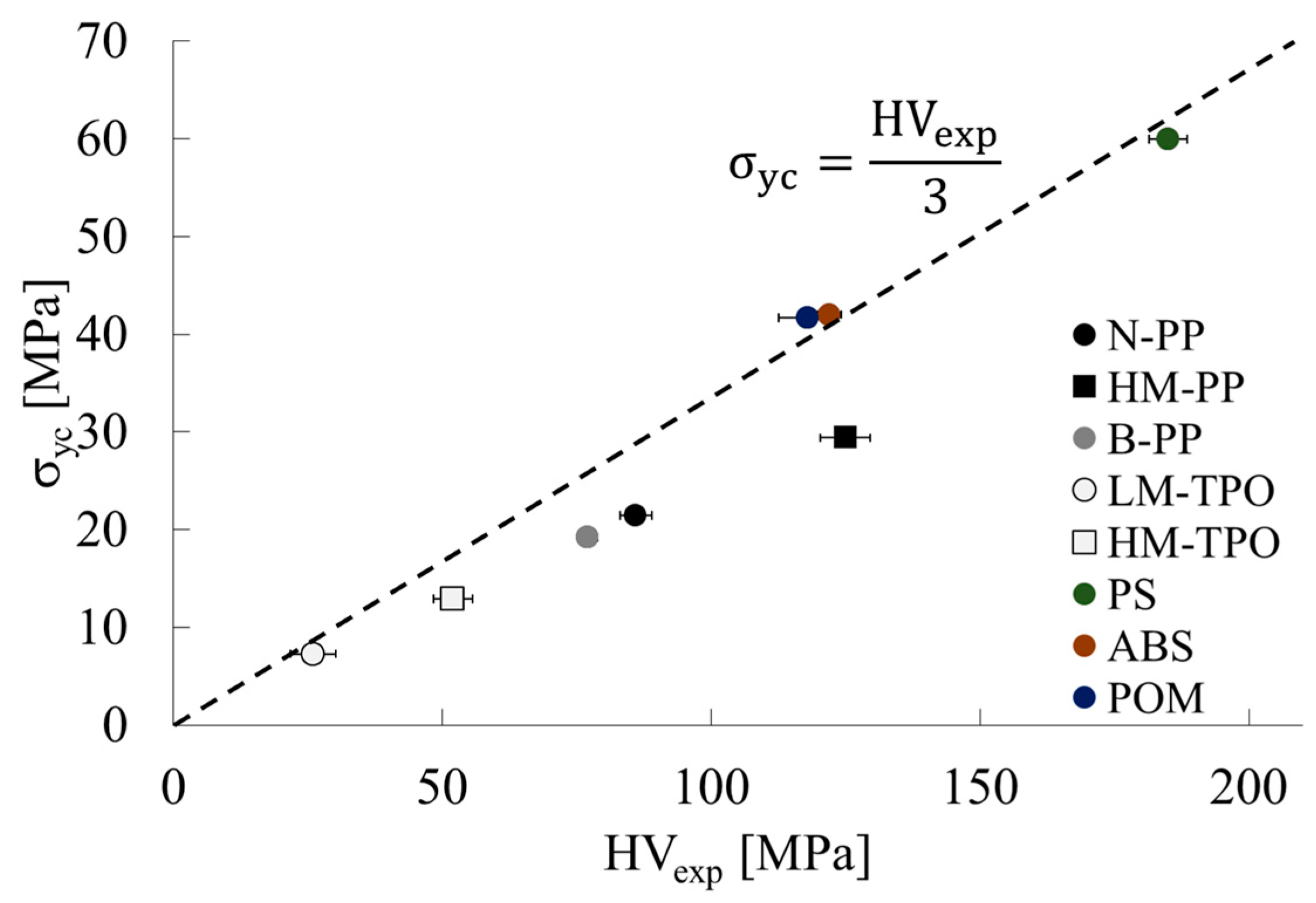
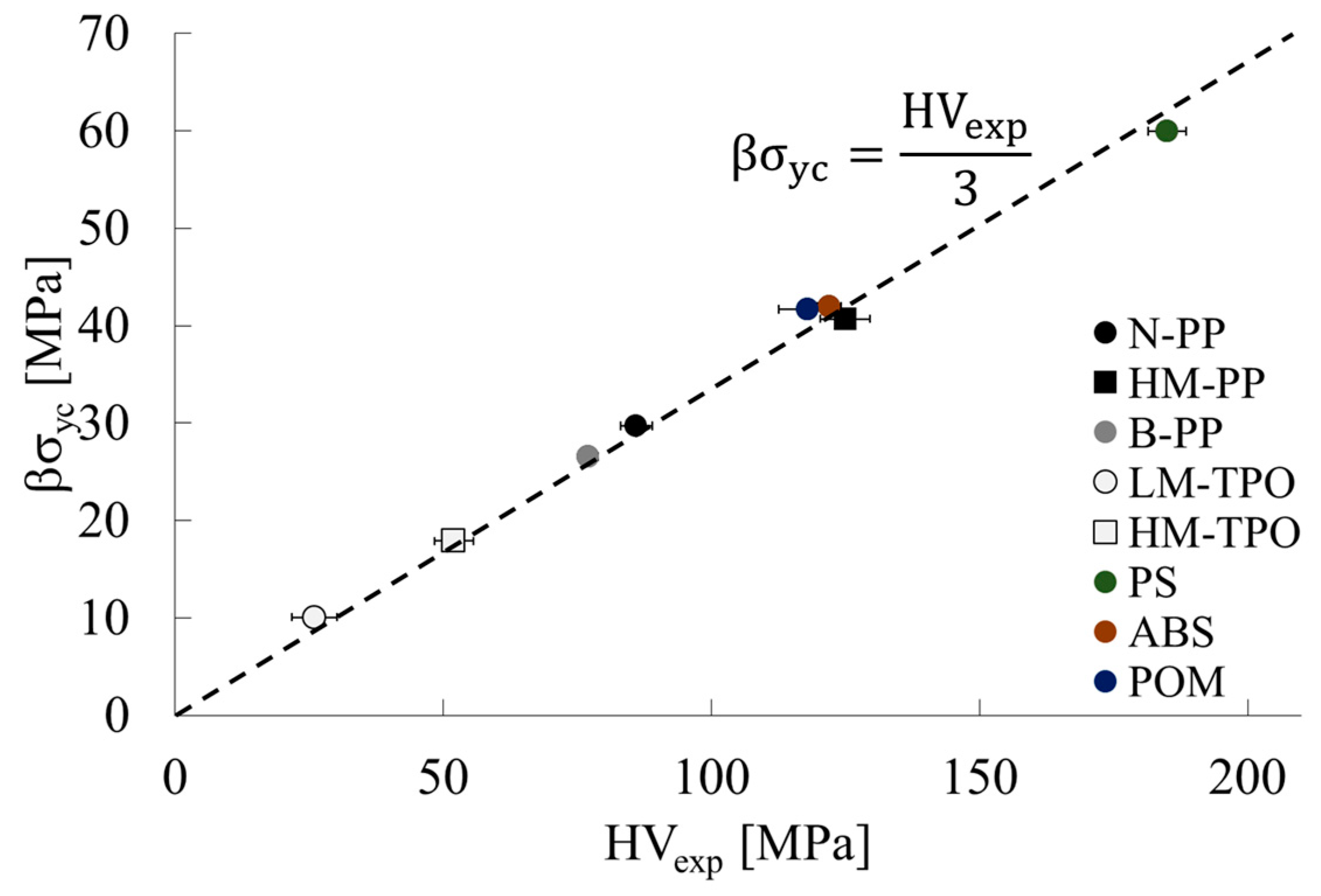
3.1. Correlation between Vickers Hardness and Yield Initiation Stress
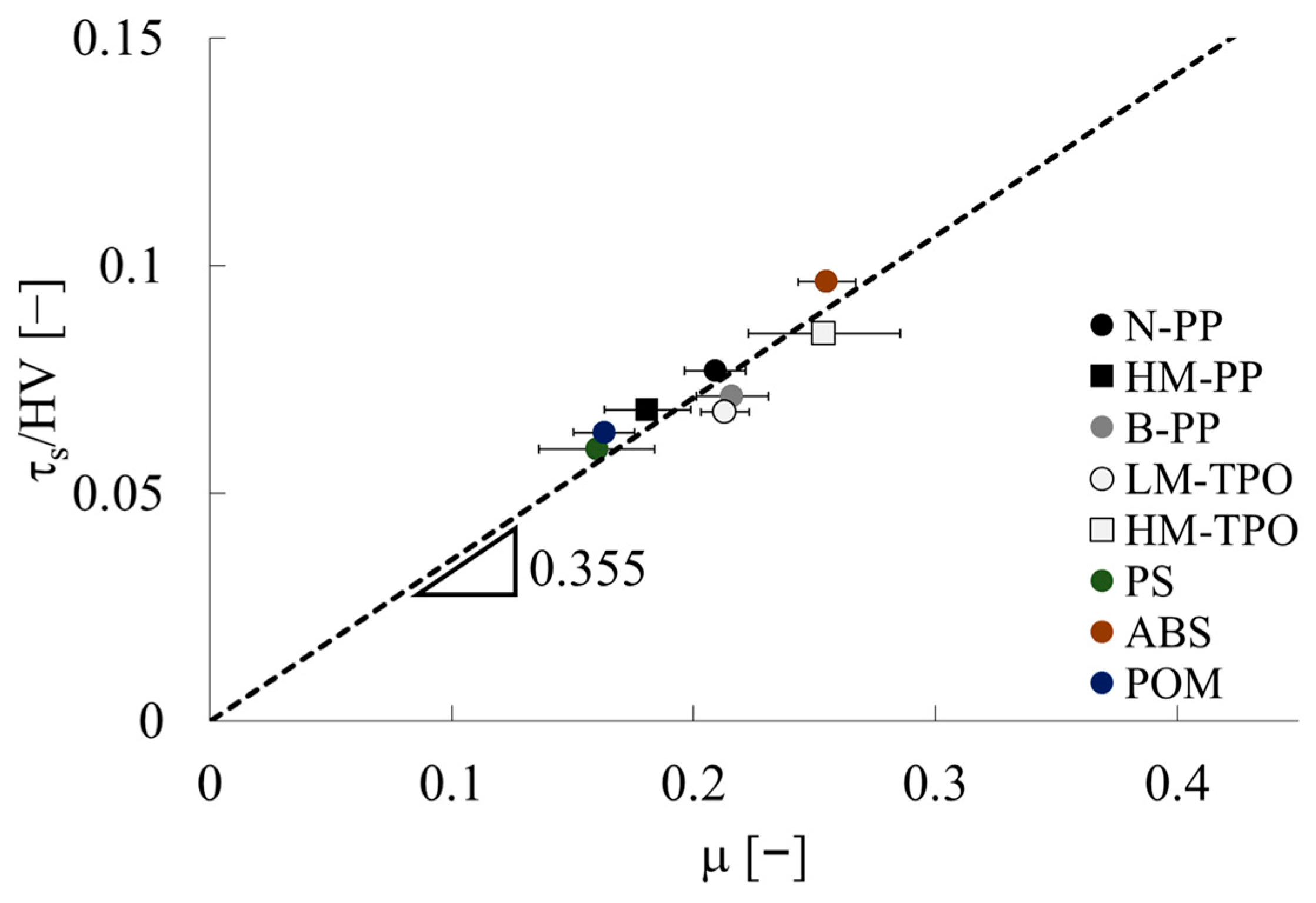
3.2. Mechanical Model for Static Friction Coefficient of Polymeric Materials
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- McCrum, N.G.; Buckley, C.P.; Bucknall, C.B. Principles of Polymer Engineering; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Juster, H.; Aar, B.; Brouwer, H. A Review on Microfabrication of Thermoplastic Polymer-Based Microneedle Arrays. Polym. Eng. Sci. 2019, 59, 877–890. [Google Scholar] [CrossRef]
- Chaudhary, B.; Li, H.; Matos, H. Long-term mechanical performance of 3D printed thermoplastics in seawater environments. Results Mater. 2023, 17, 100381. [Google Scholar] [CrossRef]
- Ge, J.; Luo, M.; Catalanotti, G.; Falzon, B.G.; Higgins, C.; McClory, C.; Thiebot, J.-A.; Zhang, L.; He, M.; Zhang, D.; et al. Process characteristics, damage mechanisms and challenges in machining of fibre reinforced thermoplastic polymer (FRTP) composites: A review. China Plast. 2023, 36, 140–149. [Google Scholar]
- Luque-Agudo, V.; Hierro-Oliva, M.; Gallardo-Moreno, A.M.; González-Martín, M.L. Effect of plasma treatment on the surface properties of polylactic acid films. Polym. Test. 2021, 96, 107097. [Google Scholar] [CrossRef]
- Yan, Y.; Chang, S.; Wang, T.; Geng, Y. Scratch on Polymer Materials Using AFM Tip-Based Approach: A Review. Polymers 2019, 11, 1590. [Google Scholar] [CrossRef] [PubMed]
- Takayama, T.; Takahashi, K. Proposal and verification of a thermoplastic surface shear-strength evaluative method. Polym. Test. 2023, 123, 108049. [Google Scholar] [CrossRef]
- ASTM D785-03; Standard Test Method for Rockwell Hardness of Plastics and Electrical Insulating Materials. ASTM International: West Conshohocken, PA, USA, 2003.
- Borc, J.; Sangwal, K.; Świetlicki, M.; Chocyk, D.; Gładyszewski, G. Vickers microindentation deformation of different cleavage faces of potassium bichromate single crystals: Anisotropy in microhardness and crack formation. Mater. Sci. Eng. A 2020, 790, 139642. [Google Scholar] [CrossRef]
- Wang, X.; Venkataraman, L.K.; Tan, C.; Li, Y. Fracture behavior in electrically poled alkaline bismuth- and potassium- based lead-free piezoceramics using Vickers indentation. Scr. Mater. 2021, 194, 113647. [Google Scholar] [CrossRef]
- Baltá-Calleja, F.J.; Bassett, D.C. Microindentation hardness of oriented chain-extended polyethylene. J. Polym. Sci. Polym. Symp. 1977, 58, 157–167. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Oxford University Press: New York, NY, USA, 1951. [Google Scholar]
- Weiler, W. Härteprüfung an Metallen und Kunststoffen, 2nd ed.; Expert Verlag: Ehningen, Germany, 1990. [Google Scholar]
- Flores, A.; Baltá Calleja, F.J.; Attenburrow, G.E.; Bassett, D.C. Microhardness studies of chain-extended PE: III. Correlation with yield stress and elastic modulus. Polymer 2000, 41, 5431–5435. [Google Scholar] [CrossRef]
- Bano, S.; Iqbal, T.; Ramzan, N.; Farooq, U. Study of Surface Mechanical Characteristics of ABS/PC Blends Using Nanoindentation. Processes 2021, 9, 637. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, L.; Zhang, P.; Yan, X.; Zhang, K.; Dou, S.; Zhao, J.; Li, Y. Measurement of viscoelastic properties for polymers by nanoindentation. Polym. Test. 2020, 83, 106353. [Google Scholar] [CrossRef]
- Koch, T.; Seidler, S. Correlations Between Indentation Hardness and Yield Stress in Thermoplastic Polymers. Strain 2009, 45, 26–33. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, F.; Deng, H.; Huang, Y.; Li, G.; Fu, Q. Morphology evolution of polymer blends under intense shear during high speed thin-wall injection molding. J. Phys. Chem. B 2017, 8, 6257–6270. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-M.; Yang, W.; Yang, S.; Huang, R.; Yang, M.-B. Morphology-tensile behavior relationship in injection molded poly(ethylene terephthalate)/polyethylene and polycarbonate/polyethylene blends (I) Part I Skin-core Structure. J. Mater. Sci. 2004, 39, 413–431. [Google Scholar] [CrossRef]
- Deng, S.; Payyappilly, S.S.; Huang, Y.; Liu, H. Multiscale simulation of shear-induced mechanical anisotropy of binary polymer blends. RSC Adv. 2016, 6, 41734–41742. [Google Scholar] [CrossRef]
- van Erp, T.B.; Govaert, L.E.; Peters, G.W.M. Mechanical performance of injection-molded poly(propylene): Characterization and Modeling. Macromol. Mater. Eng. 2013, 298, 348–358. [Google Scholar] [CrossRef]
- Guevara-Morales, A.; Figueroa-López, U. Residual stresses in injection molded products. J. Mater. Sci. 2014, 49, 4399–4415. [Google Scholar] [CrossRef]
- Straffelini, G. A simplified approach to the adhesive theory of friction. Wear 2001, 249, 78. [Google Scholar] [CrossRef]
- ISO 178:2019; Plastics—Determination of Flexural Properties. The British Standards Institution: London, UK, 2019.
- Takayama, T.; Motoyama, Y. Injection molding temperature dependence of elastic coefficients obtained using three-point bending tests to ascertain thermoplastic polymer coefficients. Mech. Eng. J. 2021, 8, 20–00414. [Google Scholar] [CrossRef]
- Giraldo-Londoño, O.; Paulino, G.H. A unified approach for topology optimization with local stress constraints considering various failure criteria: Von Mises, Drucker–Prager, Tresca, Mohr–Coulomb, Bresler–Pister and Willam–Warnke. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190861. [Google Scholar] [CrossRef] [PubMed]
- Unger, D.J. Generalized Tresca yield condition as a family of elliptic curves with application to mode I crack problems. Z. Angew. Math. Phys. 2022, 73, 184. [Google Scholar] [CrossRef]
- Ishikawa, M.; Narisawa, I.; Ogawa, H. Criterion for craze nucleation in polycarbonate. J. Polym. Sci. Polym. Phys. Ed. 1977, 36, 1791. [Google Scholar] [CrossRef]
- Comba, A.; Scotti, N.; Maravić, T.; Mazzoni, A.; Carossa, M.; Breschi, L.; Cadenaro, M. Vickers Hardness and Shrinkage Stress Evaluation of Low and High Viscosity Bulk-Fill Resin Composite. Polymers 2020, 12, 1477. [Google Scholar] [CrossRef]


| Material | Code | Manufacturer | Grade |
|---|---|---|---|
| PP | N-PP | Japan Polypropylene Corp., Tokyo, Japan | Novatec-PP MA1B |
| HM-PP | Japan Polypropylene Corp., Tokyo, Japan | Novatec-PP MA3H | |
| B-PP | Japan Polypropylene Corp., Tokyo, Japan | Novatec-PP BC03B | |
| TPO | LM-TPO | Japan Polypropylene Corp., Tokyo, Japan | WELNEX RFG4VA |
| HM-TPO | Japan Polypropylene Corp., Tokyo, Japan | WELNEX RMG06 | |
| PS | PS | Toyo Styrene Co., Ltd., Tokyo, Japan | Toyo Styrene G100 |
| ABS | ABS | Techno Polymer Co., Ltd., Chiba, Japan | TECHNO MUH E1500 |
| POM | POM | Polyplastics Co., Ltd., Tokyo, Japan | DURACON NW-02LW |
| (a) Beam | ||||||
| Code | Tinj [°C] | Tmold [°C] | Vinj [mm/s] | Phold [MPa] | tinj [s] | tcool [s] |
| N-PP | 230 | 50 | 30 | 42 | 10 | 15 |
| HM-PP | 230 | 50 | 30 | 35 | 10 | 15 |
| B-PP | 230 | 50 | 30 | 42 | 10 | 15 |
| LM-TPO | 230 | 50 | 30 | 35 | 10 | 15 |
| HM-TPO | 230 | 50 | 30 | 35 | 10 | 15 |
| PS | 230 | 60 | 30 | 63 | 10 | 15 |
| ABS | 260 | 90 | 30 | 77 | 10 | 15 |
| POM | 230 | 50 | 30 | 84 | 10 | 15 |
| (b) Disk | ||||||
| N-PP | 230 | 50 | 30 | 42 | 10 | 15 |
| HM-PP | 230 | 50 | 30 | 35 | 10 | 15 |
| B-PP | 230 | 50 | 30 | 42 | 10 | 15 |
| LM-TPO | 230 | 50 | 30 | 35 | 10 | 15 |
| HM-TPO | 230 | 50 | 30 | 35 | 10 | 15 |
| PS | 230 | 60 | 30 | 42 | 10 | 15 |
| ABS | 260 | 90 | 30 | 77 | 10 | 15 |
| POM | 230 | 50 | 30 | 91 | 10 | 15 |
| Code | σfy [MPa] | Ef [MPa] | E [MPa] | υ [−] |
|---|---|---|---|---|
| N-PP | 26.3 | 1530 | 678 | 0.407 |
| HM-PP | 35.7 | 2190 | 1096 | 0.391 |
| B-PP | 23.7 | 1570 | 618 | 0.420 |
| LM-TPO | 9.1 | 400 | 120 | 0.442 |
| HM-TPO | 16.0 | 790 | 298 | 0.424 |
| PS | 52.1 | 1940 | 1940 | 0.361 |
| ABS | 50.5 | 2640 | 1470 | 0.374 |
| POM | 35.7 | 1840 | 1000 | 0.378 |
| Code | HVexp [MPa] | σfy [MPa] | υ [−] | σy [MPa] | σyc [MPa] | β [−] | βσyc [MPa] | HVcal [MPa] |
|---|---|---|---|---|---|---|---|---|
| N-PP | 86 (3.0) | 26.3 | 0.407 | 18.7 | 21.5 | 1.384 | 29.7 | 89 |
| HM-PP | 125 (4.6) | 35.7 | 0.391 | 25.7 | 29.4 | 1.384 | 40.7 | 122 |
| B-PP | 77 (1.9) | 23.7 | 0.420 | 16.7 | 19.2 | 1.384 | 26.6 | 79 |
| LM-TPO | 26 (4.2) | 9.1 | 0.442 | 6.3 | 7.3 | 1.384 | 10.1 | 30 |
| HM-TPO | 52 (3.6) | 16.0 | 0.424 | 11.2 | 12.9 | 1.384 | 17.9 | 54 |
| PS | 185 (3.6) | 52.1 | 0.361 | 38.3 | 59.9 | 1.000 | 59.9 | 181 |
| ABS | 122 (2.2) | 50.5 | 0.374 | 36.8 | 42.0 | 1.000 | 42.0 | 125 |
| POM | 118 (5.4) | 35.7 | 0.378 | 25.9 | 41.7 | 1.000 | 41.7 | 123 |
| Code | μ [−] | σfy [MPa] | υ [−] | τys [MPa] | HV [MPa] |
|---|---|---|---|---|---|
| N-PP | 0.209 (0.013) | 26.3 | 0.407 | 6.2 | 81 |
| HM-PP | 0.181 (0.018) | 35.7 | 0.391 | 8.6 | 125 |
| B-PP | 0.216 (0.015) | 23.7 | 0.420 | 5.6 | 78 |
| LM-TPO | 0.213 (0.010) | 9.1 | 0.442 | 2.1 | 31 |
| HM-TPO | 0.254 (0.032) | 16.0 | 0.424 | 3.7 | 44 |
| PS | 0.16 (0.023) | 52.1 | 0.361 | 12.8 | 185 |
| ABS | 0.255 (0.012) | 50.5 | 0.374 | 14.1 | 127 |
| POM | 0.163 (0.013) | 35.7 | 0.378 | 8.6 | 118 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takayama, T. Vickers Hardness Mechanical Models and Thermoplastic Polymer Injection-Molded Products’ Static Friction Coefficients. J. Manuf. Mater. Process. 2024, 8, 11. https://doi.org/10.3390/jmmp8010011
Takayama T. Vickers Hardness Mechanical Models and Thermoplastic Polymer Injection-Molded Products’ Static Friction Coefficients. Journal of Manufacturing and Materials Processing. 2024; 8(1):11. https://doi.org/10.3390/jmmp8010011
Chicago/Turabian StyleTakayama, Tetsuo. 2024. "Vickers Hardness Mechanical Models and Thermoplastic Polymer Injection-Molded Products’ Static Friction Coefficients" Journal of Manufacturing and Materials Processing 8, no. 1: 11. https://doi.org/10.3390/jmmp8010011
APA StyleTakayama, T. (2024). Vickers Hardness Mechanical Models and Thermoplastic Polymer Injection-Molded Products’ Static Friction Coefficients. Journal of Manufacturing and Materials Processing, 8(1), 11. https://doi.org/10.3390/jmmp8010011






