Material Parameter Identification for a Stress-State-Dependent Ductile Damage and Failure Model Applied to Clinch Joining
Abstract
1. Introduction
2. Materials and Methods
2.1. Constitutive Model and Material Parameters
2.2. Experimental Setups
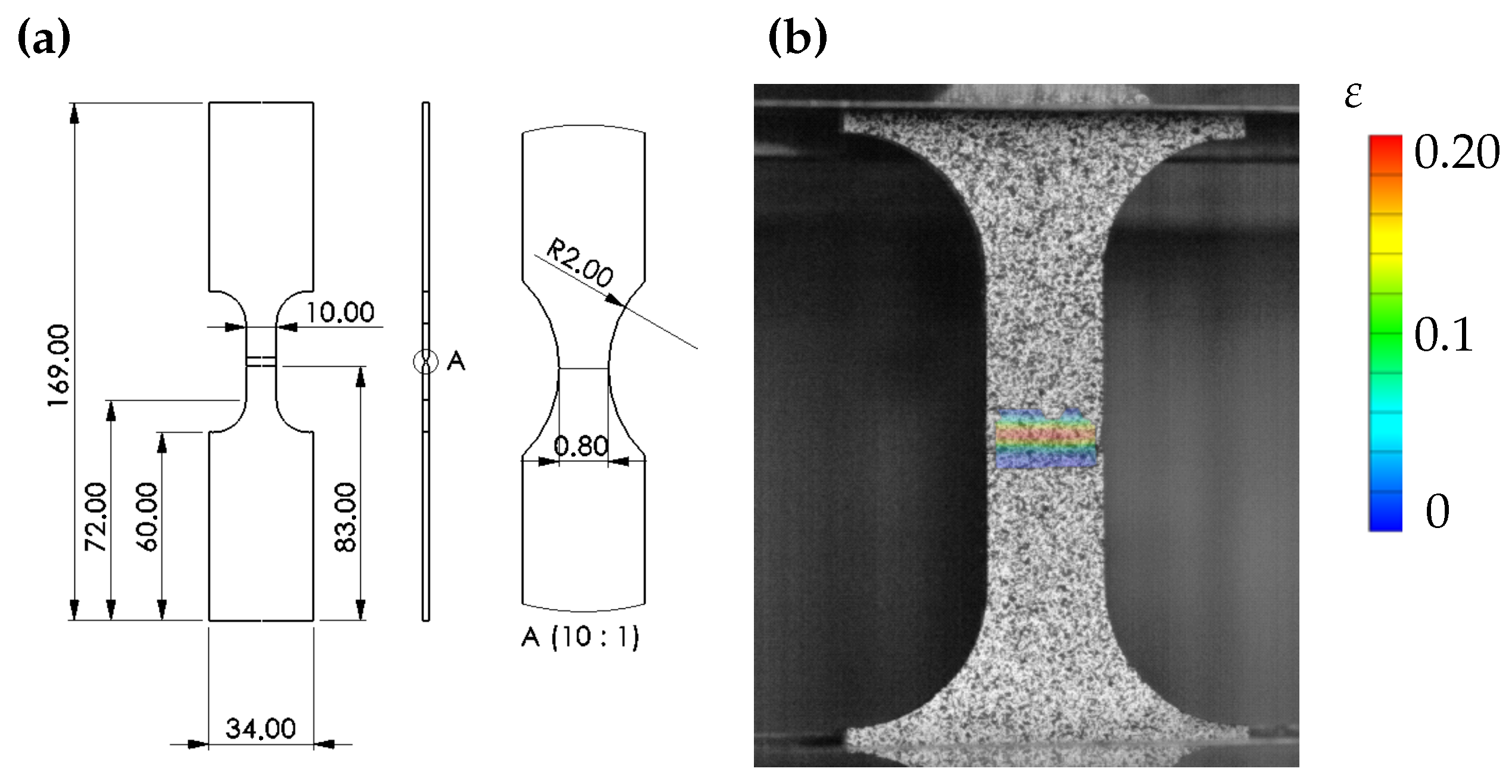
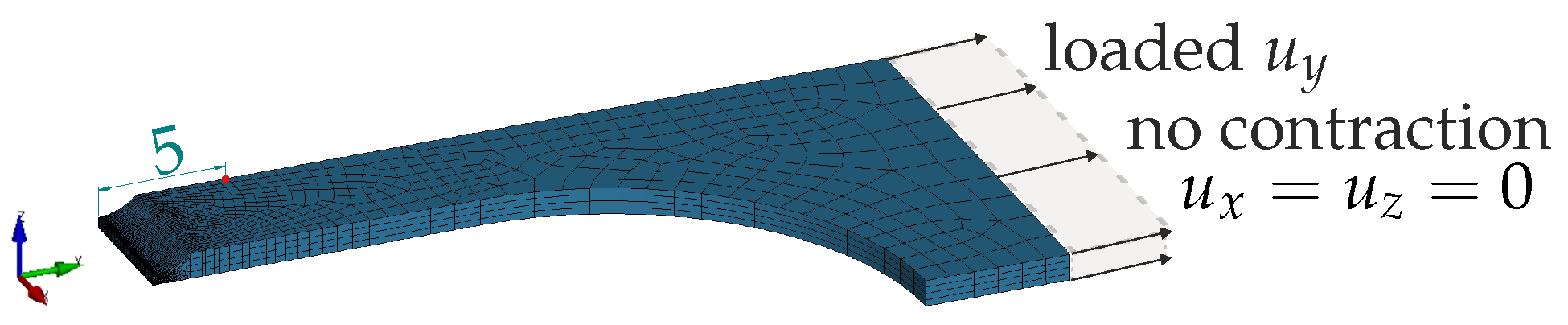
2.2.1. Tensile Tests
2.2.2. Plane-Strain Tensile Test
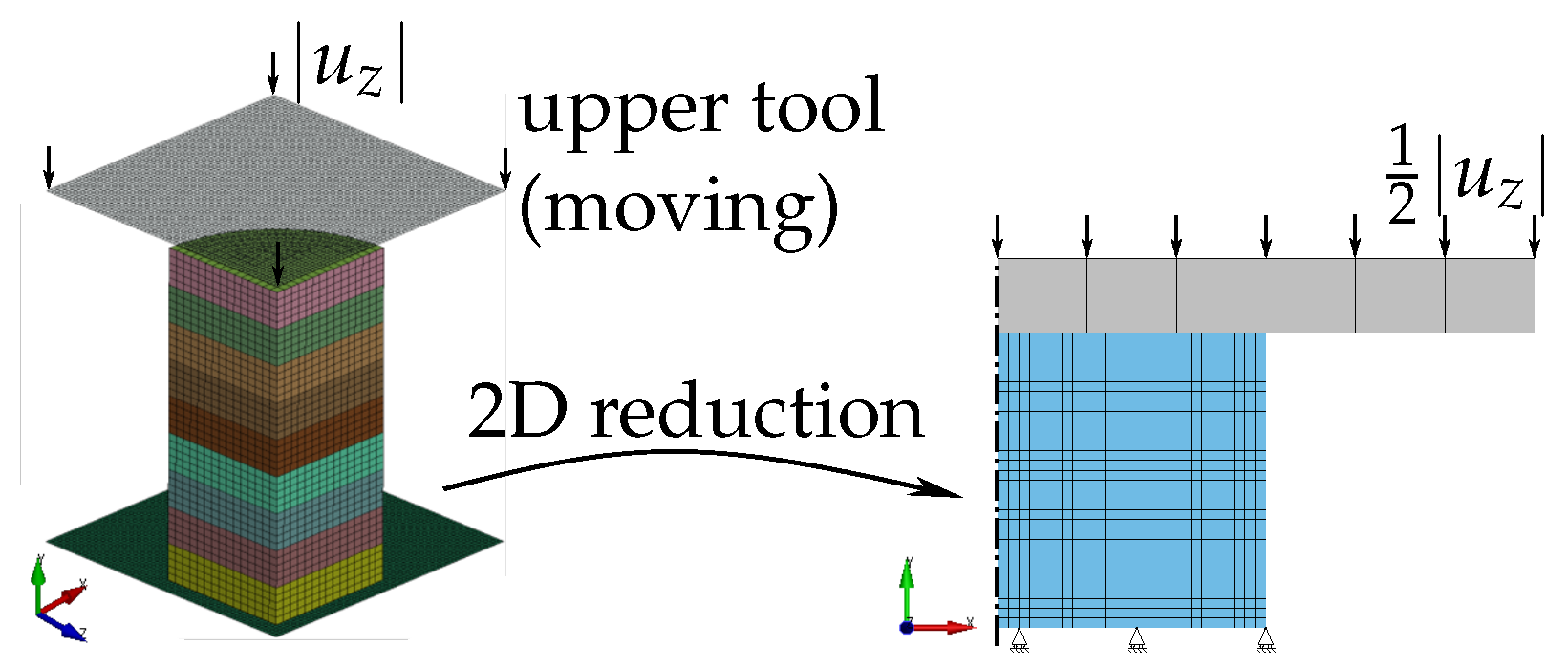
2.2.3. Layer Compression Test
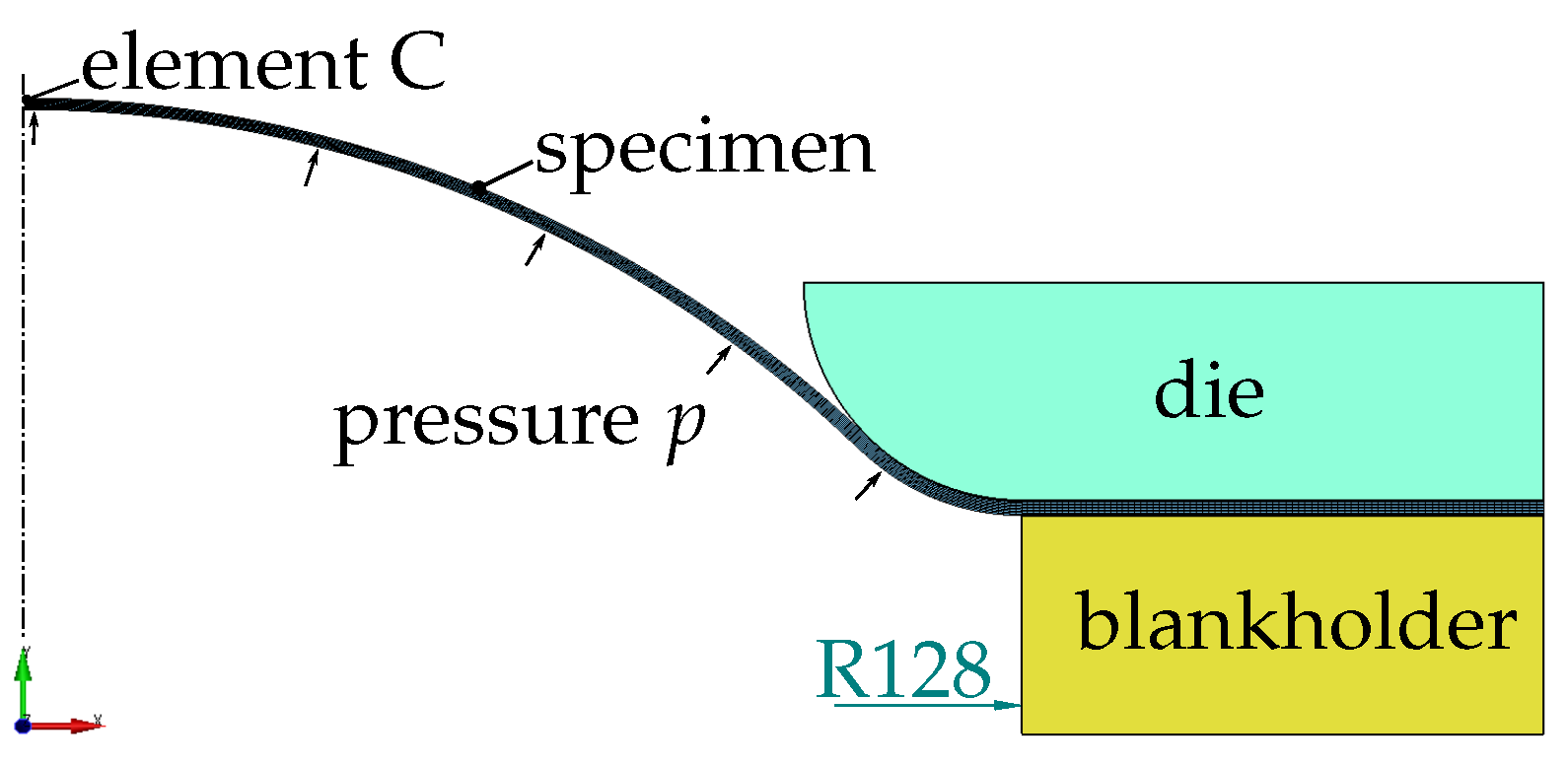
2.2.4. Bulge Test
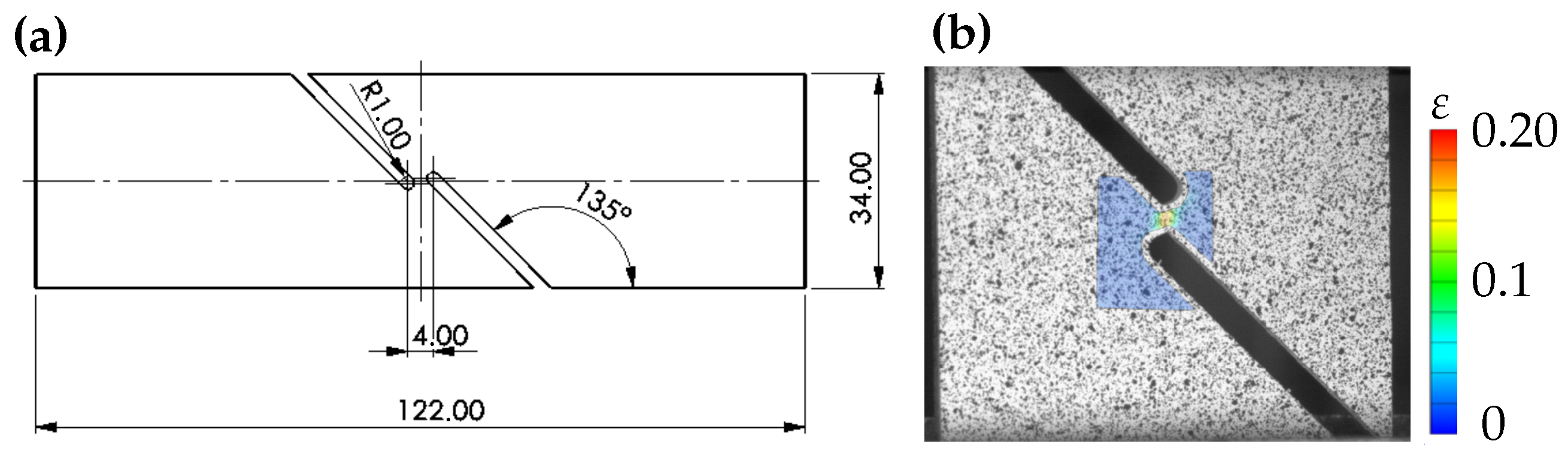
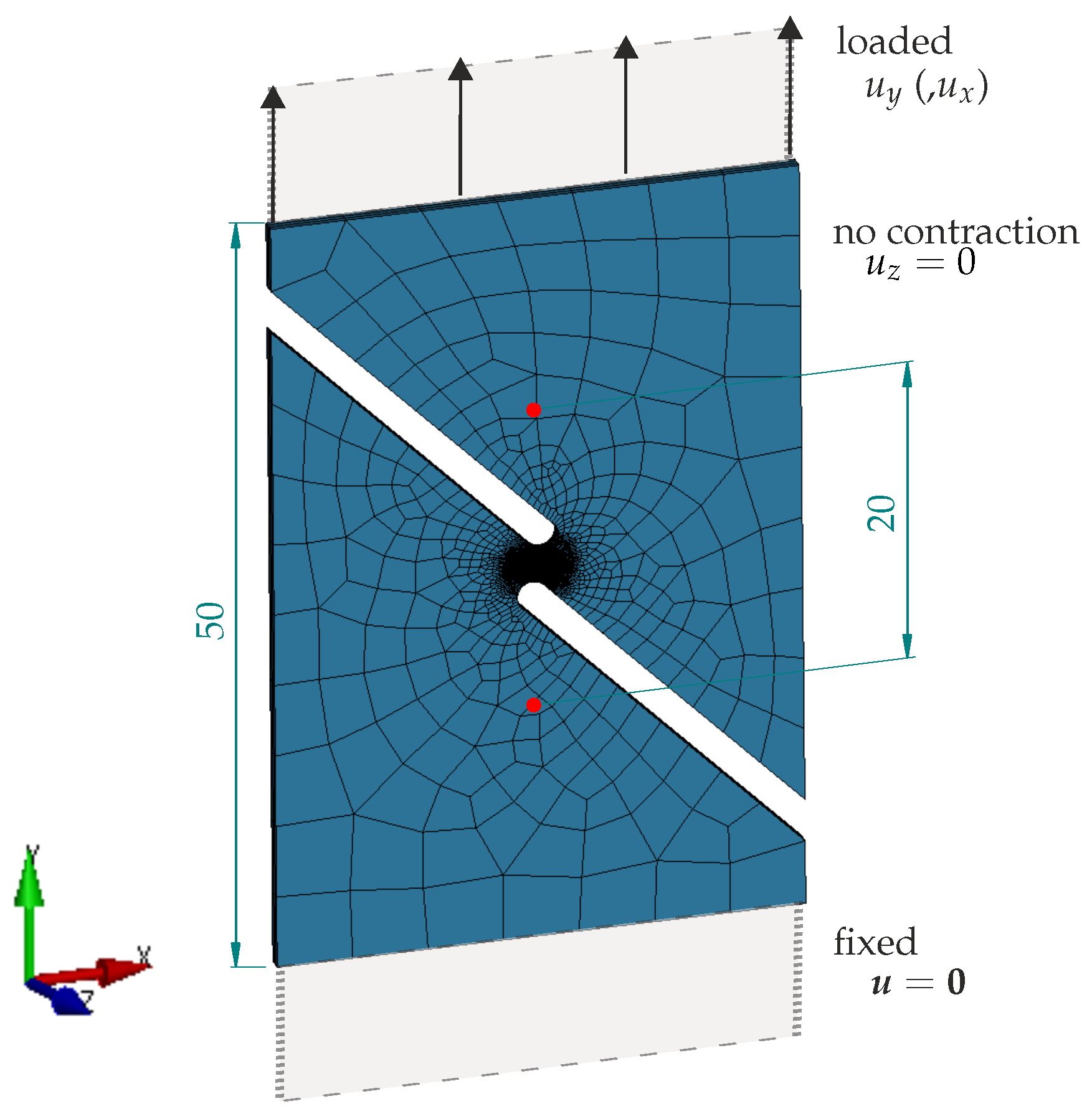
2.2.5. Mini-ASTM Shear Test
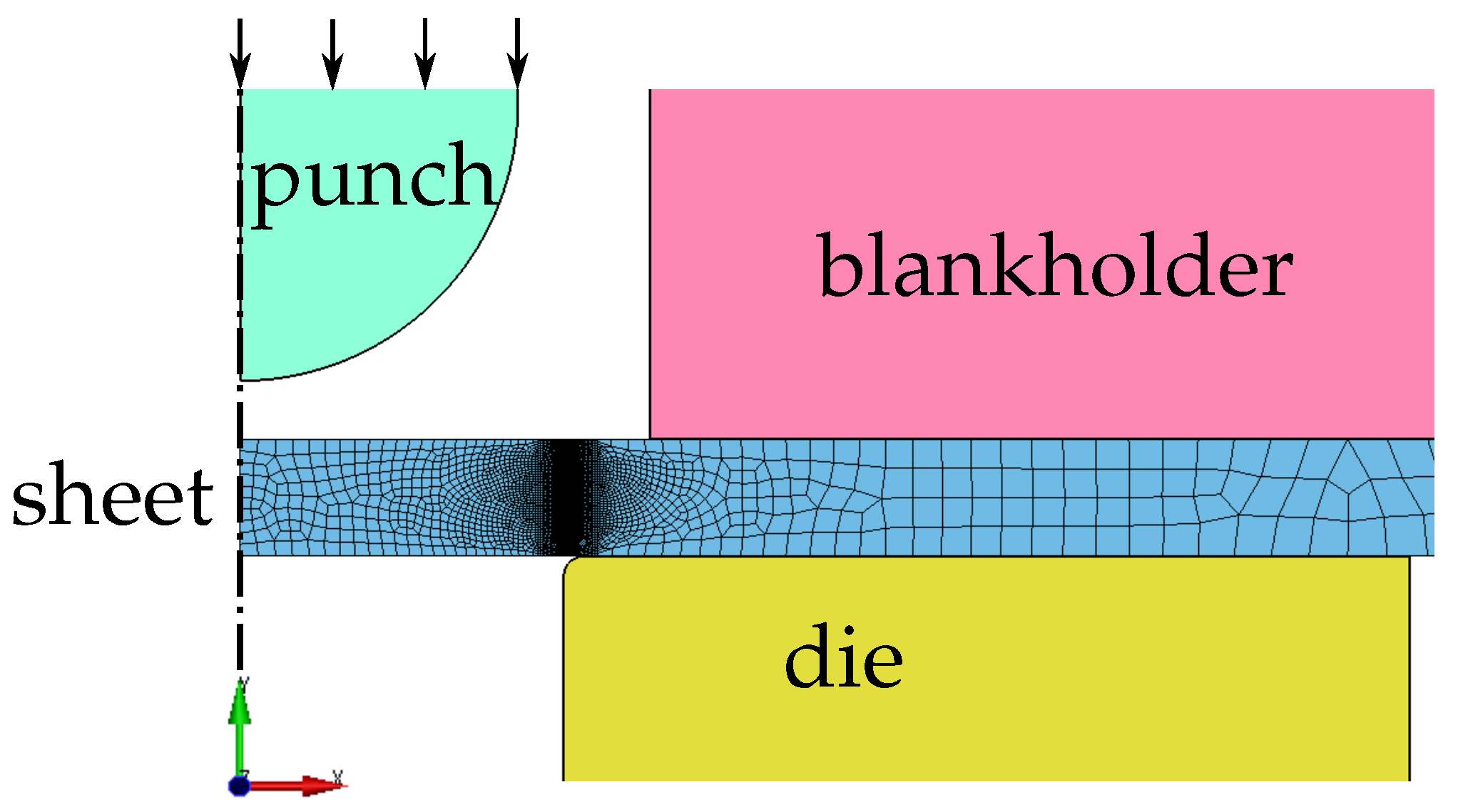
2.2.6. Classical Punch Test
2.2.7. Modified Punch Test
Variants
Experimental Procedure
2.3. Numerical Setups
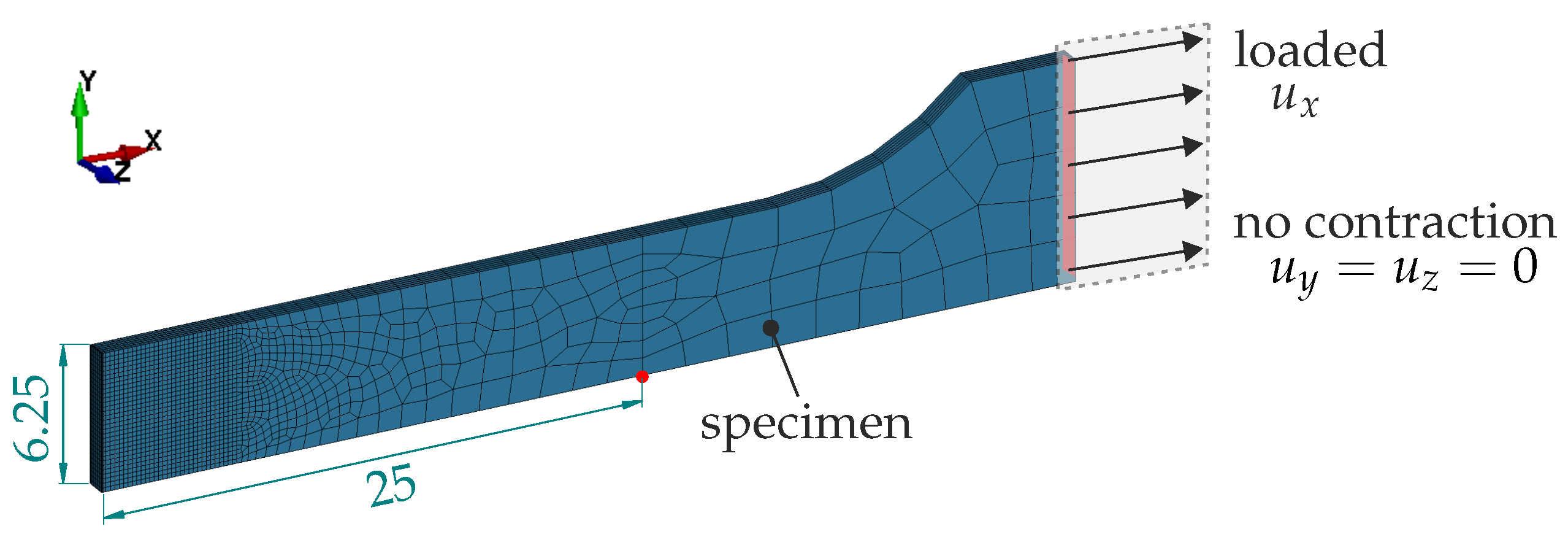
2.3.1. Tensile Tests
2.3.2. Plane-Strain Tensile Test
2.3.3. Layer Compression Test
2.3.4. Bulge Test
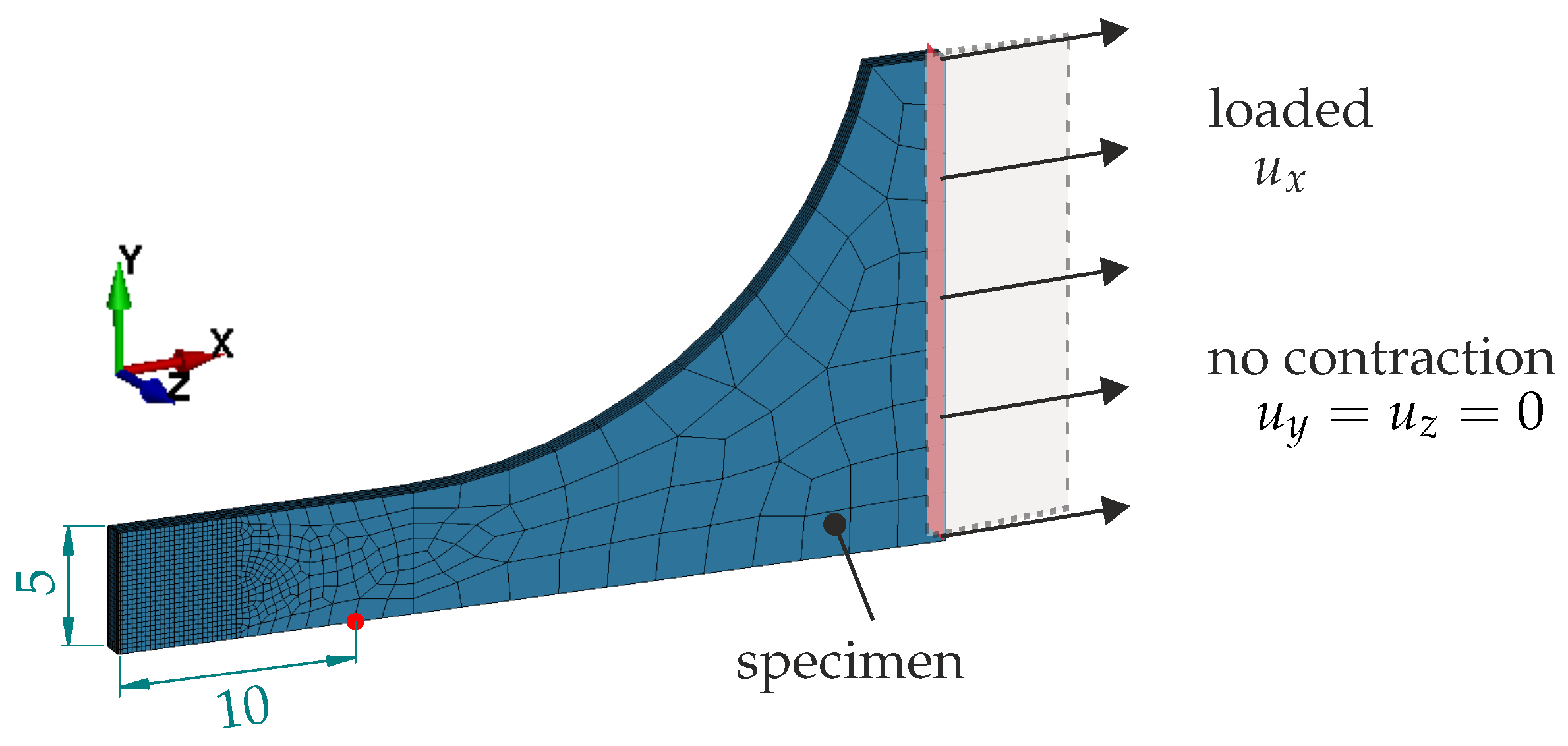
2.3.5. Mini-ASTM Shear Test
2.3.6. Classical Punch Test
2.3.7. Modified Punch Test
2.4. Material Parameter Identification Procedure
3. Results and Discussion
3.1. Dual-Phase Steel HCT590X
3.1.1. Elasticity: LAwave Measurements
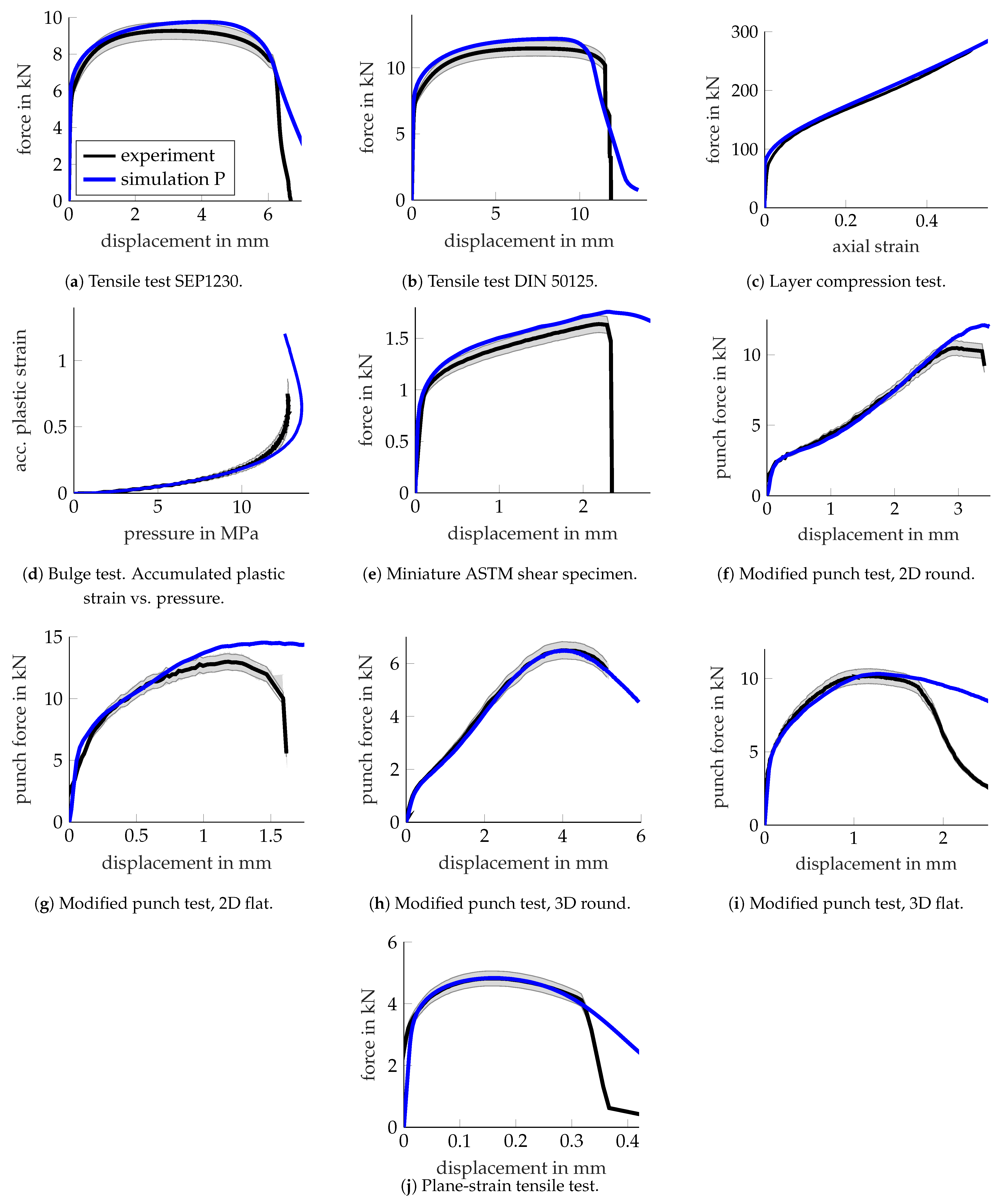
3.1.2. Plasticity: Verification and Limitations
3.1.3. Damage to Failure Mapping
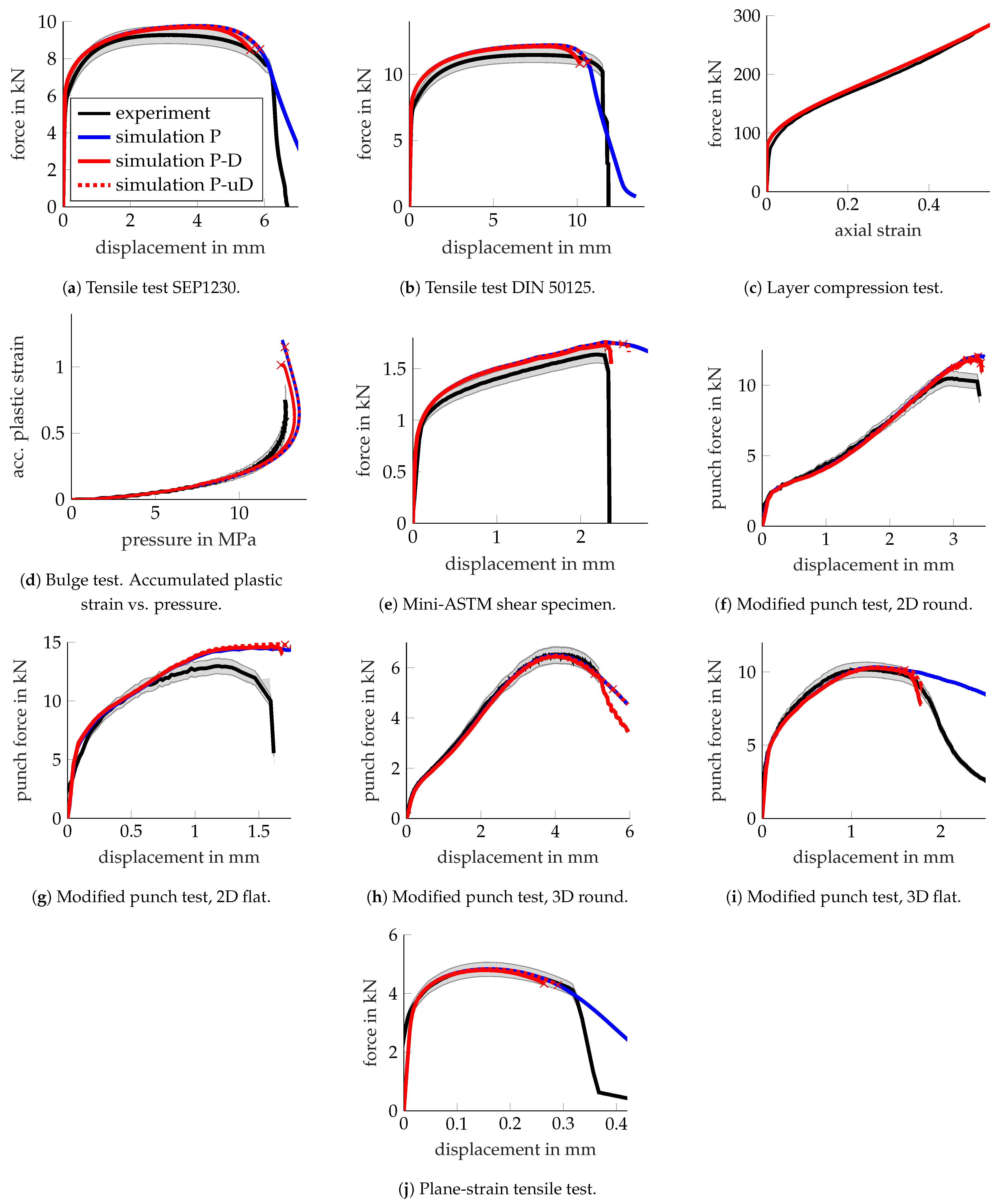
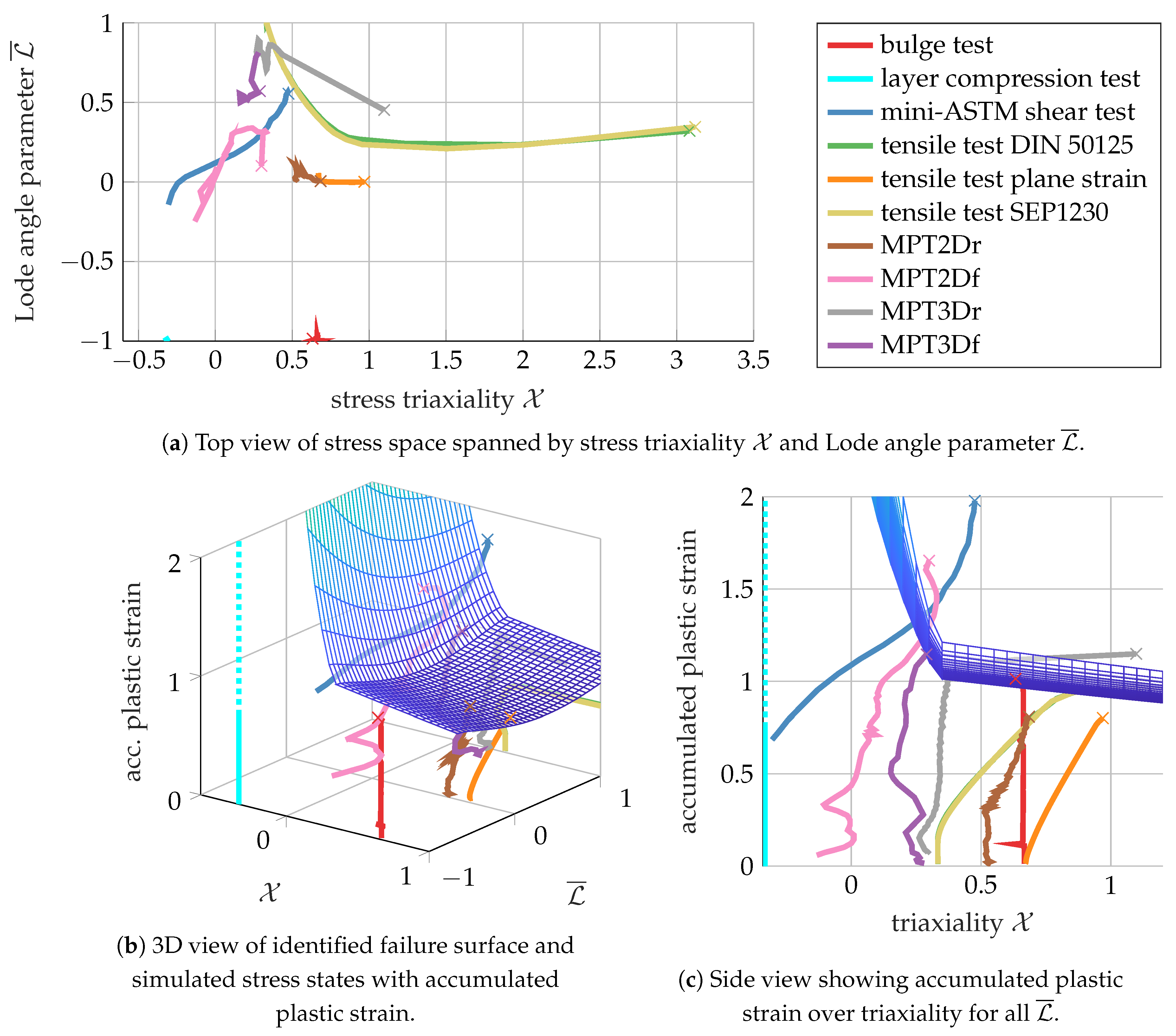
3.1.4. Failure: Inverse Identification
3.2. Aluminium Alloy EN AW-6014 T4
3.2.1. Elasticity: LAwave Measurements
3.2.2. Plasticity: Verification and Limitations
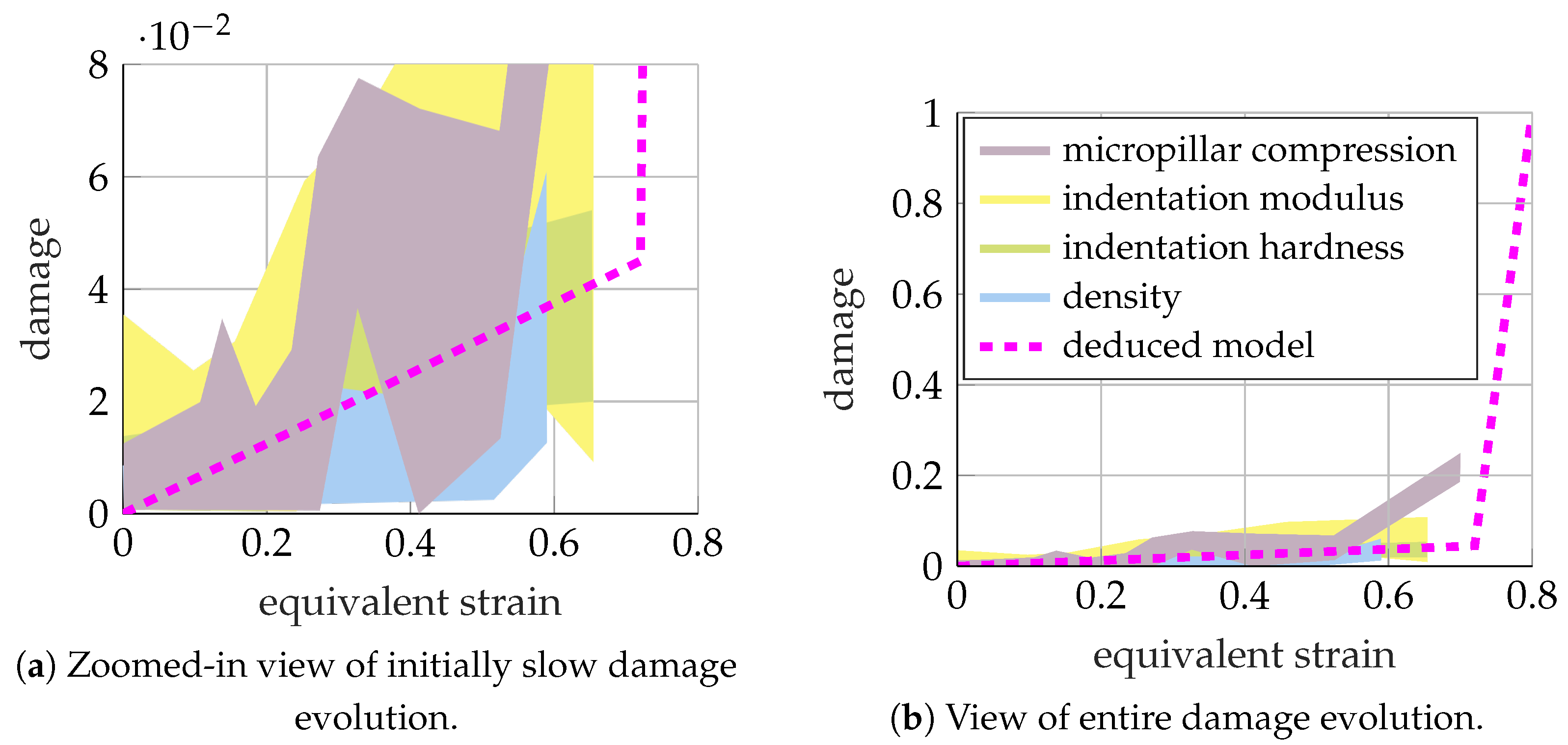
3.2.3. Damage to Failure Mapping: Deduction
3.2.4. Failure: Inverse Identification
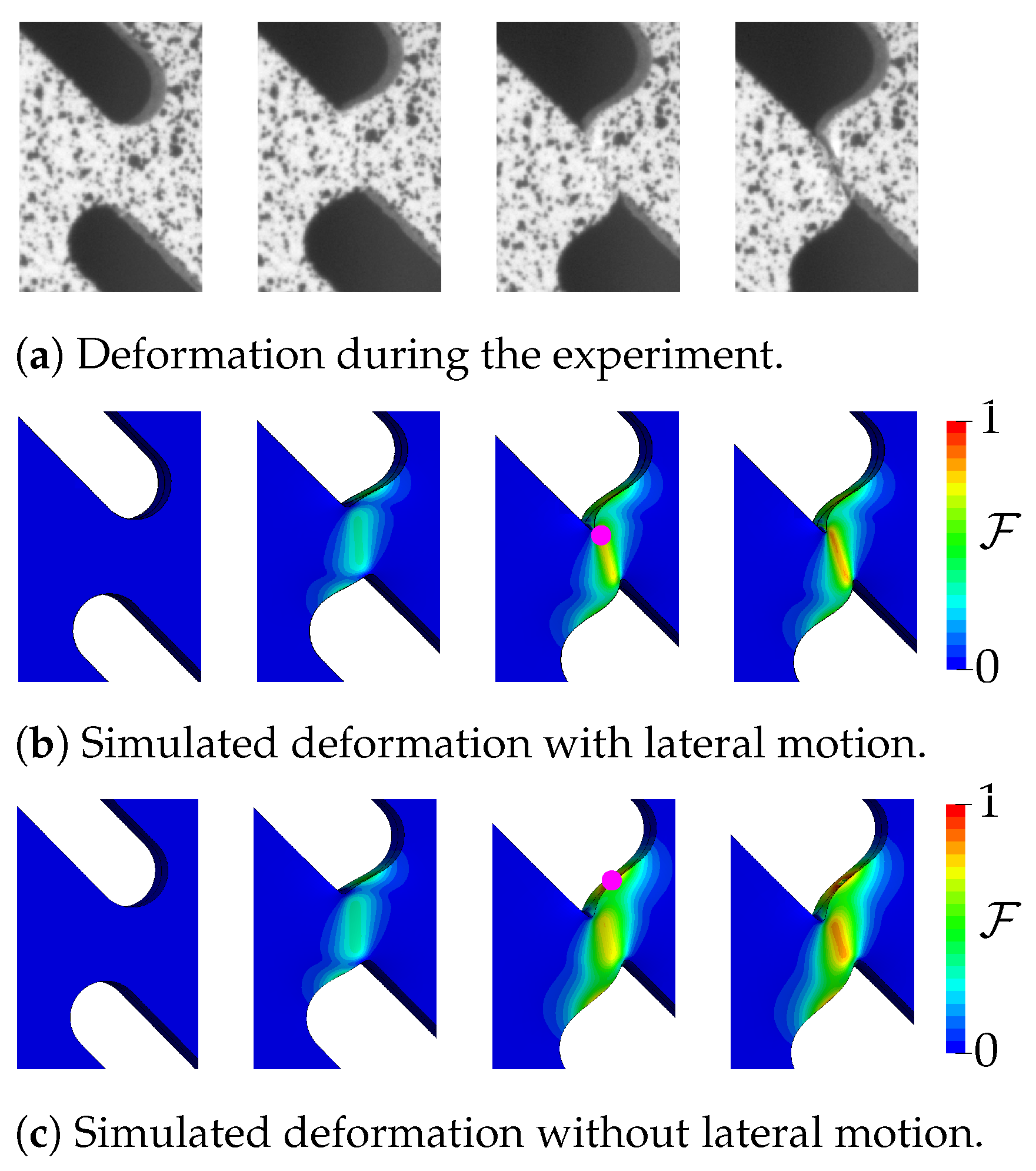
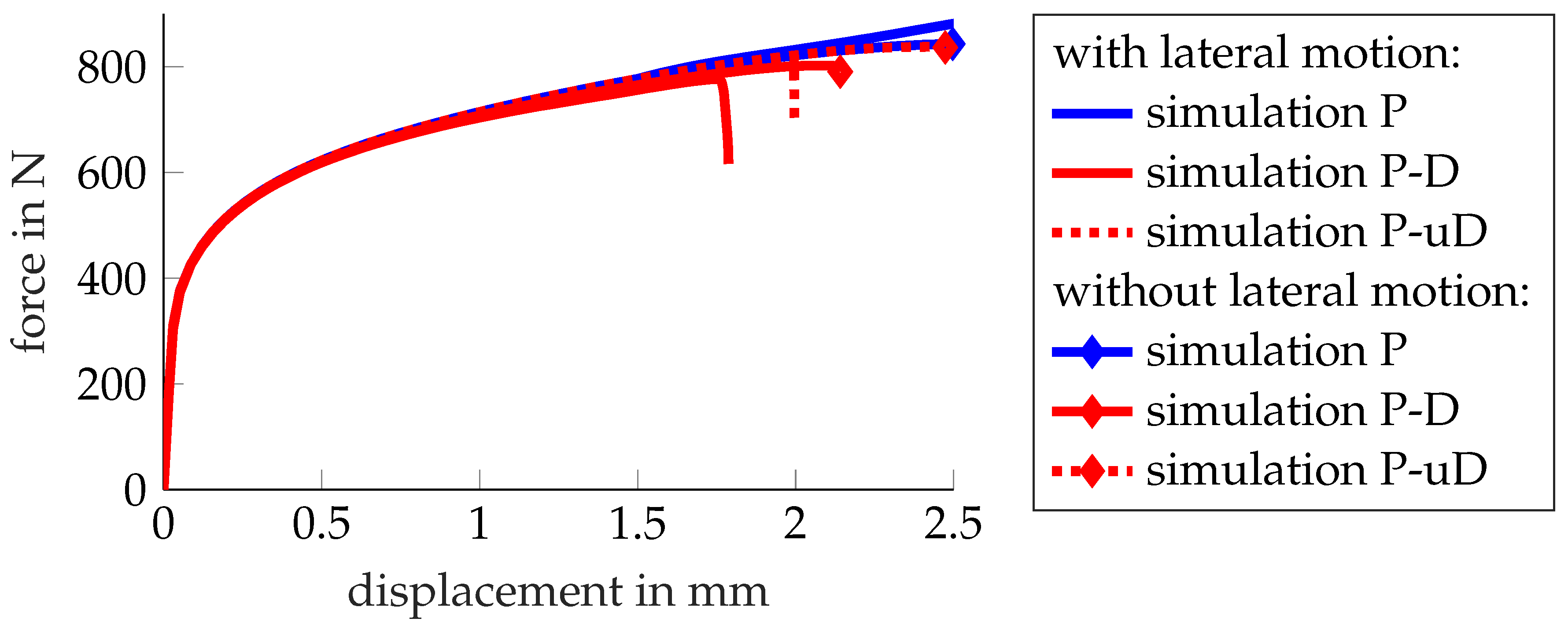
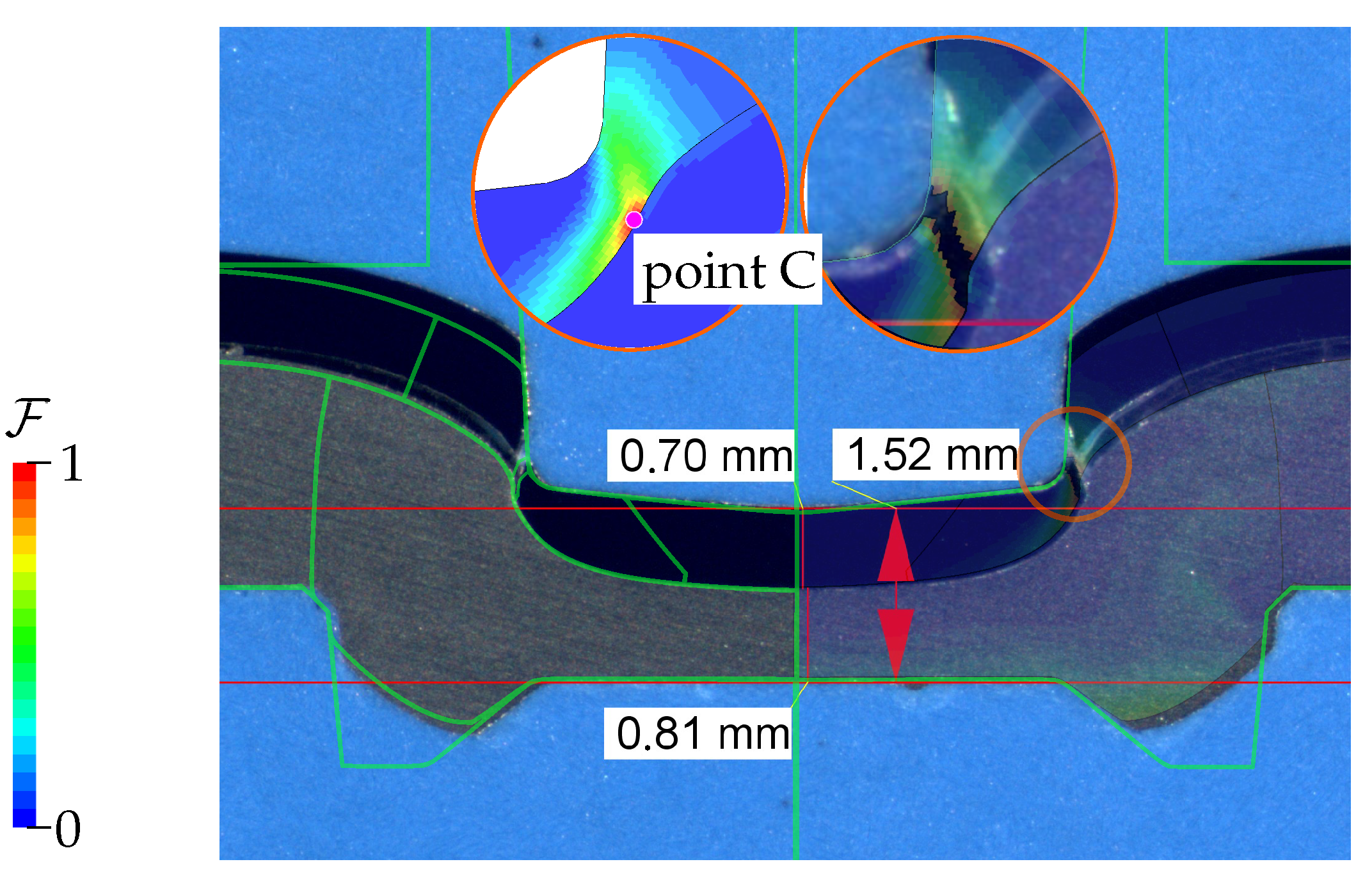
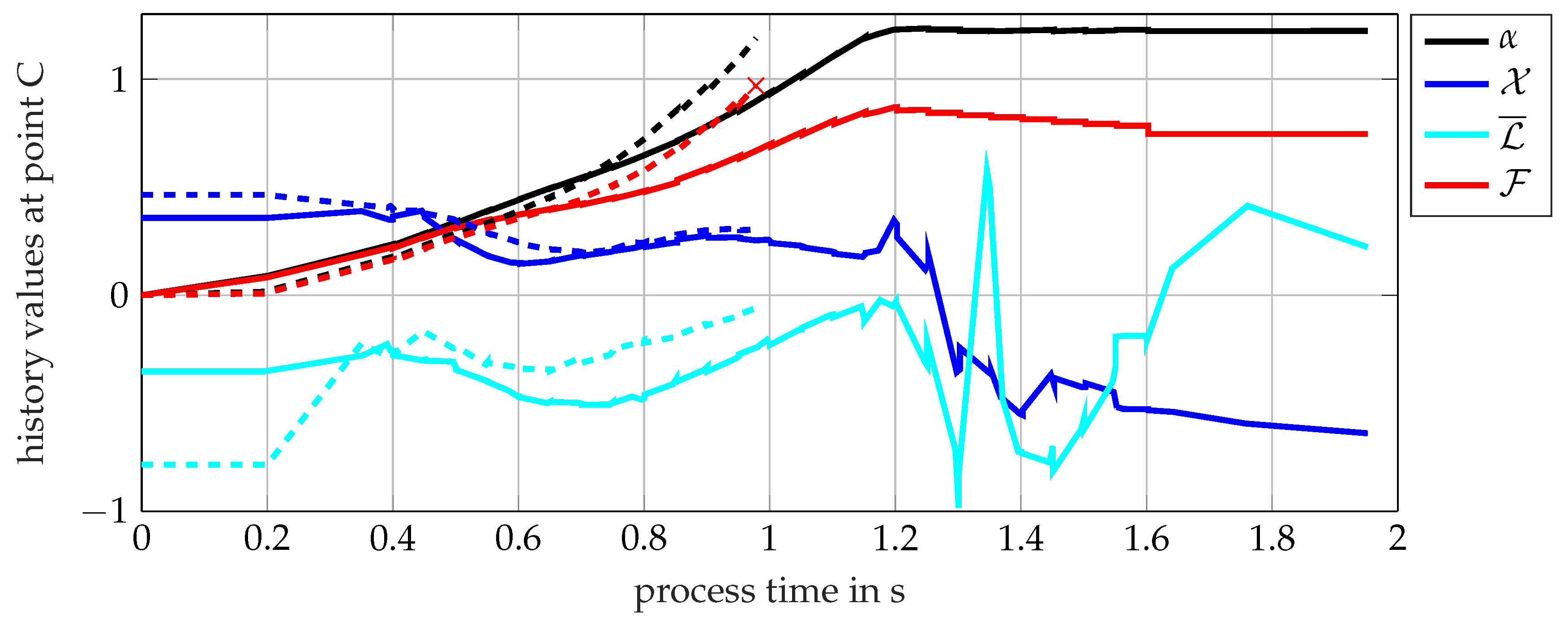
3.3. Towards Validation: A Teaser on Clinching
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tekkaya, A.; Bouchard, P.O.; Bruschi, S.; Tasan, C. Damage in metal forming. CIRP Ann. 2020, 69, 600–623. [Google Scholar] [CrossRef]
- Meschut, G.; Merkein, M.; Brosius, A.; Bobbert, M. Mechanical joining in versatile process chains. Prod. Eng. 2022, 16, 187–191. [Google Scholar] [CrossRef]
- Schramm, B.; Friedlein, J.; Gröger, B.; Bielak, C.; Bobbert, M.; Gude, M.; Meschut, G.; Wallmersperger, T.; Mergheim, J. A Review on the Modeling of the Clinching Process Chain-Part II: Joining Process. J. Adv. Join. Process. 2022, 6, 100134. [Google Scholar] [CrossRef]
- Wciślik, W.; Lipiec, S. Void-Induced Ductile Fracture of Metals: Experimental Observations. Materials 2022, 15, 6473. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Zhang, M.; Peng, Y.; Wang, J. Advances in Understanding the Evolution Mechanism of Micropore Defects in Metal Materials under External Loads. Metals 2024, 14, 522. [Google Scholar] [CrossRef]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture: With Special Emphasis on the Effects of Hydrostatic Pressure; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Brünig, M.; Gerke, S.; Koirala, S. Biaxial experiments and numerical analysis on stress-state-dependent damage and failure behavior of the anisotropic aluminum alloy EN AW-2017A. Metals 2021, 11, 1214. [Google Scholar] [CrossRef]
- Friedlein, J.; Mergheim, J.; Steinmann, P. Modelling of stress-state dependent ductile damage with gradient-enhancement exemplified for clinch joining. 2024, under review.
- Bouchard, P.O.; Bourgeon, L.; Fayolle, S.; Mocellin, K. An enhanced Lemaitre model formulation for materials processing damage computation. Int. J. Mater. Form. 2011, 4, 299–315. [Google Scholar] [CrossRef]
- Buyuk, M. Development of a Tabulated Thermo-Viscoplastic Material Model with Regularized Failure for Dynamic Ductile Failure Prediction of Structures under Impact Loading. Ph.D. Thesis, The George Washington University, Washington, DC, USA, 2013. [Google Scholar]
- Böhnke, M.; Bielak, C.R.; Bobbert, M.; Meschut, G. Development of a Modified Punch Test for Investigating the Failure Behavior in Sheet Metal Materials. In Proceedings of the 12th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes; Springer: Cham, Switzerland, 2022; pp. 575–584. [Google Scholar]
- Kupfer, R.; Köhler, D.; Römisch, D.; Wituschek, S.; Ewenz, L.; Kalich, J.; Weiß, D.; Sadeghian, B.; Busch, M.; Krüger, J.; et al. Clinching of aluminum materials–methods for the continuous characterization of process, microstructure and properties. J. Adv. Join. Process. 2022, 5, 100108. [Google Scholar] [CrossRef]
- Böhnke, M.; Bielak, C.R.; Friedlein, J.; Bobbert, M.; Mergheim, J.; Meschut, G.; Steinmann, P. A calibration method for failure modeling in clinching process simulations. Sheet Met. 2023, 25, 271. [Google Scholar]
- Ghahremaninezhad, A.; Ravi-Chandar, K. Crack nucleation from a notch in a ductile material under shear dominant loading. Int. J. Fract. 2013, 184, 253–266. [Google Scholar] [CrossRef]
- Cao, T.S. Numerical simulation of 3D ductile cracks formation using recent improved Lode-dependent plasticity and damage models combined with remeshing. Int. J. Solids Struct. 2014, 51, 2370–2381. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Determining the strain to fracture for simple shear for a wide range of sheet metals. Int. J. Mech. Sci. 2018, 149, 224–240. [Google Scholar] [CrossRef]
- Butcher, C.; Abedini, A. On phenomenological failure loci of metals under constant stress states of combined tension and shear: Issues of coaxiality and non-uniqueness. Metals 2019, 9, 1052. [Google Scholar] [CrossRef]
- Tasan, C.; Hoefnagels, J.; Geers, M. Identification of the continuum damage parameter: An experimental challenge in modeling damage evolution. Acta Mater. 2012, 60, 3581–3589. [Google Scholar] [CrossRef]
- Ghahremaninezhad, A.; Ravi-Chandar, K. Ductile failure behavior of polycrystalline Al 6061-T6. Int. J. Fract. 2012, 174, 177–202. [Google Scholar] [CrossRef]
- Khameneh, F.; Abedini, A.; Butcher, C. Lengthscale effects in optical strain measurement for fracture characterization in simple shear. Int. J. Fract. 2021, 232, 153–180. [Google Scholar] [CrossRef]
- Ghahremaninezhad, A.; Ravi-Chandar, K. Ductile failure behavior of polycrystalline Al 6061-T6 under shear dominant loading. Int. J. Fract. 2013, 180, 23–39. [Google Scholar] [CrossRef]
- Scales, M.; Tardif, N.; Kyriakides, S. Ductile failure of aluminum alloy tubes under combined torsion and tension. Int. J. Solids Struct. 2016, 97, 116–128. [Google Scholar] [CrossRef]
- Oh, S.; Chen, C.; Kobayashi, S. Ductile Fracture in Axisymmetric Extrusion and Drawing—Part 2: Workability in Extrusion and Drawing. ASME J. Eng. Ind. 1979, 101, 36–44. [Google Scholar] [CrossRef]
- Mohr, D.; Marcadet, S.J. Micromechanically-motivated phenomenological Hosford–Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67, 40–55. [Google Scholar] [CrossRef]
- HCT590X, Material Data Sheet, Salzgitter Flachstahl, Salzgitter, Germany. Available online: https://www.salzgitter-flachstahl.de/fileadmin/mediadb/szfg/informationsmaterial/produktinformationen/kaltgewalztes_feinblech/deu/hct590x.pdf (accessed on 1 June 2024).
- EN AW-6014 T4, Material Data Sheet Novelis Advanz™ 6F-e170, Novelis Global Automotive. 2019. Available online: https://de.novelis.com/product/novelis-advanz-6f-e170/ (accessed on 1 June 2024).
- ISO 6892-1:2019-11; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. ISO: Geneva, Switzerland, 2019.
- Kopp, R.; Wiegels, H. Einführung in die Umformtechnik; Verlag Mainz Aachen: Aachen, Germany, 1999. [Google Scholar]
- Bruschi, S.; Altan, T.; Banabic, D.; Bariani, P.F.; Brosius, A.; Cao, J.; Ghiotti, A.; Khraisheh, M.; Merklein, M.; Tekkaya, A.E. Testing and modelling of material behaviour and formability in sheet metal forming. CIRP Ann. 2014, 63, 727–749. [Google Scholar] [CrossRef]
- SEP 1230:2007-02; The Determination of the Mechanical Properties of Sheet Metal at High Strain Rates in High-Speed Tensile Tests. Verlag Stahleisen GmbH: Düsseldorf, Germany, 2007.
- DIN 50125:2022-08; Testing of Metallic Materials—Tensile Test Pieces. Deutsches Institut für Normung e.V. (DIN): Berlin, Germany, 2019.
- Böhnke, M.; Kappe, F.; Bobbert, M.; Meschut, G. Influence of various procedures for the determination of flow curves on the predictive accuracy of numerical simulations for mechanical joining processes. Mater. Test. 2021, 63, 493–500. [Google Scholar] [CrossRef]
- Basaran, M. Stress state dependent damage modeling with a focus on the lode angle influence. Ph.D. Thesis, Lehrstuhl und Institut für Allgemeine Mechanik, Shaker Verlag, Aachen, Germany, 2011. [Google Scholar]
- Merklein, M.; Kuppert, A. A method for the layer compression test considering the anisotropic material behavior. Int. J. Mater. Form. 2009, 2, 483–486. [Google Scholar] [CrossRef]
- Graf, M.; Henseler, T.; Ullmann, M.; Kawalla, R.; Prahl, U.; Awiszus, B. Study on determination of flow behaviour of 6060-aluminium and AZ31-magnesium thin sheet by means of stacked compression test. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Chemnitz, Germany, 6–7 March 2019; IOP Publishing: Bristol, UK, 2019; Volume 480, p. 012023. [Google Scholar]
- Pawelski, O. Über das Stauchen von Hohlzylindern und seine Eignung zur Bestimmung der Formänderungsfestigkeit dünner Bleche. Arch. Für Eisenhüttenwesen 1967, 38, 437–442. [Google Scholar] [CrossRef]
- Doege, E.; Meyer-Nolkemper, H.; Saeed, I. Fließkurvenatlas Metallischer Werkstoffe: Mit Fließkurven für 73 Werkstoffe und einer grundlegenden Einführung; Hanser: München, Germany, 1986. [Google Scholar]
- Suttner, S.; Merklein, M. Experimental and numerical investigation of a strain rate controlled hydraulic bulge test of sheet metal. J. Mater. Process. Technol. 2016, 235, 121–133. [Google Scholar] [CrossRef]
- Slota, J.; Spišák, E. Determination of flow stress by the hydraulic bulge test. Metalurgija 2008, 47, 13–17. [Google Scholar]
- ASTM B831-19; Standard Test Method for Shear Testing of Thin Aluminum Alloy Products. ASTM: West Conshohocken, PA, USA, 2005.
- Trondl, A.; Klitschke, S.; Boehme, W.; Sun, D.Z. Verformungs- und Versagensverhalten von Stählen für den Automobilbau unter crashartiger mehrachsiger Belastung. FAT-Schriftenreihe. 2016. Available online: https://www.vda.de/de/aktuelles/publikationen/publication/fat-schriftenreihe-283 (accessed on 19 July 2024).
- Otroshi, M.; Rossel, M.; Meschut, G. Stress state dependent damage modeling of self-pierce riveting process simulation using GISSMO damage model. J. Adv. Join. Process. 2020, 1, 100015. [Google Scholar] [CrossRef]
- Lee, Y.W. Fracture Prediction in Metal Sheets. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Busch, M.; Hausotte, T. Application of an edge detection algorithm for surface determination in industrial X-ray computed tomography. Prod. Eng. 2022, 16, 411–422. [Google Scholar] [CrossRef]
- Busch, M.; Butzhammer, L.; Hausotte, T. Herausforderungen bei computertomografischen Untersuchungen von Fügeverbindungen. Tech. Mess. 2022, 89, 83–88. [Google Scholar] [CrossRef]
- Graser, M.; Lenzen, M.; Merklein, M. On the inverse identification of Lankford coefficients using geometrical changes under quasi-biaxial loading. Int. J. Mater. Form. 2019, 12, 1053–1061. [Google Scholar] [CrossRef]
- Friedlein, J.; Wituschek, S.; Lechner, M.; Mergheim, J.; Steinmann, P. Inverse parameter identification of an anisotropic plasticity model for sheet metal. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Stuttgart, Germany, 21 June–2 July 2021; IOP Publishing: Bristol, UK, 2021; Volume 1157, p. 012004. [Google Scholar]
- Schneider, D. LAwave®—A Nondestructive Device for Testing Thin Films, Coatings and Material Surfaces by Laser Induced Surface Acoustic Waves. 2013. Available online: https://www.researchgate.net/publication/268034125_LAwaveR_-_A_Nondestructive_Device_for_Testing_Thin_Films_Coatings_and_Material_Surfaces_by_Laser_Induced_Surface_Acoustic_Waves?channel=doi&linkId=545f742f0cf2c1a63bfdb595&showFulltext=true (accessed on 19 July 2024).
- Nahrmann, M.; Matzenmiller, A. Modelling of nonlocal damage and failure in ductile steel sheets under multiaxial loading. Int. J. Solids Struct. 2021, 232, 111166. [Google Scholar] [CrossRef]
- Friedlein, J.; Bielak, C.; Böhnke, M.; Bobbert, M.; Meschut, G.; Mergheim, J.; Steinmann, P. Influence of plastic orthotropy on clinching of sheet metal. Sheet Met. 2023, 25, 133–140. [Google Scholar]
- Friedlein, J.; Kalich, J.; Lüder, S.; Schmale, H.C.; Böhnke, M.; Schlichter, M.; Bobbert, M.; Meschut, G.; Steinmann, P.; Mergheim, J. Application of stress-state dependent ductile damage and failure model to clinch joining for a wide range of tool and material combinations. 2024, to be submitted.
- Banabic, D. Sheet Metal Forming Processes: Constitutive Modelling and Numerical Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Schowtjak, A.; Wang, S.; Hering, O.; Clausmeyer, T.; Lohmar, J.; Schulte, R.; Ostwald, R.; Hirt, G.; Tekkaya, A.E. Prediction and analysis of damage evolution during caliber rolling and subsequent cold forward extrusion. Prod. Eng. 2020, 14, 33–41. [Google Scholar] [CrossRef]













| Symbol | Description | Identification | Unit |
|---|---|---|---|
| Elasticity | |||
| E | Young’s modulus | measurement | MPa |
| Poisson’s ratio | literature | – | |
| Plasticity | |||
| initial yield stress | direct fit to experiment | MPa | |
| K | hardening modulus | direct fit to experiment | MPa |
| power-law exponent | direct fit to experiment | – | |
| yield-stress increment | direct fit to experiment | MPa | |
| hardening saturation | direct fit to experiment | – | |
| saturation exponent | direct fit to experiment | – | |
| Damage | |||
| damage saturation | assumed value, 1 | – | |
| damage saturation (failure) | deduction from experiments | – | |
| critical failure indicator | deduction from experiments | – | |
| Failure | |||
| failure exponent | assumed value, 1 | – | |
| failure strain at shear for CLO-model | inverse identification | – | |
| Hosford–Coulomb parameter a | inverse identification | – | |
| Hosford–Coulomb parameter b | inverse identification | – | |
| Hosford–Coulomb parameter c | inverse identification | – | |
| Hosford–Coulomb parameter n | literature | – | |
| HCT590X (wt %) | EN AW-6014 T4 (wt %) | |||||
|---|---|---|---|---|---|---|
| Chemical composition | Min. | Max. | Min. | Max. | ||
| C | 0.15 | Si | 0.60 | |||
| Si | 0.75 | Fe | 0.35 | |||
| Mn | 2.5 | Cu | 0.25 | |||
| P | 0.04 | Mn | 0.05 | 0.20 | ||
| S | 0.015 | Mg | 0.40 | 0.80 | ||
| Al | 0.015 | 1.5 | Cr | 0.20 | ||
| Cr + Mo | 1.4 | Zn | 0.10 | |||
| Nb + Ti | 0.15 | Ti | 0.10 | |||
| V | 0.10 | |||||
| Physical properties | Yield strength Rp0.2 (MPa) | 330–430 | ≤130 | |||
| Ultimate tensile strength Rm (MPa) | 590–700 | ≥175 | ||||
| Elongation A80 (%) | ≥20 | ≥23 | ||||
| K | |||||
| MPa | MPa | – | MPa | – | – |
| K | |||||
| MPa | MPa | – | MPa | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friedlein, J.; Böhnke, M.; Schlichter, M.; Bobbert, M.; Meschut, G.; Mergheim, J.; Steinmann, P. Material Parameter Identification for a Stress-State-Dependent Ductile Damage and Failure Model Applied to Clinch Joining. J. Manuf. Mater. Process. 2024, 8, 157. https://doi.org/10.3390/jmmp8040157
Friedlein J, Böhnke M, Schlichter M, Bobbert M, Meschut G, Mergheim J, Steinmann P. Material Parameter Identification for a Stress-State-Dependent Ductile Damage and Failure Model Applied to Clinch Joining. Journal of Manufacturing and Materials Processing. 2024; 8(4):157. https://doi.org/10.3390/jmmp8040157
Chicago/Turabian StyleFriedlein, Johannes, Max Böhnke, Malte Schlichter, Mathias Bobbert, Gerson Meschut, Julia Mergheim, and Paul Steinmann. 2024. "Material Parameter Identification for a Stress-State-Dependent Ductile Damage and Failure Model Applied to Clinch Joining" Journal of Manufacturing and Materials Processing 8, no. 4: 157. https://doi.org/10.3390/jmmp8040157
APA StyleFriedlein, J., Böhnke, M., Schlichter, M., Bobbert, M., Meschut, G., Mergheim, J., & Steinmann, P. (2024). Material Parameter Identification for a Stress-State-Dependent Ductile Damage and Failure Model Applied to Clinch Joining. Journal of Manufacturing and Materials Processing, 8(4), 157. https://doi.org/10.3390/jmmp8040157







