Effect of Curvilinear Reinforcing Fibers on the Linear Static Behavior of Soft-Core Sandwich Structures

Abstract

The present research deals with the linear static behavior of soft-core sandwich plates and shells. The external skins are reinforced by curvilinear fibers. Their curved paths are described by a general mathematical law that allows the definition of arbitrary placements. The mechanical behavior of these structures is modeled through several Higher-order Shear Deformation Theories (HSDTs) including the zig-zag effect, based on an Equivalent Single Layer (ESL) approach. The solution of the governing equations is achieved numerically by means of the Generalized Differential Quadrature (GDQ) method. A huge number of parametric investigations is proposed in graphical and tabular forms to highlight the influence of the fiber orientation on the static response. The results prove that the structural behavior is affected by such parameters. Thus, the desired structural behavior can be modified by means of a proper choice of the fiber orientation.

1. Introduction

Advanced composite materials are mainly developed to design stiffer and lighter structures, characterized by an improved and more efficient mechanical behavior. Among them, fiber-reinforced media [1,2,3,4], laminated and sandwich composites [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], Functionally Graded Materials (FGMs) [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41], nanocomposites [42,43,44,45,46] and metamaterials [47,48,49,50,51,52,53] should be mentioned. Thus, many scientists and researchers focused their efforts on the design of optimal and optimized configurations of these innovative constituents. One of the most recurring approaches is the redistribution of the stiffness within the structural body without a weight growth, to improve or, at least, modify its static and dynamic responses. Structures characterized by variable mechanical properties arose precisely for this purpose. The present paper can be placed in this context, since it deals with variable stiffness sandwich plates and shells made of fiber-reinforced layers. The variation of the mechanical properties of these structural elements is accomplished by defining a curvilinear path of the reinforcing fibers [54,55]. To this aim, an innovative and general mathematical formulation is developed by the authors [56]. Differently from the previous paper by Tornabene et al. [56], in which the same general approach is employed for the natural frequency analysis of variable stiffness shells, the current research is focused on the linear static behavior of soft-core sandwich plates and shells.

A brief literature review is presented below to introduce this topic. For this purpose, the authors would like to apologize for the possible omissions of those contributions that could be considered as important steps in the development of this subject. A more complete literature review can be found in the PhD Thesis by Groh [57]. A pioneering application of curvilinear fibers in composite structures was presented by Hyer and Charette [58] to deal with a rectangular plate with centrally located circular hole. Hyer et al. [59] continued the same topic by studying also the manufacturing problem. A plane elasticity problem of a symmetrically laminated composite with curvilinear fibers was investigated by Gürdal and Olmedo [60] to evaluate the stiffness variation effect on the elastic response of the structure. In their work, the orientation of the fibers was defined by two parameters, which consisted of the fiber angle at the center of the laminate and the fiber angle at a specified distance from the center. The manufacturing process of the proposed approach was progressively studied by Waldarth et al. [61], Setoodeh and Gürdal [62], and Setoodeh et al. [63,64]. Jegley et al. [65] proved that the load carrying capability of panels reinforced by curvilinear fibers was superior to the one that characterized panels with straight fibers. Analogously, the stress concentrations around the hole were reduced due to the curvilinear paths of the fibers. Abdalla et al. [66] developed a maximization procedure for the natural frequency of composite panels reinforced by curved fibers. The post-buckling progressive damage behavior and the structural failure of variable-stiffness composite panels were studied by Lopes et al. [67] taking into account the residual thermal stresses caused by the curing process. Gürdal et al. [68] investigated the in-plane and buckling responses of flat rectangular composite laminates with variable stiffness. Their research proved that it was possible to vary either the buckling load or the in-plane stiffness of the structure. The variable-stiffness concept and the two-parameter law for the fiber orientation were extended also to conical and cylindrical shells by Blom et al. [69,70,71]. Akhavan and Ribeiro [72] investigated the natural frequencies and vibrational modes of variable-stiffness laminated composite plates reinforced by curvilinear fibers by means of a p-version finite element approach. The same topic was analyzed also by Honda and Narita [73], who proposed an analytical method for this purpose. Díaz et al. [74] presented a numerical method for obtaining the interlaminar stresses in variable stiffness composite panels. Coburn et al. [75] highlighted the improved buckling performances of variable-stiffness laminates compared to the ones reinforced by straight fibers. They employed the Rayleigh-Ritz procedure in the theoretical framework of the First-order Shear Deformation Theory (FSDT). Raju et al. [76] performed a geometrically nonlinear analysis of symmetric laminated composite plates with curvilinear fibers subjected to in-plane shear loads. In particular, the effect of fiber orientation on the buckling and post-buckling behavior was investigated. The same kind of analysis was performed by White et al. [77], who extended the research to variable-stiffness cylinders under axial compression forces. Yazdani and Ribeiro [78] developed a layer-wise p-version finite element approach able to capture accurately the free vibrations of thick composite laminates reinforced by curvilinear fibers. Ribeiro and Stoykov [79] and Ribeiro [80,81] investigated respectively the free and forced geometrically nonlinear vibrations of variable-stiffness cylindrical shells. Analogously, Akhavan and Ribeiro [82] developed a third-order shear deformation theory to study the geometrically nonlinear periodic forced vibrations of imperfect laminates reinforced by curvilinear fibers. To this aim, a p-version finite element method was used. An accurate variable-kinematic approach was developed instead by Vescovini and Dozio [83] for the vibration and buckling analysis of moderately thick variable-stiffness laminated and sandwich plates. Groh and Weaver [84] proposed a pseudo-spectral differential quadrature method to analyze the mechanical behavior of sandwich panels with variable-stiffness face sheets, whose governing equations are derived by using the Hellinger-Reissner model. On the other hand, the Koiter’s approach and the finite element method were employed in the paper by Madeo et al. [85] to analyze the post-buckling behavior of variable-stiffness composite plates. Khani et al. [86] investigated failure loads, failure modes and weights of variable-stiffness panels with cut-out by means of several experimental tests. Their work proved that variable-stiffness laminates could sustain larger loads before failure. Demasi et al. [87] proposed a multi-theory approach based on the Generalized Unified Formulation (GUF), including Equivalent Single Layer, zig-zag, and Layer-Wise models, for the static analysis of variable-stiffness composites. The Rayleigh-Ritz method was employed by Oliveri et al. [88] to investigate the thermo-mechanical post-buckling behavior of variable-stiffness multilayered plates, taking into account geometrical nonlinearities through the Von Kármán’s hypotheses. A theoretical framework based on higher-order theories was developed by Tornabene et al. [89,90] for the free vibration and static analyses of doubly-curved laminated composite shells reinforced by curvilinear fibers placed according to classical schemes. A numerical solution was proposed in these circumstances. Finally, it should be mentioned that the presence of defects or imperfections, such as gaps and overlaps, characterizes laminated composites reinforced by curvilinear fibers, due to the peculiar manufacturing process, as highlighted in the papers [91,92,93,94]. This aspect could be even more evident in shell structures due to their curvature. For this purpose, an innovative fiber placement method named as Continuous Tow Shearing (CTS) was recently developed by Kim et al. [95] to minimize such defects in the manufacture of variable-stiffness composites.

A structural model based on an ESL approach is developed in this paper to investigate the linear static behavior of doubly-curved shells reinforced by curvilinear fibers placed according to a general scheme. In particular, several Higher-order Shear Deformation Theories (HSDTs) are developed to this aim [96,97]. Since soft-core sandwich structures are analyzed, the Murakami’s function is embedded in the model to capture the effective zig-zag effect that occurs in this peculiar circumstance [98,99,100]. This ESL approach can reach the same accuracy of a layer-wise theory without increasing the degrees of freedom of the problem and the computational cost, consequently. Further details concerning layer-wise theories could be found in the paper by Tornabene [12] and by Naumenko and Eremeyev [101]. In addition, as highlighted in the papers [102,103,104,105,106,107,108,109,110,111,112,113,114], lower-order theories such as the well-known FSDT could be inadequate in these cases. Once the theoretical framework is introduced, a massive set of parametric investigations is presented to show the effect of the fiber orientation on the static response of these structural elements. The Generalized Differential Quadrature (GDQ) method is employed to get the numerical solution of the governing equations [115,116,117,118].

2. Shell Geometry

Let us introduce a global reference coordinate system $O{x}_1{x}_2{x}_3$ in the three-dimensional space, as shown in Figure 1. Each direction $x_i$ is clearly identified by the corresponding unit vector ${\mathbf{e}}_1$. A generic shell element is defined in such space. Its shape can be described through the position vector of the middle surface $\mathbf{r}\left({\alpha }_1,{\alpha }_2\right)$, where ${\alpha }_1,{\alpha }_2$ are the principal and orthogonal curvilinear coordinates of the surface in hand (Figure 1), for ${\alpha }_1\in \left[{\alpha }_1^0,{\alpha }_1^1\right]$ and ${\alpha }_2\in \left[{\alpha }_2^0,{\alpha }_2^1\right]$.

The coordinate $\zeta$ denotes the thickness direction. Thus, $O^{\prime }{\alpha }_1{\alpha }_2\zeta$ stands for the local reference system of the shell middle surface. The shell volume is identified by its constant thickness $h$. It should be recalled that the structure is made of $l$ layers, therefore the overall thickness is given by

$$h={\displaystyle \sum _{k=1}^l{h}_k}$$

(1)

where $h_k$ stands for the thickness of the $k$-th layer, which can be computed as follows

$$h_k={\zeta }_{k+1}-{\zeta }_k$$

(2)

Since only sandwich structures are analyzed in the present paper, the shells are made of three layers: two external thinner plies of equal thickness $h_s$, and a thicker core of thickness $h_c$. Thus, the total thickness is given by

$$h=h_c+2h_s$$

(3)

Each point of this three-dimensional structure is analytically described through the following position vector $\mathbf{R}\left({\alpha }_1,{\alpha }_2,\zeta \right)$

$$\mathbf{R}\left({\alpha }_1,{\alpha }_2,\zeta \right)=\mathbf{r}\left({\alpha }_1,{\alpha }_2\right)+\zeta \mathbf{n}\left({\alpha }_1,{\alpha }_2\right)$$

(4)

where $\mathbf{n}\left({\alpha }_1,{\alpha }_2\right)$ represents the outward unit normal vector. This quantity can be computed by means of the cross product (denoted by “$\times$”) as follows

$$\mathbf{n}=\frac{{\mathbf{r}}_{,1}\times {\mathbf{r}}_{,2}}{\left|{\mathbf{r}}_{,1}\times {\mathbf{r}}_{,2}\right|}$$

(5)

in which ${\mathbf{r}}_{,i}=\partial \mathbf{r}/\partial {\alpha }_i$. Once the position vector $\mathbf{r}\left({\alpha }_1,{\alpha }_2\right)$ of the middle surface is given, the Lamè parameters $A_1,A_2$ of the doubly-curved surface which define the shape of the shell can be easily evaluated by means of the dot product (denoted by “$\cdot$”) as shown below

$$A_1\left({\alpha }_1,{\alpha }_2\right)=\sqrt{{\mathbf{r}}_{,1}\cdot {\mathbf{r}}_{,1}},\hspace{1em}{A}_2\left({\alpha }_1,{\alpha }_2\right)=\sqrt{{\mathbf{r}}_{,2}\cdot {\mathbf{r}}_{,2}}$$

(6)

Analogously, the radii of curvature $R_1,R_2$ of the shell middle surface can be calculated through the following relations

$$R_1=-\frac{{\mathbf{r}}_{,1}\cdot {\mathbf{r}}_{,1}}{{\mathbf{r}}_{,11}\cdot \mathbf{n}},\hspace{1em}{R}_2=-\frac{{\mathbf{r}}_{,2}\cdot {\mathbf{r}}_{,2}}{{\mathbf{r}}_{,22}\cdot \mathbf{n}}$$

(7)

3. Higher-Order ESL Model

The present higher-order structural model allows the study of several displacement fields by varying the maximum order of kinematic expansion $N$. The three-dimensional displacements $U_1\left({\alpha }_1,{\alpha }_2,\zeta \right)$, $U_2\left({\alpha }_1,{\alpha }_2,\zeta \right)$, $U_3\left({\alpha }_1,{\alpha }_2,\zeta \right)$ can be written as follows

$$\begin{array}{l}{U}_1={\displaystyle \sum _{\tau =0}^{N+1}{F}_{\tau }^{}{u}_1^{\left(\tau \right)}}=F_0^{}{u}_1^{\left(0\right)}+F_1^{}{u}_1^{\left(1\right)}+F_2^{}{u}_1^{\left(2\right)}+\cdots +F_{N-1}^{}{u}_1^{\left(N-1\right)}+F_N^{}{u}_1^{\left(N\right)}+F_{N+1}^{}{u}_1^{\left(N+1\right)}\hfill \\ U_2={\displaystyle \sum _{\tau =0}^{N+1}{F}_{\tau }^{}{u}_2^{\left(\tau \right)}}=F_0^{}{u}_2^{\left(0\right)}+F_1^{}{u}_2^{\left(1\right)}+F_2^{}{u}_2^{\left(2\right)}+\cdots +F_{N-1}^{}{u}_2^{\left(N-1\right)}+F_N^{}{u}_2^{\left(N\right)}+F_{N+1}^{}{u}_2^{\left(N+1\right)}\hfill \\ U_3={\displaystyle \sum _{\tau =0}^{N+1}{F}_{\tau }^{}{u}_3^{\left(\tau \right)}}=F_0^{}{u}_3^{\left(0\right)}+F_1^{}{u}_3^{\left(1\right)}+F_2^{}{u}_3^{\left(2\right)}+\cdots +F_{N-1}^{}{u}_3^{\left(N-1\right)}+F_N^{}{u}_3^{\left(N\right)}+F_{N+1}^{}{u}_3^{\left(N+1\right)}\hfill \end{array}$$

(8)

in which $F_{\tau }\left(\zeta \right)$ are the thickness-functions that define the kinematic expansion. The generalized displacements $u_1^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2\right)$, $u_2^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2\right)$, $u_3^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2\right)$, which are defined on the shell middle surface, are the degrees of freedom. The thickness functions are assumed as power law functions. In other words, one gets

$$F_{\tau }\left(\zeta \right)={\zeta }^{\tau }$$

(9)

for $\tau =0,1,2,\dots ,N$. The $\left(N+1\right)$-th function, instead, denotes the Murakami’s function $\mathrm{Z}\left(\zeta \right)$ defined below

$$F_{N+1}=\mathrm{Z}={\left(-1\right)}^k\left(\frac{2}{{\zeta }_{k+1}-{\zeta }_k}\zeta -\frac{{\zeta }_{k+1}+{\zeta }_k}{{\zeta }_{k+1}-{\zeta }_k}\right)$$

(10)

This peculiar function must be inserted in the structural model to capture the effective behavior of soft-core sandwich structures. Otherwise, the so-called zig-zag effect cannot be properly modeled [90]. The notation $\mathrm{EDZ}N$ is used to identify the shear-deformation theory including the Murakami’s function.

For the sake of conciseness, the three-dimensional displacements can be collected in the corresponding vector $\mathbf{U}\left({\alpha }_1,{\alpha }_2,\zeta \right)$

$$\mathbf{U}={\left[\begin{array}{ccc}{U}_1& U_2& U_3\end{array}\right]}^T$$

(11)

Analogously, the vector ${\mathbf{u}}^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2\right)$ can be introduced to collect the degrees of freedom of the model for $\tau =0,1,2,\dots ,N,N+1$.

$${\mathbf{u}}^{\left(\tau \right)}={\left[\begin{array}{ccc}{u}_1^{\left(\tau \right)}& u_2^{\left(\tau \right)}& u_3^{\left(\tau \right)}\end{array}\right]}^T$$

(12)

The generalized strain components, which are defined on the shell middle surface as well, can be included in the corresponding vector ${\mathsf{\epsilon }}^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2\right)$ shown below

$${\mathsf{\epsilon }}^{\left(\tau \right)}={\left[\begin{array}{ccccccccc}{\epsilon }_1^{\left(\tau \right)}& {\epsilon }_2^{\left(\tau \right)}& {\gamma }_1^{\left(\tau \right)}& {\gamma }_2^{\left(\tau \right)}& {\gamma }_{13}^{\left(\tau \right)}& {\gamma }_{23}^{\left(\tau \right)}& {\omega }_{13}^{\left(\tau \right)}& {\omega }_{23}^{\left(\tau \right)}& {\epsilon }_3^{\left(\tau \right)}\end{array}\right]}^T$$

(13)

for $\tau =0,1,2,\dots ,N,N+1$. These quantities can be evaluated as a function of the generalized displacements as follows

$${\mathsf{\epsilon }}^{\left(\tau \right)}={\mathbf{D}}_{\Omega }^{}{\mathbf{u}}^{\left(\tau \right)}$$

(14)

in which ${\mathbf{D}}_{\Omega }$ is the kinematic differential operator defined below

$${\mathbf{D}}_{\Omega }={\left[\begin{array}{ccccccccc}\frac{1}{A_1}\frac{\partial }{\partial {\alpha }_1}& \frac{1}{A_1{A}_2}\frac{\partial A_2}{\partial {\alpha }_1}& -\frac{1}{A_1{A}_2}\frac{\partial A_1}{\partial {\alpha }_2}& \frac{1}{A_2}\frac{\partial }{\partial {\alpha }_2}& -\frac{1}{R_1}& 0& 1& 0& 0\\ \frac{1}{A_1{A}_2}\frac{\partial A_1}{\partial {\alpha }_2}& \frac{1}{A_2}\frac{\partial }{\partial {\alpha }_2}& \frac{1}{A_1}\frac{\partial }{\partial {\alpha }_1}& -\frac{1}{A_1{A}_2}\frac{\partial A_2}{\partial {\alpha }_1}& 0& -\frac{1}{R_2}& 0& 1& 0\\ \frac{1}{R_1}& \frac{1}{R_2}& 0& 0& \frac{1}{A_1}\frac{\partial }{\partial {\alpha }_1}& \frac{1}{A_2}\frac{\partial }{\partial {\alpha }_2}& 0& 0& 1\end{array}\right]}^T$$

(15)

The three-dimensional strain components can be included in the vector $\mathsf{\epsilon }\left({\alpha }_1,{\alpha }_2,\zeta \right)$, which assumes the aspect below

$$\mathsf{\epsilon }={\left[\begin{array}{cccccc}{\epsilon }_1& {\epsilon }_2& {\gamma }_{12}& {\gamma }_{1n}& {\gamma }_{2n}& {\epsilon }_n\end{array}\right]}^T$$

(16)

These quantities can be computed once the generalized strains are evaluated. The following definition can be used for this purpose

$$\mathsf{\epsilon }={\displaystyle \sum _{\tau =0}^{N+1}{\mathbf{Z}}^{\left(\tau \right)}{\mathsf{\epsilon }}^{\left(\tau \right)}}$$

(17)

where the matrix ${\mathbf{Z}}^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2,\zeta \right)$ has the meaning shown below for each order $\tau$ of kinematic expansion

$${\mathbf{Z}}^{\left(\tau \right)}=\left[\begin{array}{ccccccccc}\frac{F_{\tau }^{}}{H_1}& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& \frac{F_{\tau }^{}}{H_2}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& \frac{F_{\tau }^{}}{H_1}& \frac{F_{\tau }^{}}{H_2}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{F_{\tau }^{}}{H_1}& 0& \frac{\partial F_{\tau }^{}}{\partial \zeta }& 0& 0\\ 0& 0& 0& 0& 0& \frac{F_{\tau }^{}}{H_2}& 0& \frac{\partial F_{\tau }^{}}{\partial \zeta }& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& \frac{\partial F_{\tau }^{}}{\partial \zeta }\end{array}\right]$$

(18)

The geometric parameters $H_1,H_2$ can be evaluated as a function of the principal radii of curvature

$$H_1=1+\frac{\zeta }{R_1},\hspace{1em}{H}_2=1+\frac{\zeta }{R_2}$$

(19)

Consequentially, the three-dimensional stress components can be evaluated as a function of the strain components by using the elastic constitutive laws, assuming a linear behavior of the composite materials. The stress components at issue can be collected in the vector $\mathsf{\sigma }\left({\alpha }_1,{\alpha }_2,\zeta \right)$ defined below

$$\mathsf{\sigma }={\left[\begin{array}{cccccc}{\sigma }_1& {\sigma }_2& {\tau }_{12}& {\tau }_{1n}& {\tau }_{2n}& {\sigma }_n\end{array}\right]}^T$$

(20)

The following relation written in compact matrix form allows a definition of such quantities as a function of the corresponding stress components

$$\mathsf{\sigma }={\overline{\mathbf{C}}}^{\left(k\right)}\mathsf{\epsilon }$$

(21)

where ${\overline{\mathbf{C}}}^{\left(k\right)}$ is the constitutive operator for the $k$-th orthotropic layer defined in the local reference system of the structure. It assumes the following aspect

$${\overline{\mathbf{C}}}^{\left(k\right)}=\left[\begin{array}{cccccc}{\overline{C}}_{11}^{\left(k\right)}& {\overline{C}}_{12}^{\left(k\right)}& {\overline{C}}_{16}^{\left(k\right)}& 0& 0& {\overline{C}}_{13}^{\left(k\right)}\\ {\overline{C}}_{12}^{\left(k\right)}& {\overline{C}}_{22}^{\left(k\right)}& {\overline{C}}_{26}^{\left(k\right)}& 0& 0& {\overline{C}}_{23}^{\left(k\right)}\\ {\overline{C}}_{16}^{\left(k\right)}& {\overline{C}}_{26}^{\left(k\right)}& {\overline{C}}_{66}^{\left(k\right)}& 0& 0& {\overline{C}}_{36}^{\left(k\right)}\\ 0& 0& 0& {\overline{C}}_{44}^{\left(k\right)}& {\overline{C}}_{45}^{\left(k\right)}& 0\\ 0& 0& 0& {\overline{C}}_{45}^{\left(k\right)}& {\overline{C}}_{55}^{\left(k\right)}& 0\\ {\overline{C}}_{13}^{\left(k\right)}& {\overline{C}}_{23}^{\left(k\right)}& {\overline{C}}_{36}^{\left(k\right)}& 0& 0& {\overline{C}}_{33}^{\left(k\right)}\end{array}\right]$$

(22)

Quantities included in ${\overline{\mathbf{C}}}^{\left(k\right)}$ take into account the orientation of the reinforcing fibers ${\theta }^{\left(k\right)}$ for the $k$-th ply. The following relations can be used to evaluate them

$${\overline{C}}_{11}^{\left(k\right)}=C_{11}^{\left(k\right)}{c}^4+2\left(C_{12}^{\left(k\right)}+2C_{66}^{\left(k\right)}\right)c^2{s}^2+C_{22}^{\left(k\right)}{s}^4$$

(23)

$${\overline{C}}_{12}^{\left(k\right)}=C_{12}^{\left(k\right)}{c}^4+\left(C_{11}^{\left(k\right)}+C_{22}^{\left(k\right)}-4C_{66}^{\left(k\right)}\right)c^2{s}^2+C_{12}^{\left(k\right)}{s}^4$$

(24)

$${\overline{C}}_{13}^{\left(k\right)}=C_{13}^{\left(k\right)}{c}^2+C_{23}^{\left(k\right)}{s}^2$$

(25)

$${\overline{C}}_{16}^{\left(k\right)}=\left(C_{11}^{\left(k\right)}-C_{12}^{\left(k\right)}-2C_{66}^{\left(k\right)}\right)c^{3}s+\left(C_{12}^{\left(k\right)}-C_{22}^{\left(k\right)}+2C_{66}^{\left(k\right)}\right)c{s}^3$$

(26)

$${\overline{C}}_{22}^{\left(k\right)}=C_{22}^{\left(k\right)}{c}^4+2\left(C_{12}^{\left(k\right)}+2C_{66}^{\left(k\right)}\right)c^2{s}^2+C_{11}^{\left(k\right)}{s}^4$$

(27)

$${\overline{C}}_{23}^{\left(k\right)}=C_{23}^{\left(k\right)}{c}^2+C_{13}^{\left(k\right)}{s}^2$$

(28)

$${\overline{C}}_{26}^{\left(k\right)}=\left(C_{12}^{\left(k\right)}-C_{22}^{\left(k\right)}+2C_{66}^{\left(k\right)}\right)c^{3}s+\left(C_{11}^{\left(k\right)}-C_{12}^{\left(k\right)}-2C_{66}^{\left(k\right)}\right)c{s}^3$$

(29)

$${\overline{C}}_{33}^{\left(k\right)}=C_{33}^{\left(k\right)}$$

(30)

$${\overline{C}}_{36}^{\left(k\right)}=\left(C_{13}^{\left(k\right)}-C_{23}^{\left(k\right)}\right)cs$$

(31)

$${\overline{C}}_{66}^{\left(k\right)}=\left(C_{11}^{\left(k\right)}+C_{22}^{\left(k\right)}-2C_{12}^{\left(k\right)}\right)c^2{s}^2+C_{66}^{\left(k\right)}{\left(c^2-s^2\right)}^2$$

(32)

$${\overline{C}}_{44}^{\left(k\right)}=C_{44}^{\left(k\right)}{c}^2+C_{55}^{\left(k\right)}{s}^2$$

(33)

$${\overline{C}}_{45}^{\left(k\right)}=\left(C_{44}^{\left(k\right)}-C_{55}^{\left(k\right)}\right)cs$$

(34)

$${\overline{C}}_{55}^{\left(k\right)}=C_{55}^{\left(k\right)}{c}^2+C_{44}^{\left(k\right)}{s}^2$$

(35)

where $c=\cos {\theta }^{\left(k\right)}$ and $s=\sin {\theta }^{\left(k\right)}$. The elastic constants in (23)–(35) can be computed as a function of the engineering constants of the materials of the $k$-th layer as shown below

$$\begin{array}{c}{C}_{11}^{\left(k\right)}=\frac{1-{\nu }_{23}^{\left(k\right)}{\nu }_{32}^{\left(k\right)}}{E_2^{\left(k\right)}{E}_3^{\left(k\right)}{\Delta }_{}^{\left(k\right)}},\hspace{1em}{C}_{12}^{\left(k\right)}=\frac{{\nu }_{21}^{\left(k\right)}+{\nu }_{31}^{\left(k\right)}{\nu }_{23}^{\left(k\right)}}{E_2^{\left(k\right)}{E}_3^{\left(k\right)}{\Delta }_{}^{\left(k\right)}},\hspace{1em}{C}_{13}^{\left(k\right)}=\frac{{\nu }_{31}^{\left(k\right)}+{\nu }_{21}^{\left(k\right)}{\nu }_{32}^{\left(k\right)}}{E_2^{\left(k\right)}{E}_3^{\left(k\right)}{\Delta }_{}^{\left(k\right)}}\\ C_{22}^{\left(k\right)}=\frac{1-{\nu }_{13}^{\left(k\right)}{\nu }_{31}^{\left(k\right)}}{E_1^{\left(k\right)}{E}_3^{\left(k\right)}{\Delta }_{}^{\left(k\right)}},\hspace{1em}{C}_{23}^{\left(k\right)}=\frac{{\nu }_{32}^{\left(k\right)}+{\nu }_{12}^{\left(k\right)}{\nu }_{31}^{\left(k\right)}}{E_1^{\left(k\right)}{E}_3^{\left(k\right)}{\Delta }_{}^{\left(k\right)}},\hspace{1em}{C}_{33}^{\left(k\right)}=\frac{1-{\nu }_{12}^{\left(k\right)}{\nu }_{21}^{\left(k\right)}}{E_1^{\left(k\right)}{E}_2^{\left(k\right)}{\Delta }_{}^{\left(k\right)}}\\ C_{44}^{\left(k\right)}=G_{13}^{\left(k\right)},\hspace{1em}{C}_{55}^{\left(k\right)}=G_{23}^{\left(k\right)},\hspace{1em}{C}_{66}^{\left(k\right)}=G_{12}^{\left(k\right)}\end{array}$$

(36)

where the quantity ${\Delta }_{}^{\left(k\right)}$ has the following meaning

$${\Delta }_{}^{\left(k\right)}=\frac{1-{\nu }_{12}^{\left(k\right)}{\nu }_{21}^{\left(k\right)}-{\nu }_{23}^{\left(k\right)}{\nu }_{32}^{\left(k\right)}-{\nu }_{31}^{\left(k\right)}{\nu }_{13}^{\left(k\right)}-2{\nu }_{21}^{\left(k\right)}{\nu }_{32}^{\left(k\right)}{\nu }_{13}^{\left(k\right)}}{E_1^{\left(k\right)}{E}_2^{\left(k\right)}{E}_3^{\left(k\right)}}$$

(37)

in which $E_1^{\left(k\right)},E_2^{\left(k\right)},E_3^{\left(k\right)}$ are the Young’s moduli, $G_{12}^{\left(k\right)},G_{13}^{\left(k\right)},G_{23}^{\left(k\right)}$ are the shear moduli, and ${\nu }_{12}^{\left(k\right)},{\nu }_{13}^{\left(k\right)},{\nu }_{23}^{\left(k\right)}$ are the Poisson’s ratios. The following relations are required for a complete mechanical characterization of the orthotropic layer, for $i,j=1,2,3$

$$\frac{{\nu }_{ij}^{\left(k\right)}}{E_i^{\left(k\right)}}=\frac{{\nu }_{ji}^{\left(k\right)}}{E_j^{\left(k\right)}},\hspace{1em}{G}_{ij}^{\left(k\right)}=G_{ji}^{\left(k\right)}$$

(38)

The evaluation of the elastic coefficients is simplified if an isotropic layer is considered, since $E_{}^{\left(k\right)}=E_1^{\left(k\right)}=E_2^{\left(k\right)}=E_3^{\left(k\right)}$, ${\nu }_{}^{\left(k\right)}={\nu }_{12}^{\left(k\right)}={\nu }_{13}^{\left(k\right)}={\nu }_{23}^{\left(k\right)}$, and the mechanical properties are not affected by the orientation of the lamina. In this circumstance, the shear modulus is given by

$$G_{}^{\left(k\right)}=\frac{E_{}^{\left(k\right)}}{2\left(1+{\nu }^{\left(k\right)}\right)}$$

(39)

In this paper, the core is always assumed as isotropic; therefore, its orientation is meaningless. On the other hand, the two external skins are orthotropic and characterized by a variable orientation of the fibers ${\theta }^{\left(k\right)}$. In other words, the reinforcing fibers are placed according to curvilinear paths. The value of ${\theta }^{\left(k\right)}$ can be defined through the following general law

$$\begin{array}{cc}\hfill {\theta }^{\left(k\right)}\left({\alpha }_1,{\alpha }_2\right)={\theta }_1^{\left(k\right)}{\psi }_1^{\left(k\right)}\left({\alpha }_1\right)& +{\theta }_2^{\left(k\right)}{\psi }_2^{\left(k\right)}\left({\alpha }_2\right)+{\theta }_3^{\left(k\right)}{\psi }_3^{\left(k\right)}\left({\alpha }_1\right)+\hfill \\ & +{\theta }_4^{\left(k\right)}{\psi }_4^{\left(k\right)}\left({\alpha }_2\right)+{\theta }_5^{\left(k\right)}{\psi }_5^{\left(k\right)}\left({\alpha }_1,{\alpha }_2\right)+{\theta }_6^{\left(k\right)}{\psi }_6^{\left(k\right)}\left({\alpha }_1,{\alpha }_2\right)+{\overline{\theta }}^{\left(k\right)}\hfill \end{array}$$

(40)

in which the constants ${\theta }_i^{\left(k\right)}$, for $i=1,2,\dots ,6$, represent the maximum values of the corresponding fiber variations denoted by the functions ${\psi }_i^{\left(k\right)}$. On the other hand, ${\overline{\theta }}^{\left(k\right)}$ is the constant orientation that define the initial straight placement of the reinforcing fibers. The meaning of the six general functions ${\psi }_i^{\left(k\right)}$ is given below in terms of the following dimensionless coordinates, for $i=1,2$

$${\overline{\alpha }}_i=\frac{{\alpha }_i-{\alpha }_i^0}{{\alpha }_i^1-{\alpha }_i^0},\hspace{1em}\hspace{1em}{\tilde{\alpha }}_i=\frac{{\alpha }_i^1-{\alpha }_i}{{\alpha }_i^1-{\alpha }_i^0}$$

(41)

The functions ${\psi }_1^{\left(k\right)},{\psi }_3^{\left(k\right)}$ denote a variation along the principal direction ${\alpha }_1$ and can assume different meanings (power law, sine-wave, or exponential), as shown below

$${\psi }_1^{\left(k\right)}\left({\alpha }_1\right)=\{\begin{array}{c}{\overline{\alpha }}_1{}^{p_1}\\ {\left(\sin \left(\pi \left(n_1{\overline{\alpha }}_1+{\alpha }_{1m}\right)\right)\right)}^{p_1}\\ e^{{\left(-\frac{{\overline{\alpha }}_1}{{\alpha }_{1m}}\right)}^{p_1}}\end{array},\hspace{1em}{\psi }_3^{\left(k\right)}\left({\alpha }_1\right)=\{\begin{array}{c}{\tilde{\alpha }}_1{}^{p_3}\\ {\left(\sin \left(\pi \left(n_3{\tilde{\alpha }}_1+{\alpha }_{3m}\right)\right)\right)}^{p_3}\\ e^{{\left(-\frac{{\tilde{\alpha }}_1}{{\alpha }_{3m}}\right)}^{p_3}}\end{array}$$

(42)

where $n_1,n_3\in {\mathbb{N}}_0^{+}$, $p_1,p_3\in ℝ$ and ${\alpha }_{1m},{\alpha }_{3m}\in \left[0,1\right]$. On the other hand, the functions ${\psi }_2^{\left(k\right)},{\psi }_4^{\left(k\right)}$ define a variation along the principal direction ${\alpha }_2$ and have the same meaning of the previous ones

$${\psi }_2^{\left(k\right)}\left({\alpha }_2\right)=\{\begin{array}{c}{\overline{\alpha }}_2{}^{p_2}\\ {\left(\sin \left(\pi \left(n_2{\overline{\alpha }}_2+{\alpha }_{2m}\right)\right)\right)}^{p_2}\\ e^{{\left(-\frac{{\overline{\alpha }}_2}{{\alpha }_{2m}}\right)}^{p_2}}\end{array},\hspace{1em}{\psi }_4^{\left(k\right)}\left({\alpha }_2\right)=\{\begin{array}{c}{\tilde{\alpha }}_2{}^{p_4}\\ {\left(\sin \left(\pi \left(n_4{\tilde{\alpha }}_2+{\alpha }_{4m}\right)\right)\right)}^{p_4}\\ e^{{\left(-\frac{{\tilde{\alpha }}_2}{{\alpha }_{4m}}\right)}^{p_4}}\end{array}$$

(43)

where $n_2,n_4\in {\mathbb{N}}_0^{+}$, $p_2,p_4\in ℝ$ and ${\alpha }_{2m},{\alpha }_{4m}\in \left[0,1\right]$. Finally, the functions ${\psi }_5^{\left(k\right)},{\psi }_6^{\left(k\right)}$ involve both the principal directions ${\alpha }_1,{\alpha }_2$ and can be expressed in the following form

$${\psi }_i^{\left(k\right)}\left({\alpha }_1,{\alpha }_2\right)=e^{-{\Psi }_i}$$

(44)

for $i=5,6$. The Gaussian distribution can be used for this purpose and one gets

$${\Psi }_5=\frac{1}{2\left(1-{\rho }_{12}^2\right)}\left({\left(\frac{{\alpha }_1-{\alpha }_{5m}}{{\Delta }_1}\right)}^2+{\left(\frac{{\alpha }_2-{\alpha }_{6m}}{{\Delta }_2}\right)}^2-2{\rho }_{12}^{}\frac{{\alpha }_1-{\alpha }_{5m}}{{\Delta }_1}\frac{{\alpha }_2-{\alpha }_{6m}}{{\Delta }_2}\right)$$

(45)

where ${\rho }_{12}^{}\in \left[-1,1\right]$ and ${\Delta }_1,{\Delta }_2>0$. This function is clearly centered in the point $\left({\alpha }_{5m},{\alpha }_{6m}\right)$ of the domain, with ${\alpha }_{5m}\in \left[{\alpha }_1^0,{\alpha }_1^1\right]$ and ${\alpha }_{6m}\in \left[{\alpha }_2^0,{\alpha }_2^1\right]$. Analogously, an ellipse-shaped function could be chosen and one gets

$${\Psi }_6=\frac{{\left(\left({\alpha }_1-{\alpha }_{7m}\right)\cos \beta +\left({\alpha }_2-{\alpha }_{8m}\right)\sin \beta \right)}^2}{a^2}+\frac{{\left(-\left({\alpha }_1-{\alpha }_{7m}\right)\sin \beta +\left({\alpha }_2-{\alpha }_{8m}\right)\cos \beta \right)}^2}{b^2}$$

(46)

in which $a,b$ define the semi-axes of the ellipse, which could be also rotated by a constant angle $\beta$ measured counter-clockwise from the direction ${\alpha }_1$. This function is centered instead in the point $\left({\alpha }_{7m},{\alpha }_{8m}\right)$ within the reference domain, with ${\alpha }_{7m}\in \left[{\alpha }_1^0,{\alpha }_1^1\right]$ and ${\alpha }_{8m}\in \left[{\alpha }_2^0,{\alpha }_2^1\right]$. The variations ${\psi }_i^{\left(k\right)}$ are activated by setting the corresponding value ${\theta }_i^{\left(k\right)}$ different from zero. It should be noted that several variations can be also combined to obtain a more complex path of the reinforcing fibers.

The present formulation does not consider any defect or imperfection that could occur in the manufacturing process. Such defects are unavoidable when the fibers are placed according to curvilinear paths, as specified in the papers by Blom et al. [91,92], Nik et al. [93] and Akbarzadeh et al. [94]. Nevertheless, several production techniques are developed to reduce these imperfections [95]. Thus, in this research paper it is assumed by hypothesis that such defects that occur during the manufacturing process are negligible. Further assumptions that involve the present formulation can be found in the recent paper by Tornabene et al. [56].

Once the constitutive laws are introduced, it is more advantageous to define the internal actions in terms of generalized stress resultants ${\mathbf{S}}^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2\right)$ as shown below for $\tau =0,1,2,\dots ,N,N+1$

$${\mathbf{S}}^{\left(\tau \right)}={\displaystyle \sum _{\eta =0}^{N+1}{\mathbf{A}}^{\left(\tau \eta \right)}{\mathbf{D}}_{\Omega }^{}{\mathbf{u}}^{\left(\eta \right)}}$$

(47)

The vector that collects the generalized stress resultants, which are defined on the shell middle surface, assumes the following aspect for each order of kinematic expansion $\tau$

$${\mathbf{S}}^{\left(\tau \right)}={\left[\begin{array}{ccccccccc}{N}_1^{\left(\tau \right)}& N_2^{\left(\tau \right)}& N_{12}^{\left(\tau \right)}& N_{21}^{\left(\tau \right)}& T_1^{\left(\tau \right)}& T_2^{\left(\tau \right)}& P_1^{\left(\tau \right)}& P_2^{\left(\tau \right)}& S_3^{\left(\tau \right)}\end{array}\right]}^T$$

(48)

On the other hand, the matrix ${\mathbf{A}}^{\left(\tau \eta \right)}$ in (47) represents the constitutive operator of the present higher-order approach which can be evaluated as follows

$${\mathbf{A}}^{\left(\tau \eta \right)}={\displaystyle \sum _{k=1}^l{\displaystyle \underset{{\zeta }_k}{\overset{{\zeta }_{k+1}}{\int }}{\left({\mathbf{Z}}^{\left(\tau \right)}\right)}^T{\overline{\mathbf{C}}}^{\left(k\right)}{\mathbf{Z}}^{\left(\eta \right)}{H}_1{H}_{2}d\zeta }}$$

(49)

for $\tau ,\eta =0,1,2,\dots ,N,N+1$. In extended notation, the following matrix is accomplished

$${\mathbf{A}}^{\left(\tau \eta \right)}=\left[\begin{array}{ccccccccc}{A}_{11\left(20\right)}^{\left(\tau \eta \right)}& A_{12\left(11\right)}^{\left(\tau \eta \right)}& A_{16\left(20\right)}^{\left(\tau \eta \right)}& A_{16\left(11\right)}^{\left(\tau \eta \right)}& 0& 0& 0& 0& A_{13\left(10\right)}^{\left(\tau \tilde{\eta }\right)}\\ A_{12\left(11\right)}^{\left(\tau \eta \right)}& A_{22\left(02\right)}^{\left(\tau \eta \right)}& A_{26\left(11\right)}^{\left(\tau \eta \right)}& A_{26\left(02\right)}^{\left(\tau \eta \right)}& 0& 0& 0& 0& A_{23\left(01\right)}^{\left(\tau \tilde{\eta }\right)}\\ A_{16\left(20\right)}^{\left(\tau \eta \right)}& A_{26\left(11\right)}^{\left(\tau \eta \right)}& A_{66\left(20\right)}^{\left(\tau \eta \right)}& A_{66\left(11\right)}^{\left(\tau \eta \right)}& 0& 0& 0& 0& A_{36\left(10\right)}^{\left(\tau \tilde{\eta }\right)}\\ A_{16\left(11\right)}^{\left(\tau \eta \right)}& A_{26\left(02\right)}^{\left(\tau \eta \right)}& A_{66\left(11\right)}^{\left(\tau \eta \right)}& A_{66\left(02\right)}^{\left(\tau \eta \right)}& 0& 0& 0& 0& A_{36\left(01\right)}^{\left(\tau \tilde{\eta }\right)}\\ 0& 0& 0& 0& A_{44\left(20\right)}^{\left(\tau \eta \right)}& A_{45\left(11\right)}^{\left(\tau \eta \right)}& A_{44\left(10\right)}^{\left(\tau \tilde{\eta }\right)}& A_{45\left(10\right)}^{\left(\tau \tilde{\eta }\right)}& 0\\ 0& 0& 0& 0& A_{45\left(11\right)}^{\left(\tau \eta \right)}& A_{55\left(02\right)}^{\left(\tau \eta \right)}& A_{45\left(01\right)}^{\left(\tau \tilde{\eta }\right)}& A_{55\left(01\right)}^{\left(\tau \tilde{\eta }\right)}& 0\\ 0& 0& 0& 0& A_{44\left(10\right)}^{\left(\tilde{\tau }\eta \right)}& A_{45\left(01\right)}^{\left(\tilde{\tau }\eta \right)}& A_{44\left(00\right)}^{\left(\tilde{\tau }\tilde{\eta }\right)}& A_{45\left(00\right)}^{\left(\tilde{\tau }\tilde{\eta }\right)}& 0\\ 0& 0& 0& 0& A_{45\left(10\right)}^{\left(\tilde{\tau }\eta \right)}& A_{55\left(01\right)}^{\left(\tilde{\tau }\eta \right)}& A_{45\left(00\right)}^{\left(\tilde{\tau }\tilde{\eta }\right)}& A_{55\left(00\right)}^{\left(\tilde{\tau }\tilde{\eta }\right)}& 0\\ A_{13\left(10\right)}^{\left(\tilde{\tau }\eta \right)}& A_{23\left(01\right)}^{\left(\tilde{\tau }\eta \right)}& A_{36\left(10\right)}^{\left(\tilde{\tau }\eta \right)}& A_{36\left(01\right)}^{\left(\tilde{\tau }\eta \right)}& 0& 0& 0& 0& A_{33\left(00\right)}^{\left(\tilde{\tau }\tilde{\eta }\right)}\end{array}\right]$$

(50)

where the following definitions are required to compute its elements for $\tau ,\eta =0,1,2,\dots ,N,N+1$, $n,m=1,2,3,4,5,6$ and $p,q=0,1,2$

$$\begin{array}{l}{A}_{nm\left(pq\right)}^{\left(\tau \eta \right)}={\displaystyle \sum _{k=1}^l{\displaystyle \underset{{\zeta }_k}{\overset{{\zeta }_{k+1}}{\int }}{\overline{C}}_{nm}^{\left(k\right)}{F}_{\eta }^{}{F}_{\tau }^{}\frac{H_1{H}_2}{H_1^p{H}_2^q}d\zeta }}\\ A_{nm\left(pq\right)}^{\left(\tilde{\tau }\eta \right)}={\displaystyle \sum _{k=1}^l{\displaystyle \underset{{\zeta }_k}{\overset{{\zeta }_{k+1}}{\int }}{\overline{C}}_{nm}^{\left(k\right)}{F}_{\eta }^{}\frac{\partial F_{\tau }^{}}{\partial \zeta }\frac{H_1{H}_2}{H_1^p{H}_2^q}d\zeta }}\\ A_{nm\left(pq\right)}^{\left(\tau \tilde{\eta }\right)}={\displaystyle \sum _{k=1}^l{\displaystyle \underset{{\zeta }_k}{\overset{{\zeta }_{k+1}}{\int }}{\overline{C}}_{nm}^{\left(k\right)}\frac{\partial F_{\eta }^{}}{\partial \zeta }{F}_{\tau }^{}\frac{H_1{H}_2}{H_1^p{H}_2^q}d\zeta }}\\ A_{nm\left(pq\right)}^{\left(\tilde{\tau }\tilde{\eta }\right)}={\displaystyle \sum _{k=1}^l{\displaystyle \underset{{\zeta }_k}{\overset{{\zeta }_{k+1}}{\int }}{\overline{C}}_{nm}^{\left(k\right)}\frac{\partial F_{\eta }^{}}{\partial \zeta }\frac{\partial F_{\tau }^{}}{\partial \zeta }\frac{H_1{H}_2}{H_1^p{H}_2^q}d\zeta }}\end{array}$$

(51)

Finally, the static equilibrium of the shell can be expressed in terms of generalized displacement components by means of the following governing equation in vector form

$${\displaystyle \sum _{\eta =0}^{N+1}{\mathbf{L}}^{\left(\tau \eta \right)}{\mathbf{u}}^{\left(\eta \right)}}+{\mathbf{q}}^{\left(\tau \right)}=\mathbf{0}$$

(52)

for $\tau =0,1,2,\dots ,N,N+1$. This system of partial derivative equations defines three equilibrium relations for each order of kinematic expansion. The fundamental operator ${\mathbf{L}}^{\left(\tau \eta \right)}$ can be evaluated according to the definition shown below

$${\mathbf{L}}^{\left(\tau \eta \right)}={\mathbf{D}}_{\Omega }^{\ast }{\mathbf{A}}^{\left(\tau \eta \right)}{\mathbf{D}}_{\Omega }^{}$$

(53)

for $\tau ,\eta =0,1,2,\dots ,N,N+1$. The equilibrium operator ${\mathbf{D}}_{\Omega }^{\ast }$, instead, assumes the following aspect

$${\mathbf{D}}_{\Omega }^{\ast }={\left[\begin{array}{ccc}\frac{1}{A_1}\frac{\partial }{\partial {\alpha }_1}+\frac{1}{A_1{A}_2}\frac{\partial A_2}{\partial {\alpha }_1}& -\frac{1}{A_1{A}_2}\frac{\partial A_1}{\partial {\alpha }_2}& -\frac{1}{R_1}\\ -\frac{1}{A_1{A}_2}\frac{\partial A_2}{\partial {\alpha }_1}& \frac{1}{A_2}\frac{\partial }{\partial {\alpha }_2}+\frac{1}{A_1{A}_2}\frac{\partial A_1}{\partial {\alpha }_2}& -\frac{1}{R_2}\\ \frac{1}{A_1{A}_2}\frac{\partial A_1}{\partial {\alpha }_2}& \frac{1}{A_1}\frac{\partial }{\partial {\alpha }_1}+\frac{1}{A_1{A}_2}\frac{\partial A_2}{\partial {\alpha }_1}& 0\\ \frac{1}{A_2}\frac{\partial }{\partial {\alpha }_2}+\frac{1}{A_1{A}_2}\frac{\partial A_1}{\partial {\alpha }_2}& \frac{1}{A_1{A}_2}\frac{\partial A_2}{\partial {\alpha }_1}& 0\\ \frac{1}{R_1}& 0& \frac{1}{A_1}\frac{\partial }{\partial {\alpha }_1}+\frac{1}{A_1{A}_2}\frac{\partial A_2}{\partial {\alpha }_1}\\ 0& \frac{1}{R_2}& \frac{1}{A_2}\frac{\partial }{\partial {\alpha }_2}+\frac{1}{A_1{A}_2}\frac{\partial A_1}{\partial {\alpha }_2}\\ -1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right]}^T$$

(54)

On the other hand, the vector ${\mathbf{q}}^{\left(\tau \right)}$ introduced for each order of kinematic equation in (52) collects three load components for $\tau =0,1,2,\dots ,N,N+1$ as shown below

$${\mathbf{q}}^{\left(\tau \right)}={\left[\begin{array}{ccc}{q}_1^{\left(\tau \right)}& q_2^{\left(\tau \right)}& q_n^{\left(\tau \right)}\end{array}\right]}^T$$

(55)

where $q_1^{\left(\tau \right)},q_2^{\left(\tau \right)},q_n^{\left(\tau \right)}$ stand for the external load components applied within the shell middle surface along the principal directions ${\alpha }_1,{\alpha }_2,\zeta$, respectively. Their value is computed once the surface loads applied on the shell external surfaces $q_1^{(\pm )},q_2^{(\pm )},q_n^{(\pm )}$ are defined. The superscript $(+)$ specifies that the load component is acting on the upper surface, whereas $(-)$ is used to characterize the force component applied on the lower surface. By means of the static equivalence principle, one gets

$$\begin{array}{l}{q}_1^{\left(\tau \right)}=q_1^{(-)}{F}_{\tau }^{(-)}{H}_1^{(-)}{H}_2^{(-)}+q_1^{(+)}{F}_{\tau }^{(+)}{H}_1^{(+)}{H}_2^{(+)}\\ q_2^{\left(\tau \right)}=q_2^{(-)}{F}_{\tau }^{(-)}{H}_1^{(-)}{H}_2^{(-)}+q_2^{(+)}{F}_{\tau }^{(+)}{H}_1^{(+)}{H}_2^{(+)}\\ q_n^{\left(\tau \right)}=q_n^{(-)}{F}_{\tau }^{(-)}{H}_1^{(-)}{H}_2^{(-)}+q_n^{(+)}{F}_{\tau }^{(+)}{H}_1^{(+)}{H}_2^{(+)}\end{array}$$

(56)

where the symbol $F_{\tau }^{(\pm )}$ denotes the value that a generic thickness function assumes on the external surfaces of the shell. Analogously, $H_1^{(\pm )},H_2^{(\pm )}$ are the values that the geometric parameters (19) assume on the same surfaces (for $\zeta =\pm h/2$).

The governing equations in (52) can be solved once the natural or essential boundary conditions are properly enforced. The compatibility requirement of the present formulation is $C^1$, since both the displacements and stress resultant components are involved in the boundary conditions. The essential boundary conditions involve the generalized displacements for each order of kinematic expansion $\tau$. The following relations are required for clamped edges

$$u_1^{\left(\tau \right)}=u_2^{\left(\tau \right)}=u_3^{\left(\tau \right)}=0$$

(57)

On the other hand, a free edge condition is expressed analytically through the natural boundary conditions. Thus, the stress resultants are involved. In particular, the following conditions are required for ${\alpha }_1={\alpha }_1^0$ (or ${\alpha }_1={\alpha }_1^1$) and ${\alpha }_2^0\le {\alpha }_2\le {\alpha }_2^1$

$$N_1^{\left(\tau \right)}=N_{12}^{\left(\tau \right)}=T_1^{\left(\tau \right)}=0$$

(58)

On the other hand, the natural boundary conditions for ${\alpha }_2={\alpha }_2^0$ (or ${\alpha }_2={\alpha }_2^1$) and ${\alpha }_1^0\le {\alpha }_1\le {\alpha }_1^1$ become

$$N_{21}^{\left(\tau \right)}=N_2^{\left(\tau \right)}=T_2^{\left(\tau \right)}=0$$

(59)

With reference to the shell element depicted in Figure 1, it can be observed that the four external edges are identified by a cardinal direction: north (N), east (E), south (S), and west (W). To simplify the definition of external restraints, the boundary conditions are specified following the sequence WSEN. The letters “C” and “F” will replace the corresponding cardinal direction notation to define a clamped or free edge, respectively. For instance, CCCC stands for a completely clamped shell. On the other hand, when the notation CCCF is used, only the northern edge is free, whereas the others are clamped.

When a structure with a closing meridian such as a complete shell of revolution is analyzed, the structural compatibility must be enforced along the two coincident edges. If the closing meridian is identified by ${\alpha }_1={\alpha }_1^0$ and ${\alpha }_1={\alpha }_1^1$, the structural compatibility is given by

$$\begin{array}{ccc}{N}_1^{\left(\tau \right)}\left({\alpha }_1^0,{\alpha }_2\right)=N_1^{\left(\tau \right)}\left({\alpha }_1^1,{\alpha }_2\right)& & u_1^{\left(\tau \right)}\left({\alpha }_1^0,{\alpha }_2\right)=u_1^{\left(\tau \right)}\left({\alpha }_1^1,{\alpha }_2\right)\\ N_{12}^{\left(\tau \right)}\left({\alpha }_1^0,{\alpha }_2\right)=N_{12}^{\left(\tau \right)}\left({\alpha }_1^1,{\alpha }_2\right)& & u_2^{\left(\tau \right)}\left({\alpha }_1^0,{\alpha }_2\right)=u_2^{\left(\tau \right)}\left({\alpha }_1^1,{\alpha }_2\right)\\ T_1^{\left(\tau \right)}\left({\alpha }_1^0,{\alpha }_2\right)=T_1^{\left(\tau \right)}\left({\alpha }_1^1,{\alpha }_2\right)& & u_3^{\left(\tau \right)}\left({\alpha }_1^0,{\alpha }_2\right)=u_3^{\left(\tau \right)}\left({\alpha }_1^1,{\alpha }_2\right)\end{array}$$

(60)

On the other hand, the following relations are required if the closing edge is characterized by ${\alpha }_2={\alpha }_2^0$ and ${\alpha }_2={\alpha }_2^1$

$$\begin{array}{ccc}{N}_{21}^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^0\right)=N_{21}^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^1\right)& & u_1^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^0\right)=u_1^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^1\right)\\ N_2^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^0\right)=N_2^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^1\right)& & u_2^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^0\right)=u_2^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^1\right)\\ T_2^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^0\right)=T_2^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^1\right)& & u_3^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^0\right)=u_3^{\left(\tau \right)}\left({\alpha }_1,{\alpha }_2^1\right)\end{array}$$

(61)

4. Numerical Technique

The governing equations are solved numerically by means of the GDQ method. In this section, only the main features of this numerical approach are presented, since a complete and accurate treatise is presented in the recent review paper by Tornabene et al. [117]. By definition, the GDQ method allows evaluation of the $n$-th order derivative of a smooth function $f\left(x\right)$ at a generic discrete point $x_i$ of the reference domain as a weighted linear sum of the values that the function assumes in each point of the domain

$${\frac{d^{n}f\left(x\right)}{d{x}^n}|}_{x=x_i}\cong {\displaystyle \sum _{j=1}^T{\varsigma }_{ij}^{\left(n\right)}f\left(x_j\right)}$$

(62)

where $T$ stands for the overall number of discrete points defined within the domain, which are placed according to the Chebyshev-Gauss-Lobatto grid distribution

$$x_i=\left(1-\cos \left(\frac{i-1}{T-1}\pi \right)\right)\frac{x_T-x_1}{2}+x_1$$

(63)

Consequently, a set of $T$ discrete nodes is introduced as follows

$$a=x_1,x_2,\dots ,x_i,\dots ,x_{T-1},x_T=b$$

(64)

where $x_1,x_T$ are the boundary points of the domain. The weighting coefficients ${\varsigma }_{ij}^{\left(n\right)}$ are computed instead through the following recursive expressions provided by Shu [115], for $i,j=1,2,\dots ,T$ and $n=1,2,\dots ,T-1$

$$\begin{array}{c}{\varsigma }_{ij}^{\left(n\right)}=n\left({\varsigma }_{ij}^{\left(1\right)}{\varsigma }_{ii}^{\left(n-1\right)}-\frac{{\varsigma }_{ij}^{\left(n-1\right)}}{x_i-x_j}\right)\hspace{1em}\mathrm{for} i\ne j\\ {\varsigma }_{ij}^{\left(n\right)}=-{\displaystyle \sum _{j=1,j\ne i}^T{\varsigma }_{ij}^{\left(n\right)}\hspace{1em}\mathrm{for} i=j}\end{array}$$

(65)

where ${\varsigma }_{ij}^{\left(1\right)}$ stands for the weighting coefficients for the first-order derivatives defined below

$${\varsigma }_{ij}^{\left(1\right)}=\frac{{\displaystyle \prod _{k=1,i\ne k}^T\left(x_i-x_k\right)}}{\left(x_i-x_j\right){\displaystyle \prod _{k=1,j\ne k}^T\left(x_j-x_k\right)}}$$

(66)

As far as two-dimensional domains are concerned, the present approach can be easily generalized as shown in [23,117]. In these circumstances, the grid distribution (63) is applied along the main directions ${\alpha }_1,{\alpha }_2$ by specifying the number of discrete points as $I_N,I_M$, respectively.

The same numerical approach can be considered as the starting point for the evaluation of integrals. The methodology in hand is known as Generalized Integral Quadrature (GIQ) method. For the sake of completeness, only the main definition is presented in the paper. Further details concerning this technique can be found in [117]. The integral of a smooth function $f\left(x\right)$ within the interval $\left[x_i,x_j\right]$ included in the reference domain, with $x_i,x_j\in \left[a,b\right]$ and $x_i>a, x_j<b$, can be computed as follows

$${\displaystyle \underset{x_i}{\overset{x_j}{\int }}f\left(x\right)dx}\cong {\displaystyle \sum _{k=1}^T{w}_k^{ij}f\left(x_k\right)}$$

(67)

where $w_k^{ij}$ stands for the weighting coefficients for the integration at issue, which can be easily evaluated starting from the weighting coefficients for the first-order derivatives (66). This numerical method is used in the present research to compute the stiffness terms (51), once the thickness direction is discretized by applying the same grid shown above.

5. Solution of the Static Problem

By means of the GDQ method, the discrete form of the fundamental system of Equation (53) is achieved, which becomes

$$\mathbf{K}\mathsf{\delta }=\mathbf{f}$$

(68)

where $\mathbf{K}$ is the global discrete stiffness matrix, $\mathsf{\delta }$ the vector of generalized displacements related to the discrete points of the domain, and $\mathbf{f}$ is the vector that collects the values of the external loads. It should be noted that the unknowns of the static problem at issue are collected in the corresponding algebraic vector $\mathsf{\delta }$. It is convenient at this point to collect such displacements so that the degrees of freedom linked to the inner points of the domain are separated from the ones related to the boundary points. The sub-vectors ${\mathsf{\delta }}_d,{\mathsf{\delta }}_b$ are introduced, respectively. Analogously, the same classification is specified for the external load vector (${\mathbf{f}}_d,{\mathbf{f}}_b$). Thus, the system of linear Equation (68) becomes

$$\left[\begin{array}{cc}{\mathbf{K}}_{bb}& {\mathbf{K}}_{bd}\\ {\mathbf{K}}_{db}& {\mathbf{K}}_{dd}\end{array}\right]\left[\begin{array}{c}{\mathsf{\delta }}_b\\ {\mathsf{\delta }}_d\end{array}\right]=\left[\begin{array}{c}{\mathbf{f}}_b\\ {\mathbf{f}}_d\end{array}\right]$$

(69)

in which the stiffness matrix is also partitioned, consequently. Finally, the proper manipulations lead to the following result, which allows the obtaining of the static solution ${\mathsf{\delta }}_d$ in terms of generalized nodal displacements

$$\left({\mathbf{K}}_{dd}-{\mathbf{K}}_{db}{\mathbf{K}}_{bb}^{-1}{\mathbf{K}}_{bd}\right){\mathsf{\delta }}_d=f_d-{\mathbf{K}}_{db}{\mathbf{K}}_{bb}^{-1}{\mathbf{f}}_b$$

(70)

The procedure just illustrated represents the so-called static condensation procedure and allows the reduction of the initial size of the problem [4].

Once the static solution in terms of generalized displacements is accomplished, the through-the-thickness profiles of stress and strain components can be evaluated by using the three-dimensional elasticity equations written in an orthogonal curvilinear coordinate system. This approach is known as recovery procedure and can be employed to evaluate the three-dimensional quantities at issue, starting from the solutions obtained by a two-dimensional shell model. The reader can find a complete treatise about this approach in the papers [21].

Finally, it should be mentioned that the present formulation is implemented in a computational code developed in MATLAB by the authors [119].

6. Applications

The numerical results are presented in this section. For this purpose, four structures reinforced by curvilinear fibers are analyzed. Their geometries are depicted in Figure 2. In particular, a square plate, a conical shell, a doubly-curved panel of revolution with catenary meridian and a doubly-curved panel of translation (obtained by moving a circumference over a parabola) are investigated. Their shape is described through the position vectors listed in

Table 1. Definition of structural geometries and corresponding lamination schemes.

Square plate

Position vector

$\mathbf{r}\left(x,y\right)=x{\mathbf{e}}_1+y{\mathbf{e}}_2$, $x\in \left[0,L_x\right],y\in \left[0,L_y\right],L_x=L_y=1.5 \mathrm{m}$

Lamination scheme

$\left({\theta }_1^{\left(1\right)}{\psi }_1^{\left(1\right)}/\mathrm{Soft}-\mathrm{core}/90+{\theta }_1^{\left(3\right)}{\psi }_1^{\left(3\right)}\right),{\theta }_1^{\left(1\right)}={\theta }_1^{\left(3\right)}=\varphi ,h_s=0.02 \mathrm{m},h_c=0.06 \mathrm{m}$ ${\psi }_1^{\left(1\right)}\left(x\right)={\psi }_1^{\left(3\right)}\left(x\right)={\left(\sin \left(\pi \left(n_1{\overline{\alpha }}_1+{\alpha }_{1m}\right)\right)\right)}^{p_1}$

Conical shell

Position vector

$\begin{array}{c}\mathbf{r}\left({\alpha }_1,y\right)=\left(a\cos {\alpha }_1+y\sin \alpha \sin \phi \right){\mathbf{e}}_1-y\cos \alpha {\mathbf{e}}_2+\left(b\sin {\alpha }_1-y\sin \alpha \cos \phi \right){\mathbf{e}}_3\\ \phi \left({\alpha }_1\right)=\arctan \left(-\frac{b\cos {\alpha }_1}{a\sqrt{1-{\cos }^2{\alpha }_1}}\right),a=b=0.5 \mathrm{m},\alpha =\pi /12, {\alpha }_1\in \left[{\alpha }_1^0,{\alpha }_1^1\right]=\left[0,2\pi \right], y\in \left[y_0,y_1\right]=\left[0,1 \mathrm{m}\right]\end{array}$

Lamination scheme

$\begin{array}{c}\left(90+{\theta }_2^{\left(1\right)}{\psi }_2^{\left(1\right)}/\mathrm{Soft}-\mathrm{core}/90+{\theta }_2^{\left(3\right)}{\psi }_2^{\left(3\right)}\right),{\theta }_2^{\left(1\right)}=-{\theta }_2^{\left(3\right)}=\varphi ,h_s=0.02 \mathrm{m},h_c=0.06 \mathrm{m}\\ {\psi }_2^{\left(1\right)}\left(y\right)={\psi }_2^{\left(3\right)}\left(y\right)={\overline{\alpha }}_2{}^{p_2},p_2=1\end{array}$

Doubly-curved panel of revolution with catenary meridian

Position vector

$\begin{array}{c}\mathbf{r}\left(\phi ,\vartheta \right)=R_0\left(\phi \right)\cos \vartheta {\mathbf{e}}_1-R_0\left(\phi \right)\sin \vartheta {\mathbf{e}}_2+a\mathrm{arcsinh}\left(\frac{1}{\tan \phi }\right){\mathbf{e}}_3\\ R_0\left(\phi \right)=a\cosh \left(\mathrm{arcsinh}\left(\frac{1}{\tan \phi }\right)\right),a=2 \mathrm{m},c=2 \mathrm{m},d=1 \mathrm{m}\\ {\alpha }_1\in \left[{\alpha }_1^0,{\alpha }_1^1\right]=\left[-2.05117,2.05117\right],{\alpha }_2\in \left[{\alpha }_2^0,{\alpha }_2^1\right]=\left[-\pi /6,\pi /6\right]\end{array}$

Lamination scheme

$\begin{array}{c}\left(30+{\theta }_1^{\left(1\right)}{\psi }_1^{\left(1\right)}/\mathrm{Soft}-\mathrm{core}/45+{\theta }_5^{\left(3\right)}{\psi }_5^{\left(3\right)}\right), {\theta }_1^{\left(1\right)}=-2{\theta }_5^{\left(3\right)}=\varphi , h_s=0.05 \mathrm{m}, h_c=0.1 \mathrm{m}\\ {\psi }_1^{\left(1\right)}\left(\phi \right)=e^{{\left(-\frac{\overline{\phi }}{{\phi }_m}\right)}^{p_1}}, p_1=1, {\phi }_m=0.9\\ {\psi }_5^{\left(3\right)}\left(\phi ,\vartheta \right)=e^{\left(-\frac{1}{2\left(1-{\rho }_{12}^2\right)}\left({\left(\frac{\phi -{\phi }_m}{{\Delta }_1}\right)}^2+{\left(\frac{\vartheta -{\vartheta }_m}{{\Delta }_2}\right)}^2-2{\rho }_{12}^{}\frac{\phi -{\phi }_m}{{\Delta }_1}\frac{\vartheta -{\vartheta }_m}{{\Delta }_2}\right)\right)}, {\phi }_m=0, {\vartheta }_m=\frac{{\vartheta }_1-{\vartheta }_0}{2}, {\Delta }_1=0.3, {\Delta }_2=100, {\rho }_{12}=0\end{array}$

Doubly-curved panel of translation (a circumference slides over a parabola)

Position vector

$\begin{array}{c}\mathbf{r}\left({\alpha }_1,{\alpha }_2\right)=\left(R_0^{{\alpha }_1}\left({\alpha }_1\right)-x_3^{{\alpha }_2}\left({\alpha }_2\right)\sin {\alpha }_1\right){\mathbf{e}}_1+-R_0^{{\alpha }_2}\left({\alpha }_2\right){\mathbf{e}}_2+\left(x_3^{{\alpha }_1}\left({\alpha }_1\right)+x_3^{{\alpha }_2}\left({\alpha }_2\right)\cos {\alpha }_1\right){\mathbf{e}}_3\\ R_0^{{\alpha }_1}\left({\alpha }_1\right)=\frac{k^{{\alpha }_1}\tan {\alpha }_1}{2}, x_3^{{\alpha }_1}\left({\alpha }_1\right)=\frac{{\left(R_0^{{\alpha }_1}\left({\alpha }_1\right)\right)}^2}{k^{{\alpha }_1}}, k^{{\alpha }_1}=\frac{a^2-d^2}{b}, a=2 \mathrm{m}, b=0.5 \mathrm{m}, c=-2 \mathrm{m}, d=0 \mathrm{m}\\ R_0^{{\alpha }_2}\left({\alpha }_2\right)=R\sin {\alpha }_2, x_3^{{\alpha }_2}\left({\alpha }_2\right)=R\left(1-\cos {\alpha }_2\right), R=3 \mathrm{m}, {\alpha }_1\in \left[{\alpha }_1^0,{\alpha }_1^1\right]=\left[-\frac{\pi }{6},\frac{\pi }{6}\right], {\alpha }_2\in \left[{\alpha }_2^0,{\alpha }_2^1\right]=\left[-\pi /4,\pi /4\right]\end{array}$

Lamination scheme

$\begin{array}{c}\left(30+{\theta }_3^{\left(1\right)}{\psi }_3^{\left(1\right)}\left({\alpha }_1\right)/\mathrm{Soft}-\mathrm{core}/60+{\theta }_1^{\left(3\right)}{\psi }_1^{\left(3\right)}\right),{\theta }_3^{\left(1\right)}=-{\theta }_1^{\left(3\right)}=\varphi ,h_s=0.02 \mathrm{m},h_c=0.06 \mathrm{m}\\ {\psi }_3^{\left(1\right)}\left({\alpha }_1\right)={\tilde{\alpha }}_1^{p_3},p_3=1,{\psi }_1^{\left(3\right)}\left({\alpha }_1\right)={\overline{\alpha }}_1{}^{p_1},p_1=1\end{array}$

. Analogously, the lamination schemes, as well as the mathematical laws that describe the curvilinear paths of the reinforcing fibers, are specified in Table 1. For the sake of clarity, the curvilinear paths are also presented in graphical form in Figure 3 for the lower and upper sheets of each structure, considering the maximum value of the fiber orientation. For conciseness purposes, the mechanical properties of the orthotropic skins and the isotropic core are listed in

Table 2. Mechanical properties of the materials used in the computations.

Material	Young’s Moduli [GPa]	Poisson’s Ratios	Shear Moduli [GPa]
Graphite-epoxy (orthotropic)	$E_1=137.90$	${\nu }_{12}=0.30$	$G_{12}=7.10$
	$E_2=8.96$	${\nu }_{13}=0.30$	$G_{13}=7.10$
	$E_3=8.96$	${\nu }_{23}=0.49$	$G_{23}=6.21$
Glass-epoxy (orthotropic)	$E_1=53.78$	${\nu }_{12}=0.25$	$G_{12}=8.96$ $G_{12}=8.96$
	$E_2=17.93$	${\nu }_{13}=0.25$
	$E_3=17.93$	${\nu }_{23}=0.34$
Foam (isotropic)	$E=0.232$	$\nu =0.20$	$G=\frac{E}{2\left(1+\nu \right)}$

. On the other hand, the mechanical composition of the four structures, which are all loaded by an external pressure $q_n^{(+)}=-10 \mathrm{kPa}$, is summarized in

Table 3. Mechanical composition of the four structures.

Structural Element	Core Material	Skin Material
Square plate	Foam	Glass-epoxy
Conical shell	Foam	Glass-epoxy
Doubly-curved panel of revolution	Foam	Graphite-epoxy
Doubly-curved panel of translation	Foam	Graphite-epoxy

.

The results are presented in terms of through-the-thickness profiles of strain, stress, and displacement components. Then, the profiles of the generalized displacements $u_1^{\left(0\right)},u_2^{\left(0\right)},u_3^{\left(0\right)}$ along two couples of orthogonal directions are also provided for each structure.

A set of parametric investigations is presented to study the effect of the fiber orientation represented by the symbol $\varphi \in \left[0°,60°\right]$ on the linear static response. Each group of analyses is repeated to investigate also the influence of the maximum order of kinematic expansion. To this aim, three higher-order theories are considered, which are $\mathrm{EDZ}2$, $\mathrm{EDZ}3$ and $\mathrm{EDZ}4$.

Finally, it should be mentioned that the same structures have been analyzed from the dynamic point of view (free vibration analysis) in the previous paper by Tornabene et al. [56].

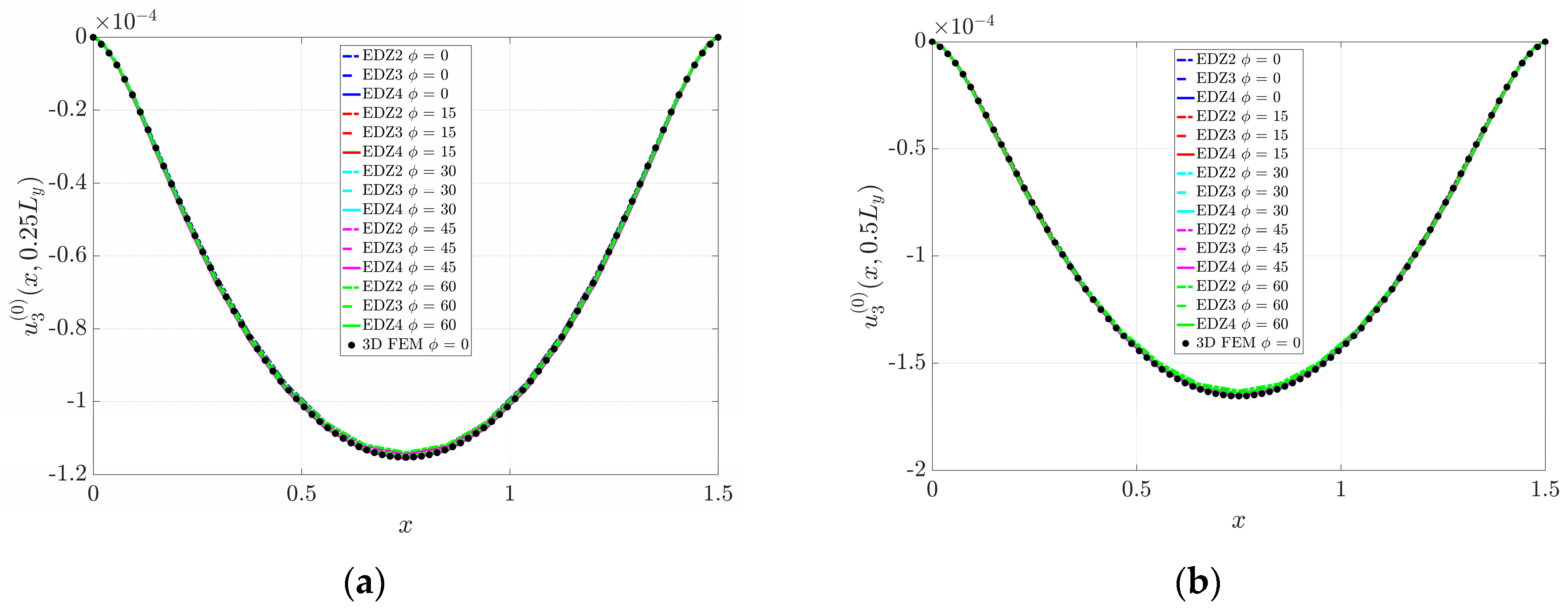
6.1. Square Plate

The discrete model of a completely clamped (CCCC) square plate is obtained by setting $I_N=I_M=25$ grid points. In this circumstance, a three-dimensional finite element model (3D-FEM) is also developed for comparison purposes, only for straight reinforcing fibers ($\varphi =0$). The commercial software Strand7 is employed for this reason, by using the Hexa20 brick elements.

The through-the-thickness variations of the strain, stress and displacement components are evaluated in $\left(0.25L_x,0.25L_y\right)$ and are shown in Figure 4, Figure 5 and Figure 6. On the other hand, the profiles of the generalized displacements are evaluated for constant values of the main coordinates, varying the values of the fiber orientation $\varphi$ and the maximum order of kinematic expansion.

These results are presented in Figure 7 and Figure 8. It can be noted that the variation of the fiber orientation mainly affects the generalized displacements defined on the middle surface than the three-dimensional profiles of strains, stresses and displacements, since the soft-core effect is prevalent. Nevertheless, also the stress and strain components are influenced by the placement of the fibers, especially for higher values of $\varphi \in \left[0°,60°\right]$. This example proves also the validity of the current formulation, both in terms of two-dimensional and three-dimensional solutions, through the great agreement with the 3D-FEM results.

6.2. Conical Shell

A completely clamped conical shell is considered in the next application. The discrete model is obtained by setting $I_N=31$ and $I_M=25$. The through-the-thickness profiles of strain, stress and displacement components are evaluated in the point $\left(0.25\left({\alpha }_1^1-{\alpha }_1^0\right)+{\alpha }_1^0,0.25\left(y_1-y_0\right)+y_0\right)$ and are presented in Figure 9, Figure 10 and Figure 11. As it can be noted from these figures, the fiber orientation $\varphi \in \left[0°,60°\right]$ affects the static response of the sandwich structure at issue. Analogously, several profiles of the generalized displacements $u_1^{\left(0\right)},u_2^{\left(0\right)},u_3^{\left(0\right)}$ for constant values of the main coordinates can be obtained by varying the fiber orientation, as it can be noted in Figure 12 and Figure 13. The influence of the curvilinear path is especially evident along the circumferential lines obtained for constant values of $y$ coordinate (Figure 12), where the corresponding displacement profiles are represented by straight segments.

6.3. Doubly-Curved Panel of Revolution

The doubly-curved panel investigated in this paragraph is obtained by the rotation of a catenary shaped profile about the axis of revolution. The corresponding discrete model is obtained by setting $I_N=31$ and $I_M=25$ as in the previous example. The boundary conditions are specified by the notation CCCF; in other words, the northern edge is free, whereas the others are clamped.

The through-the-thickness variations of three-dimensional strains, stresses and displacements are computed in the point $\left(0.25\left({\phi }_1-{\phi }_0\right)+{\phi }_0,0.25\left({\vartheta }_1-{\vartheta }_0\right)+{\vartheta }_0\right)$. The corresponding graphs are illustrated in Figure 14, Figure 15 and Figure 16, varying the values of the fiber orientation $\varphi \in \left[0°,60°\right]$ and the maximum order of kinematic expansion. Even in this circumstance, the static response is affected by the fiber orientation.

On the other hand, the profiles of the generalized displacements within the shell middle surface are collected in Figure 17 and Figure 18 for constant values of the principal coordinates.

6.4. Doubly-Curved Panel of Translation

The last structure is a completely clamped doubly-curved panel of translation. The middle surface of this peculiar geometry can be described by sliding a circumference over a parabolic arch. As far as the discrete model is concerned, the grid distribution is applied by setting $I_N=I_M=31$.

The through-the-thickness profiles of strain, stress and displacement components are evaluated respectively in $\left(0.25\left({\alpha }_1^1-{\alpha }_1^0\right)+{\alpha }_1^0,0.25\left({\alpha }_2^1-{\alpha }_2^0\right)+{\alpha }_2^0\right)$, varying the values of the fiber orientation $\varphi \in \left[0°,60°\right]$ and the maximum order of kinematic expansion $N$. Their graphs are shown in Figure 19, Figure 20 and Figure 21.

The variations of the generalized displacement components computed on the shell middle surface are shown instead in Figure 22 and Figure 23, by selecting constant values of the principal coordinates.

Finally, the deformed shapes of the four shell structures analyzed in this section are depicted in Figure 24 for three different values of the fiber orientation ($\varphi =0°,\varphi =30°,\varphi =60°$).

6.5. Remarks on the Use of the Murakami’s Function

It can be noted that the present approach is used to perform the static analysis of sandwich structures made of three layers (two external stiffer skins and a soft-core). Murakami’s function can capture their effective mechanical behavior in this circumstance. Nevertheless, sandwich structures could be characterized by more than three layers. For instance, the inner soft-core could be enclosed by couples of orthotropic stiffer layers. Consequently, a lamination scheme could be given by $\left({\theta }^{\left(1\right)}/{\theta }^{\left(2\right)}/\mathrm{Soft}-\mathrm{core}/{\theta }^{\left(4\right)}/{\theta }^{\left(5\right)}\right)$. As highlighted first in the paper by Gherlone [120], then in the work by Groh and Weaver [121], the Murakami’s function embedded in an ESL model could be inadequate to deal with these kinds of structural problems. A final application is presented to illustrate this aspect. For this purpose, a completely clamped laminated square plate with $L_x=L_y=1.5 \mathrm{m}$ and $h=0.1 \mathrm{m}$, loaded by an external pressure $q_n^{(+)}=-10 \mathrm{kPa}$, is considered. Its lamination scheme is given by $\left(0/90/\mathrm{Soft}-\mathrm{core}/90/0\right)$, assuming $h_1=h_2=0.01 \mathrm{m}$, $h_4=h_5=0.01 \mathrm{m}$ and $h_3=0.06 \mathrm{m}$. The four external layers are made of orthotropic material (Graphite-epoxy), whereas the soft-core is made of Foam. Their properties are listed in Table 2. In this circumstance, the reinforcing fibers are placed according to straight paths to perform the comparison also with the three-dimensional finite element solution (3D FEM). As far as the present ESL approach is concerned, the EDZ4 is considered to be structural theory. To prove the inadequacy of the Murakami’s function to capture the effective static behavior of this five-layered plate, a layer-wise theory is used for the sake of comparison. In particular, the LD4 model is used. The reader can find the meaning and the features of this theory in the paper by Tornabene [12]. The through-the-thickness profiles of strains, stresses and displacements are shown in Figure 25, Figure 26 and Figure 27. The following results prove the same aspects highlighted in the reference papers [120,121]. In particular, the LD4 is in excellent agreement with the reference solution (3D FEM), whereas the EDZ4 is not able to capture the effective through-the-thickness profiles, especially in terms of strains and displacements. The discrete model is obtained by setting $I_N=I_M=25$ grid points for the GDQ solutions. On the other hand, the commercial software Strand7 is employed for the 3D FEM solution, by using the Hexa20 brick elements. This final example justifies the use of the ESL zig-zag theories only for three-layered sandwich structures with an inner soft-core.

7. Discussion

A massive set of parametric investigations has been performed and presented in the paper to show the effect of the curvilinear paths of the reinforcing fibers on the linear static response of soft-core sandwich structures. A theoretical framework based on higher-order ESL theories including the Murakami’s function has been employed. As far as the values of the fiber orientation are concerned, an innovative and general mathematical formulation has been developed, to describe more complex curvilinear paths (such as power law, sine-wave, exponential, Gaussian and ellipse shaped). The following observations can be gathered:

• The soft-core effect is well-captured by means of the Murakami’s function. As highlighted in previous work [56], this function is required to model the so-called zig-zag effect. These aspects are extremely clear in the through-the-thickness profiles of strain, stress and displacement components presented in the paper.
• The higher-order theories employed in this paper provide comparable results. Thus, all these models can be used to deal with similar structural problems. With respect to first-order models, the shear correction factor and the plane stress hypothesis can be neglected, and the mechanical behavior is closer to the three-dimensional one.
• The linear static behavior is affected by the value of the fiber orientation. Therefore, the angle of the fiber orientation represents a design parameter that can be modified and optimized during the manufacturing process to obtain the desired structural behavior in terms of static response.
• The boundary conditions in terms of generalized displacements on the shell middle surface, as well as stress profiles, are well-enforced. In particular, null displacements are obtained for clamped edges, whereas the normal stress ${\sigma }_n$ coincides with the value of the corresponding applied load.
• The numerical method employed in the paper represents an accurate tool to deal with similar structural problems.