Transverse Thermal Conductivity of Epoxy Carbon Fiber Prepreg Laminates with a Graphite Filled Matrix
Abstract
:1. Introduction
2. Production and Characterization Methods
2.1. Materials
2.2. Resin Preparation and Curing
2.3. Prepreg Production
2.4. Morphological Characterization
2.5. Thermal Conductivity Measurements
3. Results and Discussions
3.1. Neat and Filled Resin Conductivity
3.2. Laminate Characterization
4. Micromechanical Calculations
5. Conclusions
- In the epoxy resin, a non-linear dependence of the thermal conductivity from the filler volume content could be found. Larger particles showed a higher conductivity, most probably due to lower phonon scattering.
- In the carbon fiber reinforced composites, the thermal conductivity was enhanced by a factor of 4 with 20 vol% of graphitic particles. The fiber reinforced laminate showed a different behavior compared to the epoxy graphite composites: Small and large particles showed very similar transverse thermal conductivities.
Author Contributions
Funding
Conflicts of Interest
References
- Scelsi, L.; Bonner, M.; Hodzic, A.; Soutis, C.; Wilson, C.; Scaife, R.; Ridgway, K. Potential emissions savings of lightweight composite aircraft components evaluated through life cycle assessment. Express Polym. Lett. 2011, 5, 209–217. [Google Scholar] [CrossRef]
- Rolfes, R.; Hammerschmidt, U. Transverse thermal conductivity of CFRP laminates: A numerical and experimental validation of approximation formulae. Compos. Sci. Technol. 1995, 54, 45–54. [Google Scholar] [CrossRef]
- Pilling, M.W.; Yates, B.; Black, M.A. The thermal conductivity of carbon fibre-reinforced composites. J. Mater. Sci. 1979, 14, 1326–1338. [Google Scholar] [CrossRef]
- Shim, H.-B.; Seo, M.-K.; Park, S.-J. Thermal conductivity and mechanical properties of various cross-section types carbon fiber-reinforced composites. J. Mater. Sci. 2002, 37, 1881–1885. [Google Scholar] [CrossRef]
- Han, S.; Chung, D.D.L. Increasing the through-thickness thermal conductivity of carbon fiber polymer–matrix composite by curing pressure increase and filler incorporation. Compos. Sci. Technol. 2011, 71, 1944–1952. [Google Scholar] [CrossRef]
- Goyal, V.; Balandin, A.A. Thermal properties of the hybrid graphene-metal nano-micro-composites: Applications in thermal interface materials. Appl. Phys. Lett. 2012, 100, 73113. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.-W. Processing-structure-multi-functional property relationship in carbon nanotube/epoxy composites. Carbon 2006, 44, 3022–3029. [Google Scholar] [CrossRef]
- Sumfleth, J.; Adroher, X.C.; Schulte, K. Synergistic effects in network formation and electrical properties of hybrid epoxy nanocomposites containing multi-wall carbon nanotubes and carbon black. J. Mater. Sci. 2009, 44, 3241–3247. [Google Scholar] [CrossRef]
- Yu, A.; Itkis, M.E.; Bekyarova, E.; Haddon, R.C. Effect of single-walled carbon nanotube purity on the thermal conductivity of carbon nanotube-based composites. Appl. Phys. Lett. 2006, 89, 133102. [Google Scholar] [CrossRef]
- Tekce, H.S.; Kumlutas, D.; Tavman, I.H. Effect of Particle Shape on Thermal Conductivity of Copper Reinforced Polymer Composites. J. Reinf. Plast. Compos. 2007, 26, 113–121. [Google Scholar] [CrossRef]
- Hammerstroem, D.W.; Burgers, M.A.; Chung, S.W.; Guliants, E.A.; Bunker, C.E.; Wentz, K.M.; Hayes, S.E.; Buckner, S.W.; Jelliss, P.A. Aluminum nanoparticles capped by polymerization of alkyl-substituted epoxides: Ratio-dependent stability and particle size. Inorg. Chem. 2011, 50, 5054–5059. [Google Scholar] [CrossRef]
- Ng, H.Y.; Lu, X.; Lau, S.K. Thermal conductivity of boron nitride-filled thermoplastics: Effect of filler characteristics and composite processing conditions. Polym. Compos. 2005, 26, 778–790. [Google Scholar] [CrossRef]
- Hong, J.-P.; Yoon, S.-W.; Hwang, T.; Oh, J.-S.; Hong, S.-C.; Lee, Y.; Nam, J.D. High thermal conductivity epoxy composites with bimodal distribution of aluminum nitride and boron nitride fillers. Thermochim. Acta 2012, 537, 70–75. [Google Scholar] [CrossRef]
- Bauhofer, W.; Kovacs, J.Z. A review and analysis of electrical percolation in carbon nanotube polymer composites. Compos. Sci. Technol. 2009, 69, 1486–1498. [Google Scholar] [CrossRef]
- Ruckdeschel, P.; Philipp, A.; Kopera, B.A.F.; Bitterlich, F.; Dulle, M.; Pech-May, N.W.; Retsch, M. Thermal transport in binary colloidal glasses: Composition dependence and percolation assessment. Phys. Rev. E 2018, 97, 22612. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, Z. Thermal conductivity of in situ epoxy composites filled with ZrB2 particles. Compos. Sci. Technol. 2015, 107, 61–66. [Google Scholar] [CrossRef]
- Liu, K.; Takagi, H.; Osugi, R.; Yang, Z. Effect of physicochemical structure of natural fiber on transverse thermal conductivity of unidirectional abaca/bamboo fiber composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1234–1241. [Google Scholar] [CrossRef]
- Shtein, M.; Nadiv, R.; Buzaglo, M.; Kahil, K.; Regev, O. Thermally Conductive Graphene-Polymer Composites: Size, Percolation, and Synergy Effects. Chem. Mater. 2015, 27, 2100–2106. [Google Scholar] [CrossRef]
- Ding, Y.; Alias, H.; Wen, D.; Williams, R.A. Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids). Int. J. Heat Mass Transf. 2006, 49, 240–250. [Google Scholar] [CrossRef]
- Burger, N.; Laachachi, A.; Ferriol, M.; Lutz, M.; Toniazzo, V.; Ruch, D. Review of thermal conductivity in composites: Mechanisms, parameters and theory. Prog. Polym. Sci. 2016, 61, 1–28. [Google Scholar] [CrossRef]
- Fan, B.; Liu, Y.; He, D.; Bai, J. Enhanced thermal conductivity for mesophase pitch-based carbon fiber/modified boron nitride/epoxy composites. Polymer 2017, 122, 71–76. [Google Scholar] [CrossRef]
- Mottram, J.T.; Taylor, R. Thermal conductivity of fibre-phenolic resin composites. Part I: Thermal diffusivity measurements. Compos. Sci. Technol. 1987, 29, 189–210. [Google Scholar] [CrossRef]
- Agari, Y.; Tanaka, M.; Nagai, S.; Tanaka, M.; Nagai, S.; Uno, T. Thermal conductivity of a polymer composite filled with mixtures of particles. J. Appl. Polym. Sci. 1987, 34, 1429–1437. [Google Scholar] [CrossRef]
- Garret, K.W.; Rosenberg, H.M. The thermal conductivity of epoxy-resin /powder composite materials. J. Appl. Phys. 1974, 7, 1247. [Google Scholar] [CrossRef]
- Boudenne, A.; Ibos, L.; Fois, M.; Majesté, J.C.; Géhin, E. Electrical and thermal behavior of polypropylene filled with copper particles. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1545–1554. [Google Scholar] [CrossRef]
- Zhu, B.L.; Ma, J.; Wu, J.; Yung, K.C.; Xie, C.S. Study on the properties of the epoxy-matrix composites filled with thermally conductive AlN and BN ceramic particles. J. Appl. Polym. Sci. 2010, 118, 2754–2764. [Google Scholar] [CrossRef]
- Monkiewitsch, M. Faservolumengehaltsbestimmung Mittels Thermogravimetrischer Analyse (TGA): Methodendarstellung und Ergebnisse eines Ringversuchs als Grundlage für Einen Normentwurf; Industrievereinigung Verstärkte Kunststoffe e.V.: Frankfurt, Germany, 2018. [Google Scholar]
- King, J.A.; Lopez Gaxiola, D.; Johnson, B.A.; Keith, J.M. Thermal Conductivity of Carbon-filled Polypropylene-based Resins. J. Compos. Mater. 2010, 44, 839–855. [Google Scholar] [CrossRef]
- Heinle, C.; Brocka, Z.; Hülder, G.; Ehrenstein, G.W.; Osswald, T.A. Thermal conductivity of polymers filled with non-isometric fillers: A process dependent, anisotropic property. In Proceedings of the 67th Annual Technical Conference of the Society of Plastics Engineers (ANTEC), Chicago, IL, USA, 22–24 June 2009. [Google Scholar]
- Corcione, C.E.; Frigione, M.; Acierno, D. Rheological characterization of UV-curable epoxy systems: Effects of o -Boehmite nanofillers and a hyperbranched polymeric modifier. J. Appl. Polym. Sci. 2009, 112, 1302–1310. [Google Scholar] [CrossRef]
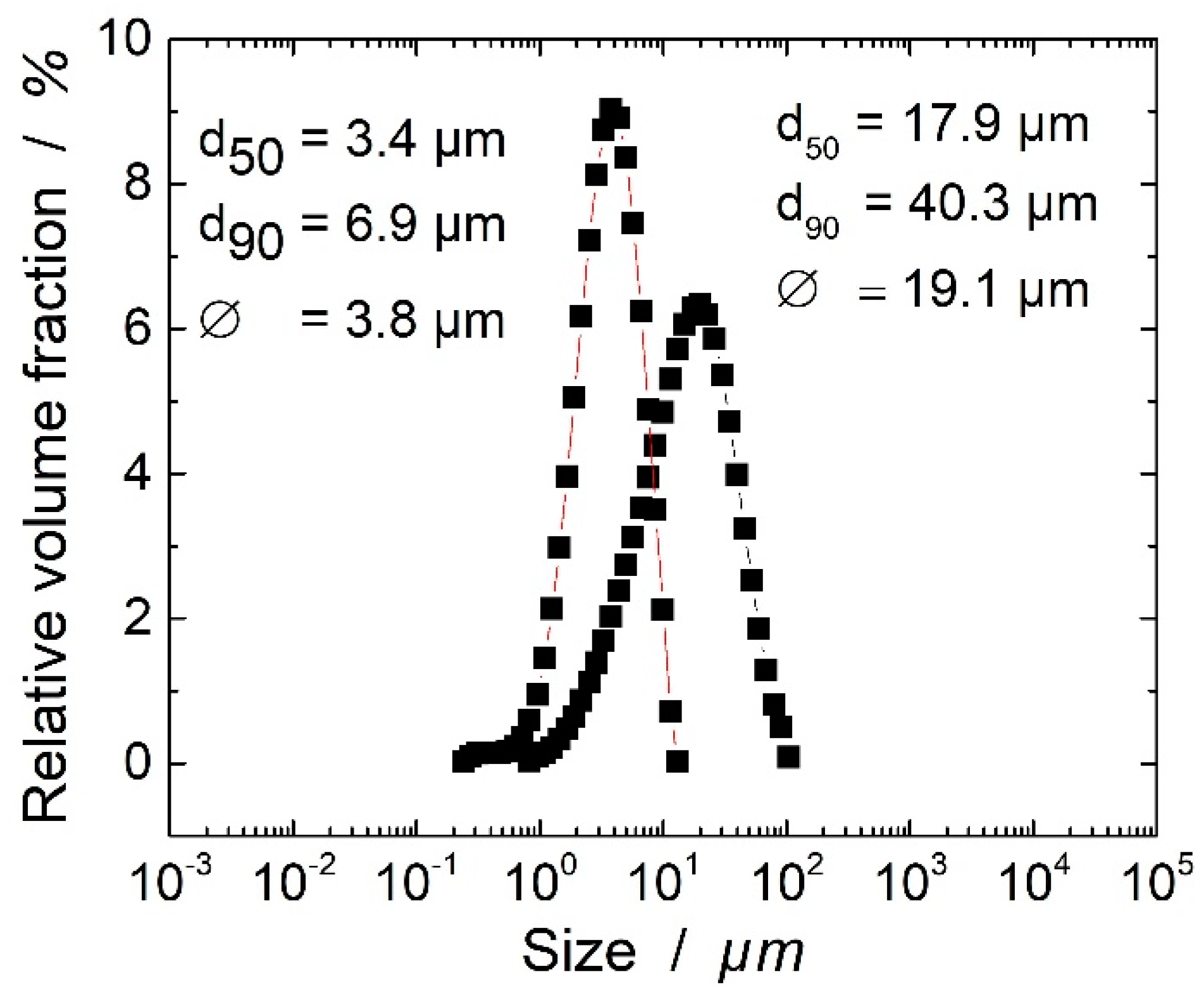





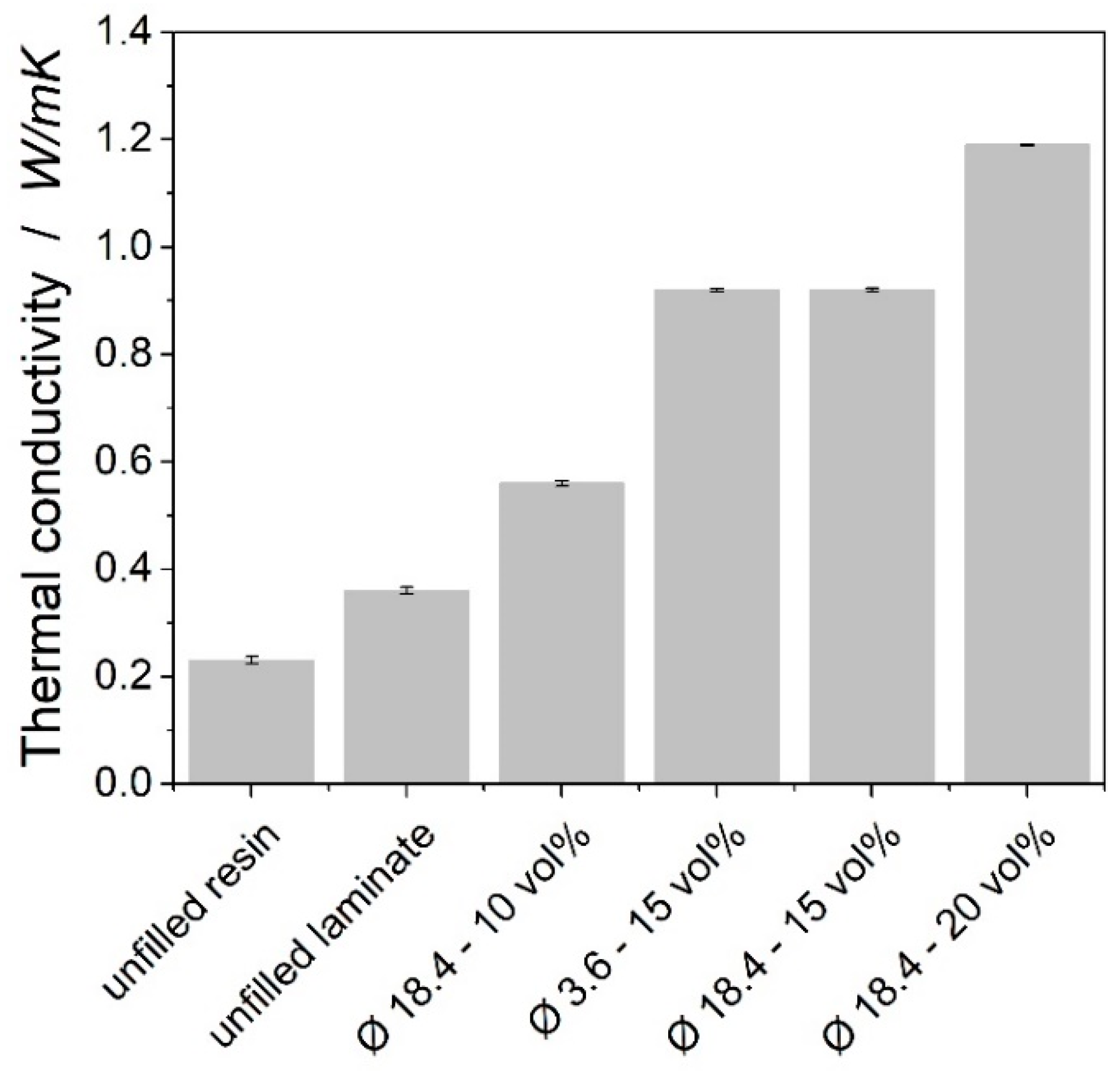




| Sample | FVC | Measuring Method | Enhancement Method | Thermal Conductivity Enhancement (%) |
|---|---|---|---|---|
| Epoxy/Carbon Fiber [5] | 65.0 | proprietary | Coating of prepreg: 0.4% SWNT | 33.2% |
| Epoxy/Mesophase Pitch Fiber [21] | n.a. | LFA | Matrix modification | 78.9% |
| Underlying research | 55 | LFA | Conductive matrix: 20 vol% graphite | 330% |
| Prepreg Laminate | Fiber Volume Content |
|---|---|
| unfilled | 48 vol% |
| Graphite ø 18.4 µm–10 vol% | 55 vol% |
| Graphite ø 18.4 µm–15 vol% | 53 vol% |
| Graphite ø 18.4 µm–20 vol% | 57 vol% |
| Graphite ø 3.6 µm–15 vol% | 56 vol% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bard, S.; Demleitner, M.; Radtke, M.; Altstädt, V. Transverse Thermal Conductivity of Epoxy Carbon Fiber Prepreg Laminates with a Graphite Filled Matrix. J. Compos. Sci. 2019, 3, 44. https://doi.org/10.3390/jcs3020044
Bard S, Demleitner M, Radtke M, Altstädt V. Transverse Thermal Conductivity of Epoxy Carbon Fiber Prepreg Laminates with a Graphite Filled Matrix. Journal of Composites Science. 2019; 3(2):44. https://doi.org/10.3390/jcs3020044
Chicago/Turabian StyleBard, Simon, Martin Demleitner, Marius Radtke, and Volker Altstädt. 2019. "Transverse Thermal Conductivity of Epoxy Carbon Fiber Prepreg Laminates with a Graphite Filled Matrix" Journal of Composites Science 3, no. 2: 44. https://doi.org/10.3390/jcs3020044
APA StyleBard, S., Demleitner, M., Radtke, M., & Altstädt, V. (2019). Transverse Thermal Conductivity of Epoxy Carbon Fiber Prepreg Laminates with a Graphite Filled Matrix. Journal of Composites Science, 3(2), 44. https://doi.org/10.3390/jcs3020044







