Mechanical Properties of Cellulose Nanocrystal (CNC) Bundles: Coarse-Grained Molecular Dynamic Simulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Coarse-Grained (CG) Model for Cellulose Nanocrystals (CNC)
2.2. Twisted Bundles of CNCs
2.3. Simulation and Analysis Protocol
3. Results and Discussion
3.1. The Effect of Interface Energy and Twist
3.2. The Effect of Bundle Size and Twist
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
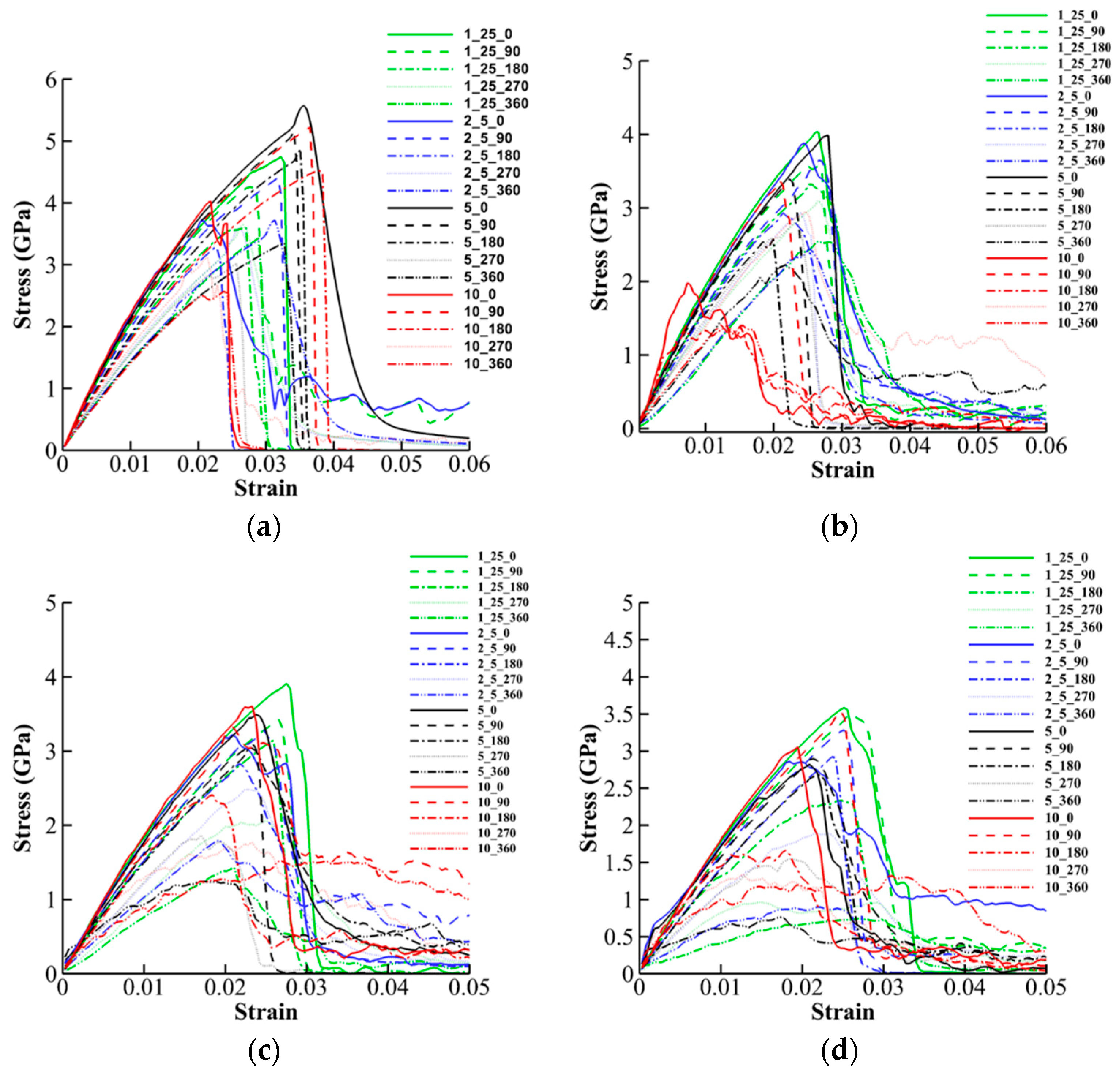
Appendix A. Stress-Strain Curves for Tensile Tests
References
- Moon, R.J.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J. Cellulose nanomaterials review: Structure, properties and nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef] [PubMed]
- Abdul Khalil, H.P.S.; Bhat, A.H.; Ireana Yusra, A.F. Green composites from sustainable cellulose nanofibrils: A review. Carbohydr. Polym. 2012, 87, 963–979. [Google Scholar] [CrossRef]
- Dufresne, A. Nanocellulose: From Nature to High Performance Tailored Materials; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2017. [Google Scholar]
- Dufresne, A. Nanocellulose: A new ageless bionanomaterial. Mater. Today 2013, 16, 220–227. [Google Scholar] [CrossRef]
- Shishehbor, M.; Zavattieri, P.D. Effects of interface properties on the mechanical properties of bio-inspired cellulose nanocrystal (CNC)-based materials. J. Mech. Phys. Solids 2019, 124, 871–896. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; Qin, Z.; Buehler, M.J. Mesoscale mechanics of twisting carbon nanotube yarns. Nanoscale 2015, 7, 5435–5445. [Google Scholar] [CrossRef]
- Shishehbor, M.; Dri, F.L.; Moon, R.J.; Zavattieri, P.D. A continuum-based structural modeling approach for cellulose nanocrystals (CNCs). J. Mech. Phys. Solids 2018, 111, 308–332. [Google Scholar] [CrossRef]
- López, C.A.; Bellesia, G.; Redondo, A.; Langan, P.; Chundawat, S.P.S.S.; Dale, B.E.; Marrink, S.J.; Gnanakaran, S.; López, C.A.; Bellesia, G.; et al. MARTINI coarse-grained model for crystalline cellulose microfibers. J. Phys. Chem. B 2015, 119, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Hadden, J.A.; French, A.D.; Woods, R.J. Unraveling cellulose microfibrils: A twisted tale. Biopolymers 2013, 99, 746–756. [Google Scholar] [CrossRef] [PubMed]
- Reising, A.B.; Moon, R.J.; Youngblood, J.P. Effect of particle alignment on mechanical properties of neat cellulose nanocrystal films. J. Sci. Technol. Prod. Process 2012, 2, 32–41. [Google Scholar]
- Cao, X.; Dong, H.; Li, C.M. New nanocomposite materials reinforced with flax cellulose nanocrystals in waterborne polyurethane. Biomacromolecules 2007, 8, 899–904. [Google Scholar] [CrossRef]
- Auad, M.L.; Mosiewicki, M.A.; Richardson, T.; Aranguren, M.I.; Marcovich, N.E. Nanocomposites made from cellulose nanocrystals and tailored segmented polyurethanes. J. Appl. Polym. Sci. 2010, 115, 1215–1225. [Google Scholar] [CrossRef]
- Miao, C.; Hamad, W.Y. Cellulose reinforced polymer composites and nanocomposites: A critical review. Cellulose 2013, 20, 2221–2262. [Google Scholar] [CrossRef]
- Wu, X.; Moon, R.J.; Martini, A. Crystalline cellulose elastic modulus predicted by atomistic models of uniform deformation and nanoscale indentation. Cellulose 2013, 20, 43–55. [Google Scholar] [CrossRef]
- Sinko, R.; Keten, S. Traction-separation laws and stick-slip shear phenomenon of interfaces between cellulose nanocrystals. J. Mech. Phys. Solids 2015, 78, 526–539. [Google Scholar] [CrossRef]
- Chen, P.; Ogawa, Y.; Nishiyama, Y.; Ismail, A.E.; Mazeau, K. Linear, non-linear and plastic bending deformation of cellulose nanocrystals. Phys. Chem. Chem. Phys. 2016, 18, 19880–19887. [Google Scholar] [CrossRef] [PubMed]
- Tian, K.; Shishehbor, M.; Zavattieri, P.D. Coarse Graining of Crystalline Cellulose. 2016. Available online: https://nanohub.org/resources/cgmcc. [CrossRef]
- Leonardo, J.; Shishehbor, M.; Zavattieri, P.D. Development of a NanoHUB Tool: Mechanical Features of Crystalline Nano Cellulose. 2017. Available online: https://nanohub.org/resources/26941.
- Wu, X.; Moon, R.J.; Martini, A. Tensile strength of Iβ crystalline cellulose predicted by molecular dynamics simulation. Cellulose 2014, 21, 2233–2245. [Google Scholar] [CrossRef]
- Wu, X.; Moon, R.; Martini, A. Calculation of single chain cellulose elasticity using fully atomistic modeling. Mol. Model. 2011, 37–43. [Google Scholar]
- Dri, F.L.; Hector, L.G.; Moon, R.J.; Zavattieri, P.D. Anisotropy of the elastic properties of crystalline cellulose Iβ from first principles density functional theory with Van der Waals interactions. Cellulose 2013, 20, 2703–2718. [Google Scholar] [CrossRef]
- Saito, T.; Kuramae, R.; Wohlert, J.; Berglund, L.A.; Isogai, A. An ultrastrong nanofibrillar biomaterial: The strength of single cellulose nanofibrils revealed via sonication-induced fragmentation. Biomacromolecules 2013, 14, 248–253. [Google Scholar] [CrossRef]
- Wohlert, J.; Berglund, L.A. A coarse-grained model for molecular dynamics simulations of native cellulose. J. Chem. Theory Comput. 2011, 7, 753–760. [Google Scholar] [CrossRef]
- Glass, D.C.; Moritsugu, K.; Cheng, X.; Smith, J.C. REACH coarse-grained simulation of a cellulose fiber. Biomacromolecules 2012, 13, 2634–2644. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Zhan, H.; Wang, H.; Ju, Y. Secondary Structure Analysis of Native Cellulose by Molecular Dynamics Simulations with Coarse Grained Model. Chin. J. Chem. Phys. 2013, 25, 191. [Google Scholar] [CrossRef]
- Srinivas, G.; Cheng, X.; Smith, J.C. A solvent-free coarse grain model for crystalline and amorphous cellulose fibrils. J. Chem. Theory Comput. 2011, 7, 2539–2548. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, G.; Cheng, X.; Smith, J.C. Coarse-grain model for natural cellulose fibrils in explicit water. J. Phys. Chem. B 2014, 118, 3026–3034. [Google Scholar] [CrossRef] [PubMed]
- Fan, B.; Maranas, J.K. Coarse-grained simulation of cellulose Iβ with application to long fibrils. Cellulose 2015, 22, 31–44. [Google Scholar] [CrossRef]
- Li, L.; Pérré, P.; Frank, X.; Mazeau, K. A coarse-grain force-field for xylan and its interaction with cellulose. Carbohydr. Polym. 2015, 127, 438–450. [Google Scholar] [CrossRef] [PubMed]
- Poma, A.B.; Chwastyk, M.; Cieplak, M. Elastic moduli of biological fibers in a coarse-grained model: Crystalline cellulose and β-amyloids. Phys. Chem. Chem. Phys. 2017, 19, 28195–28206. [Google Scholar] [CrossRef]
- Shishehbor, M.; Zavattieri, P.D. Evaluation of Coarse Grained Models for Cellulose NanoCrystals (CNCs). In Proceedings of the Engineering Mechanics Institute Conference (EMI), Metz, France, 25–27 October 2016. [Google Scholar]
- Shishehbor, M.; Pouranian, M.R.; Ramezani, M.G. Molecular investigations on the interactions of graphene, crude oil fractions and mineral aggregates at low, medium and high temperatures. Pet. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Shishehbor, M.; Pouranian, M.R.; Imaninasab, R. Evaluating the adhesion properties of crude oil fractions on mineral aggregates at different temperatures through reactive molecular dynamics. Pet. Sci. Technol. 2018, 36, 2084–2090. [Google Scholar] [CrossRef]
- Qin, X.; Feng, S.; Meng, Z.; Keten, S. Optimizing the mechanical properties of cellulose nanopaper through surface energy and critical length scale considerations. Cellulose 2017, 24, 3289–3299. [Google Scholar] [CrossRef]
- Leonardo, J.; Shishehbor, M.; Zavattieri, P.D. Mechanics of Crystalline Nano Cellulose Nanofilm. 2017. Available online: https://nanohub.org/resources/cnc. [CrossRef]
- Leonardo, J.; Shishehbor, M.; Zavattieri, P. Mechanics of CNC Nanofilm. The Summer Undergraduate Research Fellowship (SURF) Symposiu. 2017. Available online: https://docs.lib.purdue.edu/surf/2017/presentations/144.
- Liew, K.M.; Wong, C.H.; Tan, M.J. Twisting effects of carbon nanotube bundles subjected to axial compression and tension. J. Appl. Phys. 2006, 99, 114312. [Google Scholar] [CrossRef]
- Wei, X.; Naraghi, M.; Espinosa, H.D. Optimal length scales emerging from shear load transfer in natural materials: Application to carbon-based nanocomposite design. ACS Nano 2012, 6, 2333–2344. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ostanin, I.; Gaidău, C.; Dumitrică, T. Twisting carbon nanotube ropes with the mesoscopic distinct element method: Geometry, packing, and nanomechanics. Langmuir 2015, 31, 12323–12327. [Google Scholar] [CrossRef] [PubMed]
- Chang, I.L. Molecular dynamics investigation of carbon nanotube resonance. Model. Simul. Mater. Sci. Eng. 2013, 21, 045011. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Sugiyama, J.; Chanzy, H.; Langan, P. Crystal Structure and Hydrogen Bonding System in Cellulose Iα from Synchrotron X-ray and Neutron Fiber Diffraction. J. Am. Chem. Soc. 2003, 125, 14300–14306. [Google Scholar] [CrossRef]
- Cao, G.; Chen, X. Buckling of single-walled carbon nanotubes upon bending: Molecular dynamics simulations and finite element method. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 155435. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 15012. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramezani, M.G.; Golchinfar, B. Mechanical Properties of Cellulose Nanocrystal (CNC) Bundles: Coarse-Grained Molecular Dynamic Simulation. J. Compos. Sci. 2019, 3, 57. https://doi.org/10.3390/jcs3020057
Ramezani MG, Golchinfar B. Mechanical Properties of Cellulose Nanocrystal (CNC) Bundles: Coarse-Grained Molecular Dynamic Simulation. Journal of Composites Science. 2019; 3(2):57. https://doi.org/10.3390/jcs3020057
Chicago/Turabian StyleRamezani, Majid G., and Behnoush Golchinfar. 2019. "Mechanical Properties of Cellulose Nanocrystal (CNC) Bundles: Coarse-Grained Molecular Dynamic Simulation" Journal of Composites Science 3, no. 2: 57. https://doi.org/10.3390/jcs3020057
APA StyleRamezani, M. G., & Golchinfar, B. (2019). Mechanical Properties of Cellulose Nanocrystal (CNC) Bundles: Coarse-Grained Molecular Dynamic Simulation. Journal of Composites Science, 3(2), 57. https://doi.org/10.3390/jcs3020057




