Free Vibration Analysis of Laminated Functionally Graded Carbon Nanotube-Reinforced Composite Doubly Curved Shallow Shell Panels Using a New Four-Variable Refined Theory
Abstract
:1. Introduction
2. Theoretical Formulations
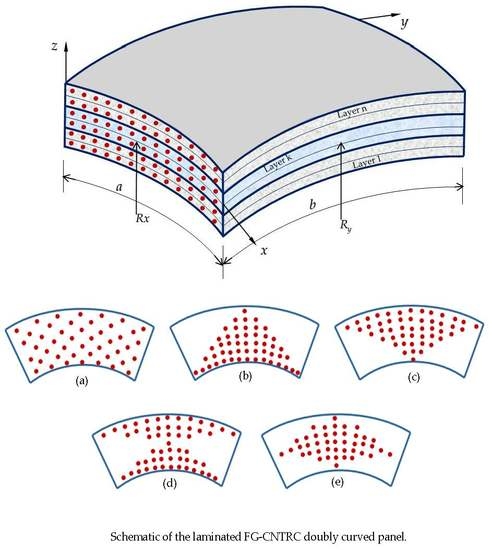
2.1. Description of the Model
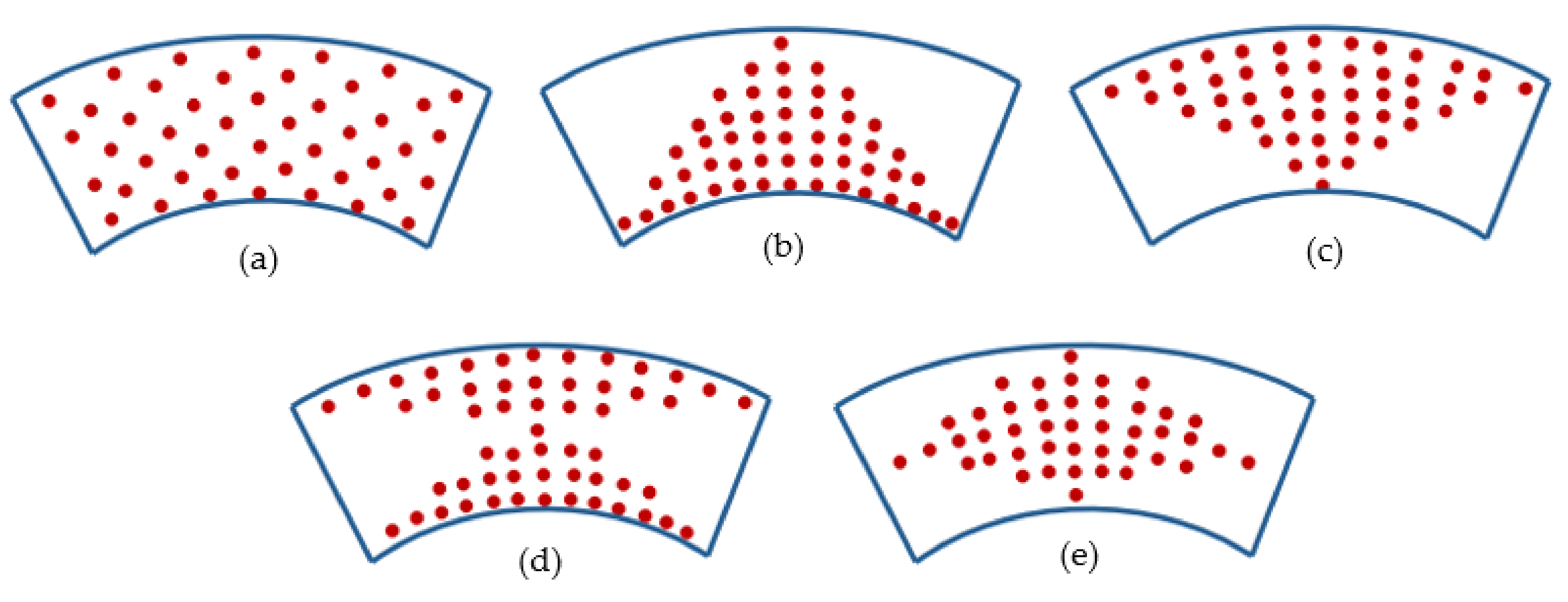
2.2. Material Properties of Functionally Graded Carbon Nanotube-Reinforced Composite
2.3. Kinematic Relations
2.4. Governing Equations
2.5. Solution Procedure
3. Numerical Results and Discussions
3.1. Comparison Studies
Example 1: Free Vibration of the Simply Supported Doubly Curved FG-CNTRC Panels
3.2. Parametric Studies
3.2.1. Effect of FG-CNTRC Parameters
3.2.2. Effect of Curvature
3.2.3. Effect of Curvature Ratio
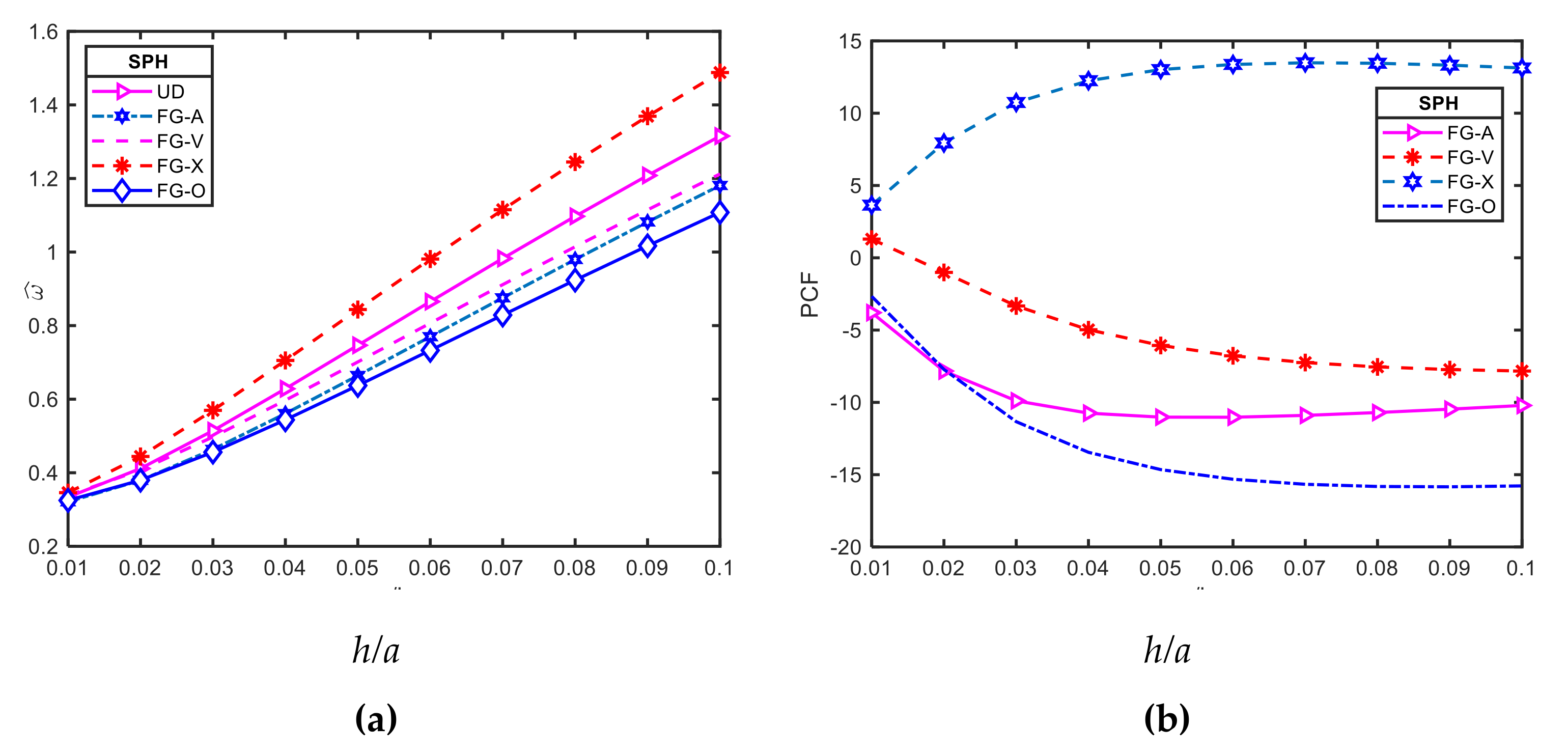
3.2.4. Effect of Thickness Ratio
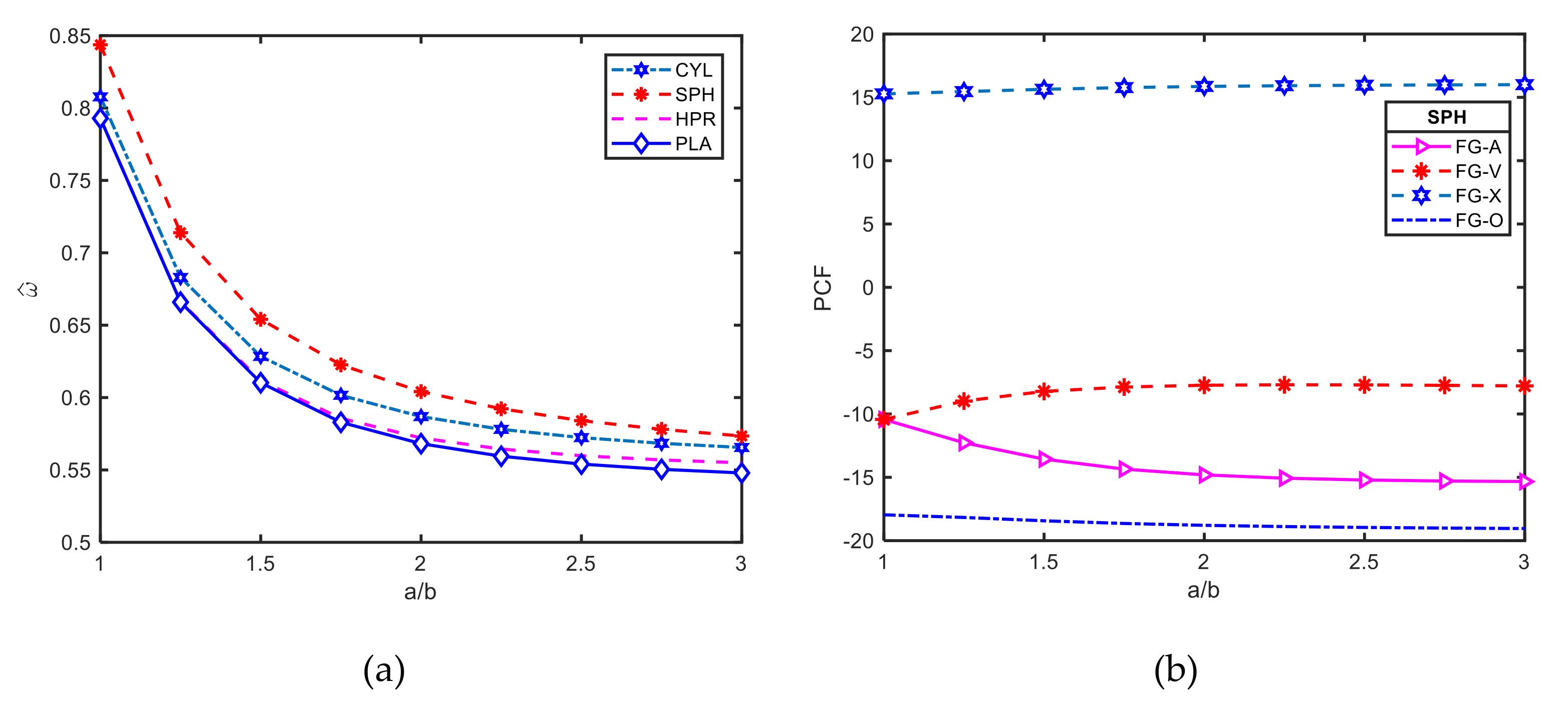
3.2.5. Effect of Aspect Ratio
3.2.6. Effect of Number of Layers
3.2.7. Effect of Different Wave Numbers
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Shen, H.-S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Qatu, M.S. Theory and vibration analysis of laminated barrel thin shells. J. Vib. Control 1999, 5, 851–889. [Google Scholar] [CrossRef]
- Reissner, E. A new derivation of the equations for the deformation of elastic shells. Am. J. Math. 1941, 63, 177–184. [Google Scholar] [CrossRef]
- Bhimaraddi, A.; Stevens, L. A higher order theory for free vibration of orthotropic, homogeneous, and laminated rectangular plates. J. Appl. Mech. 1984, 51, 195. [Google Scholar] [CrossRef]
- Eslami, M.; Shariyat, M. A high-order theory for dynamic buckling and postbuckling analysis of laminated cylindrical shells. J. Press. Vessel. Technol. 1999, 12, 94–102. [Google Scholar] [CrossRef]
- Rahmani, O.; Khalili, S.; Thomsen, O.T. A high-order theory for the analysis of circular cylindrical composite sandwich shells with transversely compliant core subjected to external loads. Compos. Struct. 2012, 94, 2129–2142. [Google Scholar] [CrossRef]
- Shimpi, R.; Patel, H. Free vibrations of plate using two variable refined plate theory. J. Sound Vib. 2006, 296, 979–999. [Google Scholar] [CrossRef]
- El Meiche, N.; Tounsi, A.; Ziane, N.; Mechab, I. A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate. Int. J. Mech. Sci. 2011, 53, 237–247. [Google Scholar] [CrossRef]
- Thai, H.-T.; Vo, T.P. A new sinusoidal shear deformation theory for bending, buckling, and vibration of functionally graded plates. Appl. Math. Model. 2013, 37, 3269–3281. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A simple quasi-3D sinusoidal shear deformation theory for functionally graded plates. Compos. Struct. 2013, 99, 172–180. [Google Scholar] [CrossRef]
- Daouadji, T.H.; Tounsi, A. A new higher order shear deformation model for static behavior of functionally graded plates. Adv. Appl. Math. Mech. 2013, 5, 351–364. [Google Scholar] [CrossRef]
- Mehrabadi, S.J.; Aragh, B.S. Stress analysis of functionally graded open cylindrical shell reinforced by agglomerated carbon nanotubes. Thin Walled Struct. 2014, 80, 130–141. [Google Scholar] [CrossRef]
- Aragh, B.S.; Barati, A.N.; Hedayati, H. Eshelby–Mori–Tanaka approach for vibrational behavior of continuously graded carbon nanotube-reinforced cylindrical panels. Compos. Part B Eng. 2012, 43, 1943–1954. [Google Scholar] [CrossRef]
- Yas, M.; Pourasghar, A.; Kamarian, S.; Heshmati, M. Three-dimensional free vibration analysis of functionally graded nanocomposite cylindrical panels reinforced by carbon nanotube. Mater. Des. 2013, 49, 583–590. [Google Scholar] [CrossRef]
- Alibeigloo, A. Free vibration analysis of functionally graded carbon nanotube-reinforced composite cylindrical panel embedded in piezoelectric layers by using theory of elasticity. Eur. J. Mech. A/Solids 2014, 44, 104–115. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, L.; Liew, K.; Yu, J. Dynamic stability analysis of carbon nanotube-reinforced functionally graded cylindrical panels using the element-free kp-Ritz method. Compos. Struct. 2014, 113, 328–338. [Google Scholar] [CrossRef]
- Moradi-Dastjerdi, R.; Foroutan, M.; Pourasghar, A. Dynamic analysis of functionally graded nanocomposite cylinders reinforced by carbon nanotube by a mesh-free method. Mater. Des. 2013, 44, 256–266. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Nonlinear vibration of nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments. Compos. Struct. 2014, 111, 291–300. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Postbuckling of nanotube-reinforced composite cylindrical shells under combined axial and radial mechanical loads in thermal environment. Compos. Part B Eng. 2013, 52, 311–322. [Google Scholar] [CrossRef]
- Shen, H.-S. Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite cylindrical shells. Compos. Part B Eng. 2012, 43, 1030–1038. [Google Scholar] [CrossRef]
- Shen, H.-S. Torsional postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments. Compos. Struct. 2014, 116, 477–488. [Google Scholar] [CrossRef]
- Liew, K.; Lei, Z.; Yu, J.; Zhang, L. Postbuckling of carbon nanotube-reinforced functionally graded cylindrical panels under axial compression using a meshless approach. Comput. Methods Appl. Mech. Eng. 2014, 268, 1–17. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, L.; Liew, K. Parametric analysis of frequency of rotating laminated CNT reinforced functionally graded cylindrical panels. Compos. Part B Eng. 2016, 90, 251–266. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Thomas, B.; Roy, T. Vibration and damping analysis of functionally graded carbon nanotubes reinforced hybrid composite shell structures. J. Vib. Control 2017, 23, 1711–1738. [Google Scholar] [CrossRef]
- Arani, A.G.; Kiani, F.; Afshari, H. Free and forced vibration analysis of laminated functionally graded CNT-reinforced composite cylindrical panels. J. Sandw. Struct. Mater. 2019, 1099636219830787. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, L.; Liew, K. Analysis of laminated CNT reinforced functionally graded plates using the element-free kp-Ritz method. Compos. Part B Eng. 2016, 84, 211–221. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 96, 165–173. [Google Scholar] [CrossRef]
- Huu Quoc, T.; Minh Tu, T.; Van Tham, V. Free vibration analysis of smart laminated functionally graded CNT reinforced composite plates via new four-variable refined plate theory. Materials 2019, 12, 3675. [Google Scholar] [CrossRef]
- Qatu, M.S. Vibration of Laminated Shells and Plates; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boka Raton, FL, USA, 2003. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wang, Q.; Shao, D.; Qin, B. A simple first-order shear deformation shell theory for vibration analysis of composite laminated open cylindrical shells with general boundary conditions. Compos. Struct. 2018, 184, 211–232. [Google Scholar] [CrossRef]
- Pouresmaeeli, S.; Fazelzadeh, S. Frequency analysis of doubly curved functionally graded carbon nanotube-reinforced composite panels. Acta Mech. 2016, 227, 2765–2794. [Google Scholar] [CrossRef]
- Huang, B.; Guo, Y.; Wang, J.; Du, J.; Qian, Z.; Ma, T.; Yi, L. Bending and free vibration analyses of antisymmetrically laminated carbon nanotube-reinforced functionally graded plates. J. Compos. Mater. 2017, 51, 3111–3125. [Google Scholar] [CrossRef]








| CNT | Matrix |
|---|---|
| - | |
| - |
| a/Rx | b/Ry | V∗CNT | UD | FG-V | FG-X | FG-O | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [34] | Present | [34] | Present | [34] | Present | [34] | Present | |||
| 0.5 | 0.5 | 0.11 | 20.238 | 20.087 | 18.543 | 17.917 | 22.432 | 22.752 | 17.140 | 16.653 |
| 0.14 | 21.655 | 21.700 | 19.779 | 19.184 | 23.997 | 24.642 | 18.267 | 17.790 | ||
| 0.17 | 25.051 | 24.691 | 22.951 | 21.848 | 27.883 | 28.023 | 21.212 | 20.419 | ||
| 0.5 | –0.5 | 0.11 | 17.106 | 17.282 | 14.809 | 14.617 | 19.588 | 20.253 | 13.364 | 13.202 |
| 0.14 | 18.626 | 19.005 | 16.181 | 16.065 | 21.225 | 22.203 | 14.610 | 14.493 | ||
| 0.17 | 21.095 | 21.214 | 18.225 | 17.875 | 24.274 | 24.879 | 16.389 | 16.149 | ||
| 0.5 | 0 | 0.11 | 18.126 | 18.210 | 16.060 | 15.698 | 20.548 | 21.120 | 14.553 | 14.297 |
| 0.14 | 19.628 | 19.890 | 17.391 | 17.065 | 22.179 | 23.044 | 15.766 | 15.525 | ||
| 0.17 | 22.380 | 22.328 | 19.799 | 19.111 | 25.488 | 25.925 | 17.903 | 17.472 | ||
| 0 | 0 | 0.11 | 18.008 | 18.201 | 15.701 | 15.55 | 20.624 | 21.332 | 14.068 | 13.907 |
| 0.14 | 19.608 | 20.016 | 17.147 | 17.089 | 22.349 | 23.391 | 15.378 | 15.265 | ||
| 0.17 | 22.207 | 22.343 | 19.315 | 19.021 | 25.557 | 26.208 | 17.252 | 17.012 | ||
| Shape | CNT Distribution | (0/90) | (0/90)2 | (0/90)4 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.11 | 0.14 | 0.17 | 0.11 | 0.14 | 0.17 | 0.11 | 0.14 | 0.17 | |||
| CYL | UD | 12.854 | 13.841 | 15.937 | 18.658 | 20.596 | 23.032 | 19.829 | 21.941 | 24.467 | |
| FG-A | 11.383 | 12.181 | 14.177 | 18.367 | 20.295 | 22.700 | 19.739 | 21.856 | 24.378 | ||
| FG-V | 12.216 | 12.969 | 15.137 | 18.624 | 20.528 | 22.998 | 19.858 | 21.963 | 24.516 | ||
| FG-X | 14.442 | 15.713 | 17.937 | 19.084 | 21.089 | 23.582 | 20.062 | 22.212 | 24.776 | ||
| FG-O | 11.067 | 11.720 | 13.753 | 18.241 | 20.121 | 22.528 | 19.610 | 21.694 | 24.207 | ||
| SPH | UD | 16.540 | 17.442 | 20.579 | 21.334 | 23.132 | 26.419 | 22.364 | 24.335 | 27.677 | |
| FG-A | 15.143 | 15.902 | 18.967 | 20.984 | 22.786 | 26.050 | 22.245 | 24.232 | 27.583 | ||
| FG-V | 16.366 | 17.080 | 20.371 | 21.426 | 23.193 | 26.560 | 22.453 | 24.423 | 27.823 | ||
| FG-X | 17.812 | 18.980 | 22.214 | 21.722 | 23.595 | 26.951 | 22.587 | 24.604 | 28.002 | ||
| FG-O | 15.214 | 15.845 | 18.990 | 20.977 | 22.723 | 26.008 | 22.175 | 24.123 | 27.472 | ||
| HPR | UD | 11.295 | 12.340 | 13.969 | 17.583 | 19.576 | 21.671 | 18.806 | 20.969 | 23.171 | |
| FG-A | 10.085 | 10.900 | 12.474 | 17.407 | 19.374 | 21.459 | 18.768 | 20.928 | 23.133 | ||
| FG-V | 10.085 | 10.900 | 12.474 | 17.407 | 19.374 | 21.459 | 18.768 | 20.928 | 23.133 | ||
| FG-X | 13.057 | 14.384 | 16.174 | 18.023 | 20.080 | 22.229 | 19.042 | 21.240 | 23.474 | ||
| FG-O | 9.219 | 9.907 | 11.409 | 17.141 | 19.075 | 21.128 | 18.574 | 20.708 | 22.889 | ||
| PLATE | Present | UD | 11.353 | 12.401 | 14.040 | 17.696 | 19.701 | 21.810 | 18.943 | 21.122 | 23.340 |
| [35] | 11.348 | 12.395 | 14.035 | 17.714 | 19.726 | 21.831 | 18.958 | 21.142 | 23.358 | ||
| Present | FG-V | 10.138 | 10.956 | 12.541 | 17.519 | 19.498 | 21.597 | 18.906 | 21.081 | 23.302 | |
| [35] | 10.056 | 10.876 | 12.435 | 17.495 | 19.484 | 21.565 | 18.883 | 21.065 | 23.271 | ||
| Present | FG-X | 13.120 | 14.453 | 16.253 | 18.139 | 20.208 | 22.372 | 19.181 | 21.395 | 23.646 | |
| [35] | 13.064 | 14.396 | 16.180 | 17.975 | 20.032 | 22.165 | 18.995 | 21.193 | 23.411 | ||
| Present | FG-O | 9.270 | 9.960 | 11.472 | 17.251 | 19.197 | 21.264 | 18.710 | 20.859 | 23.057 | |
| [35] | 9.182 | 9.874 | 11.367 | 17.378 | 19.354 | 21.421 | 18.856 | 21.036 | 23.238 | ||
| Shape | n | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | m = 6 |
|---|---|---|---|---|---|---|---|
| CYL | 1 | 17.937 | 48.140 | 99.846 | 169.706 | 254.950 | 352.930 |
| 2 | 46.027 | 64.594 | 109.402 | 176.466 | 260.683 | 358.380 | |
| 3 | 97.820 | 109.032 | 141.357 | 198.901 | 277.607 | 372.340 | |
| 4 | 168.004 | 176.095 | 198.835 | 243.742 | 311.861 | 399.381 | |
| 5 | 253.606 | 260.401 | 277.580 | 311.892 | 367.569 | 444.182 | |
| 6 | 351.923 | 358.209 | 372.384 | 399.478 | 444.253 | 508.835 | |
| SPH | 1 | 22.214 | 49.271 | 100.122 | 169.593 | 254.585 | 352.371 |
| 2 | 49.472 | 65.771 | 109.763 | 176.410 | 260.356 | 357.845 | |
| 3 | 100.573 | 109.960 | 141.685 | 198.853 | 277.285 | 371.804 | |
| 4 | 170.323 | 176.802 | 199.065 | 243.665 | 311.532 | 398.838 | |
| 5 | 255.596 | 260.940 | 277.698 | 311.759 | 367.219 | 443.632 | |
| 6 | 353.644 | 358.612 | 372.397 | 399.275 | 443.867 | 508.271 | |
| HPR | 1 | 16.174 | 47.141 | 99.497 | 169.711 | 255.202 | 353.378 |
| 2 | 47.141 | 64.179 | 109.145 | 176.475 | 260.924 | 358.816 | |
| 3 | 99.497 | 109.145 | 141.314 | 198.990 | 277.883 | 372.799 | |
| 4 | 169.711 | 176.475 | 198.990 | 243.935 | 312.190 | 399.872 | |
| 5 | 255.202 | 260.924 | 277.883 | 312.190 | 367.960 | 444.710 | |
| 6 | 353.378 | 358.816 | 372.799 | 399.872 | 444.710 | 509.403 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Tham, V.; Huu Quoc, T.; Minh Tu, T. Free Vibration Analysis of Laminated Functionally Graded Carbon Nanotube-Reinforced Composite Doubly Curved Shallow Shell Panels Using a New Four-Variable Refined Theory. J. Compos. Sci. 2019, 3, 104. https://doi.org/10.3390/jcs3040104
Van Tham V, Huu Quoc T, Minh Tu T. Free Vibration Analysis of Laminated Functionally Graded Carbon Nanotube-Reinforced Composite Doubly Curved Shallow Shell Panels Using a New Four-Variable Refined Theory. Journal of Composites Science. 2019; 3(4):104. https://doi.org/10.3390/jcs3040104
Chicago/Turabian StyleVan Tham, Vu, Tran Huu Quoc, and Tran Minh Tu. 2019. "Free Vibration Analysis of Laminated Functionally Graded Carbon Nanotube-Reinforced Composite Doubly Curved Shallow Shell Panels Using a New Four-Variable Refined Theory" Journal of Composites Science 3, no. 4: 104. https://doi.org/10.3390/jcs3040104
APA StyleVan Tham, V., Huu Quoc, T., & Minh Tu, T. (2019). Free Vibration Analysis of Laminated Functionally Graded Carbon Nanotube-Reinforced Composite Doubly Curved Shallow Shell Panels Using a New Four-Variable Refined Theory. Journal of Composites Science, 3(4), 104. https://doi.org/10.3390/jcs3040104