Modeling and Two-Step Homogenization of Aperiodic Heterogenous 3D Four-Directional Braided Composites
Abstract
:1. Introduction
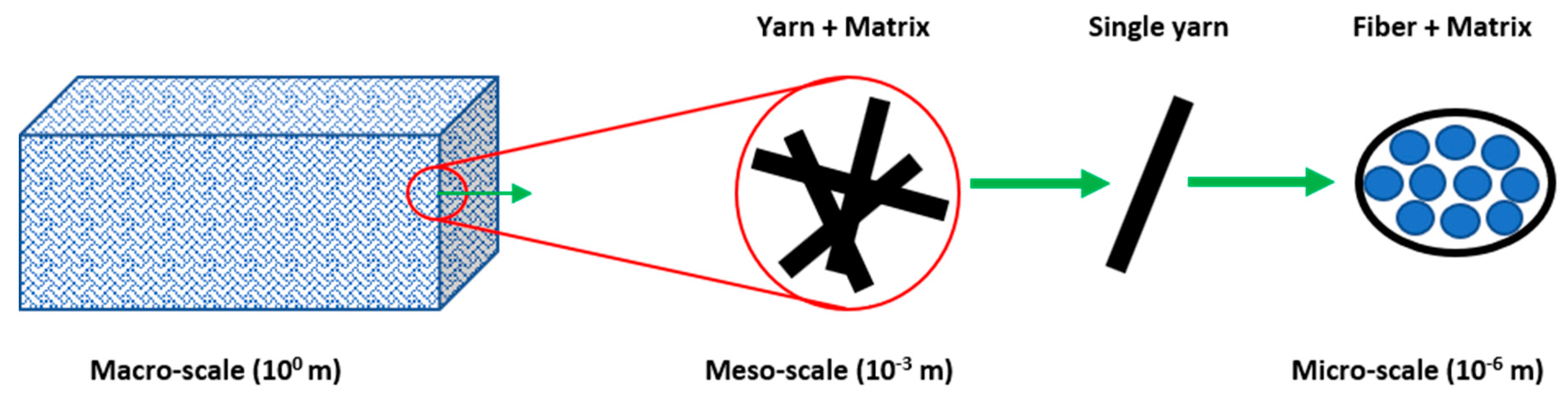
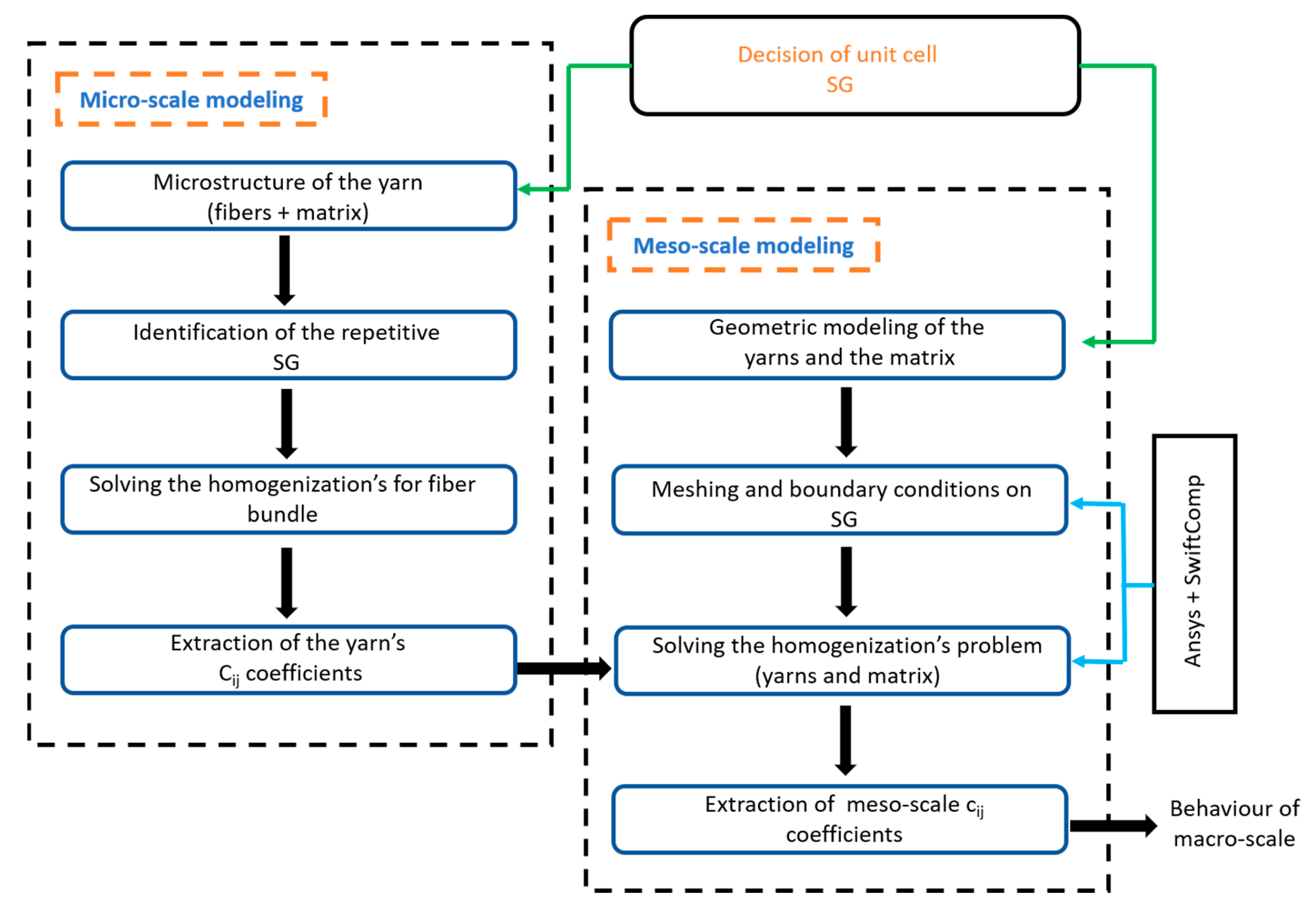
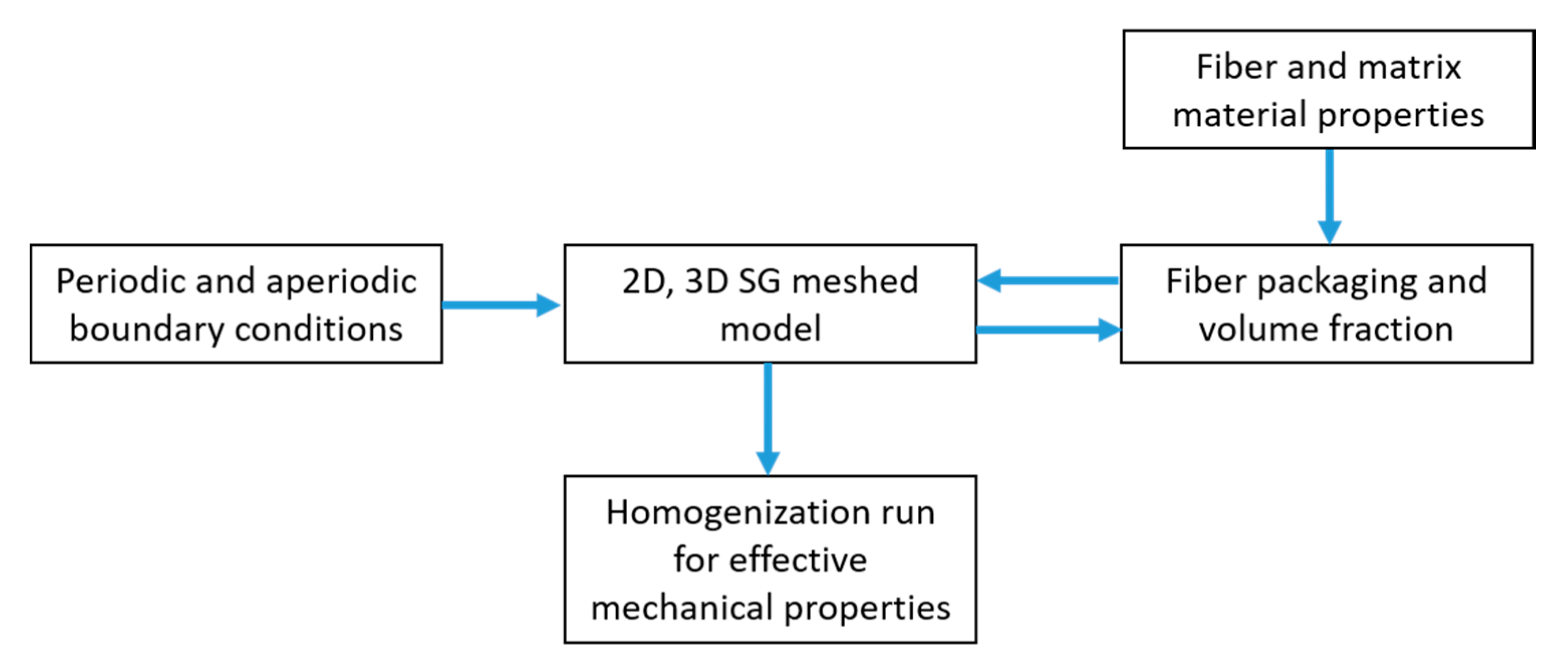
2. Modeling, Homogenization, and Finite Element Analysis
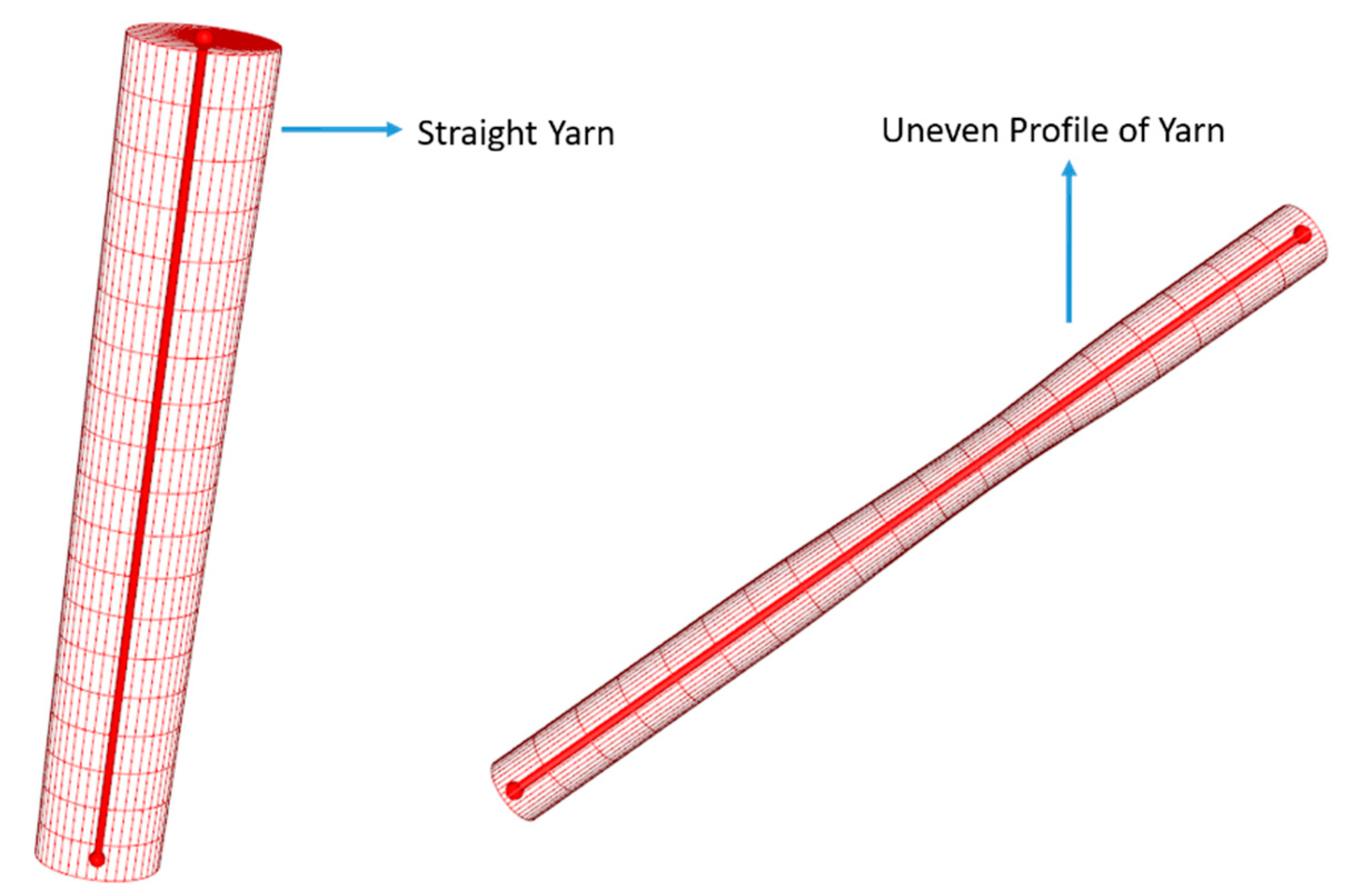
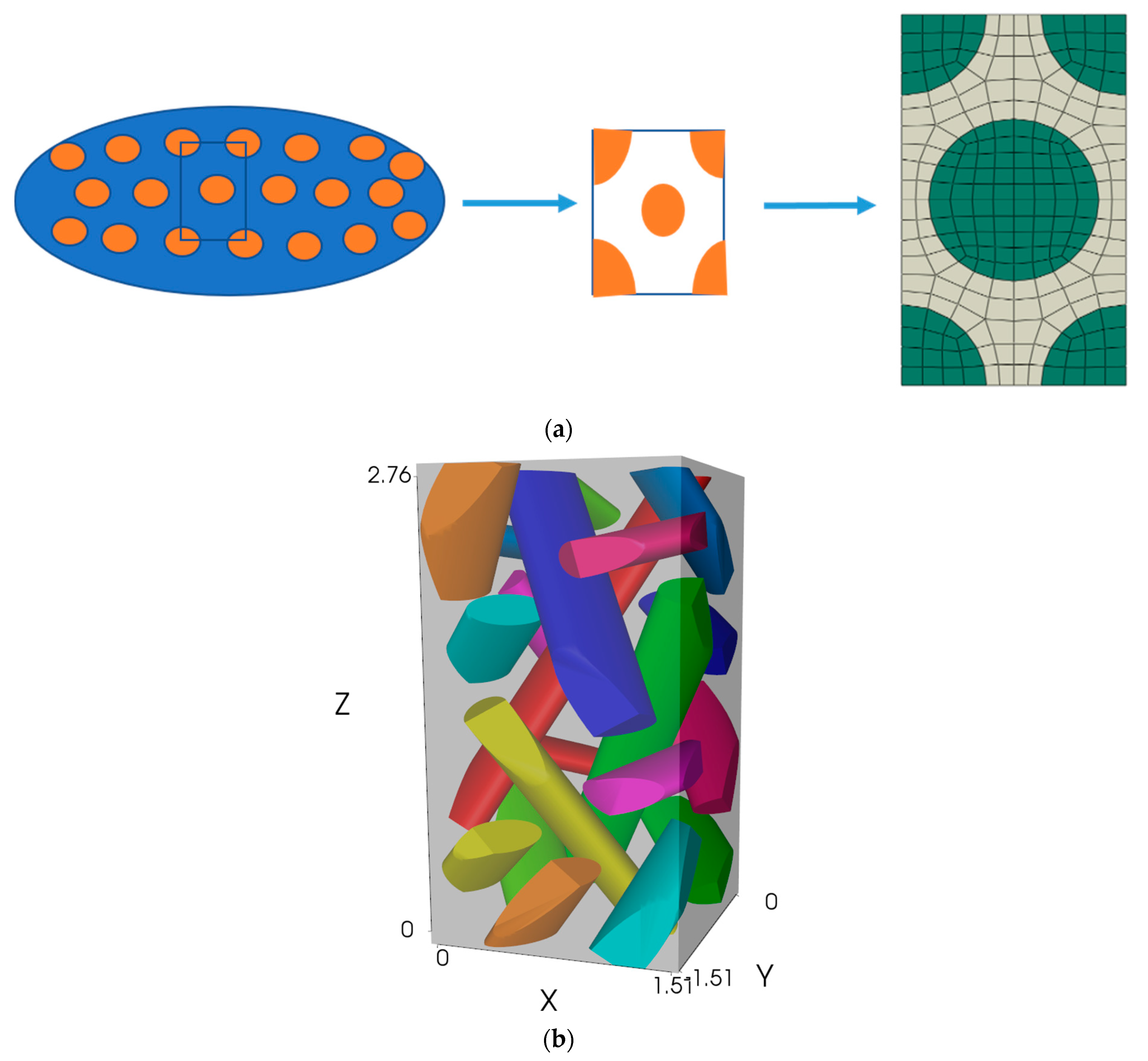
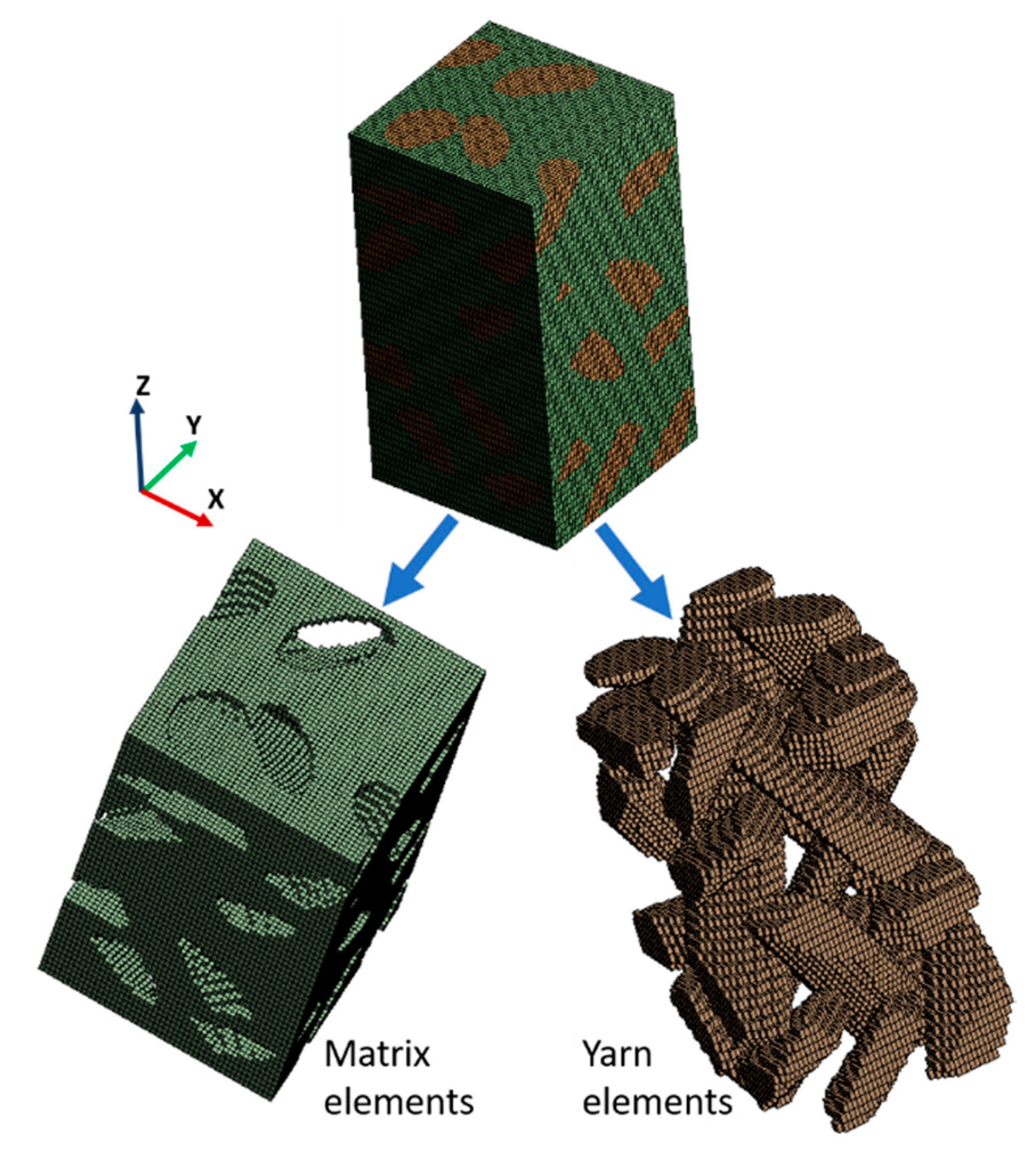
2.1. Modeling of 3D Four-Directional Braided Unit Cell
2.2. Homogenization
2.2.1. Micro-Scale Homogenization
2.2.2. Meso-Scale Homogenization
2.2.3. Effective Mechanical Properties for Braided Ceramic Matrix Composites (C/SiC)
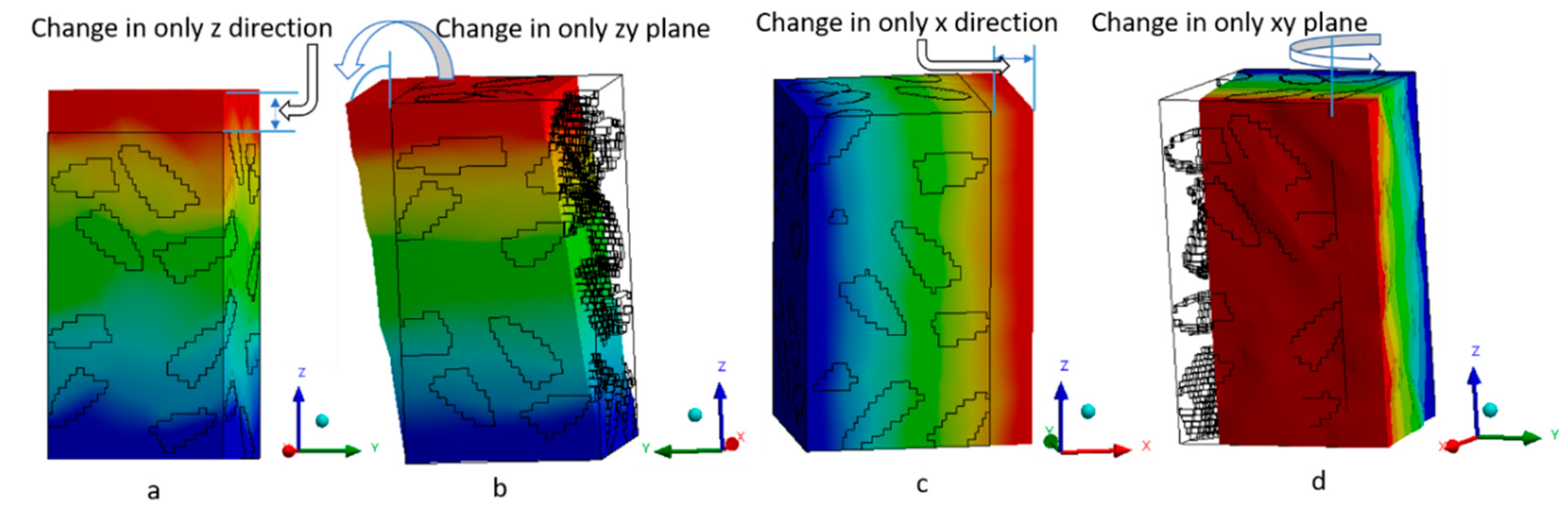
2.3. Finite Element Analysis (Numerical Analysis) at the Meso-Scale
3. Discussion and Validation
4. Conclusions
- Modeling requires manufacturing process effects such as braiding patterns and jamming conditions.
- MSG is a robust and versatile technique for the mechanical characterization of braided composite materials.
- Four-directional braided composites have high shear and transverse modulus.
- FEA is time-consuming than MSG, and while doing FEA, proper boundary and load condition is needed with exact symmetry in composite materials.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Fourth-order tensor 6 × 6 stiffness matrix | |
| Corresponding stiffness for the homogenized model | |
| U | The average strain energy of a unit cell |
| Stress field for heterogeneous body | |
| Strain field for heterogeneous body | |
| Stress field for homogeneous body | |
| Strain field for homogeneous body | |
| Unit volume of rectangular preform | |
| Pitch of a unit cell | |
| Fiber packing fraction | |
| A small parameter to describe the structure genome | |
| Difference in energy | |
| Volume average | |
| ν | Poisson ratio |
| E | Young’s modulus |
| G | Shear modulus |
| MSG | Mechanics of structure genome |
| N | Number of yarns |
| m and n | Number of rows and columns |
| The orientation angle of the yarn | |
| h | Pitch of the unit cell (1*1 rectangular pattern) |
| 2a and 2b | Yarn cross section’s major and minor axis |
| Uy | The unit volume of the rectangular preform |
| Y | The total volume of yarns |
| Vy | The volume fraction of yarns |
| Vf | Fiber volume fraction |
| κ | Fiber packing factor |
References
- Gu, Q.; Quan, Z.; Yu, J.; Yan, J.; Sun, B.; Xu, G. Structural modeling and mechanical characterizing of three-dimensional four-step braided composites: A review. Compos. Struct. 2019, 207, 119–128. [Google Scholar] [CrossRef]
- Tang, S.; Hu, C. Design, Preparation and Properties of Carbon Fiber Reinforced Ultra-High Temperature Ceramic Composites for Aerospace Applications: A Review. J. Mater. Sci. Technol. 2017, 33, 117–130. [Google Scholar] [CrossRef]
- Ko, F. Tensile Strength and Modulus of a Three-Dimensional Braid Composite. Available online: https://www.astm.org/DIGITAL_LIBRARY/STP/PAGES/STP35359S.htm (accessed on 26 November 2020).
- Ma, C.-L.; Yang, J.-M.; Chou, T.-W. Elastic Stiffness of Three-Dimensional Braided Textile Structural. Available online: https://www.astm.org/DIGITAL_LIBRARY/STP/PAGES/STP35360S.htm (accessed on 26 November 2020).
- Yang, J.-M.; Ma, C.-L.; Chou, T.-W. Fiber Inclination Model of Three-Dimensional Textile Structural Composites. J. Compos. Mater. 1986, 20, 472–484. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Franco, E. Numerical evaluation of isostrain and weighted-average models for elastic moduli of three-dimensional composites. Compos. Sci. Technol. 1997, 57, 293–305. [Google Scholar] [CrossRef]
- Jiang, L.; Zeng, T.; Yan, S.; Fang, D. Theoretical prediction on the mechanical properties of 3D braided composites using a helix geometry model. Compos. Struct. 2013, 100, 511–516. [Google Scholar] [CrossRef]
- Wu, D.L.; Hao, Z.P. 5D Braided Structural Composites. J. Astronaut. 1993, 3, 13–16. [Google Scholar]
- Wu, D. Three-cell model and 5D braided structural composites. Compos. Sci. Technol. 1996, 56, 225–233. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zhang, L.T.; Cheng, L.F. Computer geometry simulation of spatial structure of three-dimensional braided composites. J. Aeronaut. Mater. 2008, 28, 95–98. [Google Scholar]
- Chen, L.; Tao, X.-M.; Choy, C. Mechanical analysis of 3-D braided composites by the finite multiphase element method. Compos. Sci. Technol. 1999, 59, 2383–2391. [Google Scholar] [CrossRef]
- Verpoest, I.; Lomov, S.V. Virtual textile composites software WiseTex: Integration with micro-mechanical, permeability and structural analysis. Compos. Sci. Technol. 2005, 65, 2563–2574. [Google Scholar] [CrossRef]
- Nottingham, T. Geometric and Mechanical Modelling of Textiles. Ph.D. Thesis, University of Nottingham, Nottingham, UK, October 2007. [Google Scholar]
- Zhang, L.; Hu, D.; Wang, R.; Zeng, Y.; Cho, C. Establishing RVE model composed of dry fibers and matrix for 3D four-directional braided composites. J. Compos. Mater. 2019, 53, 1917–1931. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, R.; Wang, J.; Jiao, Y.; Yang, X.; Ma, M. An Efficient Method for Geometric Modeling of 3D Braided Composites. J. Eng. Fibers Fabr. 2016, 11, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Hao, W.; Liu, Y.; Huang, X.; Liu, Y.; Zhu, J. A Unit-Cell Model for Predicting the Elastic Constants of 3D Four Directional Cylindrical Braided Composite Shafts. Appl. Compos. Mater. 2017, 25, 619–633. [Google Scholar] [CrossRef]
- Wang, Y.-B.; Liu, Z.-G.; Liu, N.; Hu, L.; Wei, Y.-C.; Ou, J.-J. A new geometric modelling approach for 3D braided tubular composites base on Free Form Deformation. Compos. Struct. 2016, 136, 75–85. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Y.R.; Wei, D.S. Meso-scale modeling of 3-D four-directional braided composites. J. Aerosp. Power. 2013, 28, 1243–1249. [Google Scholar]
- Li, D.-S.; Li, J.-L.; Chen, L.; Lu, Z.-X.; Fang, D.-N. Finite Element Analysis of Mechanical Properties of 3D Four-Directional Rectangular Braided Composites Part 1: Microgeometry and 3D Finite Element Model. Appl. Compos. Mater. 2010, 17, 373–387. [Google Scholar] [CrossRef]
- Mirzavand, B.; Pourmohammad, H. Post-buckling analysis of non-uniformly heated functionally graded cylindrical shells enhanced by shape memory alloys using classical lamination theory. J. Intell. Mater. Syst. Struct. 2019, 30, 2421–2435. [Google Scholar] [CrossRef]
- Nagai, K.; Yokoyama, A.; Maekawa, Z.; Hamada, H. The study of analytical method for three-dimensional composite materials. Trans. Japan Soc. Mech. Eng. 1992, 58, 2099–2103. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-Q.; Wang, A. Microstructure/property relationships in three-dimensionally braided fiber composites. Compos. Sci. Technol. 1995, 53, 213–222. [Google Scholar] [CrossRef]
- Gowayed, Y.A.; Pastore, C.M. Analytical techniques for the prediction of elastic properties of textile reinforced composites. Mech. Compos. Mater. 1993, 28, 393–408. [Google Scholar] [CrossRef]
- Wang, C.; Cao, P.; Tang, M.; Wang, C.; Liu, K.; Liu, B. Study on Properties Prediction and Braiding Optimization of Axial Braided Carbon/Carbon Composite. Materials 2020, 13, 2588. [Google Scholar] [CrossRef] [PubMed]
- Katouzian, M.; Vlase, S. Mori–Tanaka Formalism-Based Method Used to Estimate the Viscoelastic Parameters of Laminated Composites. Polymers 2020, 12, 2481. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Baird, D. Prediction of Young’s Modulus for Injection Molded Long Fiber Reinforced Thermoplastics. J. Compos. Sci. 2018, 2, 47. [Google Scholar] [CrossRef] [Green Version]
- Bednarcyk, B.A.; Mital, S.K.; Pineda, E.J.; Arnold, S.M. Multiscale Modeling of Ceramic Matrix Composites. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Singh, D.K.; Vaidya, A.; Thomas, V.; Theodore, M.; Kore, S.; Vaidya, U. Finite Element Modeling of the Fiber-Matrix Interface in Polymer Composites. J. Compos. Sci. 2020, 4, 58. [Google Scholar] [CrossRef]
- Dodla, S. Micromechanical Analysis for Two-Phase Copper-Silver Composites under Large Deformations. J. Compos. Sci. 2018, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Yu, W. Simplified Formulation of Mechanics of Structure Genome. AIAA J. 2019, 57, 4201–4209. [Google Scholar] [CrossRef]
- Miehe, C.; Schröder, J.; Becker, M. Computational homogenization analysis in finite elasticity: Material and structural instabilities on the micro- and macro-scales of periodic composites and their interaction. Comput. Methods Appl. Mech. Eng. 2002, 191, 4971–5005. [Google Scholar] [CrossRef]
- Kassapoglou, C.; Lagace, P.A. An Efficient Method for the Calculation of Interlaminar Stresses in Composite Materials. J. Appl. Mech. 1986, 53, 744–750. [Google Scholar] [CrossRef]
- Peng, B.; Yu, W. A micromechanics theory for homogenization and dehomogenization of aperiodic heterogeneous materials. Compos. Struct. 2018, 199, 53–62. [Google Scholar] [CrossRef]
- Liu, X.; Rouf, K.; Peng, B.; Yu, W. Two-step homogenization of textile composites using mechanics of structure genome. Compos. Struct. 2017, 171, 252–262. [Google Scholar] [CrossRef]
- Rouf, K.; Liu, X.; Yu, W. Multiscale structural analysis of textile composites using mechanics of structure genome. Int. J. Solids Struct. 2018, 136–137, 89–102. [Google Scholar] [CrossRef]
- Tan, H.; Liu, L.; Guan, Y.; Chen, W.; Zhao, Z. Investigation of three-dimensional braided composites subjected to steel projectile impact: Automatically modelling mesoscale finite element model. Compos. Struct. 2019, 209, 317–327. [Google Scholar] [CrossRef]
- Bilisik, K. Three-dimensional braiding for composites: A review. Text. Res. J. 2015, 83, 1414–1436. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, L.; Hu, D.; Shen, X.; Song, J. Mesoscopic modeling of 3D four-directional braided composites. In Proceedings of the ASME Turbo Expo (Vol. 6); American Society of Mechanical Engineers (ASME): Seoul, Korea, 2016. [Google Scholar]
- Long, A.C.; Brown, L.P. Modelling the geometry of textile reinforcements for composites: TexGen. In Composite Reinforcements for Optimum Performance; Woodhead Publishing: Sawston, UK, 2011; pp. 239–264. [Google Scholar]
- Hu, L.; Tao, G.; Liu, Z.; Wang, Y.; Ya, J. Investigation on the Yarn Squeezing Effect of Three Dimensional Full Five Directional Braided Composites. Appl. Compos. Mater. 2019, 26, 371–387. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, L.; Hu, D.; Liu, C.; Shen, X.; Cho, C.; Li, B. A novel approach to impose periodic boundary condition on braided composite RVE model based on RPIM. Compos. Struct. 2017, 163, 77–88. [Google Scholar] [CrossRef]
- Qu, J.; Cherkaoui, M. Fundamentals of Micromechanics of Solidss; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kalamkarov, A.L. Asymptotic homogenization method and micromechanical models for composite materials and thin-walled composite structures. In Mathematical Methods and Models in Composites; World Scientific: Singapore, 2013. [Google Scholar]
- Xiu, Y. Numerical Analysis of Mechanical Properties of 3D Four-Step Braided Composites. Master’s Thesis, Tianjin Polytechnic University, Tianjin, China, 2001. [Google Scholar]
- Tian, S.; Yu, W.; Liu, X.; Sertse, H. Ansys Workbench Swiftcomp gui User Manual. Available online: https://cdmhub.org/groups/yugroup/resources?id=1726 (accessed on 26 November 2020).
- Liu, K.C.; Arnold, S.M. Influence of scale specific features on the progressive damage of woven ceramic matrix composites (CMCs). Comput. Mater. Contin. 2013, 35, 35–65. [Google Scholar]
- Murthy, P.L.N.; Sullivan, R.M.; Mital, S.K. Modeling of 3-D Woven Ceramic Matrix Composites. Available online: https://ntrs.nasa.gov/citations/20030020624 (accessed on 26 November 2020).
- Yu, G.; Shi, B.; Shen, Y.; Gu, J. A novel finite element method for predicting the tensile properties of 3D braided composites. Mater. Res. Express 2019, 6, 125626. [Google Scholar] [CrossRef]
- Liu, G.R.; Quek, S.S. Briefing on mechanics for solids and structures. In The Finite Element Method, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2014; pp. 13–41. [Google Scholar]
- Aboudi, J.; Arnold, S.M.; Bednarcyk, B.A. Fundamentals of the Mechanics of Multiphase Materials. In Micromechanics of Composite Materials; Elsevier Inc.: Amsterdam, The Netherlands, 2013; pp. 87–145. [Google Scholar]
- Guo, Q.; Zhang, G.; Li, J. Process parameters design of a three-dimensional and five-directional braided composite joint based on finite element analysis. Mater. Des. 2013, 46, 291–300. [Google Scholar] [CrossRef]


| Material Constituents | Mechanical Properties (GPa) |
|---|---|
| Matrix (epoxy resin) | E = 3.5, ν = 0.35 |
| Fiber (T300 fiber) | E11 = 230, E22 = E33 = 40, G12 = G13 = 24, G23 = 14.3, ν12/ν13 = 0.27, ν23 = 0.35 |
| Yarn (fiber bundle if fiber volume fraction is 0.52) properties from micro-scale homogenizations | E11=196.07 GPa, E22 = E33 = 22.10 GPa, G12 = G13 = 10.15 GPa, G23 = 8.07 GPa, ν12 = ν13= 0.27, ν23 = 0.36. |
| Material Constituents | Mechanical Properties |
|---|---|
| Matrix | E = 3.5 GPa, ν = 0.35 |
| Yarn | E11 = 196.07 GPa, E22 = E33 = 22.10 GPa, G12 = G13 = 10.15 GPa, G23= 8.07 GPa, ν12 = ν13= 0.27, ν23=0.36 |
| Calculated effective homogenized properties of the meso-scale 3D four-dimensional braided PMCs (epoxy resin/T300 carbon fiber) model | E11 = 10.712 GPa, E22 = 10.673 GPa, E33 = 17.821 GPa, G12 = 11.641 GPa, G13 = 18.152 GPa, G23 = 18.112 GPa, ν12 = 0.270, ν13 = 0.370, ν23 = 0.369. |
| X-Axis | Y-Axis | Z-Axis | ||||
|---|---|---|---|---|---|---|
| (+) Direction (Plane) | (-) Direction | (+) Direction | (-) Direction | (+) Direction | (-) Direction | |
| E11, ν12 | Ux = DB | All is fix | Sym Uy, Rz, Rx =0 | Same | Sym Uz, Ry, Rx =0 | Same |
| E22, ν23 | Sym Ux, Rz, Ry = 0 | Same | Uy = DB | All is fix | Sym Uz, Ry, Rx = 0 | Same |
| E33, ν13 | Sym Ux, Rz, Ry = 0 | Same | Sym Uy, Rz, Rx = 0 | Same | Uz = DB | All is fix |
| G12 | Uy = DB, Uz = 0 | Uy, Uz = 0 | Ux, Uz = 0 | Ux, Uz = 0 | Uz = 0 | Uz = 0 |
| G13 | Uz = DB, Uy = 0 | Uy, Uz = 0 | Uy = 0 | Uy = 0 | Ux, Uy = 0 | Ux, Uy = 0 |
| G23 | Ux = 0 | Ux = 0 | Ux, Uz = 0 | Ux, Uz = 0 | Uy = DB, Ux = 0 | Ux, Uy = 0 |
| Elastic Constants | Current Process Results | Literature FEM Results [41] | Literature (Experiment) [44] |
|---|---|---|---|
| E11 (GPa) | 10.712 | 10.645 | |
| E22 (GPa) | 10.673 | 10.651 | |
| E33 (GPa) | 17.821 | 17.266 | 17.91 |
| G12 (GPa) | 11.741 | 11.607 | |
| G13 (GPa) | 18.552 | 18.145 | |
| G23 (GPa) | 18.532 | 18.138 | |
| ν12 | 0.270 | 0.269 | |
| ν13 | 0.369 | 0.371 | |
| ν23 | 0.370 | 0.371 |
| Analysis Scale | Mechanical Properties |
|---|---|
| Micro-scale homogenization for yarn | E11 = 258.537 GPa, E22 = E33 = 58.593 GPa, G12 = G13 = 36.201 GPa, G23 = 28.098 GPa, ν12 = ν13 = 0.23, ν23 = 0.35 |
| Meso-scale homogenization (for macro-model) | E11 = 213.522 GPa, E22 = 195.171 GPa, E33 = 277.613 GPa, G12 = 214.323 GPa, G13 = 283.321 GPa, G23 = 281.305 GPa, ν12 = 0.260, ν13 = 0.341, ν23 = 0.347. |
| FEM results | E11 = 214.321 GPa, E22 = 197.153 GPa, E33 = 278.215 GPa, G12 = 214.352 GPa, G13 = 285.413 GPa, G23 = 282.315 GPa, ν12 = 0.262, ν13 = 0.342, ν23 = 0.349. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhimole, V.K.; Chen, Y.; Cho, C. Modeling and Two-Step Homogenization of Aperiodic Heterogenous 3D Four-Directional Braided Composites. J. Compos. Sci. 2020, 4, 179. https://doi.org/10.3390/jcs4040179
Dhimole VK, Chen Y, Cho C. Modeling and Two-Step Homogenization of Aperiodic Heterogenous 3D Four-Directional Braided Composites. Journal of Composites Science. 2020; 4(4):179. https://doi.org/10.3390/jcs4040179
Chicago/Turabian StyleDhimole, Vivek Kumar, Yanqin Chen, and Chongdu Cho. 2020. "Modeling and Two-Step Homogenization of Aperiodic Heterogenous 3D Four-Directional Braided Composites" Journal of Composites Science 4, no. 4: 179. https://doi.org/10.3390/jcs4040179
APA StyleDhimole, V. K., Chen, Y., & Cho, C. (2020). Modeling and Two-Step Homogenization of Aperiodic Heterogenous 3D Four-Directional Braided Composites. Journal of Composites Science, 4(4), 179. https://doi.org/10.3390/jcs4040179






