Higher-Order Free Vibration Analysis of Porous Functionally Graded Plates
Abstract
:1. Introduction
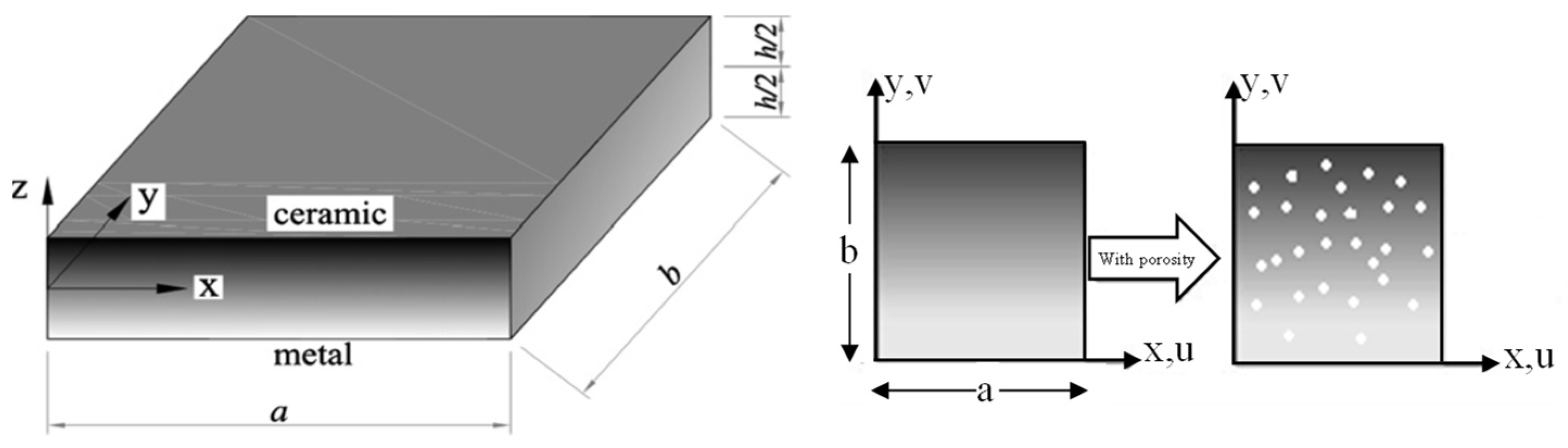
2. Theoretical Formulation
3. Equations of Motion
4. Analytical Solution
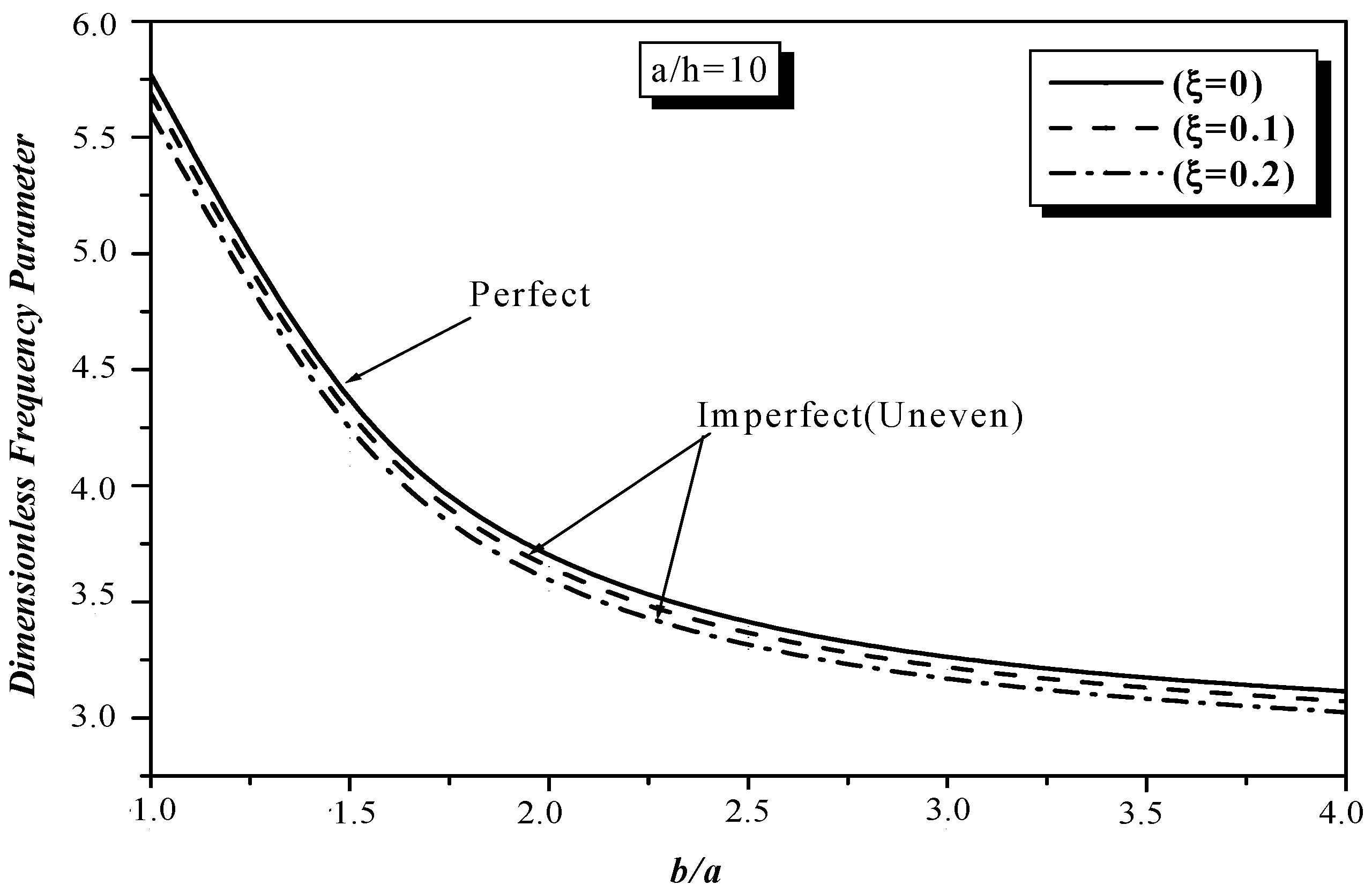
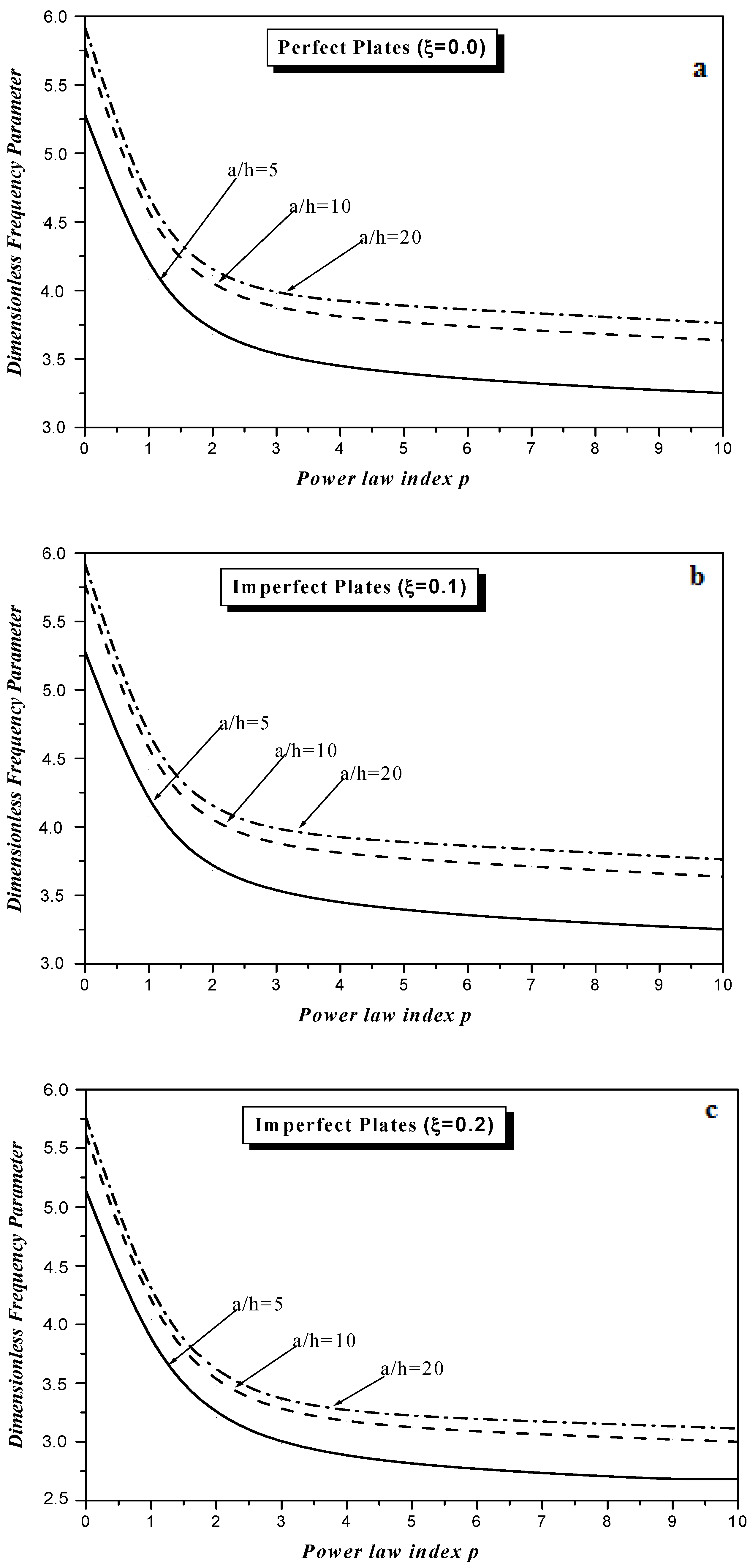
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Dehnavi, F.N.; Parvizi, A. Investigation of thermo-elasto-plastic behavior of thick-walled spherical vessels with inner functionally graded coatings. Meccanica 2017, 19, 2421–2438. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, J.; Zhang, L.; Tsutsumi, S.; Feng, J.; Ma, N. Impacts of laser cladding residual stress and material properties of functionally graded layers on titanium alloy sheet. Addit. Manuf. 2020, 35, 101303. [Google Scholar] [CrossRef]
- Huang, S.; Guo, L.; Zhang, L.; Zhang, Y.; Pan, H. The interface crack problem under steady heat flux for a functionally graded coating-substrate structure with general coating properties. Theor. Appl. Fract. Mech. 2020, 109, 102675. [Google Scholar] [CrossRef]
- Dubey, A.; Jaiswal, S.; Haldar, S.; Roy, P.; Lahiri, D. Functionally gradient magnesium-based composite for temporary orthopaedic implant with improved corrosion resistance and osteogenic properties. Biomed. Mater. 2021, 16, 015017. [Google Scholar] [CrossRef]
- Mondal, K.; Nuñez, L.; Downey, C.M.; Van Rooyen, I.J. Thermal barrier coatings overview: Design, manufacturing, and applications in high-temperature industries. Ind. Eng. Chem. Res. 2021, 60, 6061–6077. [Google Scholar] [CrossRef]
- Khaleghi, F.; Tajally, M.; Emadoddin, E.; Mohri, M. Functionally-graded shape memory alloy by diffusion annealing of palladium-coated NiTi plates. Met. Mater. Int. 2017, 23, 915–922. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, J.; Li, S.R. Finite element analysis for the buckling of functionally graded material plates based on physical neutral surface. Jisuan Lixue Xuebao/Chin. J. Comput. Mech. 2020, 37, 560–566. [Google Scholar]
- Benyamina, A.B.; Bouderba, B.; Saoula, A. Bending response of composite material plates with specific properties, case of a typical fgm “ceramic/metal” in thermal environments. Period. Polytech. Civil Eng. 2018, 62, 930–938. [Google Scholar] [CrossRef]
- Smith, J.A.; Mele, E.; Rimington, R.P.; Capel, A.J.; Lewis, M.P.; Silberschmidt, V.V.; Li, S. Polydimethylsiloxane and poly(ether) ether ketone functionally graded composites for biomedical applications. J. Mech. Behav. Biomed. Mater. 2019, 93, 130–142. [Google Scholar] [CrossRef] [Green Version]
- Rousseau, C.E.; Chalivendra, V.B.; Tippur, H.V.; Shukla, A. Experimental Fracture Mechanics of Functionally Graded Materials: An Overview of Optical Investigations. Exp. Mech. 2010, 50, 845–865. [Google Scholar] [CrossRef]
- Tornabene, F.; Liverani, A.; Caligiana, G. FGM and laminated doubly curved shells and panels of revolution with a free-form meridian: A 2-D GDQ solution for free vibrations. Int. J. Mech. Sci. 2011, 53, 446–470. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Batra, R.C.; Roque, C.M.C.; Qian, L.F.; Jorge, R.M.N. Natural frequencies of functionally graded plates by a meshless method. Compos. Struct. 2006, 75, 593–600. [Google Scholar] [CrossRef]
- Qian, L.F.; Batra, R.C.; Chen, L.M. Static and dynamic deformations of thick functionally graded elastic plates by using higher-order shear and normal deformable plate theory and meshless local Petrov–Galerkin method. Compos. Part B Eng. 2004, 35, 685–697. [Google Scholar] [CrossRef]
- Tornabene, F.; Brischetto, S.; Fantuzzi, N.; Viola, E. Numerical and exact models for free vibration analysis of cylindrical and spherical shell panels. Compos. Part B Eng. 2015, 81, 231–250. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Free vibrations of composite oval and elliptic cylinders by the generalized differential quadrature method. Thin Wall Struct. 2015, 97, 114–129. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. Application of Carrera Unified Formulation to study the effect of porosity on natural frequencies of thick porous-cellular plates. Compos. Part B Eng. 2016, 91, 361–370. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. On the effect of coupled solid-fluid deformation on natural frequencies of fluid saturated porous plates. Eur. J. Mech. A. Solids 2017, 63, 99–109. [Google Scholar] [CrossRef]
- Kamranfard, M.R.; Saidi, A.R.; Naderi, A. Analytical solution for vibration and buckling of annular sectorial porous plates under in-plane uniform compressive loading. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 2211–2228. [Google Scholar] [CrossRef]
- Benachour, A.; Tahar, H.D.; Atmane, H.A.; Tounsi, A.; Ahmed, M.S. A four variable refined plate theory for free vibrations of functionally graded plates with arbitrary gradient. Compos. Part B Eng. 2011, 42, 1386–1394. [Google Scholar] [CrossRef]
- Belabed, Z.; Houari, M.S.A.; Tounsi, A.; Mahmoud, S.R.; Bég, O.A. An efficient and simple higher order shear and normal deformation theory for functionally graded material (FGM) plates. Compos. Part B Eng. 2014, 60, 274–283. [Google Scholar] [CrossRef]
- Bîrsan, M.; Altenbach, H.; Sadowski, T.; Eremeyev, V.A.; Pietras, D. Deformation analysis of functionally graded beams by the direct approach. Compos. Part B Eng. 2012, 43, 1315–1328. [Google Scholar] [CrossRef] [Green Version]
- Bîrsan, M.; Sadowski, T.; Marsavina, L.; Linulc, E.; Pietras, D. Mechanical behavior of sandwich composite beams made of foams and functionally graded materials. Int. J. Solids Struct. 2013, 50, 519–530. [Google Scholar] [CrossRef] [Green Version]
- Vyacheslav Burlayenko, N.; Sadowski, T. Free vibrations and static analysis of functionally graded sandwich plates with three-dimensional finite elements. Meccanica 2020, 55, 815–832. [Google Scholar] [CrossRef] [Green Version]
- Bîrsan, M.; Pietras, D.; Sadowski, T. Determination of effective stiffness properties of multilayered composite beams. Contin. Mech. Thermodyn. 2021, 33, 1781–1803. [Google Scholar] [CrossRef]
- Vyacheslav Burlayenko, N.; Sadowski, T.; Altenbach, H. Efficient free vibration analysis of FGM sandwich flat panels with conventional shell elements. Mech. Adv. Mater. Struct. 2021. [Google Scholar] [CrossRef]
- Shimpi, R.P. Refined plate theory and its variants. AIAA J. 2002, 40, 137–146. [Google Scholar] [CrossRef]
- Merdaci, S.; Tounsi, A.; Houari, M.S.A.; Mechab, I.; Hebali, H.; Benyoucef, S. Two new refined shear displacement models for functionally graded sandwich plates. Arch. Appl. Mech. 2011, 81, 1507–1522. [Google Scholar] [CrossRef]
- Ameur, M.; Tounsi, A.; Mechab, I.; Adda Bedia, E.A. A New Trigonometric Shear Deformation Theory for Bending Analysis of Functionally Graded Plates Resting on Elastic Foundations. KSCE J. Civ. Eng. 2011, 15, 1405–1414. [Google Scholar] [CrossRef]
- Tounsi, A.; Houari, M.S.A.; Benyoucef, S.; Adda Bedia, E.A. A refined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates. Aerosp. Sci. Technol. 2013, 24, 209–220. [Google Scholar] [CrossRef]
- Mohamed, Z.; Tounsi, A.; Houari, M.S.A.; Adda Bedia, E.A.; Anwar Bég, O. Bending analysis of FGM plates under hygro-thermo-mechanical loading using a four variable refined plate theory. Aerosp. Sci. Technol. 2014, 34, 24–34. [Google Scholar]
- Zhu, J.; Lai, Z.; Yin, Z.; Jeon, J.; And Lee, S. Fabrication of ZrO2–NiCr functionally graded material by powder metallurgy. Mater. Chem. Phys. 2001, 68, 130–135. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; And Ungbhakorn, V. Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp. Sci. Technol. 2014, 32, 111–120. [Google Scholar] [CrossRef]
- Magnucka-Blandzi, E.; Magnucki, K. Effective design of a sandwich beam with a metal foam core. Thin-Walled Struct. 2007, 45, 432–438. [Google Scholar] [CrossRef]
- Biot, M. Theory of buckling of a porous slab and its thermoelastic analogy. J. Appl. Mech. 1964, 31, 194–198. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.H.D. Fundamentals of poroelasticity. In Comprehensive Rock Engineering: Principles, Practice and Projects; Chapter 5; Pergamon Press: Oxford, UK, 1993; Volume 2. [Google Scholar]
- Jabbari, M.; Mojahedin, A.; Khorshidvand, A.; Eslami, M. Buckling analysis of a functionally graded thin circular plate made of saturated porous materials. J. Eng. Mech. 2014, 140, 287–295. [Google Scholar] [CrossRef]
- Ait Yahia, S.; Ait Atmane, H.; Houari, M.S.A.; Tounsi, A. Wave propagation in functionally graded plates with porosities using various higher-order shear deformation plate theories. Struct. Eng. Mech. 2015, 53, 1143–1165. [Google Scholar] [CrossRef]
- Mouaici, F.; Benyoucef, S.; Ait Atmane, H.; Tounsi, A. Effect of porosity on vibrational characteristics of non-homogeneous plates using hyperbolic shear deformation theory. Wind Struct. 2016, 22, 429–454. [Google Scholar] [CrossRef]
- Merdaci, S. Analysis of Bending of Ceramic-Metal Functionally Graded Plates with Porosities Using of High Order Shear Theory. Adv. Eng. Forum. 2018, 30, 54–70. [Google Scholar]
- Merdaci, S.; Belghoul, H. High Order Shear Theory for Static Analysis Functionally Graded Plates with Porosities. C. R. Mec. 2019, 347, 207–217. [Google Scholar] [CrossRef]
- Merdaci, S.; Mostefa, A.H. Influence of porosity on the analysis of sandwich plates FGM using of high order shear-deformation theory. Frat. Int. Strutt. 2020, 14, 199–214. [Google Scholar] [CrossRef]
- Merdaci, S.; Mostefa, A.H.; Beldjelili, Y.; Mohamed, M.; Boutaleb, S.; Hellal, H. Analytical solution for static bending analysis of functionally graded plates with porosities. Frat. Int. Strutt. 2021, 15, 65–75. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Merdaci, S. Free Vibration Analysis of Composite Material Plates “Case of a Typical Functionally Graded FG Plates Ceramic/Metal with Porosities”. Nano Hybrids Compos. (NHC) 2019, 25, 69–83. [Google Scholar] [CrossRef]
- Merdaci, S.; Mostefa, A.H.; Boutaleb, S.; Hellal, H. Free Vibration Analysis of Functionally Graded FG Nano-Plates with Porosities. J. Nano Res. 2020, 64, 61–74. [Google Scholar]
- Arshid, E.; Khorshidvand, A.R. Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin Wall. Struct. 2018, 125, 220–233. [Google Scholar] [CrossRef]
- Li, H.; Pang, F.; Chen, H.; Du, Y. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Compos. Part B 2019, 164, 249–264. [Google Scholar] [CrossRef]
- Xue, Y.; Jin, G.; Ma, X.; Chen, H.; Ye, T.; Chen, M.; Zhang, Y. Free vibration analysis of porous plates with porosity distributions in the thickness and in-plane directions using isogeometric approach. Int. J. Mech. Sci. 2019, 152, 346–362. [Google Scholar] [CrossRef]
- Mashat, D.S.; Zenkour, A.M.; Radwan, A.F. A quasi-3D higher-order plate theory for bending of FG plates resting on elastic foundations under hygro-thermo-mechanical loads with porosity. Eur. J. Mech. A. Solid 2020, 82, 103985. [Google Scholar] [CrossRef]
- Xie, K.; Wang, Y.; Niu, H.; Chen, H. Large-amplitude nonlinear free vibrations of functionally graded plates with porous imperfection: A novel approach based on energy balance method. Compos. Struct. 2020, 246, 112367. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, G.; Chen, M.; Ye, T.; Yang, C.; Yin, Y. Free vibration and damping analysis of porous functionally graded sandwich plates with a viscoelastic core. Compos. Struct. 2020, 244, 112298. [Google Scholar] [CrossRef]
- Belarbi, M.O.; Khechai, A.; Bessaim, A.; Houari, M.S.A.; Garg, A.; Hirane, H.; Chalak, H.D. Finite element bending analysis of symmetric and non-symmetric functionally graded sandwich beams using a novel parabolic shear deformation theory. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 2482–2504. [Google Scholar] [CrossRef]
- Belarbi, M.O.; Zenkour, A.M.; Tati, A.; Salami, S.J.; Khechai, A.; Houari, M.S.A. An efficient eight-node quadrilateral element for free vibration analysis of multilayer sandwich plates. Int. J. Numer. Methods Eng. 2021, 122, 2360–238715. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Belarbi, M.O.; Chakraverty, S.; Eltaher, M.A. Analysis of axially temperature-dependent functionally graded carbon nanotube-reinforced composite plates. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, S.J.; Saran, V.H.; Harsha, S.P. Vibration characteristics of porous FGM plate with variable thickness resting on Pasternak’s foundation. Eur. J. Mech. A. Solids 2021, 85, 104124. [Google Scholar] [CrossRef]
- Kumar Sah, S.; Ghosh, A. Influence of Porosity Distribution on Free Vibration and Buckling Analysis of Multi- Directional Functionally Graded Sandwich Plates. Compos. Struct. 2021, 279, 114795. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R.; Antonietta Aiello, M. Higher-order modeling of anisogrid composite lattice structures with complex geometries. Eng. Struct. 2021, 244, 112686. [Google Scholar] [CrossRef]
- Van Vinh, P.; Huy, L.Q. Finite element analysis of functionally graded sandwich plates with porosity via a new hyperbolic shear deformation theory. Def. Technol. 2021. [Google Scholar] [CrossRef]
- Yin, Z.; Gao, H.; Lin, G. Bending and free vibration analysis of functionally graded plates made of porous materials according to a novel the semi-analytical method. Eng. Anal. Bound. Elem. 2021, 133, 185–199. [Google Scholar] [CrossRef]
- Zghal, S.; Ataoui, D.; Dammak, F. Free vibration analysis of porous beams with gradually varying mechanical properties. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2021. [Google Scholar] [CrossRef]
- Belarbi, M.O.; Houari, M.S.A.; Hirane, H.; Daikh, A.A.; Bordas, S.P.A. On the finite element analysis of functionally graded sandwich curved beams via a new refined higher order shear deformation theory. Compos. Struct. 2022, 279, 114715. [Google Scholar] [CrossRef]
- Merdaci, S.; Hadj, M.A.; Merazi, M.; Belghoul, H.; Hellal, H.; Boutaleb, S. Effects of even pores distribution of functionally graded plate porous rectangular and square. Procedia Struct. Integr. 2020, 26, 35–45. [Google Scholar]
- Rezaei, A.S.; Saidi, A.R.; Abrishamdari, M.; Pour Mohammadi, M.H. Natural frequencies of functionally graded plates with porosities via a simple four variable plate theory: An analytical approach. Thin-Walled Struct. 2017, 120, 366–377. [Google Scholar] [CrossRef]
- Askari, M.; Saidi, A.R.; Rezaei, A.S.; Badizi, M.A. Navier-type Free Vibration Analysis of Porous Smart Plates According to Reddy’s Plate Theory. In Proceedings of the First International Conference on Mechanics of Advanced Materials and Equipment, Ahvaz, Iran, 31 January 2018. [Google Scholar]
- Shi, J.W.; Nakatani, A.; Kitagawa, H. Vibration analysis of fully clamped arbitrarily laminated plate. Compos. Struct. 2004, 63, 115–122. [Google Scholar] [CrossRef]
- Shi, J.W.; Nakatani, A.; Kitagawa, H. Approximate vibration analysis of laminated curved panel using higher-order shear deformation theory. Acta Mech. Sinica 2004, 20, 238–246. [Google Scholar]


| Properties | Aluminum (Al) | Alumina (Al2O3) |
|---|---|---|
| Young’s modulus (N/m2) | 70 × 109 | 38 × 108 |
| Poisson’s ratio | 0.3 | 0.3 |
| Mass density (kg/m3) | 2702 | 3800 |
| Method | ||||
|---|---|---|---|---|
| 0 | 1 | 4 | ||
| 20 | Ref. [21] | 0.0148 | 0.0113 | 0.0098 |
| Ref. [22] | 0.0148 | 0.0113 | 0.0098 | |
| Ref. [65] | 0.0148 | 0.0113 | 0.0098 | |
| Ref. [66] | 0.0148 | 0.0113 | 0.0098 | |
| Proposed formulation | 0.0148 | 0.0113 | 0.0098 | |
| 10 | Ref. [21] | 0.0576 | 0.0441 | 0.0380 |
| Ref. [22] | 0.0578 | 0.0449 | 0.0389 | |
| Ref. [65] | 0.0578 | 0.0442 | 0.0383 | |
| Ref. [66] | 0.0577 | 0.0442 | 0.0380 | |
| Proposed formulation | 0.0577 | 0.0442 | 0.0381 | |
| 5 | Ref. [21] | 0.2112 | 0.1628 | 0.1375 |
| Ref. [22] | 0.2121 | 0.1640 | 0.1383 | |
| Ref. [65] | 0.2127 | 0.1630 | 0.1405 | |
| Ref. [66] | 0.2112 | 0.1631 | 0.1377 | |
| Proposed formulation | 0.2113 | 0.1631 | 0.1378 | |
| Porosity | Method | ||||
|---|---|---|---|---|---|
| (1, 1) | (1, 2) | (2, 2) | (1, 3) | ||
| Ref. [65] | 0.0224 | 0.0553 | 0.0874 | 0.1085 | |
| Ref. [66] | 0.0223 | 0.0552 | 0.0873 | 0.1083 | |
| Proposed formulation | 0.0224 | 0.0554 | 0.0874 | 0.1084 | |
| Ref. [65] | 0.0225 | 0.0555 | 0.0879 | 0.1091 | |
| Ref. [66] | 0.0224 | 0.0554 | 0.0877 | 0.1087 | |
| Proposed formulation | 0.0225 | 0.0555 | 0.0879 | 0.1089 | |
| Model | Perfect | Imperfect | |||
|---|---|---|---|---|---|
| 5 | Ref. [56] | 2.6476 | 2.5934 | 2.5150 | |
| Proposed formulation | 2.6475 | 2.5930 | 2.5140 | ||
| 10 | Ref. [56] | 2.7937 | 2.7328 | 2.6452 | |
| Proposed formulation | 2.7937 | 2. 7320 | 2.6448 | ||
| 5 | Ref. [56] | 4.0782 | 3.9982 | 3.8821 | |
| Proposed formulation | 4.0781 | 3.9978 | 3.8818 | ||
| 10 | Ref. [56] | 4.4193 | 4.3243 | 4.1875 | |
| Proposed formulation | 4.4192 | 4.3224 | 4.1863 | ||
| 5 | Ref. [56] | 6.2664 | 6.1508 | 6.9033 | |
| Proposed formulation | 6.2663 | 6.1502 | 6.9024 | ||
| 10 | Ref. [56] | 7.0516 | 5.9821 | 6.6891 | |
| Proposed formulation | 7.0515 | 5.9818 | 6.6886 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merdaci, S.; Adda, H.M.; Hakima, B.; Dimitri, R.; Tornabene, F. Higher-Order Free Vibration Analysis of Porous Functionally Graded Plates. J. Compos. Sci. 2021, 5, 305. https://doi.org/10.3390/jcs5110305
Merdaci S, Adda HM, Hakima B, Dimitri R, Tornabene F. Higher-Order Free Vibration Analysis of Porous Functionally Graded Plates. Journal of Composites Science. 2021; 5(11):305. https://doi.org/10.3390/jcs5110305
Chicago/Turabian StyleMerdaci, Slimane, Hadj Mostefa Adda, Belghoul Hakima, Rossana Dimitri, and Francesco Tornabene. 2021. "Higher-Order Free Vibration Analysis of Porous Functionally Graded Plates" Journal of Composites Science 5, no. 11: 305. https://doi.org/10.3390/jcs5110305
APA StyleMerdaci, S., Adda, H. M., Hakima, B., Dimitri, R., & Tornabene, F. (2021). Higher-Order Free Vibration Analysis of Porous Functionally Graded Plates. Journal of Composites Science, 5(11), 305. https://doi.org/10.3390/jcs5110305








