Multi-Objective Optimization of Functionally Graded Beams Using a Genetic Algorithm with Non-Dominated Sorting
Abstract
:1. Introduction
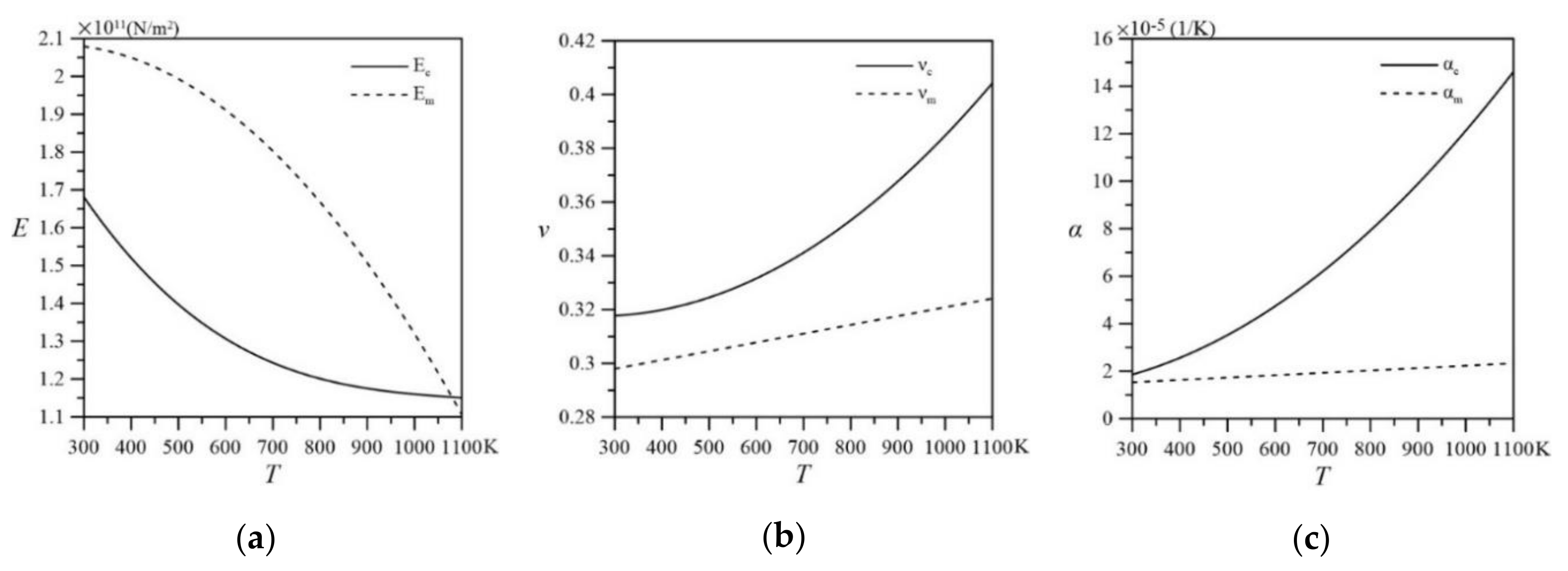
2. Effective Material Properties
2.1. The Rule of Mixtures
2.2. The Mori-Tanaka Scheme
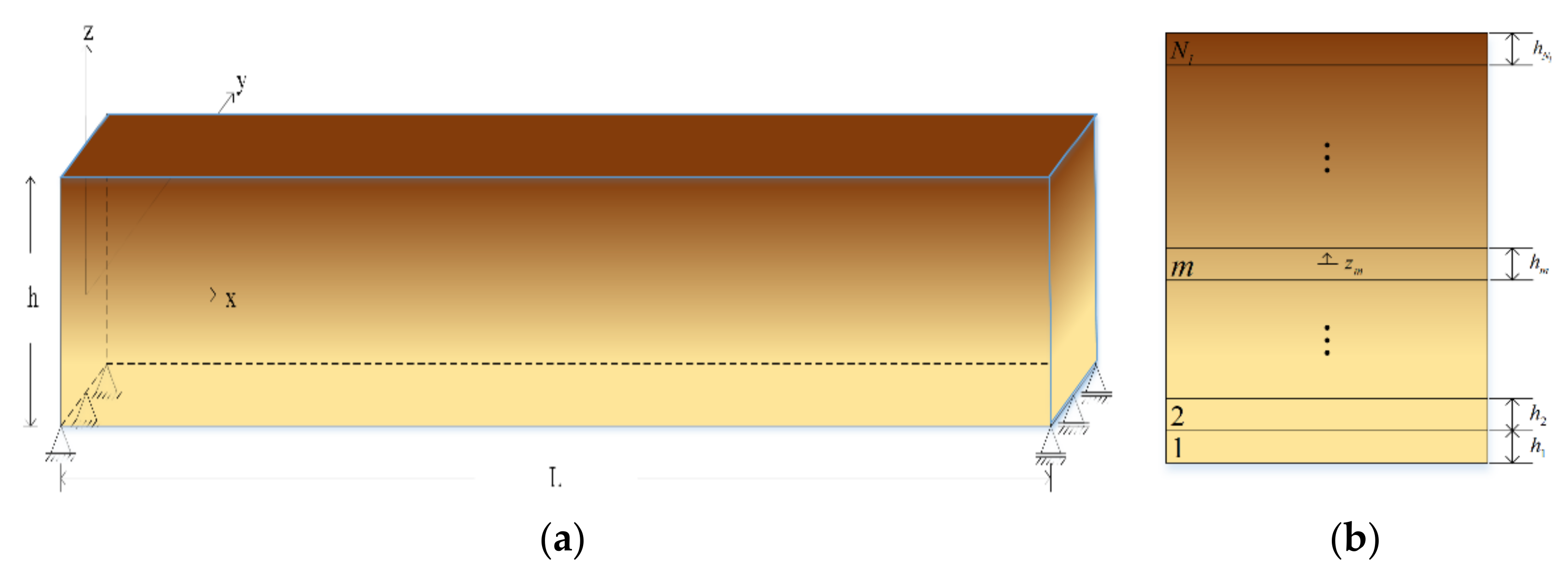
3. The Mixed LW HSDT for FG Beams
3.1. Strong-Form Formulation
3.2. Applications
4. Optimal Design
4.1. Statement of the Optimization Problem
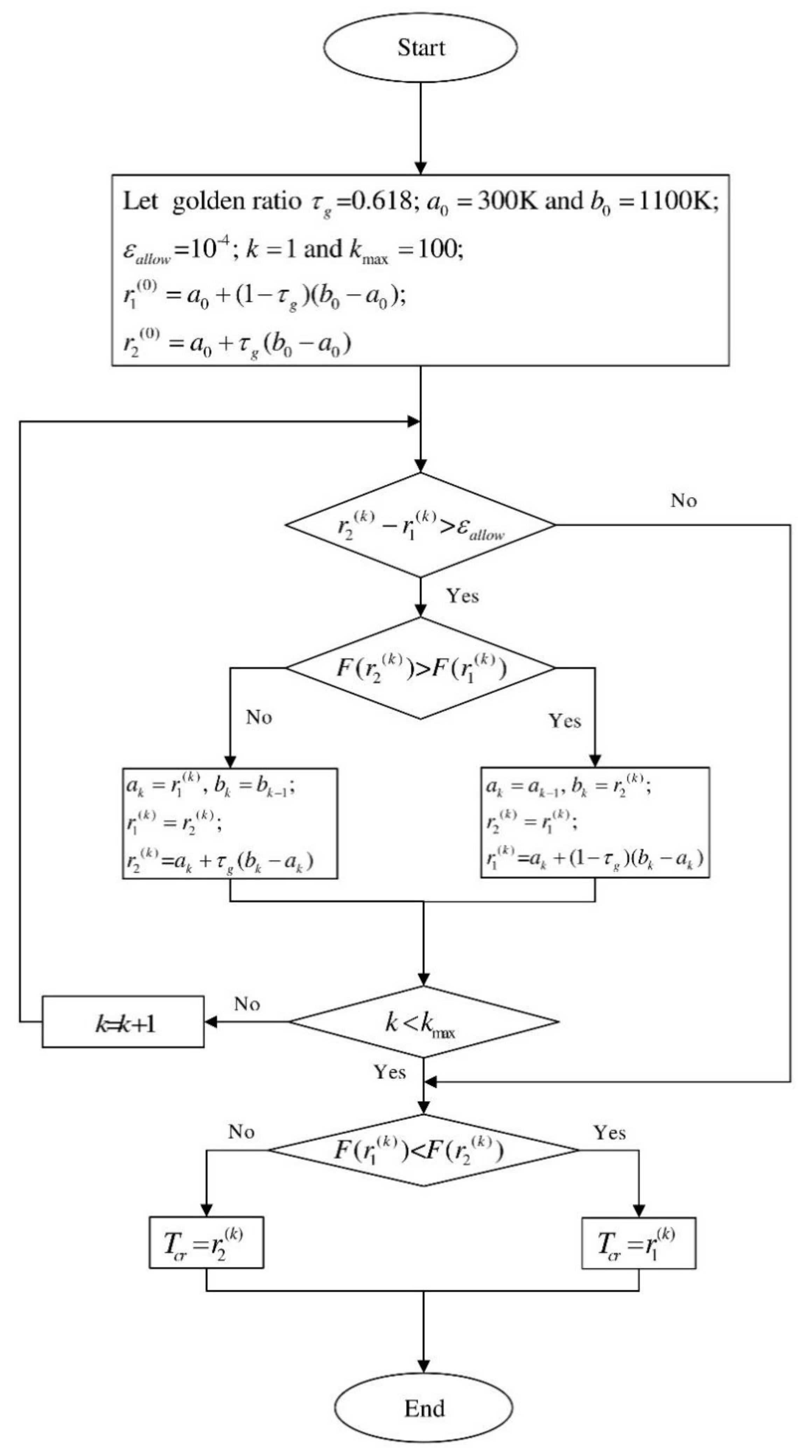
4.2. The Non-Dominated Sorting-Based GA
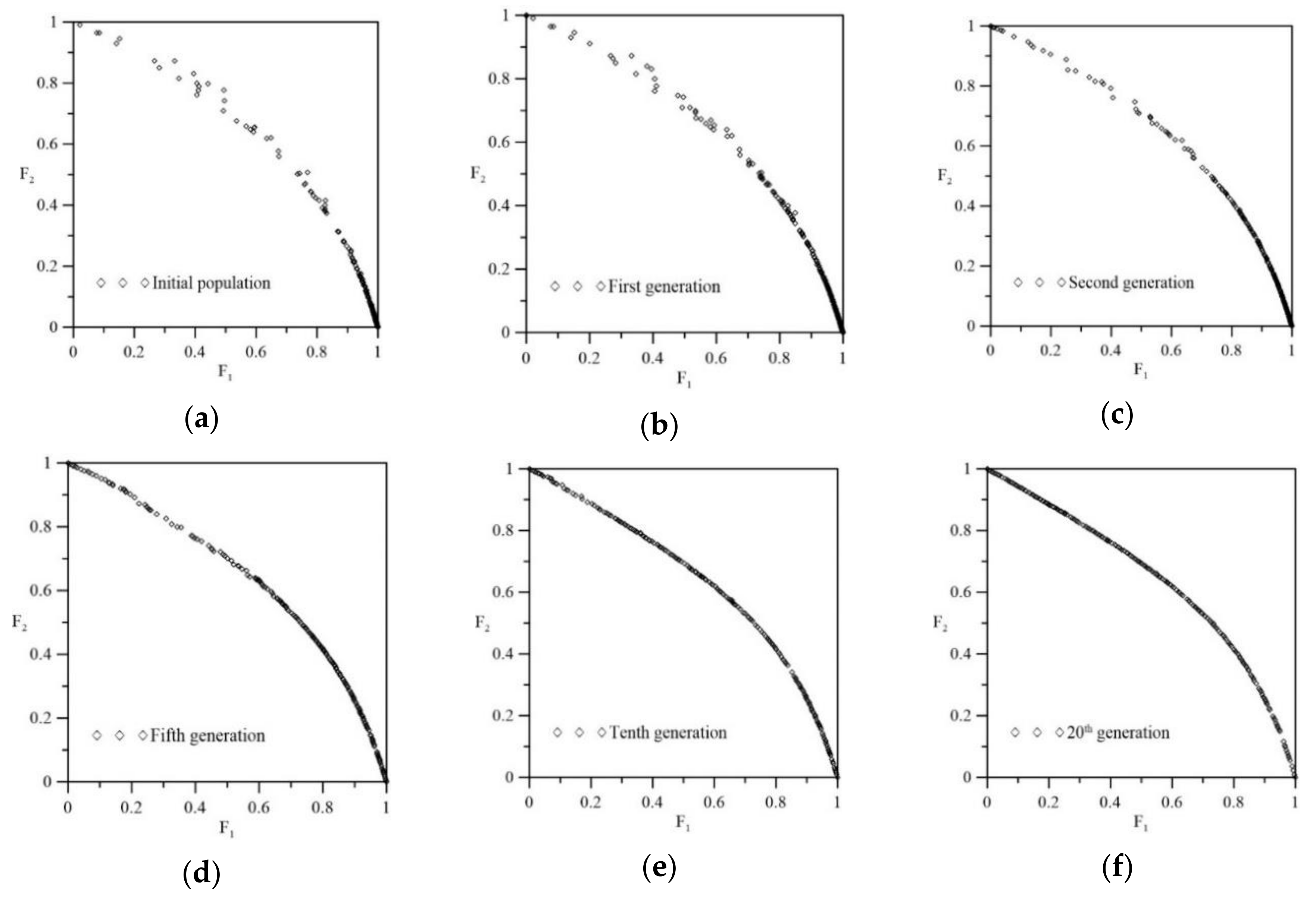
- (a)
- Initial population
- (b)
- Fitness value
- (c)
- Selection
- (d)
- Crossover
- (e)
- Mutation
- (f)
- Elitist
- (g)
- End criteria
5. Illustrative Examples
5.1. Thermal Buckling Analysis of Laminated Composite Beams and FG Beams
5.2. Optimization of Material Composition of FG beams
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Relations between the Generalized Force/Moment Resultants and the Generalized Displacements
References
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing, and Applications; Springer: Manhattan, NY, USA, 1999. [Google Scholar]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Reddy, J.N.; Chin, C.D. Thermomechanical analysis of functionally graded cylinders and plates. J. Therm. Stresses 1998, 21, 593–626. [Google Scholar] [CrossRef]
- Shen, H.S. Functionally Graded Materials: Nonlinear Analysis of Plates and Shells; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Koizumi, M. The concept of FGM. Ceram. Tran. 1993, 34, 3–10. [Google Scholar]
- Koizumi, M. FGM activities in Japan. Compos. Part B 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Liew, K.M.; Ferreira, A.J.M. A review of meshless methods for laminated and functionally graded plates and shells. Compos. Struct. 2011, 93, 2013–2041. [Google Scholar] [CrossRef]
- Punera, D.; Kant, T. A critical review of stress and vibration analyses of functionally graded shell structures. Compos. Struct. 2019, 210, 787–809. [Google Scholar] [CrossRef]
- Swaminathan, K.; Naveenkumar, D.T.; Zenkour, A.M.; Carrera, E. Stress, vibration and buckling analyses of FGM plates-A state-of-the-art review. Compos. Struct. 2015, 120, 10–31. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Ghugal, Y.M. Modeling and analysis of functionally graded sandwich beams: A review. Mech. Adv. Mater. Struct. 2019, 26, 1776–1795. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Wu, C.P.; Chiu, K.H.; Wang, Y.M. A review on the three-dimensional analytical approaches of multilayered and functionally graded piezoelectric plates and shells. CMC-Comput. Mater. Continua 2008, 8, 93–132. [Google Scholar]
- Wu, C.P.; Liu, Y.C. A review of semi-analytical numerical methods for laminated composite and multilayered functionally graded elastic/piezoelectric plates and shells. Compos. Struct. 2016, 147, 1–15. [Google Scholar] [CrossRef]
- Kiani, Y.; Eslami, M.R. Thermal buckling analysis of functionally graded material beams. Int. J. Mech. Mater. Des. 2010, 6, 229–238. [Google Scholar] [CrossRef]
- Tauchert, T.R. Thermal buckling of antisymmetric angle-ply laminates. J. Therm. Stresses 1987, 10, 113–124. [Google Scholar] [CrossRef]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Tran, T.T.; Nguyen, N.H.; Do, T.V.; Minh, P.V.; Duc, N.D. Bending and thermal buckling of unsymmetric functionally graded sandwich beams in high-temperature environment based on a new third-order shear deformation theory. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Prusty, B.G.; Kelly, D.W. Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int. J. Mech. Sci. 2011, 53, 734–743. [Google Scholar] [CrossRef]
- Soldatos, K.P.; Elishakoff, I. A transverse shear and normal deformable orthotropic beam theory. J. Sound Vibr. 1992, 155, 528–533. [Google Scholar] [CrossRef]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Bouazza, M.; Benseddiq, N.; Zenkour, A.M. Thermal buckling analysis of laminated composite beams using hyperbolic refined shear deformation theory. J. Therm. Stresses 2019, 42, 332–340. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Nguyen, T.T.P.; Vo, T.P.; Thai, H.T. Vibration and buckling analysis of functionally graded sandwich beams by a new higher-order shear deformation theory. Compos. Part B 2015, 76, 273–285. [Google Scholar] [CrossRef] [Green Version]
- Mantari, J.L.; Oktem, A.S.; Soares, C.G. A new higher order shear deformation theory for sandwich and composite laminated plates. Compos. Part B 2012, 43, 1489–1499. [Google Scholar] [CrossRef]
- Liu, N. An isogeometric continuum shell element for modeling the nonlinear response of functionally graded material structures. Compos. Struct. 2020, 237, 111893. [Google Scholar] [CrossRef]
- Liu, N.; Plucinsky, P.; Jeffers, A.E. Combining load-controlled and displacement-controlled algorithms to model thermal-mechanical snap-through instabilities in structures. J. Eng. Mech. 2017, 143, 04017051. [Google Scholar] [CrossRef]
- Refrafi, S.; Bousahla, A.A.; Bousahla, A.; Menasria, A.; Bourada, F.; Tounsi, A.; Bedia, E.A.A.; Mahmoud, S.R.; Benrahou, K.H.; Tounsi, A. Effects of hygro-thermo-mechanical conditions on the buckling of FG sandwich plates resting on elastic foundations. Comput. Concrete 2020, 25, 311–325. [Google Scholar]
- Carrera, E. Theories and finite elements for multilayered plates and shells: A unified compact formulation with numerical assessment and benchmarking. Arch. Comput. Methods Eng. 2003, 10, 215–296. [Google Scholar] [CrossRef]
- Carrera, E.; Giunta, G.; Petrolo, M. Beam Structures: Classical and Advanced Theories; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- She, G.L.; Yuan, F.G.; Ren, Y.R. Thermal buckling and post-buckling analysis of functionally graded beams based on a general higher-order shear deformation theory. Appl. Math. Modell. 2017, 47, 340–357. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P. Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int. J. Mech. Sci. 2012, 62, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Aydogdu, M. Thermal buckling analysis of cross-ply laminated composite beams with general boundary conditions. Compos. Sci. Tech. 2007, 67, 1096–1104. [Google Scholar] [CrossRef]
- Simsek, M. Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nucl. Eng. Des. 2010, 240, 697–705. [Google Scholar] [CrossRef]
- Timarci, T.; Soldatos, K.P. Comparative dynamic studies for symmetric cross-ply circular cylindrical shells on the basis of a unified shear deformable shell theory. J. Sound Vib. 1995, 187, 609–624. [Google Scholar] [CrossRef]
- Tahani, M. Analysis of laminated composite beams using layerwise displacement theories. Compos. Struct. 2007, 79, 535–547. [Google Scholar] [CrossRef]
- Lee, H.J.; Saravanos, D.A. Coupled layerwise analysis of thermopiezoelectric composite beams. AIAA J. 1996, 34, 1231–1237. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Ainapure, A.V. A beam finite element based on layerwise trigonometric shear deformation theory. Compos. Struct. 2001, 53, 153–162. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Ghugal, Y.M. A new layerwise trigonometric shear deformation theory for two-layered cross-ply beams. Compos. Sci. Technol. 2001, 61, 1271–1283. [Google Scholar] [CrossRef]
- Pandey, S.; Pradyumna, S. Analysis of functionally graded sandwich plates using a higher-order layerwise theory. Compos. Part B 2018, 153, 325–336. [Google Scholar] [CrossRef]
- Bayat, Y.; Toussi, H.E. Exact solution of thermal buckling and post buckling of composite and SMA hybrid composite beam by layerwise theory. Aerosp. Sci. Technol. 2017, 67, 484–494. [Google Scholar] [CrossRef]
- Washizu, K. Variational Methods in Elasticity and Plasticity; Pergamon Press: New York, NY, USA, 1982. [Google Scholar]
- Reddy, J.N. Energy and Variational Methods in Applied Mechanics: With an Introduction to the Finite Element Method; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1984. [Google Scholar]
- Wu, C.P.; Kuo, H.C. Interlaminar stresses analysis for laminated composite plates based on a local high order lamination theory. Compos. Struct. 1992, 20, 237–247. [Google Scholar] [CrossRef]
- Wu, C.P.; Chen, W.Y. Vibration and stability of laminated plates based on a local high order plate theory. J. Sound Vib. 1994, 177, 503–520. [Google Scholar] [CrossRef]
- Wu, C.P.; Xu, Z.R. Strong and weak formulations of a mixed higher-order shear deformation theory for the static analysis of functionally graded beams under thermo-mechanical loads. J. Compos. Sci. 2020, 4, 158. [Google Scholar] [CrossRef]
- Liew, K.M.; Pan, Z.Z.; Zhang, L.W. An overview of layerwise theories for composite laminates and structures: Development, numerical implementation and application. Compos. Struct. 2019, 216, 240–259. [Google Scholar] [CrossRef]
- Walker, M.; Reiss, T.; Adali, S. A procedure to select the best material combinations and optimally design hybrid composite plates for minimum weight and cost. Eng. Opt. 1997, 29, 65–83. [Google Scholar] [CrossRef]
- Walker, M.; Smith, R. A procedure to select the best material combinations and optimally design composite sandwich cylindrical shells for minimum mass. Mater. Des. 2006, 27, 160–165. [Google Scholar] [CrossRef]
- Houmat, A. Optimal lay-up design of variable stiffness laminated composite plates by a layer-wise optimization technique. Eng. Opt. 2018, 50, 205–217. [Google Scholar] [CrossRef]
- Guenanou, A.; Houmat, A. Optimum stacking sequence design of laminated composite circular plates with curvilinear fibres by a layer-wise optimization method. Eng. Opt. 2018, 50, 766–780. [Google Scholar] [CrossRef]
- Cho, J.R.; Ha, D.Y. Volume fraction optimization for minimizing thermal stress in Ni-Al2O3 functionally graded materials. Mater. Sci. Eng. A 2002, 334, 147–155. [Google Scholar] [CrossRef]
- Vlasov, V.Z. Thin-Walled Elastic Beams; Program for Scientific Translation: Jerusalem, Israel, 1961. [Google Scholar]
- Nguyen, T.T.; Lee, J. Optimal design of thin-walled functionally graded beams for buckling problems. Compos. Struct. 2017, 179, 459–467. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithms & Engineering Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Publishing Company, Inc.: White Plains, NY, USA, 1989. [Google Scholar]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behavior of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Yas, M.H.; Kamarian, S.; Jam, J.E.; Pourasghar, A. Optimization of functionally graded beams resting on elastic foundations. J Solid Mech. 2011, 3, 365–378. [Google Scholar]
- Yas, M.H.; Kamarian, S.; Pourasghar, A. Application of imperialist competitive algorithm and neural networks to optimise the volume fraction of three-parameter functionally graded beams. J. Exper. Theoret. Art. Intell. 2014, 26, 1–12. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M. Neural Network Design; PWS Publishing Company: Boston, MA, USA, 1995. [Google Scholar]
- Bert, C.W.; Malik, M. Differential quadrature: A powerful new technique for analysis of composite structures. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Du, H.; Lim, M.K.; Lin, R.M. Application of generalized differential quadrature method to structural problems. Int. J. Numer. Methods Eng. 1994, 37, 1881–1896. [Google Scholar] [CrossRef]
- Wu, C.P.; Lee, C.Y. Differential quadrature solution for the free vibration analysis of laminated conical shells with variable stiffness. Int. J. Mech. Sci. 2001, 43, 1853–1869. [Google Scholar] [CrossRef]
- Goupee, A.J.; Vel, S. Optimization of natural frequencies of bidirectional functionally graded beams. Struct. Multidiscipl. Opt. 2006, 32, 473–484. [Google Scholar] [CrossRef]
- Na, K.S.; Kim, J.H. Optimization of volume fractions for functionally graded panels considering stress and critical temperature. Compos. Struct. 2009, 89, 509–516. [Google Scholar] [CrossRef]
- Na, K.S.; Kim, J.H. Volume fraction optimization of functionally graded composite panels for stress reduction and critical temperature. Fin. Elem. Anal. Des. 2009, 45, 845–851. [Google Scholar] [CrossRef]
- Na, K.S.; Kim, J.H. Volume fraction optimization for step-formed functionally graded plates considering stress and critical temperature. Compos. Struct. 2010, 92, 1283–1290. [Google Scholar] [CrossRef]
- Walker, M.; Smith, R.E. A technique for the multiobjective optimization of laminated composite structures using genetic algorithms and finite element analysis. Compos. Struct. 2003, 62, 123–128. [Google Scholar] [CrossRef]
- Tornabene, F.; Ceruti, A. Mixed static and dynamic optimization of four-parameter functionally graded completely doubly curved and degenerate shells and panels using GDQ method. Math. Problems Eng. 2013, 2013, 867079. [Google Scholar] [CrossRef] [Green Version]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E. Vibration analysis of spherical structural elements using the GDQ method. Comput. Math. Appl. 2007, 53, 1538–1560. [Google Scholar] [CrossRef] [Green Version]
- Tornabene, F.; Viola, E. 2-D solution for free vibrations of parabolic shells using generalized differential quadrature method. Eur. J. Mech. A/Solids 2008, 27, 1001–1025. [Google Scholar] [CrossRef]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proc. Roy. Soc. A 1959, 252, 561–569. [Google Scholar]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. Roy. Soc. A 1959, 241, 376–396. [Google Scholar]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Ramirez, F.; Heyliger, P.R. Discrete layer solution to free vibrations of functionally graded magneto-electro-elastic plates. Mech. Adv. Mater. Struct. 2006, 13, 249–266. [Google Scholar] [CrossRef]
- Ramirez, F.; Heyliger, P.R.; Pan, E. Static analysis of functionally graded elastic anisotropic plates using a discrete layer approach. Compos. Part B 2006, 37, 10–20. [Google Scholar] [CrossRef]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. J. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Khdeir, A.A. Thermal buckling of cross-ply laminated composite beams. Acta Mech. 2001, 149, 201–213. [Google Scholar] [CrossRef]
- Li, Z.M.; Qiao, P. Thermal postbuckling analysis of anisotropic laminated beams with different boundary conditions resting on two-parameter elastic foundation. Eur. J. Mech. A/Solids 2015, 54, 30–43. [Google Scholar] [CrossRef]




| L/h | Theories | |
|---|---|---|
| 10 | Current LW1 (nl = 1) | 0.8315 |
| Current LW1 (nl = 3) | 0.8123 | |
| Current LW1 (nl = 6) | 0.7995 | |
| Current LW1 (nl = 9) | 0.7970 | |
| Current LW2 (nl = 1) | 0.8306 | |
| Current LW2 (nl = 3) | 0.7953 | |
| Current LW2 (nl = 6) | 0.7950 | |
| Current LW3 (nl = 1) | 0.8010 | |
| Current LW3 (nl = 3) | 0.7950 | |
| Current LW3 (nl = 6) | 0.7950 | |
| a Current LW3 (nl = 6) | 0.8001 | |
| b Current LW3 (nl = 6) | 0.8383 | |
| a, b Current LW3 (nl = 6) | 0.8438 | |
| HSDT [80] | 0.78912 | |
| HRSDT [22] | 0.8230 | |
| TSDT [79] | 0.8229 | |
| FSDT [79] | 0.8281 | |
| EBT [79] | 1.1072 | |
| 50 | Current LW1 (nl = 1) | 1.0411 |
| Current LW1 (nl = 3) | 1.0370 | |
| Current LW1 (nl = 6) | 1.0359 | |
| Current LW1 (nl = 9) | 1.0357 | |
| Current LW2 (nl = 1) | 1.0392 | |
| Current LW2 (nl = 3) | 1.0355 | |
| Current LW2 (nl = 6) | 1.0355 | |
| Current LW3 (nl = 1) | 1.0373 | |
| Current LW3 (nl = 3) | 1.0355 | |
| Current LW3 (nl = 6) | 1.0355 | |
| a Current LW3 (nl = 6) | 1.0360 | |
| b Current LW3 (nl = 6) | 1.0931 | |
| a, b Current LW3 (nl = 6) | 1.0936 | |
| HSDT [80] | 1.04656 | |
| HRSDT [22] | 1.0921 | |
| TSDT [79] | 1.0921 | |
| FSDT [79] | 1.0925 | |
| EBT [79] | 1.1072 |
| Theories | ||
|---|---|---|
| 10 | Current LW1 (nl = 1) | 0.8335 |
| Current LW1 (nl = 3) | 0.8162 | |
| Current LW1 (nl = 6) | 0.8088 | |
| Current LW1 (nl = 9) | 0.8073 | |
| Current LW2 (nl = 1) | 0.8302 | |
| Current LW2 (nl = 3) | 0.8063 | |
| Current LW2 (nl = 6) | 0.8062 | |
| Current LW3 (nl = 1) | 0.8134 | |
| Current LW3 (nl = 3) | 0.8061 | |
| Current LW3 (nl = 6) | 0.8061 | |
| a Current LW3 (nl = 6) | 0.8123 | |
| b Current LW3 (nl = 6) | 0.8896 | |
| a, b Current LW3 (nl = 6) | 0.8965 | |
| HSDT [80] | 0.81683 | |
| HRSDT [22] | 0.8833 | |
| TSDT [79] | 0.8832 | |
| FSDT [79] | 0.8868 | |
| EBT [79] | 1.0370 | |
| 30 | Current LW1 (nl = 1) | 0.7828 |
| Current LW1 (nl = 3) | 0.7622 | |
| Current LW1 (nl = 6) | 0.7463 | |
| Current LW1 (nl = 9) | 0.7432 | |
| Current LW2 (nl = 1) | 0.7824 | |
| Current LW2 (nl = 3) | 0.7411 | |
| Current LW2 (nl = 6) | 0.7407 | |
| Current LW3 (nl = 1) | 0.7454 | |
| Current LW3 (nl = 3) | 0.7406 | |
| Current LW3 (nl = 6) | 0.7406 | |
| a Current LW3 (nl = 6) | 0.7445 | |
| b Current LW3 (nl = 6) | 0.7680 | |
| a, b Current LW3 (nl = 6) | 0.7720 | |
| HSDT [80] | 0.72608 | |
| HRSDT [22] | 0.7472 | |
| TSDT [79] | 0.7471 | |
| FSDT [79] | 0.7528 | |
| EBT [79] | 1.1329 |
| L/h | Micromechanical Models | Theories | |||
|---|---|---|---|---|---|
| 10 | 1 | Mori–Tanaka | Current LW1 (nl = 2) | 0.5151 | 0.3757 |
| Current LW1 (nl = 4) | 0.5043 | 0.3692 | |||
| Current LW1 (nl = 8) | 0.5015 | 0.3674 | |||
| Current LW2 (nl = 2) | 0.5007 | 0.3674 | |||
| Current LW2 (nl = 4) | 0.5006 | 0.3667 | |||
| Current LW3 (nl = 2) | 0.5006 | 0.3667 | |||
| Current LW3 (nl = 4) | 0.5006 | 0.3667 | |||
| 10 | 1 | Rule of mixtures | Current LW1 (nl = 2) | 0.5122 | 0.3678 |
| Current LW1 (nl = 4) | 0.5014 | 0.3614 | |||
| Current LW1 (nl = 8) | 0.4987 | 0.3600 | |||
| Current LW2 (nl = 2) | 0.4978 | 0.3595 | |||
| Current LW2 (nl = 4) | 0.4978 | 0.3595 | |||
| Current LW3 (nl = 2) | 0.4977 | 0.3595 | |||
| Current LW3 (nl = 4) | 0.4977 | 0.3595 | |||
| 10 | 5 | Mori–Tanaka | Current LW1 (nl = 2) | 0.5315 | 0.4525 |
| Current LW1 (nl = 4) | 0.5202 | 0.4436 | |||
| Current LW1 (nl = 8) | 0.5172 | 0.4412 | |||
| Current LW2 (nl = 2) | 0.5164 | 0.4405 | |||
| Current LW2 (nl = 4) | 0.5163 | 0.4405 | |||
| Current LW3 (nl = 2) | 0.5163 | 0.4405 | |||
| Current LW3 (nl = 4) | 0.5163 | 0.4405 | |||
| 10 | 5 | Rule of mixtures | Current LW1 (nl = 2) | 0.5307 | 0.4467 |
| Current LW1 (nl = 4) | 0.5193 | 0.4381 | |||
| Current LW1 (nl = 8) | 0.5164 | 0.4358 | |||
| Current LW2 (nl = 2) | 0.5155 | 0.4350 | |||
| Current LW2 (nl = 4) | 0.5154 | 0.4350 | |||
| Current LW3 (nl = 2) | 0.5154 | 0.4350 | |||
| Current LW3 (nl = 4) | 0.5154 | 0.4350 | |||
| 20 | 5 | Mori–Tanaka | Current LW1 (nl = 2) | 0.5432 | 0.5194 |
| Current LW1 (nl = 4) | 0.5322 | 0.5081 | |||
| Current LW1 (nl = 8) | 0.5295 | 0.5066 | |||
| Current LW2 (nl = 2) | 0.5286 | 0.5042 | |||
| Current LW2 (nl = 4) | 0.5285 | 0.5042 | |||
| Current LW3 (nl = 2) | 0.5285 | 0.5042 | |||
| Current LW3 (nl = 4) | 0.5285 | 0.5042 | |||
| 20 | 5 | Rule of mixtures | Current LW1 (nl = 2) | 0.5423 | 0.5170 |
| Current LW1 (nl = 4) | 0.5314 | 0.5066 | |||
| Current LW1 (nl = 8) | 0.5286 | 0.5042 | |||
| Current LW2 (nl = 2) | 0.5277 | 0.5026 | |||
| Current LW2 (nl = 4) | 0.5277 | 0.5026 | |||
| Current LW3 (nl = 2) | 0.5277 | 0.5026 | |||
| Current LW3 (nl = 4) | 0.5277 | 0.5026 |
| Materials | P0 | P−1 | P1 | P2 | P3 | P at 300K |
|---|---|---|---|---|---|---|
| ZrO2 | ||||||
| E | 244.27 × 109 | 0 | −1.371 × 10−3 | 1.214 × 10−6 | −3.681 × 10−10 | 168.06 × 109 |
| 12.766 × 10−6 | 0 | −1.491 × 10−3 | 1.006 × 10−5 | −6.778 × 10−11 | 18.591 × 10−6 | |
| 0.2882 | 0 | 1.133 × 10−4 | 0 | 0 | 0.298 | |
| 3657 | 0 | 0 | 0 | 0 | 3657 | |
| SUS304 | ||||||
| E | 201.04 × 109 | 0 | 3.079 ×10−4 | −6.534 × 10−7 | 0 | 207.79 × 109 |
| 12.330 × 10−6 | 0 | 8.086 × 10−4 | 0 | 0 | 15.321 × 10−6 | |
| 0.3262 | 0 | −2.002 × 10−4 | 3.797 × 10−7 | 0 | 0.318 | |
| 8166 | 0 | 0 | 0 | 0 | 8166 |
| Order Number of Pareto- Optimal Solutions | (F1, F2) | ||||
|---|---|---|---|---|---|
| 1 | (0.000, 1.000) | 3658.1 | 300.7326 | (0.358, 1.829, 0.000) | (0.565, 0.435) |
| 10 | (0.037, 0.953) | 3820.7 | 303.1011 | (0.000, 1.000, 0.037) | (0.558, 0.442) |
| 20 | (0.072, 0.910) | 3975.6 | 305.2840 | (0.000, 2.392, 0.076) | (0.549, 0.451) |
| 30 | (0.113, 0.861) | 4157.9 | 307.7473 | (0.000, 3.000, 0.125) | (0.537, 0.463) |
| 40 | (0.154, 0.815) | 4337.3 | 310.0472 | (0.000, 2.831, 0.178) | (0.523, 0.477) |
| 50 | (0.206, 0.760) | 4565.6 | 312.7782 | (0.000, 2.759, 0.253) | (0.502, 0.498) |
| 60 | (0.251, 0.716) | 4768.5 | 315.0162 | (0.000, 2.714, 0.328) | (0.482, 0.518) |
| 70 | (0.309, 0.665) | 5023.2 | 317.5743 | (0.000, 3.000, 0.435) | (0.456, 0.544) |
| 80 | (0.380, 0.610) | 5335.0 | 320.3524 | (0.000, 2.967, 0.591) | (0.424, 0.576) |
| 90 | (0.433, 0.572) | 5570.0 | 322.2288 | (0.002, 2.958, 0.736) | (0.403, 0.597) |
| 100 | (0.496, 0.531) | 5851.2 | 324.2938 | (0.001, 2.958, 0.945) | (0.385, 0.615) |
| 110 | (0.576, 0.482) | 6204.6 | 326.7625 | (0.004, 2.820, 1.300) | (0.381, 0.619) |
| 120 | (0.644, 0.439) | 6502.7 | 328.9122 | (0.000, 3.000, 1.723) | (0.399, 0.601) |
| 130 | (0.695, 0.403) | 6731.2 | 330.7254 | (0.000, 2.745, 2.190) | (0.428, 0.572) |
| 140 | (0.741, 0.367) | 6934.5 | 332.5478 | (0.653, 1.122, 7.805) | (0.459, 0.541) |
| 150 | (0.801, 0.311) | 7199.1 | 335.3457 | (0.864, 1.065, 22.95) | (0.506, 0.494) |
| 160 | (0.844, 0.264) | 7387.2 | 337.7239 | (0.864, 1.082, 25.69) | (0.545, 0.455) |
| 170 | (0.883, 0.213) | 7559.9 | 340.2622 | (0.881, 1.179, 24.36) | (0.580, 0.420) |
| 180 | (0.926, 0.148) | 7751.7 | 343.5581 | (0.954, 1.146, 50.00) | (0.621, 0.379) |
| 190 | (0.967, 0.076) | 7930.0 | 347.1474 | (0.537, 1.000, 45.04) | (0.661, 0.339) |
| 200 | (1.000, 0.008) | 8077.5 | 350.5544 | (0.000, 2.005, 50.00) | (0.684, 0.316) |
| Order Number of Pareto- Optimal Solutions | (F1, F2) | ||||
|---|---|---|---|---|---|
| 1 | (0.000, 0.994) | 3657.0 | 172.5 | (0.465, 1.620, 0.000) | (0.272, 0.728) |
| 10 | (0.040, 0.977) | 3833.8 | 174.4 | (0.000, 3.000, 0.041) | (0.315, 0.685) |
| 20 | (0.098, 0.947) | 4090.2 | 177.7 | (0.000, 3.000, 0.105) | (0.354, 0.646) |
| 30 | (0.151, 0.917) | 4326.6 | 181.1 | (0.000, 1.799, 0.173) | (0.375, 0.625) |
| 40 | (0.199, 0.888) | 4535.2 | 184.4 | (0.000, 1.787, 0.241) | (0.385, 0.615) |
| 50 | (0.246, 0.858) | 4743.0 | 187.7 | (0.000, 3.000, 0.318) | (0.390, 0.610) |
| 60 | (0.311, 0.816) | 5031.9 | 192.4 | (0.000, 1.000, 0.440) | (0.391, 0.609) |
| 70 | (0.364, 0.781) | 5268.3 | 196.2 | (0.000, 2.613, 0.560) | (0.391, 0.609) |
| 80 | (0.424, 0.743) | 5532.8 | 200.6 | (0.000, 1.561, 0.716) | (0.393, 0.607) |
| 90 | (0.483, 0.705) | 5791.1 | 204.8 | (0.000, 1.474, 0.901) | (0.400, 0.600) |
| 100 | (0.531, 0.672) | 6002.2 | 208.5 | (0.000, 2.792, 1.086) | (0.411, 0.589) |
| 110 | (0.585, 0.633) | 6242.9 | 212.9 | (0.013, 1.444, 1.364) | (0.431, 0.569) |
| 120 | (0.651, 0.579) | 6533.8 | 218.8 | (0.000, 2.239, 1.746) | (0.465, 0.535) |
| 130 | (0.697, 0.537) | 6736.6 | 223.6 | (0.000, 1.443, 2.132) | (0.496, 0.504) |
| 140 | (0.746, 0.484) | 6956.2 | 229.5 | (0.046, 2.894, 2.754) | (0.535, 0.465) |
| 150 | (0.793, 0.425) | 7164.5 | 236.1 | (0.343, 1.047, 5.655) | (0.575, 0.425) |
| 160 | (0.836, 0.362) | 7353.8 | 243.1 | (0.373, 1.592, 5.894) | (0.612, 0.388) |
| 170 | (0.884, 0.281) | 7562.9 | 252.1 | (0.428, 1.210, 10.03) | (0.652, 0.348) |
| 180 | (0.915, 0.219) | 7703.5 | 259.1 | (0.798, 1.231, 21.23) | (0.677, 0.323) |
| 190 | (0.965, 0.105) | 7924.0 | 271.9 | (0.879, 1.297, 34.51) | (0.713, 0.287) |
| 200 | (1.000, 0.013) | 8077.6 | 282.1 | (0.117, 1.000, 49.74) | (0.736, 0.264) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-P.; Li, K.-W. Multi-Objective Optimization of Functionally Graded Beams Using a Genetic Algorithm with Non-Dominated Sorting. J. Compos. Sci. 2021, 5, 92. https://doi.org/10.3390/jcs5040092
Wu C-P, Li K-W. Multi-Objective Optimization of Functionally Graded Beams Using a Genetic Algorithm with Non-Dominated Sorting. Journal of Composites Science. 2021; 5(4):92. https://doi.org/10.3390/jcs5040092
Chicago/Turabian StyleWu, Chih-Ping, and Kuan-Wei Li. 2021. "Multi-Objective Optimization of Functionally Graded Beams Using a Genetic Algorithm with Non-Dominated Sorting" Journal of Composites Science 5, no. 4: 92. https://doi.org/10.3390/jcs5040092
APA StyleWu, C.-P., & Li, K.-W. (2021). Multi-Objective Optimization of Functionally Graded Beams Using a Genetic Algorithm with Non-Dominated Sorting. Journal of Composites Science, 5(4), 92. https://doi.org/10.3390/jcs5040092







