Chemical Supercritical Fluid Infiltration of Pyrocarbon with Thermal Gradients: Deposition Kinetics and Multiphysics Modeling
Abstract
:1. Introduction
2. Materials and Methods
Experimental Materials and Methods
3. Experimental Results
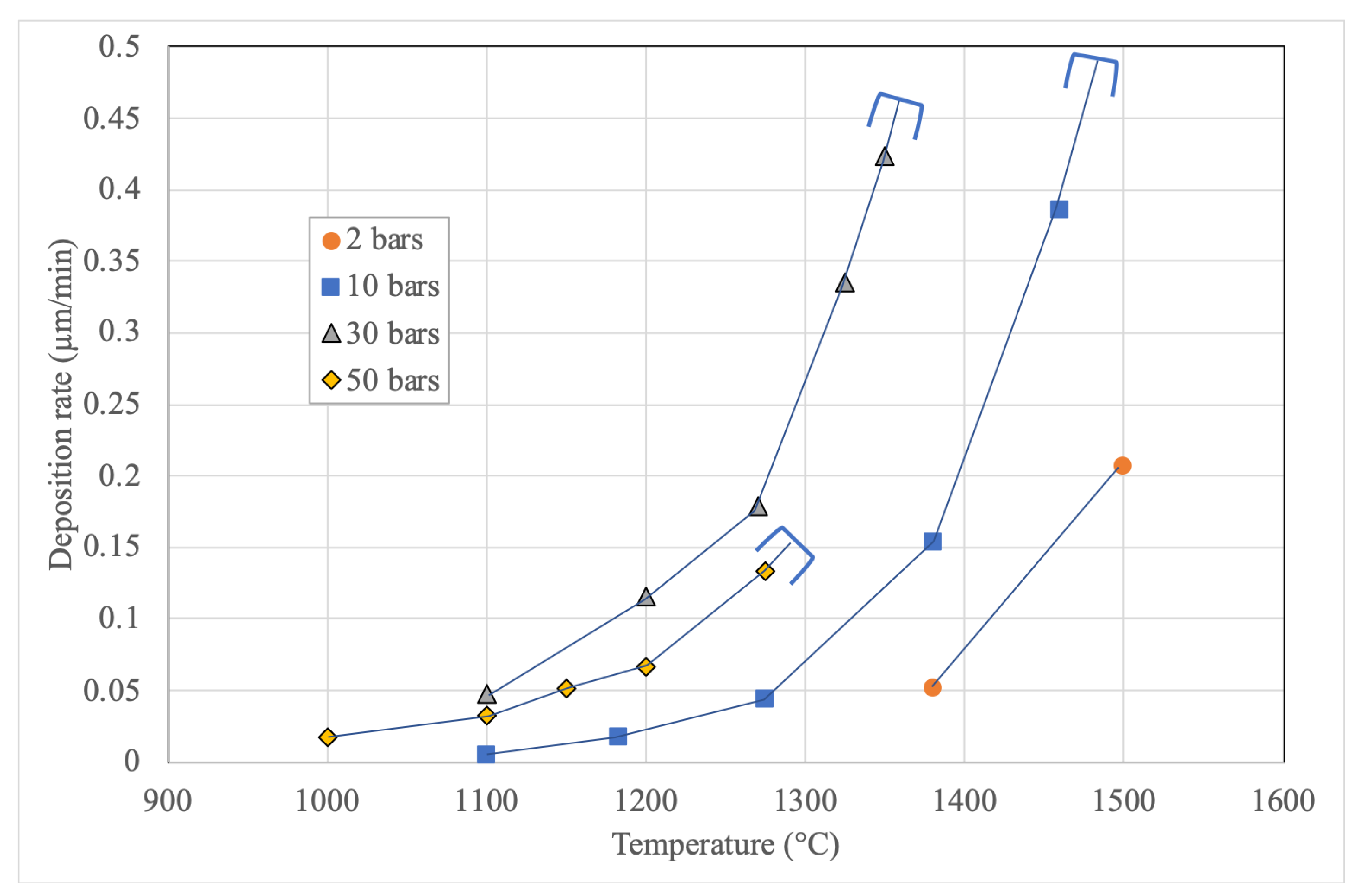
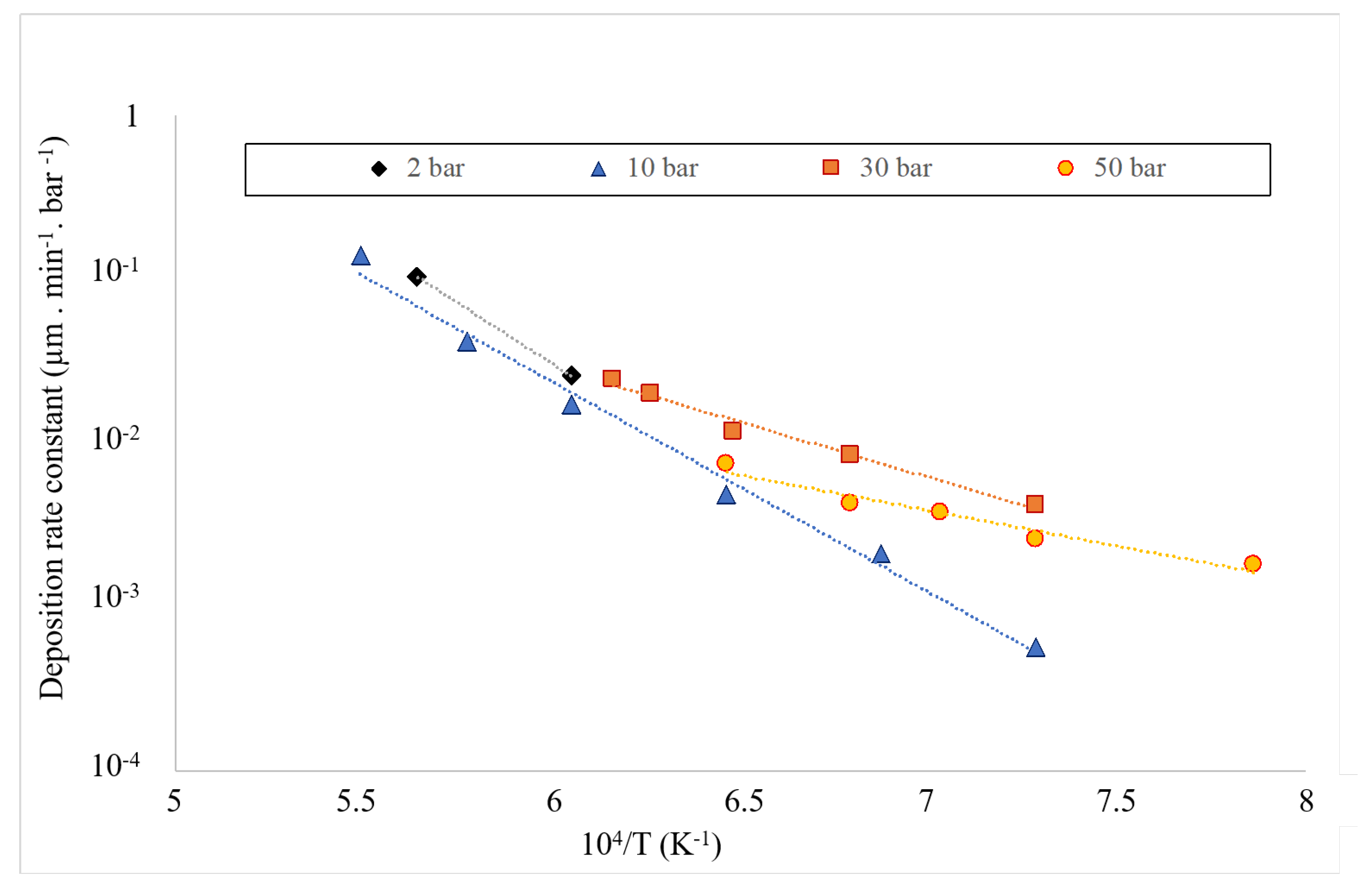
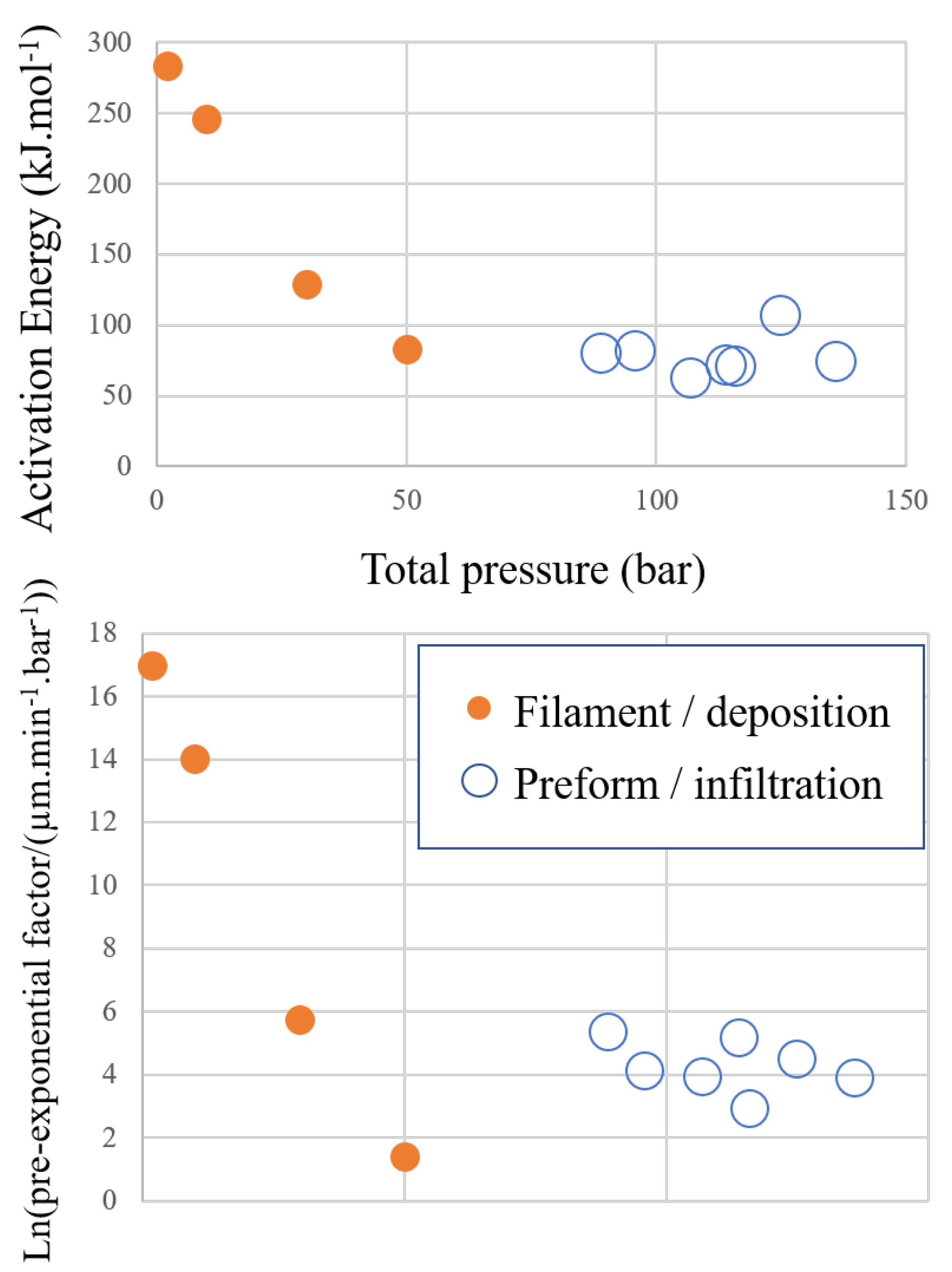
3.1. Kinetics of the Deposition Reaction on a Single Filament
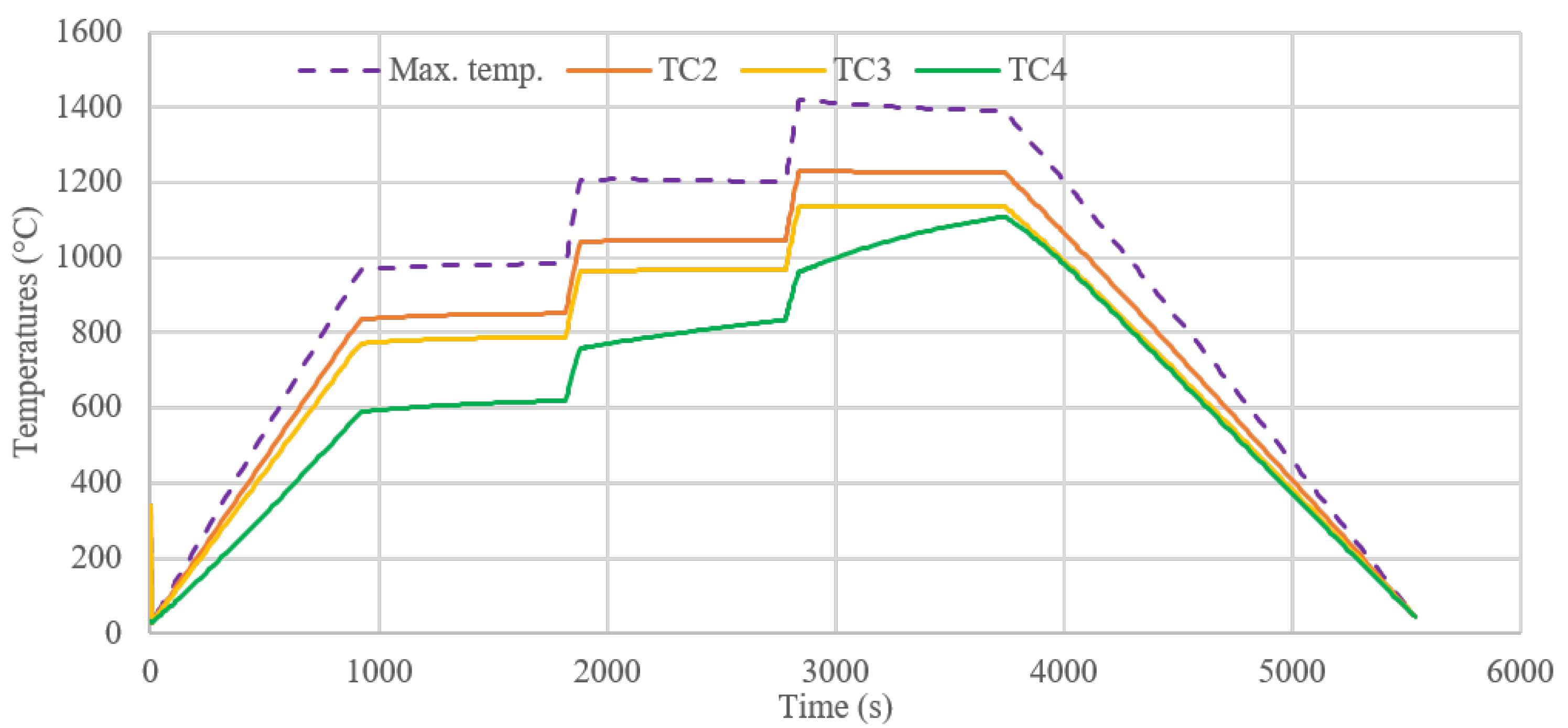
3.2. Thermal Study of an Infiltration Reactor
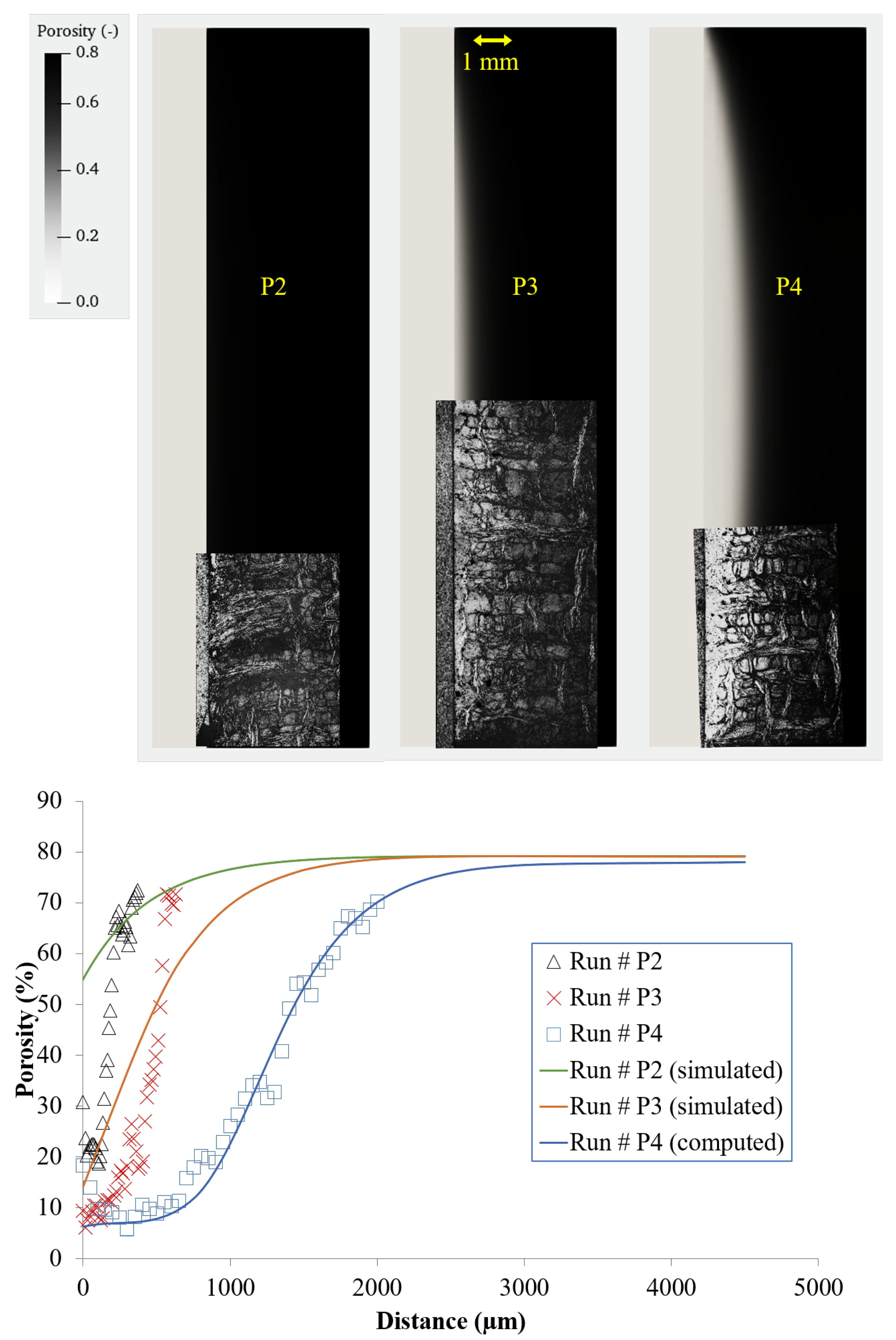
3.3. Infiltrations: Kinetics and Densification Profiles
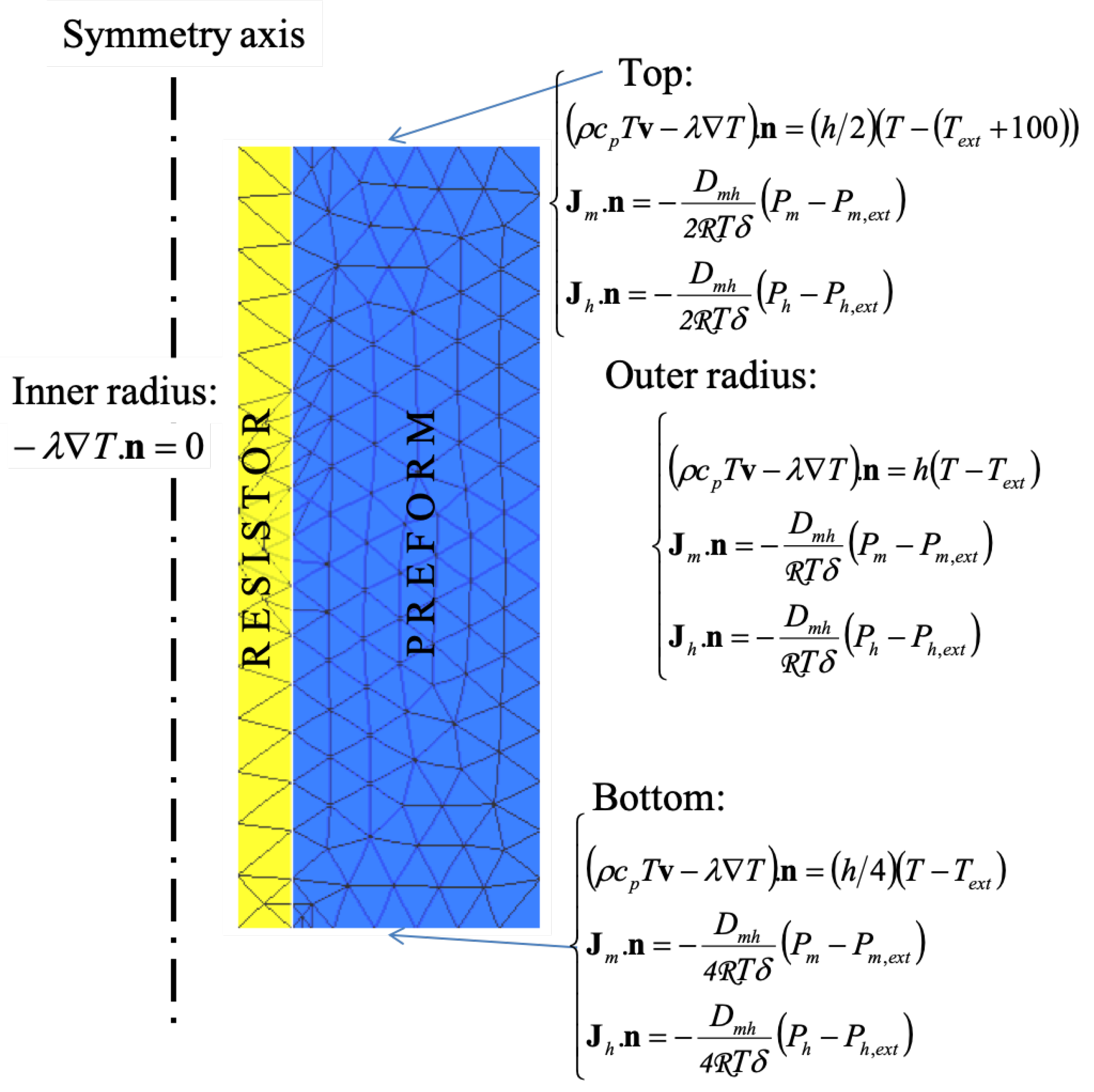
4. Infiltration Modeling
Model Setup
5. Numerical Results and Discussion
5.1. Thermal Study
5.2. Evolution of Pressure during the Infiltration Runs
5.3. Infiltration Fronts
6. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Langlais, F.; Vignoles, G.L. Chemical Vapor Infiltration Processing of Ceramic Matrix Composites. In Comprehensive Composite Materials II, 2nd ed.; Beaumont, P.W.R., Zweben, C.H., Ruggles-Wrenn, M.B., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 5, Chapter 4; pp. 86–129. [Google Scholar] [CrossRef]
- Lazzeri, A. CVI Processing of Ceramic Matrix Composites. In Ceramics and Composites Processing Methods; Bansal, N.P., Boccaccini, A.R., Eds.; John Wiley and Sons/The American Ceramic Society: New York, NY, USA, 2012; Chapter 9; pp. 313–349. [Google Scholar] [CrossRef]
- Naslain, R. Design, preparation and properties of non-oxide CMCs for application in engines and nuclear reactors: An overview. Compos. Sci. Technol. 2004, 64, 155–170. [Google Scholar] [CrossRef]
- Naslain, R. SiC-matrix composites: Nonbrittle ceramics for thermo-structural application. Int. J. Appl. Ceram. Technol. 2005, 2, 75–84. [Google Scholar] [CrossRef]
- Arai, Y.; Inoue, R.; Goto, K.; Kogo, Y. Carbon fiber reinforced ultra-high temperature ceramic matrix composites: A review. Ceram. Int. 2019, 45, 14481–14489. [Google Scholar] [CrossRef]
- Savage, G. Carbon/Carbon Composites; Chapman & Hall: London, UK, 1993; ISBN 0-412-36150-7. [Google Scholar]
- Hatta, H.; Weiß, R.; David, P. Carbon/Carbons and their Industrial Applications. In Ceramic Matrix Composites: Materials, Modeling and Technology; Bansal, N.P., Lamon, J., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; Chapter 5; pp. 85–146. [Google Scholar]
- Choy, K. Chemical vapour deposition of coatings. Prog. Mater. Sci. 2003, 48, 57–170. [Google Scholar] [CrossRef]
- Pramanik, S.; Manna, A.; Tripathy, A.; Kar, K. Current Advancements in Ceramic Matrix Composites; Springer: Berlin/Heidelberg, Germany, 2016; pp. 457–496. [Google Scholar] [CrossRef]
- Kopeliovich, D. Advances in Manufacture of Ceramic Matrix Composites by Infiltration Techniques; Elsevier Inc.: Amsterdam, The Netherlands, 2018; pp. 93–119. [Google Scholar] [CrossRef]
- Golecki, I. Rapid vapor-phase densification of refractory composites. Mater. Sci. Eng. R Rep. 1997, 20, 37–124. [Google Scholar] [CrossRef]
- Vignoles, G.L. Chemical Vapor Deposition/Infiltration Processes For Ceramic Composites. In Advances in Composites Manufacturing and Process Design; Boisse, P., Ed.; Elsevier Woodhead Scientific: Cambridge, UK, 2016; Chapter 8; pp. 147–176. [Google Scholar] [CrossRef]
- David, P.; Bénazet, J.D.; Ravel, F. Rapid deposition of carbon and ceramic matrices by film-boiling technique. Adv. Sci. Technol. 1999, 22, 135–140. [Google Scholar]
- Rovillain, D.; Trinquecoste, M.; Bruneton, E.; Derré, A.; David, P.; Delhaès, P. Film-boiling chemical vapor infiltration. An experimental study on carbon/carbon composites. Carbon 2001, 39, 1355–1365. [Google Scholar] [CrossRef]
- Deng, H.L.; Li, K.Z.; Li, H.J.; Yang, Z.L.; Cao, W.F.; Lu, J.H. Densification of C/C composites using film boiling chemical vapor infiltration with two heaters. New Carbon Mater. 2013, 28, 442–447. [Google Scholar] [CrossRef]
- Besnard, C.; Allemand, A.; David, P.; Léon, J.; Maillé, L. An original concept for the synthesis of an oxide coating: The film boiling process. J. Eur. Ceram. Soc. 2021, 41, 3013–3018. [Google Scholar] [CrossRef]
- Maillé, L.; Le Petitcorps, Y.; Guette, A.; Vignoles, G.; Roger, J. Synthesis of carbon coating and carbon matrix for C/C composites based on a hydrocarbon in its supercritical state. J. Supercrit. Fluids 2017, 127, 41–47. [Google Scholar] [CrossRef]
- Maille, L.; Guette, A.; Pailler, R.; Petitcorps, Y.; Weisbecker, P. Elaboration of C/C composites based on the infiltration of a hydrocarbon precursor in supercritical state into the preform. Powder Metall. Met. Ceram. 2014, 52, 669–673. [Google Scholar] [CrossRef] [Green Version]
- Henry, L.; Roger, J.; Le Petitcorps, Y.; Aymonier, C.; Maillé, L. Preparation of ceramic materials using supercritical fluid chemical deposition. J. Supercrit. Fluids 2018, 141, 113–119. [Google Scholar] [CrossRef]
- Vignoles, G.L. Modeling of Chemical Vapor Infiltration Processes. In Advances in Composites Manufacturing and Process Design; Boisse, P., Ed.; Elsevier Woodhead Scientific: Cambridge, UK, 2016; Chapter 17; pp. 415–458. [Google Scholar] [CrossRef]
- Pandey, A.; Selvam, P.; Dhindaw, B.; Pati, S. Multiscale modeling of chemical vapor infiltration process for manufacturing of carbon-carbon composite. In Proceedings of the 6th International Conference on Recent Advances in Composite Materials, ICRACM 2019, Tamil Nadu, India, 25–28 February 2019; Krenkel, W., Pegoretti, A.S.V., Eds.; Elsevier Ltd.: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Leutard, D.; Vignoles, G.L.; Lamouroux, F.; Bernard, B. Monitoring density and temperature in C/C composites elaborated by CVI with radio-frequency heating. J. Mater. Synth. Process. 2002, 9, 259–273. [Google Scholar] [CrossRef] [Green Version]
- Vignoles, G.L.; Goyhénèche, J.M.; Sébastian, P.; Puiggali, J.R.; Lines, J.F.; Lachaud, J.; Delhaès, P.; Trinquecoste, M. The film-boiling densification process for C/C composite fabrication: From local scale to overall optimization. Chem. Eng. Sci. 2006, 61, 5636–5653. [Google Scholar] [CrossRef]
- Vignoles, G.L.; Nadeau, N.; Brauner, C.M.; Lines, J.F.; Puiggali, J.R. The notion of densification front in CVI processing with temperature gradients. In Mechanical Properties and Performance of Engineering Ceramics and Composites; Lara-Curzio, D.Z., Kriven, W.M., Eds.; The American Ceramic Society: Westerville, OH, USA, 2005; Volume 26, pp. 187–195. [Google Scholar] [CrossRef]
- Nadeau, N.; Vignoles, G.L.; Brauner, C.M. Analytical and numerical study of the densification of carbon/carbon composites by a film-boiling chemical vapor infiltration process. Chem. Eng. Sci. 2006, 61, 7509–7527. [Google Scholar] [CrossRef]
- Lines, J.F.; Vignoles, G.L.; Goyheneche, J.M.; Puiggali, J.R. Thermal modelling of a carbon/carbon composite material fabrication process. J. Phys. IV 2004, 120, 291–297. [Google Scholar] [CrossRef]
- Schneider, S.; Bajohr, S.; Graf, F.; Kolb, T. State of the Art of Hydrogen Production via Pyrolysis of Natural Gas. ChemBioEng Rev. 2020, 7, 150–158. [Google Scholar] [CrossRef]
- Abney, M.B.; Childers, A.; Skomurski, S.; Lo, C.; Yates, S.F.; Brom, N. Hydrogen Recovery by Methane Pyrolysis to Elemental Carbon. In Proceedings of the 49th International Conference on Environmental Systems, Boston, MA, USA, 7–11 July 2019; Available online: https://ttu-ir.tdl.org/bitstream/handle/2346/84507/ICES-2019-103.pdf (accessed on 9 December 2021).
- Lide, D.R. Handbook of Chemistry and Physics, 71st ed.; CRC Press, Inc.: Boca Raton, FL, USA, 1990. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Ning, X.; Pirouz, P. The microstructure of SCS-6 SiC fiber. J. Mater. Res. 1991, 6, 2234–2248. [Google Scholar] [CrossRef]
- Brüggert, M.; Hu, Z.; Hüttinger, K. Chemistry and kinetics of chemical vapor deposition of pyrocarbon: VI. influence of temperature using methane as a carbon source. Carbon 1999, 37, 2021–2030. [Google Scholar] [CrossRef]
- Tesner, P.A. Kinetics of Pyrolytic Carbon Formation. In Chemistry and Physics of Carbon; M. Dekker: New York, NY, USA, 1984; Volume 19, pp. 65–161. [Google Scholar]
- Reid, R.; Prausnitz, J.; Poling, B.E. The Properties of Gases and Liquids, 4th ed.; McGraw-Hill: New York, NY, USA, 1987; ISBN 0-07-051799-1. [Google Scholar]
- Pradère, C.; Batsale, J.; Goyhénèche, J.; Pailler, R.; Dilhaire, S. Thermal properties of carbon fibers at very high temperature. Carbon 2009, 47, 737–743. [Google Scholar] [CrossRef]
- PDE Solutions, Inc. FlexPDE Software, v. 7.19. Available online: https://www.pdesolutions.com (accessed on 6 September 2021).
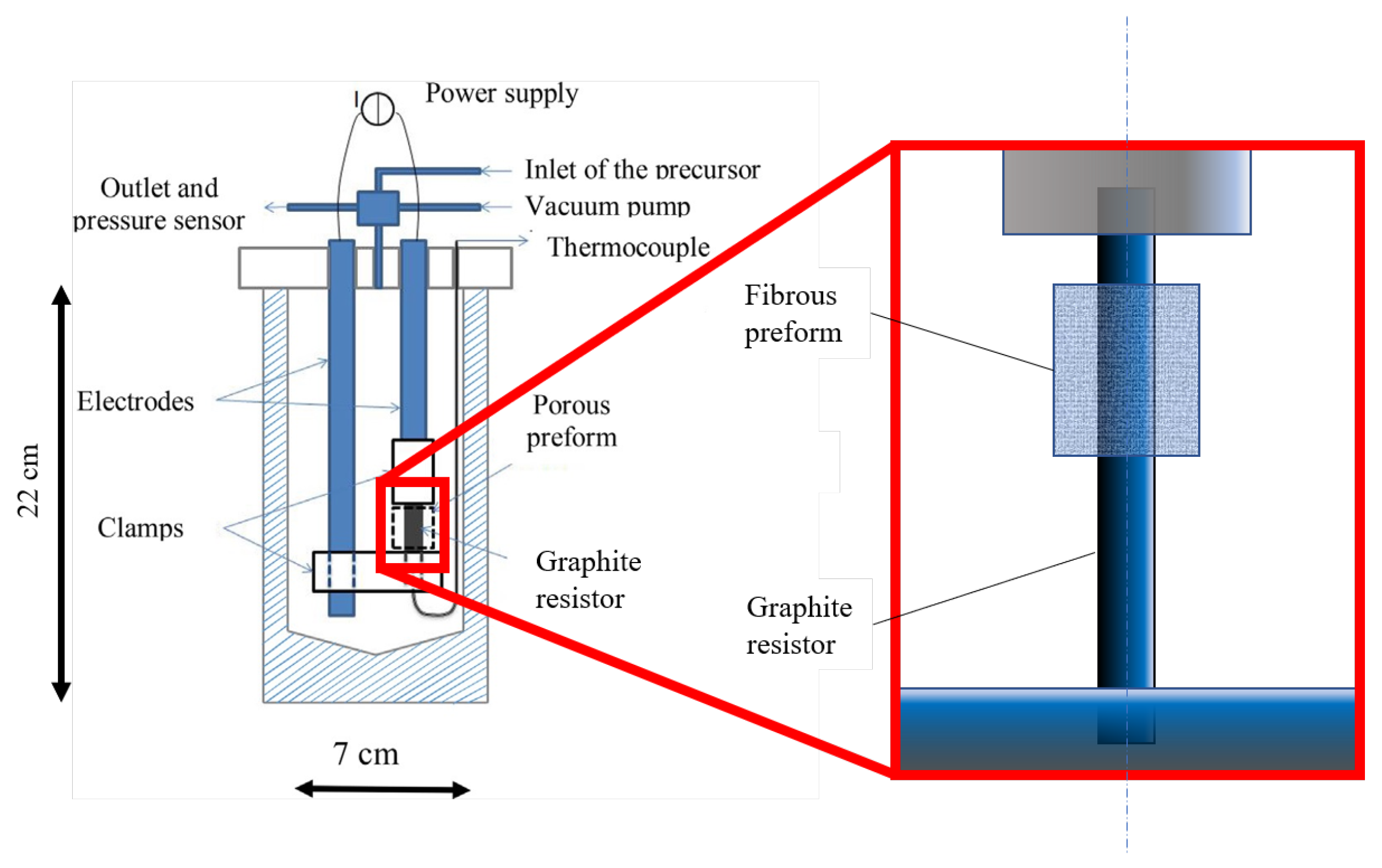
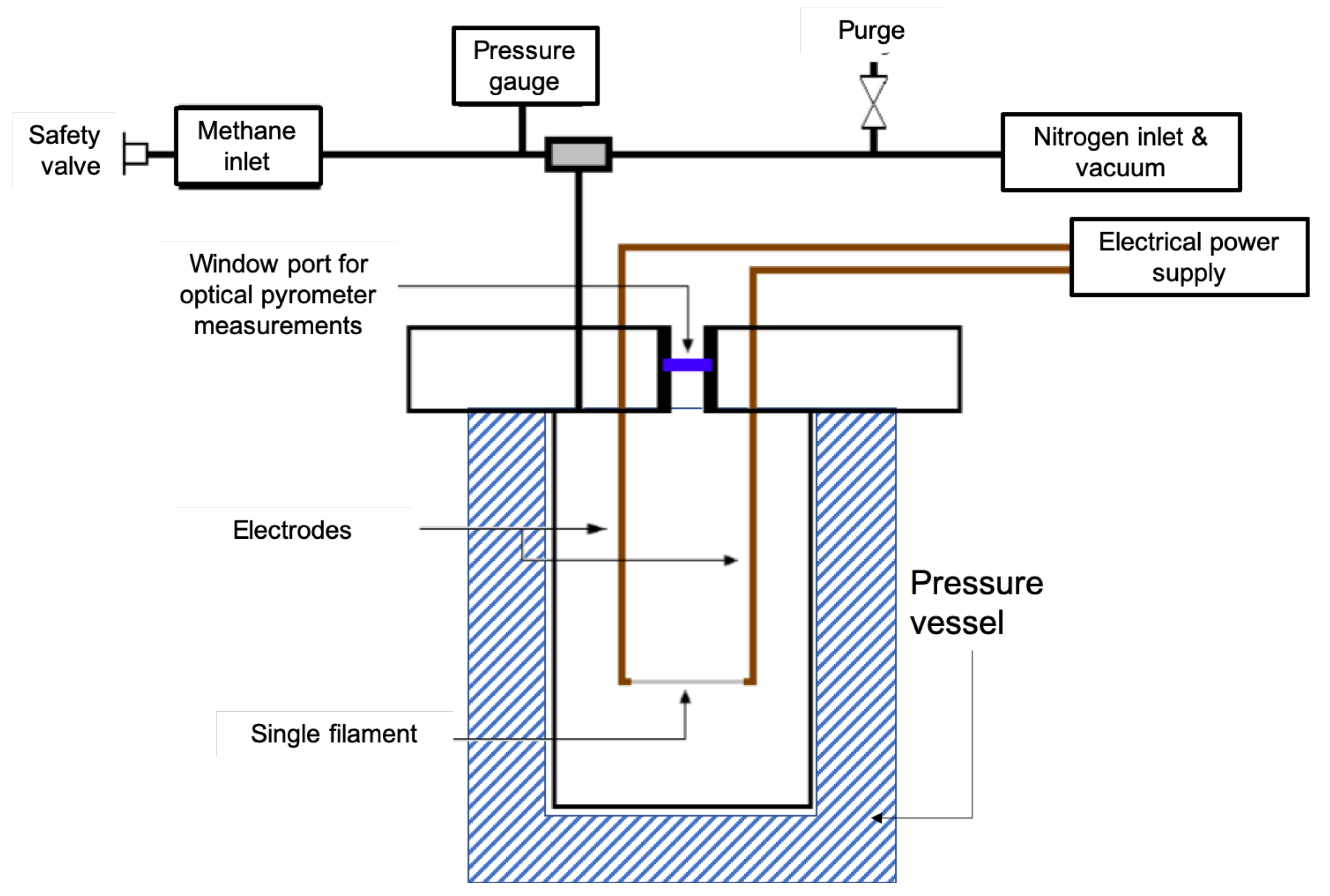








| Part | Material | Dimensions |
|---|---|---|
| Reactor | Inconel | L |
| Gas inlet | Inconel | |
| Sealing cap | Inconel | |
| Electrodes | Inconel | |
| Clamps | Steel | |
| Resistor | Graphite tube | mm; mm; = 3 mm |
| Preform | Carbon fibers ( = 7 m) | mm; 15 mm |
| Run | Initial Pressure | Power | Time | Measured Temperature * |
|---|---|---|---|---|
| # | (bar) | (kW) | (min) | (C) |
| P1 | 50 | 1.87 | 15 | ≈850 |
| P2 | 50 | 2.0 | 15 | ≈900 |
| P3 | 50 | 2.0 | 15 | ≈900 |
| then 2.5 | 15 | ≈1050 | ||
| P4 | 50 | 2.0 | 15 | ≈900 |
| then 2.5 | 15 | ≈1050 | ||
| then 3.0 | 15 | ≈1200 | ||
| P5 | 60 | 2.0 | 15 | ≈900 |
| P6 | 60 | 2.0 | 15 | ≈900 |
| then 2.5 | 15 | ≈1050 | ||
| P7 | 60 | 2.0 | 15 | ≈900 |
| then 2.5 | 15 | ≈1050 | ||
| then 3.0 | 15 | ≈1200 | ||
| P8 | 70 | 2.0 | 15 | ≈900 |
| P9 | 70 | 2.0 | 15 | ≈900 |
| then 2.5 | 15 | ≈1050 | ||
| P10 | 70 | 2.0 | 15 | ≈900 |
| then 2.5 | 15 | ≈1050 | ||
| then 3.0 | 15 | ≈1200 |
| Total Pressure | Pre-Exponential Constant A | Activation Energy | Ref. |
|---|---|---|---|
| (bar) | (·bar) | (kJ·mol) | |
| 1 | 451.9 | [32] | |
| 1 | 272 | [33] | |
| 2 | This work | ||
| 10 | This work | ||
| 30 | This work | ||
| 50 | This work |
| Parameter | Value or Expression | Unit |
|---|---|---|
| Reactor | ||
| Initial outer wall temperature | K | |
| Initial total pressure | Pa | |
| Diffusion boundary layer thickness | m | |
| Heat capacity of the reactor | J·K | |
| Reactor volume | m | |
| Outer heat exchange coefficient | W·K | |
| Preform/fluid heat transfer coefficient | W·m·K | |
| Resistor/exterior heat transfer coefficient | W·m·K | |
| Preform | ||
| Fiber density | kg·m | |
| Fiber initial diameter | m | |
| Initial porosity | - | |
| Mass transfer parameters | ||
| Carbon density | kg·m | |
| Carbon molar volume | m·mol | |
| Internal surface area | m | |
| Effective pore diameter | m | |
| Viscous flow tortuosity | - | |
| Darcy Permeability | m | |
| Diffusion tortuosity | - | |
| Mutual diffusion coefficient | m·s | |
| Fluid dynamic viscosity | Pa·s | |
| Heat transfer parameters | ||
| Conductivity, effective | W·m·K | |
| Conductivity, fibers | W·m·K | |
| Conductivity, deposit | W·m·K | |
| Conductivity, gas | W·m·K | |
| Molar heat capacities | J·K·mol | |
| J·K·mol | ||
| Run | Power | TC1 | TC2 | TC3 | TC4 | Max. Temp. | Radial Flux |
|---|---|---|---|---|---|---|---|
| # | kW | C | C | C | C | C | MW·m |
| P1 | 1.87 | 715 | 843 | 783 | 608 | 1113 | 4.94 |
| P2, P5, P8 | 2 | 950 | 922 | 854 | 638 | 1154 | 5.31 |
| P3, P6, P9 | 2.5 | 1025 | 1124 | 1033 | 778 | 1409 | 6.64 |
| P4, P7, P10 | 3 | 1200 | 1334 | 1245 | 945 | 1425 | 7.97 |
| Run | ln(A) | ||||||
|---|---|---|---|---|---|---|---|
| # | bar | bar | mm | mm | nm·s | kJ·mol | m·min·bar |
| P2 | 81 | 14.72 | |||||
| P3 | 89 | 24.45 | 1.2 | 1.4 | 1.56 | 80 | 5.35 |
| P4 | 96 | 25.35 | 1.0 | 1.95 | 0.61 | 81 | 4.09 |
| P5 | 98 | 14.97 | |||||
| P6 | 107 | 25.11 | 1.55 | 1.45 | 1.6 | 62 | 3.91 |
| P7 | 116 | 26.02 | 1.15 | 1.85 | 0.45 | 71 | 2.92 |
| P8 | 114 | 15.14 | 1.2 | 1.1 | 1.22 | 72 | 5.14 |
| P9 | 125 | 25.59 | 0.9 | 1.2 | 1.11 | 106 | 4.48 |
| P10 | 136 | 26.50 | 1.1 | 2.45 | 1.39 | 74 | 3.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vignoles, G.L.; Talué, G.; Badey, Q.; Guette, A.; Pailler, R.; Le Petitcorps, Y.; Maillé, L. Chemical Supercritical Fluid Infiltration of Pyrocarbon with Thermal Gradients: Deposition Kinetics and Multiphysics Modeling. J. Compos. Sci. 2022, 6, 20. https://doi.org/10.3390/jcs6010020
Vignoles GL, Talué G, Badey Q, Guette A, Pailler R, Le Petitcorps Y, Maillé L. Chemical Supercritical Fluid Infiltration of Pyrocarbon with Thermal Gradients: Deposition Kinetics and Multiphysics Modeling. Journal of Composites Science. 2022; 6(1):20. https://doi.org/10.3390/jcs6010020
Chicago/Turabian StyleVignoles, Gerard L., Gaëtan Talué, Quentin Badey, Alain Guette, René Pailler, Yann Le Petitcorps, and Laurence Maillé. 2022. "Chemical Supercritical Fluid Infiltration of Pyrocarbon with Thermal Gradients: Deposition Kinetics and Multiphysics Modeling" Journal of Composites Science 6, no. 1: 20. https://doi.org/10.3390/jcs6010020
APA StyleVignoles, G. L., Talué, G., Badey, Q., Guette, A., Pailler, R., Le Petitcorps, Y., & Maillé, L. (2022). Chemical Supercritical Fluid Infiltration of Pyrocarbon with Thermal Gradients: Deposition Kinetics and Multiphysics Modeling. Journal of Composites Science, 6(1), 20. https://doi.org/10.3390/jcs6010020






