A Hyperbolic Shear Deformation Theory for Natural Frequencies Study of Functionally Graded Plates on Elastic Supports
Abstract
:1. Introduction
2. Analytical Method
2.1. Basic Assumptions
- The displacements are small compared to the thickness of the plate and therefore the stresses involved are infinitesimal;
- The transversal normal stress is negligible compared to the stresses in the plane and ;
- The transverse displacement includes two components of bending and shear . These components are functions of coordinates and time only. They can be written as:
- The planar displacements and consist of components of extension, bending and shear:
- The bending components and are assumed to be similar to the displacements given by classical plate theory. Therefore, the expressions for and can be written as:
- The shear components and give rise, together with , to the parabolic variations in the shear strains , and hence to the shear stresses , through the thickness of the plate so that the shear stresses are zero on the upper and lower plate boundaries. Therefore, the expression for et can be given by:
2.2. Kinematics
2.3. Constitutive Equations
2.4. Equations of Movement
3. Analytical Solutions for Rectangular Plates
4. Analysis of the Free Vibration of Different Types of Plates
4.1. Study of Simply Supported Isotropic Plates
4.2. Analysis of Simply Supported Functionally Graded Plates
4.3. Investigation of Functionally Graded Plates on Elastic Supports
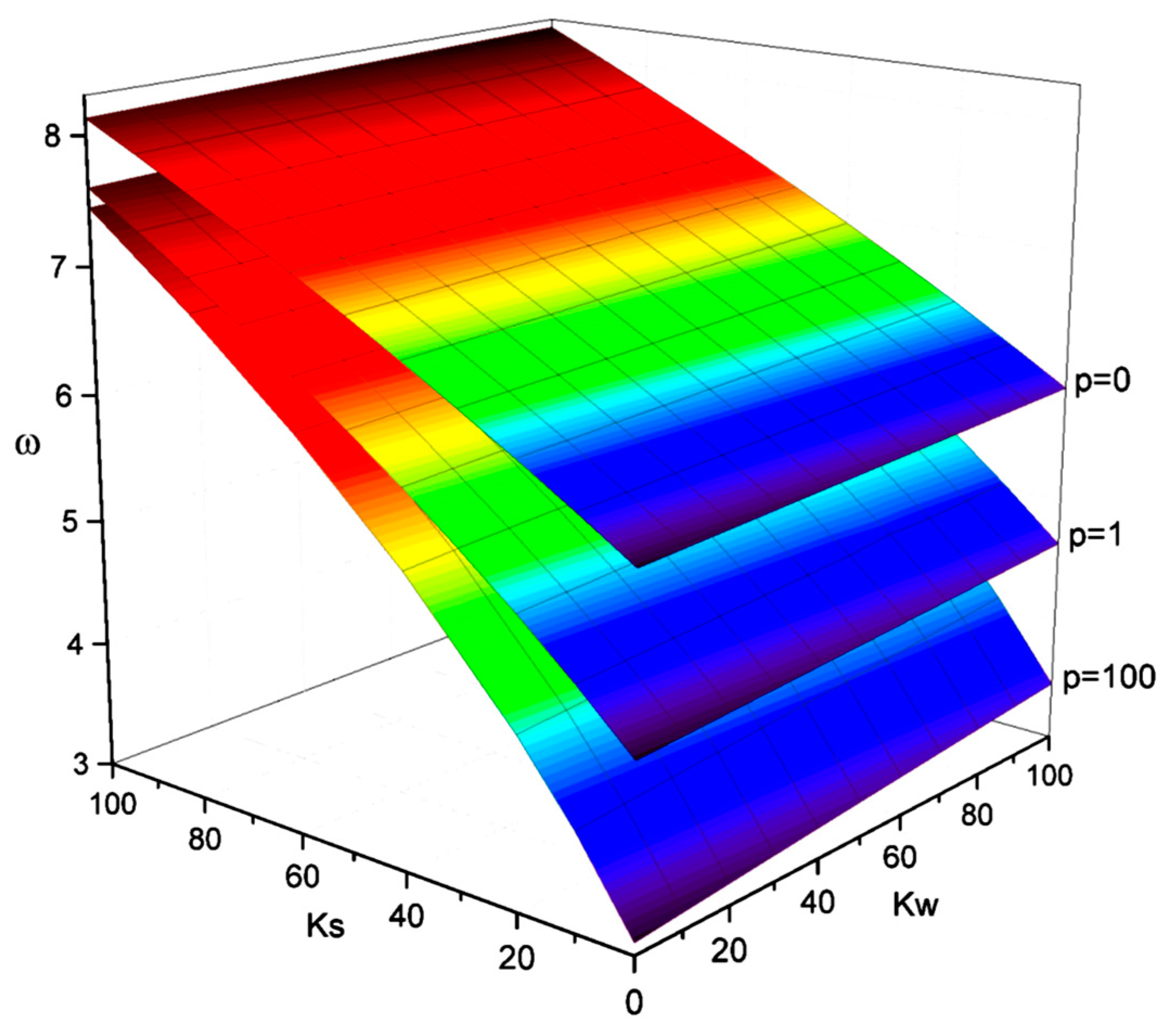
4.4. Parametric Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kar, V.R.; Panda, S.K. Free Vibration Responses of Temperature Dependent Functionally Graded Curved Panels under Thermal Environment. Lat. Am. J. Solids Struct. 2015, 12, 2006–2024. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Ghasemi, F.; Salari, E. Investigating Thermal Effects on Vibration Behavior of Temperature-Dependent Compositionally Graded Euler Beams with Porosities. Meccanica 2016, 51, 223–249. [Google Scholar] [CrossRef]
- Shahsavari, D.; Shahsavari, M.; Li, L.; Karami, B. A Novel Quasi-3D Hyperbolic Theory for Free Vibration of FG Plates with Porosities Resting on Winkler/Pasternak/Kerr Foundation. Aerosp. Sci. Technol. 2018, 72, 134–149. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R. Thermal Buckling and Post-Buckling Analysis of Functionally Graded Beams Based on a General Higher-Order Shear Deformation Theory. Appl. Math. Model. 2017, 47, 340–357. [Google Scholar] [CrossRef]
- Taati, E.; Fallah, F. Exact Solution for Frequency Response of Sandwich Microbeams with Functionally Graded Cores. J. Vib. Control 2019, 25, 2641–2655. [Google Scholar] [CrossRef]
- Zaoui, F.Z.; Ouinas, D.; Tounsi, A.; Viña Olay, J.A.; Achour, B.; Touahmia, M. Fundamental Frequency Analysis of Functionally Graded Plates with Temperature-Dependent Properties Based on Improved Exponential-Trigonometric Two-Dimensional Higher Shear Deformation Theory. Arch. Appl. Mech. 2021, 91, 859–881. [Google Scholar] [CrossRef]
- Bakora, A.; Tounsi, A. Thermo-Mechanical Post-Buckling Behavior of Thick Functionally Graded Plates Resting on Elastic Foundations. Struct. Eng. Mech. 2015, 56, 85–106. [Google Scholar] [CrossRef]
- Hebali, H.; Bakora, A.; Tounsi, A.; Kaci, A. A Novel Four Variable Refined Plate Theory for Bending, Buckling, and Vibration of Functionally Graded Plates. Steel Compos. Struct. 2016, 22, 473–495. [Google Scholar] [CrossRef]
- Udupa, G.; Rao, S.S.; Gangadharan, K.V. Functionally Graded Composite Materials: An Overview. Procedia Mater. Sci. 2014, 5, 1291–1299. [Google Scholar] [CrossRef]
- Zaoui, F.Z.; Hanifi, H.A.L.; Younsi, A.; Meradjah, M.; Tounsi, A.; Ouinas, D. Free Vibration Analysis of Functionally Graded Beams Using a Higher-Order Shear Deformation Theory. Math. Model. Eng. Probl. 2017, 4, 7–12. [Google Scholar] [CrossRef]
- Zaoui, F.Z.; Tounsi, A.; Ouinas, D. Free Vibration of Functionally Graded Plates Resting on Elastic Foundations Based on Quasi-3D Hybrid-Type Higher Order Shear Deformation Theory. Smart Struct. Syst. 2017, 20, 509–524. [Google Scholar]
- Mohammadi, M.; Saidi, A.R.; Jomehzadeh, E. Levy Solution for Buckling Analysis of Functionally Graded Rectangular Plates. Appl. Compos. Mater. 2010, 17, 81–93. [Google Scholar] [CrossRef]
- Ebrahimi, M.J.; Najafizadeh, M.M. Free Vibration Analysis of Two-Dimensional Functionally Graded Cylindrical Shells. Appl. Math. Model. 2014, 38, 308–324. [Google Scholar] [CrossRef]
- Ruan, M.; Wang, Z.-M. Transverse Vibrations of Moving Skew Plates Made of Functionally Graded Material. J. Vib. Control 2016, 22, 3504–3517. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Meskini, M. Free Vibration Analysis of Porous Laminated Rotating Circular Cylindrical Shells—Ahmad Reza Ghasemi, Mohammad Meskini, 2019. J. Vib. Control 2019, 25, 2494–2508. [Google Scholar] [CrossRef]
- Bouazza, M.; Tounsi, A.; Adda-Bedia, E.A.; Megueni, A. Thermoelastic Stability Analysis of Functionally Graded Plates: An Analytical Approach. Comput. Mater. Sci. 2010, 49, 865–870. [Google Scholar] [CrossRef]
- Golmakani, M.E.; Alamatian, J. Large Deflection Analysis of Shear Deformable Radially Functionally Graded Sector Plates on Two-Parameter Elastic Foundations. Eur. J. Mech.—ASolids 2013, 42, 251–265. [Google Scholar] [CrossRef]
- Memar Ardestani, M.; Soltani, B.; Shams, S. Analysis of Functionally Graded Stiffened Plates Based on FSDT Utilizing Reproducing Kernel Particle Method. Compos. Struct. 2014, 112, 231–240. [Google Scholar] [CrossRef]
- Meksi, A.; Benyoucef, S.; Houari, M.S.A.; Tounsi, A. A Simple Shear Deformation Theory Based on Neutral Surface Position for Functionally Graded Plates Resting on Pasternak Elastic Foundations. Struct. Eng. Mech. 2015, 53, 1215–1240. [Google Scholar] [CrossRef]
- Bellifa, H.; Benrahou, K.H.; Hadji, L.; Houari, M.S.A.; Tounsi, A. Bending and Free Vibration Analysis of Functionally Graded Plates Using a Simple Shear Deformation Theory and the Concept the Neutral Surface Position. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 265–275. [Google Scholar] [CrossRef]
- Hadji, L.; Daouadji, T.H.; Meziane, M.A.A.; Tlidji, Y.; Bedia, E.A.A. Analysis of Functionally Graded Beam Using a New First-Order Shear Deformation Theory. Struct. Eng. Mech. 2016, 57, 315–325. [Google Scholar] [CrossRef]
- Mantari, J.L.; Granados, E.V. An Original FSDT to Study Advanced Composites on Elastic Foundation. Thin-Walled Struct. 2016, 107, 80–89. [Google Scholar] [CrossRef]
- Mantari, J.L.; Guedes Soares, C. A Novel Higher-Order Shear Deformation Theory with Stretching Effect for Functionally Graded Plates. Compos. Part B Eng. 2013, 45, 268–281. [Google Scholar] [CrossRef]
- Nguyen, V.-H.; Nguyen, T.-K.; Thai, H.-T.; Vo, T.P. A New Inverse Trigonometric Shear Deformation Theory for Isotropic and Functionally Graded Sandwich Plates. Compos. Part B Eng. 2014, 66, 233–246. [Google Scholar] [CrossRef]
- Abdelbari, S.; Fekrar, A.; Heireche, H.; Said, H.; Tounsi, A.; Adda Bedia, E.A. An Efficient and Simple Shear Deformation Theory for Free Vibration of Functionally Graded Rectangular Plates on Winkler-Pasternak Elastic Foundations. Wind Struct. 2016, 22, 329–348. [Google Scholar] [CrossRef]
- Akavci, S.S. Mechanical Behavior of Functionally Graded Sandwich Plates on Elastic Foundation. Compos. Part B Eng. 2016, 96, 136–152. [Google Scholar] [CrossRef]
- Benchohra, M.; Driz, H.; Bakora, A.; Tounsi, A.; Bedia, E.A.A.; Mahmoud, S.R. A New Quasi-3D Sinusoidal Shear Deformation Theory for Functionally Graded Plates. Struct. Eng. Mech. 2018, 65, 19–31. [Google Scholar]
- Rachid, A.; Ouinas, D.; Lousdad, A.; Zaoui, F.Z.; Achour, B.; Gasmi, H.; Butt, T.A.; Tounsi, A. Mechanical Behavior and Free Vibration Analysis of FG Doubly Curved Shells on Elastic Foundation via a New Modified Displacements Field Model of 2D and Quasi-3D HSDTs. Thin-Walled Struct. 2022, 172, 108783. [Google Scholar] [CrossRef]
- Akavci, S.S. An Efficient Shear Deformation Theory for Free Vibration of Functionally Graded Thick Rectangular Plates on Elastic Foundation. Compos. Struct. 2014, 108, 667–676. [Google Scholar] [CrossRef]
- Mantari, J.L. A Refined Theory with Stretching Effect for the Dynamics Analysis of Advanced Composites on Elastic Foundation. Mech. Mater. 2015, 86, 31–43. [Google Scholar] [CrossRef]
- Meksi, R.; Benyoucef, S.; Mahmoudi, A.; Tounsi, A.; Adda Bedia, E.A.; Mahmoud, S.R. An Analytical Solution for Bending, Buckling and Vibration Responses of FGM Sandwich Plates—Rafik Meksi, Samir Benyoucef, Abdelkader Mahmoudi, Abdelouahed Tounsi, El Abbas Adda Bedia, SR Mahmoud, 2019. J. Sandw. Struct. Mater. 2019, 21, 727–757. [Google Scholar] [CrossRef]
- Thai, H.-T.; Park, M.; Choi, D.-H. A Simple Refined Theory for Bending, Buckling, and Vibration of Thick Plates Resting on Elastic Foundation. Int. J. Mech. Sci. 2013, 73, 40–52. [Google Scholar] [CrossRef]
- Xiang, S.; Kang, G.; Liu, Y. A Nth-Order Shear Deformation Theory for Natural Frequency of the Functionally Graded Plates on Elastic Foundations. Compos. Struct. 2014, 111, 224–231. [Google Scholar] [CrossRef]
- Meftah, A.; Bakora, A.; Zaoui, F.Z.; Tounsi, A.; Bedia, E.A.A. A Non-Polynomial Four Variable Refined Plate Theory for Free Vibration of Functionally Graded Thick Rectangular Plates on Elastic Foundation. Steel Compos. Struct. 2017, 23, 317–330. [Google Scholar] [CrossRef]
- Sidhoum, I.A.; Boutchicha, D.; Benyoucef, S.; Tounsi, A. A Novel Quasi-3D Hyperbolic Shear Deformation Theory for Vibration Analysis of Simply Supported Functionally Graded Plates. Smart Struct. Syst. 2018, 22, 303–314. [Google Scholar]
- Taleb, O.; Houari, M.S.A.; Bessaim, A.; Tounsi, A.; Mahmoud, S.R. A New Plate Model for Vibration Response of Advanced Composite Plates in Thermal Environment. Struct. Eng. Mech. 2018, 67, 369–383. [Google Scholar]
- Zaoui, F.Z.; Ouinas, D.; Tounsi, A. New 2D and Quasi-3D Shear Deformation Theories for Free Vibration of Functionally Graded Plates on Elastic Foundations. Compos. Part B Eng. 2019, 159, 231–247. [Google Scholar] [CrossRef]
- Soldatos, K.P. A Transverse Shear Deformation Theory for Homogeneous Monoclinic Plates. Acta Mech. 1992, 94, 195–220. [Google Scholar] [CrossRef]
- Younsi, A.; Tounsi, A.; Zaoui, F.Z.; Bousahla, A.A.; Mahmoud, S.R. Novel Quasi-3D and 2D Shear Deformation Theories for Bending and Free Vibration Analysis of FGM Plates. Geomech. Eng. 2018, 14, 519–532. [Google Scholar]
- Zaoui, F.Z.; Tounsi, A.; Ouinas, D.; Olayet, J.A.V. A Refined HSDT for Bending and Dynamic Analysis of FGM Plates. Struct. Eng. Mech. 2020, 74, 105–119. [Google Scholar]
- Hosseini-Hashemi, S.; Fadaee, M.; Rokni Damavandi Taher, H. Exact Solutions for Free Flexural Vibration of Lévy-Type Rectangular Thick Plates via Third-Order Shear Deformation Plate Theory. Appl. Math. Model. 2011, 35, 708–727. [Google Scholar] [CrossRef]
- Thai, H.-T.; Choi, D.-H. A Refined Shear Deformation Theory for Free Vibration of Functionally Graded Plates on Elastic Foundation. Compos. Part B Eng. 2012, 43, 2335–2347. [Google Scholar] [CrossRef]
- Jin, G.; Su, Z.; Shi, S.; Ye, T.; Gao, S. Three-Dimensional Exact Solution for the Free Vibration of Arbitrarily Thick Functionally Graded Rectangular Plates with General Boundary Conditions. Compos. Struct. 2014, 108, 565–577. [Google Scholar] [CrossRef]
- Baferani, A.H.; Saidi, A.; Ehteshami, H. Accurate Solution for Free Vibration Analysis of Functionally Graded Thick Rectangular Plates Resting on Elastic Foundation—ScienceDirect. Compos. Struct. 2011, 93, 1842–1853. [Google Scholar] [CrossRef]




| Materials | Properties | ||
|---|---|---|---|
| (Gpa) | (kg/m3) | ||
| Metal: Al | 70 | 2702 | 1/3 |
| Ceramic: Al2O3 | 380 | 3800 | 1/3 |
| Ceramic: ZrO2 | 200 | 5700 | 1/3 |
| Method | Modes | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 0.01 | Hosseini et al. [41] | 19.7320 | 49.3032 | 49.3032 | 78.8421 | 98.5169 | 98.5169 | 128.0024 | 128.0024 |
| Thai and Choi [42] | 19.7320 | 49.3032 | 49.3032 | 78.8421 | 98.5169 | 98.5169 | 128.0024 | 128.0024 | |
| Present | 19.7320 | 49.3031 | 49.3031 | 78.8421 | 98.5169 | 98.5169 | 128.0024 | 128.0024 | |
| 0.1 | Hosseini et al. [41] | 19.0653 | 45.4869 | 45.4869 | 69.8093 | 85.0646 | 85.0646 | 106.7350 | 106.7350 |
| Thai and Choi [42] | 19.0653 | 45.4869 | 45.4869 | 69.8093 | 85.0646 | 85.0646 | 106.7350 | 106.7350 | |
| Present | 19.0653 | 45.4869 | 45.4869 | 69.8091 | 85.0642 | 85.0642 | 106.7342 | 106.7342 | |
| 0.2 | Hosseini et al. [41] | 17.4523 | 38.1883 | 38.1883 | 55.2543 | 65.3135 | 65.3135 | 78.9865 | 78.9865 |
| Thai and Choi [42] | 17.4523 | 38.1883 | 38.1883 | 55.2543 | 65.3135 | 65.3135 | 78.9865 | 78.9865 | |
| Present | 17.4522 | 38.1876 | 38.1876 | 55.2524 | 65.3104 | 65.3104 | 78.9812 | 78.9812 | |
| 0.3 | Hosseini et al. [41] | 15.5745 | 31.6413 | 31.6413 | 44.0236 | 51.1314 | 51.1314 | 60.6549 | 60.6549 |
| Thai and Choi [42] | 15.5744 | 31.6413 | 31.6413 | 44.0236 | 51.1314 | 51.1314 | 60.6549 | 60.6549 | |
| Present | 15.5742 | 31.6396 | 31.6396 | 44.0190 | 51.1244 | 51.1244 | 60.6436 | 60.6436 | |
| 0.4 | Hosseini et al. [41] | 13.8136 | 26.5910 | 26.5910 | 36.1319 | 41.5668 | 41.5668 | 48.8370 | 48.8370 |
| Thai and Choi [42] | 13.8136 | 26.5908 | 26.5908 | 36.1319 | 41.5668 | 41.5668 | 48.8370 | 48.8370 | |
| Present | 13.8131 | 26.5877 | 26.5877 | 36.1242 | 41.5550 | 41.5550 | 48.8194 | 48.8194 | |
| Theory | ||||||
|---|---|---|---|---|---|---|
| Jin et al. [43] | Mantari [30] | Thai and Choi [42] | Present | |||
| 1 | 10 | 0 | 0.1135 | 0.1137 | 0.1134 | 0.1134 |
| 1 | 0.0870 | 0.0883 | 0.0868 | 0.0868 | ||
| 2 | 0.0789 | 0.0806 | 0.0788 | 0.0788 | ||
| 5 | 0.0741 | 0.0756 | 0.0740 | 0.0740 | ||
| 5 | 0 | 0.4169 | 0.4183 | 0.4151 | 0.4150 | |
| 1 | 0.3222 | 0.3271 | 0.3205 | 0.3205 | ||
| 2 | 0.2905 | 0.2965 | 0.2892 | 02892 | ||
| 5 | 0.2676 | 0.2726 | 0.2665 | 0.2667 | ||
| 2 | 0 | 1.8470 | 1.8543 | 1.8266 | 1.8265 | |
| 1 | 1.4687 | 1.4803 | 1.4452 | 1.4451 | ||
| 2 | 1.3095 | 1.3224 | 1.2891 | 1.2891 | ||
| 5 | 1.1450 | 1.1565 | 1.1319 | 1.1320 | ||
| 2 | 10 | 0 | 0.0719 | 0.0719 | 0.0717 | 0.0717 |
| 1 | 0.0550 | 0.0558 | 0.0549 | 0.0549 | ||
| 2 | 0.0499 | 0.0510 | 0.0498 | 0.0498 | ||
| 5 | 0.0471 | 0.0480 | 0.0470 | 0.0470 | ||
| 5 | 0 | 0.2713 | 0.2721 | 0.2705 | 0.2704 | |
| 1 | 0.2088 | 0.2121 | 0.2081 | 0.2081 | ||
| 2 | 01888 | 0.1928 | 0.1882 | 0.1882 | ||
| 5 | 0.1754 | 0.1789 | 0.1749 | 0.1750 | ||
| 2 | 0 | 0.9570 | 1.3075 | 1.2904 | 1.2904 | |
| 1 | 0.7937 | 1.0371 | 1.0134 | 1.0134 | ||
| 2 | 0.7149 | 0.9297 | 0.9066 | 0.9066 | ||
| 5 | 0.6168 | 0.8248 | 0.8070 | 0.8071 | ||
| Method | ||||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | |||
| (0,0) | 0.05 | Baferani et al. [44] | 0.0291 | 0.0227 | 0.0209 | 0.0197 |
| Thai and choi [42] | 0.0291 | 0.0222 | 0.0202 | 0.0191 | ||
| Present | 0.0291 | 0.0222 | 0.0202 | 0.0191 | ||
| 0.1 | Baferani et al. [44] | 0.1134 | 0.0891 | 0.0819 | 0.0767 | |
| Thai and choi [42] | 0.1134 | 0.0868 | 0.0788 | 0.0740 | ||
| Present | 0.1134 | 0.0868 | 0.0788 | 0.0740 | ||
| 0.2 | Baferani et al. [44] | 0.4154 | 0.3299 | 0.03016 | 0.2765 | |
| Thai and choi [42] | 0.4150 | 0.3205 | 0.2892 | 0.2667 | ||
| Present | 0.4150 | 0.3205 | 0.2892 | 0.2667 | ||
| (0,100) | 0.05 | Baferani et al. [44] | 0.0406 | 0.0382 | 0.0380 | 0.0381 |
| Thai and choi [42] | 0.0406 | 0.0378 | 0.0374 | 0.0377 | ||
| Present | 0.0406 | 0.0378 | 0.0374 | 0.0376 | ||
| 0.1 | Baferani et al. [44] | 0.1599 | 0.1517 | 0.1508 | 0.1515 | |
| Thai and choi [42] | 0.1597 | 0.1494 | 0.1478 | 0.1487 | ||
| Present | 0.1597 | 0.1494 | 0.1478 | 0.1486 | ||
| 0.2 | Baferani et al. [44] | 0.6080 | 0.5876 | 0.5861 | 0.5879 | |
| Thai and choi [42] | 0.6075 | 0.5753 | 0.5694 | 0.5722 | ||
| Present | 0.6074 | 0.5752 | 0.5694 | 0.5722 | ||
| (100,0) | 0.05 | Baferani et al. [44] | 0.0298 | 0.0238 | 0.0221 | 0.0210 |
| Thai and choi [42] | 0.0298 | 0.0233 | 0.0214 | 0.0204 | ||
| Present | 0.0298 | 0.0232 | 0.0214 | 0.0204 | ||
| 0.1 | Baferani et al. [44] | 0.1162 | 0.0933 | 0.0867 | 0.0821 | |
| Thai and choi [42] | 0.1161 | 0.0910 | 0.0836 | 0.0795 | ||
| Present | 0.1161 | 0.0910 | 0.0836 | 0.0795 | ||
| 0.2 | Baferani et al. [44] | 0.4273 | 0.3476 | 0.3219 | 0.2999 | |
| Thai and choi [42] | 0.4269 | 0.3381 | 0.3097 | 0.2901 | ||
| Present | 0.4268 | 0.3381 | 0.3096 | 0.2901 | ||
| (100,100) | 0.05 | Baferani et al. [44] | 0.0411 | 0.0388 | 0.0386 | 0.0388 |
| Thai and choi [42] | 0.0411 | 0.0384 | 0.0381 | 0.0384 | ||
| Present | 0.0411 | 0.0384 | 0.0381 | 0.0384 | ||
| 0.1 | Baferani et al. [44] | 0.1619 | 0.1542 | 0.1535 | 01543 | |
| Thai and choi [42] | 0.1617 | 0.1519 | 0.1505 | 0.1515 | ||
| Present | 0.1617 | 0.1519 | 0.1504 | 0.1514 | ||
| 0.2 | Baferani et al. [44] | 0.6162 | 0.5978 | 0.5970 | 0.5993 | |
| Thai and choi [42] | 0.6156 | 0.5852 | 0.5800 | 0.5834 | ||
| Present | 0.6156 | 0.5852 | 0.5800 | 0.5834 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaoui, F.Z.; Ouinas, D.; Achour, B.; Tounsi, A.; Latifee, E.R.; Al-Naghi, A.A.A. A Hyperbolic Shear Deformation Theory for Natural Frequencies Study of Functionally Graded Plates on Elastic Supports. J. Compos. Sci. 2022, 6, 285. https://doi.org/10.3390/jcs6100285
Zaoui FZ, Ouinas D, Achour B, Tounsi A, Latifee ER, Al-Naghi AAA. A Hyperbolic Shear Deformation Theory for Natural Frequencies Study of Functionally Graded Plates on Elastic Supports. Journal of Composites Science. 2022; 6(10):285. https://doi.org/10.3390/jcs6100285
Chicago/Turabian StyleZaoui, Fatima Zohra, Djamel Ouinas, Belkacem Achour, Abdelouahed Tounsi, Enamur R. Latifee, and Ahmed A. Alawi Al-Naghi. 2022. "A Hyperbolic Shear Deformation Theory for Natural Frequencies Study of Functionally Graded Plates on Elastic Supports" Journal of Composites Science 6, no. 10: 285. https://doi.org/10.3390/jcs6100285
APA StyleZaoui, F. Z., Ouinas, D., Achour, B., Tounsi, A., Latifee, E. R., & Al-Naghi, A. A. A. (2022). A Hyperbolic Shear Deformation Theory for Natural Frequencies Study of Functionally Graded Plates on Elastic Supports. Journal of Composites Science, 6(10), 285. https://doi.org/10.3390/jcs6100285







