Fundamental Frequency Optimization of Variable Angle Tow Laminates with Embedded Gap Defects
Abstract
1. Introduction
2. Materials and Methods
2.1. Variable Angle Tow Laminates
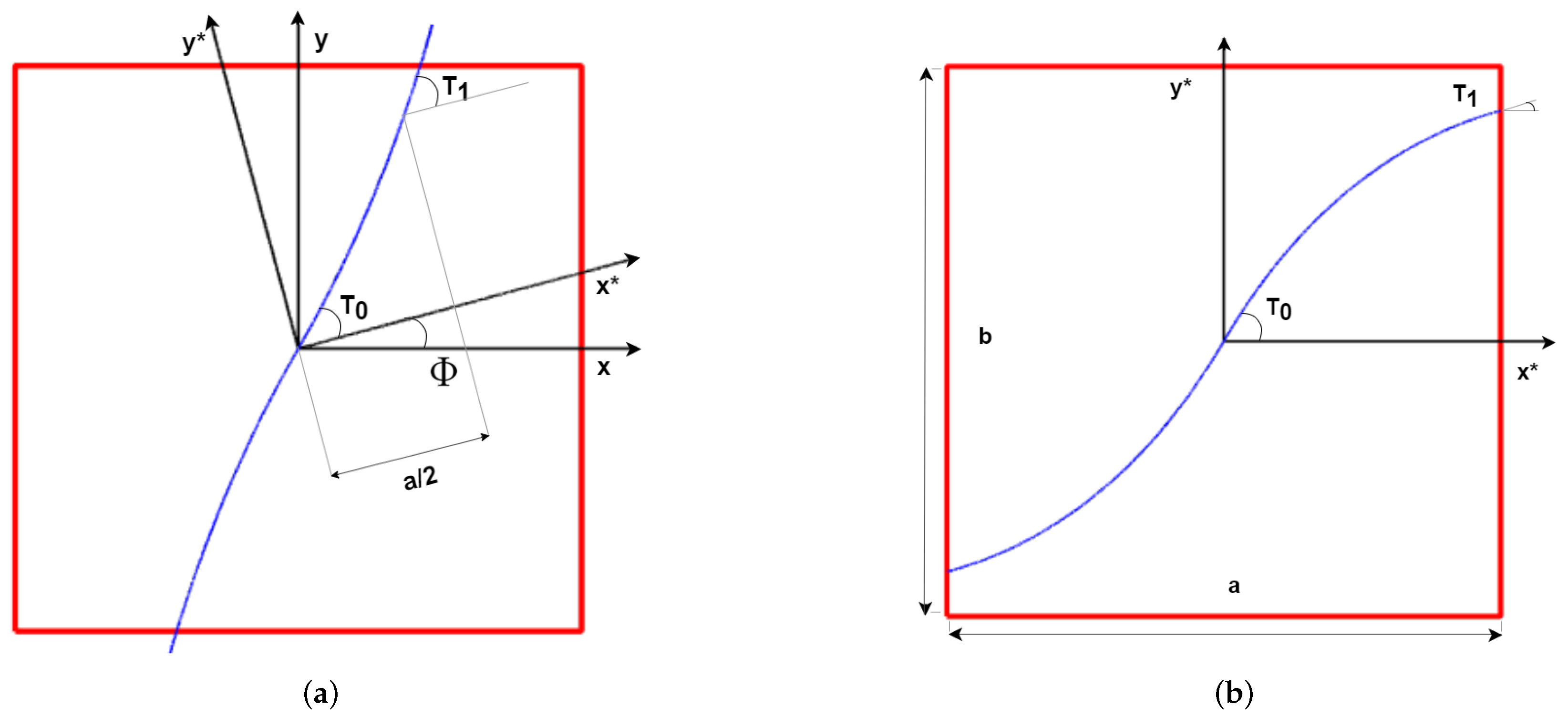
2.1.1. Fiber Path Definition
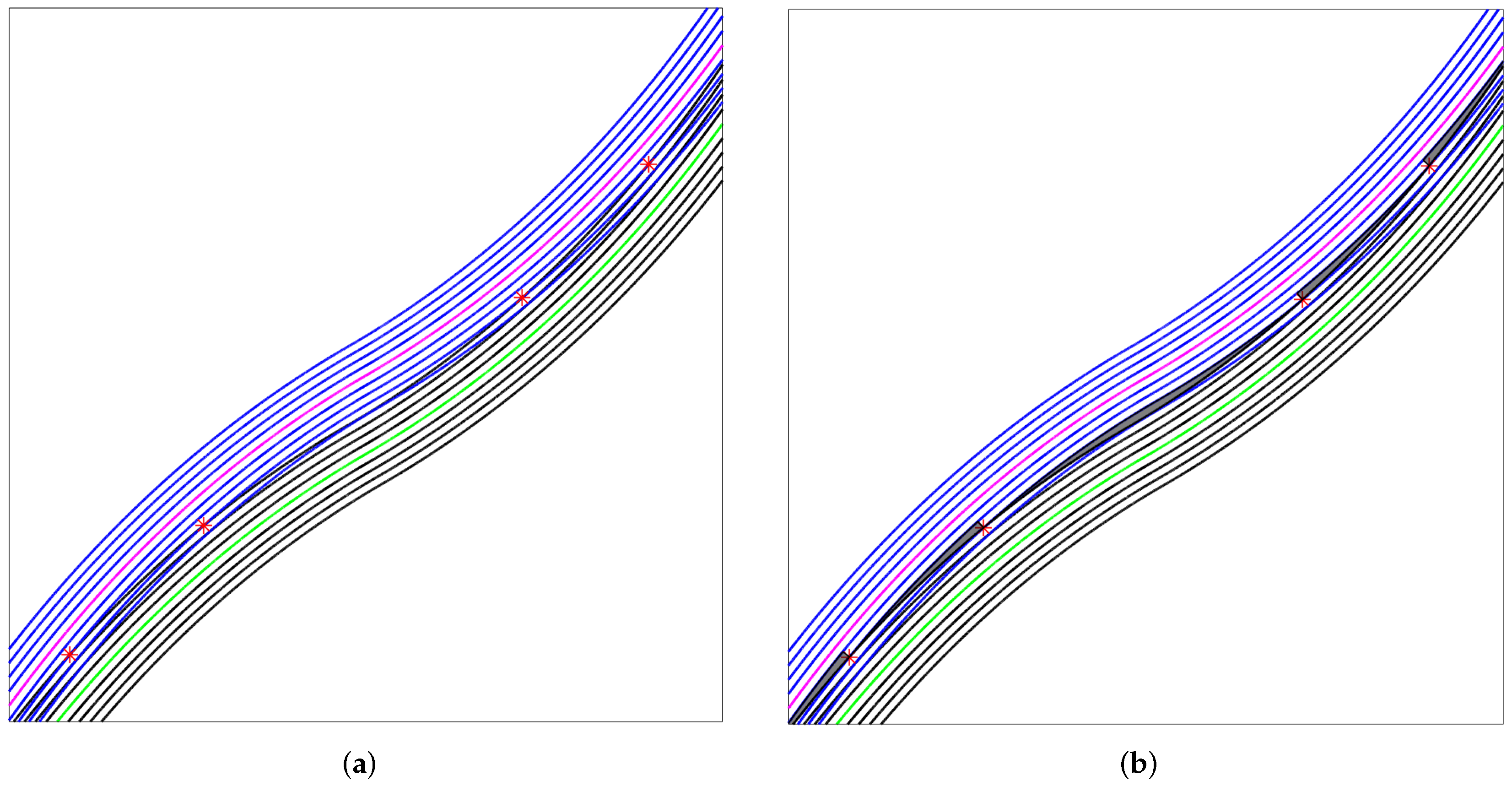
2.1.2. Induced Defects
2.1.3. Manufacturing Constraints
3. Optimization
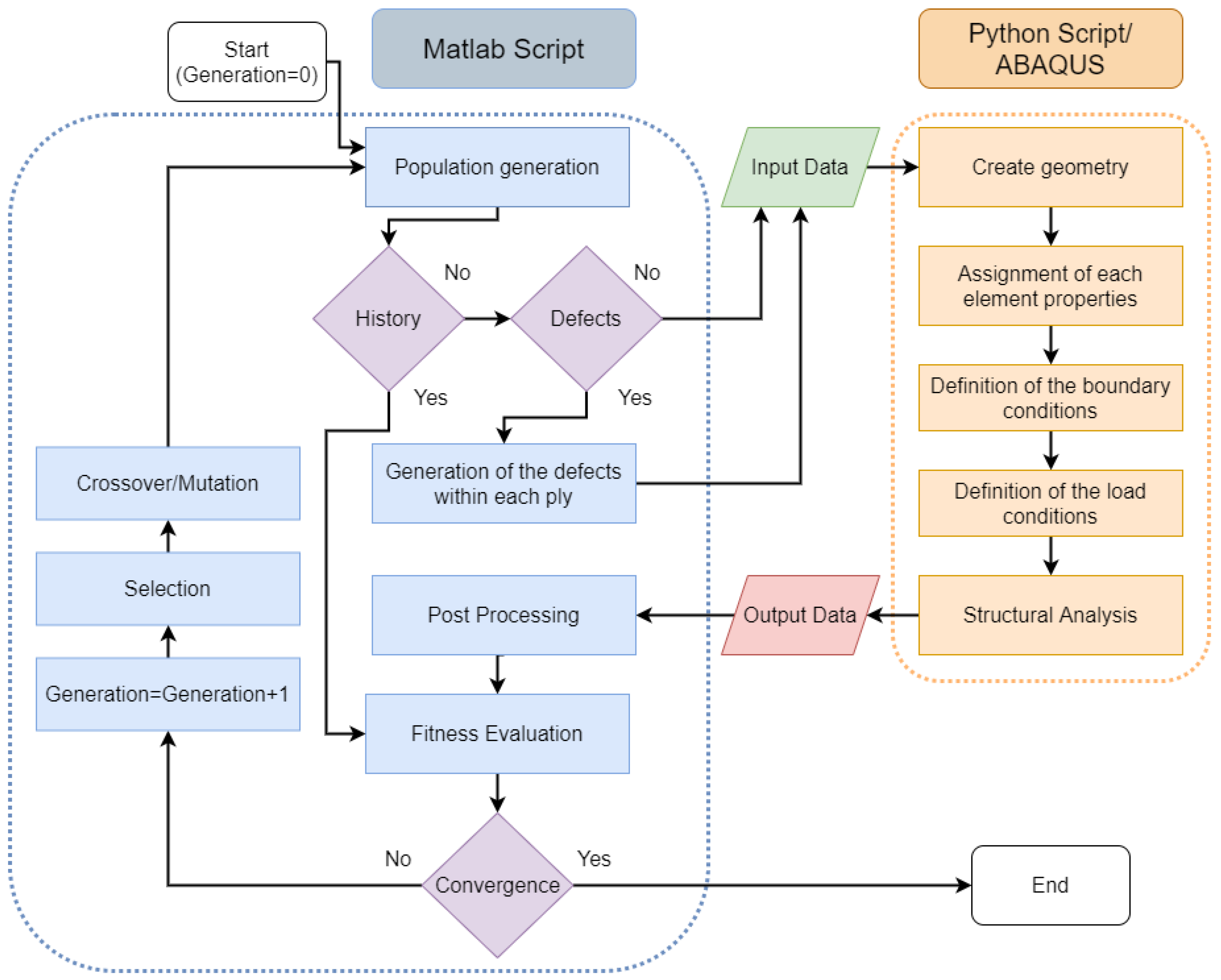
4. Implementation
4.1. Finite Element Model
4.2. Matlab Environment
4.3. Validation
5. Results and Discussions
5.1. Non Steered Plates
5.2. Defect Free Steered Optimization Results
5.3. Defect Free Steered Results with Complete Gap
5.4. Complete Gap Steered Optimization Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFP | Automated Fiber Placement |
| VAT | Variable Angle Tow |
| LS | Linearly Steered |
| NS | Non Steered |
| C | Boundary Condition Fully Clamped |
| S | Boundary Condition Fully Simply Supported |
| VSCL | Variable Stiffness Composite Laminate |
| SDC | Specific Damping Capacity |
| CPT | Classical Plate Theory |
| FSDT | First-Order Shear Deformation Theory |
| FEM | Finite Element Method |
| GA | Genetic Algorithm |
References
- Gürdal, Z.; Tatting, B.F.; Wu, C. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response. Compos. Part A Appl. Sci. Manuf. 2008, 39, 911–922. [Google Scholar] [CrossRef]
- Alhajahmad, A.; Mittelstedt, C. Design tailoring of curvilinearly grid-stiffened variable-stiffness composite cylindrically curved panels for maximum buckling capacity. Thin-Walled Struct. 2020, 157, 107132. [Google Scholar] [CrossRef]
- Setoodeh, S.; Abdalla, M.M.; IJsselmuiden, S.T.; Gürdal, Z. Design of variable-stiffness composite panels for maximum buckling load. Compos. Struct. 2009, 87, 109–117. [Google Scholar] [CrossRef]
- Honda, S.; Narita, Y.; Sasaki, K. Maximizing the fundamental frequency of laminated composite plates with optimally shaped curvilinear fibers. J. Syst. Des. Dyn. 2009, 3, 867–876. [Google Scholar] [CrossRef][Green Version]
- Honda, S.; Igarashi, T.; Narita, Y. Multi-objective optimization of curvilinear fiber shapes for laminated composite plates by using NSGA-II. Compos. Part B Eng. 2013, 45, 1071–1078. [Google Scholar] [CrossRef]
- Pereira, D.; Guimarães, T.; Resende, H.; Rade, D. Numerical and experimental analyses of modal frequency and damping in tow-steered CFRP laminates. Compos. Struct. 2020, 244, 112190. [Google Scholar] [CrossRef]
- Serhat, G.; Basdogan, I. Lamination parameter interpolation method for design of manufacturable variable-stiffness composite panels. AIAA J. 2019, 57, 3052–3065. [Google Scholar] [CrossRef]
- Serhat, G.; Bediz, B.; Basdogan, I. Unifying lamination parameters with spectral-Tchebychev method for variable-stiffness composite plate design. Compos. Struct. 2020, 242, 112183. [Google Scholar] [CrossRef]
- Farsadi, T.; Asadi, D.; Kurtaran, H. Fundamental frequency optimization of variable stiffness composite skew plates. Acta Mech. 2021, 232, 555–573. [Google Scholar] [CrossRef]
- Akhavan, H.; Ribeiro, P. Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers. Compos. Struct. 2011, 93, 3040–3047. [Google Scholar] [CrossRef]
- Van Campen, J.M.; Kassapoglou, C.; Gürdal, Z. Generating realistic laminate fiber angle distributions for optimal variable stiffness laminates. Compos. Part B Eng. 2012, 43, 354–360. [Google Scholar] [CrossRef]
- Dodwell, T.J.; Butler, R.; Rhead, A.T. Optimum fiber steering of composite plates for buckling and manufacturability. AIAA J. 2016, 54, 1146–1149. [Google Scholar] [CrossRef]
- Parnas, L.; Oral, S.; Ceyhan, Ü. Optimum design of composite structures with curved fiber courses. Compos. Sci. Technol. 2003, 63, 1071–1082. [Google Scholar] [CrossRef]
- Demir, E.; Yousefi-Louyeh, P.; Yildiz, M. Design of variable stiffness composite structures using lamination parameters with fiber steering constraint. Compos. Part B Eng. 2019, 165, 733–746. [Google Scholar] [CrossRef]
- Rashed, A.; Demir, E. Design of variable stiffness composites for maximum fundamental frequency considering manufacturing constraints of tow steering. Compos. Struct. 2022, 284, 115151. [Google Scholar] [CrossRef]
- Blom, A.W.; Lopes, C.S.; Kromwijk, P.J.; Gurdal, Z.; Camanho, P.P. A theoretical model to study the influence of tow-drop areas on the stiffness and strength of variable-stiffness laminates. J. Compos. Mater. 2009, 43, 403–425. [Google Scholar] [CrossRef]
- Fayazbakhsh, K.; Nik, M.A.; Pasini, D.; Lessard, L. Defect layer method to capture effect of gaps and overlaps in variable stiffness laminates made by Automated Fiber Placement. Compos. Struct. 2013, 97, 245–251. [Google Scholar] [CrossRef]
- Fayazbakhsh, K.; Nik, M.A.; Pasini, D.; Lessard, L. The effect of gaps and overlaps on the in-plane stiffness and buckling load of variable stiffness laminates made by automated fiber placement. In Proceedings of the 15th European Conference on Composite Materials, Venice, Italy, 24–28 June 2012. [Google Scholar]
- Marouene, A.; Boukhili, R.; Chen, J.; Yousefpour, A. Effects of gaps and overlaps on the buckling behavior of an optimally designed variable-stiffness composite laminates—A numerical and experimental study. Compos. Struct. 2016, 140, 556–566. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Nik, M.A.; Pasini, D. The role of shear deformation in laminated plates with curvilinear fiber paths and embedded defects. Compos. Struct. 2014, 118, 217–227. [Google Scholar] [CrossRef]
- Arranz, S.; Sohouli, A.; Suleman, A. Buckling Optimization of Variable Stiffness Composite Panels for Curvilinear Fibers and Grid Stiffeners. J. Compos. Sci. 2021, 5, 324. [Google Scholar] [CrossRef]
- Brooks, T.R.; Martins, J.R. On manufacturing constraints for tow-steered composite design optimization. Compos. Struct. 2018, 204, 548–559. [Google Scholar] [CrossRef]
- Mishra, V.; Peeters, D.M.; Abdalla, M.M. Stiffness and buckling analysis of variable stiffness laminates including the effect of automated fibre placement defects. Compos. Struct. 2019, 226, 111233. [Google Scholar] [CrossRef]
- Heinecke, F.; Willberg, C. Manufacturing-induced imperfections in composite parts manufactured via automated fiber placement. J. Compos. Sci. 2019, 3, 56. [Google Scholar] [CrossRef]
- Marrouze, J.; Housner, J.; Abdi, F. Effect of manufacturing defects and their uncertainties on strength and stability of stiffened panels. In Proceedings of the 19th International Conference on Composite Materials, Montreal, QC, Canada, 28 July–2 August 2013; p. 10. [Google Scholar]
- Heinecke, F.; van den Brink, W.; Wille, T. Assessing the structural response of automated fibre placement composite structures with gaps and overlaps by means of numerical approaches. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Denmark, 19–24 July 2015; p. 12. [Google Scholar]
- Heinecke, F.; Wille, T. In-situ structural evaluation during the fibre deposition process of composite manufacturing. CEAS Aeronaut. J. 2018, 9, 123–133. [Google Scholar] [CrossRef]
- Li, X.; Hallett, S.R.; Wisnom, M.R. Modelling the effect of gaps and overlaps in automated fibre placement (AFP)-manufactured laminates. Sci. Eng. Compos. Mater. 2015, 22, 115–129. [Google Scholar] [CrossRef]
- Antunes, A.M.; Ribeiro, P.; Rodrigues, J.D.; Akhavan, H. Modal analysis of a variable stiffness composite laminated plate with diverse boundary conditions: Experiments and modelling. Compos. Struct. 2020, 239, 111974. [Google Scholar] [CrossRef]
- Rodrigues, J.D.; Ribeiro, P.; Akhavan, H. Experimental and finite element modal analysis of variable stiffness composite laminated plates. In Proceedings of the 11th Biennial International Conference on Vibration Problems (ICOVP-2013), Lisbon, Portugal, 9–12 September 2013; p. 30. [Google Scholar]
- Gurdal, Z.; Olmedo, R. In-plane response of laminates with spatially varying fiber orientations-variable stiffness concept. AIAA J. 1993, 31, 751–758. [Google Scholar] [CrossRef]
- Waldhart, C. Analysis of Tow-Placed, Variable-Stiffness Laminates. Master’s Thesis, Faculty of the Virginia Plytechnic Institute and State University, Blacksburg, VA, USA, 1996. [Google Scholar]
- Langley, P.T. Finite Element Modeling of Tow-Placed Variable-Stiffness Composite Laminates. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 1999. [Google Scholar]
- Blom, A.W. Structural Performance of Fiber-Placed, Variable-Stiffness Composite Conical and Cylindrical Shelss. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2009. [Google Scholar]



| Tow Width | Typical Minimum Turning Radius | Typical Maximum Curvature |
|---|---|---|
| (mm) | (mm) | (m) |
| 3.175 | 635 | 1.57 |
| 6.35 | 1778 | 0.56 |
| 12.7 | 8890 | 0.1125 |
| Property | E1 [GPa] | E2 [GPa] | G12 [GPa] | ν12 | ρ [kg/m3] |
|---|---|---|---|---|---|
| G40-800/5276-1 | 143 | 9.1 | 4.8 | 0.3 | 1650 |
| resin | 3.7 | 3.7 | 1.4 | 0.3 | 1310 |
| Characteristic | a [m] | b [m] | h [mm] | E1 [GPa] | E2 [GPa] | G [GPa] | ν12 | ρ [kg/m3] |
|---|---|---|---|---|---|---|---|---|
| Value | 1 | 1 | 0.01 | 173 | 7.2 | 3.76 | 0.29 | 1540 |
| Layup [°] | f1 [Hz] | f2 [Hz] | f3 [Hz] | |
|---|---|---|---|---|
| Ref. [10] | 579.398 | 821.532 | 1225.79 | |
| Abaqus | 579.790 | 822.538 | 1230.008 | |
| Difference (%) | 0.07 | 0.12 | 0.34 | |
| >, <>, < | Ref. [10] | 667.177 | 862.919 | 1234.64 |
| Abaqus | 667.492 | 863.899 | 1239.187 | |
| Difference (%) | 0.05 | 0.11 | 0.37 | |
| >, <>, < | Ref. [10] | 710.771 | 912.183 | 1335.49 |
| Abaqus | 710.597 | 912.246 | 1336.922 | |
| Difference (%) | 0.02 | 0.01 | 0.11 |
| Property | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | kg/m | |
|---|---|---|---|---|---|---|---|
| Prepreg | 143 | 1500 | |||||
| Resin | 1100 |
| Layup | Manufacturing Defects | —Literature Results FSDT [20] | —Present Results | Difference (%) | |
|---|---|---|---|---|---|
| 200 | <58|39 | Defect free | |||
| Complete gap |
| Design | [°] | [°] | [°] | [°] | [Hz] | [Hz] | [Hz] | Gen. | |
|---|---|---|---|---|---|---|---|---|---|
| NS-C | 39 | ||||||||
| NS-S | 44 | ||||||||
| NS-C | 55 | ||||||||
| NS-S | 55 | ||||||||
| NS-C | 61 | ||||||||
| NS-S | 43 |
| Design | LS-C | LS-S | LS-C | LS-S | LS-C | LS-S | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| CON | CON | UN | CON | UN | CON | CON | CON | |||
| A | A | - | A | B | - | A | B | A | A | |
| <, | <0.0, 0.3> | <0.1, 22.6> | <90.0, −1.9> | <−74.9, −43.7> | <−81.8, −28.4> | <−42.8, −45.9> | <42.3, 46.0> | <42.1, 46.0> | <89.9, 90.0> | <−90.0, −52.9> |
| <, | <0.2, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > |
| <, | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > |
| <, | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > | <, > |
| Gen. | 59 | 66 | 66 | 89 | 76 | 74 | 55 | 80 | 82 | 117 |
| 32 tows | 16 tows | 8 tows | ||||||||||
| Design | LS-C-CON | LS-S-CON | LS-C-CON | LS-S-CON | LS-C-CON | LS-S-CON | ||||||
| A | B | A | B | A | B | A | B | A | B | A | B | |
| [Hz] | ||||||||||||
| [Hz] | ||||||||||||
| [Hz] | ||||||||||||
| [%] | ||||||||||||
| 32 tows | 16 tows | 8 tows | 32 tows | 16 tows | 8 tows | |||||||
| Design | LS-C | LS-S | LS-C | LS-S | LS-C | LS-S | LS-C | LS-S | LS-C | LS-S | LS-C | LS-S |
| CON-A | CON-A | |||||||||||
| [Hz] | ||||||||||||
| [Hz] | ||||||||||||
| [Hz] | ||||||||||||
| [%] | ||||||||||||
| Design | LS-C-CON | LS-S-CON | LS-C-CON | LS-S-CON | LS-C-CON | LS-S-CON | ||
|---|---|---|---|---|---|---|---|---|
| A | A | A | B | A | B | A | A | |
| <, | < > | < > | <, > | <, > | <, > | <, > | < > | <, > |
| <, | < > | < > | <, > | <, > | <, > | <, > | < > | <, > |
| <, | < > | < > | <, > | <, > | <, > | <, > | < > | <, > |
| <, | < > | < > | <, > | <, > | <, > | <, > | < > | <, > |
| Gen. | 66 | 62 | 122 | 75 | 83 | 88 | 84 | 91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, J.; Sohouli, A.; Suleman, A. Fundamental Frequency Optimization of Variable Angle Tow Laminates with Embedded Gap Defects. J. Compos. Sci. 2022, 6, 64. https://doi.org/10.3390/jcs6020064
Carvalho J, Sohouli A, Suleman A. Fundamental Frequency Optimization of Variable Angle Tow Laminates with Embedded Gap Defects. Journal of Composites Science. 2022; 6(2):64. https://doi.org/10.3390/jcs6020064
Chicago/Turabian StyleCarvalho, João, Abdolrasoul Sohouli, and Afzal Suleman. 2022. "Fundamental Frequency Optimization of Variable Angle Tow Laminates with Embedded Gap Defects" Journal of Composites Science 6, no. 2: 64. https://doi.org/10.3390/jcs6020064
APA StyleCarvalho, J., Sohouli, A., & Suleman, A. (2022). Fundamental Frequency Optimization of Variable Angle Tow Laminates with Embedded Gap Defects. Journal of Composites Science, 6(2), 64. https://doi.org/10.3390/jcs6020064







