Atomic Insights into the Structural Properties and Displacement Cascades in Ytterbium Titanate Pyrochlore (Yb2Ti2O7) and High-Entropy Pyrochlores
Abstract
:1. Introduction
2. Computational Details and Methodology
2.1. Crystal Structures
2.2. Interatomic Potential
2.3. Displacement Cascades Simulations
3. Results and Discussion
3.1. Calculation for Equilibrium Lattice Constant and Ionic Radii
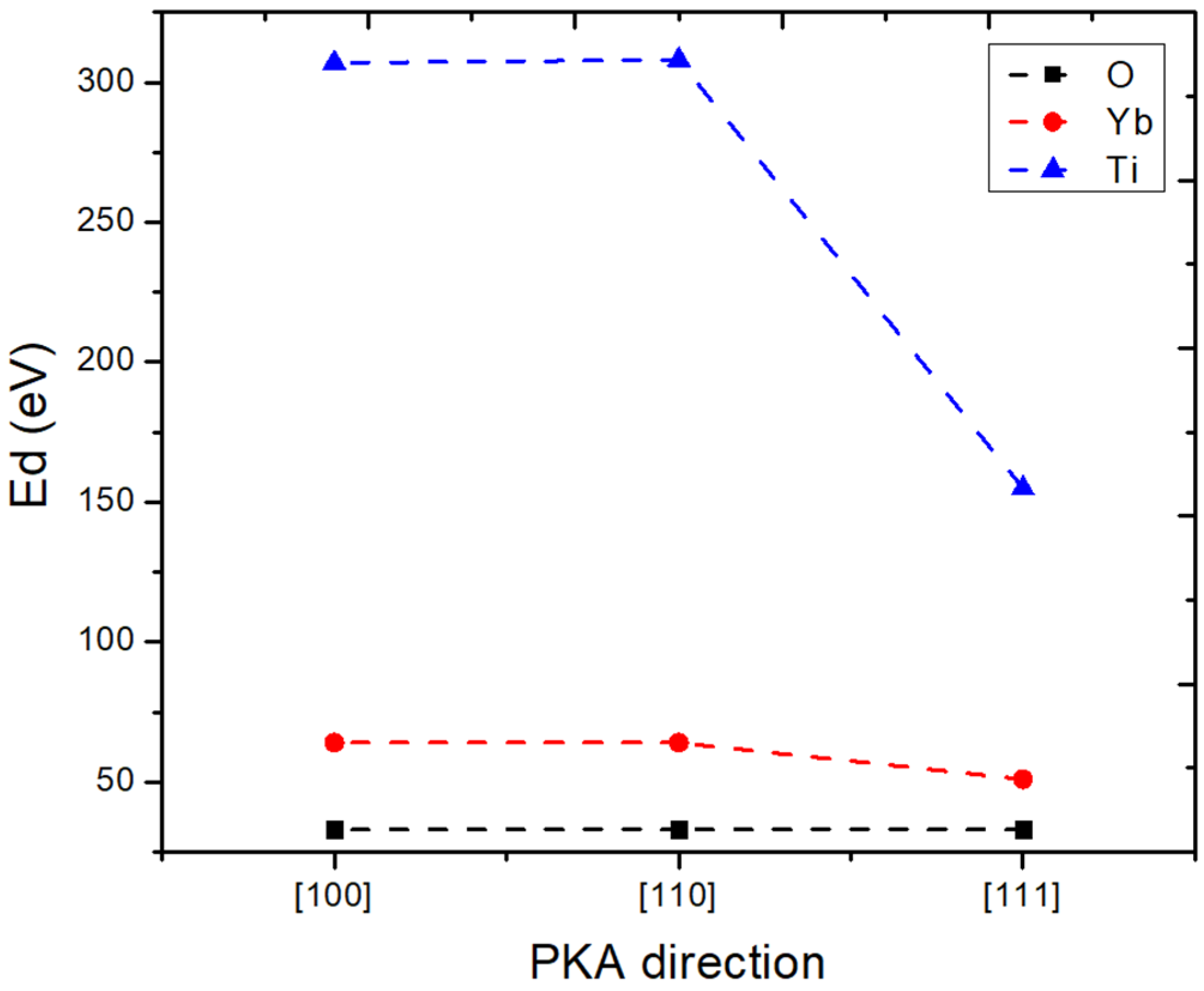
3.2. Threshold Displacement Energy (Ed)
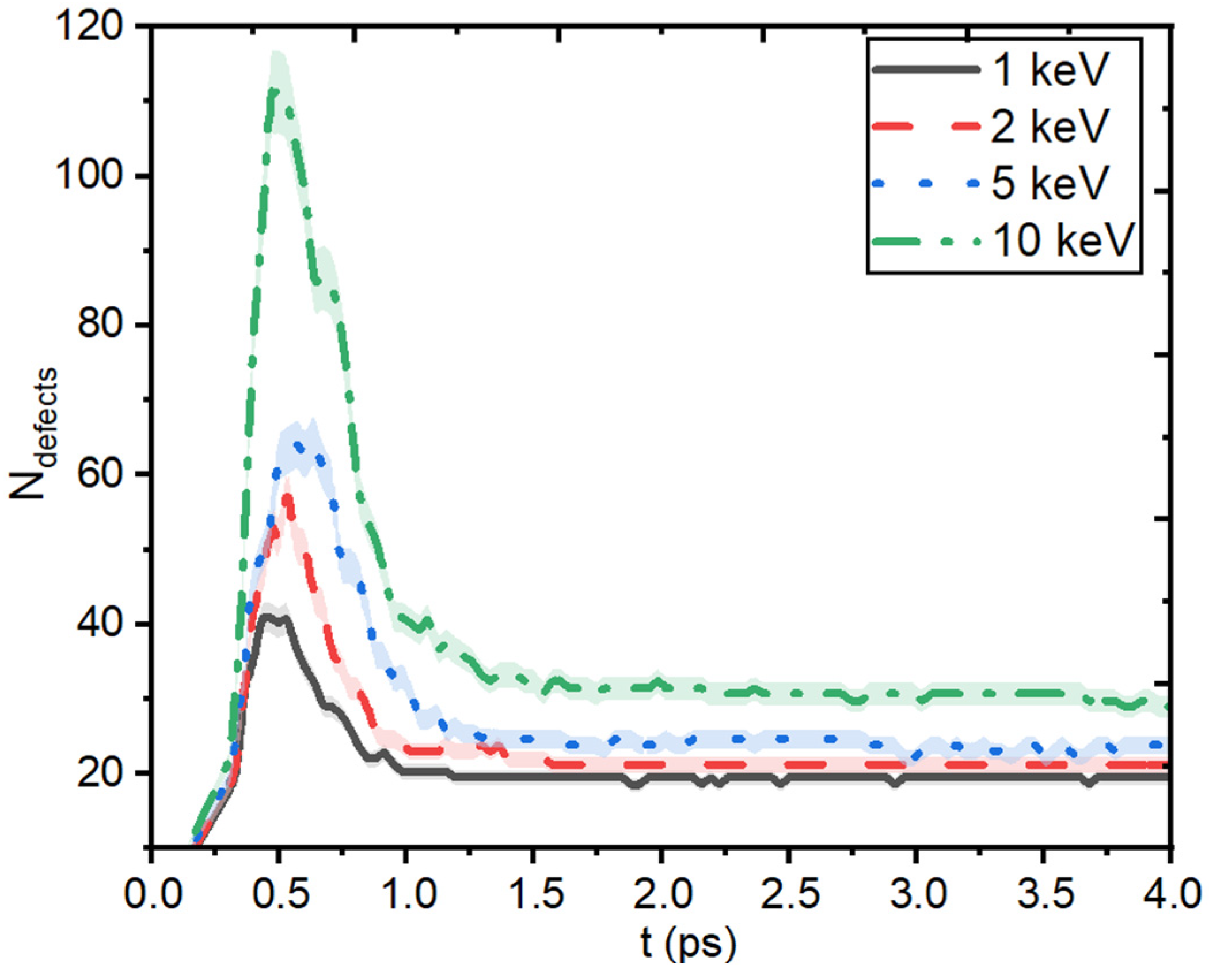
3.3. Effect of Displacement Cascades on Energy and Direction of PKA
3.4. Displacement Cascades in HEPy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abram, T.; Ion, S. Generation-IV nuclear power: A review of the state of the science. Energy Policy 2008, 36, 4323–4330. [Google Scholar] [CrossRef]
- Dungan, K.; Gregg, R.W.H.; Morris, K.; Livens, F.R.; Butler, G. Assessment of the disposability of radioactive waste inventories for a range of nuclear fuel cycles: Inventory and evolution over time. Energy 2021, 221, 119826. [Google Scholar] [CrossRef]
- Amiard, J. Nuclear Waste Disposal Methods. Manag. Radioact. Waste 2021, 5, 23–66. [Google Scholar] [CrossRef]
- Kong, L.; Karatchevtseva, I.; Zhang, Y.; Wei, T. The incorporation of Nd or Ce in CaZrTi2O7 zirconolite: Ceramic versus glass-ceramic. J. Nucl. Mater. 2021, 543, 152583. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, K.; Zheng, X.; Wang, Y.; Sun, X.; Xue, P.; Li, C.; Du, M. Formulation of Poly(ionic liquids)@COF Nanotrap for Efficient Perrhenate Sequestration from Alkaline Nuclear Waste. Chem. Mater. 2022, 34, 5452–5456. [Google Scholar] [CrossRef]
- Guo, X.; Gin, S.; Frankel, G.S. Review of corrosion interactions between different materials relevant to disposal of high-level nuclear waste. npj Mater. Degrad. 2020, 4, 34. [Google Scholar] [CrossRef]
- Frankel, G.S.; Vienna, J.D.; Lian, J.; Guo, X.; Gin, S.; Kim, S.H.; Du, J.; Ryan, J.V.; Wang, J.; Windl, W.; et al. Recent Advances in Corrosion Science Applicable To Disposal of High-Level Nuclear Waste. Chem. Rev. 2021, 121, 12327–12383. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Zhao, P.; Bourcier, W.L.; Van Konynenburg, R.; Shaw, H.F. Investigation of Pyrochlore-Based U-Bearing Ceramic Nuclear Waste: Uranium Leaching Test and TEM Observation. Environ. Sci. Technol. 2004, 38, 1480–1486. [Google Scholar] [CrossRef]
- Dholakia, M.; Chandra, S.; Jaya, S.M. Comparative study of radiation damage in Gd2Zr2O7 and Y2Ti2O7 crystal: A molecular dynamics investigation. AIP Conf. Proc. 2020, 2265, 30373. [Google Scholar] [CrossRef]
- Zhang, Y. Ceramic Materials for Nuclear Energy Applications. JOM 2019, 71, 4806–4807. [Google Scholar] [CrossRef]
- Marra, J. Advanced ceramic materials for next-generation nuclear applications. IOP Conf. Ser. Mater. Sci. Eng. 2011, 18, 16001. [Google Scholar] [CrossRef]
- Lee, W.H.; Cheong, J.H. Potential radiological hazard and options to cope with consequences from recycling of activated metal waste disposed of at a near-surface disposal facility. Ann. Nucl. Energy 2021, 152, 107993. [Google Scholar] [CrossRef]
- Hand, M.L.; Stennett, M.C.; Hyatt, N.C. Rapid low temperature synthesis of a titanate pyrochlore by molten salt mediated reaction. J. Eur. Ceram. Soc. 2012, 32, 3211–3219. [Google Scholar] [CrossRef]
- Dholakia, M.; Chandra, S. Structural stability of titanate pyrochlores undergoing radiation damage. Comput. Mater. Sci. 2022, 201, 110889. [Google Scholar] [CrossRef]
- Mohan, S.; Kaur, G.; David, C.; Panigrahi, B.K.; Amarendra, G. Ab initio molecular dynamics simulation of threshold displacement energies and defect formation energies in Y4Zr3O12. J. Appl. Phys. 2020, 127, 235901. [Google Scholar] [CrossRef]
- Minervini, L.; Grimes, R.W.; Sickafus, K.E. Disorder in pyrochlore oxides. J. Am. Ceram. Soc. 2000, 83, 1873–1878. [Google Scholar] [CrossRef]
- Zhang, Y. Machine learning the lattice constant of cubic pyrochlore compounds. Int. J. Appl. Ceram. Technol. 2021, 18, 661–676. [Google Scholar] [CrossRef]
- Kennedy, B.J.; Hunter, B.A.; Howard, C.J. Structural and Bonding Trends in Tin Pyrochlore Oxides. J. Solid State Chem. 1997, 130, 58–65. [Google Scholar] [CrossRef]
- Sakai, H.; Yoshimura, K.; Ohno, H.; Kato, H.; Kambe, S.; Walstedt, R.E.; Matsuda, T.D.; Haga, Y.; Onuki, Y. Superconductivity in a pyrochlore oxide, Cd2Re2O7. J. Phys. Condens. Matter 2001, 13, L785. [Google Scholar] [CrossRef]
- Dong, L.; Li, Y.; Devanathan, R.; Setyawan, W.; Gao, F. Low energy ion-solid interactions and chemistry effects in a series of pyrochlores. J. Am. Ceram. Soc. 2017, 100, 3132–3144. [Google Scholar] [CrossRef]
- Chartier, A.; Meis, C.; Crocombette, J.P.; Corrales, L.R.; Weber, W.J. Atomistic modeling of displacement cascades in (formula presented) pyrochlore. Phys. Rev. B-Condens. Matter Mater. Phys. 2003, 67, 174102. [Google Scholar] [CrossRef]
- Whittle, K.R.; Blackford, M.G.; Aughterson, R.D.; Lumpkin, G.R.; Zaluzec, N.J. Ion irradiation of novel yttrium/ytterbium-based pyrochlores: The effect of disorder. Acta Mater. 2011, 59, 7530–7537. [Google Scholar] [CrossRef]
- Archer, A.; Foxhall, H.R.; Allan, N.L.; Shearer, J.R.W.; Gunn, D.S.D.; Harding, J.H.; Todorov, I.T.; Travis, K.P.; Purton, J.A. Multiple cascade radiation damage simulations of pyrochlore. Mol. Simul. 2021, 47, 273–283. [Google Scholar] [CrossRef]
- Subramani, T.; Voskanyan, A.; Jayanthi, K.; Abramchuk, M.; Navrotsky, A. A Comparison of Order-Disorder in Several Families of Cubic Oxides. Front. Chem. 2021, 9, 719169. [Google Scholar] [CrossRef]
- Annamareddy, A.; Eapen, J.; Eapen, J. Decoding ionic conductivity and reordering in cation-disordered pyrochlores Subject Areas: Author for correspondence. Philos. Trans. A 2021, 379, 20190452. [Google Scholar] [CrossRef] [PubMed]
- Teng, Z.; Tan, Y.; Zhang, H. High-entropy pyrochlore a2b2o7 with both heavy and light rare-earth elements at the a site. Materials 2022, 15, 129. [Google Scholar] [CrossRef]
- Xiang, H.; Xing, Y.; Dai, F.; Wang, H.; Su, L.; Miao, L.; Zhang, G.; Wang, Y.; Qi, X.; Yao, L.; et al. High-Entropy Ceramics: Present Status, Challenges, and a Look Forward. J. Adv. Ceram. 2021, 10, 385–441, ISBN 4014502104. [Google Scholar] [CrossRef]
- Widom, M. Modeling the structure and thermodynamics of high-entropy alloys. J. Mater. Res. 2018, 33, 2881–2898. [Google Scholar] [CrossRef]
- Zhi, Q.; Tan, X.; Liu, Z.; Liu, Y.; Zhang, Q.; Chen, Y.; Li, M. Effect of Zr content on microstructure and mechanical properties of lightweight Al2NbTi3V2Zrx high entropy alloy. Micron 2021, 144, 103031. [Google Scholar] [CrossRef]
- Ji, G.; Zhou, Z.; Meng, F.; Yang, X.; Sheng, R.; Qiao, J.; Liaw, P.K.; Li, M.; Jiang, L.; Chen, S.; et al. Effect of Zr addition on the local structure and mechanical properties of Ti–Ta–Nb–Zr refractory high-entropy alloys. J. Mater. Res. Technol. 2022, 19, 4428–4438. [Google Scholar] [CrossRef]
- Brixner, L. Preparation and Properties of the Ln2Ti20-Type Rare Earth Titanates. Inorg. Chem. 1964, 3, 1065–1067. [Google Scholar] [CrossRef]
- Devanathan, R.; Weber, W.J. Insights into the radiation response of pyrochlores from calculations of threshold displacement events. J. Appl. Phys. 2005, 98, 086110. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, S. First-principles design of refractory high entropy alloy VMoNbTaW. Entropy 2018, 20, 965. [Google Scholar] [CrossRef] [PubMed]
- Lipkina, K.; Savchenko, A.; Skupov, M.; Glushenkov, A.; Vatulin, A.; Uferov, O.; Ivanov, Y.; Kulakov, G.; Ershov, S.; Maranchak, S.; et al. Metallic inert matrix fuel concept for minor actinides incineration to achieve ultra-high burn-up. J. Nucl. Mater. 2014, 452, 378–381. [Google Scholar] [CrossRef]
- Mustafa Azeem, M.; Li, Z.; Wang, Q.; Zubair, M. Molecular dynamics studies and irradiation effects in ODSS alloys. Int. J. Nucl. Energy Sci. Technol. 2018, 12, 381–399. [Google Scholar] [CrossRef]
- Azeem, M.M.; Wang, Q.; Li, Z.; Zhang, Y. Dislocation-oxide interaction in Y2O3 embedded Fe: A molecular dynamics simulation study. Nucl. Eng. Technol. 2020, 52, 337–343. [Google Scholar] [CrossRef]
- Azeem, M.M.; Wang, Q.; Zubair, M. Atomistic simulations of nanoindentation response of irradiation defects in iron. Sains Malays. 2019, 48, 2029–2039. [Google Scholar] [CrossRef]
- Azeem, M.M.; Wang, Q.; Zhang, Y.; Liu, S.; Zubair, M. Effect of Grain Boundary on Diffusion of P in Alpha-Fe: A Molecular Dynamics Study. Front. Phys. 2019, 7, 97. [Google Scholar] [CrossRef]
- Mustafa Azeem, M.; Abd El Gawad, K.; Zubair, M.; Ibrahim, S.A.; Ado, M.; Mehdi, G. Radiation damage effects in oxide dispersion strengthened steel alloys. In Proceedings of the International Conference on Nuclear Engineering, Tsukuba, Japan, 19–24 May 2019. [Google Scholar]
- Mustafa, A.M.; Li, Z.; Shao, L. Molecular Dynamics Simulations of Damage Cascades Creation in Oxide-Particle-Embedded Fe. In Proceedings of the 25th International Conference on Nuclear Engineering, Shanghai, China, 2–6 July 2017; Volume 5, pp. 1–5. [Google Scholar]
- Azeem, M.M.; Li, Z.; Wang, Q.; Amjad, Q.M.N.; Zubair, M.; Ahmed, O.M.H. Classical molecular dynamics study for defect sink behavior in oxide dispersed strengthened alloys. In Proceedings of the Proceedings of 2018 15th International Bhurban Conference on Applied Sciences and Technology, Islamabad, Pakistan, 9–13 January 2018; pp. 12–15. [Google Scholar]
- Talanov, M.V.; Talanov, V.M. Structural Diversity of Ordered Pyrochlores. Chem. Mater. 2021, 33, 2706–2725. [Google Scholar] [CrossRef]
- Connor, T.; Cheong, O.; Bornhake, T.; Shad, A.C.; Tesch, R.; Sun, M.; He, Z.; Bukayemsky, A.; Vinograd, V.L. Pyrochlore Compounds From Atomistic Simulations. Front. Chem. 2021, 9, 733321. [Google Scholar] [CrossRef]
- Ewing, R.C.; Weber, W.J.; Lian, J. Nuclear waste disposal-pyrochlore (A 2B 2O 7): Nuclear waste form for the immobilization of plutonium and “minor” actinides. J. Appl. Phys. 2004, 95, 5949–5971. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Wiberg, K.B. A Scheme for Strain Energy Minimization. Application to the Cycloalkanes. J. Am. Chem. Soc. 1965, 87, 1070–1078. [Google Scholar] [CrossRef]
- Kocevski, V.; Pilania, G.; Uberuaga, B.P. Modeling Disorder in Pyrochlores and Other Anion-Deficient Fluorite Structural Derivative Oxides. Front. Chem. 2021, 9, 712543. [Google Scholar] [CrossRef]
- Chakoumakos, B.C. Systematics of the pyrochlore structure type, ideal A2B2X6Y. J. Solid State Chem. 1984, 53, 120–129. [Google Scholar] [CrossRef]
- Sickafus, K.E.; Minervini, L.; Grimes, R.W.; Valdez, J.A.; Ishimaru, M.; Li, F.; McClellan, K.J.; Hartmann, T. Radiation tolerance of complex oxides. Science 2000, 289, 748–751. [Google Scholar] [CrossRef]
- Plimpton, S.; Hendrickson, B. A New Parallel Method for Molecular Dynamics Simulation of Macromolecular Systems. J. Comput. Chem. 1996, 17, 326–337. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Dholakia, M.; Chandra, S.; Jaya, S.M. A comparative study of topology and local disorder in Y2O3, Y2TiO5, and Y2Ti2O7 crystals Manan. J. Alloys Compd. 2018, 739, 1037–1047. [Google Scholar] [CrossRef]
- Minervini, L.; Zacate, M.O.; Grimes, R.W. Defect cluster formation in M2O3-doped CeO2. Solid State Ion. 1999, 116, 339–349. [Google Scholar] [CrossRef]
- Minervini, L.; Grimes, R.W.; Tabira, Y.; Withers, R.L.; Sickafus, K.E. The oxygen positional parameter in pyrochlores and its dependence on disorder. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 2002, 82, 123–135. [Google Scholar] [CrossRef]
- Balducci, G.; Kašpar, J.; Fornasiero, P.; Graziani, M.; Islam, M.S. Surface and reduction energetics of the CeO2-ZrO2 catalysts. J. Phys. Chem. B 1998, 102, 557–561. [Google Scholar] [CrossRef]
- Luty, B.A.; Davis, M.E.; Tironi, I.G.; Van Gunsteren, W.F. A comparison of particle-particle, particle-mesh and ewald methods for calculating electrostatic interactions in periodic molecular systems. Mol. Simul. 1994, 14, 11–20. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Biersack, J.P. The Stopping and Range of Ions in Matter BT—Treatise on Heavy-Ion Science: Volume 6: Astrophysics, Chemistry, and Condensed Matter; Bromley, D.A., Ed.; Springer: Boston, MA, USA, 1985; pp. 93–129. ISBN 978-1-4615-8103-1. [Google Scholar]
- Cooper, M.W.D.; Rushton, M.J.D.; Grimes, R.W. A many-body potential approach to modelling the thermomechanical properties of actinide oxides. J. Phys. Condens. Matter 2014, 26, 105401. [Google Scholar] [CrossRef] [PubMed]
- Ado, M.; Wang, Q.; Ibrahim, S.A.; Adede, S.O. Effect of radiation and substitution of Ce4+ at Zr site in Y4Zr3O12 using collision cascades: A molecular dynamics simulation study. J. Nucl. Sci. Technol. 2022, 60, 415–424. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Anupama, M.K.; Rudraswamy, B.; Dhananjaya, N. Influence of trivalent (Gd3+, Cr3+) ion substitution on the structural and magnetic properties of Ni0.4Zn0.6Cr0.5GdxFe1.5−xO4 ferrite nanoparticles. Int. J. Nanotechnol. 2017, 14, 867–874. [Google Scholar] [CrossRef]
- Nakamoto, R.; Xu, B.; Xu, C.; Xu, H.; Bellaiche, L. Properties of rare-earth iron garnets from first principles. Phys. Rev. B 2017, 95, 024434. [Google Scholar] [CrossRef]
- Patel, K.; Prosandeev, S.; Yang, Y.; Xu, B.; Íñiguez, J.; Bellaiche, L. Atomistic mechanism leading to complex antiferroelectric and incommensurate perovskites. Phys. Rev. B 2016, 94, 054107. [Google Scholar] [CrossRef]
- Lee, W.; Chen, S.Y.; Tseng, E.; Gloter, A.; Chen, C.L. Study of defect structure in ferromagnetic nanocrystalline CeO2: Effect of ionic radius. J. Phys. Chem. C 2016, 120, 14874–14882. [Google Scholar] [CrossRef]
- Martel, L.; Naji, M.; Popa, K.; Vigier, J.F.; Somers, J. Fingerprint of local disorder in long range ordered isometric pyrochlores. Sci. Rep. 2017, 7, 12269. [Google Scholar] [CrossRef] [PubMed]
- Anupama, M.K.; Rudraswamy, B. Effect of Gd3+-Cr3+ ion substitution on the structural, electrical and magnetic properties of Ni-Zn ferrite nanoparticles. IOP Conf. Ser. Mater. Sci. Eng. 2016, 149, 012194. [Google Scholar] [CrossRef]
- Dong, L.; Li, Y.; Devanathan, R.; Gao, F. Molecular dynamics simulation of the structural, elastic, and thermal properties of pyrochlores. RSC Adv. 2016, 6, 41410–41419. [Google Scholar] [CrossRef]
- Dong, L.; Setyawan, W.; Li, Y.; Devanathan, R.; Gao, F. Molecular dynamics simulation of low-energy recoil events in titanate pyrochlores. RSC Adv. 2017, 7, 35403–35410. [Google Scholar] [CrossRef]
- El-Atwani, O.; Li, N.; Li, M.; Devaraj, A.; Baldwin, J.K.S.; Schneider, M.M.; Sobieraj, D.; Wróbel, J.S.; Nguyen-Manh, D.; Maloy, S.A.; et al. Outstanding radiation resistance of tungsten-based high-entropy alloys. Sci. Adv. 2019, 5, eaav2002. [Google Scholar] [CrossRef] [PubMed]
- Pickering, E.J.; Carruthers, A.W.; Barron, P.J.; Middleburgh, S.C.; Armstrong, D.E.J.; Gandy, A.S. High-entropy alloys for advanced nuclear applications. Entropy 2021, 23, 98. [Google Scholar] [CrossRef]
- Mandal, B.P.; Bhattacharyya, K.; Zain, J.H.; Sudarsan, V.; Nigam, S.; Nayak, C.; Tyagi, A.K. Variation of structural disorder in Zr substituted Y2Sn2O7: Its impact on photocatalysis. J. Solid State Chem. 2021, 303, 122472. [Google Scholar] [CrossRef]
- Cai, L.; Arias, A.L.; Nino, J.C. The tolerance factors of the pyrochlore crystal structure. J. Mater. Chem. 2011, 21, 3611–3618. [Google Scholar] [CrossRef]
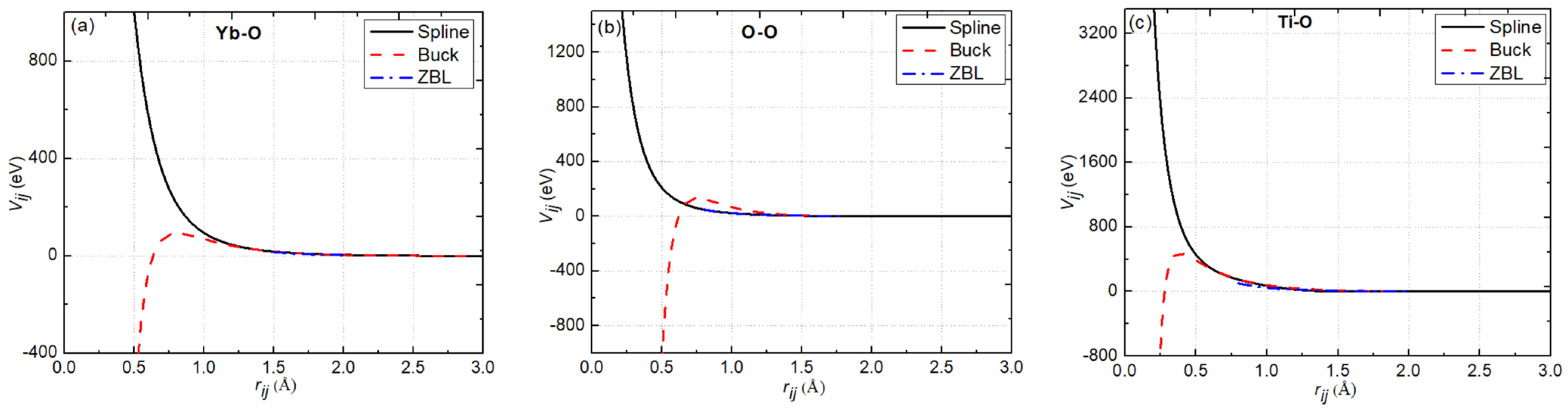


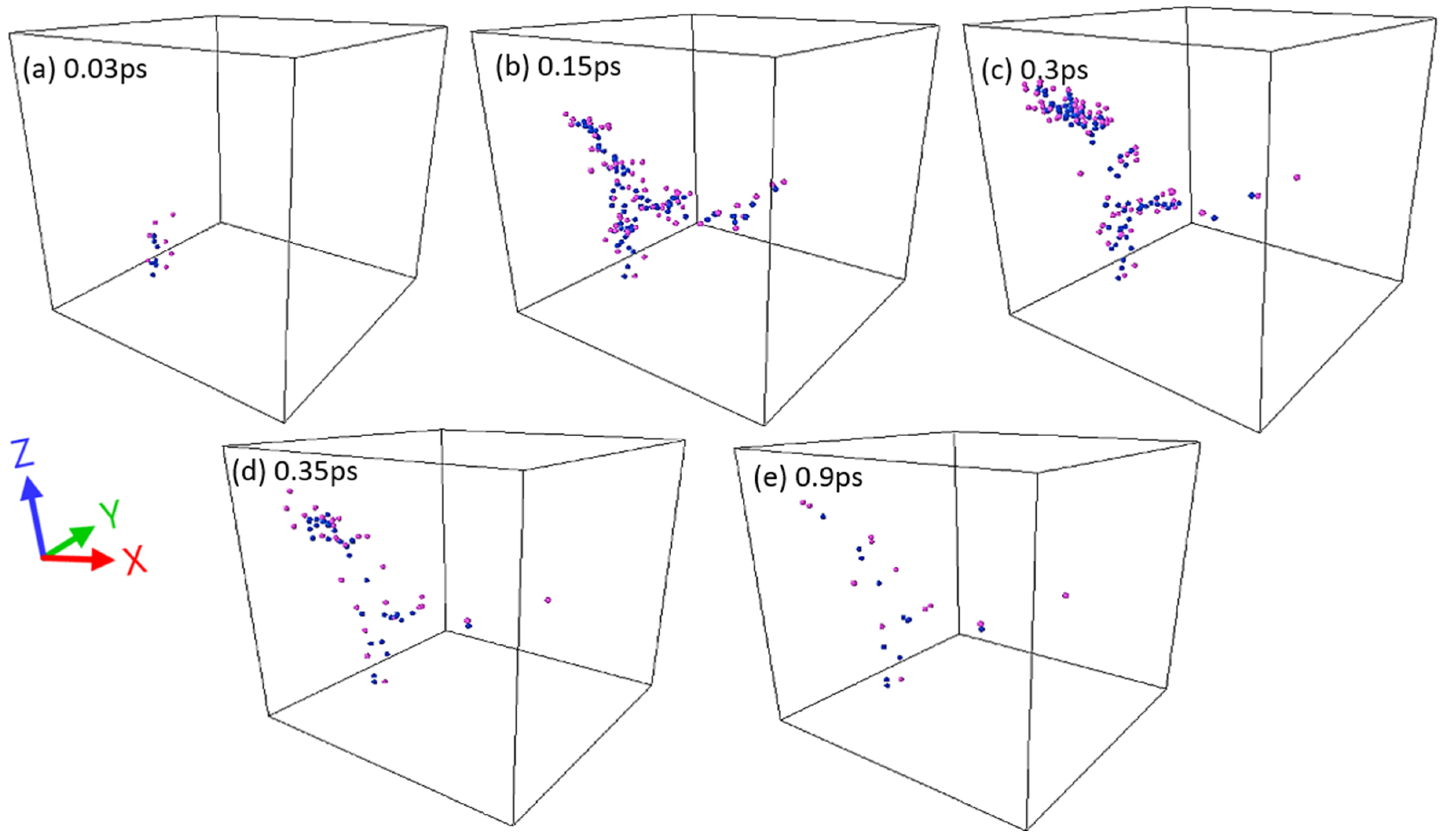


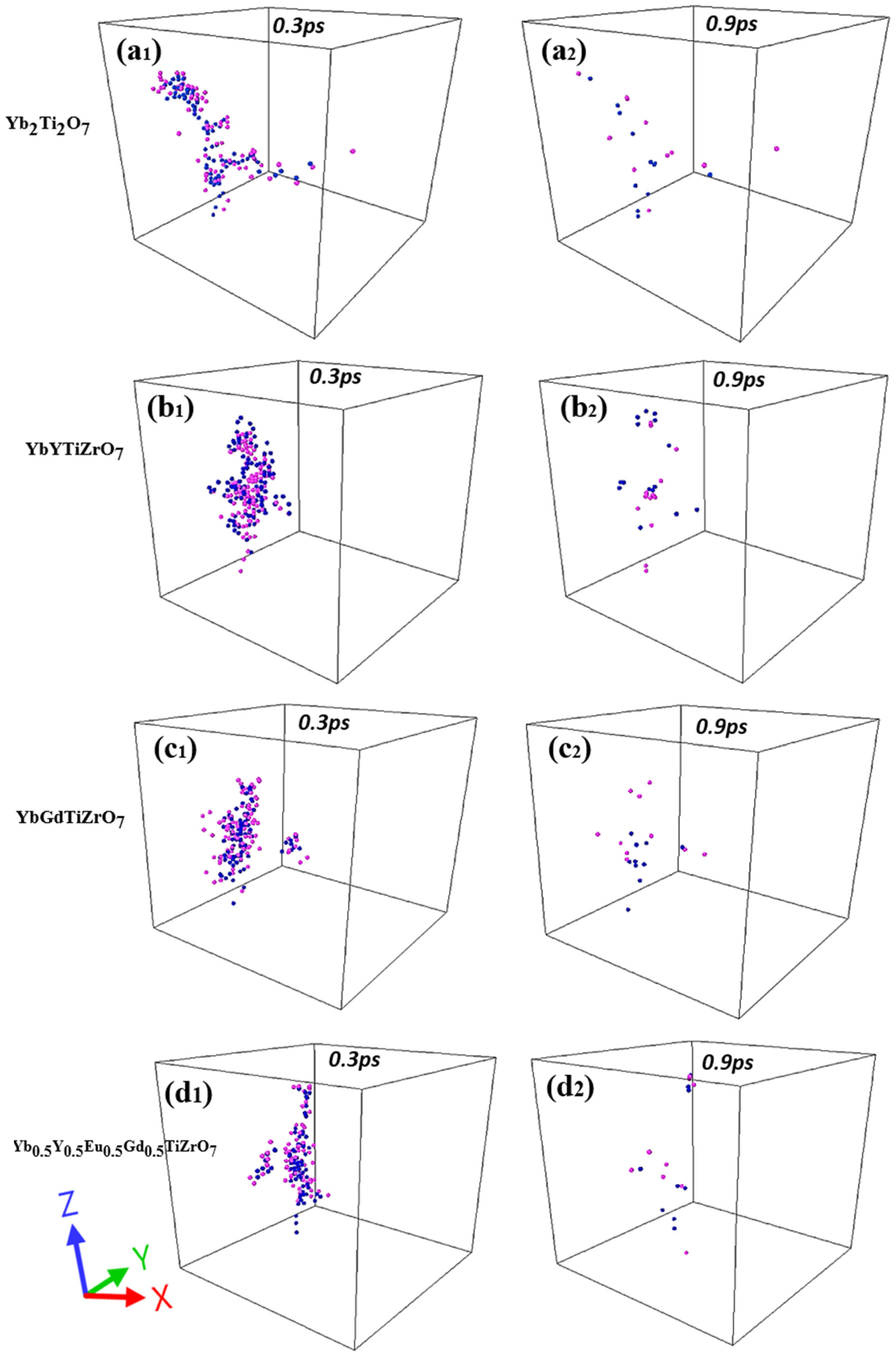
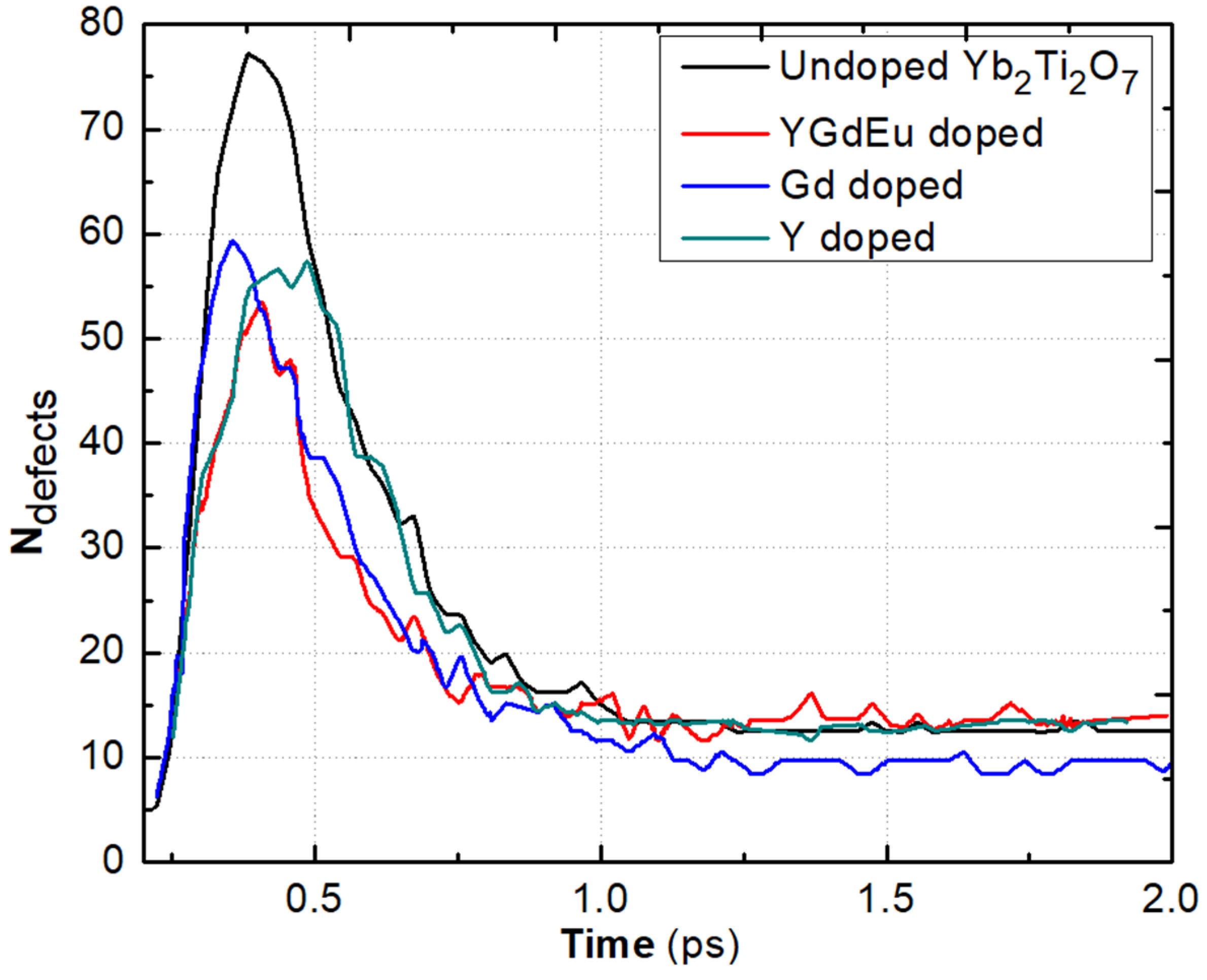
| Pair (s) | (eV) | (Å) | ) | (Å) | (Å) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Yb-O | 1649.80 | 0.3386 | 16.57 | 10.40 | −8.38 | 3.08 | −0.55 | 0.6 | 1.3 |
| Ti-O | 2131.40 | 0.3038 | 0.400 | 10.62 | −14.80 | −14.74 | −6.28 | 0.3 | 2.0 |
| O-O | 9547.96 | 0.2192 | 32.00 | 9.355 | −10.71 | 6.23 | −1.68 | 0.8 | 2.1 |
| Ion (s) | rionic (Å) | ao (Å) |
|---|---|---|
| 0.977, 0.861 [18], 1.032 [62] | 9.988, 10.291 [18], 10.011 [61] | |
| 0.985, 0.87 [18], 1.042 [62] | 10.007, 10.34 [18], 10.03 [63] | |
| 1.004, 0.89 [18], 1.004 [62] | 10.055, 10.35 [18], 10.069 [63] | |
| 1.019, 0.90 [18] | 10.056, 10.37 [18], 10.080 [61] | |
| 1.053, 1.107 [61] | 10.136, 8.34 [61], 10.171 [61] | |
| 1.066, 1.120 [62] | 10.159, 10.192 [63] | |
| 1.062, 1.079 [62] | 10.184, 10.211 [63] | |
| 1.109, 0.98 [18], 1.163 [62] | 10.231, 10.56 [18] | |
| 1.143, 1.196 [62], 1.14 [63] | 10.343, 10.65 [18], 10.6 [63] | |
| 1.164, 1.03 [18], 1.16 [64] | 10.324, 10.7026 [18] |
| Types of PKA | PKA Direction | Ed (eV) | Types of PKA | PKA Direction | Ed (eV) |
|---|---|---|---|---|---|
| Yb | [100] | 60 | Ti | [100] | 1182 |
| [110] | 60 | [110] | 1177 | ||
| [111] | 66 | [111] | 625 | ||
| Y | [100] | 146 | Zr | [100] | 430 |
| [110] | 146 | [110] | 431 | ||
| [111] | 174 | [111] | 426 | ||
| Gd | [100] | 93 | O | [100] | 1769 |
| [110] | 93 | [110] | 1521 | ||
| [111] | 84 | [111] | 343 | ||
| Eu | [100] | 85 | |||
| [110] | 85 | ||||
| [111] | 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azeem, M.M.; Wang, Q. Atomic Insights into the Structural Properties and Displacement Cascades in Ytterbium Titanate Pyrochlore (Yb2Ti2O7) and High-Entropy Pyrochlores. J. Compos. Sci. 2023, 7, 413. https://doi.org/10.3390/jcs7100413
Azeem MM, Wang Q. Atomic Insights into the Structural Properties and Displacement Cascades in Ytterbium Titanate Pyrochlore (Yb2Ti2O7) and High-Entropy Pyrochlores. Journal of Composites Science. 2023; 7(10):413. https://doi.org/10.3390/jcs7100413
Chicago/Turabian StyleAzeem, M. Mustafa, and Qingyu Wang. 2023. "Atomic Insights into the Structural Properties and Displacement Cascades in Ytterbium Titanate Pyrochlore (Yb2Ti2O7) and High-Entropy Pyrochlores" Journal of Composites Science 7, no. 10: 413. https://doi.org/10.3390/jcs7100413
APA StyleAzeem, M. M., & Wang, Q. (2023). Atomic Insights into the Structural Properties and Displacement Cascades in Ytterbium Titanate Pyrochlore (Yb2Ti2O7) and High-Entropy Pyrochlores. Journal of Composites Science, 7(10), 413. https://doi.org/10.3390/jcs7100413






