A Mathematical Approach for Sound Insulation Characteristics and Cost Optimization of Double-Layer Composite Structures
Abstract
1. Introduction
2. Sound Insulation Mechanism and Test Method of a Sound Insulation Structure
3. Influence of Different Schemes on Sound Insulation Structure Performance
4. Mathematical Model for Fast Calculation of Sound Transmission Loss of a Double-Layer Sound Insulation Structure and Accuracy Verification
4.1. Mathematical Model for the Rapid Calculation of Sound Insulation
4.2. Test of the Rapid Calculation Mathematical Model
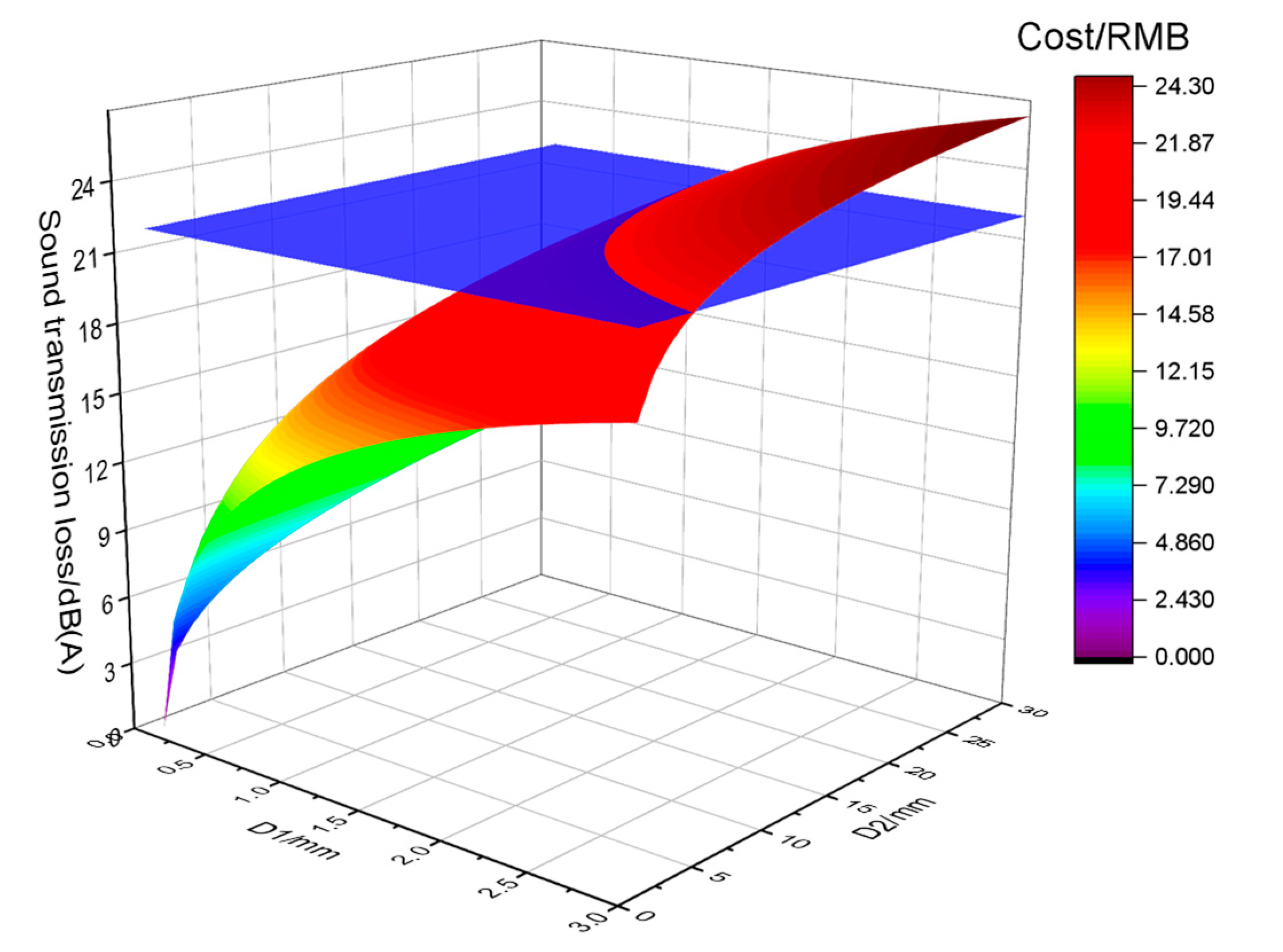
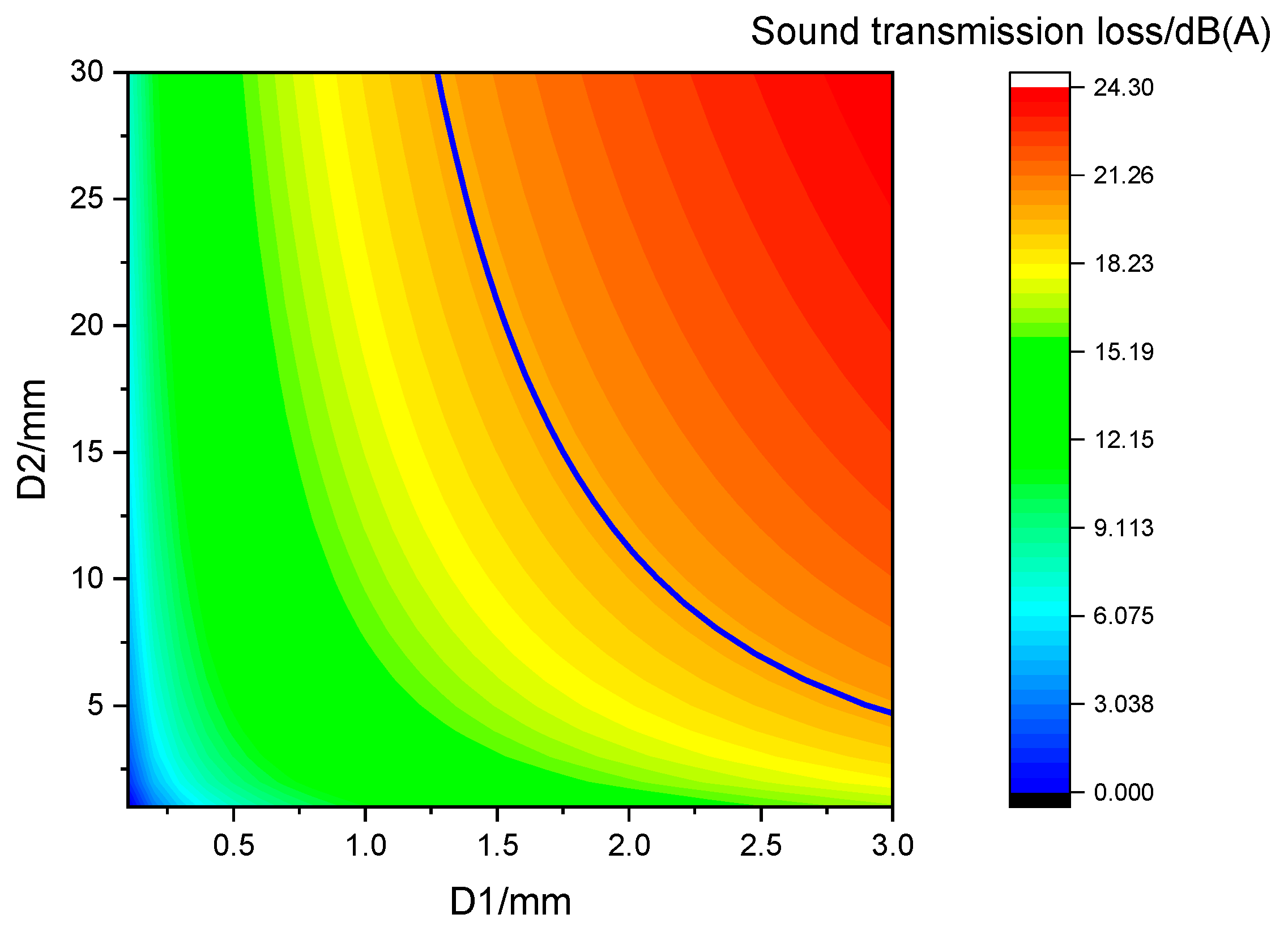
5. Optimal Cost Numerical Model of Double-Layer Sound Insulation Structures
5.1. Cost Calculation of Double-Layer Sound Insulation Structures
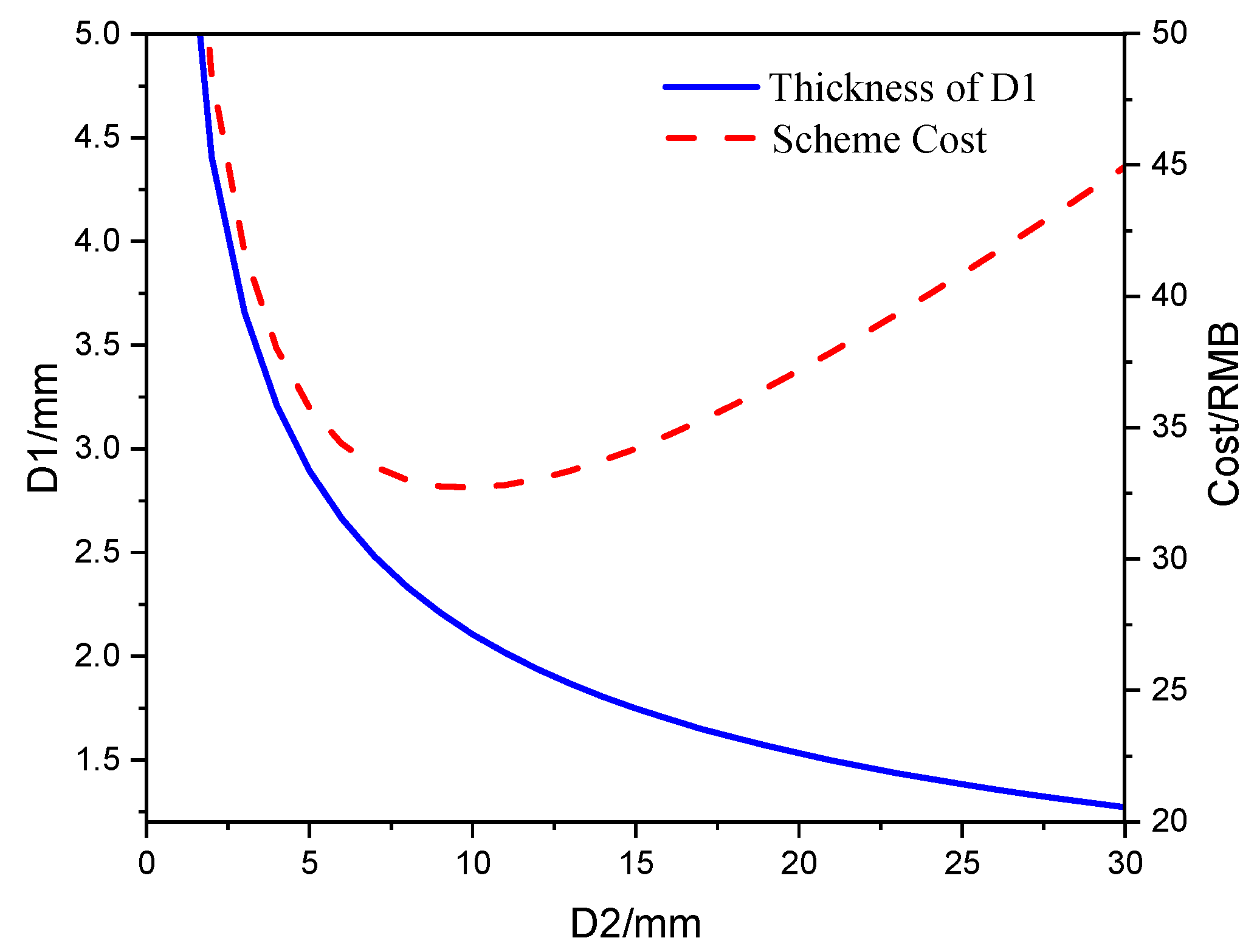
5.2. Optimal Cost Calculation Model of Double-Layer Sound Insulation Structures
6. Conclusions
- The sound transmission loss of the sound insulation structure composed of polyvinyl chloride and non-woven fibers with different thicknesses was obtained via the experimental method. The results showed that the noise reduction in the sound insulation structure increased with the increase in the polyvinyl chloride’s thickness; when the thickness of the non-woven fiber increased from 5 to 20 mm, the noise reduction in the sound insulation structure also increased.
- The undetermined coefficient in the calculation formula of the sound transmission loss of the double-layer sound insulation structure was calculated by the least square method, and the numerical model for the rapid calculation of the sound transmission loss of the double-layer sound insulation structure was obtained.
- The accuracy of the model was evaluated by the statistical determination coefficient, and the degree of coincidence of the model was 99.891%. The results proved the effectiveness of the numerical model for the rapid calculation of the sound transmission loss of the double-layer sound insulation structure obtained in this paper.
- Based on the experimental and mathematical methods, an optimal cost numerical model was established to quickly determine the optimal cost design for different schemes with the same effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| D1/mm | D2/mm | Cost/RMB |
|---|---|---|
| 6.059 | 1 | 64.970 |
| 4.408 | 2 | 48.605 |
| 3.660 | 3 | 41.759 |
| 3.207 | 4 | 38.034 |
| 2.895 | 5 | 35.791 |
| 2.662 | 6 | 34.389 |
| 2.481 | 7 | 33.521 |
| 2.333 | 8 | 33.015 |
| 2.210 | 9 | 32.770 |
| 2.106 | 10 | 32.719 |
| 2.016 | 11 | 32.818 |
| 1.937 | 12 | 33.036 |
| 1.867 | 13 | 33.349 |
| 1.805 | 14 | 33.740 |
| 1.749 | 15 | 34.197 |
| 1.697 | 16 | 34.709 |
| 1.651 | 17 | 35.267 |
| 1.608 | 18 | 35.866 |
| 1.569 | 19 | 36.501 |
| 1.532 | 20 | 37.165 |
| 1.498 | 21 | 37.857 |
| 1.467 | 22 | 38.574 |
| 1.437 | 23 | 39.311 |
| 1.409 | 24 | 40.068 |
| 1.383 | 25 | 40.842 |
| 1.358 | 26 | 41.632 |
| 1.335 | 27 | 42.436 |
| 1.313 | 28 | 43.253 |
| 1.292 | 29 | 44.081 |
| 1.272 | 30 | 44.921 |
References
- Zouani, A.; Hanim, S. Overview of noise and vibration in automotive engines. Int. J. Veh. Noise Vib. 2016, 12, 162–181. [Google Scholar] [CrossRef]
- Amares, S.; Sujatmika, E.; Hong, T.W.; Durairaj, R.; Hamid, H.S.H.B. A Review: Characteristics of Noise Absorption Material. J. Phys. Conf. Ser. 2017, 908, 012005. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, H.-M.; Zeng, X.-H.; Zhuang, Z. Theoretical and Experimental Study on the Transmission Loss of a Side Outlet Muffler. Shock. Vib. 2020, 2020, 6927574. [Google Scholar] [CrossRef]
- Wyrwal, J.; Pawelczyk, M.; Liu, L.; Rao, Z. Double-panel active noise reducing casing with noise source enclosed inside—Modelling and simulation study. Mech. Syst. Signal Process. 2020, 152, 107371. [Google Scholar] [CrossRef]
- He, Z.; Han, Y.; Chen, W.; Zhou, M.; Xing, Z. Noise control of a two-stage screw refrigeration compressor. Appl. Acoust. 2020, 167, 107383. [Google Scholar] [CrossRef]
- Dąbrowski, Z.; Dziurdź, J. Simultaneous Analysis of Noise and Vibration of Machines in Vibroacoustic Diagnostics. Arch. Acoust. 2016, 41, 783–789. [Google Scholar] [CrossRef]
- Berardi, U.; Iannace, G. Acoustic characterization of natural fibers for sound absorption applications. Build. Environ. 2015, 94, 840–852. [Google Scholar] [CrossRef]
- Yang, T.; Xiong, X.; Mishra, R.; Novák, J.; Militký, J. Sound absorption and compression properties of perpendicular-laid nonwovens. Text. Res. J. 2018, 89, 612–624. [Google Scholar] [CrossRef]
- Segura-Alcaraz, P.; Segura-Alcaraz, J.; Montava, I.; Bonet-Aracil, M. The effect of the combination of multiple woven fabric and nonwoven on acoustic absorption. J. Ind. Text. 2019, 50, 1262–1280. [Google Scholar] [CrossRef]
- Yang, T.; Hu, L.; Xiong, X.; Petrů, M.; Noman, M.T.; Mishra, R.; Militký, J. Sound Absorption Properties of Natural Fibers: A Review. Sustainability 2020, 12, 8477. [Google Scholar] [CrossRef]
- Rwawiire, S.; Tomkova, B.; Militky, J.; Hes, L.; Kale, B.M. Acoustic and thermal properties of a cellulose nonwoven natural fabric (barkcloth). Appl. Acoust. 2017, 116, 177–183. [Google Scholar] [CrossRef]
- Taban, E.; Tajpoor, A.; Faridan, M.; Samaei, S.E.; Beheshti, M.H. Acoustic Absorption Characterization and Prediction of Natural Coir Fibers. Acoust. Aust. 2019, 47, 67–77. [Google Scholar] [CrossRef]
- Soltani, P.; Norouzi, M. Prediction of the sound absorption behavior of nonwoven fabrics: Computational study and experimental validation. J. Sound Vib. 2020, 485, 115607. [Google Scholar] [CrossRef]
- Gokulkumar, S.; Thyla, P.; Prabhu, L.; Sathish, S. Measuring Methods of Acoustic Properties and Influence of Physical Parameters on Natural Fibers: A Review. J. Nat. Fibers 2019, 17, 1719–1738. [Google Scholar] [CrossRef]
- Zhang, L. Wave propagation characteristics and absorbed energy capability of the electrically doubly curved system rein-forced by nanocomposite on viscoelastic substrate. Mech. Based Des. Struct. Mach. 2021. [Google Scholar] [CrossRef]
- Sun, C.; Li, R.; Chen, Z.; Mei, Y.; Wang, X.; Li, C.; Liu, Y. Research on Vibration Suppression Method Based on Coaxial Stacking Measurement. Mathematics 2021, 9, 1438. [Google Scholar] [CrossRef]
- Gao, N.; Hou, H. Low frequency acoustic properties of a honeycomb-silicone rubber acoustic metamaterial. Mod. Phys. Lett. B 2017, 31, 1750118. [Google Scholar] [CrossRef]
- Gao, N.; Hou, H.; Mu, Y. Low frequency acoustic properties of bilayer membrane acoustic metamaterial with magnetic oscillator. Theor. Appl. Mech. Lett. 2017, 7, 252–257. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Asadijafari, M.H.; Talebitooti, R. Acoustic wave transmission characteristics of stiffened composite shell systems with double curvature. Compos. Struct. 2022, 292, 115688. [Google Scholar] [CrossRef]
- Seilsepour, H.; Zarastvand, M.; Talebitooti, R. Acoustic insulation characteristics of sandwich composite shell systems with double curvature: The effect of nature of viscoelastic core. J. Vib. Control. 2022, 29, 1076–1090. [Google Scholar] [CrossRef]
- Asadijafari, M.H.; Zarastvand, M.R.; Talebitooti, R. The effect of considering Pasternak elastic foundation on acoustic insulation of the finite doubly curved composite structures. Compos. Struct. 2021, 256, 113064. [Google Scholar] [CrossRef]
- Pollice, R.; Gomes, G.D.P.; Aldeghi, M.; Hickman, R.J.; Krenn, M.; Lavigne, C.; Lindner-D’Addario, M.; Nigam, A.; Ser, C.T.; Yao, Z.; et al. Data-Driven Strategies for Accelerated Materials Design. Acc. Chem. Res. 2021, 54, 849–860. [Google Scholar] [CrossRef]
- Carrara, P.; De Lorenzis, L.; Stainier, L.; Ortiz, M. Data-driven fracture mechanics. Comput. Methods Appl. Mech. Eng. 2020, 372, 113390. [Google Scholar] [CrossRef]
- Karapiperis, K.; Stainier, L.; Ortiz, M.; Andrade, J.E. Data-driven multiscale modeling in mechanics. J. Mech. Phys. Solids 2021, 147, 104239. [Google Scholar] [CrossRef]
- Salissou, Y.; Panneton, R. A general wave decomposition formula for the measurement of normal incidence sound transmission loss in impedance tube. J. Acoust. Soc. Am. 2009, 125, 2083–2090. [Google Scholar] [CrossRef]
- Su, J.; Zheng, L.; Deng, Z. Study on acoustic properties at normal incidence of three-multilayer composite made of glass wool, glue and polyurethane foam. Appl. Acoust. 2019, 156, 319–326. [Google Scholar] [CrossRef]
- Li, Z.; Chen, S.; Wu, Z.; Yang, L. An improved approach for normal-incidence sound transmission loss measurement using a four-microphone impedance tube. J. Vib. Control. 2020, 27, 332–342. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computing in dynamics. Int. J. Numer. Methods Eng. 2018, 113, 1697–1710. [Google Scholar] [CrossRef]
- Arridge, S.; Maass, P.; Öktem, O.; Schönlieb, C.B. Solving inverse problems using data-driven models. Acta Numer. 2019, 28, 1–174. [Google Scholar] [CrossRef]
- Li, X.; Yan, Z.; Liu, Z.; Zhuo, Z. Advanced structural material design based on simulation and data-driven method. Adv. Mech. 2021, 51, 82–105. [Google Scholar]
- Li, X.; Ning, S.; Liu, Z.; Yan, Z.; Luo, C.; Zhuang, Z. Designing phononic crystal with anticipated band gap through a deep learning based data-driven method. Comput. Methods Appl. Mech. Eng. 2019, 361, 112737. [Google Scholar] [CrossRef]
- Malkiel, I.; Mrejen, M.; Nagler, A.; Arieli, U.; Wolf, L.; Suchowski, H. Deep learning for the design of nano-photonic structures. In Proceedings of the 2018 IEEE International Conference on Computational Photography (ICCP), Pittsburgh, PA, USA, 4–6 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–14. [Google Scholar]
- Li, X.; Liu, Z.; Cui, S.; Luo, C.; Li, C.; Zhuang, Z. Predicting the effective mechanical property of heterogeneous materials by image based modeling and deep learning. Comput. Methods Appl. Mech. Eng. 2019, 347, 735–753. [Google Scholar] [CrossRef]
- Luo, C.; Ning, S.; Liu, Z.; Zhuang, Z. Interactive inverse design of layered phononic crystals based on reinforcement learning. Extrem. Mech. Lett. 2020, 36, 100651. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L. Physics-informed neural networks: A deep learning framework for solving the vibrational problems. Adv. Nano Res. 2021, 11, 495–519. [Google Scholar]
- Zeng, X.; Zhang, L.; Yu, Y.; Shi, M.; Zhou, J. The stiffness and damping characteristics of a dual-chamber air spring device applied to motion suppression of marine structures. Appl. Sci. 2016, 6, 74. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, L.; Yu, F.; Zhou, J. The effect of an orifice plate with different orifice numbers and shapes on the damping characteristics of a dual-chamber air spring. J. Vibroengineering 2017, 19, 2375–2389. [Google Scholar] [CrossRef]
- Renaud, O.; Victoria-Feser, M.P. A robust coefficient of determination for regression. J. Stat. Plan. Inference 2010, 140, 1852–1862. [Google Scholar] [CrossRef]
- Dougherty, E.R.; Kim, S.; Chen, Y. Coefficient of determination in nonlinear signal processing. Signal Process. 2000, 80, 2219–2235. [Google Scholar] [CrossRef]






| Polyvinyl Chloride Thickness/mm | Non-Woven Fiber Thickness/mm | ||||
|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 20 | |
| 0 | a | ||||
| 1.5 | b | ||||
| 2 | c | e | g | ||
| 3 | d | f | h | i | |
| Scheme No. | Noise Value/dB (A) | Sound Insulation/dB (A) |
|---|---|---|
| a | 73.75 | 0 |
| b | 55.03 | 18.72 |
| c | 53.65 | 20.1 |
| d | 51.58 | 22.17 |
| e | 51.88 | 21.87 |
| f | 49.9 | 23.85 |
| g | 51.1 | 22.65 |
| h | 49.12 | 24.63 |
| i | 48.49 | 25.26 |
| No. | Name | Price |
|---|---|---|
| 1 | Polyvinyl Chloride | 10.55 |
| 2 | Non-Woven Fiber | 1.05 |
| D1/mm | D2/mm | Cost/RMB |
|---|---|---|
| 2.106 | 10 | 32.719 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, H.; Chen, Q.; Long, D. A Mathematical Approach for Sound Insulation Characteristics and Cost Optimization of Double-Layer Composite Structures. J. Compos. Sci. 2023, 7, 110. https://doi.org/10.3390/jcs7030110
Zhang L, Zhang H, Chen Q, Long D. A Mathematical Approach for Sound Insulation Characteristics and Cost Optimization of Double-Layer Composite Structures. Journal of Composites Science. 2023; 7(3):110. https://doi.org/10.3390/jcs7030110
Chicago/Turabian StyleZhang, Liang, Huawei Zhang, Qiyu Chen, and Danfeng Long. 2023. "A Mathematical Approach for Sound Insulation Characteristics and Cost Optimization of Double-Layer Composite Structures" Journal of Composites Science 7, no. 3: 110. https://doi.org/10.3390/jcs7030110
APA StyleZhang, L., Zhang, H., Chen, Q., & Long, D. (2023). A Mathematical Approach for Sound Insulation Characteristics and Cost Optimization of Double-Layer Composite Structures. Journal of Composites Science, 7(3), 110. https://doi.org/10.3390/jcs7030110






