Wear Behavior of AZ61 Matrix Hybrid Composite Fabricated via Friction Stir Consolidation: A Combined RSM Box–Behnken and Genetic Algorithm Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. RSM Box–Behnken Experimental Design
3. Pin-On-Disc Wear Testing
4. Genetic Algorithm Optimization
5. Results
5.1. Wear Rate Parametric Optimization Using RSM Box–Behnken Design
5.2. Analysis of Variance
5.3. Mathematical Model
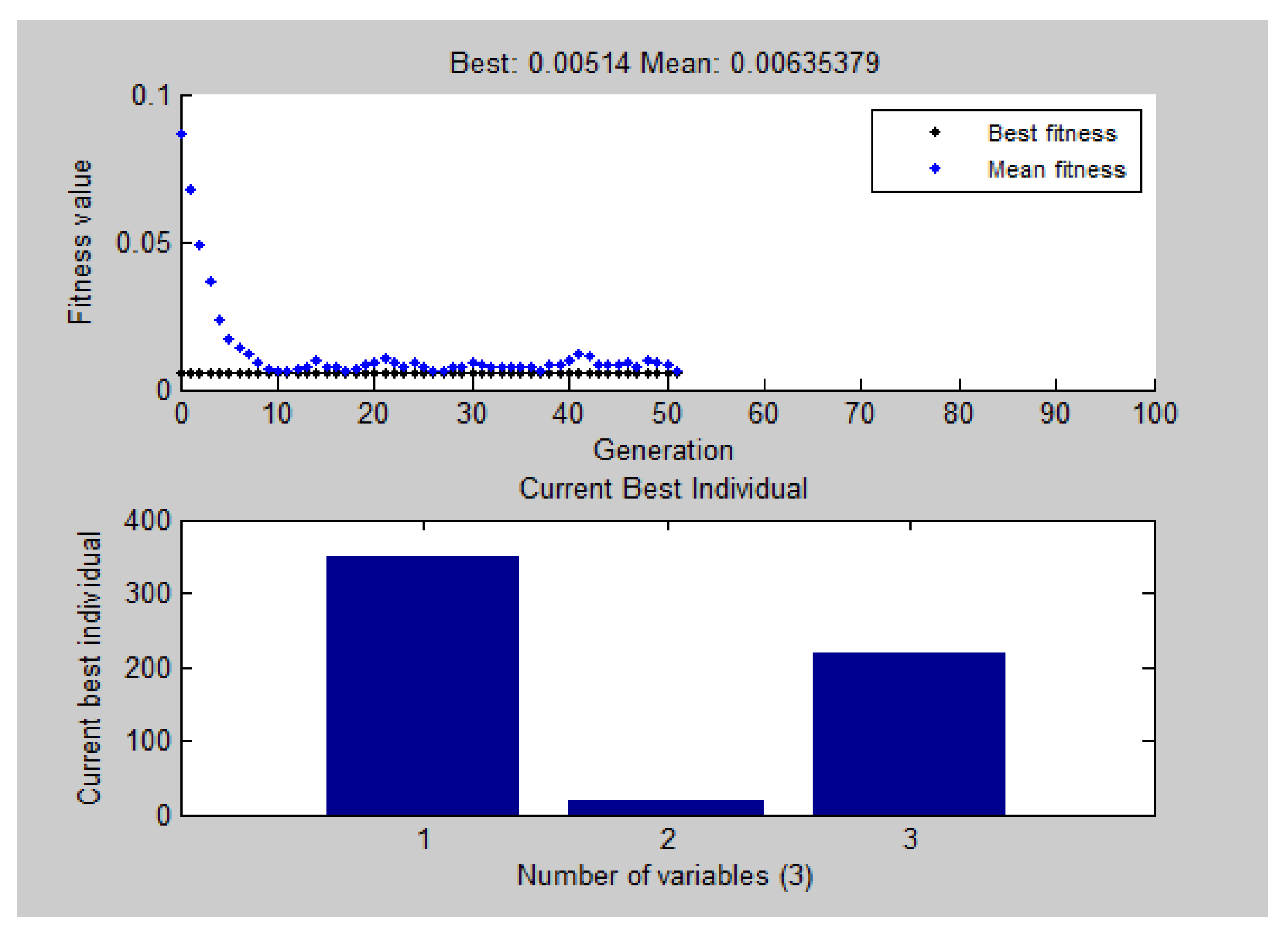
5.4. Parametric Optimization Using Genetic Algorithm
5.5. Verification Experiment for RSM and GA
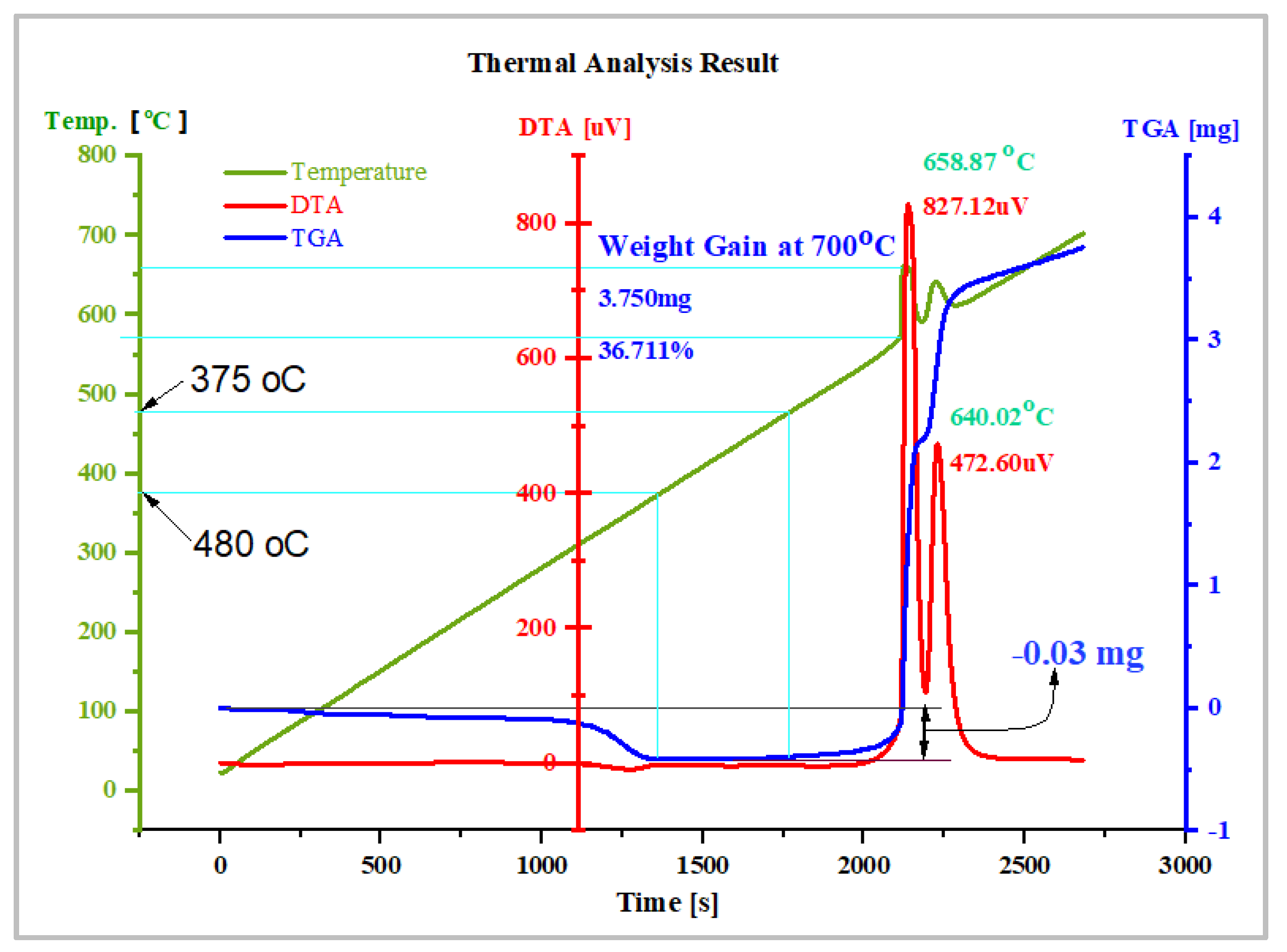
5.6. Thermogravimetric Analysis of Optimized Composite
5.7. SEM Metallographic Structure of Metal Matrix Hybrid Composite
5.8. SEM Analysis of Worn-Out Optimum Sample Predicted by GA and RSM Box–Behnken
6. Conclusions
- Using RSM optimization, the optimal wear rate of 0.008 mg/m was achieved with the following parameter combination: a sliding distance of 350 m, a sliding speed of 240 rpm and a load of 20 N. These findings demonstrate that RSM optimization effectively reduces wear and improves the wear resistance of the metal matrix hybrid composite. However, the GA optimization outperformed the RSM, achieving a minimum wear rate of 0.00514 mg/m. The optimized parameter combination for the GA was identical to that of the RSM, with a sliding distance of 350 m, a sliding speed of 220 rpm and a load of 20 N. This suggests that GA optimization further enhanced the wear resistance of the composite, surpassing the optimization achieved by RSM.
- In summary, this research study demonstrates the effectiveness of both RSM and GA techniques in optimizing the wear behavior of the metal matrix hybrid composite fabricated via the friction stir consolidation process. While RSM yielded significant improvements in the wear rate, GA optimization further reduced the wear rate, achieving a lower value. These findings highlight the potential of these optimization methods to enhance the wear resistance of metal matrix hybrid composites. Likewise, thermogravimetric results showed that, from the temperature 375 °C to 480 °C, the MMHC showed thermal stability with no weight loss or gain.
- Future research can be applied to the study of microstructural changes and mechanisms responsible for the improved wear behavior observed with RSM and GA optimization. Additionally, long-term performance and durability studies should be conducted to evaluate the practical applicability of the optimized composite materials in real-world scenarios.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, A.; Vichare, O.; Debnath, K.; Paswan, M. Fabrication methods of metal matrix composites (MMCs). Mater. Today Proc. 2020, 46, 6840–6846. [Google Scholar] [CrossRef]
- Manjunatha, L.; Yunus, M.; Alsoufi, M.; Dinesh, P. Development and Comparative Studies of Aluminum-Based Carbon Nano Tube Metal Matrix Composites using Powder Metallurgy and Stir Casting Technology. Int. J. Sci. Eng. Res. 2017, 8, 521–526. [Google Scholar]
- Sankhla, A.M.; Patel, K.M.; Makhesana, M.A.; Giasin, K.; Pimenov, D.Y.; Wojciechowski, S.; Khanna, N. Effect of mixing method and particle size on hardness and compressive strength of aluminium based metal matrix composite prepared through powder metallurgy route. J. Mater. Res. Technol. 2022, 18, 282–292. [Google Scholar] [CrossRef]
- Annigeri, U.K.; Veeresh Kumar, G.B. Method of stir casting of Aluminum metal matrix Composites: A review. Mater. Today Proc. 2017, 4, 1140–1146. [Google Scholar] [CrossRef]
- Shivalingaiah, K.; Nagarajaiah, V.; Selvan, C.P.; Kariappa, S.T.; Chandrashekarappa, N.G.; Lakshmikanthan, A.; Chandrashekarappa, M.P.G.; Linul, E. Stir Casting Process Analysis and Optimization for Better Properties in Al-MWCNT-GR-Based Hybrid Composites. Metals 2022, 12, 1297. [Google Scholar] [CrossRef]
- Lai, S.; Chung, D.D.L. Consumption of S i c whiskers by the AI-Sic reaction in aluminium-matrix SiC whisker composites. J. Mater. Chem. 1996, 6, 469–477. [Google Scholar] [CrossRef]
- Swamy, P.K.; Mylaraiah, S.; Gowdru Chandrashekarappa, M.P.; Lakshmikanthan, A.; Pimenov, D.Y.; Giasin, K.; Krishna, M. Corrosion behaviour of high-strength Al 7005 alloy and its composites reinforced with industrial waste-based fly ash and glass fibre: Comparison of stir cast and extrusion conditions. Materials 2021, 14, 3929. [Google Scholar] [CrossRef]
- Krishnaraj, V.; Prabukarthi, A.; Ramanathan, A.; Elanghovan, N.; Kumar, M.S.; Zitoune, R.; Davim, J.P. Optimization of machining parameters at high speed drilling of carbon fiber reinforced plastic (CFRP) laminates. Compos. Part B Eng. 2012, 43, 1791–1799. [Google Scholar] [CrossRef]
- Zitoune, R.; El Mansori, M.; Krishnaraj, V. Tribo-functional design of double cone drill implications in tool wear during drilling of copper mesh/CFRP/woven ply. Wear 2013, 302, 1560–1567. [Google Scholar] [CrossRef]
- Abd-Elwahed, M.S.; Ibrahim, A.F.; Reda, M.M. Effects of ZrO2 nanoparticle content on microstructure and wear behavior of titanium matrix composite. J. Mater. Res. Technol. 2020, 9, 8528–8534. [Google Scholar] [CrossRef]
- Yilmaz, O.; Buytoz, S. Abrasive wear of Al2O3-reinforced aluminium-based MMCs. Compos. Sci. Technol. 2001, 61, 2381–2392. [Google Scholar] [CrossRef]
- Sivanesh Prabhu, M.; Elaya Perumal, A.; Arulvel, S.; Franklin Issac, R. Friction and wear measurements of friction stir processed aluminium alloy 6082/CaCO3 composite. Meas. J. Int. Meas. Confed. 2019, 142, 10–20. [Google Scholar] [CrossRef]
- Cardoso-jaime, V.; Broderick, N.A.; Maya-maldonado, K. Metal ions in insect reproduction: A crosstalk between reproductive physiology and immunity. Curr. Opin. Insect Sci. 2022, 52, 100924. [Google Scholar] [CrossRef]
- Sheelwant, A.; Jadhav, P.M.; Narala, S.K.R. ANN-GA based parametric optimization of Al-TiB2 metal matrix composite material processing technique. Mater. Today Commun. 2021, 27, 102444. [Google Scholar] [CrossRef]
- Cao, X.; Li, Z.; Zhou, X.; Luo, Z.; Duan, J. Modeling and optimization of resistance spot welded aluminum to Al-Si coated boron steel using response surface methodology and genetic algorithm. Meas. J. Int. Meas. Confed. 2021, 171, 108766. [Google Scholar] [CrossRef]
- Panwar, V.; Kumar Sharma, D.; Pradeep Kumar, K.V.; Jain, A.; Thakar, C. Experimental investigations and optimization of surface roughness in turning of en 36 alloy steel using response surface methodology and genetic algorithm. Mater. Today Proc. 2020, 46, 6474–6481. [Google Scholar] [CrossRef]
- Fan, M.; Li, T.; Hu, J.; Cao, R.; Wei, X.; Shi, X.; Ruan, W. Artificial neural network modeling and genetic algorithm optimization for cadmium removal from aqueous solutions by reduced graphene oxide-supported nanoscale zero-valent iron (nZVI/rGO) composites. Materials 2017, 10, 544. [Google Scholar] [CrossRef]
- Álvarez, M.J.; Ilzarbe, L.; Viles, E.; Tanco, M. The Use of Genetic Algorithms in Response Surface Methodology. Qual. Technol. Quant. Manag. 2009, 6, 295–307. [Google Scholar] [CrossRef]
- Omrani, E.; Moghadam, A.D.; Menezes, P.L.; Rohatgi, P.K. Influences of graphite reinforcement on the tribological properties of self-lubricating aluminum matrix composites for green tribology, sustainability, and energy efficiency—A review. Int. J. Adv. Manuf. Technol. 2016, 83, 325–346. [Google Scholar] [CrossRef]
- Sanjay, M.R.; Madhu, P.; Jawaid, M.; Senthamaraikannan, P.; Senthil, S.; Pradeep, S. Characterization and Properties of Natural Fiber Polymer Composites: A Comprehensive Review; Elsevier: Amsterdam, The Netherlands, 2018; Volume 172, ISBN 9198944711. [Google Scholar]
- Kumar, B.S.P.; Shobha, K.R.; Singh, M.K.; Rinawa, M.L.; Madhavarao, S.; Wadhawa, G.C.; Alrebdi, T.A.; Christopher, D. Optimization and Wear Properties for the Composites of Metal Matrix AA8011/Boron Nitride Using Taguchi Method. J. Nanomater. 2022, 2022, 6957545. [Google Scholar] [CrossRef]
- Shanmugavel, R.; Sundaresan, T.K.; Marimuthu, U.; Manickaraj, P. Process Optimization and Wear Behavior of Red Mud Reinforced Aluminum Composites. Adv. Tribol. 2016, 2016, 9082593. [Google Scholar] [CrossRef]
- Morampudi, P.; Venkata Ramana, V.S.N.; Vikas, K.S.; Rahul; Prasad, C. Enhancing wear properties of Al6061 metal-matrix composites by reinforcement of ZrB2 nano particles. Mater. Today Proc. 2022, 59, A45–A51. [Google Scholar] [CrossRef]
- Jojith, R.; Radhika, N.; Govindaraju, M. Reciprocating Wear Behavioural Analysis of Heat-treated Aluminium ZrO2/Al7Si0.3Mg Functionally Graded Composite Through Taguchi’s Optimization Method. Silicon 2022, 14, 11337–11354. [Google Scholar] [CrossRef]
- Seeman, M.; Ganesan, G.; Karthikeyan, R.; Velayudham, A. Study on tool wear and surface roughness in machining of particulate aluminum metal matrix composite-response surface methodology approach. Int. J. Adv. Manuf. Technol. 2010, 48, 613–624. [Google Scholar] [CrossRef]
- Stojanović, B.; Gajević, S.; Kostić, N.; Miladinović, S.; Vencl, A. Optimization of parameters that affect wear of A356/Al2O3 nanocomposites using RSM, ANN, GA and PSO methods. Ind. Lubr. Tribol. 2022, 74, 350–359. [Google Scholar] [CrossRef]
- Umanath, K.; Palanikumar, K.; Sankaradass, V.; Uma, K. Materials Today: Proceedings Optimization of wear properties on AA7075/Sic/Mos2 hybrid metal matrix composite by response surface methodology. Mater. Today Proc. 2021, 46, 4019–4024. [Google Scholar] [CrossRef]
- Uthayakumar, M.; Kumaran, S.T.; Aravindan, S. Dry sliding friction and wear studies of fly ash reinforced AA-6351 metal matrix composites. Adv. Tribol. 2013, 2013, 365602. [Google Scholar] [CrossRef]
- Baradeswaran, A.; Elayaperumal, A.; Franklin Issac, R. A statistical analysis of optimization of wear behaviour of Al- Al2O3 composites using taguchi technique. Procedia Eng. 2013, 64, 973–982. [Google Scholar] [CrossRef]
- Gangwar, S.; Sharma, S.; Pathak, V.K. Preliminary Evaluation and Wear Properties Optimization of Boron Carbide and Molybdenum Disulphide Reinforced Copper Metal Matrix Composite Using Adaptive Neuro-fuzzy Inference System. J. Bio- Tribo-Corrosion 2021, 7, 1–19. [Google Scholar] [CrossRef]
- Das, A.; Sarkar, S.; Karanjai, M.; Sutradhar, G. RSM Based Study on the Influence of Sintering Temperature on MRR for Titanium Powder Metallurgy Products using Box-Behnken Design. Mater. Today Proc. 2018, 5, 6509–6517. [Google Scholar] [CrossRef]
- Radhika, N.; Sai Charan, K. Experimental Analysis on Three Body Abrasive Wear Behaviour of Stir Cast Al LM 25/TiC Metal Matrix Composite. Trans. Indian Inst. Met. 2017, 70, 2233–2240. [Google Scholar] [CrossRef]
- Kalhapure, V.A.; Khairnar, H.P. Taguchi method optimization of operating parameters for automotive disc brake pad wear. Appl. Eng. Lett. 2021, 6, 47–53. [Google Scholar] [CrossRef]
- Nasrollahzadeh, M.; Atarod, M.; Sajjadi, M.; Sajadi, S.M.; Issaabadi, Z. Plant-Mediated Green Synthesis of Nanostructures: Mechanisms, Characterization, and Applications, 1st ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2019; Volume 28, ISBN 9780128135860. [Google Scholar]
- Lal, S.; Kumar, S.; Khan, Z.A. Microstructure evaluation, thermal and mechanical characterization of hybrid metal matrix composite. IEEE J. Sel. Top. Quantum Electron. 2018, 25, 1187–1196. [Google Scholar] [CrossRef]
- Ashebir, D.A.; Mengesha, G.A.; Sinha, D.K. The Role of Tetra Hybrid Reinforcements on the Behavior of Aluminum Metal Matrix Composites. J. Nanomater. 2022, 2022, 1988293. [Google Scholar] [CrossRef]
- Kefyalew Abebe, S.; Sinha, D.K.; Beri Tufa, H.; Mengesha, G.A. Physical and mechanical behavior of aluminum-magnesium alloy matrix hybrid composite fabricated through friction stir consolidation process. Adv. Mech. Eng. 2023, 15, 16878132231180013. [Google Scholar] [CrossRef]
- Jojith, R.; Radhika, N. Reciprocal dry sliding wear of SiCp/Al–7Si-0.3 Mg functionally graded composites: Influence of T6 treatment and process parameters. Ceram. Int. 2021, 47, 30459–30470. [Google Scholar] [CrossRef]
- Kumar, R.; Deshpande, R.G.; Gopinath, B.; Harti, J.; Nagaral, M.; Auradi, V. Mechanical Fractography and Worn Surface Analysis of Nanographite and ZrO2-Reinforced Al7075 Alloy Aerospace Metal Composites. J. Fail. Anal. Prev. 2021, 21, 525–536. [Google Scholar] [CrossRef]
- Ram Kumar, S.; Gowtham, S.; Radhika, N. Fabrication of Cu-Sn/SiC Metal Matrix Composites and Investigation of its Mechanical and Dry Sliding Wear Properties. Mater. Today Proc. 2018, 5, 12757–12771. [Google Scholar] [CrossRef]
- Alpas, A.T.; Bhattacharya, S.; Hutchings, I.M. Wear of Particulate Metal Matrix Composites; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; Volume 4, ISBN 9780081005330. [Google Scholar]







| Compositions | Al | Zn | Mn | Ni | Cu | Fe | Si | Pb | Ca | Sn |
|---|---|---|---|---|---|---|---|---|---|---|
| Weight % | 6.4 | 0.74 | 0.35 | 0.0012 | 0.0029 | 0.001 | 0.015 | 0.001 | 0.001 | <0.001 |
| Factors | ||||
|---|---|---|---|---|
| Speed [rpm] | Load [N] | Thickness [mm] | Time [min.] | Composition [%wt] |
| 800 | 500 | 12 | 6 | 15 |
| Factors | Coded | Unit | Level | Level | level |
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| Load | X2 | N | 20 | 30 | 40 |
| Sliding Speed | X3 | Rpm | 220 | 240 | 260 |
| Sliding Distance | X1 | m | 350 | 500 | 650 |
| Run | Coded Factors | Actual Factors | ||||
|---|---|---|---|---|---|---|
| X1 | X2 | X3 | Load | Sliding Speed | Sliding Distance | |
| 1 | −1 | −1 | 0 | 20 | 220 | 500 |
| 2 | 0 | −1 | 1 | 30 | 220 | 650 |
| 3 | 1 | −1 | 0 | 40 | 220 | 500 |
| 4 | 0 | 0 | 0 | 30 | 240 | 500 |
| 5 | −1 | 0 | −1 | 20 | 240 | 350 |
| 6 | 0 | 0 | 0 | 30 | 240 | 500 |
| 7 | 1 | 0 | 1 | 40 | 240 | 650 |
| 8 | 1 | 1 | 0 | 40 | 260 | 500 |
| 9 | 0 | −1 | −1 | 30 | 220 | 350 |
| 10 | 0 | 1 | 1 | 30 | 260 | 650 |
| 11 | 1 | 0 | −1 | 40 | 240 | 350 |
| 12 | 0 | 0 | 0 | 30 | 240 | 500 |
| 13 | 0 | 1 | −1 | 30 | 260 | 350 |
| 14 | −1 | 1 | 0 | 20 | 260 | 500 |
| 15 | −1 | 0 | 1 | 20 | 240 | 650 |
| Run | Coded Factors | Actual Factors | Responses | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | Load | Sliding Speed | Sliding Distance | Weight before Test (g) | Weight after Test (g) | Weight Loss (g) | Conversion into mg | Wear Rate (mg/m) | |
| 1 | −1 | −1 | 0 | 20 | 220 | 500 | 0.6428 | 0.6344 | 0.0084 | 8.4 | 0.0450 ± 0.0002 |
| 2 | 0 | −1 | 1 | 30 | 220 | 650 | 0.6428 | 0.5873 | 0.0555 | 55.5 | 0.0854 ± 0.0004 |
| 3 | 1 | −1 | 0 | 40 | 220 | 500 | 0.6427 | 0.5774 | 0.0653 | 65.3 | 0.1310 ± 0.0003 |
| 4 | 0 | 0 | 0 | 30 | 240 | 500 | 0.6427 | 0.59465 | 0.0661 | 48.4 | 0.0961 ± 0.0005 |
| 5 | −1 | 0 | −1 | 20 | 240 | 350 | 0.6428 | 0.6401 | 0.0027 | 2.7 | 0.0080 ± 0.0004 |
| 6 | 0 | 0 | 0 | 30 | 240 | 500 | 0.6427 | 0.6022 | 0.0405 | 40.5 | 0.0830 ± 0.0005 |
| 7 | 1 | 0 | 1 | 40 | 240 | 650 | 0.6429 | 0.5454 | 0.0975 | 97.5 | 0.1500 ± 0.0003 |
| 8 | 1 | 1 | 0 | 40 | 260 | 500 | 0.6429 | 0.5524 | 0.0905 | 90.5 | 0.1750 ± 0.0007 |
| 9 | 0 | −1 | −1 | 30 | 220 | 350 | 0.6428 | 0.625 | 0.0178 | 17.8 | 0.0480 ± 0.0005 |
| 10 | 0 | 1 | 1 | 30 | 260 | 650 | 0.6427 | 0.5623 | 0.0804 | 80.4 | 0.1240 ± 0.0005 |
| 11 | 1 | 0 | −1 | 40 | 240 | 350 | 0.6428 | 0.5864 | 0.0546 | 56.4 | 0.1610 ± 0.0006 |
| 12 | 0 | 0 | 0 | 30 | 240 | 500 | 0.6427 | 0.5942 | 0.0665 | 48.5 | 0.0970 ± 0.0005 |
| 13 | 0 | 1 | −1 | 30 | 260 | 350 | 0.6427 | 0.6280 | 0.0427 | 14.7 | 0.0510 ± 0.00025 |
| 14 | −1 | 1 | 0 | 20 | 260 | 500 | 0.6428 | 0.6094 | 0.0334 | 33.4 | 0.0668 ± 0.0004 |
| 15 | −1 | 0 | 1 | 20 | 240 | 650 | 0.6428 | 0.6024 | 0.0404 | 40.4 | 0.0623 ± 0.0005 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 0.031095 | 0.003455 | 16.79 | 0.003 |
| Linear | 3 | 0.028037 | 0.009346 | 45.41 | 0.000 |
| Load | 1 | 0.023642 | 0.023642 | 114.87 | 0.000 |
| Speed | 1 | 0.001442 | 0.001442 | 7.01 | 0.046 |
| Distance | 1 | 0.002953 | 0.002953 | 14.35 | 0.013 |
| Square | 3 | 0.001551 | 0.000517 | 2.51 | 0.173 |
| Load X Oad | 1 | 0.000867 | 0.000867 | 4.21 | 0.095 |
| Speed X Speed | 1 | 0.000031 | 0.000031 | 0.15 | 0.713 |
| Distance X Distance | 1 | 0.000534 | 0.000534 | 2.60 | 0.168 |
| 2-Way Interaction | 3 | 0.001506 | 0.000502 | 2.44 | 0.180 |
| Load X Speed | 1 | 0.000123 | 0.000123 | 0.60 | 0.474 |
| Load X Distance | 1 | 0.001066 | 0.001066 | 5.18 | 0.072 |
| Speed X Distance | 1 | 0.000317 | 0.000317 | 1.54 | 0.270 |
| Error | 5 | 0.001029 | 0.000206 | ||
| Lack-of-Fit | 3 | 0.000906 | 0.000302 | 4.92 | 0.174 |
| Pure Error | 2 | 0.000123 | 0.000061 | ||
| Total | 14 | R2 = 96.80% and R2(Adj) = 91.03% | |||
| S.No. | Factors | |||||
|---|---|---|---|---|---|---|
| Load | Speed | Distance | Regression Wear | Experimental Wear | Error | |
| 1 | 40 | 260 | 650 | 0.18 mg/m | 0.187 | 3.89% |
| 2 | 30 | 260 | 500 | 0.11 mg/m | 0.115 | 4.55% |
| 3 | 30 | 220 | 350 | 0.059 mg/m | 0.061 | 3.39% |
| Parameter Function | Parameter Value |
|---|---|
| Population size | 50 |
| Population type | Double vector |
| Creation Function | Constraint dependent |
| Fitness Scaling Function | Rank |
| Selection Function | Roulette |
| Reproduction: Elite Count | Default (0.05 × Population size) = 2.5 |
| Reproduction: Crossover Fraction | Default: 0.8 |
| Mutation Function | Uniform: Rate at 0.15 |
| Crossover Function | Constraint dependent |
| Number of Generations | 100 |
| Function Tolerance | 1 × 10−6 |
| Constraint Tolerance | 1 × 10−6 |
| Process Parameters | Levels |
|---|---|
| Load | 20 N |
| Sliding Speed | 220 rpm |
| Sliding Distance | 350 m |
| Methods | Optimized Parameters | Wear Rate (WR) | Sample-1 | Sample-2 | Sample-3 | Average WR (mg)/m |
|---|---|---|---|---|---|---|
| RSM | Load = 20 N | Experiment | 0.0085 | 0.0083 | 0.0084 | 0.0084 |
| Sliding Speed = 240 rpm | Predicted | 0.008 | 0.008 | 0.008 | 0.008 | |
| Sliding Distance = 350 m | % Error | 6.25 | 3.75 | 5 | 5% | |
| GA | Load = 20 N | Experiment | 0.0054 | 0.00538 | 0.00532 | 0.00537 |
| Sliding Speed = 220 rpm | Predicted | 0.00514 | 0.00514 | 0.00514 | 0.00514 | |
| Sliding Distance = 350 m | % Error | 5.06 | 4.67 | 3.5 | 4.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abebe, S.K.; Beri, H.; Sinha, D.K.; Rajhi, A.A.; Hossain, N.; Duhduh, A.A.; Zainuddin, S.; Ahmed, G.M.S. Wear Behavior of AZ61 Matrix Hybrid Composite Fabricated via Friction Stir Consolidation: A Combined RSM Box–Behnken and Genetic Algorithm Optimization. J. Compos. Sci. 2023, 7, 275. https://doi.org/10.3390/jcs7070275
Abebe SK, Beri H, Sinha DK, Rajhi AA, Hossain N, Duhduh AA, Zainuddin S, Ahmed GMS. Wear Behavior of AZ61 Matrix Hybrid Composite Fabricated via Friction Stir Consolidation: A Combined RSM Box–Behnken and Genetic Algorithm Optimization. Journal of Composites Science. 2023; 7(7):275. https://doi.org/10.3390/jcs7070275
Chicago/Turabian StyleAbebe, Samuel Kefyalew, Habtamu Beri, Devendra Kumar Sinha, Ali A. Rajhi, Nazia Hossain, Alaauldeen A. Duhduh, Shaik Zainuddin, and Gulam Mohammed Sayeed Ahmed. 2023. "Wear Behavior of AZ61 Matrix Hybrid Composite Fabricated via Friction Stir Consolidation: A Combined RSM Box–Behnken and Genetic Algorithm Optimization" Journal of Composites Science 7, no. 7: 275. https://doi.org/10.3390/jcs7070275
APA StyleAbebe, S. K., Beri, H., Sinha, D. K., Rajhi, A. A., Hossain, N., Duhduh, A. A., Zainuddin, S., & Ahmed, G. M. S. (2023). Wear Behavior of AZ61 Matrix Hybrid Composite Fabricated via Friction Stir Consolidation: A Combined RSM Box–Behnken and Genetic Algorithm Optimization. Journal of Composites Science, 7(7), 275. https://doi.org/10.3390/jcs7070275








