An Efficient Method for Simulating the Temperature Distribution in Regions Containing YAG:Ce3+ Luminescence Composites of White LED
Abstract
:1. Introduction
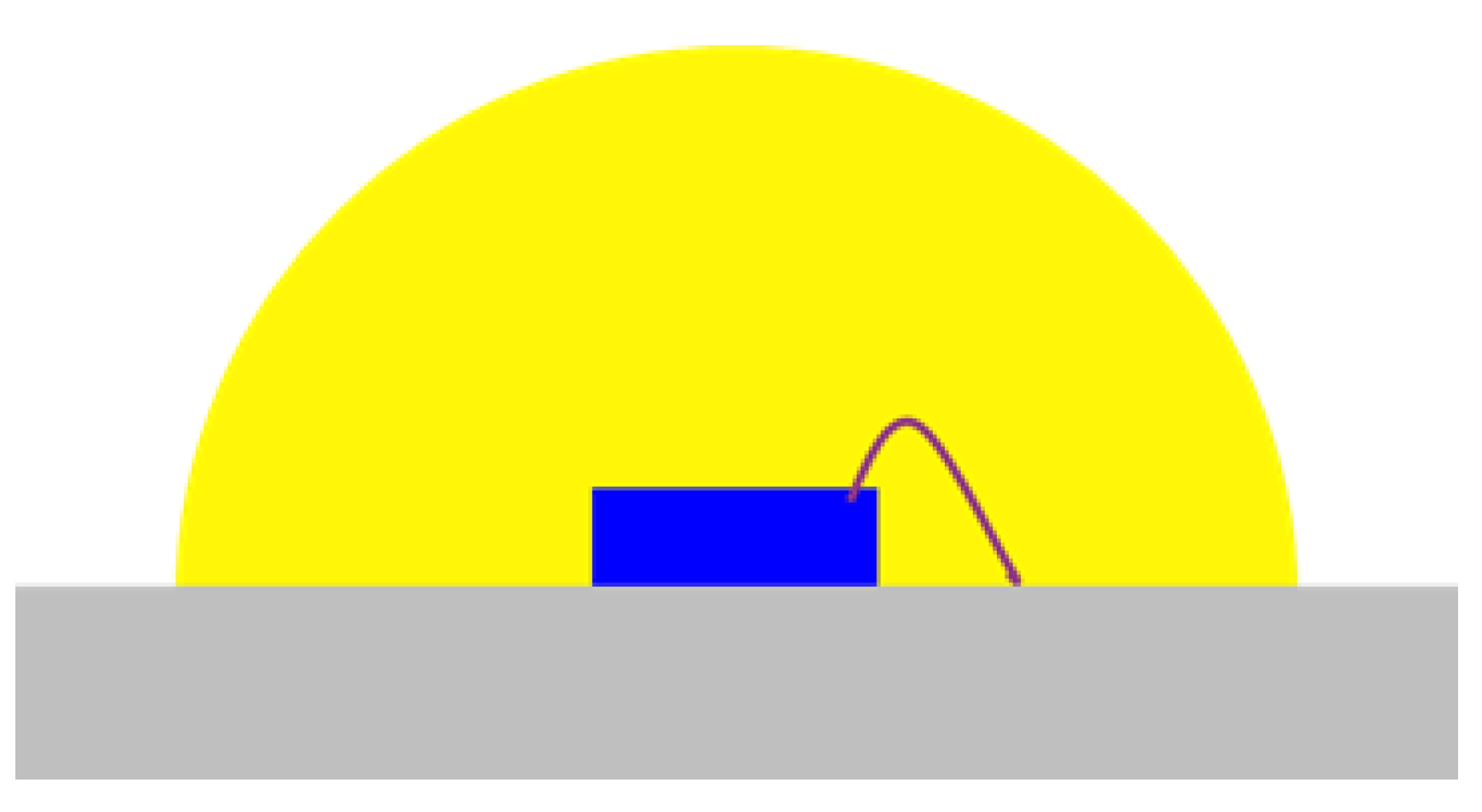
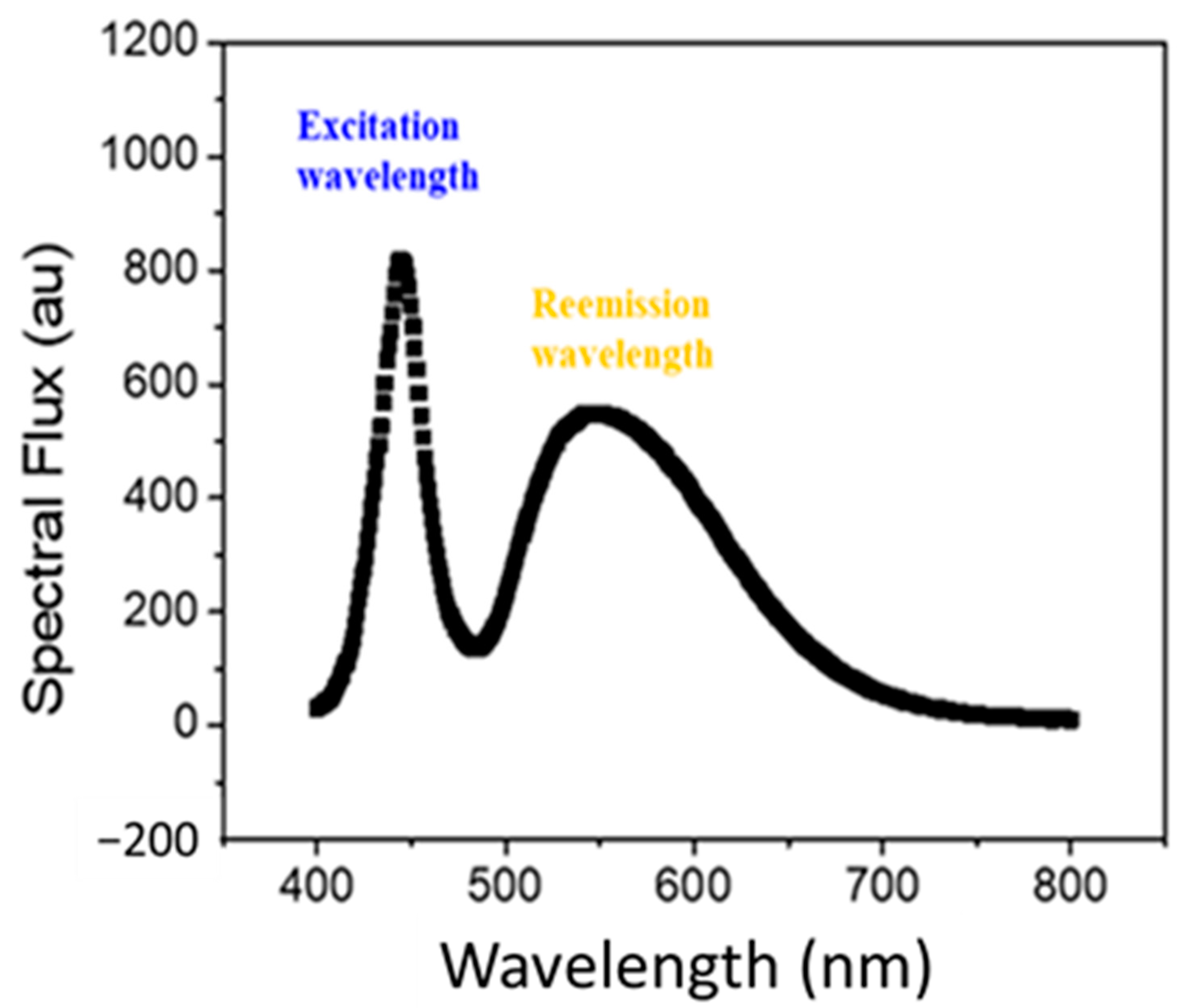
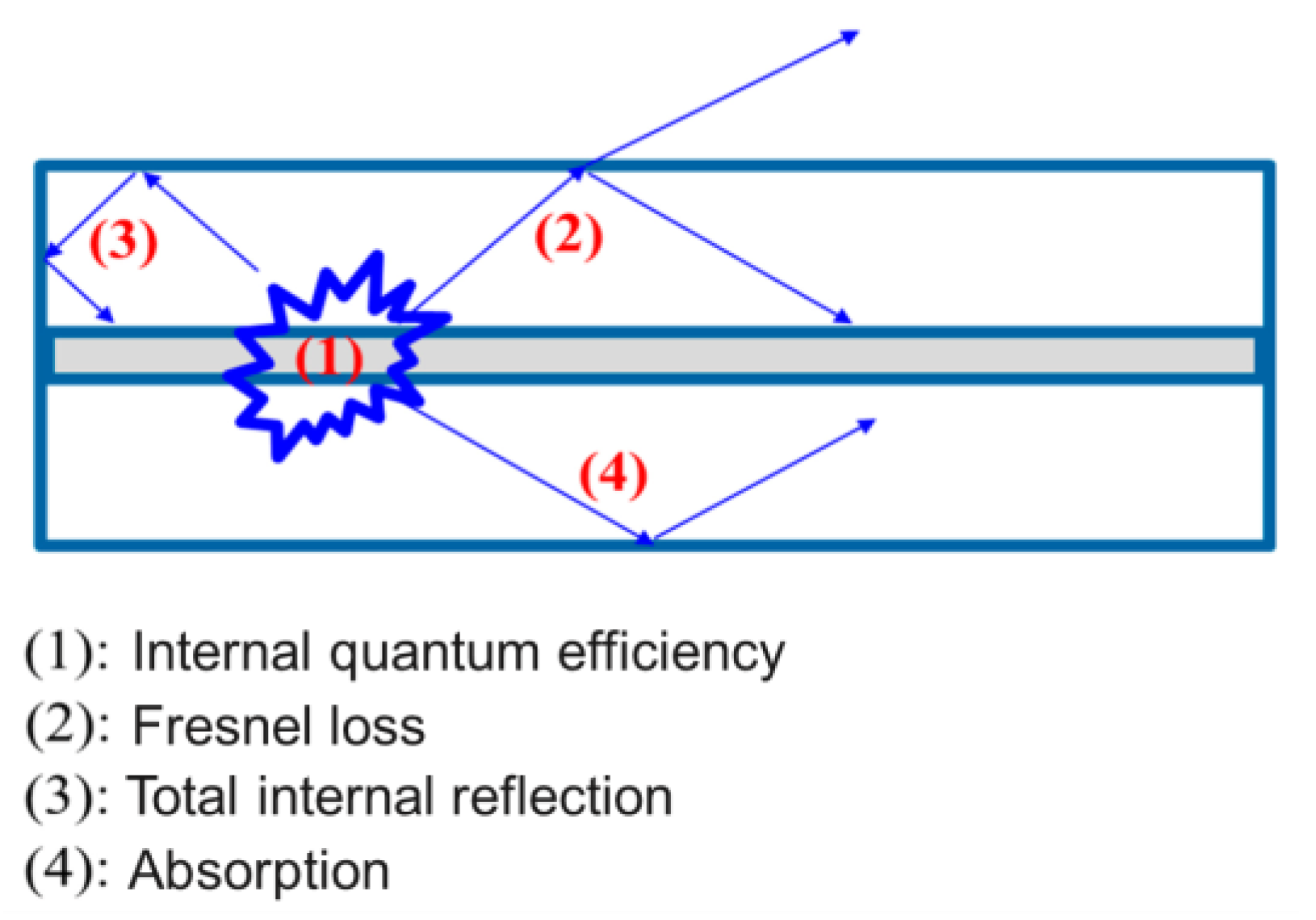
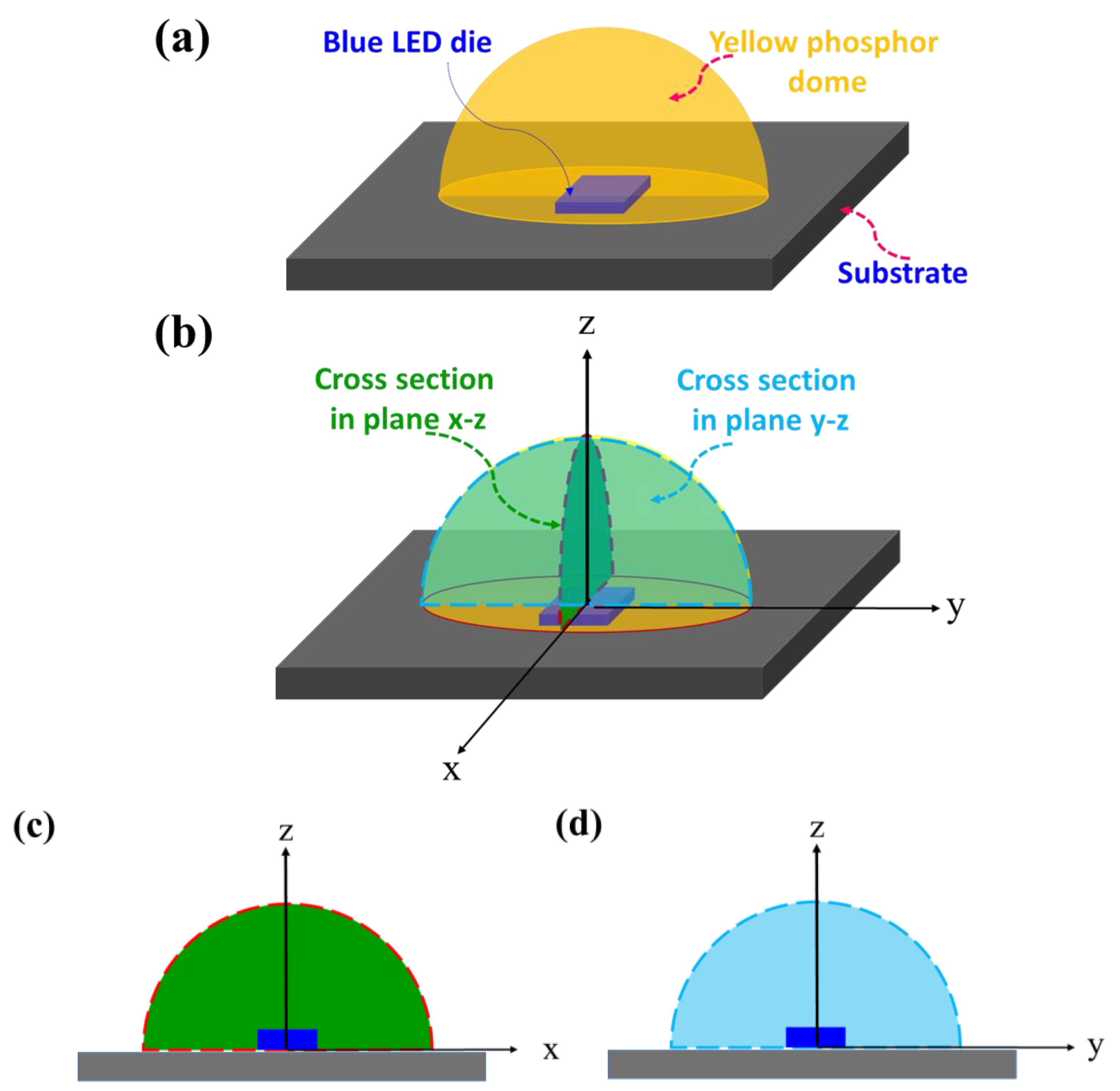
2. Two Main Heat Sources in pc-WLEDs Using a Hemispherical Silicone–Phosphor Matrix Distribution
3. Thermal Simulation
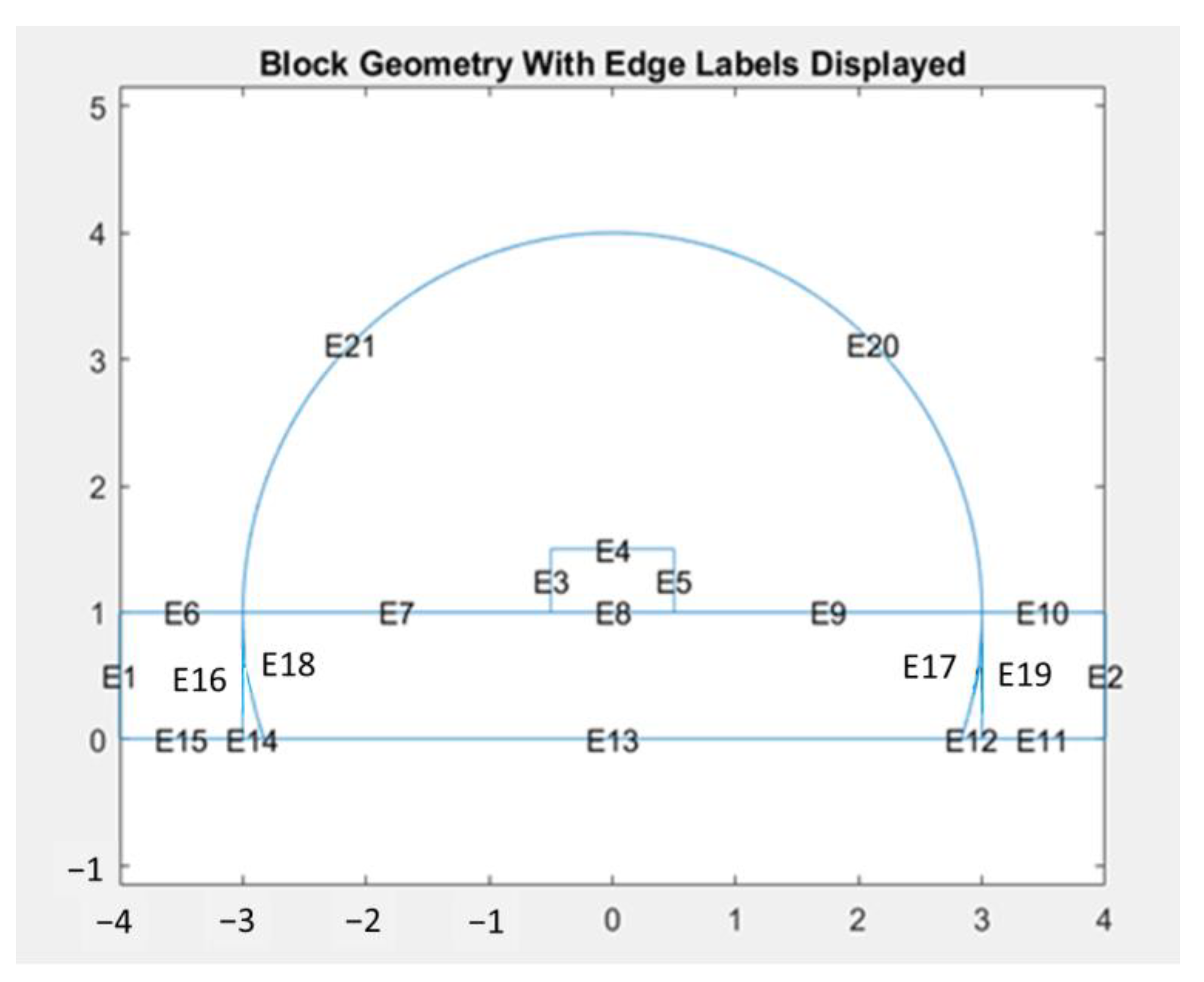
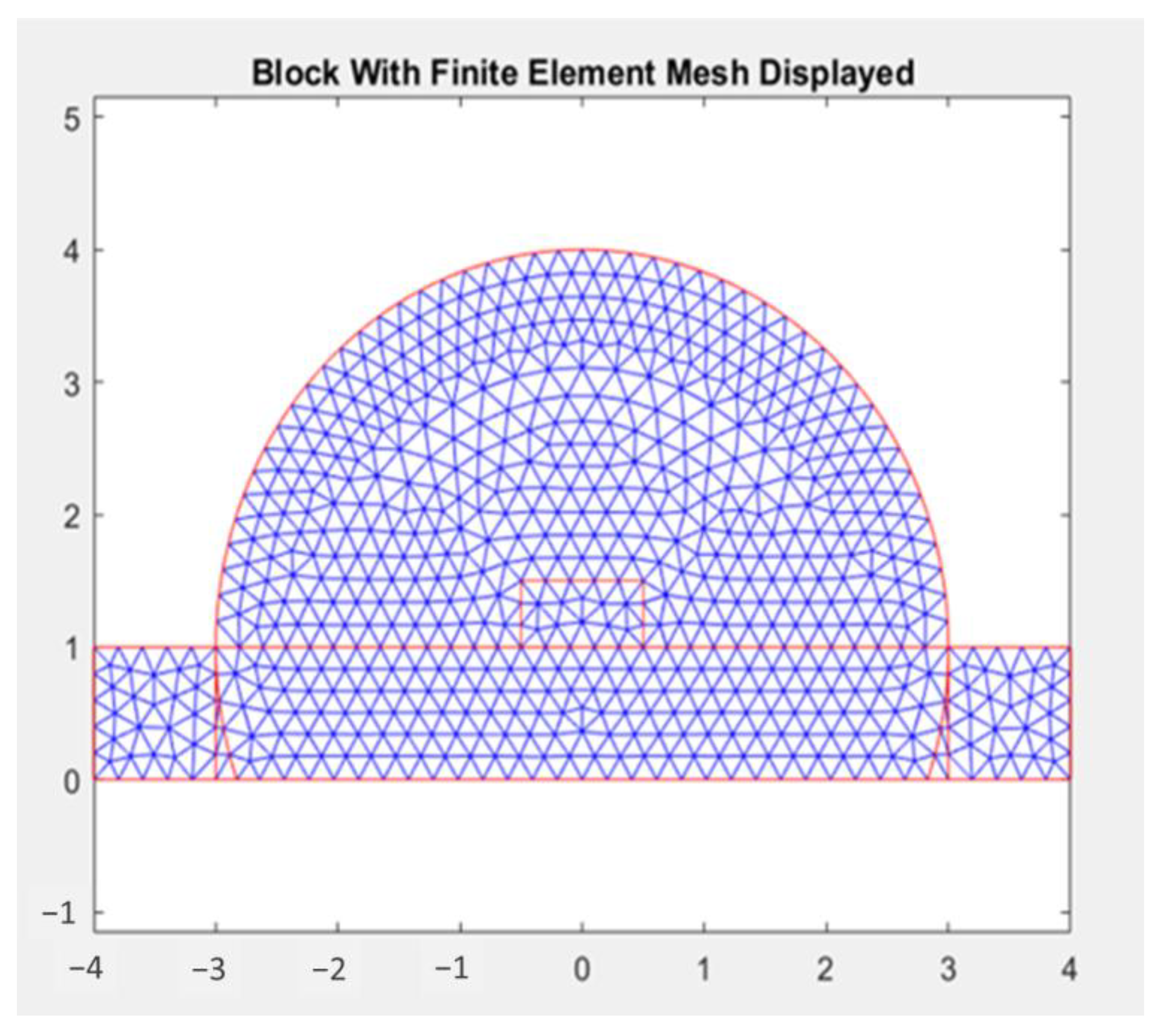
3.1. Simplify from 3D to 2D Thermal Modeling for Steady State
3.2. The Boundary Conditions
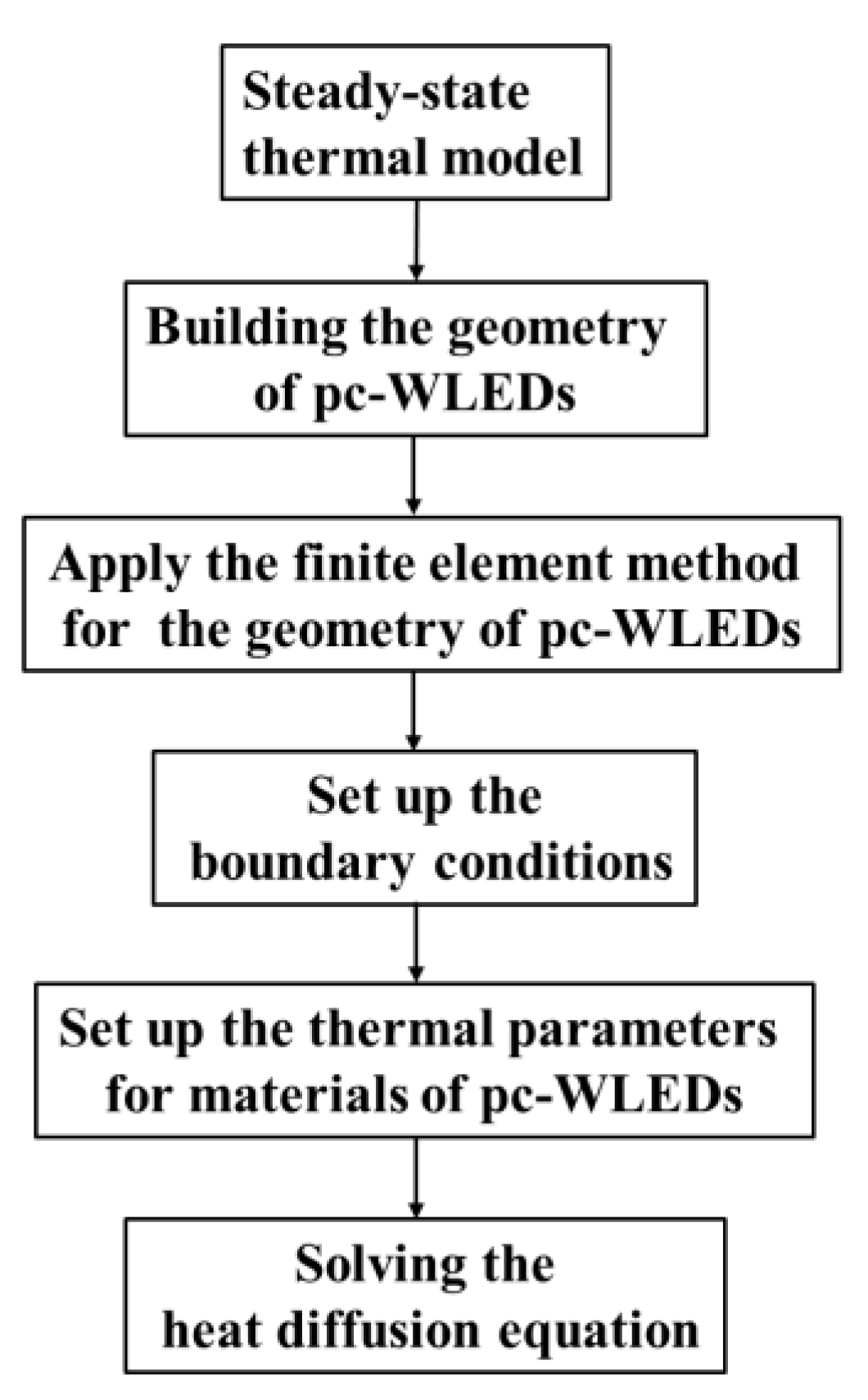
3.3. Simulation Flowchart
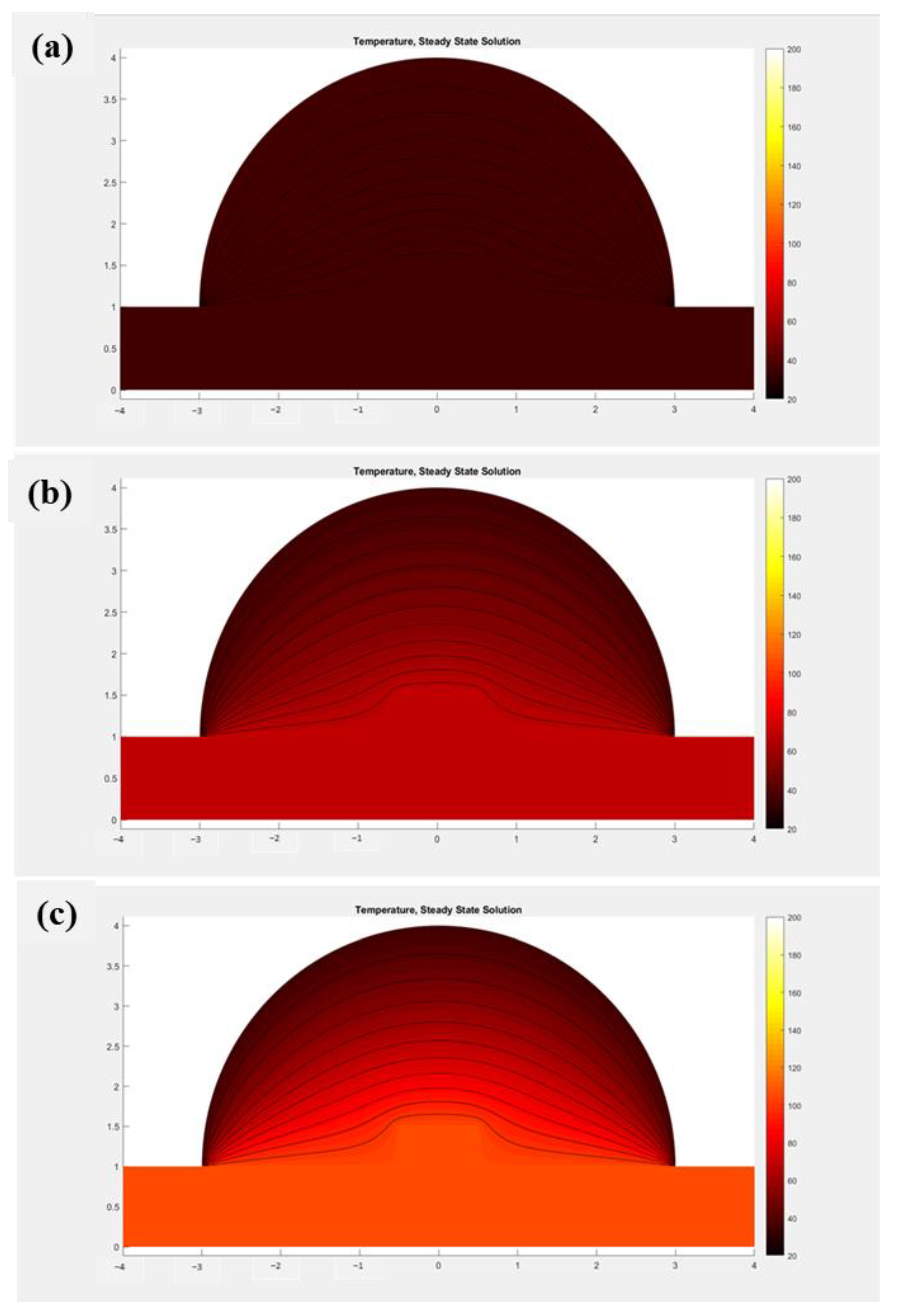
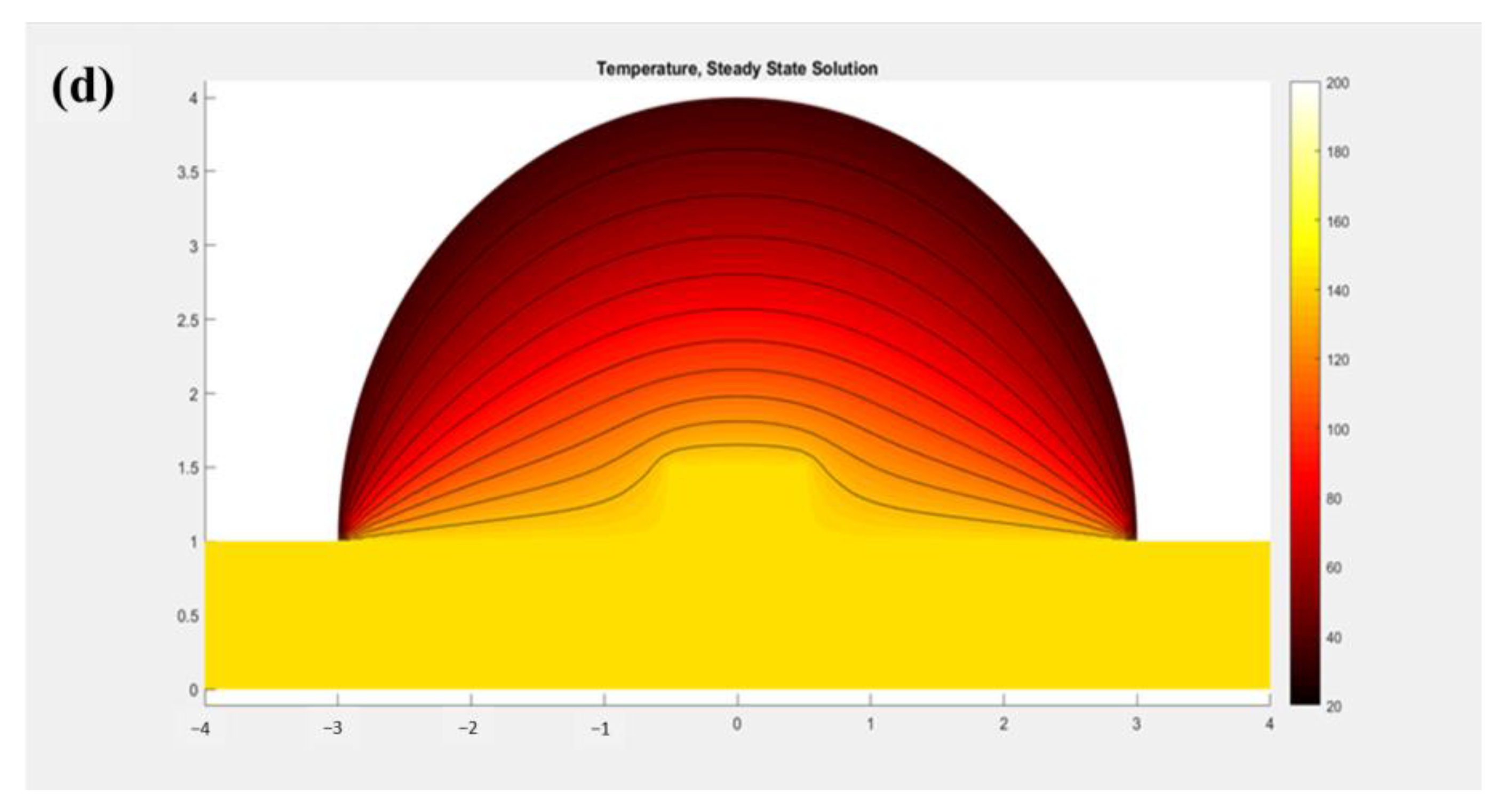
4. Simulation Results and Discussion
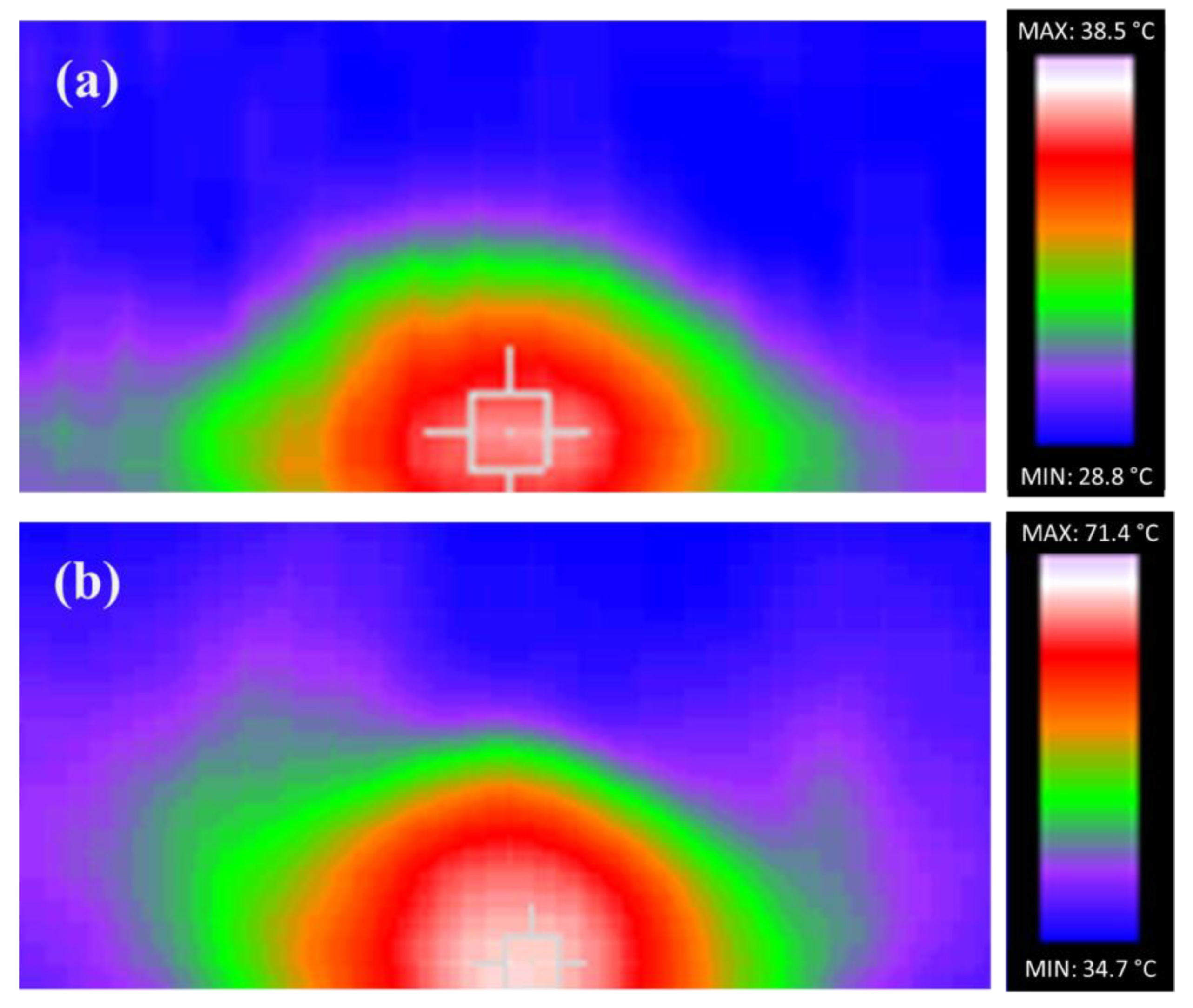
5. Experiments for the Determination of the Temperature Distribution of the Phosphor Region in the Hemispherical Packaging Structure
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schubert, E.-F.; Kim, J.-K. Solid-state light sources getting smart. Science 2005, 308, 1274–1278. [Google Scholar] [CrossRef] [PubMed]
- Narendran, N.; Gu, Y. Life of LED-Based White Light Sources. J. Disp. Technol. 2005, 1, 167–171. [Google Scholar] [CrossRef]
- Schubert, E. Light-Emitting Diodes, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Chang, M.-H.; Das, D.; Varde, P.; Pecht, M. Light emitting diodes reliability review. Microelectron. Reliab. 2012, 52, 762–782. [Google Scholar] [CrossRef]
- Efremov, A.-A.; Bochkareva, N.-I.; Gorbunov, R.-I.; Lavrinovich, D.-A.; Rebane, Y.-T.; Tarkhin, D.-V.; Shreter, Y.-G. Effect of the joule heating on the quantum efficiency and choice of thermal conditions for high-power blue InGaN/GaN LEDs. Semiconductors 2006, 40, 605–610. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Bettinelli, M.; Sharma, S.-K.; Redlich, B.; Speghini, A.; Karlsson, M. Unraveling the impact of different thermal quenching routes on the luminescence efficiency of the Y3Al5O12:Ce3+ phosphor for white light emitting diodes. J. Mater. Chem. C 2020, 8, 14015. [Google Scholar] [CrossRef]
- Narendran, N.; Gu, Y.; Jayasinghe, L.; Freyssinier, J.-P.; Zhu, Y. Long-term performance of white LEDs and systems. In Proceedings of the First International Conference on White LEDs and Solid-State lighting, Tokyo, Japan, 26–30 November 2007; pp. 174–179. [Google Scholar]
- Singh, P.; Tan, C.-M. Degradation Physics of High-Power LEDs in Outdoor Environment and the Role of Phosphor in the degradation process. Sci. Rep. 2016, 6, 24052. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.L.; Mills, K.-C.; Bobashev, G.; Rountree, K.-J.; Lamvik, M.; Yaga, R.; Johnson, C. Understanding chromaticity shifts in LED devices through analytical models. Microelectron. Reliab. 2018, 84, 149–156. [Google Scholar] [CrossRef]
- Yazdan Mehr, M.; Bahrami, A.; Van Driel, W.-D.; Fan, X.-J.; Davis, J.-L.; Zhang, G.-Q. Degradation of optical materials in solid-state lighting systems. Int. Mater. Rev. 2020, 65, 102–128. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.-F.; Yang, S.-Y.; Hung, T.-Y.; Lee, C.-C.; Chiang, K.-N. Light degradation test and design of thermal performance for high-power light-emitting diodes. Microelectron. Reliab. 2012, 52, 794–803. [Google Scholar] [CrossRef]
- Baran, K.; Leśko, M.; Wachta, H.; Różowicz, A. Thermal Modeling and Simulation of High Power LED Module. AIP Conf. Proc. 2019, 2078, 020048. [Google Scholar] [CrossRef]
- Fu, H.K.; Wang, C.P.; Chiang, H.C.; Chen, T.T.; Chen, C.L.; Chou, P.T. Evaluation of temperature distribution of LED module. Microelectron. Reliab. 2013, 53, 554–559. [Google Scholar] [CrossRef]
- Chen, M.; Xu, C.; Xu, K.; Zheng, L. Thermal simulation and analysis of flat surface flip-chip high power light-emitting diodes. J. Semicond. 2013, 34, 124005. [Google Scholar] [CrossRef]
- Smet, P.F.; Parmentier, A.B.; Poelman, D. Selecting Conversion Phosphors for White Light-Emitting Diodes. J. Electrochem. Soc. 2011, 158, R37. [Google Scholar] [CrossRef] [Green Version]
- Ying, S.-P.; Fu, H.-K.; Tang, W.-F.; Hong, R.-C. The Study of Thermal Resistance Deviation of High-Power LEDs. IEEE Trans. Electron Devices 2014, 61, 2843–2848. [Google Scholar] [CrossRef]
- Górecki, K.; Ptak, P. Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB. Energies 2021, 14, 1286. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Wang, K.; Luo, X. Optical Analysis of Phosphor’s Location for High-Power Light-Emitting Diodes. IEEE Trans. Device Mater. Reliab. 2009, 9, pp. 65–73. [Google Scholar] [CrossRef]
- Chen, K.J.; Lin, B.C.; Chen, H.C.; Shih, M.H.; Wang, C.H.; Kuo, H.T.; Tsai, H.H.; Kuo, M.Y.; Chien, S.H.; Lee, P.T. Effect of the Thermal Characteristics of Phosphor for the Conformal and Remote Structures in White Light-Emitting Diodes. IEEE Photonics J. 2013, 5, 8200508. [Google Scholar] [CrossRef]
- Tan, C.M.; Singh, P.; Zhao, W.; Kuo, H.C. Physical Limitations of Phosphor layer thickness and concentration for White LEDs. Sci. Rep. 2018, 8, 2452. [Google Scholar] [CrossRef] [Green Version]
- Nemitz, W.; Fulmek, P.; Nicolics, J.; Reil, F.; Wenzl, F.P. On the determination of the temperature distribution within the color conversion elements of phosphor converted LEDs. Sci. Rep. 2017, 7, 9964. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.Z.; Li, C.X.; Wang, Y.; Ran, L.L. Thermal simulation and analysis of high-power white LED light. In Advances in Materials Science, Energy Technology and Environmental Engineering; Patty, A., Zhou, P., Eds.; Taylor & Francis Group: London, UK, 2017; ISBN 978-1-138-19668-1. [Google Scholar]
- Chatterjee, A.; Senawiratne, J.; Li, Y.; Detchprohm, T.; Zhu, M.; Xia, Y.; Zhao, W.; Plawsky, J.L.; Wetzel, C. Junction Temperature Simulation of Gallium Nitride Green Light Emitting Diodes Using COMSOL. In Proceedings of the COMSOL Conference, Boston, MA, USA, 24 October 2007. [Google Scholar]
- Kim, J.P.; Jeon, S. Investigation of Light Extraction by Refractive Index of an Encapsulant, a Package Structure, and Phosphor. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 1815–1819. [Google Scholar] [CrossRef]
- Ma, M.; Mont, F.W.; Yan, X.; Cho, J.; Schubert, E.F.; Kim, G.B.; Sone, C. Effects of the refractive index of the encapsulant on the light-extraction efficiency of light-emitting diodes. Opt. Express 2011, 19, A1135–A1140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 5th ed.; J. Wiley: New York, NY, USA, 2002. [Google Scholar]
- Stefanie, R.; Rainer, H. The Thermal Measurement Point of LEDs; Application Note No. AN085; OSRAM Opto Semiconductors: Munich, Germany, 2021. [Google Scholar]
- Ying, S.; Fu, H.; Hong, R. The Study of Thermal Resistance Measurement of Multichip LED. IEEE Trans. Electron Devices 2015, 62, 3291–3295. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Partial Differential Equation Toolbox for Use with MATLAB; The MathWorks, Inc.: Natick, MA, USA, 1995. [Google Scholar]
- Heat Transfer. Mathwork.com. Available online: https://www.mathworks.com/help/pde/heat-transfer-and-diffusion-equations.htmls_tid=CRUX_lftnav (accessed on 19 April 2022).



| Name | Value | Unit |
|---|---|---|
| Substrate thickness | 1 | mm |
| Blue LED die thickness | 0.5 | mm |
| Blue LED die width | 0.7 | mm |
| Silicone–phosphor matrix radius | 3.0 | mm |
| Driven Current (mA) | Temperature of pc-WLED Substrate (°C) | Temperature of LED Die (°C) |
|---|---|---|
| 50 | 36 | 37 |
| 200 | 69 | 71 |
| 350 | 103 | 108 |
| 500 | 142 | 149 |
| Name | Value | Unit |
|---|---|---|
| Substrate thermal conductivity | 400 | W/(m·K) |
| Blue LED die thermal conductivity | 130 | W/(m·K) |
| Silicone–phosphor matrix thermal conductivity | 0.2 | W/(m·K) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, Q.-K.; Vu, T.-H.-T. An Efficient Method for Simulating the Temperature Distribution in Regions Containing YAG:Ce3+ Luminescence Composites of White LED. J. Compos. Sci. 2023, 7, 301. https://doi.org/10.3390/jcs7070301
Nguyen Q-K, Vu T-H-T. An Efficient Method for Simulating the Temperature Distribution in Regions Containing YAG:Ce3+ Luminescence Composites of White LED. Journal of Composites Science. 2023; 7(7):301. https://doi.org/10.3390/jcs7070301
Chicago/Turabian StyleNguyen, Quang-Khoi, and Thi-Hanh-Thu Vu. 2023. "An Efficient Method for Simulating the Temperature Distribution in Regions Containing YAG:Ce3+ Luminescence Composites of White LED" Journal of Composites Science 7, no. 7: 301. https://doi.org/10.3390/jcs7070301
APA StyleNguyen, Q.-K., & Vu, T.-H.-T. (2023). An Efficient Method for Simulating the Temperature Distribution in Regions Containing YAG:Ce3+ Luminescence Composites of White LED. Journal of Composites Science, 7(7), 301. https://doi.org/10.3390/jcs7070301







