Experimental and Numerical Analysis of Axial Behavior of Triaxial Woven Fabric Confined Concrete Columns
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.1.1. Triaxial Woven Fabric
2.1.2. Concrete Column
2.2. Confinement of Concrete
2.3. Equipment and Instruments
3. Non-Linear Finite Element Analysis
3.1. Materials Modelling for the FE Model
3.1.1. Geometric Model of Triaxial Woven Fabric
3.1.2. Modeling of TWF Materials
3.2. Modeling of Concrete
3.3. FEA Methodology
4. Results and Discussion
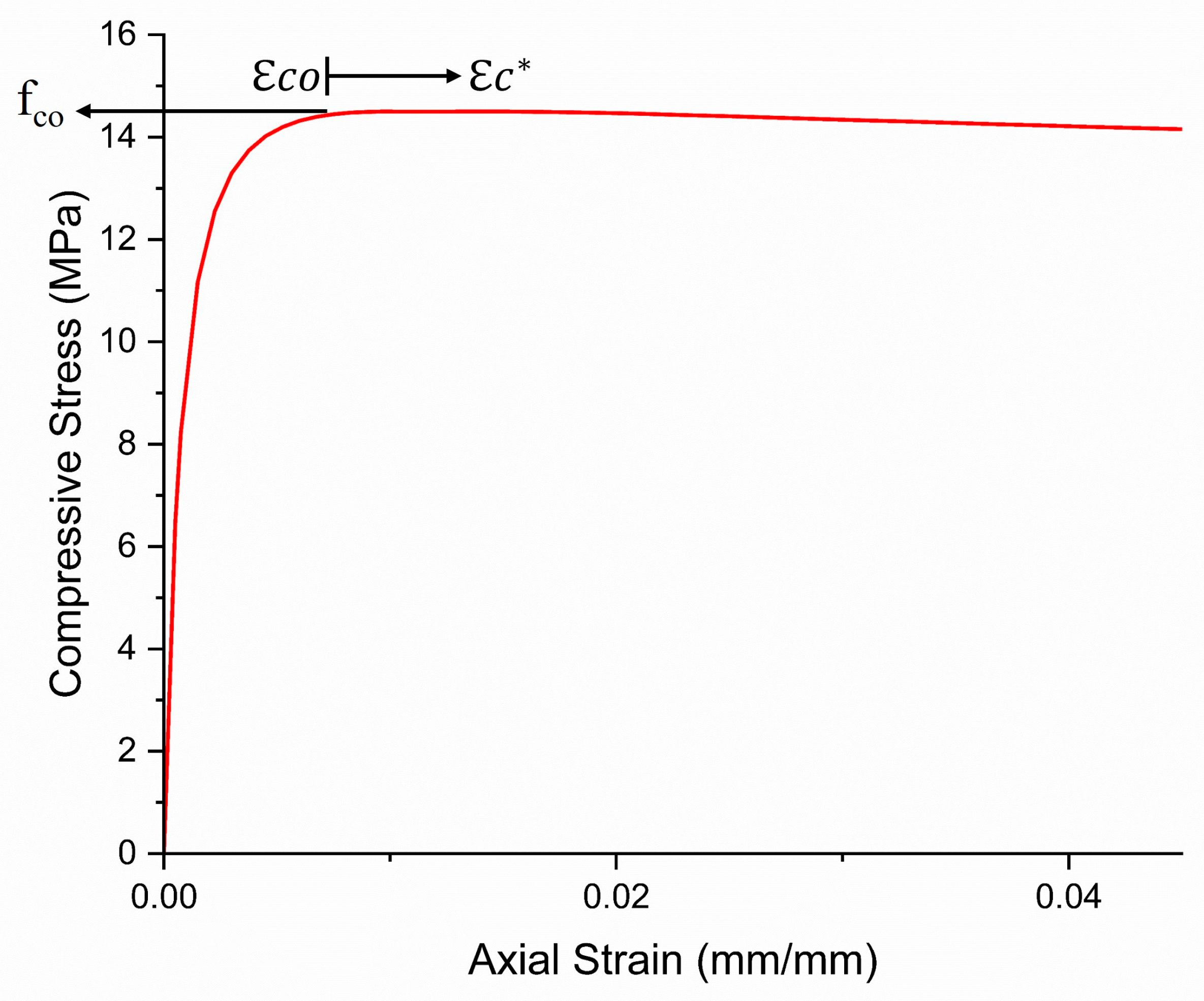
4.1. Stress–Strain Behavior of Concrete Column Confined by TWF
4.2. Effect of TWF Confinement on Compressive Stress and Axial Strain
4.3. Failure Mode
4.4. Comparative Analysis of Experimental and Simulated Results
5. Conclusions
- The stress–strain curve shape, compressive stress, and strain behavior of TWF-confined materials are affected by the fibers used in TWF warp and weft directions. The choice of fibers in these orientations affects the confinement mechanism and overall performance of the material under compressive loads. Fibers in the warp direction help increase the material’s resistance to lateral expansion, which affects compressive stress. Conversely, fibers in the weft direction help improve the material’s ability to withstand axial deformation, affecting compressive strain.
- TWF-C confinement resulted in a significant enhancement of 118% in compressive stress. In contrast, TWF g confinement showed the most significant improvement, with a significant increase of 161% in axial strain. Furthermore, the mechanical properties of TWF samples with different fiber orientations exhibited variations. Specifically, the sample with glass fiber as weft and carbon fiber as warp (TWF-GC2) exhibited more significant improvement than the sample with glass fiber as warp and carbon fiber as weft (TWF-CG2). TWF-GC2 exhibited a 22.5% increase in compressive strength and an 8% increase in axial strain compared to TWF-CG2. The findings highlight the importance of considering specific arrangements of fiber orientations in TWF confinement to optimize concrete column performance.
- The final failure morphology and crack evolution of each group of samples are different due to the different tensile and shear properties of different materials. Most of the samples with glass fiber as the weft show a “gradual crack” during the loading process, while the samples with carbon fiber as the weft show “instantaneous” damage.
- The comparison between the finite element modelling results and experimental data confirms the accuracy of the proposed finite element approach for investigating the confinement processes in TWF confined columns. The successful replication of experimental fracture patterns using maximum positive primary plastic strains demonstrates the reliability and usefulness of the finite element method as a tool for studying complex confinement phenomena.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malla, P.; Khedmatgozar Dolati, S.S.; Ortiz, J.D.; Mehrabi, A.; Nanni, A. Damage and Defects in Fiber-Reinforced Polymer Reinforced and Strengthened Concrete Elements. J. Compos. Constr. 2023, 27, 04023035. [Google Scholar] [CrossRef]
- Sharma, E.M. Processing. Use Of Frp Sheets to Strengthen The Existing Beams. J. Data Acquis. Process. 2023, 38, 3481. [Google Scholar]
- Banaeipour, A.; Tavakkolizadeh, M.; Akbar, M.; Hussain, Z.; Ostrowski, K.A.; Bahadori, A.; Spyrka, M. Effects of Small Deviations in Fiber Orientation on Compressive Characteristics of Plain Concrete Cylinders Confined with FRP Laminates. Materials 2023, 16, 261. [Google Scholar] [CrossRef]
- Ghani, M.U.; Siddique, A.; Abraha, K.G.; Yao, L.; Li, W.; Khan, M.Q.; Kim, I.-S. Performance evaluation of jute/glass-fiber-reinforced Polybutylene Succinate (PBS) hybrid composites with different layering configurations. Materials 2022, 15, 1055. [Google Scholar] [CrossRef]
- Benny, B.; Bazli, M.; Rajabipour, A.; Arashpour, M. Durability of tubular sea water sea sand concrete and fibre-reinforced polymer hybrid structures: Mechanisms and effective parameters: Critical overview and discussion. Constr. Build. Mater. 2023, 366, 130206. [Google Scholar] [CrossRef]
- Zeng, J.-J.; Guo, Y.-C.; Gao, W.-Y.; Chen, W.-P.; Li, L.-J. Stress-strain behavior of concrete in circular concrete columns partially wrapped with FRP strips. Compos. Struct. 2018, 200, 810–828. [Google Scholar] [CrossRef]
- Li, G.; Maricherla, D.; Singh, K.; Pang, S.-S.; John, M. Effect of fiber orientation on the structural behavior of FRP wrapped concrete cylinders. Compos. Struct. 2006, 74, 475–483. [Google Scholar] [CrossRef]
- Pham, T.M.; Hadi, M.N.S.; Youssef, J. Optimized FRP Wrapping Schemes for Circular Concrete Columns under Axial Compression. J. Compos. Constr. 2015, 19, 04015015. [Google Scholar] [CrossRef]
- Zeng, J.-J.; Duan, Z.-J.; Guo, Y.-C.; Xie, Z.-H.; Li, L.-J. Novel fiber-reinforced polymer cross wrapping strengthening technique: A comparative study. Adv. Struct. Eng. 2019, 23, 979–996. [Google Scholar] [CrossRef]
- Sadeghian, P.; Rahai, A.R.; Ehsani, M.R. Effect of Fiber Orientation on Compressive Behavior of CFRP-confined Concrete Columns. J. Reinf. Plast. Compos. 2009, 29, 1335–1346. [Google Scholar] [CrossRef]
- Piekarczyk, J.; Piekarczyk, W.; Blazewicz, S. Compression strength of concrete cylinders reinforced with carbon fiber laminate. Constr. Build. Mater. 2011, 25, 2365–2369. [Google Scholar] [CrossRef]
- Fanaradelli, T.; Rousakis, T. Assessment of analytical stress and strain at peak and at ultimate conditions for fiber-reinforcement polymer-confined reinforced concrete columns of rectangular sections under axial cyclic loading. Struct. Concr. 2020, 22, 95–108. [Google Scholar] [CrossRef]
- Mohamed, H.; Masmoudi, R.; Chaallal, O. Compressive behaviour of filament winded GFRP tube-encased concrete columns. In Proceedings of the 4th International Conference on FRP Composites in Civil Engineering (CICE), Zurich, Switzerland, 22–24 July 2008. [Google Scholar]
- Hyer, M.W.; White, S.R. Stress Analysis of Fiber-Reinforced Composite Materials; DEStech Publications, Inc.: Lancaster, PA, USA, 2009. [Google Scholar]
- Fam, A.; Flisak, B.; Rizkalla, S. Experimental and analytical modeling of concrete-filled FRP tubes subjected to combined bending and axial loads. ACI Struct. J. 2003, 100, 499–509. [Google Scholar]
- Seffo, M.; Hamcho, M. Strength of Concrete Cylinder Confined by Composite Materials (CFRP). Energy Procedia 2012, 19, 276–285. [Google Scholar] [CrossRef]
- Ziaadiny, H.; Abbasnia, R. Unified cyclic stress-strain model for FRP-confined concrete circular, square and rectangular prisms. Struct. Concr. 2016, 17, 220–234. [Google Scholar] [CrossRef]
- Rao, Y.; Zhang, C.; Li, W. Structural analysis for triaxial woven fabric composites of carbon fiber. Compos. Struct. 2019, 219, 42–50. [Google Scholar] [CrossRef]
- El Messiry, M.; Eltahan, E. Stab resistance of triaxial woven fabrics for soft body armor. J. Ind. Text. 2016, 45, 1062–1082. [Google Scholar] [CrossRef]
- Zhou, H.; Xiao, X.; Qian, K.; Zhang, K.; Zhang, D. Numerical and experimental analyses of out-of-plane de-formation of triaxial woven fabric. Mater. Res. Express 2018, 5, 055305. [Google Scholar] [CrossRef]
- Fujita, A.; Hamada, H.; Maekawa, Z. Tensile Properties of Carbon Fiber Triaxial Woven Fabric Composites. J. Compos. Mater. 1993, 27, 1428–1442. [Google Scholar] [CrossRef]
- Dano, M.-L.; Gendron, G.; Picard, A. Mechanical behavior of a triaxial woven fabric composite. Mech. Compos. Mater. Struct. 2000, 7, 207–224. [Google Scholar] [CrossRef]
- Zhao, Q.; Hoa, S.; Ouellette, P. Progressive failure of triaxial woven fabric (TWF) composites with open holes. Compos. Struct. 2004, 65, 419–431. [Google Scholar] [CrossRef]
- Kueh, A.; Soykasap, O.; Pellegrino, S. Thermo-mechanical behaviour of singleply triaxial weave carbon fibre reinforced plastic. In Proceedings of the Spacecraft Structures, Materials and Mechanical Testing, Noordwijk, The Netherlands, 10–12 May 2005. [Google Scholar]
- Zhao, Q.; Hoa, S.V. Triaxial Woven Fabric (TWF) Composites with Open Holes (Part I): Finite Element Models for Analysis. J. Compos. Mater. 2003, 37, 763–789. [Google Scholar] [CrossRef]
- Zhao, Q.; Hoa, S.V.; Ouellette, P. Triaxial Woven Fabric (TWF) Composites with Open Holes (Part II): Verification of the Finite Element Models. J. Compos. Mater. 2003, 37, 849–873. [Google Scholar] [CrossRef]
- Díaz Valdés, S.H.; Soutis, C. Real-time nondestructive evaluation of fiber composite laminates using low-frequency Lamb waves. J. Acoust. Soc. Am. 2002, 111, 2026–2033. [Google Scholar] [CrossRef]
- Shi, Y.; Swait, T.; Soutis, C. Modelling damage evolution in composite laminates subjected to low velocity impact. Compos. Struct. 2012, 94, 2902–2913. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ansys, I.J.A.R. Engineering data, composite materials library. ANSYS Release 2017, 18, 1. [Google Scholar]
- Hashin, Z.; Rotem, A. A Fatigue Failure Criterion for Fiber Reinforced Materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Barbero, E.; Cosso, F.; Roman, R.; Weadon, T. Determination of material parameters for Abaqus progressive damage analysis of E-glass epoxy laminates. Compos. Part B Eng. 2012, 46, 211–220. [Google Scholar] [CrossRef]
- Rahimian Koloor, S.S.; Karimzadeh, A.; Yidris, N.; Petrů, M.; Ayatollahi, M.R.; Tamin, M.N. An Energy-Based Concept for Yielding of Multidirectional FRP Composite Structures Using a Mesoscale Lamina Damage Model. Polymers 2020, 12, 157. [Google Scholar] [CrossRef]
- Ferrotto, M.; Fischer, O.; Cavaleri, L. A strategy for the finite element modeling of FRP-confined concrete columns subjected to preload. Eng. Struct. 2018, 173, 1054–1067. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Nayal, R.; Rasheed, H.A. Tension stiffening model for concrete beams reinforced with steel and FRP bars. J. Mater. Civ. Eng. 2006, 18, 831–841. [Google Scholar] [CrossRef]
- Wahalathantri, B.; Thambiratnam, D.; Chan, T.; Fawzia, S. A material model for flexural crack simulation in reinforced concrete elements using ABAQUS. In Proceedings of the First International Conference on Engineering, Designing and Developing the Built Environment for Sustainable Wellbeing, Kochi, India, 22–24 July 2011; pp. 260–264. [Google Scholar]
- Genikomsou, A.S.; Polak, M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- Ellobody, E.; Young, B.; Lam, D. Behaviour of normal and high strength concrete-filled compact steel tube circular stub columns. J. Constr. Steel Res. 2006, 62, 706–715. [Google Scholar] [CrossRef]
- Ghernouti, Y.; Rabehi, B. Effectiveness of Hybrid and Partially Confined Concrete Subjected to Axial Compressive Loading Using CFRP and GFRP Composite Materials. Slovak J. Civ. Eng. 2020, 28, 8–14. [Google Scholar] [CrossRef]
- Karouche, A.; Hebbache, K.; Belebchouche, C.; Lahbari, N.; Kessal, O.; Czarnecki, S. External Confined Concrete Cylinders Behavior under Axial Compression Using CFRP Wrapping. Materials 2022, 15, 8232. [Google Scholar] [CrossRef]
- Zheng, L.; Xiao, Y.; Liu, L.; Xu, F. Experimental and numerical study of the behavior of epoxy foam-filled 3D woven spacer composites under bending load. Polym. Compos. 2022, 43, 3057–3067. [Google Scholar] [CrossRef]
- Raza, A.; Ahmad, A. Numerical investigation of load-carrying capacity of GFRP-reinforced rectangular concrete members using CDP model in ABAQUS. Adv. Civ. Eng. 2019, 2019, 1745341. [Google Scholar] [CrossRef]













| Density | ||||||
|---|---|---|---|---|---|---|
| Swancor 2511-1A | Swancor 2511-1BS | Tensile strength (MPa) | Tensile modulus (MPa) | Extensibility (%) | Flexural strength (MPa) | Flexural modulus (MPa) |
| 1.1–1.2 | 0.9–1.0 | 67–80 | 2700–3500 | 4.5–8.5 | 110–140 | 2800–3600 |
| Materials | E11 GPa | E22 GPa | E33 GPa | Nu12 | Nu13 | Nu23 | G12 GPa | G13 GPa | G23 GPa |
|---|---|---|---|---|---|---|---|---|---|
| Carbon | 105 | 10.0 | 10.0 | 0.32 | 0.32 | 0.44 | 3.3 | 3.3 | 3.6 |
| Glass | 40.0 | 8.40 | 8.40 | 0.315 | 0.315 | 0.39 | 4.3 | 4.3 | 3.2 |
| Property | Parameter | TWF-C | TWF-G |
|---|---|---|---|
| Strength properties | Tensile strength in the normal direction (MPa) | 1340 | 820 |
| Compressive strength in the normal direction (MPa) | 1192 | 500 | |
| Tensile strength in transverse dir. of fiber (MPa) | 19.6 | 80.6 | |
| Compressive strength in transverse dir. of fiber (MPa) | 92.3 | 322 | |
| Shear strength in the normal direction of fiber (MPa) | 51 | 54.5 | |
| Shear strength in transverse dir. of fiber (MPa) | 23 | 161.2 | |
| Damage properties | Fracture tensile energy in fibers’ dir. (mJ/mm2) | 48.4 | 32 |
| Fracture tensile energy in transverse dir. (mJ/mm2) | 60.3 | 20 | |
| Fracture compressive energy in fibers’ dir. (mJ/mm2) | 4.5 | 4.5 | |
| Fracture compressive energy in transverse dir. (mJ/mm2) | 8.5 | 4.5 |
| Elastic Properties | |
| Young’s modulus (MPa) | 19039 |
| Poisson’s ratio | 0.2 |
| Plastic Properties | |
| Dilation angle (degree) | 30 |
| Eccentricity | 0.1 |
| fb′/fco′ | 1.16 |
| Kc | 0.667 |
| Specimen | fco (MPa)/fcc (MPa) | εco/εcc | |
|---|---|---|---|
| Control | Mean | 14.6 | 0.011 |
| Upper CI | 16.65 | 0.012 | |
| Lower CI | 12.65 | 0.010 | |
| TWF-C | Mean | 32.00 | 0.023 |
| Upper CI | 33.87 | 0.028 | |
| Lower CI | 30.21 | 0.018 | |
| TWF-G | Mean | 24.73 | 0.030 |
| Upper CI | 26.43 | 0.034 | |
| Lower CI | 22.96 | 0.026 | |
| TWF-CG2) | Mean | 25.00 | 0.025 |
| Upper CI | 25.78 | 0.030 | |
| Lower CI | 23.98 | 0.020 | |
| TWF-GC2 | Mean | 30.00 | 0.027 |
| Upper CI | 31.86 | 0.031 | |
| Lower CI | 28.13 | 0.024 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghani, M.U.; Sun, T.; Zhang, H.; Abraha, K.G.; Ahmad, N.; Ahmed, K.; Saeed, R.; Sadannavar, M.K.; Li, W. Experimental and Numerical Analysis of Axial Behavior of Triaxial Woven Fabric Confined Concrete Columns. J. Compos. Sci. 2023, 7, 358. https://doi.org/10.3390/jcs7090358
Ghani MU, Sun T, Zhang H, Abraha KG, Ahmad N, Ahmed K, Saeed R, Sadannavar MK, Li W. Experimental and Numerical Analysis of Axial Behavior of Triaxial Woven Fabric Confined Concrete Columns. Journal of Composites Science. 2023; 7(9):358. https://doi.org/10.3390/jcs7090358
Chicago/Turabian StyleGhani, Muhammad Usman, Tingting Sun, Honghua Zhang, Kahsay Gebresilassie Abraha, Nauman Ahmad, Khalil Ahmed, Rehan Saeed, Mohmadarslan Kutubuddin Sadannavar, and Wei Li. 2023. "Experimental and Numerical Analysis of Axial Behavior of Triaxial Woven Fabric Confined Concrete Columns" Journal of Composites Science 7, no. 9: 358. https://doi.org/10.3390/jcs7090358
APA StyleGhani, M. U., Sun, T., Zhang, H., Abraha, K. G., Ahmad, N., Ahmed, K., Saeed, R., Sadannavar, M. K., & Li, W. (2023). Experimental and Numerical Analysis of Axial Behavior of Triaxial Woven Fabric Confined Concrete Columns. Journal of Composites Science, 7(9), 358. https://doi.org/10.3390/jcs7090358






