A Comparison of Three Simulation Techniques for Modeling the Fan Blade–Composite Abradable Rub Strip Interaction in Turbofan Engines

Abstract

Turbofan engine models for foreign object impact simulations must include a representation of fan blade interactions with surrounding components of the engine, including rubbing against the abradable lining. In this study, three numerical techniques, namely, the finite element method (FEM), smoothed particles hydrodynamics (SPH), and the adaptive (hybrid) FEM/SPH approach (ADT), were evaluated for their applicability to modeling of the blade–abradable rub strip (ARS) interaction. Models developed using these methods in the commercial code LS-DYNA were compared in terms of their computational cost, robustness, sensitivity to mesh density, and certain physical and non-physical parameters. As a result, the applicability of the models to represent the blade-ARS interaction was ranked as follows (1—most applicable, 3—least applicable): 1—SPH, 2—FEM, and 3—ADT.

1. Introduction

An aircraft turbofan engine certification must demonstrate compliance with fan blade-off, bird ingestion, and other high-speed impact requirements determined by airworthiness standards [1]. The corresponding destructive physical tests usually involve substantial complexity and high cost [2]. Engine manufacturers have made substantial progress in developing high-fidelity simulation models for modeling the response of the engines to dynamic loading (see e.g., [3,4]). These models, capable of representing processes and interactions evolving within the engine subjected to impact, provide an efficient design practice and target engine certification via only a limited number of physical tests, thus enabling multimillion-dollar cost avoidance.

In modeling, it is usually critically important to simulate the interaction of fan blades with other parts of the turbofan engine. Such interactions may result from deflection of the blades upon a bird strike, ice shedding, or other events that may lead to rotor unbalance. Some typical components in the fan section are schematically shown in Figure 1, and include a metal case, flexible ballistic materials, and a thick layer of honeycomb. In the areas adjacent to the rotating fan blades, the honeycomb is often enhanced with a lightweight potting compound that comprises the abradable rub strip (ARS) (see, e.g., [5]). The abradable’s main function is to minimize the clearance between the blade tips and the fan case, thus reducing possible parasitic leakage through this area and increasing the overall engine efficiency [6]. In the event of being hit by a foreign object, such as a bird entering the air intake of the engine, the blade may make a radial excursion coming into contact with the ARS.

While significant progress has been made in modeling the blade interaction with flexible ballistic fabrics [7,8,9] and metal casings [4,10,11], blade–ARS interaction modeling is a largely underexplored area. Previously published studies in this field were mainly concerned with structural dynamics problems (e.g., blade vibrations due to contact with abradable coating [12]) rather than impact simulations. In structural dynamics, the explicit representation of abradable rub strips using continuum elements is generally too computationally expensive due to the large timescales required for the dynamic response to fully develop (tens of revolutions of the rotor). As a result, reduced engine models are combined with simplified abradable representations [12,13,14]. In contrast, in high-speed impact simulations, relatively small timescales (usually, only one or a few rotor revolutions) allow for explicit continuum elements-based representation of the abradable layer, thus potentially enabling a high level of accuracy in predicting deformation and loading of the fan blades during impact, as well as damage to the abradable lining.

A comprehensive methodology for modeling fan blade–ARS interactions is yet to be developed. As a step toward this goal, the objective of this study was to compare three simulation techniques, namely, the finite element method (FEM) in Lagrangian formulation, the smoothed particles hydrodynamics (SPH) technique [15], and the adaptive (hybrid) FEM/SPH approach [16], for their applicability to modeling of this interaction. These techniques were chosen to represent the spectrum of methods available to engineers and researchers for blade–ARS impact modeling, including the conventional mesh-based approach (FEM), the meshless method often employed in extreme deformation problems (SPH), and the relatively new and experimental technique combining mesh-based and meshless procedures (ADT)—a feature that is considered to be promising for this application. LS-DYNA—a simulation platform commonly used in industry for modeling impact scenarios in aircraft engines (see e.g., [17,18,19])—was employed in this work.

2. Metrics for the Description of the Blade–ARS Interaction

In this study, the interaction of a fan blade with the abradable lining was characterized using the following metrics:

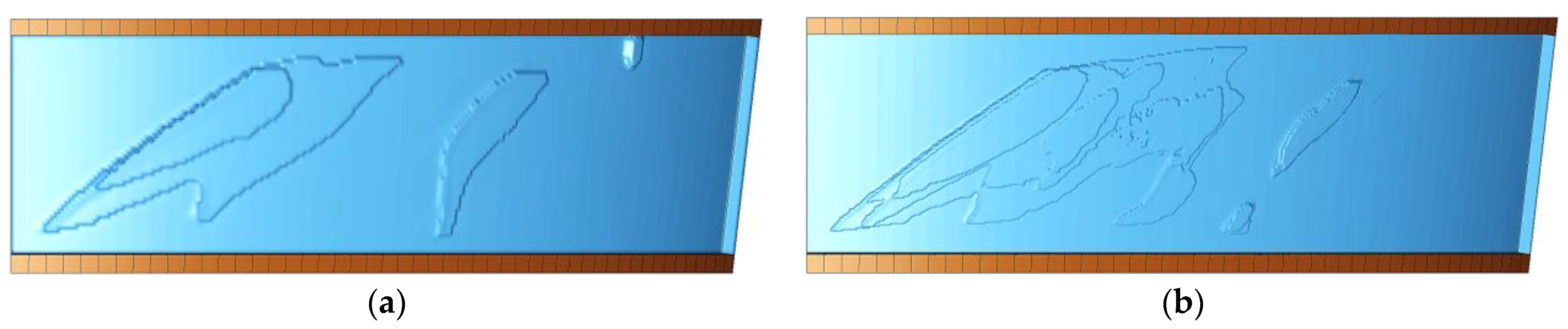
2.1. Rub Morphology

This metric, being qualitative, encompasses any feature related to the shape of the damaged region formed in the abradable as a result of the blade–ARS interaction. It also allows describing scenarios where the damaged region represents a series of disconnected areas, as illustrated in Figure 2. In this case, the largest of such regions is denoted as a “primary rub”, while the remaining regions are collectively referred to as “secondary rubs”.

2.2. Damaged Area

This metric represents the projected area of the damaged region formed in the abradable as a result of fan blade–ARS interaction and calculated on the 5 mm × 5 mm grid, as shown in Figure 2. If secondary rubs were present, the damaged area was calculated separately for the first rub and for the entire (total) damaged region that included both primary and secondary rubs. It should be emphasized that this metric represents only the two-dimensional projected area of the rub zone and does not quantify the volume of the damaged material.

2.3. Peak Force

The peak force represents a maximum resultant contact force during the first (primary) rub seen on the contact force–time diagram, as shown in Figure 3.

2.4. Process Duration

A time interval corresponding to the duration of the primary rub, as seen on the contact force–time diagram: $∆\mathrm{t}={\mathrm{t}}_2-{\mathrm{t}}_1$ (see Figure 3).

2.5. Average Force

The area under the segment of the force–time curve corresponding to the primary rub, divided by the process duration:

$${\mathrm{F}}_{\mathrm{a}\mathrm{v}\mathrm{e}}=\frac{{\int }_{{\mathrm{t}}_2}^{{\mathrm{t}}_1}\mathrm{F}\mathrm{d}\mathrm{t}}{{\mathrm{t}}_2-{\mathrm{t}}_1}$$

(1)

In the case of the adaptive method, the calculation of ${\mathrm{F}}_{\mathrm{a}\mathrm{v}\mathrm{e}}$ involved an intermediate step of summation of contact force–time outputs resulting from the blade–FE abradable and the blade–SPH abradable interactions (using the “sum curves” option in LS Pre-Post software).

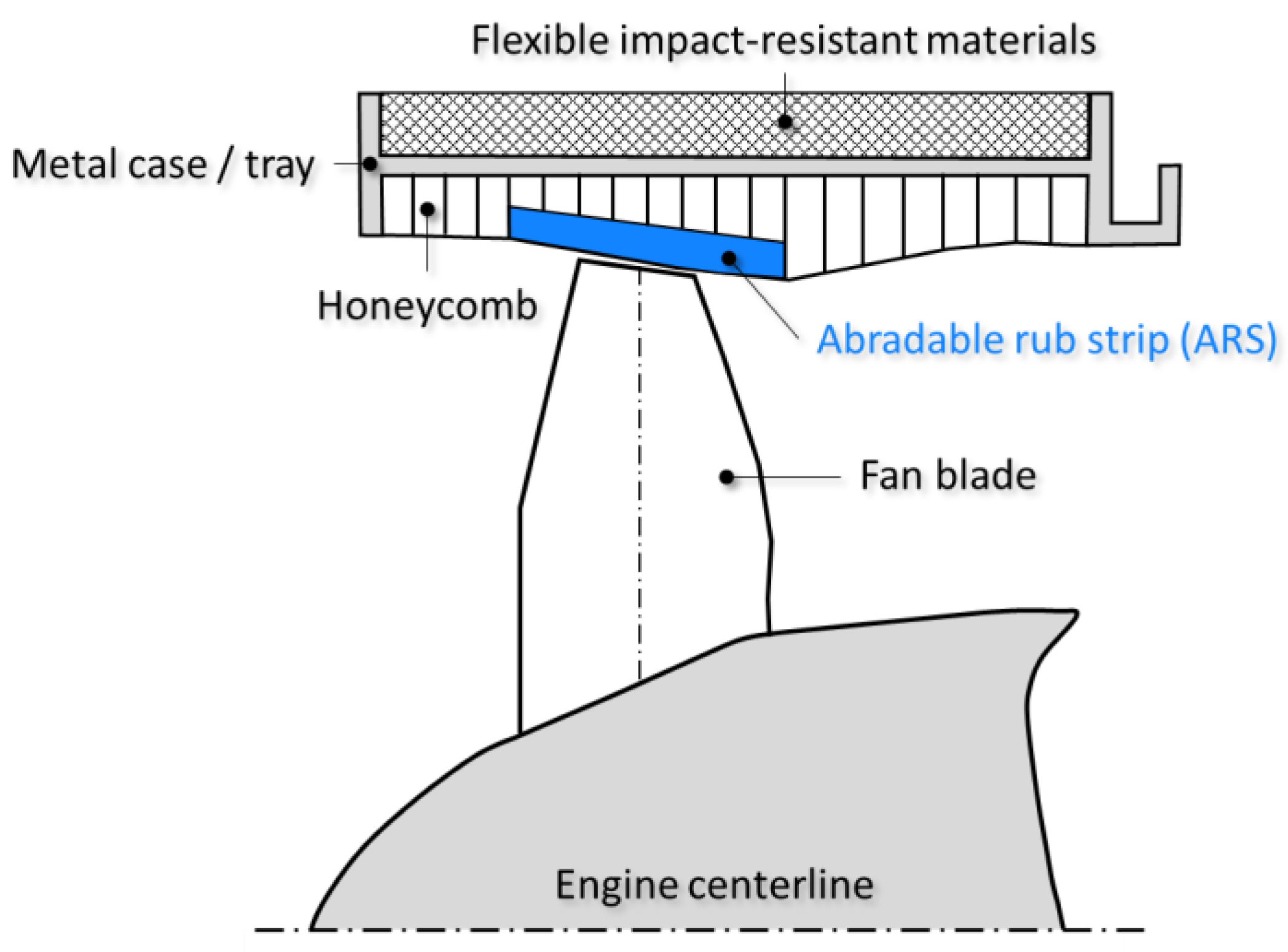
3. Material Modeling

3.1. Experimental Observations and Modeling Implications

The microstructure of a generic abradable rub strip material is exemplified in Figure 4. It comprises hollow glass microspheres randomly distributed in a polymer matrix, such as epoxy resin. Due to this composition, the material exhibits the following features.

• Temperature dependence of properties, owing to the known influence of heat on the behavior of polymers (softening, plasticization). Experimental uniaxial tension curves for an abradable rub strip material at room temperature (RT) and an elevated temperature (ET) corresponding to the glass transition region of its polymer matrix are shown in Figure 5a. As can be deduced from the figure, at ET the material exhibits nearly elastic–perfectly plastic behavior with the strength of only a fraction of its RT value. Near or above T_g, the abradable strength drops to “structurally insignificant” values, usually of the order of only a few megapascals.
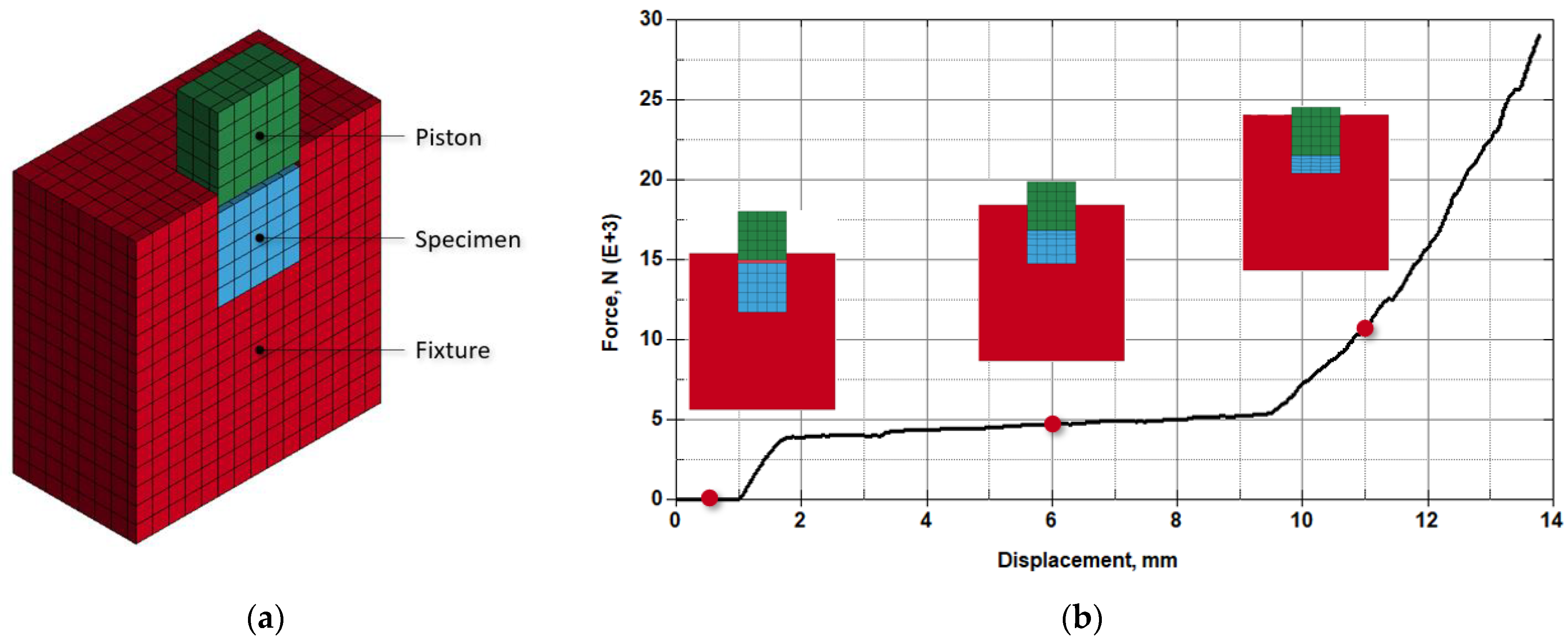
• Compaction under compressive loading, due to the progressive collapse of hollow glass microspheres, resulting in significant volume changes until densification. An experimental curve depicting the behavior of an abradable under confined compression loading is shown in Figure 5b. The pore collapse corresponds to the plateau stage on the curve.

A typical material model requires equations that relate stress to the deformation and internal energy (or temperature). A stress tensor describes the “stress state” at a point in the body subjected to external loading:

$$\mathsf{\sigma }=\left[\begin{array}{ccc}{\mathsf{\sigma }}_{11}& {\mathsf{\sigma }}_{12}& {\mathsf{\sigma }}_{13}\\ {\mathsf{\sigma }}_{21}& {\mathsf{\sigma }}_{22}& {\mathsf{\sigma }}_{23}\\ {\mathsf{\sigma }}_{31}& {\mathsf{\sigma }}_{32}& {\mathsf{\sigma }}_{33}\end{array}\right]$$

(2)

Here, ${\mathsf{\sigma }}_{\mathrm{i}\mathrm{i}}$—normal stresses, and ${\mathsf{\sigma }}_{\mathrm{i}\mathrm{j}}$—shear stresses. In most cases, the stress tensor may be separated into a uniform hydrostatic pressure $\left(\mathrm{p}\right)$:

$$\mathrm{p}=-\frac{1}{3}·\left({\mathsf{\sigma }}_{11}+{\mathsf{\sigma }}_{22}+{\mathsf{\sigma }}_{33}\right)$$

(3)

and a stress deviatoric tensor $\left({\mathsf{\sigma }}^{\mathrm{\prime }}\right)$ associated with the resistance of the material to shear distortion:

$${\mathsf{\sigma }}^{\mathrm{\prime }}=\left[\begin{array}{ccc}{\mathsf{\sigma }}_{11}-\mathrm{p}& {\mathsf{\sigma }}_{12}& {\mathsf{\sigma }}_{13}\\ {\mathsf{\sigma }}_{21}& {\mathsf{\sigma }}_{22}-\mathrm{p}& {\mathsf{\sigma }}_{23}\\ {\mathsf{\sigma }}_{31}& {\mathsf{\sigma }}_{32}& {\mathsf{\sigma }}_{33}-\mathrm{p}\end{array}\right]$$

(4)

such that

$$\mathsf{\sigma }={\mathsf{\sigma }}^{\mathrm{\prime }}-\mathrm{p}·\mathsf{\delta }$$

(5)

Here, $\mathsf{\delta }$ is a 3 × 3 identity (unit) matrix.

As the material will exhibit a significant deviation from the linear relationship between the hydrostatic pressure and the volume due to the noted compaction and densification, the pressure in modeling was calculated using an equation of state (*EOS in LS-DYNA), while the deviatoric stresses were computed separately using a strength model (*MAT in LS-DYNA).

3.2. Strength Model

High-speed impact scenarios, such as blade rub, plastic work–heat conversion, and friction, often result in a dramatic increase in local temperatures in the impact region. Temperatures during the blade rubs often reach or exceed the glass transition temperature of the polymer matrix of the ARS material, leading to its plasticization and reduction in strength to “structurally insignificant” levels, as described above.

To represent this behavior, the material was modeled as elastic–perfectly plastic using *MAT_ELASTIC_PLASTIC_HYDRO (*MAT_010). The following values were assigned to the material’s shear modulus and the yield strength: G = 100 MPa, σ_Y = 5 MPa. These parameters were purposely defined not to represent any particular abradable material tested by the author.

It should be noted that, for the sake of simplicity, the whole rub strip was assumed to be in the softened state (same values of G and σ_Y), regardless of the vicinity of the material to the rub zone. A more accurate representation would require a material model with temperature-dependent properties and a coupled thermo-mechanical analysis.

3.3. Equation of State

As was shown in Figure 5a, abradables demonstrate typical porous material-like behavior when subjected to triaxial compression, which is characterized by (i) a linear-elastic region; (ii) a near-constant load plateau; and (iii) a densification stage. *EOS_TABULATED_COMPACTION (*EOS_008) was employed to describe the considerable volume changes that the material exhibits under compressive loading due to the crushing of microspheres. The EOS defines the hydrostatic pressure $\left(\mathrm{p}\right)$ as a function of the volumetric strain $\left({\mathsf{\epsilon }}_{\mathrm{V}}\right)$, where ${\mathsf{\epsilon }}_{\mathrm{V}}$ is the natural logarithm of the relative volume:

$${\mathsf{\epsilon }}_{\mathrm{V}}=\mathrm{l}\mathrm{n}\left(\frac{\mathrm{V}}{{\mathrm{V}}_0}\right)$$

(6)

The parameters of the EOS were mainly determined using “first principles” and do not represent any particular abradable material tested by the author.

In the linear elastic regime, the ${\mathrm{p}-\mathsf{\epsilon }}_{\mathrm{V}}$ relationship is given by the bulk modulus of the material, calculated as

$$\mathrm{K}=\frac{2}{3}\mathrm{G}·\frac{\left(1+\mathsf{\nu }\right)}{\left(1-2\mathsf{\nu }\right)}$$

(7)

where G = 100 MPa is the shear modulus of the material at the elevated temperature and $\mathsf{\nu }=0.35$ is its Poisson’s ratio.

Pressure at the start of the plateau region (${\mathrm{p}}_{\mathrm{c}\mathrm{r}}$ that corresponds to the initiation of microsphere crushing) was evaluated using the following criterion:

$${\mathrm{p}}_{\mathrm{c}\mathrm{r}}=\mathrm{m}\mathrm{i}\mathrm{n}\left(\mathrm{k}·\frac{2{\mathrm{E}}_{\mathrm{g}\mathrm{l}}}{\sqrt{3\left(1-{\mathsf{\nu }}_{\mathrm{g}\mathrm{l}}^2\right)}}·{\left(\frac{\mathrm{t}}{\mathrm{R}}\right)}^2;{2\mathsf{\sigma }}_{\mathrm{c},\mathrm{m}\mathrm{a}\mathrm{x}}·\frac{\mathrm{t}}{\mathrm{R}}\right)$$

(8)

Here, the first condition corresponds to a buckling pressure of a microsphere submersed in plasticized polymer resin if idealized as a thin-walled spherical shell under uniform external pressure [20], where ${\mathrm{E}}_{\mathrm{g}\mathrm{l}}$ and ${\mathsf{\nu }}_{\mathrm{g}\mathrm{l}}$ are the Young’s modulus and the Poisson’s ratio of glass—the material of the microsphere; t and R are the wall thickness and the radius of the microsphere; and k is a coefficient that was added to the shell buckling formula to account for deviations in the experimental critical load from the value predicted by the equation when k = 1. As suggested by the data presented in [21], for small radius-to-thickness ratios, such as $\frac{\mathrm{R}}{\mathrm{t}}<200$, the coefficient of k = 0.5 can be used. The second condition stands for the hydrostatic pressure that causes failure of the microsphere due to stress in its wall exceeding its material’s compressive strength ${\mathsf{\sigma }}_{\mathrm{c},\mathrm{m}\mathrm{a}\mathrm{x}}$. It can be speculated that ${\mathsf{\sigma }}_{\mathrm{c},\mathrm{m}\mathrm{a}\mathrm{x}}$ used in Equation (8)—due to microsphere shells usually being only a few microns thick—should correspond to the strength of their base material (glass) with a very low content of defects, such as the strength of glass fibers (approximately 1000 MPa).

For a generic abradable material with glass microspheres (${\mathrm{E}}_{\mathrm{g}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{s}}=\mathrm{75,000}$ MPa, ${\mathsf{\nu }}_{\mathrm{g}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{s}}=0.2$) of $\mathrm{R}=50\mathsf{\mu }\mathrm{m}$ and $\mathrm{t}=1\mathsf{\mu }\mathrm{m}$, ${\mathrm{p}}_{\mathrm{c}\mathrm{r}}$ was estimated using Equation (8) at the level of 15 MPa.

The initiation of the densification phase was marked by the volumetric strain of 80%, which is within the range of experimentally observed values for closed-cell porous materials in compression tests [22].

The “first principles”-based ${\mathrm{p}-\mathsf{\epsilon }}_{\mathrm{V}}$ relationship used as input for the EOS in this study is shown in Figure 6. For numerical stability, the curve was smoothed by adding additional points at the transition from the linear-elastic region to the plateau and from the plateau to the densification stage. For the same purpose (numerical stability), a small non-zero slope was added to the plateau region.

The ability of the proposed material model to qualitatively represent the behavior observed experimentally was ensured by conducting a virtual confined compression test, in which a rectangular abradable material specimen placed within a rigid confinement was crushed by a rigid piston (Figure 7a). As seen in Figure 7b, the simulation with the proposed material model replicates the expected linear-elastic, plateau, and densification stages on the force–displacement curve obtained in the virtual experiment.

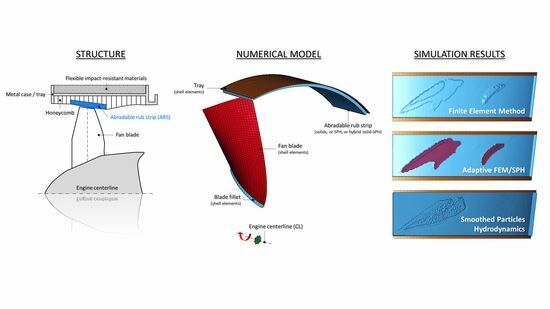
4. Simulation Model

4.1. General Description

The numerical model used in the present study to investigate the fan blade–ARS interaction is shown in Figure 8. It comprises the models of a fan blade and a 60° ARS segment attached to a flexible support (tray). The models of the blade and the tray, including their discretization, pre-loading, and boundary conditions, were supplied by the industry partner. Modeling of the abradable rub strips (FEM, ADT, and SPH implementations) and contact modeling was conducted at the University of Windsor. In all simulations, the size of the timestep in explicit time integration was held constant and equal to 5 × 10⁻⁵ ms.

The fan blade was discretized with shell elements. The nodal thicknesses of the shell elements were mapped from the solid geometry of the blade and stored using the *ELEMENT_SHELL_THICKNESS keyword. To achieve the steady state prior to the transient phase, the blade was preloaded to the centrifugal load using static explicit dynamic relaxation (IDRFLG = −1 in *CONTROL_DYNAMIC_RELAXATION keyword). The centrifugal load was applied using *LOAD_BODY_GENERALIZED_SET_PART. The load was set to smoothly increase throughout the dynamic relaxation phase. The convergence criterion was set to DRTOL = 1 × 10⁻⁵ in the *CONTROL_DYNAMIC_RELAXATION card. There was a 1.27 mm gap between the tip of the preloaded blade and the abradable.

The transient phase begins upon completion of the pre-loading phase, and the velocities on all rotating parts are initialized using the *INITIAL_VELOCITY_GENERATION keyword. The fan blade–ARS interaction during the transient phase was triggered by a forced excursion of the blade. For this purpose, a rigid body (referred to as a “CL rigid body” in Figure 8) was created at the assumed centerline (CL) of the engine. The rigid body was connected to the root edges of the blade and the fillet using *CONSTRAINED_EXTRA_NODES and was forced to move along a loop-like path in the XY plane, as shown in Figure 9 (this motion was assigned using the *BOUNDARY_PRESCRIBED_MOTION_RIGID keyword), while rotating around the z-axis (this axis was aligned with the reversed flow direction).

4.2. Numerical Schemes

The following numerical techniques were considered in the present study as possible options for ARS representation:

• Finite Element Method (FEM) with the element erosion. This approach usually provides a good balance between simulation accuracy and computational efficiency in impact problems; however, its applicability may vary depending on the levels of deformation experienced by elements in simulations. In addition, identifying erosion strain—a non-physical parameter determining the upper limit of deformation that an element can tolerate before removal from simulation—is often non-trivial.
• Smoothed Particles Hydrodynamics (SPH) meshless technique, in which the continuum is modeled as the arbitrary lattice of interacting particles/interpolation points. This method eliminates mesh tangling problems inherent to the Lagrangian finite element method and does not require an erosion algorithm, which often makes it very suitable for high-speed impact problems. The SPH method is, however, known to be more computationally expensive compared to FEM. Therefore, further study was required to decide if the cost–benefit ratio of this method makes it a suitable replacement for FEM in the considered problem.
• Adaptive (Hybrid) FEM/SPH formulation, which permits the adaptive conversion of finite elements to SPH particles at high deformation levels when the traditional finite element method becomes inefficient. In this method, the SPH particles replacing the failed solid Lagrangian elements inherit all the nodal and integration point quantities of the failed solid elements. Potential benefits of this technique, that required evaluation, are the reduced sensitivity to erosion strain compared to the traditional FEM, and a possible reduction in computational time compared to SPH.

Discretization of a representative element of ARS using the three techniques is depicted in Figure 10. It corresponds to the case of using four elements through the thickness of the rub strip. For the hybrid method, the inactive SPH particles (activated upon finite element erosion), are shown as dots inside the solid elements. For the SPH model, as centers of the particles occupy the same positions as nodes in the FEM model, the term “number of particles through-the-thickness”, used in the present study to describe SPH discretization of ARS, should be understood as “the number of particle diameters through-the-thickness”.

4.3. Contact Modeling

The multiplicity of contact algorithms in LS-DYNA creates a challenge of identifying a robust and stable procedure, which could properly represent the blade–abradable interaction. Multiple contact options were studied by the author; observations along with the best practices for each numerical scheme are discussed below.

First, it should be noted that the treatment of shell edges plays a significant role in rub simulations when the blade is modeled with shell elements. In LS-DYNA, contact at shell edges by default is treated assuming the presence of “caps” along the free edges of the shell parts with the size of such caps equal to half the thickness of the shell (i.e., the default settings force automatic extension of the shell edges). For segment-based contacts (option SOFT = 2), this behavior is controlled by the parameter SHLEDG in the *CONTROL_CONTACT card. Setting SHLEDG = 1 (the default is 0), allows for preventing the undesired extension of the shell edges, as illustrated in Figure 11, using a simulation that involved one shell element and one solid element.

Therefore, to ensure the presence of the intended tip clearance and to prevent premature rubbing of the blade into the rub strip, the interaction of a shell blade and a solid ARS must be modeled using a segment-based contact, such as *CONTACT_…_SURFACE_TO_SURFACE with option SOFT = 2, setting SHLEDG = 1 in the *CONTROL_CONTACT card.

For shell–SPH interactions, *CONTACT_…_NODES_TO_SURFACE must be used in LS-DYNA. This contact does not support the SOFT = 2 option and, thus, the SHLEDG parameter has no effect on the treatment of shell edges with this algorithm. However, the undesired shell edge extension can be prevented by setting parameter SRNDE = 2 in the *CONTACT_…_NODES_TO_SURFACE card (for the MPP solver, option GRPABLE = 1 must also be set).

The effect of shell edge treatment on the results of blade rub simulations is shown in Figure 12. As can be deduced from the figure, premature (unintended) rubbing occurs before the initiation of blade excursion in the model if shell edges extension is not suppressed. Moreover, excitation of the blade following premature rubbing causes changes to the resulting morphology of the rub zone.

For the ADT method, the definition of contacts involved several additional steps. In particular, the user has to ensure that contact between the blade and SPH is established, as SPH particles can be “born” upon erosion of the solid elements but contact with the blade would not engage. This can be verified by means of a trial simulation in which solid elements are set to erode at the very beginning (using time as the erosion criterion) making the blade–SPH interaction, if it takes place, clearly visible. Although both the AUTOMATIC and ERODING options of the *CONTACT_…_NODES_TO_SURFACE are suitable for modeling blade–adaptive SPH interaction, the latter algorithm with option SOFT = 1 was found to be more reliable. It was also discovered that in LS-DYNA R13.0, the birth time of the NODES_TO_SURFACE contact has to be set to a small but non-zero value for the contact to engage between the blade and the SPH particles that are activated after erosion of the finite elements. Furthermore, these particles are “born” coupled with the adjacent solid elements, but, upon erosion of these elements, will not have contact with the rest of the solids around them by default. Therefore, an additional NODES_TO_SURFACE card was required for this interaction to happen. This contact must be eroding, as it is expected that the solid elements will continue to be deleted, and the SPH–solid contact surface will need to be updated continuously.

A description of the contact algorithms and their parameters used in this study is provided in

Table 1. A summary of the contact algorithms used and their main parameters.

Interacting Entities	Contact Type and Parameters	Model(s)
Solid ARS—Shell blade	*CONTACT_ERODING_SURFACE_TO_SURFACE (SOFT = 2) *CONTROL_CONTACT (SHLEDG = 1)	FEM, ADT
SPH ARS—Shell blade	*CONTACT_AUTOMATIC_NODES_TO_SURFACE_MPP (GRPABLE =1, SOFT = 0, SRNDE = 2)	SPH
SPH ARS—Shell blade/Solid ARS/Shell Tray	*CONTACT_ERODING_NODES_TO_SURFACE_MPP (BT > 0, SOFT = 1)	ADT
Shell Tray—Solid ARS (adhesion of matting surfaces)	*CONTACT_TIED_NODES_TO_SURFACE	FEM, ADT
Shell Tray—SPH ARS (adhesion of matting surfaces)	*CONTACT_TIED_NODES_TO_SURFACE	SPH
Shell Tray—SPH ARS (no particles-through-tray penetration)	*CONTACT_AUTOMATIC_NODES_TO_SURFACE (SOFT = 1)	SPH

.

5. Results and Discussion

5.1. Mesh Sensitivity

In the mesh sensitivity study, the ARS was represented in the models using 3, 4, or 6 elements through the thickness, which corresponded to element/particle sizes of 3.39 mm, 2.54, and 1.69 mm, respectively (element size increments remained constant and equal to 0.85 mm).

The rub morphologies for different densities of discretization and the corresponding contact force–time diagrams are shown in Figure 13 and Figure 14, respectively. As can be deduced from the figures, all the finite element and adaptive models predict secondary rubs, while in the SPH models those rubs are either lacking or negligibly small in terms of force and area. This behavior of the models will be discussed in more detail in the following sections. The predicted morphologies of the primary rubs also varied noticeably depending on the modeling approach and discretization density. Variation in the other metrics is shown in Figure 15.

Analogous trends are seen for the contact forces (see Figure 14 and Figure 15b). Here, the variation is ±17% (FEM), ±28% (ADT), and ±10% (SPH) of the corresponding mean values. As with the peak force, the most consistent predictions of the average load with respect to the element size were obtained using the SPH model. The same is true for the duration of the primary rub (Figure 15c), which varied between ±15% (FEM), ±28% (ADT), and ±6% (SPH) of the corresponding mean values.

The damaged area predictions differed somewhat between the models; however, each model demonstrated only moderate variations in the damaged areas with change in the element size: ±14% (FEM), ±11% (ADT), and ±13% (SPH) of the corresponding mean values (see Figure 15d).

As can be deduced from Figure 15e, depending on the mesh density and the numerical method, the computational time can vary from approx. 3.5 min to approx. 3.5 h. Notably, while ADT and SPH models with the same mesh density required approximately the same computational time, the FEM model of the same element size was solved much faster. For example, the SPH and ADT models with four elements/particles through-the-thickness of the ARS consumed 64.98 and 58.10 min of the machine time, respectively, while the FEM model with the same density of discretization required only 5.98 min! Therefore, it was decided, in addition to the “equivalent element size” FE model, (EES; “equivalent” with respect to the other two methods—ADT and SPH), to introduce the “equivalent computational time” FE model (ECT), which would have a denser mesh and computational time of approximately 1 h. After several trials, the results of which are also shown in Figure 15e, it was found that, in such an FEM model, the ARS must be discretized using 10 elements through the depth (element size of 1.02 mm; 58.67 min run time).

As can be deduced from Figure 16, similarly to the EES model, the ECT model predicts secondary rubs; however, for the latter, the predicted rub area is significantly larger: 200 cm² ECT vs. 137 cm² EES (+46%) for the first rub, and 219 cm² vs. 180 cm² (+22%) for the total damaged area. This is in line with the fact the ECT model predicts that the blade will stay in contact with the ARS for a longer period of time during the first rub: 0.610 ms vs. 0.377 ms for the EES model (+62%). In addition, the ECT model predicts no distinct peak on the force–time plot (see. Figure 17). The ECT model prediction of the average contact force is 26% lower than that of the EET model: 9672 N vs. 13,130 N.

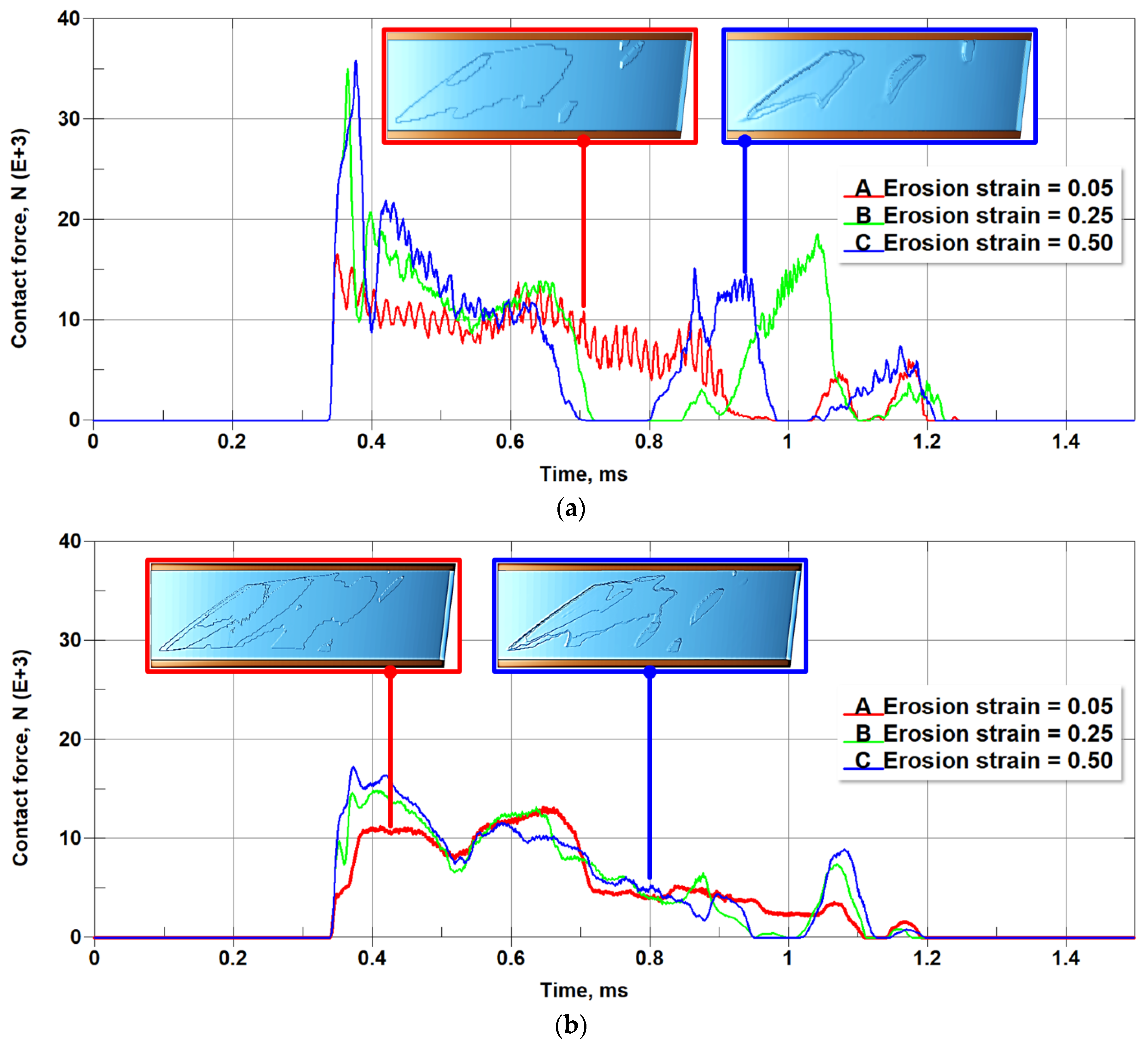
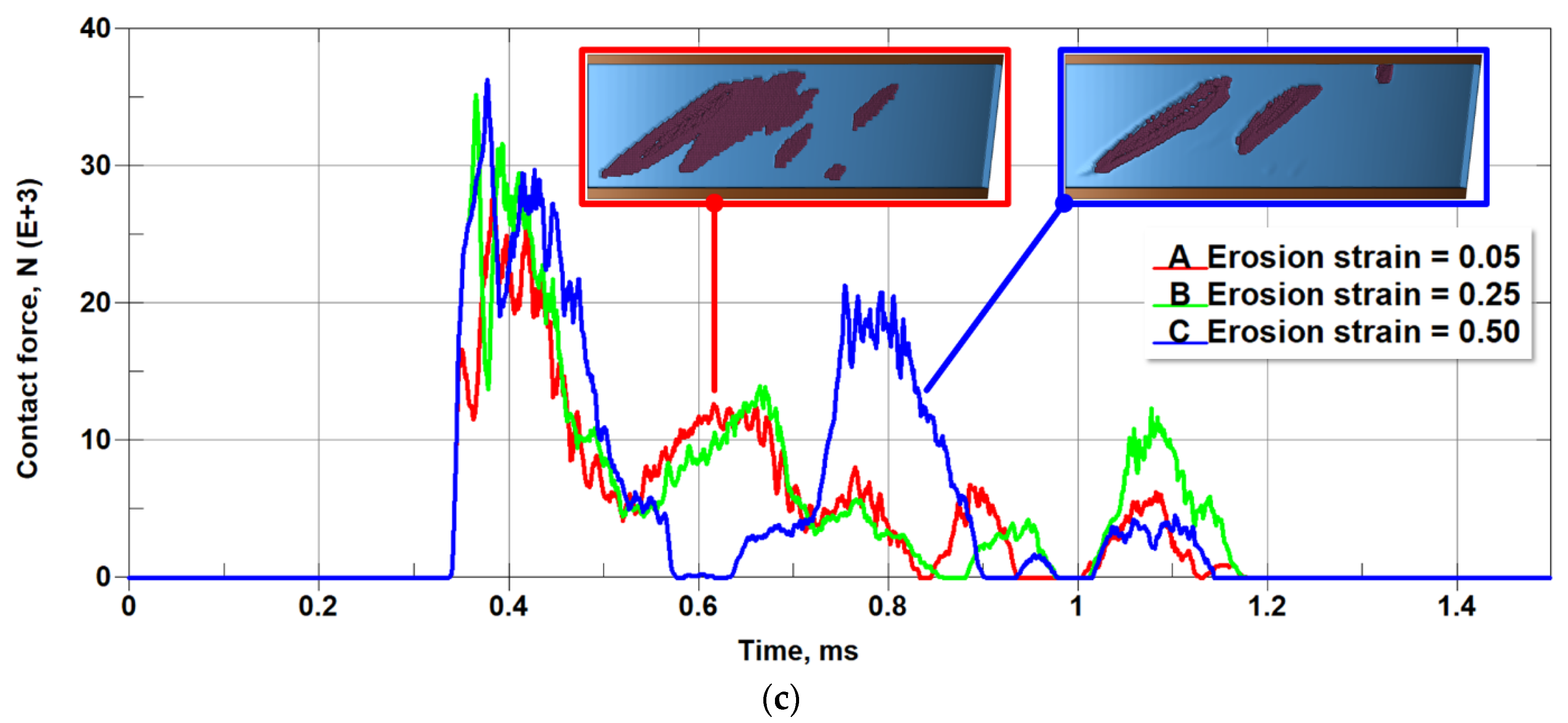
5.2. Sensitivity to Non-Physical Parameters: Element Erosion Strain and Number of Neighboring Particles

The element erosion strain in the finite element method and the number of neighbors per particle in the SPH technique are artifacts of the corresponding numerical schemes rather than physical properties. It was, therefore, imperative to study how they affect the output of the rub simulations.

In this study, element erosion in the FEM and ADT techniques was controlled using the EFFEPS parameter (maximum effective strain at failure) on the *MAT_ADD_EROSION card, while the NMNEIGH parameter in the *CONROL_SPH keyword was used to define the number of neighbors per particle in the SPH method.

The results of simulations with erosion strains of 5%, 25%, and 50% are shown in Figure 18 and Figure 19 for the FEM (the EES model with 4 and the EET model with 10 particles through-the-thickness of the ARS) and the ADT (4 particles through-the-thickness) methods.

The observations can be summarized as follows. First, the rub morphology changes dramatically with change in the erosion strain, as can be seen in Figure 18. This also reveals itself in the change to the damaged area, which varies as a function of the erosion strain: ±38% (EES FEM), ±25% (ECT FEM) and ±39% (ADT) of the corresponding mean values, as depicted in Figure 19c. Second, the average rub force changes considerably with the value of the erosion strain, especially for the EES (±25% of the mean) and the ADT (±32% of the mean) models. For the ECT model, this variation is less pronounced, as it constitutes only ±13% of the respective mean value. Notably, estimates of the rub force calculated using the ECT model are significantly lower than those obtained using the EES and the ADT models (see Figure 19a). Finally, the choice of erosion strain will also affect the prediction of the process duration, as can be seen in Figure 19b.

The number of neighboring particles in the SPH method varied within the 50–150 range. It was kept constant throughout a simulation for static memory allocation (default—would adjust adaptively) by setting the NMNEIGH parameter as a negative value in the *CONROL_SPH card. For the given mesh density (four particles through-the-thickness of ARS) and the parameter’s range, no influence on the results was observed: the force–time graphs for simulations with NMNEIGH values of −50, −100, and −150 almost exactly repeat each other.

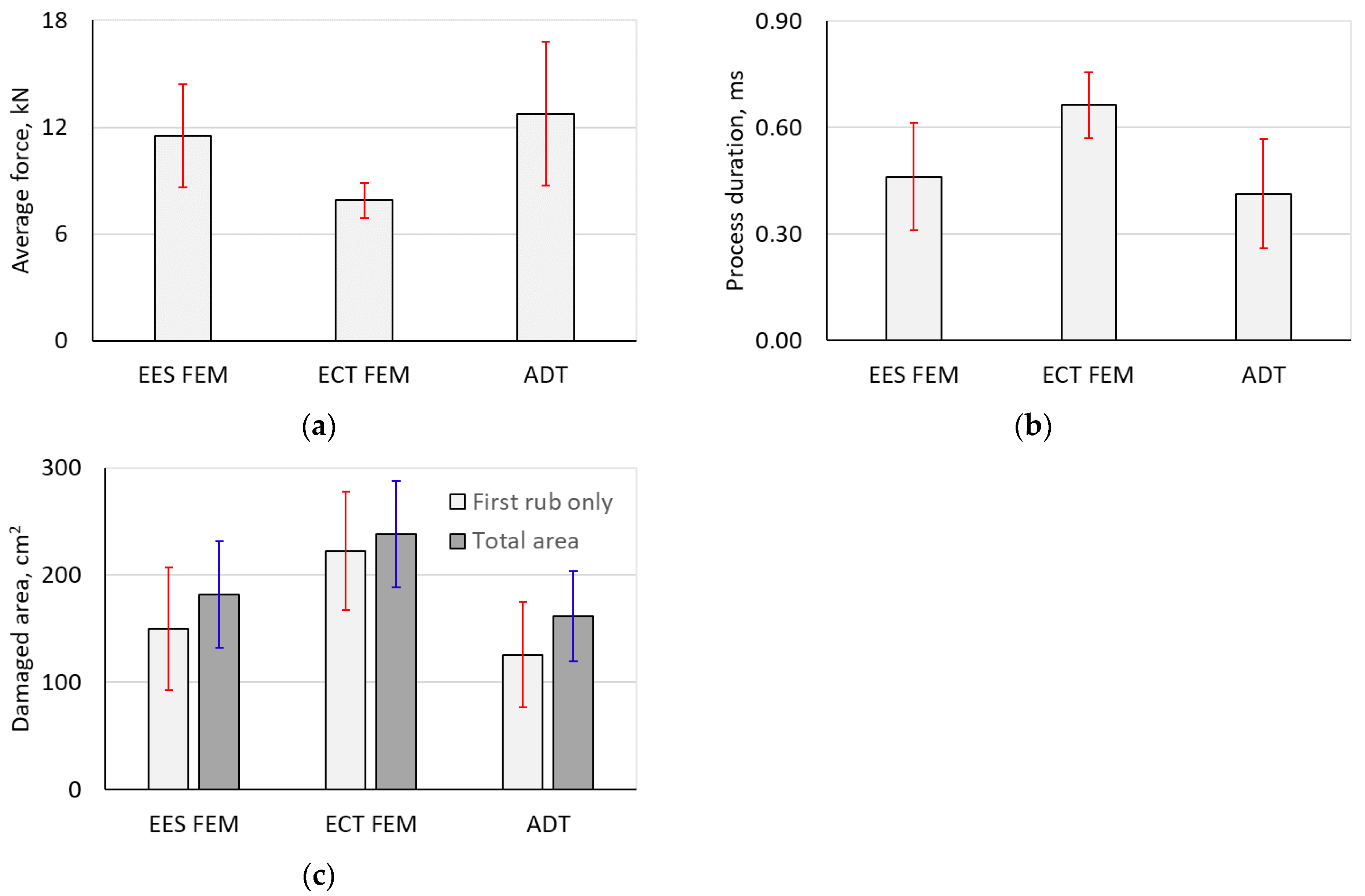
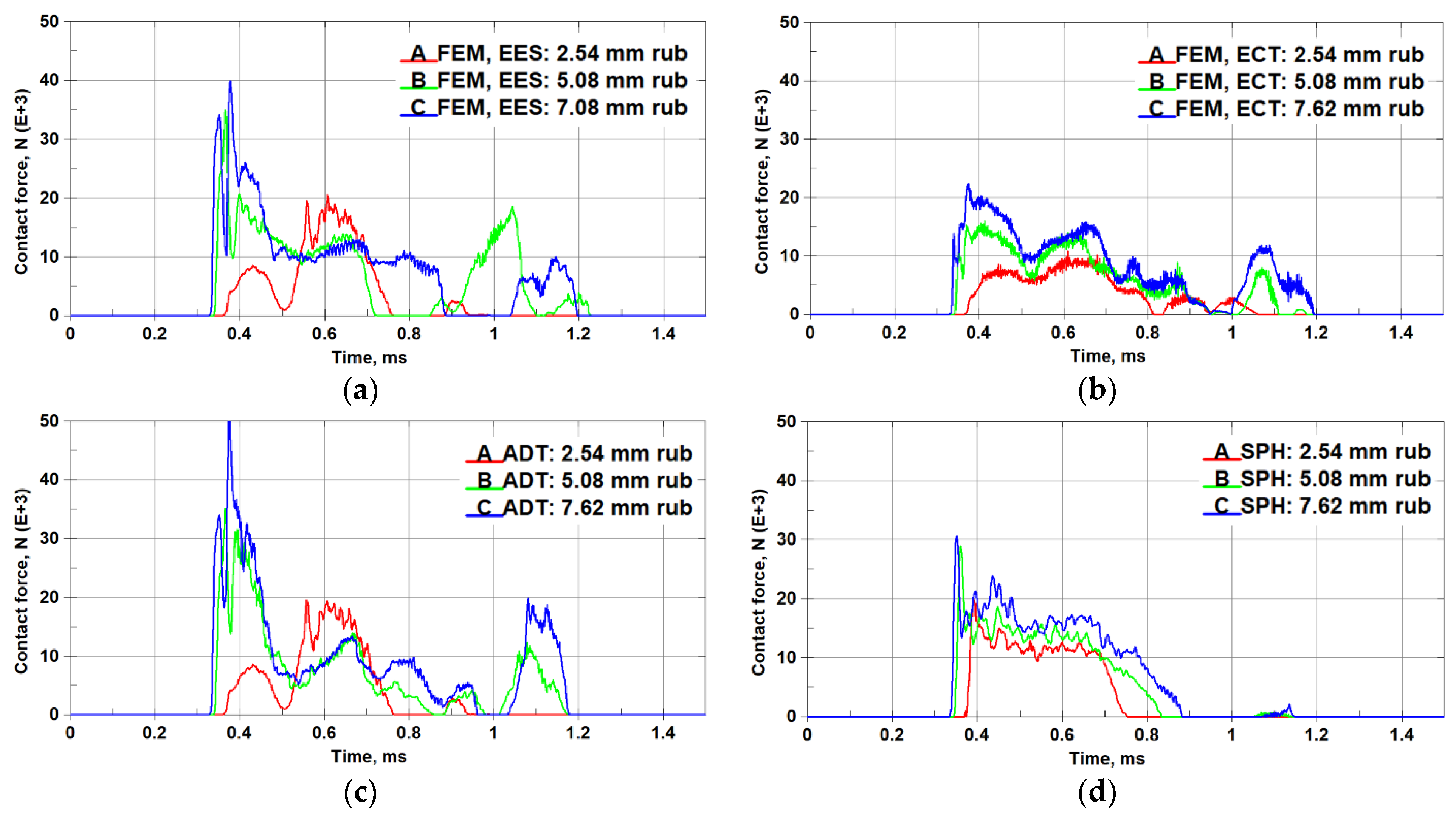
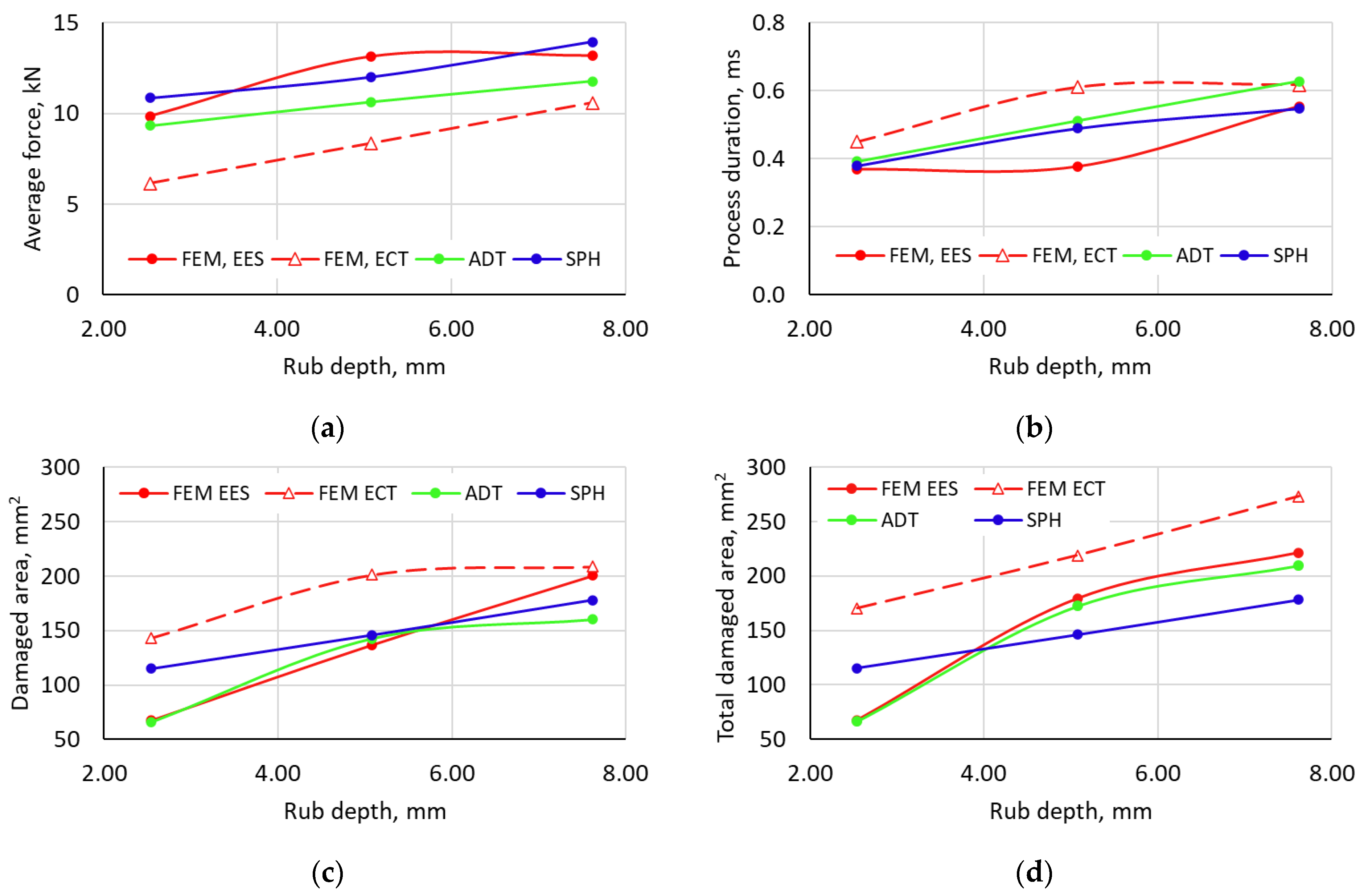
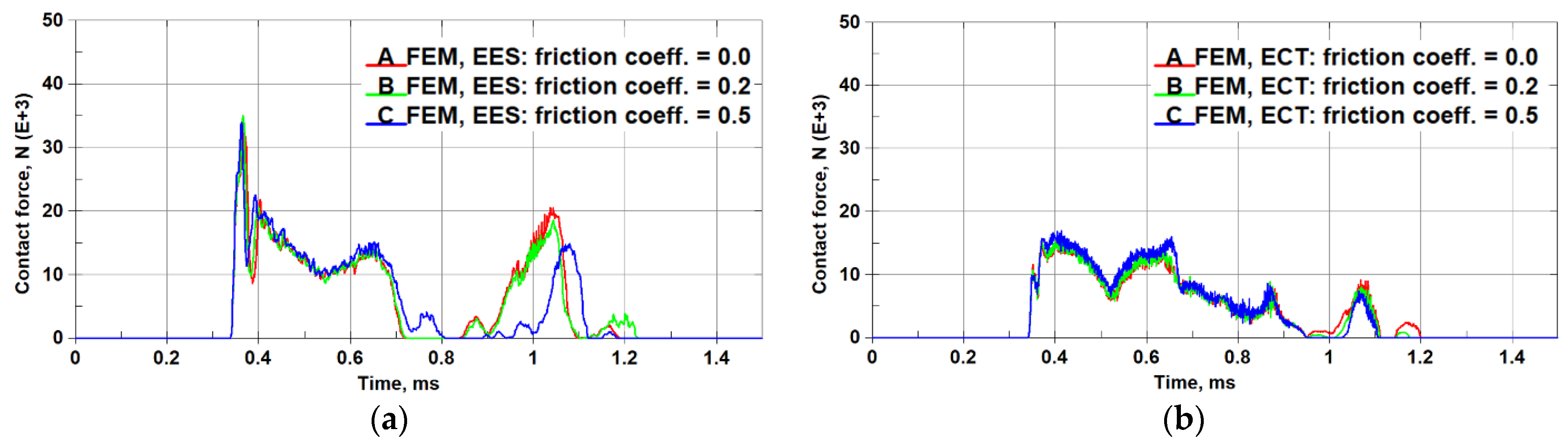
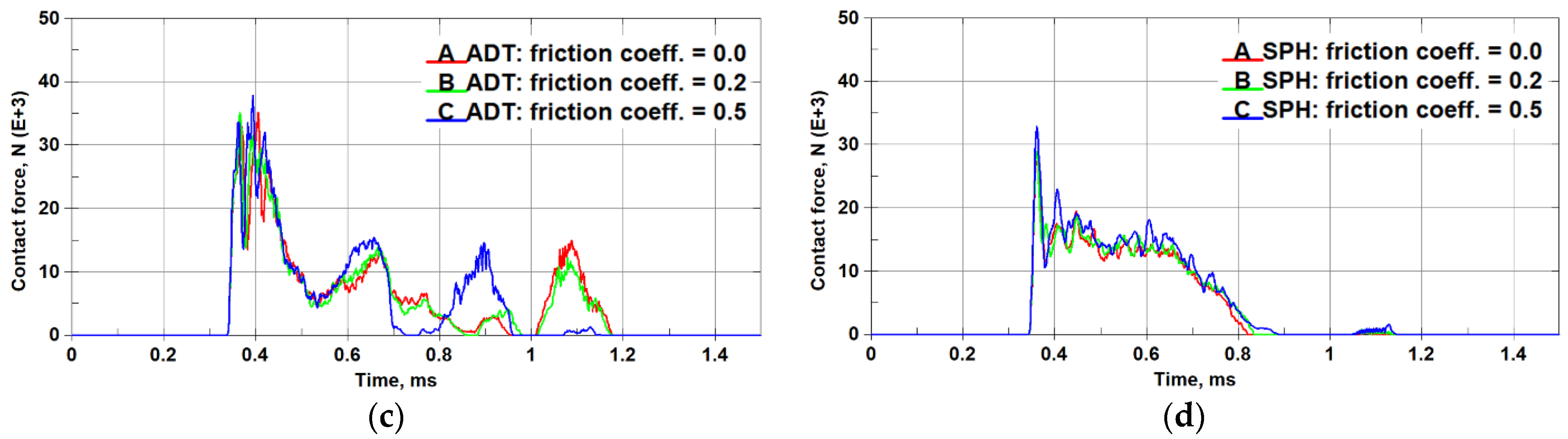
5.3. Sensitivity to Process Parameters: Incursion Depth and Friction Coefficient

Further analyses were performed to study the response of the models to variations in the blade incursion depth. The following blade incursions were considered: 2.54 mm, 5.08 mm (used in all models considered in the previous sections), and 7.62 mm. The constant element erosion strain of 25% was used in the FEM and the ADT models. Predictions of the models are compared in Figure 20 and Figure 21.

As expected, the rub depth influences the contact force significantly: larger forces were predicted by all models for deeper blade incursions. The predictions, however, had some notable differences:

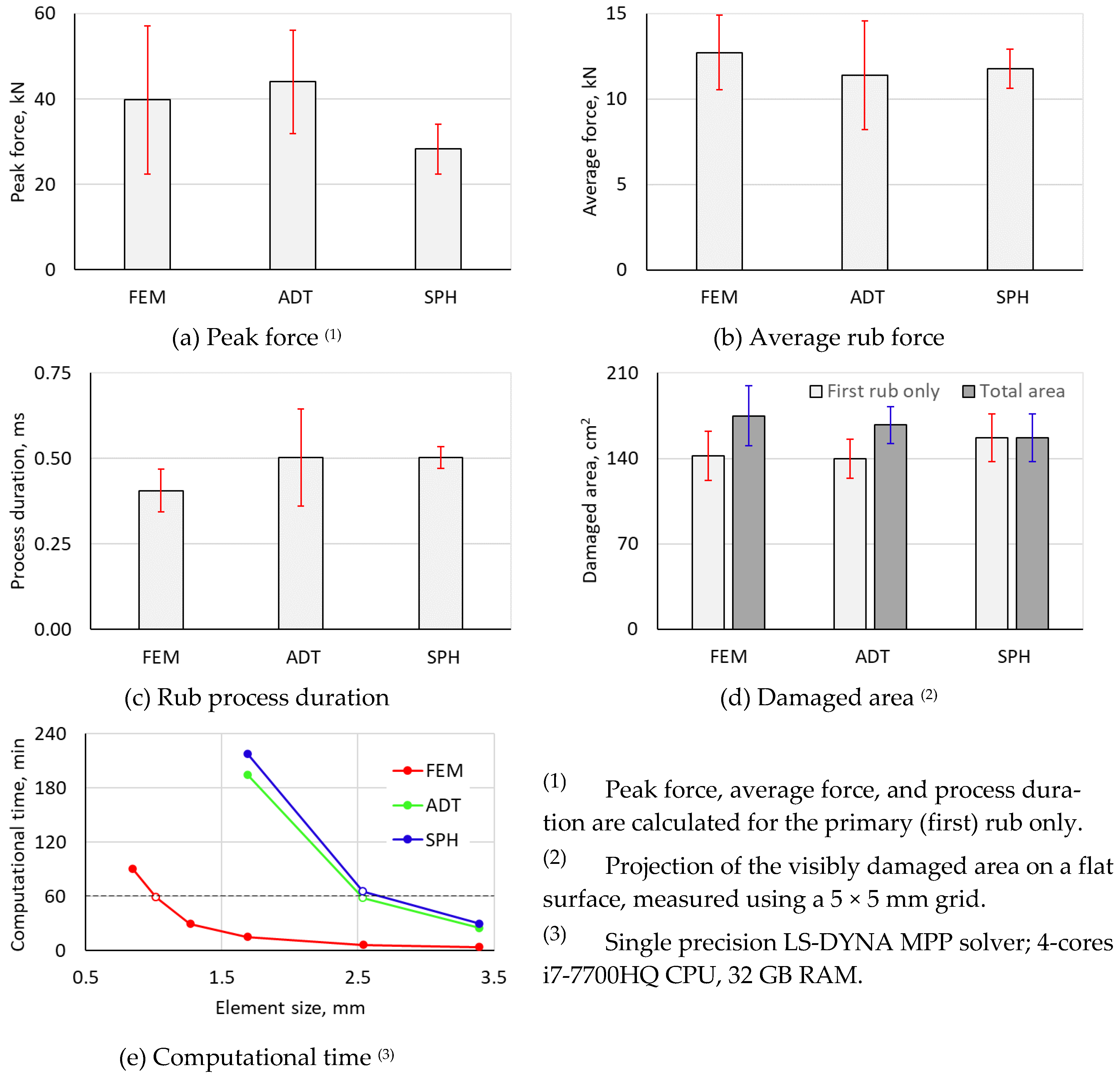
• Large oscillations were noted on the F-t plots of the FEM EES and ADT models (4 elements through the ARS thickness) and, thus, required data filtering. Such effects were not seen with the FEM ECT (10 elements through the thickness) and SPH (4 particles through-the-thickness) models.
• The FEM (both EES and ECT) and ADT models predicted deep secondary rubs for all three considered incursion depth scenarios. Notably, predictions of the initiation of the secondary rubs, their duration, and force magnitudes are not consistent between the three models (see Figure 20a–c). In contrast, although secondary rubs were also predicted by the SPH model, their magnitudes are negligibly small compared to the primary (first) rub for all the considered rub depths, as can be seen in Figure 20d.
• The shapes/profiles of the F-t curves in the case of the 2.54 mm rub, as predicted by the FEM (both EES and ECT) and ADT models, are notably different from those predicted for the deeper rubs (see Figure 20a–c). In contrast, the SPH model predicted similar “impulse” shapes for all three rub depths (Figure 20d).

The calculated process metrics are shown as a function of the rub depth in Figure 21. The following can be deduced from the figure:

• The SPH model consistently predicts a linear or nearly linear increase in all metrics (average force, process duration, and damaged area) with increase in the rub depth. Such consistency is not seen with all other models.
• With increase in incursion, the FEM ECT model predicts a notably non-linear change to the first rub damage (almost no difference for 5.08 mm and 7.62 mm rubs) and a linear change in the total damaged area. The opposite is true for the FEM EES model.
• The contact force predicted by the FEM ECT model is generally lower compared to the predictions of the other models.
• The predictions of the total damaged area with all incursion depths are notably different for the SPH and the FEM ECT models.

The influence of the friction coefficient input on the predictions of the models is shown in Figure 22. As can be deduced from the figure, it mainly affects the output of the FEM EES and ADT models, shifting the initiation of the secondary rub (FEM EES model—the secondary rub is delayed with the larger value of the coefficient; ADT model—starts earlier). For the FEM ECT and the SPH models, the value of the friction coefficient does not seem to have a significant effect on the results. It should be noted, however, that current implementation of the models does not account for frictional heating.

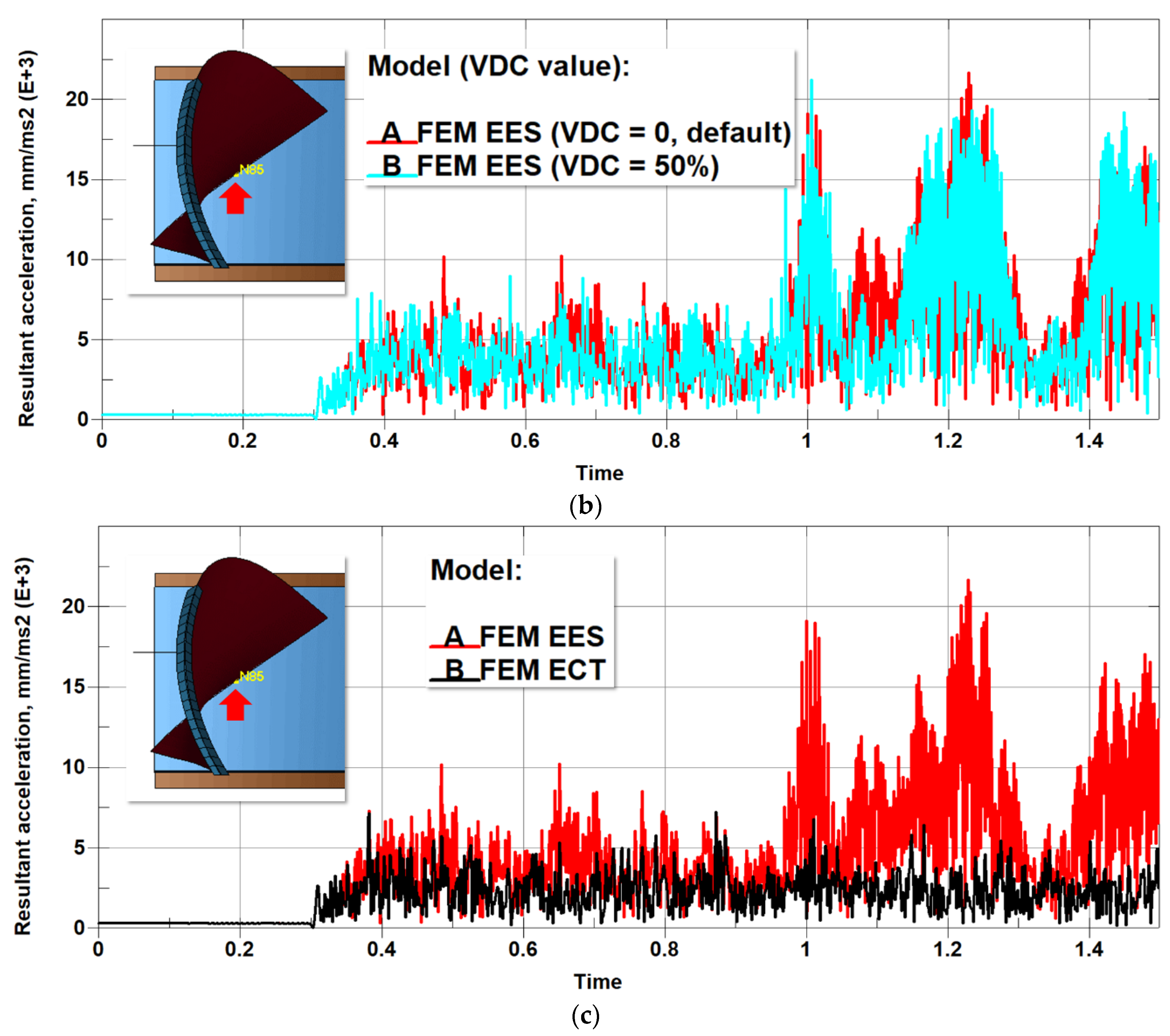
5.4. Additional Remarks

As seen in the previous sections, the mesh-based techniques (FEM and ADT) predicted noticeable secondary rubs, which were not observed at all or were negligibly small when the mesh-free technique was used. Therefore, an additional study was conducted to understand possible reasons for such a difference. The following factors that could possibly contribute to this behavior were considered:

• Excitation of the blade resulting from erosion of finite elements.
• Differences in the contact algorithms used to represent blade–FE ARS and blade–SPH ARS interactions.

In the FEM and the ADT models, upon element erosion, the blade temporarily and abruptly loses its contact with the ARS and has to travel some distance, proportional to the element size, before it can re-establish contact with the next row of elements, as schematically illustrated in Figure 23. The abrupt loss of contact due to erosion of elements can give rise to ‘spurious’ oscillations of the blade. Erosion of particles is not used in the SPH method; thus, the contact between the blade and the ARS can be maintained continuously during the incursion phase and no artificial excitation of the blade should happen.

Figure 24 represents the acceleration of a node on the tip of the blade as a function of time. As can be deduced from Figure 24a, the nodes on the tip of the blade in the EES and the ADT model (both require element erosion for the ARS) oscillate notably compared to the SPH model. An attempt was made to reduce the oscillations by applying contact damping (viscous damping coefficient in the contact cards, VDC; defined as percent of critical damping). However, no significant effect was observed, as seen in Figure 24b. As expected, the measure that helped reduce the artificial blade excitation due to element erosion was reduction in the element size (see Figure 24c): in the FEM ECT model (10 elements through the ARS, run time ~1 h), the tip node oscillations had approximately the same amplitude as in the SPH model (4 particles through the ARS, run time ~1 h).

It should be noted, however, that, despite the lack of spurious oscillations, the FEM ECT model still predicts secondary rubs, as was seen in the previous sections. Therefore, the presence or lack of secondary rubs cannot be attributed to the element erosion alone and is likely also influenced by the second factor mentioned above—the different contact algorithms used for blade–FEM and blade–SPH interactions. However, the choice of a contact algorithm for a given modeling technique, as discussed in the Contact Modeling section, is often limited in LS-DYNA. In particular, the only option to model the interaction of the FEM (blade) and SPH (ARS) parts is the *CONTACT_…_NODES_TO_SURFACE algorithm. For the FEM blade–FEM ARS interaction, more options are available theoretically; however, only the *CONTACT_…_SURFACE_TO_SURFACE was found to provide adequate and stable results. For example, in multiple attempts to utilize *CONTACT_… _NODES_TO_SURFACE for modeling of the FEM blade–FEM ARS interaction, it was observed that, with this algorithm, the blade tended to remove only one layer of elements in the ARS, regardless of the element size, the depth of incursion (!),or the contact parameters used, thus making it not suitable for the purposes of this study. Therefore, although the contact algorithms can likely affect the appearance or lack of secondary rubs in the results, it was not possible to test this hypothesis at this time.

6. Conclusions

The purpose of this study was to compare three numerical techniques that can be used for the simulation of a deep incursion of fan blades into the abradable rub strip in turbofan engines, namely, the finite element method (FEM), smoothed particles hydrodynamics (SPH), and the adaptive FEM-SPH technique (ADT). The main observed features of the models developed using these methods are summarized below.

FEM model:

• Strong mesh sensitivity of the results.
• A strong influence of element erosion strain (a non-physical parameter) on the results.
• Fine meshes are required to reduce spurious oscillations of the blade induced by element erosion, restricting the realization of the computational time benefit.
• Contact definition complexity (number of contact cards required to define interactions between parts of the model) is lower compared to other methods.

ADT (Hybrid FEM/SPH) model:

• Strong mesh sensitivity of the results.
• A strong influence of element erosion strain (a non-physical parameter) on the re/sults.
• Increasing mesh density to reduce spurious oscillations of the blade may result in an enormous increase in computational time due to the presence of embedded SPH particles.

SPH model:

• No sensitivity to non-physical parameters, such as erosion strain (not used with SPH) and the number of neighboring particles (for models considered in this study).
• Unlike the other models, predicted a consistent trend in change of all the process metrics (rub force, process duration, damaged area) with increase in the rub depth.
• No artificial excitation of the blade was observed.

All models required measures to suppress the undesired extension of shell edges of the blade to prevent its premature rubbing into the ARS.

Based on the above, the suggested ranking of the methods for the fan blade–abradable strip interaction is as follows (1—most applicable, 3—least applicable): 1—SPH, 2—FEM, and 3—ADT. It appears that the ADT technique in its current state of development has only limited applicability to the blade–ARS interaction modeling. Both the FEM and SPH models are applicable, with a slight preference for the meshless technique due to the noted lower sensitivity to non-physical parameters, better consistency in predictions, and the lack of artificial excitation of the blade. Modeling recommendations, therefore, include: (1) using the SPH or the FEM (second choice) solvers; (2) conducting a thorough sensitivity analysis and calibration for the non-physical parameters, such as erosion, if an FEM solver is used; and (3) following the solver-specific recommendations for the contact algorithms, as discussed in Section 4.3.

Further studies involving collection of experimental evidence are recommended.