Optimization of a Tapered Specimen Geometry for Short-Term Dynamic Tensile Testing of Continuous Fiber Reinforced Thermoplastics
Abstract
:1. Introduction
2. Materials and Methods
3. Results
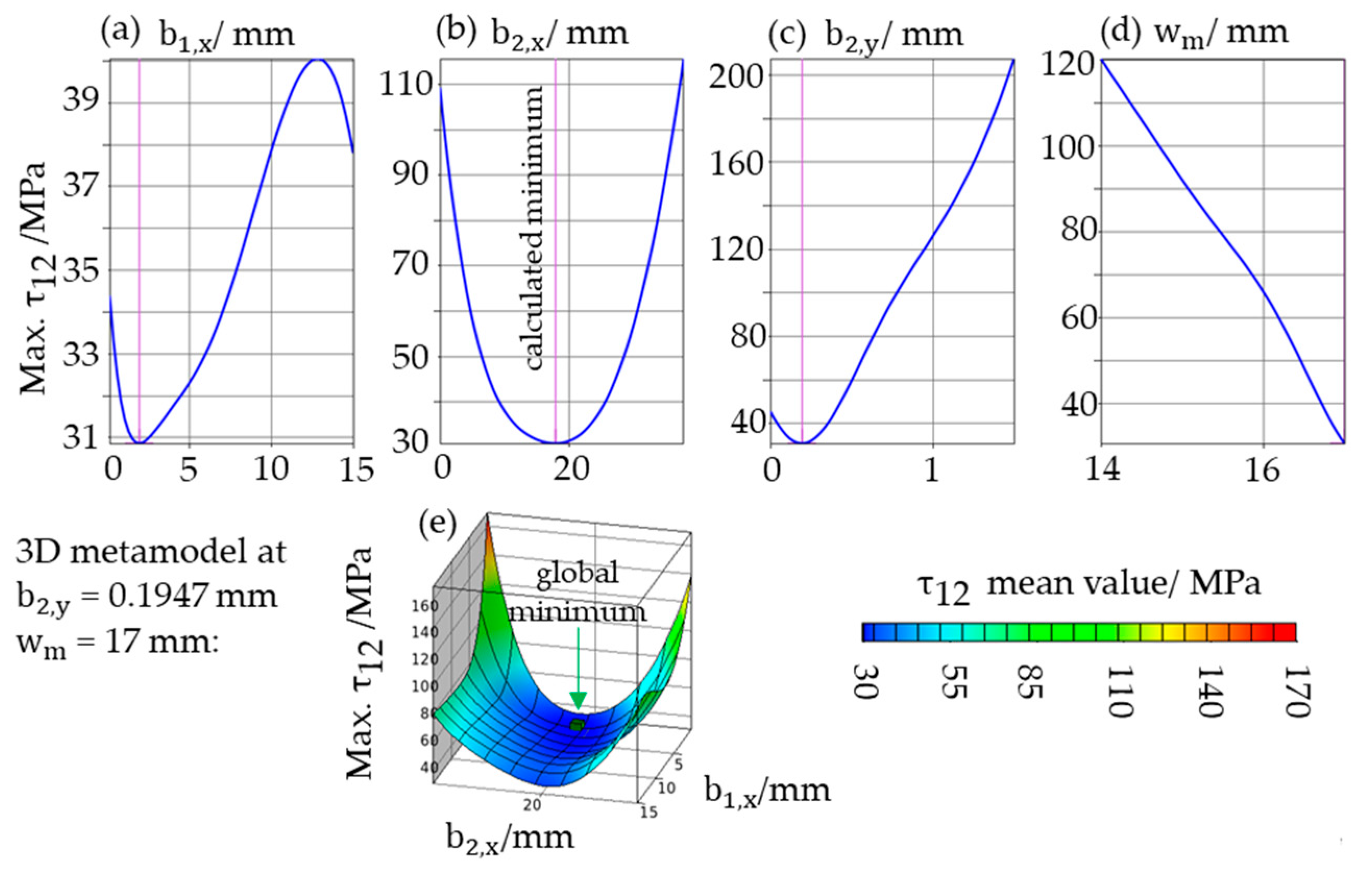
3.1. Optimization Results
3.2. Experimental Validation Results
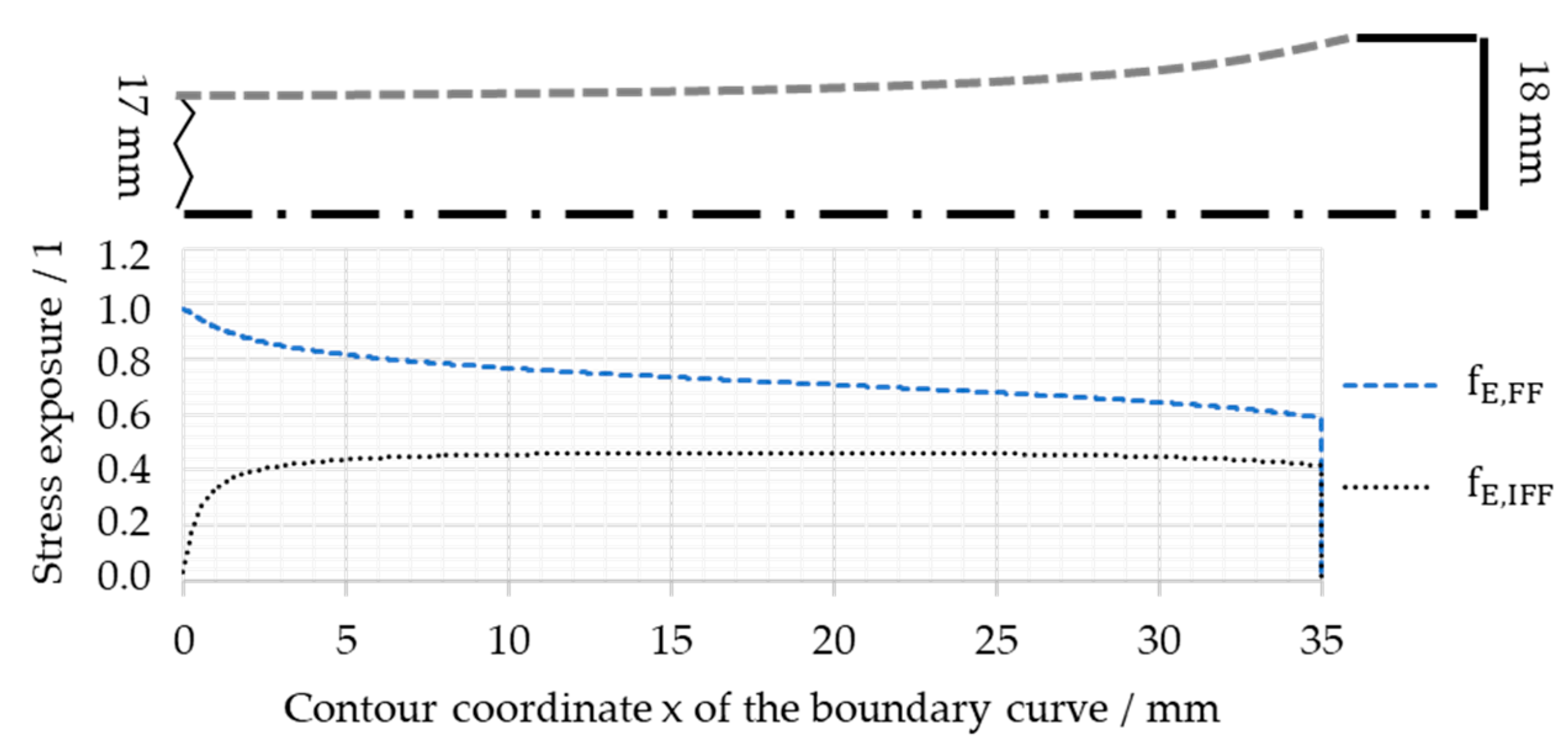
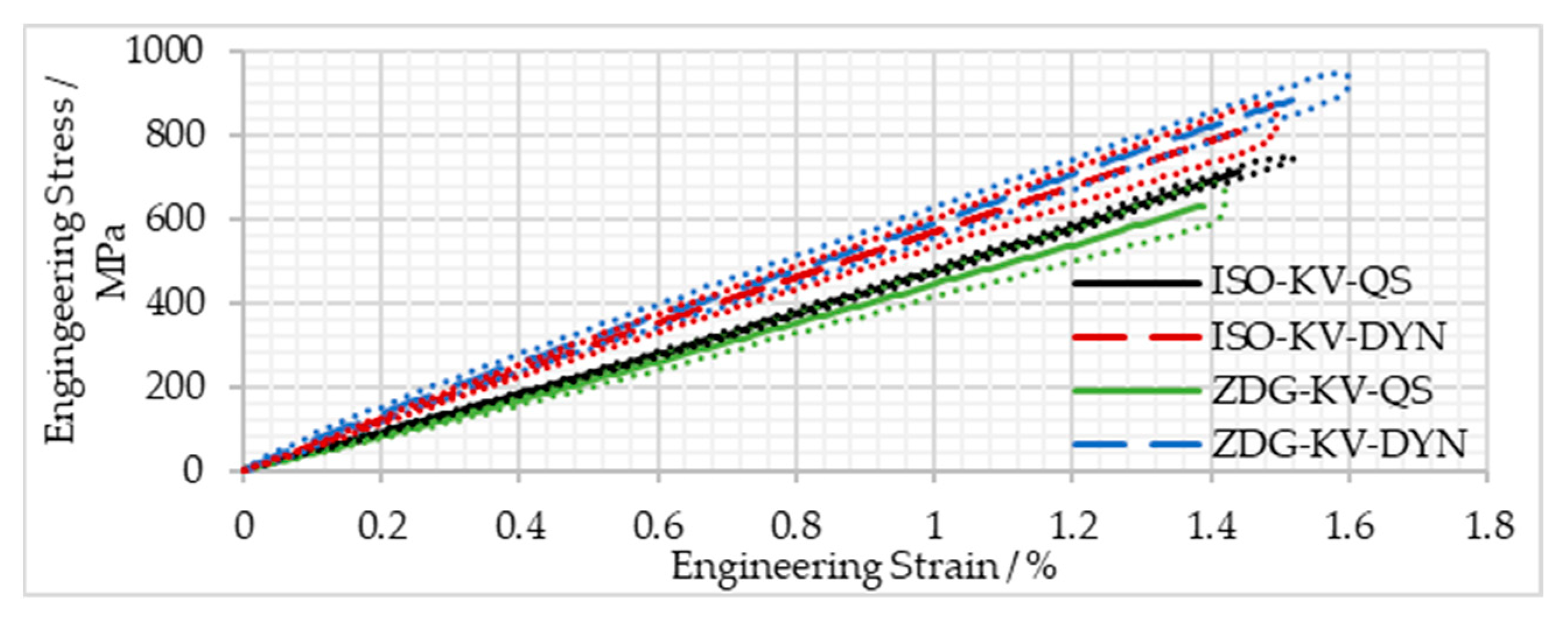
4. Discussion of Experimental Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schürmann, H. Konstruieren Mit Faser-Kunststoff-Verbunden, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 9783540721895. [Google Scholar]
- Premium AEROTEC. Premium AEROTEC Zeigt Zukunftspotenzial von CFK mit Thermoplastischer Matrix: Weltweit Erster Demonstrator für A320-Druckkalotte Steht im Mittelpunkt des ILA-Auftritts; Premium AEROTEC: Augsburg, Germany, 2018. [Google Scholar]
- ElringKlinger, A.G. ElringKlinger Erhält Großserienauftrag für ein Globales Leichtbau-Projekt. 2016. Available online: https://www.elringklinger.de/sites/default/files/releases/pressemitteilungen/2016/160607_elringklinger_pressemitteilung.pdf (accessed on 28 February 2022).
- Friedrich, H.E. (Ed.) Leichtbau in der Fahrzeugtechnik, 2nd ed.; Springer Vieweg: Wiesbaden, Germany; Heidelberg, Germany, 2017; ISBN 978-3-658-12294-2. [Google Scholar]
- DIN. DIN EN ISO 527-4: 2022-03; Kunststoffe-Bestimmung der Zugeigenschaften- Teil 4: Prüfbedingungen Für isotrop und Anisotrop Faserverstärkte Kunststoffverbundwerkstoffe. Beuth Verlag GmbH: Berlin, Germany, 2022.
- Eriksen, R.N.W. High Strain Rate Characterisation of Composite Materials; Technical University of Denmark: Kongens Lyngby, Denmark, 2014. [Google Scholar]
- Forschungsvereinigung Automobiltechnik. FAT-Richtlinie Dynamische Werkstoffkennwerte für die Crashsimulation; VDA, FAT: Frankfurt, Germany, 2007. [Google Scholar]
- Spronk, S.W.F.; Verboven, E.; Gilabert, F.A.; Sevenois, R.D.B.; Garoz, D.; Kersemans, M.; van Paepegem, W. Stress-strain synchronization for high strain rate tests on brittle composites. Polym. Test. 2018, 67, 477–486. [Google Scholar] [CrossRef]
- Harding, J.; Welsh, L.M. A tensile testing technique for fibre-reinforced composites at impact rates of strain. J. Mater. Sci. 1983, 18, 1810–1826. [Google Scholar] [CrossRef]
- Taniguchi, N.; Nishiwaki, T.; Kawada, H. Tensile strength of unidirectional CFRP laminate under high strain rate. Adv. Compos. Mater. 2007, 16, 167–180. [Google Scholar] [CrossRef]
- Kawata, K.; Hashimoto, S.; Takeda, N. Mechanical Behaviours in High Velocity Tension of Composites. Presented at the 4th International Conference on Composite Materials, Tokyo, Japan, 25–28 October 1982. [Google Scholar]
- Naik, N.K.; Yernamma, P.; Thoram, N.M.; Gadipatri, R.; Kavala, V.R. High strain rate tensile behavior of woven fabric E-glass/epoxy composite. Polym. Test. 2010, 29, 14–22. [Google Scholar] [CrossRef]
- Ploeckl, M. Effect of Strain Rate on the Tensile, Compressive, and Shear Response of Carbon-Fiber-Reinforced Thermoplastic Composites. Ph.D. Thesis, TU München, München, Germany, 2019. [Google Scholar]
- Schmack, T. Entwicklung einer Ganzheitlichen Methode zur Bestimmung des Dehnratenabhängigen Verhaltens Faserverstärkter Kunststoffe; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2019; ISBN 978-3-658-26930-2. [Google Scholar]
- Junginger, M. Charakterisierung und Modellierung Unverstärkter Thermoplastischer Kunststoffe zur Numerischen Simulation von Crashvorgängen; Fraunhofer IRB Verlag: Freiburg Breisgau, Germany, 2004. [Google Scholar]
- DIN. DIN EN ISO 26203-2: 2012-01; Metallische Werkstoffe—Zugversuch bei Hohen Dehngeschwindigkeiten—Teil 2: Servohydraulische und Andere Systeme. Beuth Verlag GmbH: Berlin, Germany, 2012.
- European Structural Integrity Society. ESIS P7-00: Procedure for Dynamic Tensile Tests; European Structural Integrity Society: Rimini, Italy, 2000. [Google Scholar]
- Stahl Eisen Prüfblatt. Ermittlung Mechanischer Eigenschaften an SEO 1230: Blechwerkstoffen Bei Hohen Dehnraten im Hochgeschwindigkeitsdehnversuch; Beuth Verlag GmbH: Berlin, Germany, 2007. [Google Scholar]
- ISO. ISO 18872; Plastics—Determination of Tensile Properties at High Strain Rates. International Organization for Standardization: Geneva, Switzerland, 2007; 83.080.10. Available online: https://www.iso.org/standard/38914.html (accessed on 18 October 2022).
- SAE. SAE J 2749: High Strain Rate Tensile Testing Of Polymers; Beuth Verlag GmbH: Berlin, Germany, 2017; Available online: https://www.beuth.de/de/norm/sae-j-2749/277331661 (accessed on 18 October 2022).
- VDA. VDA 287; Dehnratenabhängige Zugprüfung für nicht Faserverstärkte Thermoplaste bei Raumtemperatur. Verband der Automobilindustrie e. V.: Berlin, Germany, 2022. (287). Available online: https://webshop.vda.de/VDA/de/vda-287-032022 (accessed on 3 February 2023).
- Fitoussi, J.; Meraghni, F.; Jendli, Z.; Hug, G.; Baptiste, D. Experimental methodology for high strain-rates tensile behaviour analysis of polymer matrix composites. Compos. Sci. Technol. 2005, 65, 2174–2188. [Google Scholar] [CrossRef]
- Todo, M.; Takahashi, K.; Béguelin, P.; Kausch, H.H. Strain-rate dependence of the tensile fracture behaviour of woven-cloth reinforced polyamide composites. Compos. Sci. Technol. 2000, 60, 763–771. [Google Scholar] [CrossRef]
- Chen, W.; Meng, Q.; Hao, H.; Cui, J.; Shi, Y. Quasi-static and dynamic tensile properties of fiberglass/epoxy laminate sheet. Constr. Build. Mater. 2017, 143, 247–258. [Google Scholar] [CrossRef]
- De Baere, I.; van Paepegem, W.; Hochard, C.; Degrieck, J. On the tension–tension fatigue behaviour of a carbon reinforced thermoplastic part II: Evaluation of a dumbbell-shaped specimen. Polym. Test. 2011, 30, 663–672. [Google Scholar] [CrossRef]
- Gilat, A.; Goldberg, R.K.; Roberts, G.D. Strain Rate Sensitivity of Epoxy Resin in Tensile and Shear Loading. J. Aerosp. Eng. 2007, 20, 75–89. [Google Scholar] [CrossRef]
- Hufner, D.R.; Hill, S.I. High strain rate testing and modeling of a woven E-glass–vinylester composite in dry and saturated conditions. J. Compos. Mater. 2017, 51, 3017–3039. [Google Scholar] [CrossRef]
- Schmeer, S.; Mischo, F.; Scheliga, D. Tapered geometry for testing continuous fiber reinforced thermoplastics under tension. In Proceedings of the 20th European Conference on Composite Materials—Composites Meet Sustainability (Vol 1–6), Lausanne, Switzerland, 26–30 June 2022; EPFL Lausanne, Composite Construction Laboratory: Lausanne, Switzerland, 2022; pp. 181–188, ISBN 978-2-9701614-0-0. [Google Scholar]
- Spronk, S.; Verboven, E.; Gilabert, F.; Sevenois, R.; Garoz, D.; Kersemans, M.; van Paepegem, W. Dynamic tensile testing of brittle composites using a hydraulic pulse machine: Stress-strain synchronization and strain rate limits. In Proceedings of the Eighteenth International Conference of Experimental Mechanics, Brussels, Belgium, 1–5 July 2018; MDPI: Basel, Switzerland, 2018; p. 5274. [Google Scholar]
- Ryberg, A.-B.; Domeij Bäckryd, R.; Nilsson, L. Metamodel-Based Multidisciplinary Design Optimization for Automotive Applications; Technical Report; Linköping University: Linköping, Sweden, 2012. [Google Scholar]
- Seiler, M.S. Geometrische Restriktionen Bei der Geometriebasierten Strukturoptimierung von Maschinenbauteilen mit Freiformgeometrien. Ph.D. Thesis, RWTH, Aachen, Germany, 2012. [Google Scholar]
- Hussain, M.F.; Barton, R.R.; Joshi, S.B. Metamodeling: Radial Basis Functions, versus Polynomials. Eur. J. Oper. Res. 2002, 138, 142–154. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural networks and their applications. Rev. Sci. Instrum. 1994, 65, 1803–1832. [Google Scholar] [CrossRef]
- Sheldon, A.; Helwig, E.; Cho, Y.-B. Investigation and Application of Multi-Disciplinary Optimization for Automotive Body-in-White Development. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Kremer, T.; Schürmann, H. Über die Verwendung und Bedeutung von Kerbformzahlen bei der Auslegung von Faser-Kunststoff-Verbunden. Mat. Wiss. u. Werkstofftech. 2008, 39, 385–390. [Google Scholar] [CrossRef]
- Mischo, F.; Kenf, A.; Kammler, M.; Schmeer, S. Influence of Manufacturing Procedure on Mechanical Properties of Continous Fiber Reinforced Thermoplastics. In Proceedings of the 20th European Conference on Composite Materials—Composites Meet Sustainability (Vol 1–6), Lausanne, Switzerland, 26–30 June 2022; EPFL Lausanne, Composite Construction Laboratory: Lausanne, Switzerland, 2022; pp. 1125–1132, ISBN 978-2-9701614-0-0. [Google Scholar]
- De Casteljau, P. Courbes et Surfaces à Pôles No. 66; André Citroën Automobiles SA: Paris, France, 1963. [Google Scholar]
- Bezier, P. How a Simple System Was Born: Curves and Surfaces for Computer Aided Geometric Design. A Practical Guide; Elsevier Science: Amsterdam, Netherlands, 1993. [Google Scholar]
- Prautzsch, H.; Boehm, W.; Paluszny, M. Bézier and B-Spline Techniques; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 978-3-662-04919-8. [Google Scholar]
- Krautter, J.; Parizot, S. Systeme d’aide a la définition et a l’usinage des surfâces de carosserie. J. de la SIA 1971, 44, 581–586. [Google Scholar]
- Boehm, W.; Müller, A. On de Casteljau’s algorithm. Comput. Aided Geom. Des. 1999, 16, 587–605. [Google Scholar] [CrossRef]
- Puck, A. Festigkeitsanalyse von Faser-Matrix-Laminaten: Modelle für die Praxis; Hanser: München, Germany, 1996; ISBN 3446181946. [Google Scholar]
- VDI. Entwicklung von Bauteilen aus Faser-Kunststoff-Verbund—Berechnungen. 2006. (VDI 2014 Blatt3). Available online: https://www.vdi.de/en/home/vdi-standards/details/vdi-2014-blatt-3-entwicklung-von-bauteilen-aus-faser-kunststoff-verbund-berechnungen-1 (accessed on 4 December 2022).
- Stander, N.; Basudhar, A.; Roux, W.; Liebold, K.; Eggleston, T.; Goel, T.; Craig, K. LS-OPT ® User’s Manual: A Design Optimization and Probabilistic Analysis Tool for the Engineering Analyst; Version 7.0; Livermore Software Technology Corporation: Livermore, CA, USA, 2020. [Google Scholar]
- Liu, C.J.; Sterk, J.C.; Nijhof, A.; Marissen, R. Matrix-Dominated Damage in Notched Cross-Ply Composite Laminates: Experimental Observations. Appl. Compos. Mater. 2002, 9, 155–168. [Google Scholar] [CrossRef]
- Hufenbach, W.; Kroll, L. Kerbspannungsanalyse anisotrop faserverstärkter Scheiben. Arch. Appl. Mech. 1992, 62, 277–290. [Google Scholar] [CrossRef]
- DIN. DIN EN ISO 527-5:2022-05; Kunststoffe_- Bestimmung der Zugeigenschaften_- Teil_5: Prüfbedingungen für Unidirektional Faserverstärkte Kunststoffverbundwerkstoffe. Beuth Verlag GmbH: Berlin, Germany, 2022.
- Zhou, Y.; Jiang, D.; Xia, Y. Tensile mechanical behavior of T300 and M40J fiber bundles at different strain rate. J. Mater. Sci. 2001, 36, 919–922. [Google Scholar] [CrossRef]
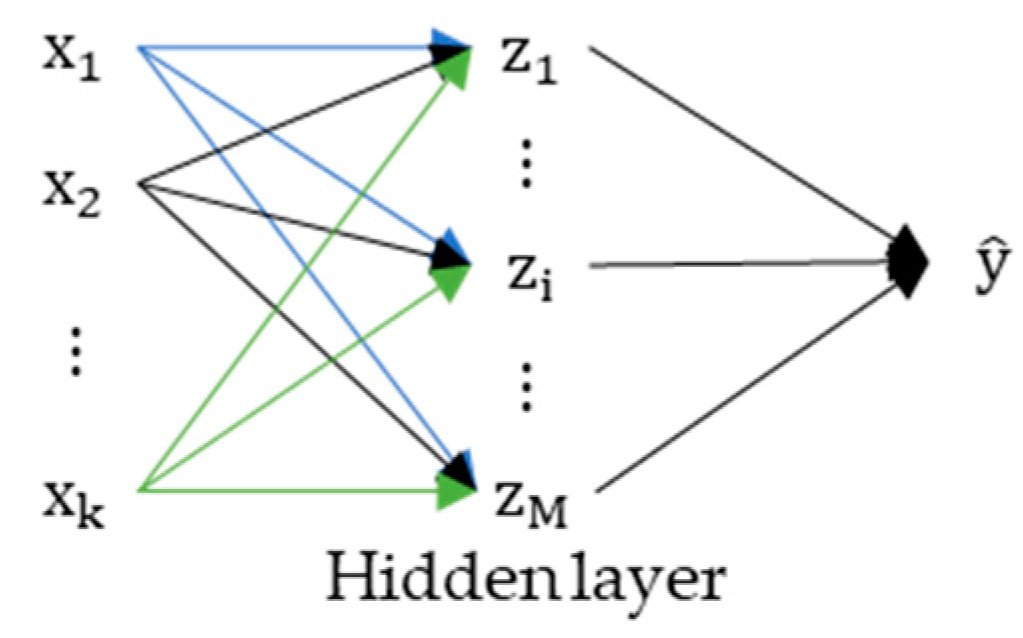




| Author | Material | Geometry | Radius r/mm | Length l0/mm | Width b/mm | Width Change over Length Δb/mm |
|---|---|---|---|---|---|---|
| Fitoussi et al. [22] | CF-Epoxy Weave | Dogbone | 7 | 29 | 6 | 14 |
| Spronk et al. [8] | CF-Epoxy Weave | Tapered | 136.57 | 50 | 15.38 | 4.62 |
| Chen et al. [24] | GF-Epoxy Weave | Tapered | 76.5 | 80 | 13 | 7 |
| De Baere et al. [25] | CF-PPS Weave | Tapered | 1446 | 210 | 23.1 | 6.9 |
| Hufner; Hill [27] | GF-VE Weave | Rectangular | - | 12.7 | 12.7 | - |
| Gilat et al. [26] | CF-Epoxy UD/Cross-ply | Tapered | 12.7 | 34.925 | 3.2 | 9 |
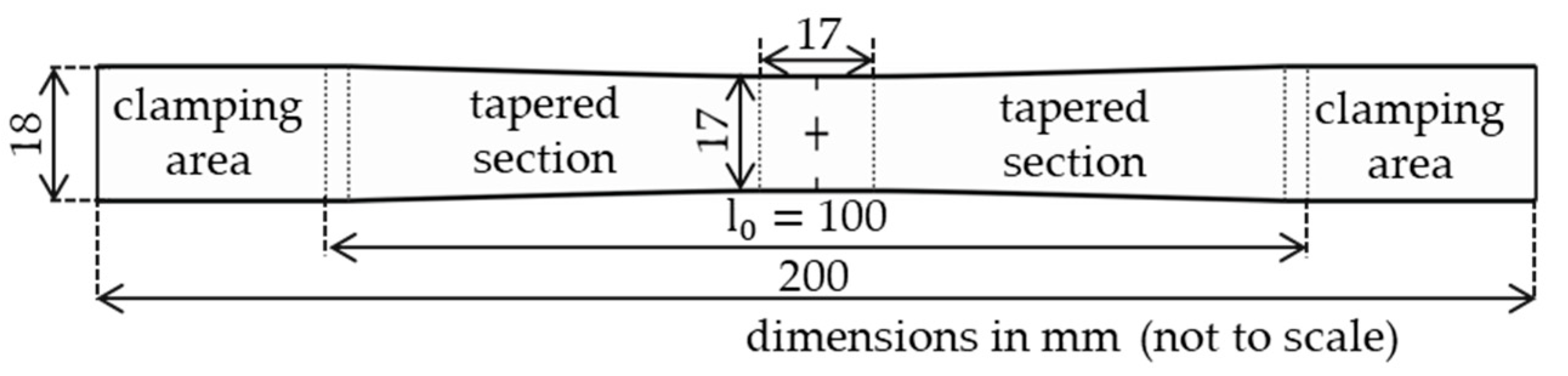
| Basic Parameter | Parameter Value (global)/mm | Bézier Point- Parameter | Parameter Value (local)/mm |
|---|---|---|---|
| 85 | (00) | ||
| 5 | (= 0) | ||
| 18 | |||
| 14–17 | (() − ) |
| RMS Error | R2 | Objective Function Result | Parameter Value (Local)/mm |
|---|---|---|---|
| 1.29 (0.92%) | 1.00 | = 31.78 MPa | (1.9100.000) |
| (17.8130.195) | |||
| = 17 |
| Laminate Layup | Ktl/1 | β/1 |
|---|---|---|
| CF-PC-UD [0]6 | 1.46 | 0.52 |
| CF-PC-KV [0/90]3s | 1.10 | 0.28 |
| Test Speed | Geometry | Young’s Modulus/GPa | Tensile Strength/MPa | |||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | |||
| KV | QS (3.33 × 10−5 m s−1) | ZDG | 41.26 | 2.99 | 632.91 | 54.72 |
| ISO | 44.50 | 1.18 | 711.61 | 37.19 | ||
| DYN (4.00 m s−1) | ZDG | 65.67 | 4.11 | 890.51 | 56.54 | |
| ISO | 60.97 | 3.99 | 809.56 | 64.67 | ||
| UD | QS (3.33 × 10−5m s−1) | ZDG | 94.28 | 3.08 | 1159.98 | 73.47 |
| ISO | 98.87 | 6.54 | 1338.15 | 95.12 | ||
| DYN (4.00 m s−1) | ZDG | 92.73 | 8.54 | 1347.40 | 119.22 | |
| ISO | 97.11 | 8.11 | 1329.94 | 138.22 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mischo, F.; Schmeer, S. Optimization of a Tapered Specimen Geometry for Short-Term Dynamic Tensile Testing of Continuous Fiber Reinforced Thermoplastics. J. Compos. Sci. 2024, 8, 93. https://doi.org/10.3390/jcs8030093
Mischo F, Schmeer S. Optimization of a Tapered Specimen Geometry for Short-Term Dynamic Tensile Testing of Continuous Fiber Reinforced Thermoplastics. Journal of Composites Science. 2024; 8(3):93. https://doi.org/10.3390/jcs8030093
Chicago/Turabian StyleMischo, Florian, and Sebastian Schmeer. 2024. "Optimization of a Tapered Specimen Geometry for Short-Term Dynamic Tensile Testing of Continuous Fiber Reinforced Thermoplastics" Journal of Composites Science 8, no. 3: 93. https://doi.org/10.3390/jcs8030093
APA StyleMischo, F., & Schmeer, S. (2024). Optimization of a Tapered Specimen Geometry for Short-Term Dynamic Tensile Testing of Continuous Fiber Reinforced Thermoplastics. Journal of Composites Science, 8(3), 93. https://doi.org/10.3390/jcs8030093







