Multiscale Modeling of Elastic Waves in Carbon-Nanotube-Based Composite Membranes
Abstract
1. Introduction
1.1. Motivation
1.2. CNT-Reinforced Composites
1.3. Dynamic Modeling of CNT-Based Composites
1.4. Problem Statement and Solution Methodology
2. Mathematical Modeling and Numerical Simulation
2.1. Mathematical Modeling
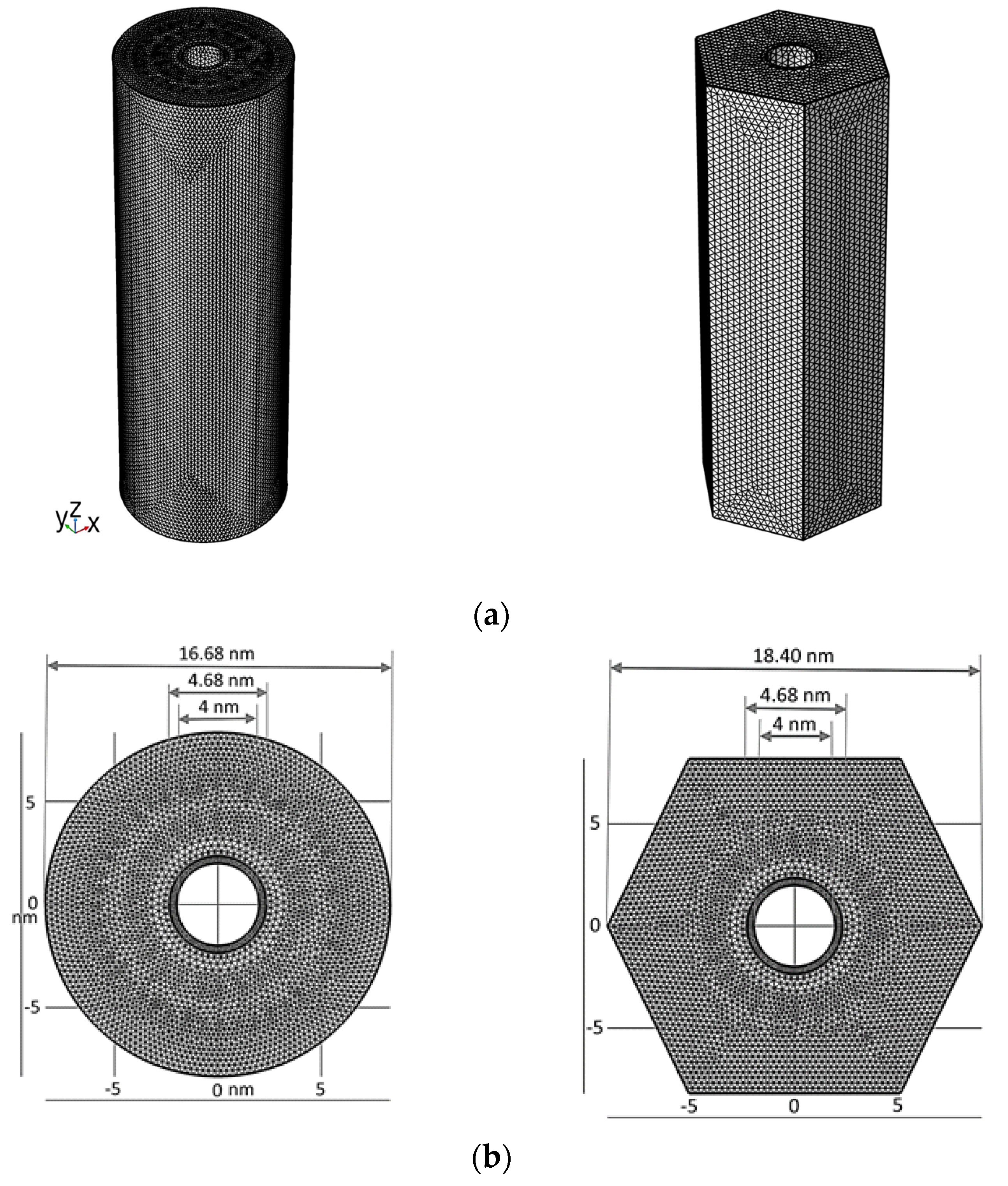
2.1.1. Representative Volume Element
2.1.2. Averaging Process
2.2. Numerical Simulation
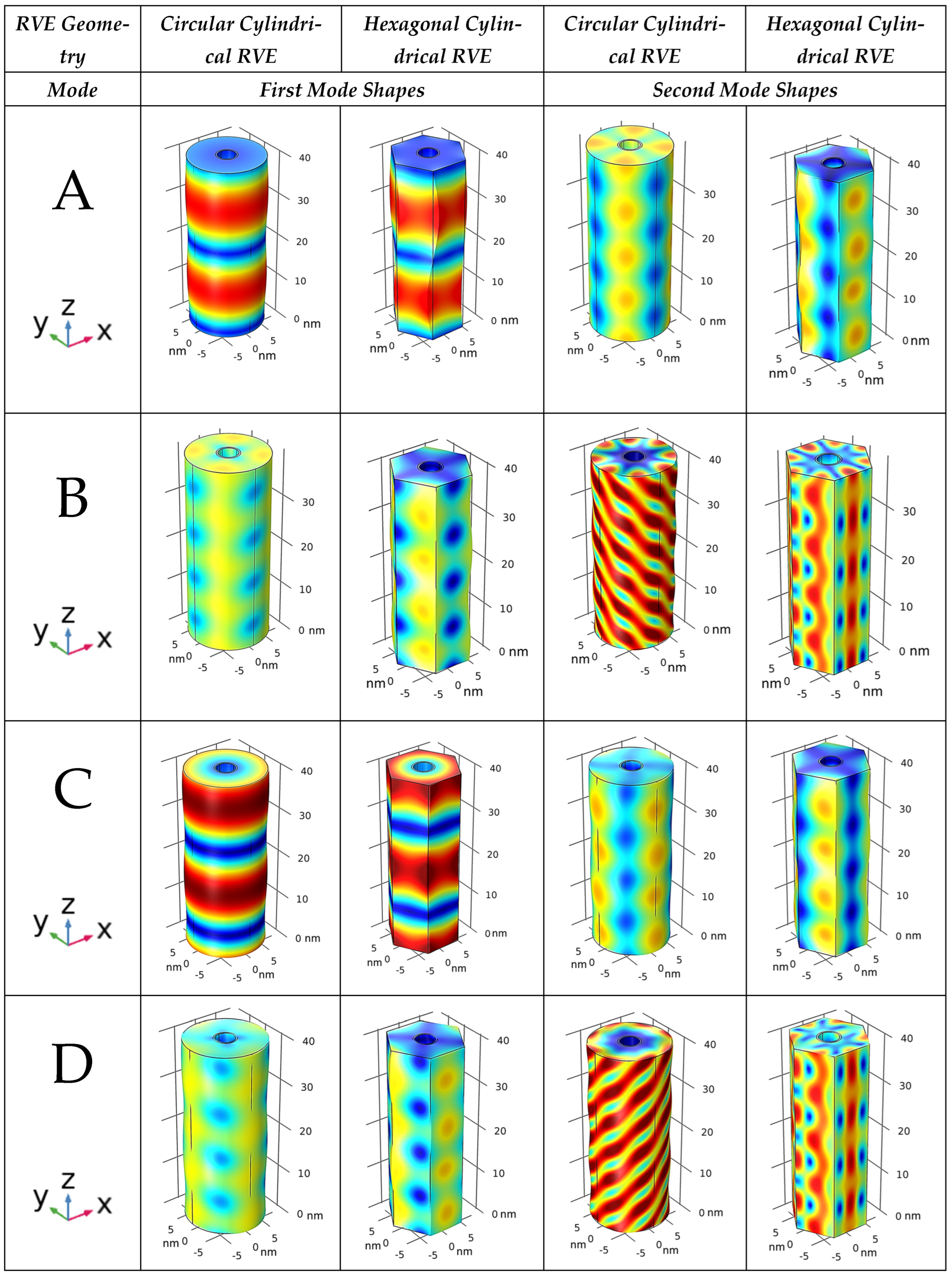
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sears, K.; Dumée, L.; Schütz, J.; She, M.; Huynh, C.; Hawkins, S.; Duke, M.; Gray, S. Recent Developments in Carbon Nanotube Membranes for Water Purification and Gas Separation. Materials 2010, 3, 127–149. [Google Scholar] [CrossRef]
- Ahn, C.H.; Baek, Y.; Lee, C.; Kim, S.O.; Kim, S.; Lee, S.; Kim, S.-H.; Bae, S.S.; Park, J.; Yoon, J. Carbon nanotube-based membranes: Fabrication and application to desalination. J. Ind. Eng. Chem. 2012, 18, 1551–1559. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Ren, Z.; Chou, T.W. Advances in the science and technology of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2001, 61, 1899–1912. [Google Scholar] [CrossRef]
- Yengejeh, S.I.; Kazemi, S.A.; Öchsner, A. Carbon nanotubes as reinforcement in composites: A review of the analytical, numerical and experimental approaches. Comput. Mater. Sci. 2017, 136, 85–101. [Google Scholar] [CrossRef]
- Qian, D.; Dickey, E.C.; Andrews, R.; Rantell, T. Load transfer and deformation mechanisms in carbon nanotube-polystyrene composites. Appl. Phys. Lett. 2000, 76, 2868–2870. [Google Scholar] [CrossRef]
- Cooper, C.A.; Cohen, S.R.; Barber, A.H.; Wagner, H.D. Detachment of carbon nanotubes from a polymer matrix. Appl. Phys. Lett. 2002, 81, 3873–3875. [Google Scholar] [CrossRef]
- Allaoui, A.; Bai, S.; Cheng, H.M.; Bai, J.B. Mechanical and electrical properties of a MWNT/epoxy composite. Compos. Sci. Technol. 2002, 62, 1993–1998. [Google Scholar] [CrossRef]
- Barber, A.H.; Cohen, S.R.; Wagner, H.D. Measurement of carbon nanotube polymer interfacial strength. Appl. Phys. Lett. 2003, 82, 4140–4142. [Google Scholar] [CrossRef]
- Yamamoto, G.; Omori, M.; Hashida, T.; Kimura, H. A novel structure for carbon nanotube reinforced alumina composites with improved mechanical properties. Nanotechnology 2008, 19, 31707–31714. [Google Scholar] [CrossRef]
- Frenkel, D.; Berend, S. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier: Amsterdam, The Netherlands, 2001; Volume 1. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Odegard, G.M.; Gates, T.S.; Nicholson, L.M.; Wise, K.E. Equivalent continuum modeling of nano-structured materials. Compos. Sci. Technol. 2002, 62, 1869–1880. [Google Scholar] [CrossRef]
- Odegard, G.M.; Gates, T.S.; Wise, K.E.; Parka, C.; Siochi, E.J. Constitutive modeling of nanotube-reinforced polymer composites. Compos. Sci. Technol. 2003, 63, 1671–1687. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.W. On the elastic properties of carbon nanotube based composites: Modeling and characterization. J. Phys. D Appl. Phys. 2003, 36, 573–582. [Google Scholar] [CrossRef]
- Liu, Y.J.; Chen, X.L. Evaluations of the effective material properties of carbon nanotube-based composites using a nanoscale representative volume element. Mech. Mater. 2003, 35, 69–81. [Google Scholar] [CrossRef]
- Karimzadeh, F.; Ziaei-Rad, S.; Adibi, S. Modeling considerations and material properties evaluation in analysis of carbon nano-tubes composite. Metall. Mater. Trans. B 2007, 38, 695–705. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Papanikos, P.; Labeas, G.; Pantelakis, S.G. Multi-scale modeling of tensile behavior of carbon nanotube reinforced composites. Theor. Appl. Fract. Mech. 2008, 49, 51–60. [Google Scholar] [CrossRef]
- Meguid, S.A.; Wernik, J.M.; Cheng, Z.Q. Atomistic-based continuum representation of the effective properties of nano-reinforced epoxies. Int. J. Solids Struct. 2010, 47, 1723–1736. [Google Scholar] [CrossRef]
- Montazeri, A.; Naghdabadi, R. Investigation of the interphase effects on the mechanical behavior of carbon nanotube polymer composites by multiscale modeling. J. Appl. Polym. Sci. 2010, 117, 361–367. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Shadlou, S.; Shokrieh, M.M. Multiscale modeling for mechanical properties of carbon nanotube reinforced nanocomposites subjected to different types of loading. Compos. Struct. 2011, 93, 2250–2259. [Google Scholar] [CrossRef]
- García-Macías, E.; Guzmán, C.F.; Flores, E.I.S.; Castro-Triguero, R. Multiscale modeling of the elastic moduli of CNT-reinforced polymers and fitting of efficiency parameters for the use of the extended rule-of-mixtures. Compos. Part B Eng. 2019, 159, 114–131. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. Mechanics of Multiscale Hybrid Nanocomposite; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Gibson, R.F.; Ayorinde, E.O.; Wen, Y.-F. Vibrations of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2007, 67, 1–28. [Google Scholar] [CrossRef]
- Palacios, J.A.; Ganesan, R. Dynamic response of Carbon-Nanotube-Reinforced-Polymer materials based on multiscale finite element analysis. Compos. Part B Eng. 2019, 166, 497–508. [Google Scholar] [CrossRef]
- Natsuki, T.; Hayashi, T.; Endo, M. Wave propagation of carbon nanotubes embedded in an elastic medium. J. Appl. Phys. 2005, 97, 044307. [Google Scholar] [CrossRef]
- Mitra, M.; Gopalakrishnan, S. Wave propagation analysis in carbon nanotubes embedded composite using wavelet based spectral finite element. Smart Mater. Struct. 2006, 15, 104–122. [Google Scholar] [CrossRef]
- Alavinasab, A.; Jha, R.; Ahmadi, G. Modeling of carbon nanotube composites based on nonlocal elasticity approach. Int. J. Comput. Methods Eng. 2014, 15, 17–25. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Enferadi, A.; Dabbagh, A. Wave Dispersion Behaviors of Multi-Scale CNT/Glass Fiber/Polymer Nanocomposite Laminated Plates. Polym. J. 2022, 14, 5448. [Google Scholar] [CrossRef] [PubMed]
- Hegemier, G.A.; Gurtman, G.A.; Nayfeh, A.H. Continuum Mixture Theory of Wave Propagation in Laminated and Fiber Reinforced Composites. Int. J. Solids Struct. 1973, 9, 395–414. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Continuum Mixture Theory of Heat Conduction in Laminated Composites. J. Appl. Mech. 1975, 42, 399–404. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Loh, J.; Jaine, I. Continuum Modeling of Electromagnetic Waves in Composite Wave Guides. J. Appl. Phys. 1979, 50, 606–609. [Google Scholar] [CrossRef]
- Hawwa, M.A.; Nayfeh, A.H. Thermoelastic waves in a laminated composite with a second sound effect. J. Appl. Phys. 1996, 80, 2733–2738. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Abdelrahman, W.G. Improved continuum mixture model for wave propagation in fibrous composites. J. Acoust. Soc. Am. 1998, 104, 867–876. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Dong, J.J.; Faidi, W. Approximate model for wave propagation in piezoelectric materials. II. Fibrous composites J. Appl. Phys. 1999, 85, 2347–2354. [Google Scholar]
- Arash, B.; Wang, Q.; Varadan, V.K. Mechanical properties of carbon nanotube/polymer composites. Sci. Rep. 2014, 4, 6479. [Google Scholar] [CrossRef] [PubMed]
- Park, J.G.; Keum, D.H.; Lee, Y.H. Strengthening mechanisms in carbon nanotube-reinforced aluminum composites. Carbon 2015, 1, 690–698. [Google Scholar] [CrossRef]
- Norouzi, S.; Barati, A.; Noroozi, R. Computational studies on mechanical properties of carbon-based nanostructures reinforced nanocomposites. J. Comput. Appl. Mech. 2019, 50, 413–419. [Google Scholar]
- Hashim, H.; Salleh, M.S.; Omar, M.Z. Homogenous dispersion and interfacial bonding of carbon nanotube reinforced with aluminum matrix composite: A review. Rev. Adv. Mater. Sci. 2019, 58, 295–303. [Google Scholar] [CrossRef]





| RVE Geometry | Circular Cylindrical RVE | Hexagonal Cylindrical RVE | ||
|---|---|---|---|---|
| Cases/Modes | Mode 1 | Mode 2 | Mode 1 | Mode 2 |
| A | 5.89 THz | 11.89 THz | 5.86 THz | 11.88 THz |
| B | 4.97 THz | 12.00 THz | 4.97 THz | 12.00 THz |
| C | 5.89 THz | 11.88 THz | 5.88 THz | 11.87 THz |
| D | 4.97 THz | 12.00 THz | 4.94 THz | 11.99 THz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahrous, E.N.; Hawwa, M.A.; Abubakar, A.A.; Al-Qahtani, H.M. Multiscale Modeling of Elastic Waves in Carbon-Nanotube-Based Composite Membranes. J. Compos. Sci. 2024, 8, 258. https://doi.org/10.3390/jcs8070258
Mahrous EN, Hawwa MA, Abubakar AA, Al-Qahtani HM. Multiscale Modeling of Elastic Waves in Carbon-Nanotube-Based Composite Membranes. Journal of Composites Science. 2024; 8(7):258. https://doi.org/10.3390/jcs8070258
Chicago/Turabian StyleMahrous, Elaf N., Muhammad A. Hawwa, Abba A. Abubakar, and Hussain M. Al-Qahtani. 2024. "Multiscale Modeling of Elastic Waves in Carbon-Nanotube-Based Composite Membranes" Journal of Composites Science 8, no. 7: 258. https://doi.org/10.3390/jcs8070258
APA StyleMahrous, E. N., Hawwa, M. A., Abubakar, A. A., & Al-Qahtani, H. M. (2024). Multiscale Modeling of Elastic Waves in Carbon-Nanotube-Based Composite Membranes. Journal of Composites Science, 8(7), 258. https://doi.org/10.3390/jcs8070258







