Next Article in Journal
Determining the Elastic Constants and Thickness of the Interphase in Fiberglass Plastic Composites from Micromechanical and Macromechanical Tests
Previous Article in Journal
Does Silane Application Affect Bond Strength Between Self-Adhesive Resin Cements and Feldspathic Porcelain?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
J. Compos. Sci.
Volume 9
Issue 2
10.3390/jcs9020053
jcs-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of Structural and Magnetic Phase Transitions in Multiferroic Y-Type Hexaferrite Systems by Means of Transverse Magnetic Susceptibility

by
Pablo Hernández-Gómez
*,
Óscar Bernardo
and
José María Muñoz
Departamento de Electricidad y Electrónica, Universidad de Valladolid, 47011 Valladolid, Spain
*
Author to whom correspondence should be addressed.
J. Compos. Sci. 2025, 9(2), 53; https://doi.org/10.3390/jcs9020053
Submission received: 13 December 2024 / Revised: 9 January 2025 / Accepted: 20 January 2025 / Published: 23 January 2025
Browse Figures
Versions Notes

Abstract

:
Transverse magnetic susceptibility is an excellent tool to study singularity points as anisotropy and switching fields in different bulk and nanostructured systems, as well as phase transitions. This technique has been carried out on polycrystalline Y-type hexaferrites, with compositions Ba2−xSrxCo2Fe12O22, (0.0 ≤ x ≤ 2.0), and Ba2−xSrxZn2Fe12O22, (1.3 ≤ x ≤ 1.7), promising candidates to exhibit multiferroic properties due to their noncollinear spin structure. In the Co2Y system, different behavior is observed depending on the Sr substitution rate, with a secondary maximum observed for samples with x ≥ 1.0 and different shapes in the measurement temperature range analyzed. In the Zn2Y system, several peaks related to the phase transitions that take place are observed, with certain variations depending on the degree of Ba substitution and the applied field in a more or less extended region around the ambient temperature. This type of measurement is a valuable tool to determine the bias field and temperature range of spin transitions.

1. Introduction

Transverse magnetic susceptibility is a measurement technique based on the application of a DC bias magnetic field in one direction and simultaneously an alternating field in a transverse direction, which is where the magnetic response is measured. It is, therefore, a measurement scheme analogous to magnetic resonance, although the alternating fields are of lower frequencies, typically from tenths to tens of KHz. By varying the bias field, peaks and cusps are obtained, which makes it possible to obtain the anisotropy and switching fields [1,2,3]. The advantage of this type of measurement is that the detection of the transverse response is more sensitive than the longitudinal response with respect to the anisotropy fields [4]. This technique was initially used on particles used in magnetic recording [5,6]. More recently, it has proven to be an excellent tool for studying singularity points in different bulk and nanostructured systems, particularly effective anisotropy fields and switching fields [7,8,9], and is also a probe of phase transitions caused by anisotropy [10,11].
Magnetoelectric multiferroics are materials that exhibit simultaneous ferroelectric and magnetic order, as well as a remarkable coupling between these properties. In this type of material, the direct or inverse magnetoelectric effect occurs, i.e., the appearance of electric polarization by the action of a magnetic field and magnetization by the application of electric fields [12]. This behavior appears in non-collinear magnetic systems, in which ferroelectricity is induced from changes in spiral magnetic ordering within the crystal, and they exhibit a number of interesting physical phenomena like electric excitation of magnon or magnetic skyrmions. The most suitable compounds are currently being sought in which the magneto-electric coupling is maximized, the coupling takes place at room temperature, and the applied field is as small as possible in order to optimize energy consumption they can present remarkable magnetoelectric effects at room temperature, with a view to its possible application in ultra-dense magnetic storage devices, spintronic devices or targeted drug delivery [13,14].
Of particular interest are single-phase multiferroics, and among them the ferroxplana type hexaferrites with Y phase ([BaSr]2Me2Fe12O22) are very promising materials, due to their temperature stability range to obtain single structural phase [15], their giant magnetoelectric coupling between ferrimagnetism and ferroelectricity caused by the spin transitions from longitudinal to transverse helimagnetic phases [16], the low magnetic fields required to switch the electric polarization [12,17,18] and the existence of spin-chirality and chiral domains [16,19]. The crystal structure of Y-type hexaferrite belongs to the R3m space group with a hexagonal structure and can be obtained with the piling up of S and T blocks along the c axis. Metal cations occupy four octahedral (18hVI, 6cVI, 3aVI and3bVI) and two tetrahedral sites (6cIV and 6cIV*). The substitution of Sr replacing Ba causes lattice deformation, which promotes the variation of the superexchange bond angles so that the compound can exhibit different spin arrangements, i.e., collinear, longitudinal conical (LC), transverse conical (TC), proper screw, and other intermediate complex helical spin systems, of which some allow the existence of ME effects, which can be improved by appropriate cation substitution and sintering conditions [20,21].
It is, therefore, to be expected that the occurrence of spin reorientations will affect the effective anisotropy in this type of material so that the measurement of the broadband transverse susceptibility will be useful in determining the temperature and bias field ranges in which these changes occur. With a view to its possible application in devices, the analysis should be carried out on polycrystalline samples, as they are the easiest to manufacture. In this work, we will demonstrate the versatility of transverse susceptibility for this task, analyzing the effect of large variations of Ba and Sr content in the BSCFO system Ba2−xSrxCo2Fe12O22 (0.0 < x < 2.0) and the effect of small variations of this content in the Ba2−xSrxZn2Fe12O22 (BSZFO) system (1.3 < x < 1.7) two systems of interest for having been described by the occurrence of multiferroic behaviors [12,22]. For this purpose, we will use a fully automated broadband system based on an LCR developed in our laboratory [23] that allows this measurement in varying ranges of DC and AC applied fields, temperature, and frequency with enhanced sensitivity.

2. Materials and Methods

Polycrystalline samples have been prepared by means of standard ceramic techniques. Stoichiometric amounts of SrCO3 (98%), BaCO3 (99%), Co3O4 (98%), and Fe2O3 (99%) with molar proportions 4.5:1.5:2:18, corresponding to the initial composition of Y type hexaferrite Ba2−xSrxCo2Fe12O22 (BSCFO) with x = 0.0, 0.5, 1.0, 1.5 and 2.0, were mixed in agate mortar, calcined at 900 °C to remove carbonates, pressed in the form of rods with 5 mm of diameter and 20 mm in length, and then sintered in air atmosphere at 1050 °C, 1150 °C and 1250 °C, according to the phase diagrams [22]. BSZFO family was prepared in a similar way with the appropriate amount of ZnO to obtain Ba2−xSrxZn2Fe12O22 with x = 1.3, 1.5, or 1.7.
X-ray diffraction patterns were obtained with a diffractometer Bruker Discover 8 at room temperature employing Cu-Kα radiation (λ = 1.54056 Å) (LTI lab at Valladolid University). Intensity data were collected by the step-counting method (step 0.02°/s) in the range 20° < 2θ < 70°. Quasi-static hysteresis loops were obtained in powdered samples with an inductive technique at room temperature with a maximum field of 4500 Oe. Homemade control program also corrects for the shape demagnetization factor. The accuracy of the measurement is ±1 Oe and ±0.25 emu/g for H and M resp.
Transverse susceptibility measurements were carried out with a broadband automatic system in which the sample rods form the core of a coil that produces a longitudinal AC magnetic field with a frequency of 1 kHz and a maximum amplitude of 2 Oe. The sample holder with the coil and a heating element is put inside a cryostat to allow temperature measurements in the range of 80 K–350 K. The cryostat tail lies into the polar pieces of an electromagnet fed by a power supply Agilent 6675A that produces a DC magnetic field, measured with a FW Bell 5080 gaussmeter (with an accuracy of ±1 Oe), perpendicular to the AC magnetic field. DC bias field sweeps run from +5000 Oe to −5000 Oe and then sweep back to +5000 Oe (i.e., bipolar scans), according to measurements found in the literature [24]. The response of the measuring coil is obtained with an LCR meter Agilent E4980A with 0.05% accuracy. Temperature control is achieved with a data logger Hewlett Packard 3497A, providing an accuracy of ±0.3 K. All the system is controlled via GPIB with a PC by means of a homemade control program with Agilent VEE software v9. The broadband nature of our system arises from the possibility of varying temperature, DC magnetic field, AC field frequency, and amplitude with enhanced sensitivity, overcoming the frequency limitations of resonant circuits.

3. Results

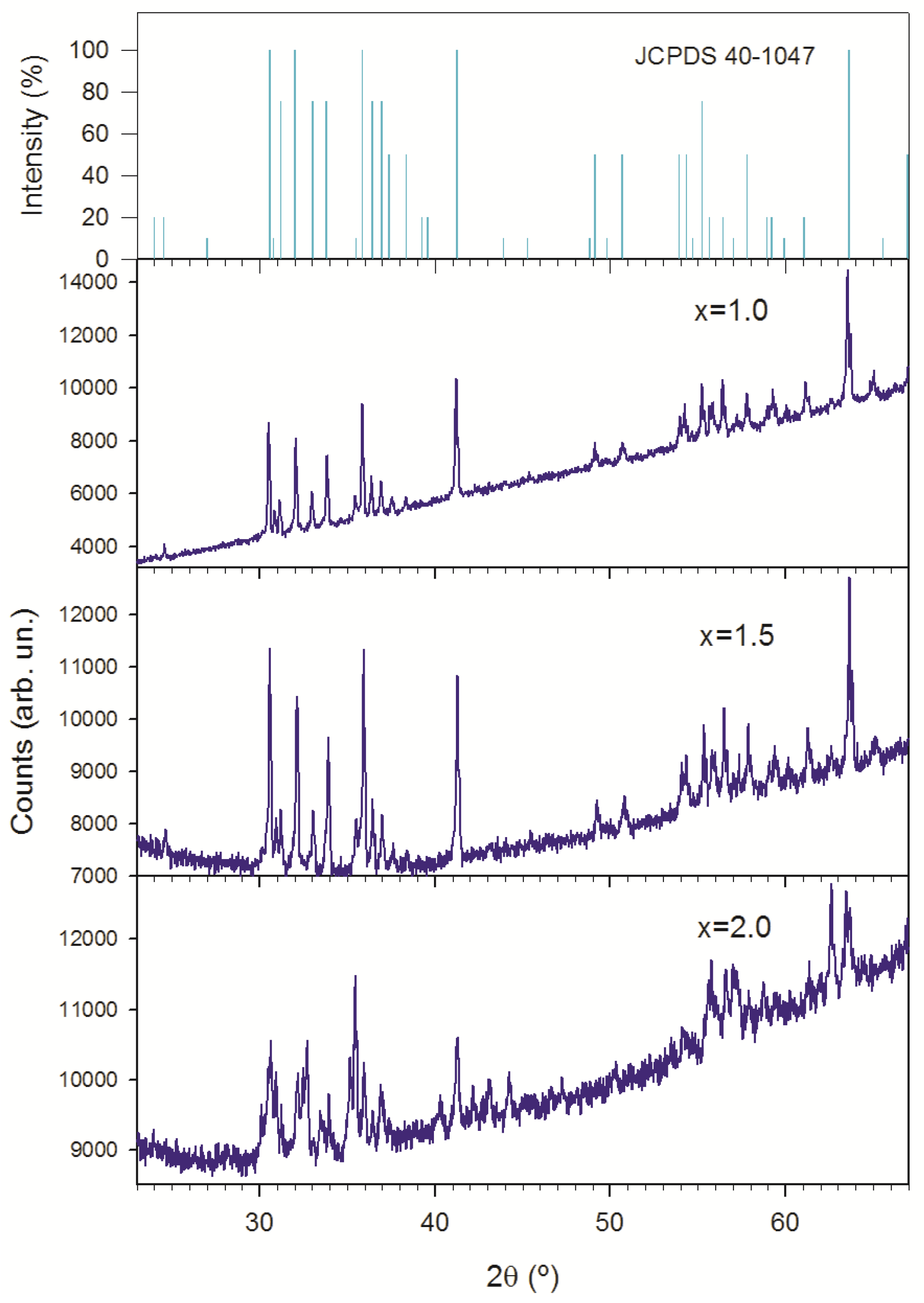
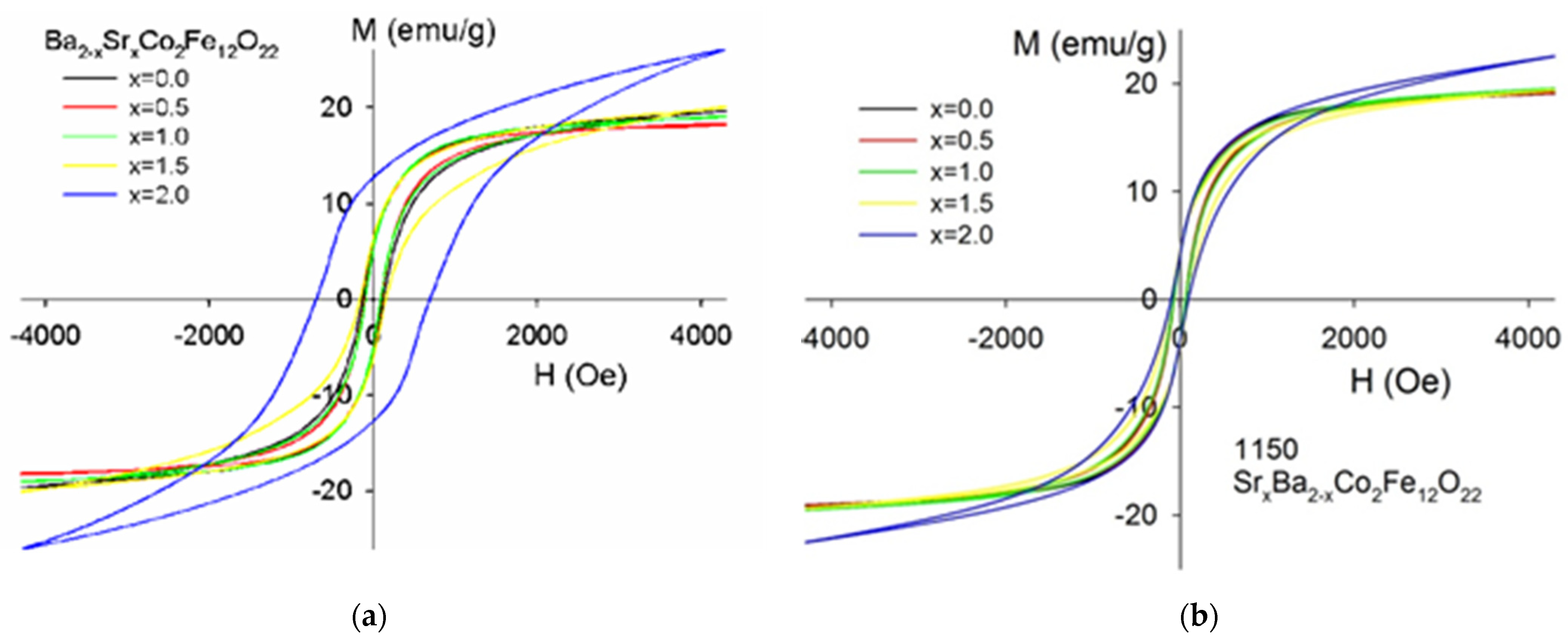
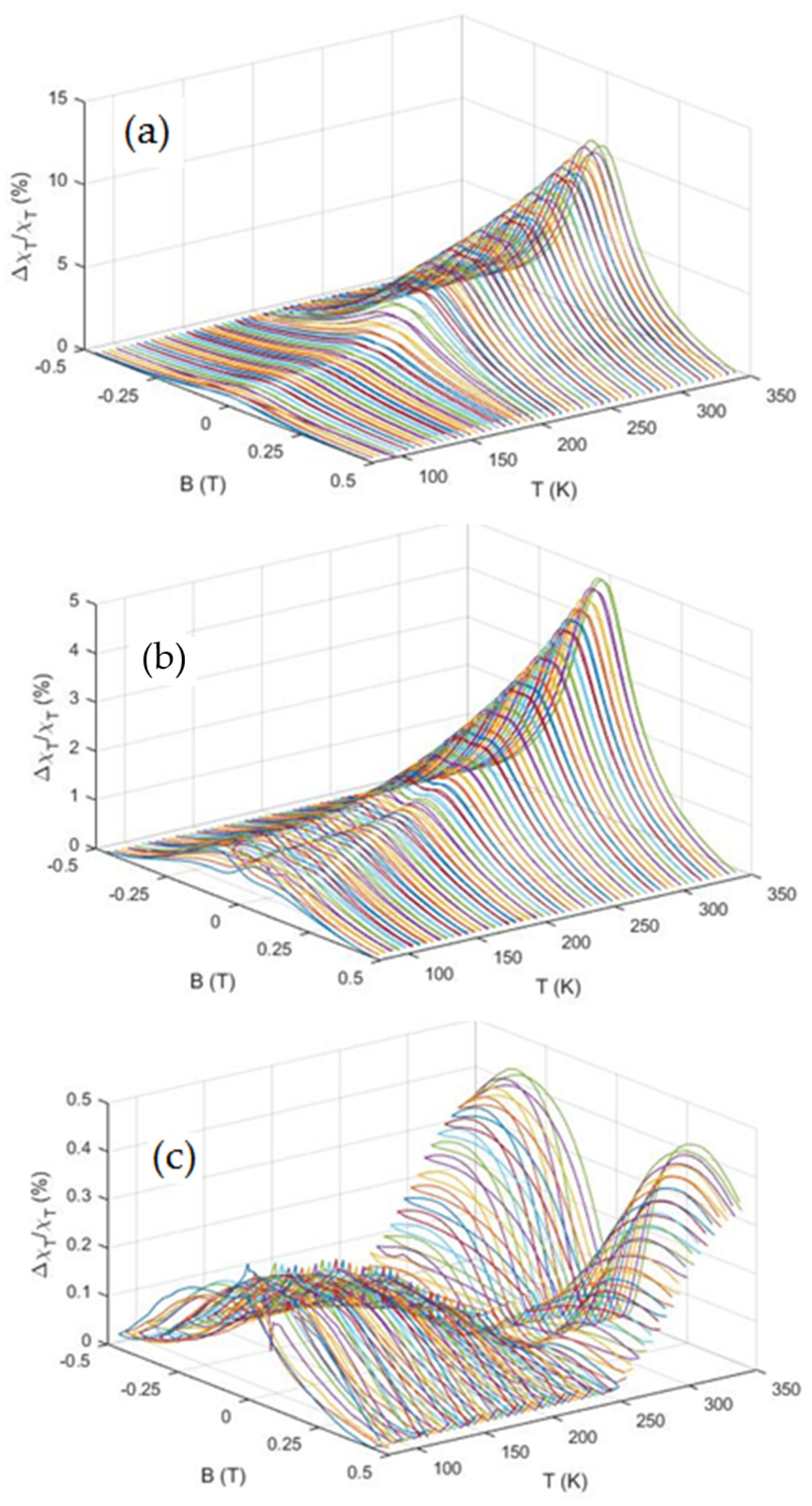
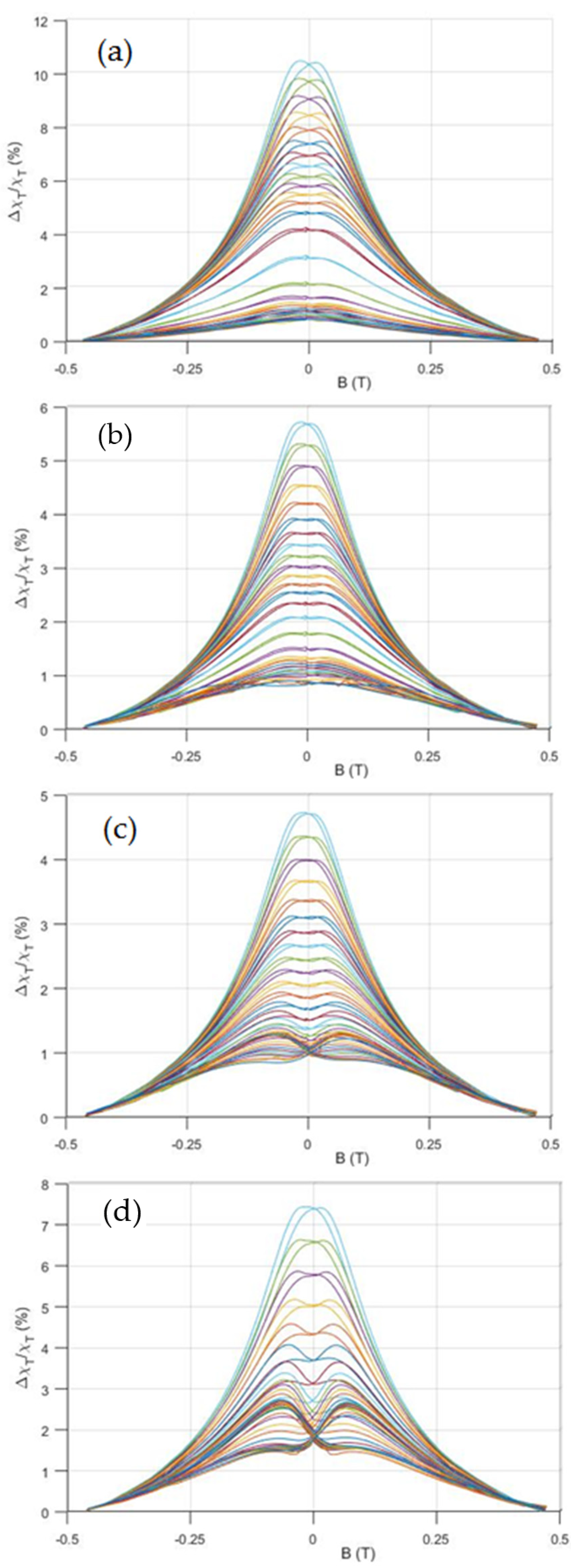
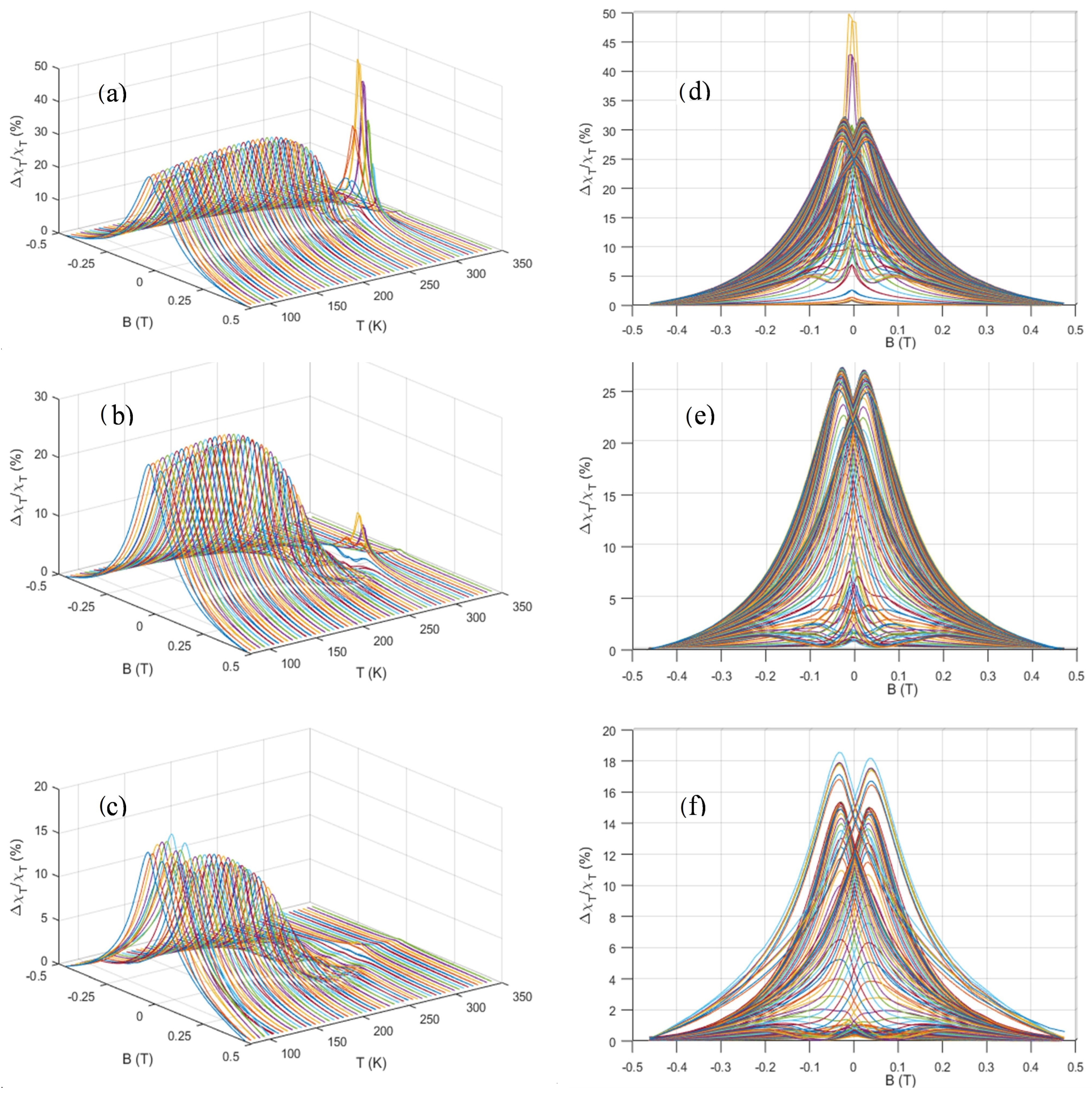
3.1. Ba2−xSrxCo2Fe12O22 System (BSCFO)

XRD patterns of selected samples are represented in Figure 1. According to phase diagram information [22] some additional phases can be present along with the main Y-type structure, namely, M-type at lower sintering temperatures, and Z-type at higher firing temperatures. The temperature range for pure Y-type formation will probably change for the different initial compositions analyzed. We can observe that pure Y-type hexagonal ferrite is obtained when sintering at 1050 °C and 1150 °C in the 0.0 < x < 2.0 range, while samples containing only Sr exhibit mixed M and Y or Y and Z phases at the low and high sintering temperatures analyzed resp. along with additional compounds like CoFe2O4, and SrFe2O4. The lattice parameters obtained for these samples reveal a smaller structure with the increase in Sr amount: a = 5.8572 Ǻ and 5.8476 Ǻ and c = 43.4681 Ǻ and 43.3647 Ǻ, for the samples with x = 1.0 and 1.5, in good agreement with the literature data [25].
Hysteresis loops represented in Figure 2 confirm the structural analysis: for pure Sr CoY composition (SCFO) the hysteresis loop is notably wider and higher, reflecting the presence of a harder sample (M-type), and with a higher saturation magnetization. This is a common behavior in all the samples after calcination at 900 °C, but after sintering at 1050 °C is only exhibited in the sample without Ba. At higher sintering temperatures (Figure 2b) the loops have similar width, but we can still observe the different saturation magnetization. In general, it is noted a small increasing trend in the saturation magnetization with the substitution rate (see Table 1), in good agreement with Cho et al. [25], related to the increased exchange involving the 18 hVI octahedral site. On the other hand, coercivities and remanence have a decreasing trend with substitution rate.
We can also observe that at room temperature the sample x = 1.5 exhibits a loop with a different shape regarding the others, as well as a higher coercivity regarding the samples with lower substitution. It has been reported [25,26] that multiferroic materials can present anomalous hysteresis loops so in this way we obtain additional proof that in this system the candidates to exhibit multiferroic behavior belong to the higher Sr substitution rate x > 1.0.
The transverse susceptibility ratio can be expressed as:
Δ χ T / χ T ( % ) = ( χ T ( H ) − χ T ( H S A T ) ) ∗ 100 / χ T ( H S A T ) ,
where χT (HSAT) is the transverse susceptibility at the saturating field (HSAT = 5000 Oe in our case). For samples filling completely the measuring coil we can deduce [27]:
Δ χ T / χ T ( % ) = ( L ( H ) − L ( H S A T ) ) ∗ 100 / L ( H S A T ) ,
In this way, the dependence on the geometrical parameters is minimized so that it is useful to extract parameters, i.e., transition temperatures, anisotropy, and switching fields [11,27]. When ΔχT/χT is represented as a function of the DC field, maxima are observed at the anisotropy field, and effective anisotropy constant can be deduced [1,2]. The accuracies of parameters are ±0.2% for TS amplitude, ±1 Oe for critical fields, and the temperature spacing used in the measurement, ±2.5 K in our case, for temperature ranges.
Representative broadband TS measurements are shown in Figure 3. The common feature is a rather broad process with low amplitude at low temperatures, then the peak increases strongly over room temperature, and at the same time approaches to zero applied field. This behavior has been observed in soft ferrites [4,27]. The maximum TS value takes place at the top measuring Tmeas tested and diminishes from 10.2% for the x = 0.0 sample to 5.8% and 4.8% for x = 0.5 and x = 1.0 samples, then increases to 7.5% when x = 1.5. On the other hand, the sample x = 2.0 (without Ba) behaves in a very different way: the TS amplitude is very small (0.5%), the peak at low temperatures vanishes at T = 250 K and then symmetrical peaks are observed with an applied DC field of 3500 Oe that corresponds to the anisotropy field of the M phase of the compound, according with the wider hysteresis loop. Taking into account the XRD results and the fact that this sample behaves in a very different way than the rest, we can conclude that the phase formation in the absence of Ba is quite different so we will not further analyze this sample in which single Y phase is not present in the sintering temperature range tested.
In Figure 4, we show the 2D plots of the TS measurements in which the effect of the DC magnetic field is highlighted. We can observe that the TS is very similar in samples up to x = 1.0, in which the TS peak is poorly defined and looks like a plateau that narrows with the increase in Tmeas. Anyway, in sample x = 1.0, we can already observe a well-defined maximum at low Tmeas and in the negative part of the DC magnetic sweep, a minimum, and a smaller maximum. In the sample x = 1.5, which corresponds to the optimal substitution rate to obtain multiferroic properties, this behavior is clearly observed, especially at low Tmeas, when measuring temperature is raised over 280 K we can just observe a maximum with a shoulder in the negative sweep.
The temperature dependence of the anisotropy field is similar in all the samples: at low temperatures, there is a plateau of about 350 Oe for x = 0.0 and 0.5 or 600 Oe for x = 1.0 and 1.5, and then HA diminishes when Tmeas is over 250 K. The measured values at 300 K are 330 Oe, 300 Oe, 250 Oe, and 390 Oe for x = 0.0 to 1.5 samples, in good agreement with previously reported data [21,28,29]. When the sintering temperature is raised, we observe that the TS plots for samples x ≥ 1.0 have different shapes in the ranges 80 K–150 K, 150–250 K, and 250 K–350 K, and the anisotropy field first increases, and then diminishes with different slopes [23]. Taking into account the sudden increase in saturation magnetization, we can state that the stability range of formation of single phase Y type hexaferrite is narrower than samples with low Sr substitution unless the differences in the TS profiles in the samples x ≥ 1.0 can also point to the existence of spin transitions, as it has been observed in the similar system BSZFO at room temperature [30] It is noteworthy that in this complex system, the magnetic response is strongly dependent on the composition, the sintering temperature and the applied magnetic field, so that subtle changes in one of the above can promote strong variation in the magnetization [20].
In BSCFO with high Sr substitution it has been reported [21,31] that the system undergoes spin transitions from alternate longitudinal conical (ALC) to transverse conical (TC) at temperatures up to 280 K. It is also known that in TC and in some intermediate spin configurations, like FE3 or double fan [12], the cycloidal component of the spiral spin order can induce ferroelectricity behavior by the spin current or inverse Dzyaloshinskii-Moriya interaction mechanism (see Figure 5). In the samples analyzed, the difference observed in the TS measurements lies in the appearance of a secondary maximum in the unipolar scan after the zero crossing of the varying DC applied field, which is absent in samples with x < 1.0, appears slightly for x = 1.0 at low measuring temperatures and is more evident when the substitution rate increases to the optimal value near x = 1.5, and lasts for higher Tmeas. The lattice distortion promotes the stabilization of noncollinear helical spin configurations, and the applied magnetic field can promote that the system undergoes a metastable change from the ALC to the FE3 state [32,33]; in this way, recent studies show that the FE3 state can be rather stable, and the spin-driven polarization can be switched by magnetic fields and magnetic moments reversed by electric fields [34]. These changes can account for the observed field dependence of the transverse susceptibility in the BSCFO system. In this way, TS measurements are a valuable tool, taking into account that ferrimagnetic spin transitions are not seen in transport measurements and are indicative of the multiferroic capabilities of this kind of compound with helical ferrimagnetic order.

3.2. Ba2−xSrxZn2Fe12O22 System (BSZFO)

In order to appreciate in detail the ability to detect spin transitions, we also analyzed the Ba2−xSrxCo2Fe12O22 (BSZFO) system, considering, in this case, a small variation of the x value around the value x = 1.5, which is the most studied since this ratio of Ba and Sr provides the optimum crystalline distance around the Sr cation in the T-block for magnetic phase transitions to take place. In particular, we studied the values x = 1.3 and x = 1.7. In the previous study [19], we already showed that the sintering temperature of 1250 °C was too high, and the Z phase appeared as the majority phase. In the samples x = 1.3 and x = 1.7, this behavior is also observed, with narrow hysteresis cycles and with maximum magnetization values around 25 emu/g. This value is notably higher than those obtained at 1050 °C and 1150 °C, which are between 5 and 15 emu/g, and in which previous XRD analyses [19] reveal that a pure Y phase is formed.
On the basis of this formation range, we analyze these lower sintering temperatures in detail. In Figure 6, we see the narrow hysteresis cycles, with magnetization values around 10 emu/g corresponding to the Y phase of Zn [35]. It is observed that the magnetization decreases with increasing x, although as we will comment later, this behavior is due to the majority magnetic phase at the ambient temperature at which the cycles have been measured. For x = 1.5 the cycle presents step-like variations, which are not observed in the rest of the samples, and the sample x = 1.3 has a narrower cycle in the vicinity of the null field. The same behavior is exhibited by the sample of the same composition sintered at 1050 °C, as well as the one at x = 1.5, while the one at x = 1.7 has a wider cycle, suggesting that the closer x approaches 2, the narrower the temperature range of pure Y-phase formation (Figure 6a).
All the loops with unusual shapes obey the same general behavior of this type of material: the existence of metamagnetic transitions for field values close to zero. The samples have been magnetized with an increasing field, and depending on the maximum value reached, the response is ferrimagnetic, which requires fields above 1 T [36], and for lower fields, we have a conical magnetization, transverse conical TC or double fan FE3 when the DC field acts on the grains of the polycrystal with c axis perpendicular to the direction of the applied field, and longitudinal conical ALC for the grains in which c is parallel to HDC. For polycrystalline samples, both situations will be present. The low-frequency hysteresis measurement allows the longitudinal effects to be observed as a priority so that wasp-waist-type cycles are observed when a metamagnetic transition takes place in which the ALC phase grows, which is associated with a fall in magnetization [37], which is the case observed for x = 1.3 and x = 1.5 at 1050 °C, as well as x = 1.3 at 1150 °C. On the other hand, step-like cycles are observed when there are also phase changes between two transverse phases from FE3 to FE2 or from FE3 to FE3 + FE2. It should be noted that at room temperature these are spin arrangements of similar energies and therefore coexist [37]. In the BSZFO system, it is only observed in compound x = 1.5 at 1150 °C.
The origin of this behavior lies in the size of the lattice. It is well known that the progressive substitution of Sr instead of Ba distorts the lattice around Sr due to its smaller size, affecting particularly the Fe(4)-O(2)-Fe(5) bonds which are decisive for the superexchange interaction. Fe(5) is a tetrahedral site in the T-block of the structure, occupied by an increasing amount of Zn as Sr is introduced [38], weakening the superexchange interaction and thus modifying the Curie temperature on the one hand, and the state of the magnetization on the other, so that for values close to x = 1.5 the collinear orientation is destabilized and various states with spiral magnetization are favored. This behavior is therefore highly sensitive to any effect that may modify the structural parameters, such as cation substitutions, Sr content replacing Ba, sintering temperature, etc. Previous works [19,39] have shown that changing the sintering temperature leads to a 15 K increase in the observed phase changes and possibly in the Curie temperature due to the variation of the lattice size. In the samples analyzed here, the same behavior is also observed for x = 1.3 and x = 1.7, and we also see that the proportion of Ba and Sr is also affected, as described below. The effect of the initial composition on the TS is going to be described in the samples made at 1050 °C.
We see in Figure 7 that in the composition x = 1.7, the maximum TS value decreases continuously from 80 K (our lowest Tmeas) and cancels out at lower temperatures than the other compositions. At 1150 °C, the further increase only starts to become noticeable at 350 K (our highest Tmeas). On the contrary, the compositions x = 1.3 and 1.5 have similar behavior in Tmeas, although in x = 1.3, the increase in TS at temperatures above 330 K is much more noticeable.
For x = 1.3, in the unipolar path from +0.5 T to −0.5 T, there is a maximum decrease from 300 Oe at 80 K to 100 Oe at 250 K. From this temperature, the value of the susceptibility decreases a lot until it becomes minimum at 285 K, and then it rises considerably. In this range, a new maximum in negative values of HDC emerges, and also a second maximum in positive values, which reflects the evolution of different magnetic phases for different temperatures and field values. In this sense, the TS measurement provides us with a complete description of the magnetic state of each composition (Figure 7).
The behavior for the sample x = 1.5 is different: the decreasing maximum is in the range of 80–180 K and has a higher value than the previous compound (350 Oe). Between 180 and 230 K, there is also a maximum and a minimum in the negative field range, and in this temperature range, the positive maximum is observed for increasing field values. From 230 K onwards, the value of the negative maximum stabilizes, and a second maximum is observed in both the positive and negative field regions. For temperatures above 250 K, which is the maximum susceptibility value, a third maximum arises in the positive zone. Subsequently, the first observed extremes disappear. At 295 and 300 K, identical behavior is observed in the bipolar path in both field directions, and at 305 K, all extremes disappear. For the composition x = 1.7, the response is analogous, although in this case, two simultaneous maxima are not observed in the negative zone, and the region with a non-zero effective field is slightly larger, reaching 310 K, as well as having a wider region in temperature with high critical field values, both in positive and negative values of HDC (Figure 6).
The results shown above allow us to affirm that the variations observed in the transverse magnetic susceptibility measurements for each temperature at different bias field values are due to changes in the spin configuration of the samples analyzed. It is known that a variety of non-collinear magnetic phases exist in these compounds. Several of them, such as the normal or alternating longitudinal conical (NLC and ALC) or the planar proper screw (PS), do not give rise to a spin configuration that induces ferroelectric behavior, while the transverse conical (TC) does. Initially, it was thought that this was the only phase with such behavior, however, due to subtle variations in the Me-O-Me bond between the S and T blocks, there is a variation of the spin rotation angle between neighboring L and S blocks, which have large and small magnetization resp (Figure 5) [37]. As already mentioned, these small variations can come from several factors, and as a consequence, the formation of non-collinear phases with helical modulation will be favored, such as the TC phase, but also others called intermediate II and III [36] or more commonly FE2 and FE3. Both can be decomposed into two spin contributions, one of which is a cycloidal elliptical component that leads to spin-induced electric polarization due to the spin current mechanism [19,40], but in particular, the FE3 or double fan phase turns out to be of particular importance in terms of magnetoelectric properties as it is quite stable at values close to room temperature and in a not excessively demanding field range, in the order of 1000 Oe [37], and therefore with quite advantageous conditions to be used in different magnetoelectric or spintronic applications. In addition, these materials are expected to show a large caloric response near the magnetic phase transitions. Usually, the entropy decreases when a field is applied isothermally, but an inverse caloric effect can take place near a phase transition; hence, the entropy increases when the field is applied, and both direct and inverse magnetocaloric peaks occur in the temperature range where the transition takes place [26,41]. This also opens up the possibility of the electric control of the magnetocaloric effect.
The results of the transverse susceptibility measurements presented in Figure 8 show for each temperature the different spin states through which the sample under study passes, so that the maxima observed in the unipolar sweep from positive field to negative field are related to the appearance next to the FE3 phase, which is the one that predominates when applying fields of the order of 0.5 T, of the FE2 phase. This happens rather abruptly at 265 K for x = 1.3 and at 220 K for x = 1.7, while it happens more gradually for x = 1.5. The decreasing positive critical field values also change markedly, especially for x = 1.3, where they do not reach 600 Oe, while they exceed 1600 Oe for the other compositions. For small positive fields, a longitudinal phase or PS appears, which decreases the magnetization as observed with the hysteresis cycle measurement. This region becomes more extensive in temperature for x = 1.5 and x = 1.7. Once the field direction is reversed, the observed extremes are related to the recovery of the initial state when increasing the bias field value, which happens asymmetrically for field values higher in modulus than those of the first quadrant, being necessary fields of up to 2200 Oe to recover this state.
Our measurement system thus allows us to scan in detail the effect of different magnetic fields over a wide range of temperatures, allowing us to observe in polycrystalline samples the responses observed for H perpendicular to c in single crystals [37], and with a similar interpretation, as the field values obtained are very similar.

4. Conclusions

Transverse susceptibility (TS) measurements have been carried out on polycrystalline Y-type BSCFO and BSZFO hexaferrites with compositions Ba2−xSrxCo2Fe12O22, (0.0 < x < 2.0) and Ba2−xSrxZn2Fe12O22, (1.3 < x < 1.7), some of them promising ones to exhibit multiferroic properties. XRD and hysteresis reveal that single-phase Y hexaferrite is obtained in a range that depends on the initial composition. TS measurements show for the BSCFO system, the appearance of a secondary maximum after the zero crossing of the varying DC applied field, which is absent in samples with x < 1.0, appears slightly for x = 1.0 at low measuring temperatures and is more evident when the substitution rate increases to the optimal value near x = 1.5. TS plots for samples x ≥ 1.0 have different shapes in the ranges 80 K–150 K, 150–250 K, and 250 K–350 K. In the case of the BSZFO system, there are several peaks related to the phase transitions that take place, with certain variations depending on the degree of Ba substitution and the applied field in a more or less extended region around the ambient temperature. This type of measurement is a valuable tool to determine the bias field and temperature range of spin transitions and, hence, the multiferroic behavior in this kind of material.

Author Contributions

Conceptualization, P.H.-G.; methodology, P.H.-G. and J.M.M.; software, J.M.M.; validation, J.M.M.; formal analysis, P.H.-G. and Ó.B.; investigation, P.H.-G. and Ó.B.; resources, P.H.-G. and J.M.M.; data curation, P.H.-G. and Ó.B.; writing—original draft preparation, P.H.-G.; writing—review and editing, P.H.-G.; visualization, P.H.-G. and Ó.B.; supervision, P.H.-G.; project administration, P.H.-G.; funding acquisition, P.H.-G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors upon request.

Acknowledgments

Óscar Bernardo acknowledges the University of Valladolid and Spanish Ministerio de Trabajo y Economía Social for Investigo-SEPE contract ref CP23/164 financed by European Union-NextGenerationEU.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Aharoni, A.; Frei, E.H.; Shtrikman, S.; Treves, D. The reversible susceptibility tensor of the Stoner-Wohlfarth model. Bull. Res. Counc. Isr. Sect. A Math. Phys. Chem. 1957, 6A, 215–238. [Google Scholar]
  2. Pareti, L.; Turilli, G. Detection of singularities in the reversible transverse susceptibility of an uniaxial ferromagnet. J. Appl. Phys. 1987, 61, 5098–5101. [Google Scholar] [CrossRef]
  3. Richter, H.J. Determination of magnetic anisotropy of magnetically hard materials. J. Appl. Phys. 1990, 67, 3081–3087. [Google Scholar] [CrossRef]
  4. Poddar, P.; Wilson, J.L.; Srikanth, H.; Farrell, D.F.; Majetich, S.A. In-plane and out-of-plane transverse susceptibility in close-packed arrays of monodisperse Fe nanoparticles. Phys. Rev. B 2003, 68, 214409. [Google Scholar] [CrossRef]
  5. Sollis, P.M.; Bissell, P.R.; Mayo, P.I.; Chantrell, R.W.; Gilson, R.G.; O’Grady, K. Characterization of the dispersion process using transverse susceptibility measurements. J. Magn. Magn. Mater. 1993, 120, 94–96. [Google Scholar] [CrossRef]
  6. Zimmerman, G.; Hempel, K.A. Transverse susceptibility of uniaxial multidomain particles. IEEE Trans. Magn. 1992, 28, 3126–3128. [Google Scholar] [CrossRef]
  7. ElBidweihy, H.; Smith, R.D.; Hughes, H. Parametric amplification of reversible transverse susceptibility in single domain magnetic nanoparticles. AIP Adv. 2019, 9, 045031. [Google Scholar] [CrossRef]
  8. Kalappattil, V.; Das, R.; Phan, M.H.; Srikanth, H. Roles of bulk and surface magnetic anisotropy on the longitudinal spin Seebeck effect of Pt/YIG. Sci. Rep. 2017, 7, 13316. [Google Scholar] [CrossRef]
  9. Chandra, S.; Biswas, A.; Datta, S.; Ghosh, B.; Raychaudhuri, A.K.; Srikanth, H. Inverse magnetocaloric and exchange bias effects in single crystalline La0:5Sr0:5MnO3 nanowires. J. Magn. Magn. Mater. 2013, 24, 505712. [Google Scholar]
  10. Woods, G.T.; Poddar, P.; Srikanth, H. Observation of charge ordering and the ferromagnetic phase transition in single crystal LSMO using rf transverse susceptibility. J. Appl. Phys. 2005, 97, 10C104. [Google Scholar] [CrossRef]
  11. Frey Huls, N.A.; Bingham, N.S.; Phan, M.H.; Srikanth, H.; Stauffer, D.D.; Leighton, C. Transverse susceptibility as a probe of the magnetocrystalline anisotropy-driven phase transition in Pr0.5Sr0.5CoO3. Phys. Rev. B 2011, 83, 024406. [Google Scholar] [CrossRef]
  12. Kimura, T. Magnetoelectric hexaferrites. Annu. Rev. Condens. Matter Phys. 2012, 3, 93–110. [Google Scholar] [CrossRef]
  13. Zhai, K.; Wu, Y.; Shen, S.; Tian, W.; Cao, H.; Chai, Y.; Chakoumakos, B.C.; Shang, D.; Yan, L.; Wang, F.; et al. Giant magnetoelectric effects achieved by tuning spin cone symmetry in Y-type hexaferrites. Nat. Commun. 2017, 8, 519. [Google Scholar] [CrossRef]
  14. Stimphil, E.; Nagesetti, A.; Guduru, R.; Stewart, T.; Rodzinski, A.; Liang, P.; Khizroev, S. Physics considerations in targeted anticancer drug delivery by magnetoelectric nanoparticles. Appl. Phys. Rev. 2017, 4, 021101. [Google Scholar] [CrossRef]
  15. Bai, Y.; Zhang, W.; Qiao, L.; Zhou, J. Low-fired Y-type hexagonal ferrite for hyper frequency applications. J. Adv. Ceram. 2012, 1, 100–109. [Google Scholar] [CrossRef]
  16. Ueda, H.; Tanaka, Y.; Nakajima, H.; Mori, S.; Ohta, K.; Haruki, K.; Hirose, S.; Wakabayashi, Y.; Kimura, T. Magnetic structure and effect of magnetic field on its domain structure in magnetoelectric Ba1.3Sr0.7CoZnFe11AlO22. Appl. Phys. Lett. 2016, 109, 182902. [Google Scholar] [CrossRef]
  17. Yang, Y.T.; Wang, L.Y.; Shen, L.J.; Zhou, W.P.; Song, Y.Q.; Lv, L.Y.; Wang, D.H.; Cao, Q.Q.; Du, Y.W.; Zhang, Y.J.; et al. Electric-field control of magnetization reversal in a Y-type hexaferrite. Solid State Commun. 2014, 178, 54–58. [Google Scholar] [CrossRef]
  18. Choi, B.; Kwon, S.; Lee, S.; Park, C.B.; Shin, K.W.; Kim, K. Fe and Co NMR studies of magnetoelectric Co2 Y-type hexaferrite BSCFAO. J. Phys. Condens. Matter 2018, 30, 065802. [Google Scholar] [CrossRef] [PubMed]
  19. Chmiel, F.P.; Prabahakaran, D.; Steadman, P.; Chen, J.; Fan, R.; Johnson, R.D.; Radaelli, P.G. Magnetoelectric domains and their switching mechanism in a Y-type hexaferrite. Phys. Rev. B 2019, 100, 104411. [Google Scholar] [CrossRef]
  20. Khanduri, H.; Chandra Dimri, M.; Kooskora, H.; Heinmaa, I.; Viola, G.; Ning, H.; Reece, M.J.; Krustok, J.; Stern, R. Structural, dielectric, magnetic, and nuclear magnetic resonance studies of multiferroic Y-type hexaferrites. J. Appl. Phys. 2012, 112, 073903. [Google Scholar] [CrossRef]
  21. Lee, H.B.; Chun, S.H.; Shin, K.W.; Jeon, B.; Chai, Y.S.; Kim, K.; Schefer, J.; Chang, H.; Yun, S.; Joung, T.; et al. Heliconical magnetic order and field-induced multiferroicity of the Co2Y-type hexaferrite Ba0.3Sr1.7Co2Fe12O22. Phys. Rev. B 2012, 86, 094435. [Google Scholar] [CrossRef]
  22. Pullar, R.C. Hexagonal ferrites: A review of the synthesis, properties and applications of hexaferrite ceramics. Prog. Mater. Sci. 2012, 57, 1191–1334. [Google Scholar] [CrossRef]
  23. Hernández-Gómez, P.; Martín-González, D.; Torres, C.; Muñoz, J.M. Broadband transverse susceptibility in multiferroic Y-type hexaferrite Ba0.5Sr1.5Co2Fe2O22. J. Magn. Magn. Mater. 2019, 476, 478–482. [Google Scholar] [CrossRef]
  24. Figueroa, A.I.; Bartolomé, J.; Garcia del Pozo, J.M.; Arauzo, A.; Guerrero, E.; Téllez, P.; Bartolomé, F.; García, L.M. Low temperature radio-frequency transverse susceptibility measurements using a CMOS oscillator circuit. J. Magn. Magn. Mater. 2012, 324, 2669–2675. [Google Scholar] [CrossRef]
  25. Cho, K.L.; Rhee, C.H.; Kim, C.S. The crystal structure and magnetic properties of Ba2−xSrxCo2Fe12O22. J. Appl. Phys. 2014, 115, 17A523. [Google Scholar]
  26. Xu, W.; Yang, J.; Shen, Y.; Bai, W.; Zhang, Y.; Liu, J.; Tang, K.; Wang, Z.; Duan, C.; Tang, X.; et al. Magnetocaloric effect in multiferroic Y-type hexaferrite Ba0.5Sr1.5Zn2(Fe0.92Al0.08)12O22. AIP Adv. 2014, 4, 067122. [Google Scholar] [CrossRef]
  27. Figueroa, A.I.; Bartolomé, J.; García, L.M.; Bartolomé, F.; Arauzo, A.; Millán, A.; Palacio, F. Magnetic Anisotropy of Maghemite Nanoparticles Probed by RF Transverse Susceptibility. Phys. Procedia 2015, 75, 1050–1057. [Google Scholar] [CrossRef]
  28. Nikzad, A.; Ghasemi, A.; Tehrani, M.K.; Gordani, G.R. Correlation between structural features and microwave analysis of substituted Sr-Co2 Y ceramic nanoparticles. J. Supercond. Nov. Magn. 2016, 29, 1657–1664. [Google Scholar] [CrossRef]
  29. Chang, Y.; Zhai, K.; Chai, Y.; Shang, D.; Sun, Y. Room-temperature magnetoelectric effects in multiferroic Y-type hexaferrites. J. Phys. D Appl. Phys. 2018, 51, 264002. [Google Scholar] [CrossRef]
  30. Hernández-Gómez, P.; Martín-González, D.; Torres, C.; Muñoz, J.M. Broadband transverse susceptibility in multiferroic Y-type hexaferrite Ba0.5Sr1.5Zn2Fe12O22. J. Magn. Magn. Mater. 2020, 506, 166808. [Google Scholar] [CrossRef]
  31. Wang, G.; Cao, S.Y.; Hu, S.; Wang, X.; Feng, Z.; Kang, B.; Chai, Y.; Zhang, J.; Ren, W. Magnetic field controllable electric polarization in Y-type hexaferrite Ba0.5Sr1.5Co2Fe12O22. J. Appl. Phys. 2015, 118, 094102. [Google Scholar] [CrossRef]
  32. Nakajima, T.; Tokunaga, Y.; Matsuda, M.; Dissanayake, S.; Fernandez-Baca, J.; Kakurai, K.; Taguchi, Y.; Tokura, Y.; Arima, T. Magnetic structures and excitations in a multiferroic Y-type hexaferrite BaSrCo2Fe11AlO22. Phys. Rev. B 2016, 94, 195154. [Google Scholar] [CrossRef]
  33. Kocsis, V.; Nakajima, T.; Matsuda, M.; Kikkawa, A.; Kaneko, Y.; Takashima, J.; Kakurai, K.; Arima, T.; Kagawa, F.; Tokunaga, Y.; et al. Magnetization-polarization cross-control near room temperature in hexaferrite single crystals. Nat. Commun. 2019, 10, 1247. [Google Scholar] [CrossRef] [PubMed]
  34. Kocsis, V.; Kaneko, Y.; Tokunaga, Y.; Tokura, Y.; Taguchi, Y. Enhanced Stability of the Multiferroic Phase in Cr-Doped Y-Type Hexaferrite Single Crystals. Phys. Rev. Appl. 2022, 18, 024050. [Google Scholar] [CrossRef]
  35. Mohammed, I.; Mohammed, J.; Kende, A.U.; Wara, A.M.; Aliero, Y.A.; Magawata, U.Z.; Umar, A.A.; Srivastava, A.K. Review on Y-type hexaferrite: Synthesis, characterization and properties. Appl. Surf. Sci. Adv. 2023, 16, 100416. [Google Scholar] [CrossRef]
  36. Kimura, T.; Lawes, G.; Ramirez, A.P. Electric Polarization Rotation in a Hexaferrite with Long-Wavelength Magnetic Structures. Phys. Rev. Lett. 2005, 94, 137201. [Google Scholar] [CrossRef] [PubMed]
  37. Kocsis, V.; Nakajima, T.; Matsuda, M.; Kikkawa, A.; Kaneko, Y.; Takashima, J.; Kakurai, K.; Arima, T.; Tokunaga, Y.; Tokura, Y.; et al. Stability of multiferroic phase and magnetization-polarization coupling in Y-type hexaferrite crystals. Phys. Rev. B 2020, 101, 075136. [Google Scholar] [CrossRef]
  38. Momozawa, N.; Yamaguchi, Y.; Takei, H.; Mita, M. Magnetic Structure of (Ba1-xSrx)2Zn2Fe12O22(x=0–1.0). J. Phys. Soc. Jpn. 1985, 54, 771–780. [Google Scholar] [CrossRef]
  39. Kamba, S.; Goian, V.; Savinov, M.; Buixaderas, E.; Nuzhnyy, D.; Maryško, M.; Kempa, M.; Bovtun, V.; Hlinka, J.; Knížek, K.; et al. Dielectric, magnetic, and lattice dynamics properties of Y-type hexaferrite Ba0.5Sr1.5Zn2Fe12O22: Comparison of ceramics and single crystals. J. Appl. Phys. 2010, 107, 104109. [Google Scholar] [CrossRef]
  40. Zhang, M.; Yin, L.; Liu, Q.; Kong, X.; Zi, Z.; Dai, J.; Sun, Y. Magnetic properties and magnetodielectric effect in Y-type hexaferrite Ba0.5Sr1.5Zn2-xMgxFe11AlO22. J. Alloys Compd. 2017, 725, 1252–1258. [Google Scholar] [CrossRef]
  41. Planes, A.; Castán, T.; Saxena, A. Thermodynamics of multicaloric effects in multiferroic materials: Application to metamagnetic shape-memory alloys and ferrotoroidics. Philos. Trans. R. Soc. A 2016, 374, 20150304. [Google Scholar] [CrossRef] [PubMed]
Jcs 09 00053 g001
Figure 1. XRD patterns of selected Ba2−xSrxCo2Fe12O22 hexaferrite samples sintered at 1150 °C, with the Y pattern.
Figure 1. XRD patterns of selected Ba2−xSrxCo2Fe12O22 hexaferrite samples sintered at 1150 °C, with the Y pattern.
Jcs 09 00053 g001
Jcs 09 00053 g002
Figure 2. Hysteresis loops of Ba2−xSrxCo2Fe12O22 hexaferrite samples: (a) sintered at 1050 °C; (b) sintered at 1150 °C.
Figure 2. Hysteresis loops of Ba2−xSrxCo2Fe12O22 hexaferrite samples: (a) sintered at 1050 °C; (b) sintered at 1150 °C.
Jcs 09 00053 g002
Jcs 09 00053 g003
Figure 3. Three-dimensional broadband TS spectra of Ba2−xSrxCo2Fe12O22 hexaferrite sample sintered at 1050 °C, (a) x = 0.0, (b) x = 1.0, (c) x = 2.0.
Figure 3. Three-dimensional broadband TS spectra of Ba2−xSrxCo2Fe12O22 hexaferrite sample sintered at 1050 °C, (a) x = 0.0, (b) x = 1.0, (c) x = 2.0.
Jcs 09 00053 g003
Jcs 09 00053 g004
Figure 4. Two-dimensional TS plots of Ba2−xSrxCo2Fe12O22 hexaferrites sintered at 1050 °C: (a) x = 0.0, (b) x = 0.5, (c) x = 1.0, (d) x = 1.5.
Figure 4. Two-dimensional TS plots of Ba2−xSrxCo2Fe12O22 hexaferrites sintered at 1050 °C: (a) x = 0.0, (b) x = 0.5, (c) x = 1.0, (d) x = 1.5.
Jcs 09 00053 g004
Jcs 09 00053 g005
Figure 5. Schematic illustration of different types of magnetic structures. Arrows represent spin blocks with large (blue) and small (red) magnetization.
Figure 5. Schematic illustration of different types of magnetic structures. Arrows represent spin blocks with large (blue) and small (red) magnetization.
Jcs 09 00053 g005
Jcs 09 00053 g006
Figure 6. Hysteresis loops of Ba2−xSrxZn2Fe12O22 (x = 1.3, 1.5, 1.7) hexaferrite samples sintered at: (a) 1050 °C and (b) 1150 °C.
Figure 6. Hysteresis loops of Ba2−xSrxZn2Fe12O22 (x = 1.3, 1.5, 1.7) hexaferrite samples sintered at: (a) 1050 °C and (b) 1150 °C.
Jcs 09 00053 g006
Jcs 09 00053 g007
Figure 7. Three-dimensional (left) and two-dimensional (right) broadband TS spectra of Ba2−xSrxZn2Fe12O22 hexaferrite sample sintered at 1050 °C, (a,d) x = 1.3, (b,e) x = 1.5, (c,f) x = 1.7.
Figure 7. Three-dimensional (left) and two-dimensional (right) broadband TS spectra of Ba2−xSrxZn2Fe12O22 hexaferrite sample sintered at 1050 °C, (a,d) x = 1.3, (b,e) x = 1.5, (c,f) x = 1.7.
Jcs 09 00053 g007
Jcs 09 00053 g008
Figure 8. Effective anisotropy and critical field temperature for Ba2−xSrxZn2Fe12O22 hexaferrite samples sintered at 1050 °C (a) x = 1.3, (b) x = 1.5, (c) x = 1.7. The evolution of magnetic field is represented with an arrow, i.e., positive fields are with field descending and negative fields are with the field ascending after zero crossing. Proposed magnetic phase diagram is pointed, based on results with similar systems [37].
Figure 8. Effective anisotropy and critical field temperature for Ba2−xSrxZn2Fe12O22 hexaferrite samples sintered at 1050 °C (a) x = 1.3, (b) x = 1.5, (c) x = 1.7. The evolution of magnetic field is represented with an arrow, i.e., positive fields are with field descending and negative fields are with the field ascending after zero crossing. Proposed magnetic phase diagram is pointed, based on results with similar systems [37].
Jcs 09 00053 g008
Table 1. Magnetic parameters of the Ba2−xSrxCo2Fe12O22 hexaferrites (0.0 ≤ x ≤ 2.0) sintered at 1050 °C, 1150 °C and 1250 °C.
Table 1. Magnetic parameters of the Ba2−xSrxCo2Fe12O22 hexaferrites (0.0 ≤ x ≤ 2.0) sintered at 1050 °C, 1150 °C and 1250 °C.
Substitution RateSintering TemperatureMs (emu/g)Mr (emu/g)Hc (Oe)
x = 0.01050 °C19.655.9129
1150 °C 19.104.475
1250 °C20.952.940
x = 0.51050 °C18.255.4103
1150 °C 19.154.166
1250 °C19.803.047
x = 1.01050 °C19.105.295
1150 °C 19.504.170
1250 °C29.753.761
x = 1.51050 °C20.106.3158
1150 °C 19.354.6104
1250 °C31.453.961
x = 2.01050 °C26.1512.7695
1150 °C 22.554.1101
1250 °C37.355.671
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Hernández-Gómez, P.; Bernardo, Ó.; Muñoz, J.M. Analysis of Structural and Magnetic Phase Transitions in Multiferroic Y-Type Hexaferrite Systems by Means of Transverse Magnetic Susceptibility. J. Compos. Sci. 2025, 9, 53. https://doi.org/10.3390/jcs9020053

AMA Style

Hernández-Gómez P, Bernardo Ó, Muñoz JM. Analysis of Structural and Magnetic Phase Transitions in Multiferroic Y-Type Hexaferrite Systems by Means of Transverse Magnetic Susceptibility. Journal of Composites Science. 2025; 9(2):53. https://doi.org/10.3390/jcs9020053

Chicago/Turabian Style

Hernández-Gómez, Pablo, Óscar Bernardo, and José María Muñoz. 2025. "Analysis of Structural and Magnetic Phase Transitions in Multiferroic Y-Type Hexaferrite Systems by Means of Transverse Magnetic Susceptibility" Journal of Composites Science 9, no. 2: 53. https://doi.org/10.3390/jcs9020053

APA Style

Hernández-Gómez, P., Bernardo, Ó., & Muñoz, J. M. (2025). Analysis of Structural and Magnetic Phase Transitions in Multiferroic Y-Type Hexaferrite Systems by Means of Transverse Magnetic Susceptibility. Journal of Composites Science, 9(2), 53. https://doi.org/10.3390/jcs9020053

Article Metrics

Back to TopTop