Impact of Uncertainty in the Input Variables and Model Parameters on Predictions of a Long Short Term Memory (LSTM) Based Sales Forecasting Model
Abstract
1. Introduction
2. Theoretical Foundations
LSTM Architecture
- : Represents the elementwise product or Hadamard product.
- : Represents the outer product.
- : Represents the inner product.
| Input activation: | (1) | |
| Input gate: | (2) | |
| Forget gate: | (3) | |
| Output gate: | (4) | |
| Internal state: | (5) | |
| Output | (6) |
3. Materials and Methods
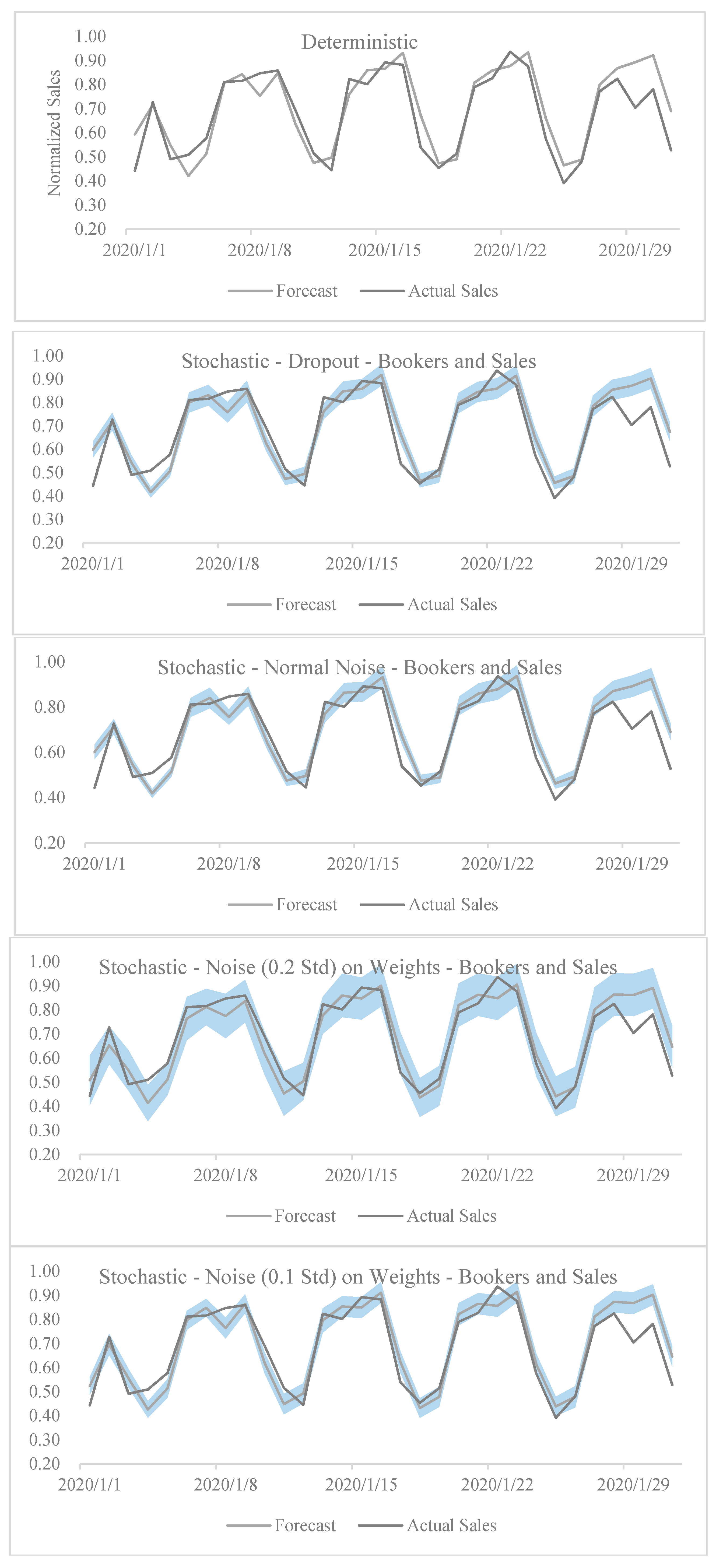
- The dropouts are only used in the active booker count model and not in the sales model at the time of prediction,
- The dropouts are only used in the sales model and not in the active booker count model at the time of prediction,
- The dropouts are used in both the sales and the active booker count models at the time of prediction.
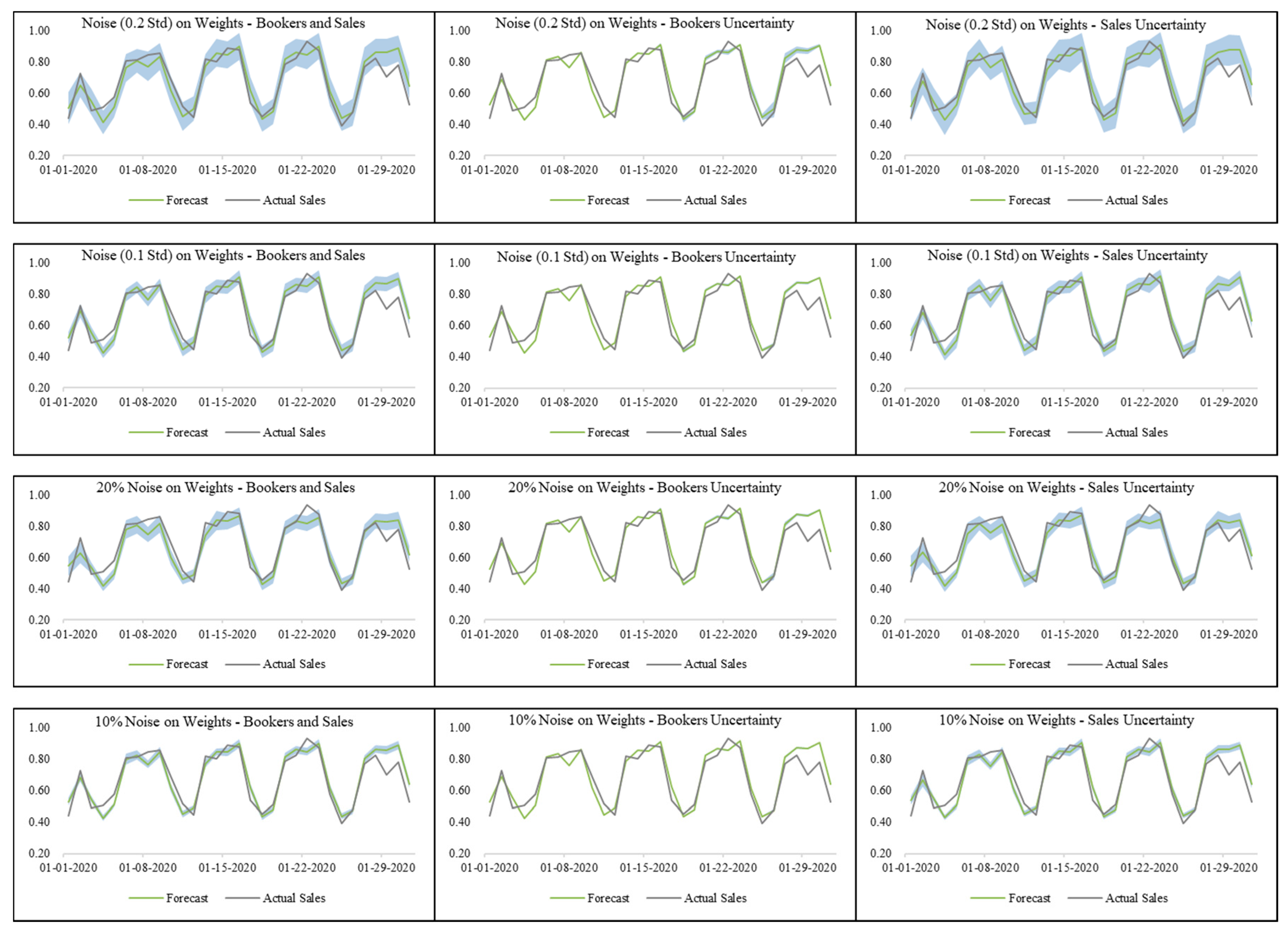
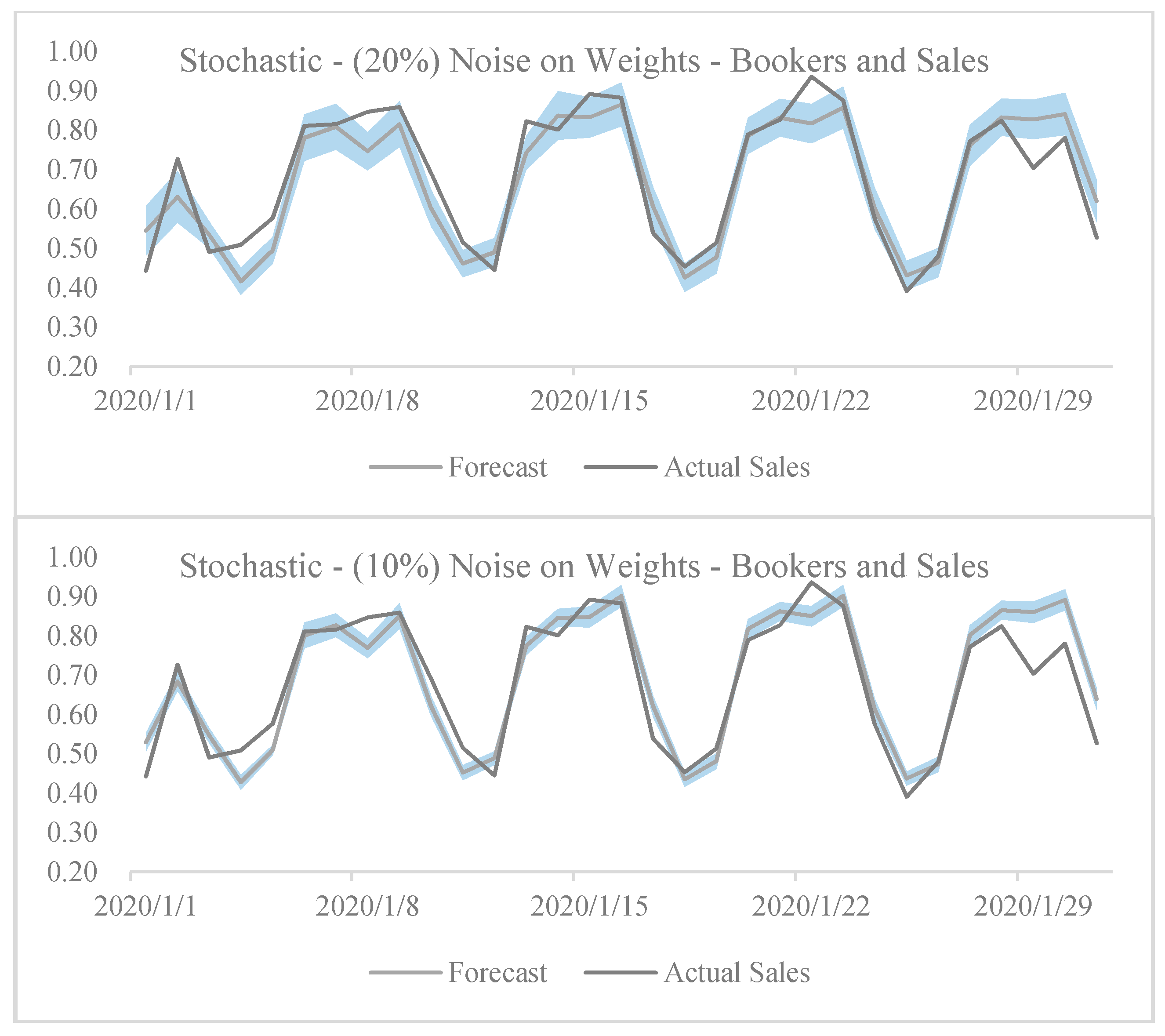
- 0 mean and fixed (0.1 and 0.2) standard deviation;
- 0 mean and fixed percentage (10% and 20%) of weight.
4. Tests and Results
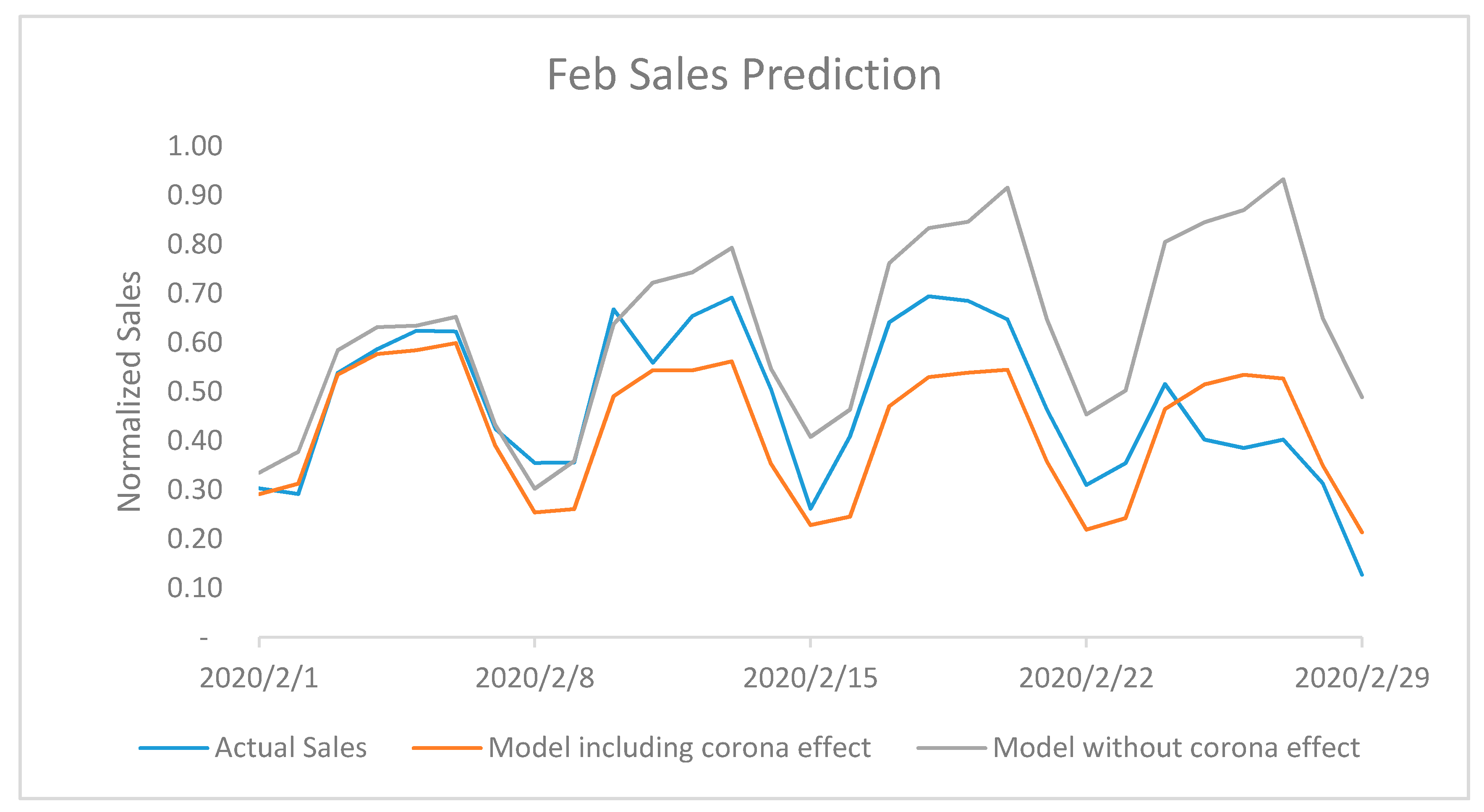
Impact of Corona Virus Outbreak on February 2020 and March 2020 Sales
- Stochastic dropout model with both active booker count and sales uncertainty;
- Noise in weights with 0.2 standard deviation in active booker count and sales models;
- Noise in weights with 20% standard deviation in active booker count and sales models.
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
References
- Jiang, C.; Jiang, M.; Xu, Q.; Huang, X. Expectile regression neural network model with applications. Neurocomputing 2017, 247, 73–86. [Google Scholar] [CrossRef]
- Castañeda-Miranda, A.; Castaño, V.M. Smart frost control in greenhouses by neural networks models. Comput. Electron. Agric. 2017, 137, 102–114, ISSN 0168-1699. [Google Scholar] [CrossRef]
- Arora, S.; Taylor, J.W. Rule-based autoregressive moving average models for forecasting load on special days: A case study for France. Eur. J. Oper. Res. 2018, 266, 259–268. [Google Scholar] [CrossRef]
- Hassan, M.M.; Huda, S.; Yearwood, J.; Jelinek, H.F.; Almogren, A. Multistage fusion approaches based on a generative model and multivariate exponentially weighted moving average for diagnosis of cardiovascular autonomic nerve dysfunction. Inf. Fusion 2018, 41, 105–118. [Google Scholar] [CrossRef]
- Barrow, D.K.; Kourentzes, N.; Sandberg, R.; Niklewski, J. Automatic robust estimation for exponential smoothing: Perspectives from statistics and machine learning. Expert Syst. Appl. 2020, 160, 113637. [Google Scholar] [CrossRef]
- Bafffour, A.A.; Feng, J.; Taylor, E.K.; Jingchun, F. A hybrid artificial neural network-GJR modeling approach to forecasting currency exchange rate volatility. Neurocomputing 2019, 365, 285–301. [Google Scholar] [CrossRef]
- Castañeda-Miranda, A.; Castaño, V.M. Smart frost measurement for anti-disaster intelligent control in greenhouses via embedding IoT and hybrid AI methods. Measurement 2020, 164, 108043. [Google Scholar] [CrossRef]
- Pradeepkumar, D.; Ravi, V. Soft computing hybrids for FOREX rate prediction: A comprehensive review. Comput. Oper. Res. 2018, 99, 262–284. [Google Scholar] [CrossRef]
- Panigrahi, S.; Behera, H. A hybrid ETS–ANN model for time series forecasting. Eng. Appl. Artif. Intell. 2017, 66, 49–59. [Google Scholar] [CrossRef]
- Buyuksahin, U.C.; Ertekin, Ş. Improving forecasting accuracy of time series data using a new ARIMA-ANN hybrid method and empirical mode decomposition. Neurocomputing 2019, 361, 151–163. [Google Scholar] [CrossRef]
- Siami, N.S.; Tavakoli, N.; Siami, N.A. A Comparison of ARIMA and LSTM in Forecasting Time Series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar] [CrossRef]
- Helmini, S.; Jihan, N.; Jayasinghe, M.; Perera, S. Sales forecasting using multivariate long shortterm memory network models. PeerJ PrePrints 2019, 7, e27712v1. [Google Scholar] [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Zhu, L.; Laptev, N. Deep and Confident Prediction for Time Series at Uber. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW); Institute of Electrical and Electronics Engineers (IEEE), New Orleans, LA, USA, 18–21 November 2017; pp. 103–110. [Google Scholar]
- Alonso, A.M.; Nogales, F.J.; Ruiz, C. A Single Scalable LSTM Model for Short-Term Forecasting of Disaggregated Electricity Loads. arXiv 2019, arXiv:1910.06640.2019. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. arXiv 2015, arXiv:1506.02142. [Google Scholar]
- De Franco, C.; Nicolle, J.; Pham, H. Dealing with Drift Uncertainty: A Bayesian Learning Approach. Risks 2019, 7, 5. [Google Scholar] [CrossRef]
- Kabir, H.D.; Khosravi, A.; Hosen, M.A.; Nahavandi, S. Neural Network-Based Uncertainty Quantification: A Survey of Methodologies and Applications. IEEE Access 2018, 6, 36218–36234. [Google Scholar] [CrossRef]
- Akusok, A.; Miche, Y.; Björk, K.-M.; Lendasse, A. Per-sample prediction intervals for extreme learning machines. Int. J. Mach. Learn. Cybern. 2018, 10, 991–1001. [Google Scholar]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef]
- Krzywinski, M.; Altman, N. Points of significance: Importance of being uncertain. Nat. Methods 2013, 10, 809–810. [Google Scholar] [CrossRef]
- Longford, N.T. Estimation under model uncertainty. Stat. Sin. 2017, 27, 859–877. [Google Scholar] [CrossRef]
- Chen, G. A Gentle Tutorial of Recurrent Neural Network with Error Backpropagation. arXiv 2016, arXiv:1610.02583. [Google Scholar]
- Ben Taieb, S.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. arXiv 2011, arXiv:1108.3259. [Google Scholar] [CrossRef]
- Davies, R.; Coole, T.; Osipyw, D. The Application of Time Series Modelling and Monte Carlo Simulation: Forecasting Volatile Inventory Requirements. Appl. Math. 2014, 5, 1152–1168. [Google Scholar] [CrossRef]
- Wright, W. Bayesian approach to neural-network modeling with input uncertainty. IEEE Trans. Neural Netw. 1999, 10, 1261–1270. [Google Scholar] [CrossRef] [PubMed]
- Labach, A.; Salehinejad, H.; Valaee, S. Survey of Dropout Methods for Deep Neural Networks. arXiv 2019, arXiv:1904.13310. [Google Scholar]
- Samuel, P.; Thomas, P.Y. Estimation of the Parameters of Triangular Distribution by Order Statistics. Calcutta Stat. Assoc. Bull. 2003, 54, 45–56. [Google Scholar] [CrossRef]
- Gupta, R.P.; Jayakumar, K.; Mathew, T. On Logistic and Generalized Logistic Distributions. Calcutta Stat. Assoc. Bull. 2004, 55, 277–284. [Google Scholar] [CrossRef]
- Qaffou, A.; Zoglat, A. Discriminating Between Normal and Gumbel Distributions. REVSTAT Stat. J. 2017, 15, 523–536. [Google Scholar]
- Toulias, T.; Kitsos, C.P. On the Generalized Lognormal Distribution. J. Probab. Stat. 2013, 2013, 432642. [Google Scholar] [CrossRef]
- Jiang, L.; Wong, A.C.M. Interval Estimations of the Two-Parameter Exponential Distribution. J. Probab. Stat. 2012, 2012, 734575. [Google Scholar] [CrossRef][Green Version]
- Ognawala, S.; Bayer, J. Regularizing recurrent networks—On injected noise and norm-based methods. arXiv 2014, arXiv:1410.5684. [Google Scholar]
- Li, Y.; Liu, F. Whiteout: gaussian adaptive noise injection regularization in deep neural networks. arXiv 2018, arXiv:1612.01490. [Google Scholar]
- Jim, K.-C.; Giles, C.; Horne, B. An analysis of noise in recurrent neural networks: Convergence and generalization. IEEE Trans. Neural Netw. 1996, 7, 1424–1438. [Google Scholar] [CrossRef] [PubMed]
- Student. The Probable Error of a Mean. Biometrika 1908, 6, 1–25. [Google Scholar] [CrossRef]





| Model Description | Observed Error | p-Value of t-Test vs. Deterministic Model | ||
|---|---|---|---|---|
| Deterministic | 4.02% | - | ||
| Stochastic—Dropout | Active Booker Count and Sales Uncertainty | 2.81% | <0.001 * | |
| Active Booker Count Only Uncertainty | 3.88% | <0.001 * | ||
| Sales Only Uncertainty | 3.10% | <0.001 * | ||
| Stochastic—Noise on Bookers and Sales | Active Booker Count Uncertainty | Normal Noise | 4.17% | 0.008 * |
| Uniform Noise | 4.50% | 0.001 * | ||
| Triangular Noise | 4.16% | 0.032 * | ||
| Logistic Noise | 4.13% | 0.239 | ||
| Gumbel Noise | 5.09% | <0.001 * | ||
| Sales Uncertainty | Normal Noise | 3.92% | 0.240 | |
| Uniform Noise | 4.00% | 0.877 | ||
| Triangular Noise | 4.18% | 0.558 | ||
| Logistic Noise | 3.33% | 0.043 * | ||
| Gumbel Noise | 8.00% | <0.001 * | ||
| Active Booker Count and Sales Uncertainty | Normal Noise | 4.12% | 0.422 | |
| Uniform Noise | 4.47% | 0.016 * | ||
| Triangular Noise | 4.02% | 0.960 | ||
| Logistic Noise | 4.68% | 0.007 * | ||
| Gumbel Noise | 9.42% | <0.001 * | ||
| Stochastic—Noise on Weights | Active Booker Count and Sales Uncertainty | Noise STD: 0.1 | 2.13% | 0.010 * |
| Noise STD: 0.2 | 1.06% | <0.001 * | ||
| Noise STD: 10% | 1.48% | <0.001 * | ||
| Noise STD: 20% | −1.58% | <0.001 * | ||
| Active Booker Count Uncertainty | Noise STD: 0.1 | 2.45% | 0.024 * | |
| Noise STD: 0.2 | 2.70% | 0.067 | ||
| Noise STD: 10% | 2.27% | 0.014 * | ||
| Noise STD: 20% | 2.07% | 0.008* | ||
| Sales Uncertainty | Noise STD: 0.1 | 2.00% | 0.002 * | |
| Noise STD: 0.2 | 1.40% | <0.001 * | ||
| Noise STD: 10% | 1.50% | <0.001 * | ||
| Noise STD: 20% | −1.33% | <0.001* | ||
| Stochastic Dropout—Active Booker Count and Sales Uncertainty | |||
| Duration | Actual Sales | Predicted Sales | Business Impact |
| 15 February to 29 February | 7.46 | 9.90 | −24.7% |
| 1 March to 15 March | 1.19 | 10.77 | −89.0% |
| Total (15 February to 15 March) | 8.65 | 20.68 | −58.2% |
| Noise STD: 0.2 Active Booker Count and Sales Uncertainty | |||
| Duration | Actual Sales | Predicted Sales | Business Impact |
| 15 February to 29 February | 7.46 | 11.19 | −33.3% |
| 1 March to 15 March | 1.19 | 11.62 | −89.8% |
| Total (15 February to 15 March) | 8.65 | 22.81 | −62.1% |
| Noise STD: 20% Active Booker Count and Sales Uncertainty | |||
| Duration | Actual Sales | Predicted Sales | Business Impact |
| 15 February to 29 February | 7.46 | 10.66 | −30.0% |
| 1-March to 15-March | 1.19 | 11.12 | −89.3% |
| Total (15 February to 15 March) | 8.65 | 21.78 | −60.3% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goel, S.; Bajpai, R. Impact of Uncertainty in the Input Variables and Model Parameters on Predictions of a Long Short Term Memory (LSTM) Based Sales Forecasting Model. Mach. Learn. Knowl. Extr. 2020, 2, 256-270. https://doi.org/10.3390/make2030014
Goel S, Bajpai R. Impact of Uncertainty in the Input Variables and Model Parameters on Predictions of a Long Short Term Memory (LSTM) Based Sales Forecasting Model. Machine Learning and Knowledge Extraction. 2020; 2(3):256-270. https://doi.org/10.3390/make2030014
Chicago/Turabian StyleGoel, Shakti, and Rahul Bajpai. 2020. "Impact of Uncertainty in the Input Variables and Model Parameters on Predictions of a Long Short Term Memory (LSTM) Based Sales Forecasting Model" Machine Learning and Knowledge Extraction 2, no. 3: 256-270. https://doi.org/10.3390/make2030014
APA StyleGoel, S., & Bajpai, R. (2020). Impact of Uncertainty in the Input Variables and Model Parameters on Predictions of a Long Short Term Memory (LSTM) Based Sales Forecasting Model. Machine Learning and Knowledge Extraction, 2(3), 256-270. https://doi.org/10.3390/make2030014




