A New Rough Set Classifier for Numerical Data Based on Reflexive and Antisymmetric Relations
Abstract
1. Introduction
2. Directional Neighborhood Rough Set Approach
2.1. Decision Table [35]
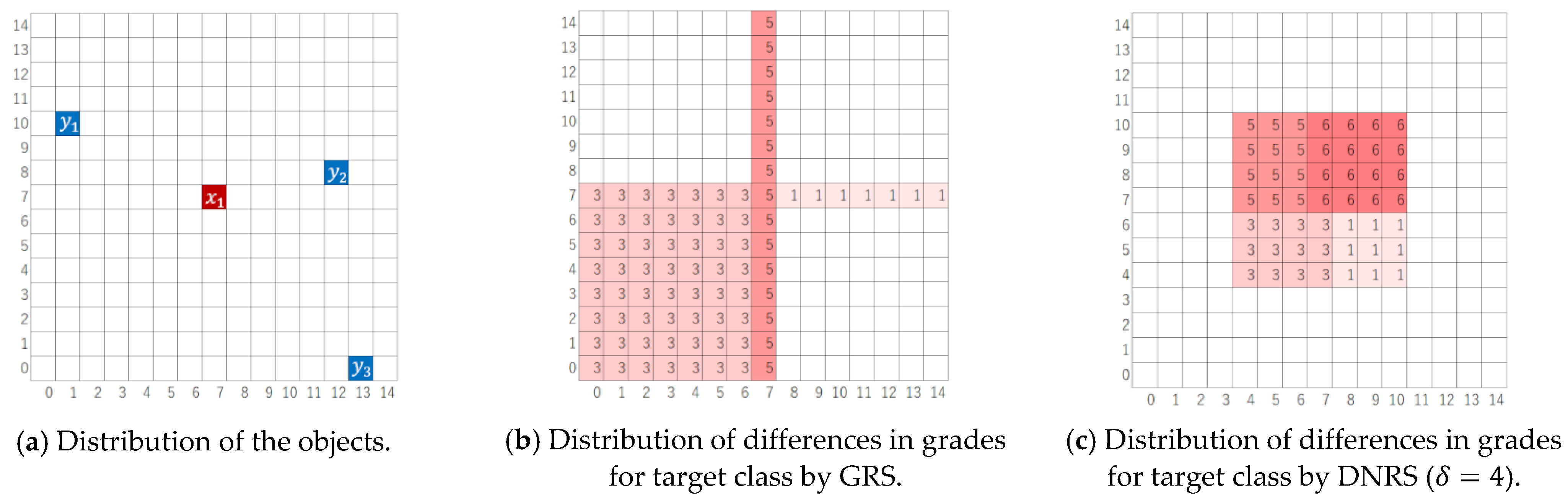
2.2. Grade and Difference in Grade
2.3. Intersection of Half-Space
2.4. Neighborhood
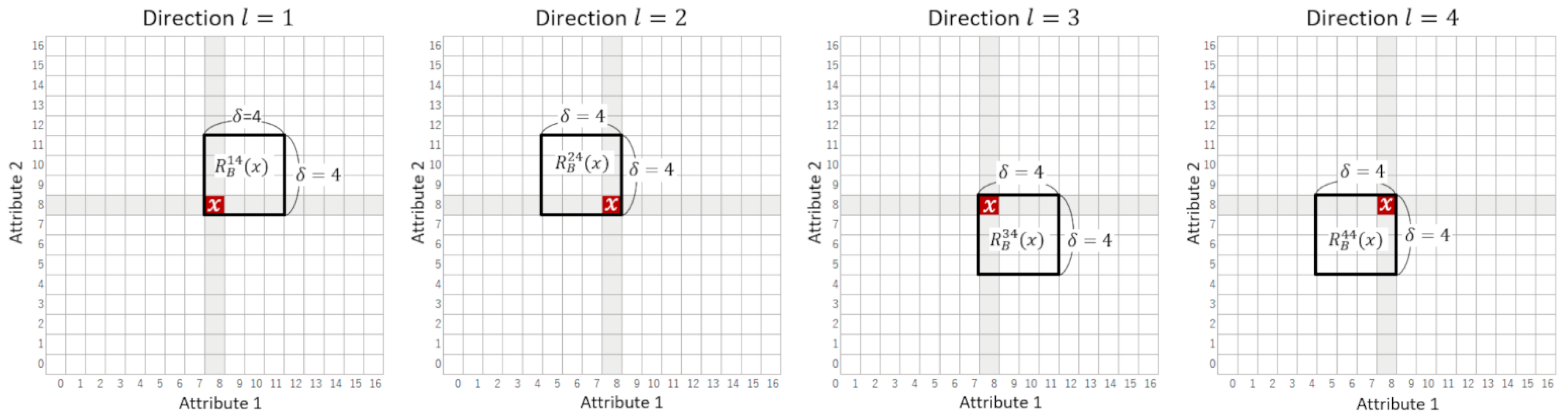
2.5. Directional Neighborhood
2.6. DN-Lower and DN-Upper Approximations
2.7. Decision Rule Extraction
2.8. Classification
2.9. Comparison between DNRS and GRS
3. Directional Neighborhood Rough Set Model
4. Experiments
4.1. Dataset
4.2. Methods
4.2.1. Experiment Demonstrating the Characteristics of the DNRS Model
4.2.2. Experiments to Demonstrate the Improvements by DNRS Model
4.2.3. Experiments to Assess the Performance of the DNRS Model
4.2.4. Accuracy Assessment
5. Results and Discussion
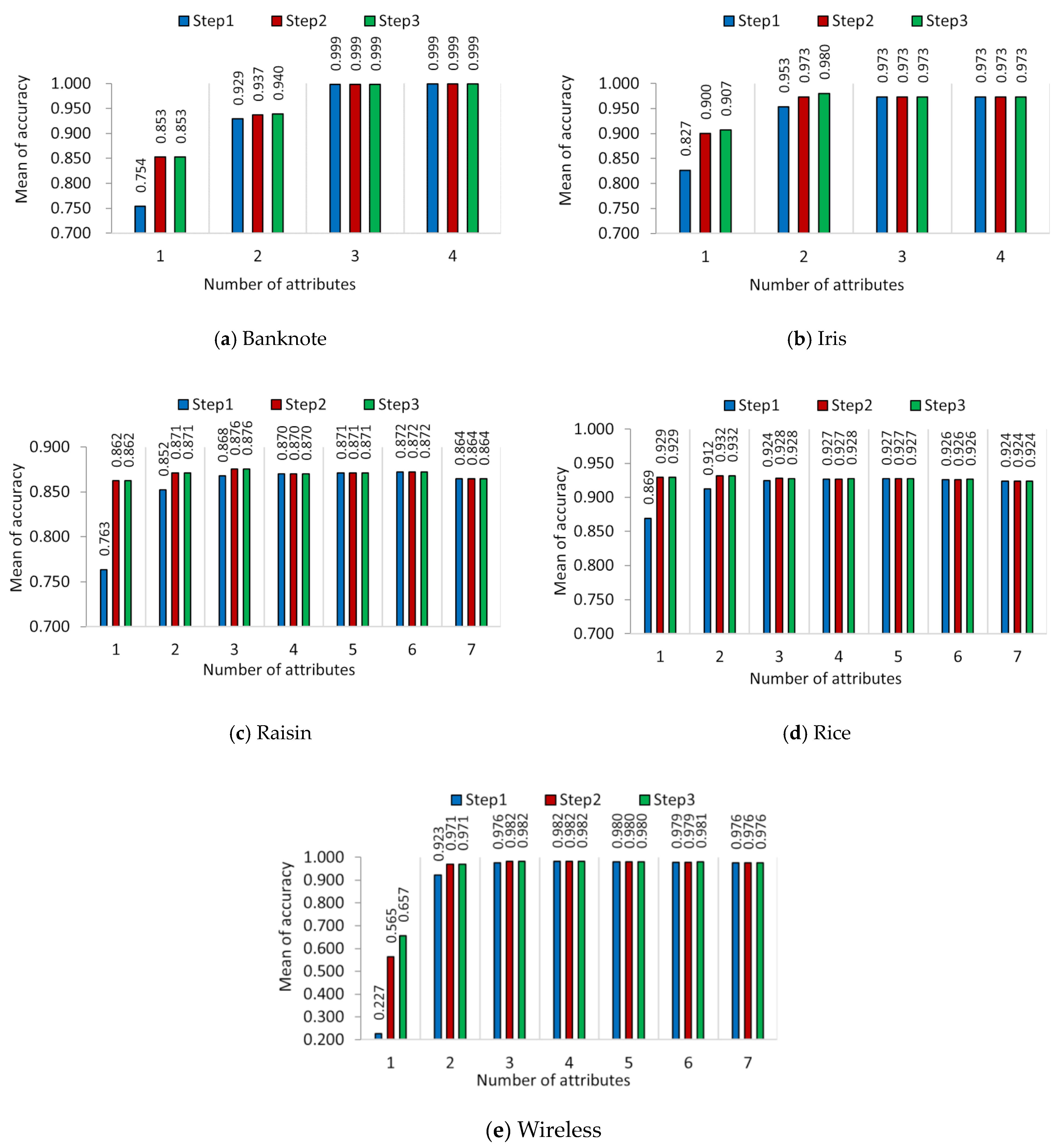
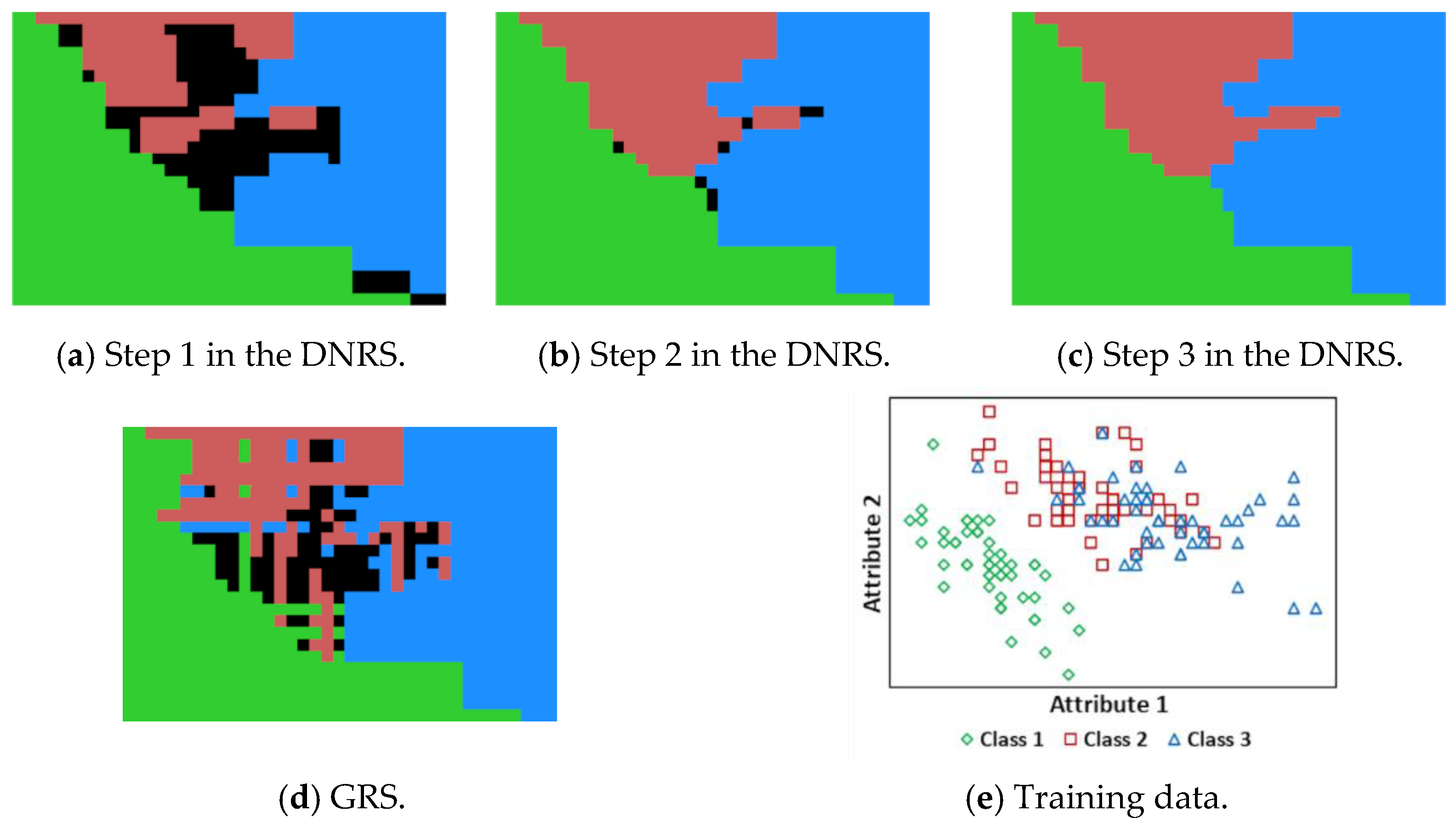
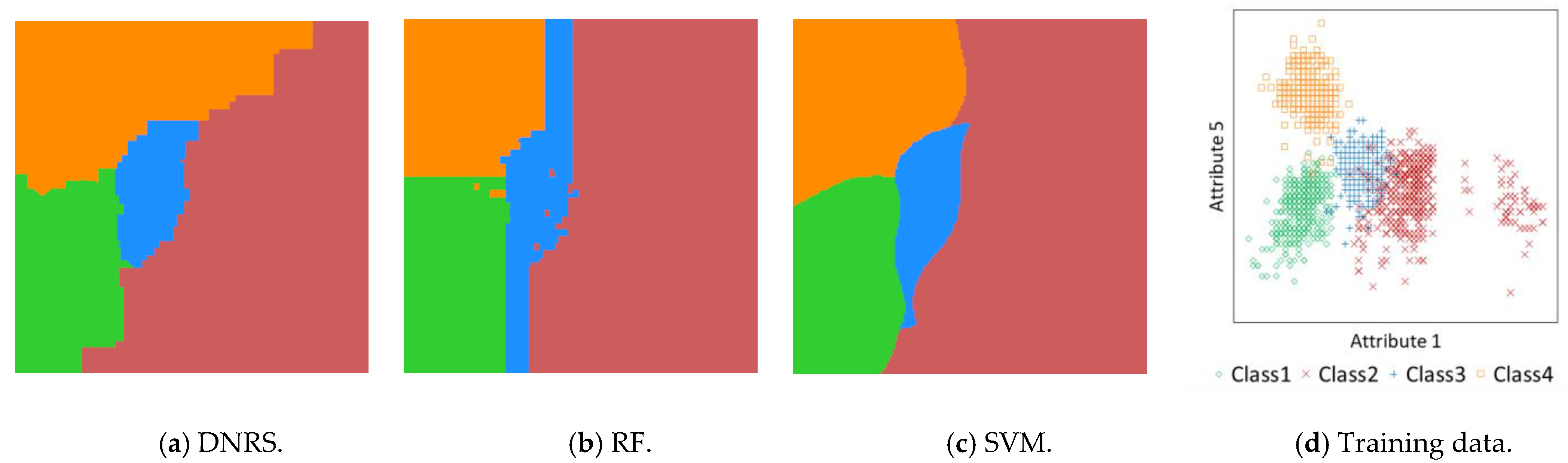
5.1. Experiment Demonstrating the Characteristics of the DNRS Model
5.2. Experiments to Demonstrate the Improvements by the DNRS Model
5.3. Experiments to Assess the Performance of the DNRS Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets: Theoretical Aspects of Reasoning About Data, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherland, 1991; pp. 1–231. [Google Scholar]
- Grzymala-Busse, J.W. Knowledge acquisition under uncertainty—A rough set approach. J. Intell. Robot. Syst. 1988, 1, 3–16. [Google Scholar] [CrossRef]
- Tsumoto, S. Automated extraction of medical expert system rules from clinical databases based on rough set theory. Inf. Sci. 1998, 112, 67–84. [Google Scholar] [CrossRef]
- Shan, N.; Ziarko, W. An incremental learning algorithm for constructing decision rules. In Rough Sets, Fuzzy Sets and Knowledge Discovery; Springer: London, UK, 1994; pp. 326–334. [Google Scholar]
- Pawlak, Z.; Skowron, A. Rudiments of rough sets. Inf. Sci. 2007, 177, 3–27. [Google Scholar] [CrossRef]
- Guan, L.; Wang, G. Generalized Approximations Defined by Non-Equivalence Relations. Inf. Sci. 2012, 193, 163–179. [Google Scholar] [CrossRef]
- Ciucci, D.; Mihálydeák, T.; Csajbók, Z.E. On exactness, definability and vagueness in partial approximation spaces. Tech. Sci. Univ. Warm. Maz. Olsztyn 2015, 18, 203–212. [Google Scholar]
- Ishii, Y.; Bagan, H.; Iwao, K.; Kinoshita, T. A new land cover classification method using grade-added rough sets. IEEE Geosci. Remote Sens. Lett. 2021, 18, 8–12. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Jia, X.; Cai, X. Neighborhood based decision-theoretic rough set models. Int. J. Approx. Reason. 2016, 69, 1–17. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Sáez, J.A.; López, V.; Herrera, F. A survey of discretization techniques: Taxonomy and empirical analysis in supervised learning. IEEE Trans. Knowl. Data Eng. 2013, 25, 734–750. [Google Scholar] [CrossRef]
- Dwiputranto, T.H.; Setiawan, N.A.; Adji, T.B. Rough-Set-Theory-Based Classification with Optimized k-Means Discretization. Technologies 2022, 10, 51. [Google Scholar] [CrossRef]
- Li, X.; Shen, Y. Discretization Algorithm for Incomplete Economic Information in Rough Set Based on Big Data. Symmetry 2020, 12, 1245. [Google Scholar] [CrossRef]
- Hu, Q.; Xie, Z.; Yu, D. Hybrid attribute reduction based on a novel fuzzy-rough model and information granulation. Pattern Recognit. 2007, 40, 3509–3521. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 1990, 17, 191–209. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems; World Scientific: Singapore, 1965; pp. 394–432. ISBN 9780784413616. [Google Scholar]
- Ji, W.; Pang, Y.; Jia, X.; Wang, Z.; Hou, F.; Song, B.; Liu, M.; Wang, R. Fuzzy rough sets and fuzzy rough neural networks for feature selection: A review. Wiley Data Min. Knowl. Discov. 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Yang, X.; Chen, H.; Li, T.; Luo, C. A Noise-Aware Fuzzy Rough Set Approach for Feature Selection. Knowl. Based Syst. 2022, 250, 109092. [Google Scholar] [CrossRef]
- Che, X.; Chen, D.; Mi, J. Label Correlation in Multi-Label Classification Using Local Attribute Reductions with Fuzzy Rough Sets. Fuzzy Sets Syst. 2022, 426, 121–144. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Y.; Ding, W.; Cao, Z. Attribute Reduction with Fuzzy Rough Self-Information Measures. Inf. Sci. 2021, 549, 68–86. [Google Scholar] [CrossRef]
- Hu, Q.; Yu, D.; Liu, J.; Wu, C. Neighborhood rough set based heterogeneous feature subset selection. Inf. Sci. 2008, 178, 3577–3594. [Google Scholar] [CrossRef]
- Yao, Y.; Yao, B. Covering based rough set approximations. Inf. Sci. 2012, 200, 91–107. [Google Scholar] [CrossRef]
- Xie, J.; Hu, B.Q.; Jiang, H. A novel method to attribute reduction based on weighted neighborhood probabilistic rough sets. Int. J. Approx. Reason. 2022, 144, 1–17. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Y.; Shao, M.; Hu, Q.; Chen, D. Feature Selection Based on Neighborhood Self-Information. IEEE Trans. Cybern. 2020, 50, 4031–4042. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Liang, S.; Yu, H.; Gao, S.; Qian, Y. Pseudo-Label Neighborhood Rough Set: Measures and Attribute Reductions. Int. J. Approx. Reason. 2019, 105, 112–129. [Google Scholar] [CrossRef]
- Sun, L.; Wang, L.; Ding, W.; Qian, Y.; Xu, J. Feature Selection Using Fuzzy Neighborhood Entropy-Based Uncertainty Measures for Fuzzy Neighborhood Multigranulation Rough Sets. IEEE Trans. Fuzzy Syst. 2021, 29, 19–33. [Google Scholar] [CrossRef]
- Xu, J.; Shen, K.; Sun, L. Multi-Label Feature Selection Based on Fuzzy Neighborhood Rough Sets. Complex Intell. Syst. 2022, 8, 2105–2129. [Google Scholar] [CrossRef]
- Skowron, A.; Stepaniuk, J. Tolerance approximation spaces. Fundam. Inform. 1996, 27, 245–253. [Google Scholar] [CrossRef]
- Parthaláin, N.M.; Shen, Q. Exploring the boundary region of tolerance rough sets for feature selection. Pattern Recognit. 2009, 42, 655–667. [Google Scholar] [CrossRef]
- Zhao, S.; Tsang, E.C.C.; Chen, D.; Wang, X. Building a rule-based classifier—A fuzzy-rough set approach. IEEE Trans. Knowl. Data Eng. 2010, 22, 624–638. [Google Scholar] [CrossRef]
- Hu, Q.; Yu, D.; Xie, Z. Neighborhood classifiers. Expert Syst. Appl. 2008, 34, 866–876. [Google Scholar] [CrossRef]
- Kumar, S.U.; Inbarani, H.H. A novel neighborhood rough set based classification approach for medical diagnosis. Procedia Comput. Sci. 2015, 47, 351–359. [Google Scholar] [CrossRef]
- Kim, D. Data Classification based on tolerant rough set. Pattern Recognit. 2001, 34, 1613–1624. [Google Scholar] [CrossRef]
- Mori, N.; Takanashi, R. Knowledge acquisition from the data consisting of categories added with degrees of conformity. Kansei Eng. Int. 2000, 1, 19–24. [Google Scholar] [CrossRef][Green Version]
- Pawlak, Z. Information systems theoretical foundations. Inf. Syst. 1981, 6, 205–218. [Google Scholar] [CrossRef]
- Mani, A.; Radeleczki, S. Algebraic approach to directed rough sets. arXiv 2020. [Google Scholar] [CrossRef]
- Mani, A. Comparative approaches to granularity in general rough sets. In Rough Sets; Bello, R., Miao, D., Falcon, R., Nakata, M., Rosete, A., Ciucci, D., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 500–517. ISBN 978-3-030-52705-1. [Google Scholar]
- Yu, B.; Cai, M.; Li, Q. A λ-rough set model and its applications with TOPSIS method to decision making. Knowl. Based Syst. 2019, 165, 420–431. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 25 September 2022).
- Ilkay, C.; Murat, K.; Sakir, T. Classification of raisin grains using machine vision and artificial intelligence methods. Gazi Muhendis. Bilim. Derg. 2020, 6, 200–209. [Google Scholar] [CrossRef]
- Ilkay, C.; Murat, K. Classification of rice varieties using artificial intelligence methods. Int. J. Intell. Syst. Appl. Eng. 2019, 7, 188–194. [Google Scholar] [CrossRef]
- Rohra, J.G.; Perumal, B.; Narayanan, S.J.; Thakur, P.; Bhatt, R.B. User localization in an indoor environment using fuzzy hybrid of particle swarm optimization & gravitational search algorithm with neural networks. Adv. Intell. Syst. Comput. 2019, 741, 217–225. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Boateng, E.Y.; Otoo, J.; Abaye, D.A. Basic tenets of classification algorithms k-nearest-neighbor, support vector machine, random forest and neural network: A review. J. Data Anal. Inf. Process. 2020, 8, 341–357. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector machine versus random forest for remote sensing image classification: A meta-analysis and systematic review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]


| Dataset Name | Number of Instances | Number of Condition Attributes | Number of Classes | Correspondence between the Attributes and the No. Used in This Article |
|---|---|---|---|---|
| Banknote | 1372 | 4 | 2 | 1: Variance of Wavelet Transformed image 2: Skewness of Wavelet Transformed image 3: Cortosis of Wavelet Transformed image 4: Entropy of image |
| Iris | 150 | 4 | 3 | 1: Sepal length 2: Sepal width 3: Petal length 4: Petal width |
| Raisin [40] | 900 | 7 | 2 | 1: Area 2: Perimeter 3: Major Axis Length 4: Minor Axis Length 5: Eccentricity 6: Convex Area 7: Extent |
| Rice [41] | 3810 | 7 | 2 | 1: Area 2: Perimeter 3: Major Axis Length 4: Minor Axis Length 5: Eccentricity 6: Convex Area 7: Extent |
| Wireless [42] | 2000 | 7 | 4 | 1:WS1 2:WS2 3:WS3 4:WS4 5:WS5 6:WS6 7:WS7 |
| Classifier | Hyperparameters |
|---|---|
| DNRS | Delta(t) t: 1–20 |
| RF | Max_depth = None N_estimators = 50, 100, 300, 500 Max_features = sqrt, log2 Criterion = Gini |
| SVM | C = 0.01, 0.1, 1, 10, 100, 1000 Gamma = 0.001, 0.01, 0.1, 1, 10 Kernel = rbf |
| Number of Attributes | DN-lower Approximation Classification (Step 1) | DN-Lower and DN-Upper Approximation Classification (Step 2, Step 3) | |||
|---|---|---|---|---|---|
| Combination of Attributes | (Hyperparameter) | Combination of attributes | (Hyperparameter) | Mean Rate of DN-Lower Approximation Training Data | |
| 1 | 1 | 2 | 1 | 17 | 46.2% |
| 2 | 1, 2 | 3 | 1, 2 | 4 | 96.6% |
| 3 | 1, 2, 3 | 8 | 1, 2, 3 | 8 | 100.0% |
| 4 | 1, 2, 3, 4 | 8 | 1, 2, 3, 4 | 8 | 100.0% |
| Number of Attributes | DN-Lower Approximation Classification (Step 1) | DN-Lower and DN-Upper Approximation Classification (Step 2, Step 3) | |||
|---|---|---|---|---|---|
| Combination of Attributes | (Hyperparameter) | Combination of Attributes | (Hyperparameter) | Mean Rate of DN-Lower Approximation Training Data | |
| 1 | 3 | 6 | 4 | 17 | 75.9% |
| 2 | 3, 4 | 9 | 3, 4 | 14 | 96.8% |
| 3 | 2, 3, 4 | 11 | 2, 3, 4 | 11 | 99.9% |
| 4 | 1, 2, 3, 4 | 9 | 1, 2, 3, 4 | 9 | 100.0% |
| Number of Attributes | DN-lower Approximation Classification (Step 1) | DN-lower and DN-Upper Approximation Classification (Step 2, Step 3) | |||
|---|---|---|---|---|---|
| Combination of Attributes | (Hyperparameter) | Combination of attributes | (Hyperparameter) | Mean Rate of DN-Lower Approximation Training Data | |
| 1 | 2 | 2 | 7 | 18 | 42.0% |
| 2 | 2, 5 | 3 | 6, 7 | 8 | 72.6% |
| 3 | 2, 3, 6 | 3 | 4, 6, 7 | 11 | 83.6% |
| 4 | 1, 3, 6, 7 | 5 | 1, 3, 6, 7 | 5 | 100.0% |
| 2, 4, 6, 7 | 3 | 2, 4, 6, 7 | 3 | 100.0% | |
| 5 | 1, 4, 5, 6, 7 | 9 | 1, 3, 5, 6, 7 | 9 | 100.0% |
| 1, 4, 5, 6, 7 | 9 | 100.0% | |||
| 6 | 1, 2, 3, 5, 6, 7 | 3 | 1, 2, 3, 5, 6, 7 | 3 | 100.0% |
| 7 | 1, 2, 3, 4, 5, 6, 7 | 6 | 1, 2, 3, 4, 5, 6, 7 | 6 | 100.0% |
| Number of Attributes | DN-lower Approximation Classification (Step 1) | DN-Lower and DN-Upper Approximation Classification (Step 2, Step 3) | |||
|---|---|---|---|---|---|
| Combination of Attributes | (Hyperparameter) | Combination of Attributes | (Hyperparameter) | Mean Rate of DN-Lower Approximation Training Data | |
| 1 | 3 | 2 | 3 | 15 | 69.4% |
| 2 | 1, 5 | 3 | 4, 6 | 19 | 77.5% |
| 3, 5 | 3 | ||||
| 3 | 1, 2, 3 1, 2, 5 2, 4, 6 | 3 3 4 | 1, 5, 6 2, 3, 7 3, 5, 7 4, 6, 7 | 5 20 15 11 | 97.5% 86.9% 88.2% 93.6% |
| 4 | 1, 2, 3, 5 | 3 | 1, 2, 3, 4 | 8 | 100.0% |
| 5 | 1, 2, 3, 5, 6 | 3 | 1, 2, 3, 5, 6 | 3 | 100.0% |
| 1, 3, 5, 6, 7 | 6 | 1, 3, 5, 6, 7 | 6 | 100.0% | |
| 6 | 1, 3, 4, 5, 6, 7 | 8 | 1, 3, 4, 5, 6, 7 | 8 | 100.0% |
| 7 | 1, 2, 3, 4, 5, 6, 7 | 5 | 1, 2, 3, 4, 5, 6, 7 | 5 | 100.0% |
| Number of Attributes | DN-lower Approximation Classification (Step 1) | DN-Lower and DN-Upper Approximation Classification (Step 2, Step 3) | |||
|---|---|---|---|---|---|
| Combination of Attributes | (Hyperparameter) | Combination of Attributes | (Hyperparameter) | Mean Rate of DN-Lower Approximation Training Data | |
| 1 | 5 | 2 | 1 | 9 | 21.5% |
| 2 | 1, 5 | 7 | 1, 5 | 20 | 89.5% |
| 3 | 1, 4, 5 | 5 | 1, 4, 5 | 17 | 97.6% |
| 4 | 1, 4, 5, 7 | 12 | 1, 4, 5, 7 | 12 | 99.6% |
| 5 | 1, 3, 4, 5, 6 | 8 | 1, 3, 4, 5, 6 | 8 | 100.0% |
| 1, 4, 5, 6, 7 | 4 | 100.0% | |||
| 6 | 1, 3, 4, 5, 6, 7 | 5 | 1, 3, 4, 5, 6, 7 | 1 | 100.0% |
| 7 | 1, 2, 3, 4, 5, 6, 7 | 19 | 1, 2, 3, 4, 5, 6, 7 | 1 | 100.0% |
| True Class | |||
|---|---|---|---|
| Class 1 | Class 2 | ||
| Predicted class | Class 1 | 323 | 61 |
| Class 2 | 45 | 359 | |
| Unclassified | 82 | 30 | |
| True Class | |||
|---|---|---|---|
| Class 1 | Class 2 | ||
| Predicted class | Class 1 | 206 | 17 |
| Class 2 | 25 | 328 | |
| Unclassified | 219 | 105 | |
| True Class | |||
|---|---|---|---|
| Class 1 | Class 2 | ||
| Predicted class | Class 1 | 319 | 83 |
| Class 2 | 59 | 367 | |
| Unclassified | 0 | 0 | |
| True class | |||
|---|---|---|---|
| Class 1 | Class 2 | ||
| Predicted class | Class 1 | 402 | 64 |
| Class 2 | 48 | 386 | |
| Unclassified | 0 | 0 | |
| Dataset | DNRS | RF | SVM | Dunnett’s Test (D-Value = 2.333) | |
|---|---|---|---|---|---|
| DNRS vs. RF | DNRS vs. SVM | ||||
| Banknote | 0.999 0.002 (4) | 0.994 0.005 (4) | 1.000 0.000 (3) | * 3.196 | −0.454 |
| Iris | 0.980 0.032 (2) | 0.973 (2) | 0.973 (2) | 0.442 | 0.442 |
| Raisin | 0.876 0.036 (3) | 0.876 0.032 (4) | 0.876 0.028 (4) | 0.000 | 0.000 |
| Rice | 0.932 0.012 (2) | 0.927 0.011 (1) | 0.933 0.014 (5) | 0.948 | −0.190 |
| Wireless | 0.982 0.004 (4) | 0.983 0.009 (6) | 0.985 0.008 (6) | −0.441 | −1.029 |
| Mean | 0.954 | 0.950 | 0.953 | ||
| Classification Time for the Largest Number of Attributes | |||
|---|---|---|---|
| DNRS | RF | SVM | |
| Banknote | 0.073 0.007 | 0.052 0.013 | 0.037 0.010 |
| Iris | 0.057 0.009 | 0.026 0.010 | 0.010 0.007 |
| Raisin | 0.135 0.039 | 0.188 0.027 | 0.026 0.009 |
| Rice | 0.468 0.034 | 0.156 0.023 | 0.112 0.013 |
| Wireless | 0.325 0.028 | 0.182 0.030 | 0.035 0.011 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishii, Y.; Iwao, K.; Kinoshita, T. A New Rough Set Classifier for Numerical Data Based on Reflexive and Antisymmetric Relations. Mach. Learn. Knowl. Extr. 2022, 4, 1065-1087. https://doi.org/10.3390/make4040054
Ishii Y, Iwao K, Kinoshita T. A New Rough Set Classifier for Numerical Data Based on Reflexive and Antisymmetric Relations. Machine Learning and Knowledge Extraction. 2022; 4(4):1065-1087. https://doi.org/10.3390/make4040054
Chicago/Turabian StyleIshii, Yoshie, Koki Iwao, and Tsuguki Kinoshita. 2022. "A New Rough Set Classifier for Numerical Data Based on Reflexive and Antisymmetric Relations" Machine Learning and Knowledge Extraction 4, no. 4: 1065-1087. https://doi.org/10.3390/make4040054
APA StyleIshii, Y., Iwao, K., & Kinoshita, T. (2022). A New Rough Set Classifier for Numerical Data Based on Reflexive and Antisymmetric Relations. Machine Learning and Knowledge Extraction, 4(4), 1065-1087. https://doi.org/10.3390/make4040054






