Tabular Machine Learning Methods for Predicting Gas Turbine Emissions
Abstract
1. Introduction
2. Background
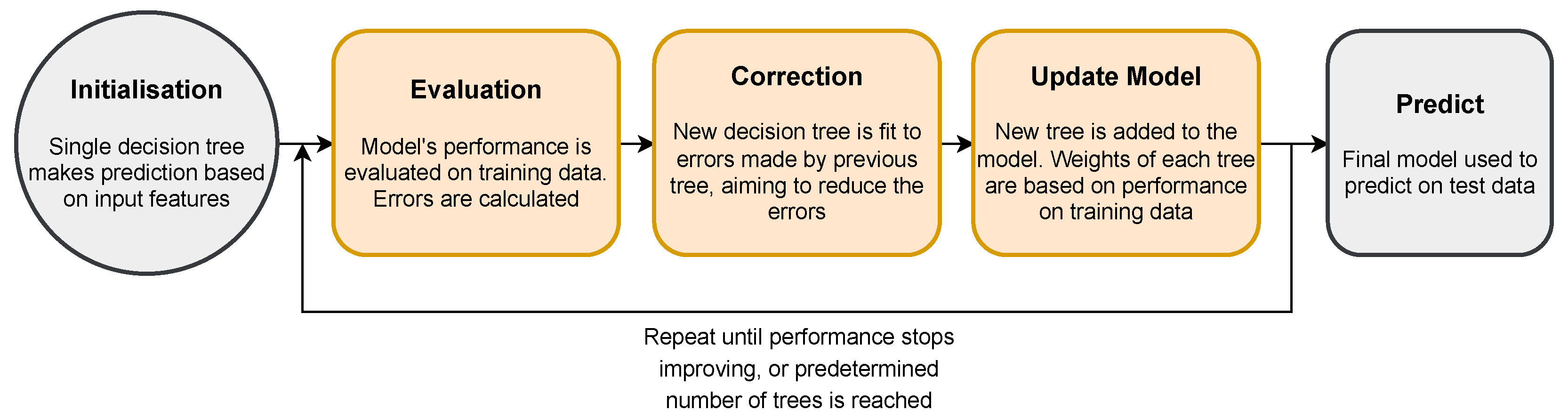
2.1. Gradient-Boosted Decision Trees
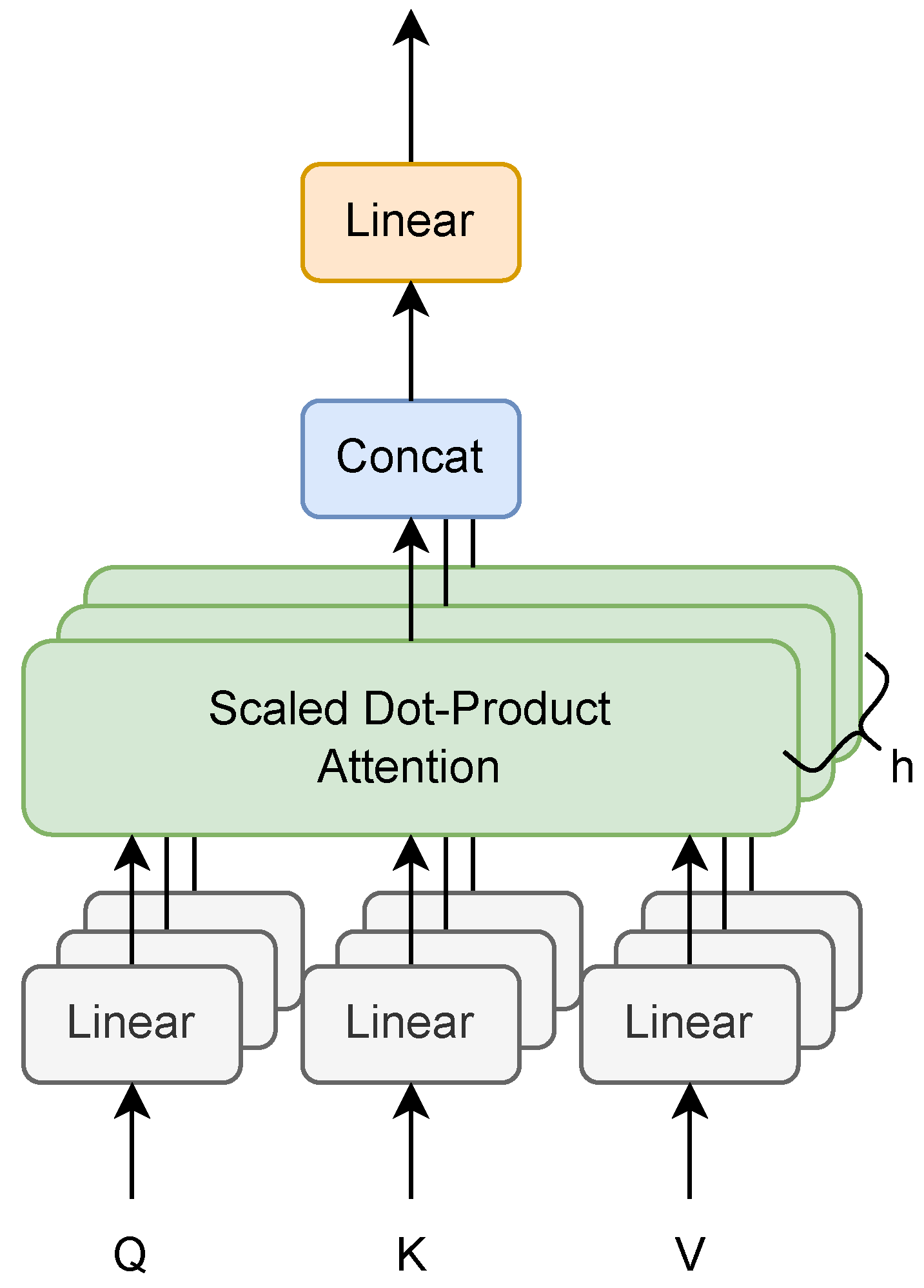
2.2. Attention and Transformers
Chemical Kinetics
3. Related Works
3.1. Gas Turbine Emissions Prediction
3.1.1. First Principles
3.1.2. Machine Learning
3.1.3. Machine Learning in Industry
3.2. Tabular Prediction
3.2.1. Tree-Based
3.2.2. Attention and Transformers
4. Materials and Methods
4.1. Data
4.2. Pre-Processing
4.3. Models
4.3.1. SAINT
4.3.2. XGBoost
4.3.3. Chemical Kinetics
4.4. Metrics and Evaluation
4.5. Impact of Number of Features
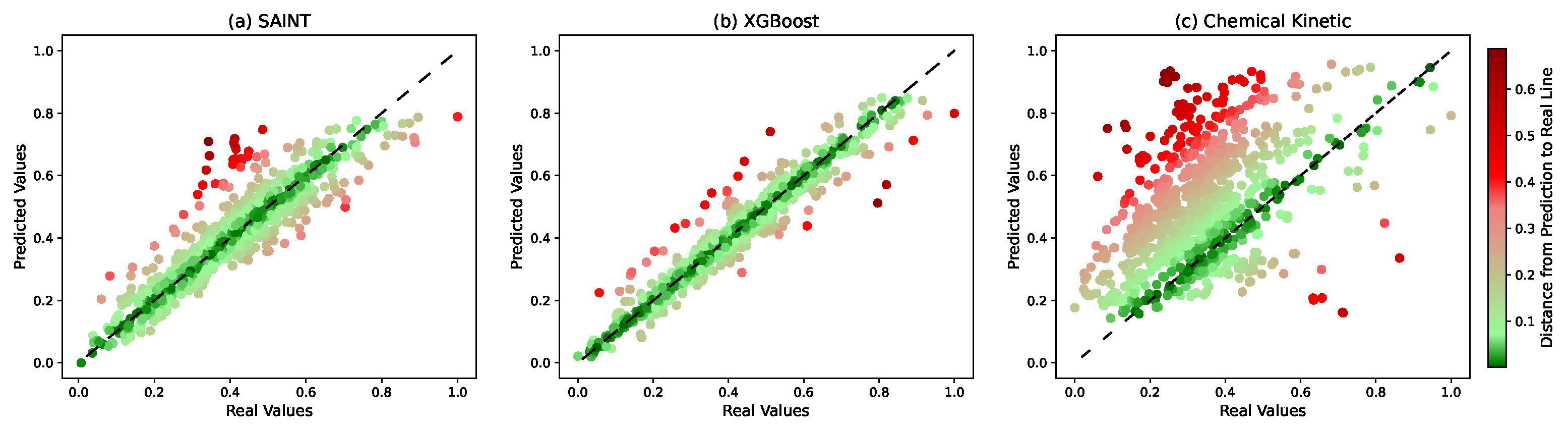
5. Results and Discussion
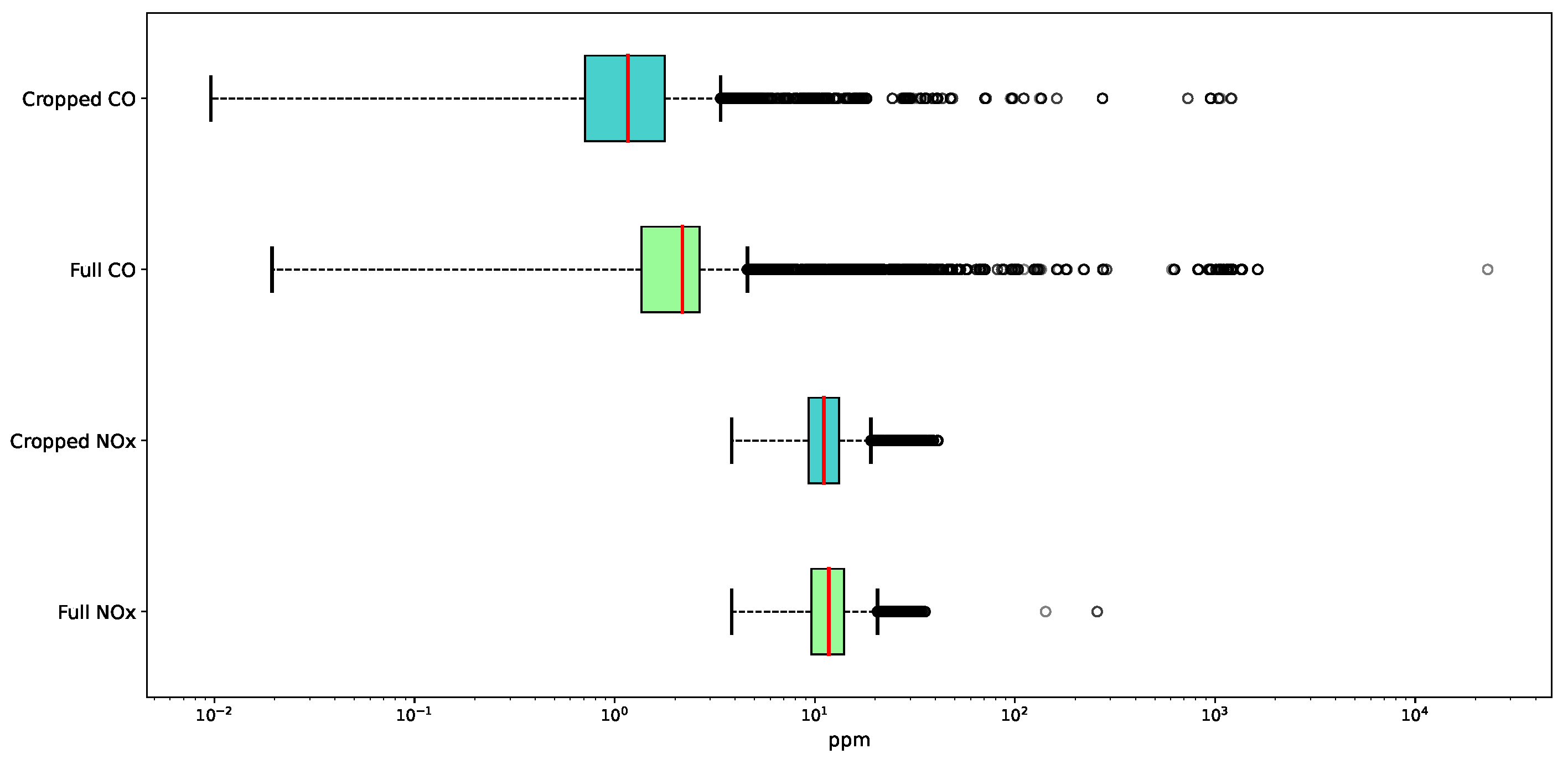
5.1. Impact of Pre-Processing
5.2. Number of Features: Impact and Importance
6. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Description | Unit | Missing Values | Full Importance | Cropped Importance |
|---|---|---|---|---|
| Compressor exit pressure | barg | 6 | 0 | 80 |
| Turbine interduct temperature | °C | 6 | 1 | 2 |
| Pressure drop across exhaust ducting | mbar | 6 | 4 | 70 |
| Exhaust temperature | °C | 6 | 5 | 51 |
| Turbine interduct temperature | °C | 6 | 6 | 5 |
| Turbine interduct temperature | °C | 6 | 7 | 23 |
| Power turbine shaft speed | rpm | 6 | 18 | 76 |
| Turbine interduct temperature | °C | 6 | 20 | 7 |
| Pressure drop across inlet ducting | mbar | 6 | 21 | 11 |
| Exhaust temperature | °C | 6 | 24 | 64 |
| Turbine interduct temperature | °C | 6 | 37 | 34 |
| Temperature after inlet ducting | °C | 6 | 38 | 21 |
| Temperature after inlet ducting | °C | 6 | 39 | 62 |
| Turbine interduct temperature | °C | 6 | 49 | 44 |
| Exhaust temperature | °C | 6 | 58 | 67 |
| Exhaust temperature | °C | 6 | 59 | 24 |
| Exhaust temperature | °C | 6 | 74 | 27 |
| Compressor shaft speed | rpm | 6 | 78 | 12 |
| Turbine interduct temperature | °C | 6 | 82 | 19 |
| Exhaust temperature | °C | 6 | 83 | 75 |
| Exhaust temperature | °C | 6 | 90 | 18 |
| Exhaust temperature | °C | 6 | 91 | 41 |
| Exhaust temperature | °C | 6 | 96 | 74 |
| Temperature in filter house (ambient temperature) | °C | 6 | 110 | 54 |
| Exhaust temperature | °C | 6 | 111 | 86 |
| Compressor exit temperature | °C | 6 | 112 | 68 |
| Turbine interduct temperature | °C | 6 | 114 | 52 |
| Compressor exit temperature | °C | 6 | 115 | 13 |
| Exhaust temperature | °C | 6 | 125 | 48 |
| Turbine interduct temperature | °C | 6 | 126 | 56 |
| Temperature after inlet ducting | °C | 6 | 147 | 38 |
| Turbine interduct temperature | °C | 6 | 149 | 16 |
| Exhaust temperature | °C | 6 | 150 | 79 |
| Turbine interduct temperature | °C | 6 | 153 | 25 |
| Turbine interduct pressure | barg | 6 | 156 | 15 |
| Turbine interduct temperature | °C | 6 | 159 | 26 |
| Exhaust temperature | °C | 6 | 163 | 87 |
| Turbine interduct temperature | °C | 6 | 171 | 58 |
| Temperature after inlet ducting | °C | 23 | 32 | 30 |
| Ambient pressure | bara | 33 | 40 | 49 |
| Temperature after inlet ducting | °C | 50 | 105 | 22 |
| Variable guide vanes position | 58 | 3 | 39 | |
| Temperature after inlet ducting | °C | 88 | 36 | 28 |
| Inlet air mass flow | kg/s | 214 | 41 | 43 |
| Turbine inlet pressure | Pa | 219 | 22 | 82 |
| Fuel mass flow | kg/s | 219 | 27 | 84 |
| Calculated heat input (fuel flow method) | W | 219 | 33 | 72 |
| Turbine inlet temperature | K | 219 | 35 | 6 |
| Mass flow into combustor (after bleeds) | kg/s | 219 | 66 | |
| Power | MW | 219 | 109 | 83 |
| Calculated heat input (heat balance method) | W | 219 | 123 | 47 |
| Exhaust mass flow | kg/s | 219 | 151 | 66 |
| Bleed mass flow | kg/s | 219 | 68 | 65 |
| Lower calorific value of fuel | kJ/kg | 468 | 162 | 37 |
| Combustor 2 pilot-tip temperature | °C | 970 | 12 | 1 |
| Combustor 4 pilot-tip temperature | °C | 970 | 14 | 3 |
| Combustor 6 pilot-tip temperature | °C | 970 | 29 | 8 |
| Combustor 5 pilot-tip temperature | °C | 970 | 106 | 4 |
| Combustor 1 pilot-tip temperature | °C | 970 | 121 | 36 |
| Combustor 3 pilot-tip temperature | °C | 970 | 127 | 14 |
| Firing temperature | K | 2178 | 79 | 42 |
| Load % 1 | % | 2837 | 46 | 78 |
| Load % 2 | % | 2837 | 30 | 59 |
| Bleed valve angle | % | 2837 | 26 | 85 |
| Main/pilot burner split | % | 3806 | 102 | 10 |
| Fuel demand | kW | 3806 | 119 | 40 |
| Main/pilot burner split | % | 3806 | 168 | 0 |
| Bleed valve angle | Degrees | 3854 | 154 | 9 |
| Gas Generator inlet journal bearing temperature 2 | °C | 4172 | 10 | 46 |
| Gas Generator exit journal bearing temperature 2 | °C | 4172 | 70 | 57 |
| Gas Generator Thrust Bearing temperature 2 | °C | 4172 | 73 | 20 |
| Gas Generator Thrust Bearing temperature 1 | °C | 4172 | 113 | 63 |
| Power Turbine Thrust Bearing temperature 2 | °C | 4597 | 64 | 29 |
| Power Turbine exit journal bearing temperature 2 | °C | 4597 | 80 | 31 |
| Power Turbine Thrust Bearing temperature 1 | °C | 4597 | 88 | 35 |
| Power Turbine inlet journal bearing temperature 1 | °C | 4597 | 140 | 32 |
| Compressor exit pressure | bara | 8973 | ||
| Gas Generator inlet journal bearing temperature 1 | °C | 9389 | 77 | 45 |
| Gas Generator exit journal bearing temperature 1 | °C | 9389 | 144 | 71 |
| Power Turbine Exit Journal Y | µm | 9814 | 8 | 55 |
| Power Turbine Exit Journal X | µm | 9814 | 11 | 50 |
| Gas Generator Exit Journal Y | µm | 9814 | 13 | 81 |
| Power Turbine Inlet Journal Y | µm | 9814 | 28 | 69 |
| Power Turbine exit journal bearing temperature 1 | °C | 9814 | 69 | 33 |
| Gas Generator Exit Journal X | µm | 9814 | 75 | 73 |
| Power Turbine Inlet Journal X | µm | 9814 | 87 | 77 |
| Gas Generator Inlet Journal X | µm | 9814 | 101 | 53 |
| Gas Generator Inlet Journal Y | µm | 9814 | 120 | 60 |
| Power Turbine inlet journal bearing temperature 2 | °C | 9814 | 141 | 61 |
| Combustor can 3, magnitude in second peak frequency in band 2 | psi | 15,020 | 2 | |
| Combustor can 1, second peak frequency in band 1 | hz | 15,020 | 9 | |
| Combustor can 3, magnitude in third peak frequency in band 2 | psi | 15,020 | 15 | |
| Combustor can 5, magnitude in first peak frequency in band 2 | psi | 15,020 | 16 | |
| Combustor can 1, first peak frequency in band 1 | hz | 15,020 | 17 | |
| Combustor can 6, magnitude in first peak frequency in band 1 | psi | 15,020 | 23 | |
| Combustor can 2, first peak frequency in band 2 | hz | 15,020 | 25 | |
| Combustor can 2, first peak frequency in band 1 | hz | 15,020 | 31 | |
| Combustor can 5, first peak frequency in band 1 | hz | 15,020 | 42 | |
| Combustor can 4, magnitude in first peak frequency in band 2 | psi | 15,020 | 43 | |
| Combustor can 4, third peak frequency in band 2 | hz | 15,020 | 44 | |
| Combustor can 1, magnitude inthird peak frequency in band 2 | psi | 15,020 | 45 | |
| Combustor can 3, first peak frequency in band 2 | hz | 15,020 | 47 | |
| Combustor can 4, magnitude in third peak frequency in band 2 | psi | 15,020 | 50 | |
| Combustor can 1, third peak frequency in band 2 | hz | 15,020 | 54 | |
| Combustor can 6, magnitude in second peak frequency in band 2 | psi | 15,020 | 55 | |
| Combustor can 6, first peak frequency in band 2 | hz | 15,020 | 62 | |
| Combustor can 3, magnitude in first peak frequency in band 2 | psi | 15,020 | 63 | |
| Combustor can 4, second peak frequency in band 2 | hz | 15,020 | 65 | |
| Combustor can 2, second peak frequency in band 1 | hz | 15,020 | 67 | |
| Combustor can 1, second peak frequency in band 2 | hz | 15,020 | 71 | |
| Combustor can 5, magnitude in third peak frequency in band 2 | psi | 15,020 | 72 | |
| Combustor can 2, third peak frequency in band 2 | hz | 15,020 | 76 | |
| Combustor can 5, magnitude in first peak frequency in band 1 | psi | 15,020 | 81 | |
| Combustor can 6, second peak frequency in band 2 | hz | 15,020 | 89 | |
| Combustor can 4, magnitude in second peak frequency in band 2 | psi | 15,020 | 94 | |
| Combustor can 2, magnitude in first peak frequency in band 1 | psi | 15,020 | 95 | |
| Combustor can 5, third peak frequency in band 2 | hz | 15,020 | 97 | |
| Combustor can 1, magnitude in second peak frequency in band 1 | psi | 15,020 | 98 | |
| Combustor can 3, magnitude in first peak frequency in band 1 | psi | 15,020 | 99 | |
| Combustor can 6, first peak frequency in band 1 | hz | 15,020 | 100 | |
| Combustor can 3, second peak frequency in band 1 | hz | 15,020 | 104 | |
| Combustor can 3, magnitude in second peak frequency in band 1 | psi | 15,020 | 107 | |
| Combustor can 2, magnitude in second peak frequency in band 2 | psi | 15,020 | 108 | |
| Combustor can 5, second peak frequency in band 2 | hz | 15,020 | 116 | |
| Combustor can 4, magnitude in second peak frequency in band 1 | psi | 15,020 | 117 | |
| Combustor can 5, first peak frequency in band 2 | hz | 15,020 | 118 | |
| Combustor can 4, magnitude in first peak frequency in band 1 | psi | 15,020 | 129 | |
| Combustor can 1, magnitude in first peak frequency in band 2 | psi | 15,020 | 130 | |
| Combustor can 6, magnitude in first peak frequency in band 2 | psi | 15,020 | 132 | |
| Combustor can 6, magnitude in third peak frequency in band 2 | psi | 15,020 | 133 | |
| Combustor can 1, first peak frequency in band 2 | hz | 15,020 | 134 | |
| Combustor can 2, magnitude in third peak frequency in band 2 | psi | 15,020 | 135 | |
| Combustor can 6, third peak frequency in band 2 | hz | 15,020 | 136 | |
| Combustor can 5, magnitude in second peak frequency in band 2 | psi | 15,020 | 143 | |
| Combustor can 3, second peak frequency in band 2 | hz | 15,020 | 145 | |
| Combustor can 4, first peak frequency in band 2 | hz | 15,020 | 146 | |
| Combustor can 2, magnitude in first peak frequency in band 2 | psi | 15,020 | 148 | |
| Combustor can 2, magnitude in second peak frequency in band 1 | psi | 15,020 | 152 | |
| Combustor can 3, third peak frequency in band 2 | hz | 15,020 | 155 | |
| Combustor can 1, magnitude in second peak frequency in band 2 | psi | 15,020 | 157 | |
| Combustor can 2, second peak frequency in band 2 | hz | 15,020 | 165 | |
| Combustor can 3, first peak frequency in band 1 | hz | 15,020 | 166 | |
| Combustor can 4, first peak frequency in band 1 | hz | 15,020 | 167 | |
| Combustor can 1, magnitude in first peak frequency in band 1 | psi | 15,020 | 170 | |
| Combustor can 4, second peak frequency in band 1 | hz | 15,020 | 172 | |
| Combustor can 6, second peak frequency in band 1 | hz | 15,020 | 19 | |
| Combustor can 6, magnitude in second peak frequency in band 1 | psi | 15,020 | 53 | |
| Combustor can 5, magnitude in second peak frequency in band 1 | psi | 15,020 | 84 | |
| Combustor can 5, second peak frequency in band 1 | hz | 15,020 | 139 | |
| Combustor can 3, magnitude in third peak frequency in band 1 | psi | 15,020 | 131 | |
| Combustor can 3, third peak frequency in band 1 | hz | 15,020 | 160 | |
| Combustor can 6, magnitude in third peak frequency in band 1 | psi | 15,020 | 92 | |
| Combustor can 6, third peak frequency in band 1 | hz | 15,020 | 128 | |
| Combustor can 1, magnitude in third peak frequency in band 1 | psi | 15,020 | 86 | |
| Combustor can 1, third peak frequency in band 1 | hz | 15,020 | 161 | |
| Combustor can 4, magnitude in third peak frequency in band 1 | psi | 15,020 | 85 | |
| Combustor can 4, third peak frequency in band 1 | hz | 15,020 | 122 | |
| Combustor can 2, third peak frequency in band 1 | hz | 15,020 | 34 | |
| Combustor can 2, magnitude in third peak frequency in band 1 | psi | 15,020 | 124 | |
| Combustor can 5, magnitude in third peak frequency in band 1 | psi | 15,020 | 51 | |
| Combustor can 5, third peak frequency in band 1 | hz | 15,020 | 56 | |
| Center casing, magnitude in first peak frequency in band 2 | psi | 16,226 | 93 | |
| Center casing, first peak frequency in band 2 | hz | 16,226 | 164 | |
| Center casing, magnitude in second peak frequency in band 2 | psi | 16,226 | 60 | |
| Center casing, second peak frequency in band 2 | hz | 16,226 | 142 | |
| Center casing, third peak frequency in band 2 | hz | 16,226 | 158 | |
| Center casing, magnitude in third peak frequency in band 2 | psi | 16,226 | 173 | |
| Center casing, first peak frequency in band 1 | hz | 16,226 | 48 | |
| Center casing, second peak frequency in band 1 | hz | 16,226 | 52 | |
| Center casing, magnitude in second peak frequency in band 1 | psi | 16,226 | 57 | |
| Center casing, magnitude in first peak frequency in band 1 | psi | 16,226 | 103 | |
| Center casing, magnitude in third peak frequency in band 1 | psi | 16,226 | 138 | |
| Center casing, third peak frequency in band 1 | hz | 16,226 | 169 | |
| Combustion chamber exit mass flow | kg/s | 17,713 | 61 | 17 |
| Lube Oil Pressure | °C | 18,021 | 137 | |
| Pressure drop across venturi | mbar | 19,528 | ||
| Center casing, first peak frequency in band 3 | hz | 20,489 | ||
| Center casing, second peak frequency in band 3 | hz | 20,489 | ||
| Center casing, third peak frequency in band 3 | hz | 20,489 | ||
| Center casing, magnitude in first peak frequency in band 3 | psi | 20,489 | ||
| Center casing, magnitude in second peak frequency in band 3 | psi | 20,489 | ||
| Center casing, magnitude in third peak frequency in band 3 | psi | 20,489 | ||
| Turbine interduct pressure | bara | 23,497 |
References
- Potts, R.L.; Leontidis, G. Attention-Based Deep Learning Methods for Predicting Gas Turbine Emissions. In Proceedings of the Northern Lights Deep Learning Conference 2023 (Extended Abstracts), Tromso, Norway, 9–13 January 2023. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar]
- Somepalli, G.; Schwarzschild, A.; Goldblum, M.; Bruss, C.B.; Goldstein, T. SAINT: Improved neural networks for tabular data via row attention and contrastive pre-training. In NeurIPS 2022 First Table Representation Workshop; NeurIPS: London, UK, 2022. [Google Scholar]
- Chen, J.; Yan, J.; Chen, D.Z.; Wu, J. Excelformer: A neural network surpassing gbdts on tabular data. arXiv 2023, arXiv:2301.02819. [Google Scholar]
- Hackney, R.; Sadasivuni, S.; Rogerson, J.; Bulat, G. Predictive emissions monitoring system for small siemens dry low emissions combustors: Validation and application. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 49767, p. V04BT04A032. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hung, W. An experimentally verified nox emission model for gas turbine combustors. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 1975; Volume 79771, p. V01BT02A009. [Google Scholar]
- Rudolf, C.; Wirsum, M.; Gassner, M.; Zoller, B.T.; Bernero, S. Modelling of gas turbine nox emissions based on long-term operation data. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 49767, p. V04BT04A006. [Google Scholar]
- Lipperheide, M.; Weidner, F.; Wirsum, M.; Gassner, M.; Bernero, S. Long-term nox emission behavior of heavy duty gas turbines: An approach for model-based monitoring and diagnostics. J. Eng. Gas Turbines Power 2018, 140, 101601. [Google Scholar]
- Bainier, F.; Alas, P.; Morin, F.; Pillay, T. Two years of improvement and experience in pems for gas turbines. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 49873, p. V009T24A005. [Google Scholar]
- Cuccu, G.; Danafar, S.; Cudré-Mauroux, P.; Gassner, M.; Bernero, S.; Kryszczuk, K. A data-driven approach to predict nox-emissions of gas turbines. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; pp. 1283–1288. [Google Scholar]
- Kaya, H.; Tüfekci, P.; Uzun, E. Predicting co and nox emissions from gas turbines: Novel data and a benchmark pems. Turk. J. Electr. Eng. Comput. Sci. 2019, 27, 4783–4796. [Google Scholar] [CrossRef]
- Si, M.; Tarnoczi, T.J.; Wiens, B.M.; Du, K. Development of predictive emissions monitoring system using open source machine learning library–keras: A case study on a cogeneration unit. IEEE Access 2019, 7, 113463–113475. [Google Scholar]
- Rezazadeh, A. Environmental pollution prediction of nox by process analysis and predictive modelling in natural gas turbine power plants. arXiv 2020, arXiv:2011.08978. [Google Scholar]
- Azzam, M.; Awad, M.; Zeaiter, J. Application of evolutionary neural networks and support vector machines to model nox emissions from gas turbines. J. Environ. Chem. Eng. 2018, 6, 1044–1052. [Google Scholar] [CrossRef]
- Kochueva, O.; Nikolskii, K. Data analysis and symbolic regression models for predicting co and nox emissions from gas turbines. Computation 2021, 9, 139. [Google Scholar] [CrossRef]
- Botros, K.; Selinger, C.; Siarkowski, L. Verification of a neural network based predictive emission monitoring module for an rb211-24c gas turbine. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2009; Volume 48869, pp. 431–441. [Google Scholar]
- Botros, K.; Cheung, M. Neural network based predictive emission monitoring module for a ge lm2500 gas turbine. In Proceedings of the International Pipeline Conference, Calgary, AB, Canada, 27 September–1 October 2010; Volume 44229, pp. 77–87. [Google Scholar]
- Botros, K.; Williams-Gossen, C.; Makwana, S.; Siarkowski, L. Predictive emission monitoring (pem) systems development and implementation. In Proceedings of the 19th Symposium on Industrial Applications of Gas Turbines Committee, Banff, AB, Canada, 17–19 October 2011. [Google Scholar]
- Guo, L.; Zhang, S.; Huang, Q. Nox prediction of gas turbine based on dual attention and lstm. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 4036–4041. [Google Scholar]
- Garg, A.; Aggarwal, P.; Aggarwal, Y.; Belarbi, M.; Chalak, H.; Tounsi, A.; Gulia, R. Machine learning models for predicting the compressive strength of concrete ontaining nano silica. Comput. Concr. 2022, 30, 33. [Google Scholar]
- Nasiri, S.; Khosravani, M. Machine learning in predicting mechanical behavior of additively manufactured parts. J. Mater. Res. Technol. 2021, 14, 1137–1153. [Google Scholar] [CrossRef]
- Garg, A.; Belarbi, M.; Tounsi, A.; Li, L.; Singh, A.; Mukhopadhyay, T. Predicting elemental stiffness matrix of FG nanoplates using Gaussian Process Regression based surrogate model in framework of layerwise model. Eng. Anal. Bound. Elem. 2022, 143, 779–795. [Google Scholar] [CrossRef]
- Onoufriou, G.; Bickerton, R.; Pearson, S.; Leontidis, G. Nemesyst: A hybrid parallelism deep learning-based framework applied for internet of things enabled food retailing refrigeration systems. Comput. Ind. 2019, 113, 103133. [Google Scholar] [CrossRef]
- Onoufriou, G.; Hanheide, M.; Leontidis, G. Premonition Net, a multi-timeline transformer network architecture towards strawberry tabletop yield forecasting. Comput. Electron. Agric. 2023, 208, 107784. [Google Scholar] [CrossRef]
- Durrant, A.; Leontidis, G.; Kollias, S.; Torres, A.; Montalvo, C.; Mylonakis, A.; Demaziere, C.; Vinai, P. Detection and localisation of multiple in-core perturbations with neutron noise-based self-supervised domain adaptation. In Proceedings of the International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering (M&C2021), Online, 3–7 October 2021. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. Catboost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Borisov, V.; Leemann, T.; Seßler, K.; Haug, J.; Pawelczyk, M.; Kasneci, G. Deep neural networks and tabular data: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–21. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on tabular data? arXiv 2022, arXiv:2207.08815. [Google Scholar]
- Kadra, A.; Lindauer, M.; Hutter, F.; Grabocka, J. Well-tuned simple nets excel on tabular datasets. Adv. Neural Inf. Process. Syst. 2021, 34, 23928–23941. [Google Scholar]
- Ye, A.; Wang, A. Applying attention to tabular data. In Modern Deep Learning for Tabular Data: Novel Approaches to Common Modeling Problems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 452–548. [Google Scholar]
- Arik, S.Ö.; Pfister, T. Tabnet: Attentive interpretable tabular learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 6679–6687. [Google Scholar] [CrossRef]
- Gorishniy, Y.; Rubachev, I.; Khrulkov, V.; Babenko, A. Revisiting deep learning models for tabular data. Adv. Neural Inf. Process. Syst. 2021, 34, 18932–18943. [Google Scholar]
- Huang, X.; Khetan, A.; Cvitkovic, M.; Karnin, Z. Tabtransformer: Tabular data modeling using contextual embeddings. arXiv 2020, arXiv:2012.06678. [Google Scholar]
- Kossen, J.; Band, N.; Lyle, C.; Gomez, A.N.; Rainforth, T.; Gal, Y. Self-attention between datapoints: Going beyond individual input-output pairs in deep learning. Adv. Neural Inf. Process. Syst. 2021, 34, 28742–28756. [Google Scholar]
- Rubachev, I.; Alekberov, A.; Gorishniy, Y.; Babenko, A. Revisiting pretraining objectives for tabular deep learning. arXiv 2022, arXiv:2207.03208. [Google Scholar]
- Gorishniy, Y.; Rubachev, I.; Babenko, A. On embeddings for numerical features in tabular deep learning. Adv. Neural Inf. Process. Syst. 2022, 35, 24991–25004. [Google Scholar]




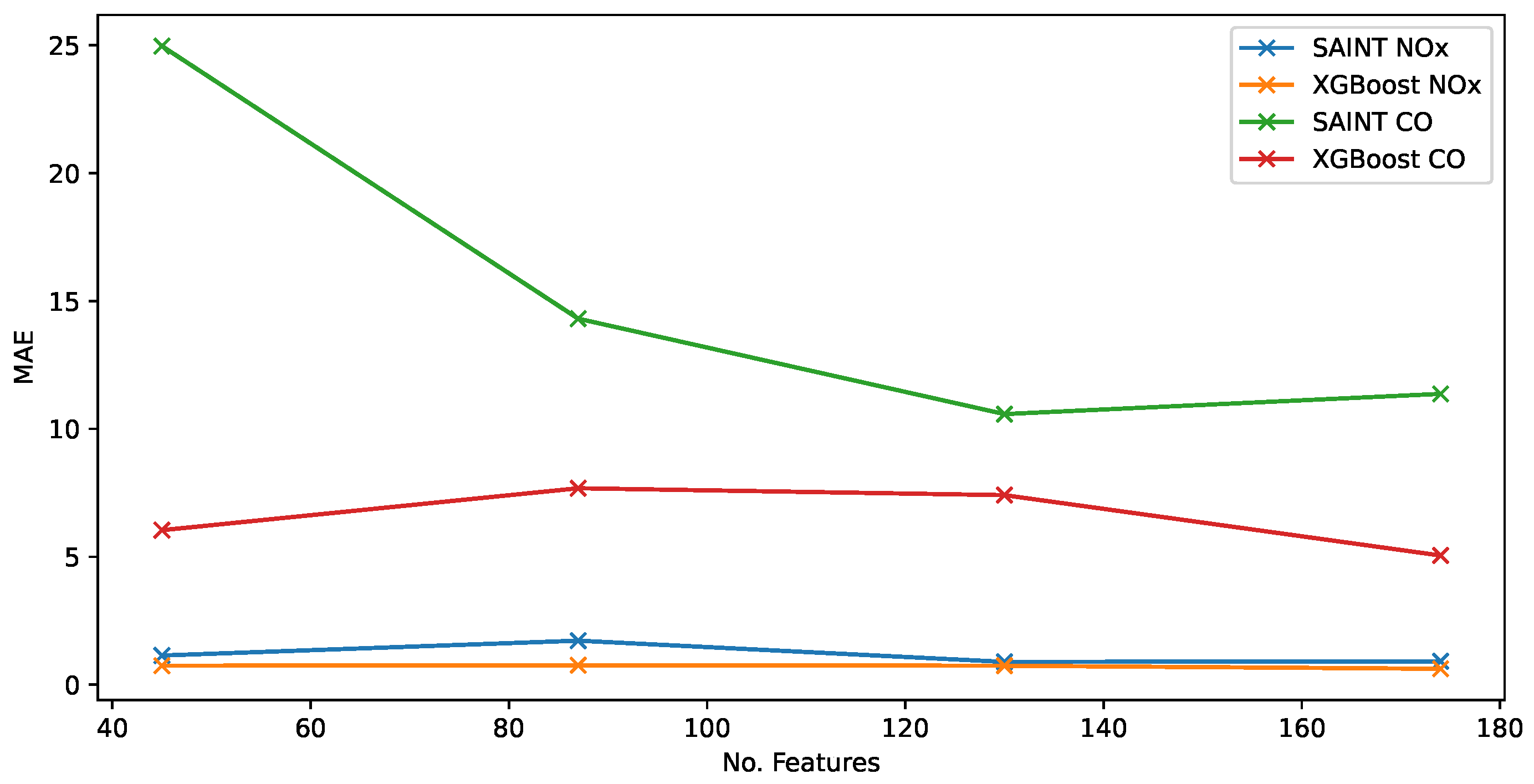
| Action | Full | Cropped |
|---|---|---|
| Start | 37,204 rows, 183 features | 9873 rows, 183 features |
| Remove low data features | Removes 9 features | Removes 95 features |
| Remove liquid fuel data | Removes 5752 rows | No change |
| Remove negative emissions | Removes 16,977 rows | Removes 744 rows |
| Remove all missing values | Removes 8615 rows | Removes 2700 rows |
| End | 5860 rows, 174 features | 6429 rows, 88 features |
| Methods | SAINT | XGBoost | Chemical Kinetic | ||||
|---|---|---|---|---|---|---|---|
| Metric | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| NOx Full | 174 | 0.91 ± 0.11 | 2.82 ± 2.45 | 0.62 ± 0.14 | 4.08 ± 3.09 | 4.46 ± 0.15 | 6.59 ± 1.43 |
| 130 | 0.89 ± 0.21 | 2.92 ± 2.02 | 0.74 ± 0.18 | 4.48 ± 3.65 | 4.09 ± 0.10 | 6.14 ± 1.14 | |
| 87 | 1.72 ± 0.70 | 3.83 ± 1.62 | 0.76 ± 0.12 | 4.04 ± 2.62 | 4.09 ± 0.10 | 6.14 ± 1.14 | |
| 45 | 1.14 ± 0.38 | 2.96 ± 1.64 | 0.74 ± 0.08 | 3.00 ± 1.99 | 3.68 ± 0.12 | 5.55 ± 0.94 | |
| NOx Cropped | 88 | 0.54 ± 0.08 | 0.92 ± 0.1 | 0.47 ± 0.02 | 0.95 ± 0.17 | 2.67 ± 0.06 | 3.84 ± 0.33 |
| 45 | 0.56 ± 0.07 | 0.94 ± 0.07 | 0.44 ± 0.02 | 0.92 ± 0.16 | 2.67 ± 0.06 | 3.84 ± 0.33 | |
| CO Full | 174 | 11.37 ± 6.61 | 117.61 ± 191.07 | 5.05 ± 6.45 | 117.83 ± 197.50 | 2.49 × 10 ± 7.54 × 10 | 3.79 × 10 ± 7.35 × 10 |
| 130 | 10.58 ± 5.84 | 164.20 ± 225.07 | 7.41 ± 8.09 | 220.53 ± 260.67 | 1.47 × 10 ± 5.98 × 10 | 2.85 × 10 ± 7.37 × 10 | |
| 87 | 14.31 ± 6.33 | 152.70 ± 225.24 | 7.68 ± 10.80 | 214.44 ± 317.08 | 1.50 × 10 ± 5.98 × 10 | 2.85 × 10 ± 7.37 × 10 | |
| 45 | 24.97 ± 30.58 | 292.55 ± 236.71 | 6.04 ± 6.30 | 219.92 ± 262.52 | 1.38 × 10 ± 8.93 × 10 | 2.64 × 10 ± 1.28 × 10 | |
| CO Cropped | 88 | 2.46 ± 0.72 | 20.02 ± 10.14 | 0.59 ± 0.31 | 9.13 ± 8.15 | 5.97 × 10 ± 3.32 × 10 | 1.80 × 10 ± 9.34 × 10 |
| 45 | 2.73 ± 2.30 | 20.01 ± 10.15 | 0.63 ± 0.37 | 10.50 ± 9.31 | 5.96 × 10 ± 3.32 × 10 | 1.80 × 10 ± 9.34 × 10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Potts, R.; Hackney, R.; Leontidis, G. Tabular Machine Learning Methods for Predicting Gas Turbine Emissions. Mach. Learn. Knowl. Extr. 2023, 5, 1055-1075. https://doi.org/10.3390/make5030055
Potts R, Hackney R, Leontidis G. Tabular Machine Learning Methods for Predicting Gas Turbine Emissions. Machine Learning and Knowledge Extraction. 2023; 5(3):1055-1075. https://doi.org/10.3390/make5030055
Chicago/Turabian StylePotts, Rebecca, Rick Hackney, and Georgios Leontidis. 2023. "Tabular Machine Learning Methods for Predicting Gas Turbine Emissions" Machine Learning and Knowledge Extraction 5, no. 3: 1055-1075. https://doi.org/10.3390/make5030055
APA StylePotts, R., Hackney, R., & Leontidis, G. (2023). Tabular Machine Learning Methods for Predicting Gas Turbine Emissions. Machine Learning and Knowledge Extraction, 5(3), 1055-1075. https://doi.org/10.3390/make5030055







