High-Throughput Ensemble-Learning-Driven Band Gap Prediction of Double Perovskites Solar Cells Absorber
Abstract
1. Introduction
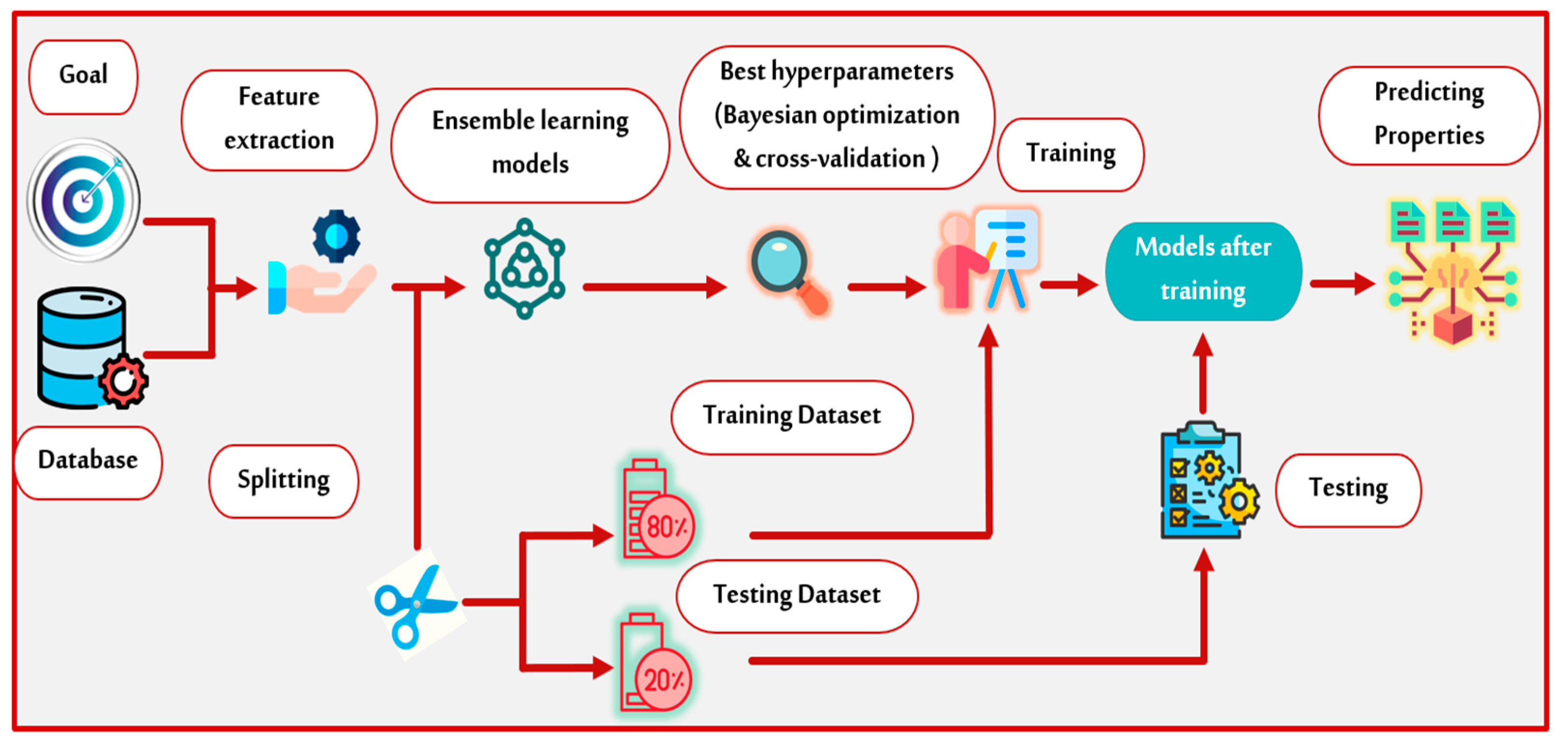
2. Methodology
2.1. Machine Learning
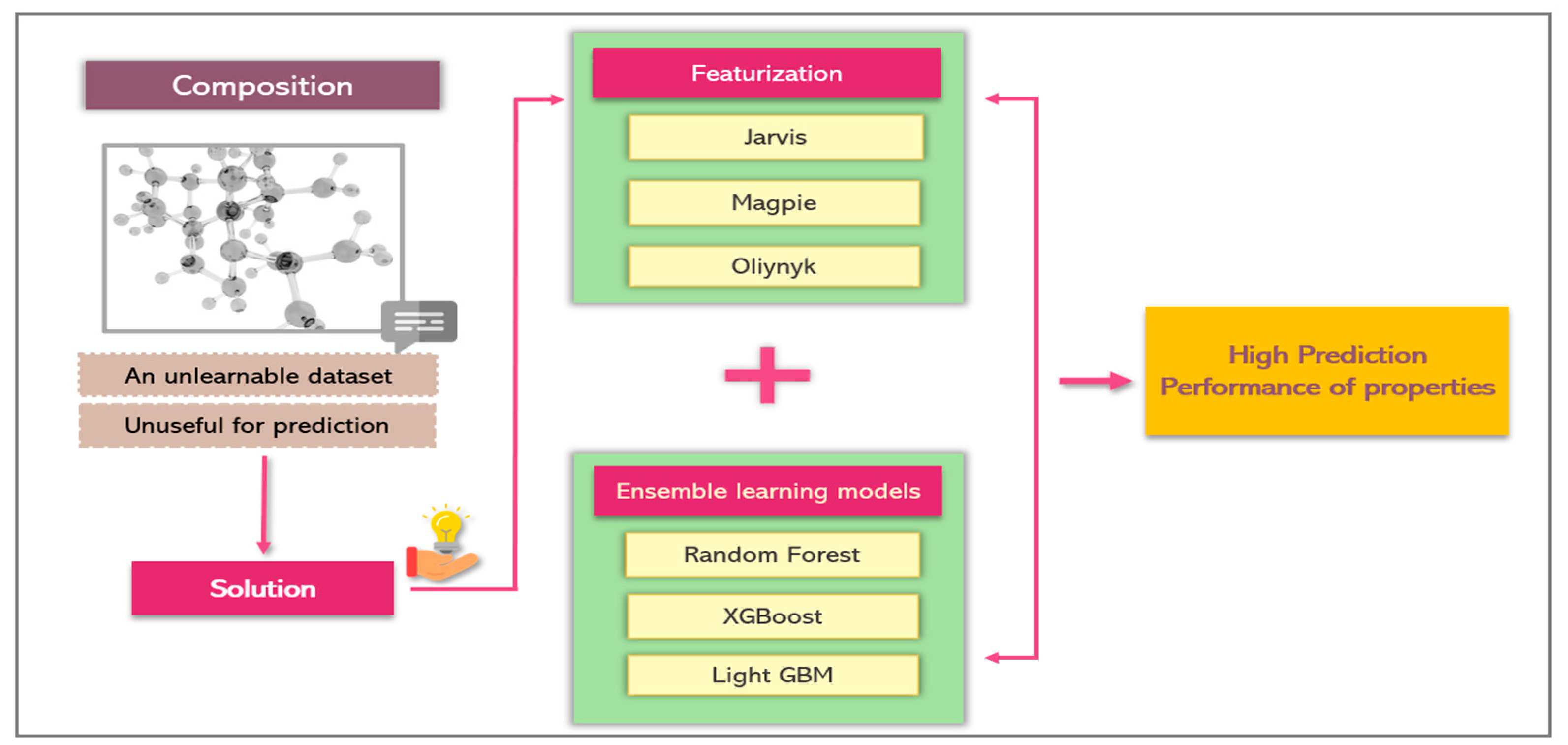
2.2. Ensemble Learning Models
2.2.1. Random Forest
2.2.2. XGBoost
2.2.3. Light GBM
3. Results and Discussions
3.1. Data Acquisition
3.2. Features Extraction
3.3. Model Selection
3.4. Model Developing
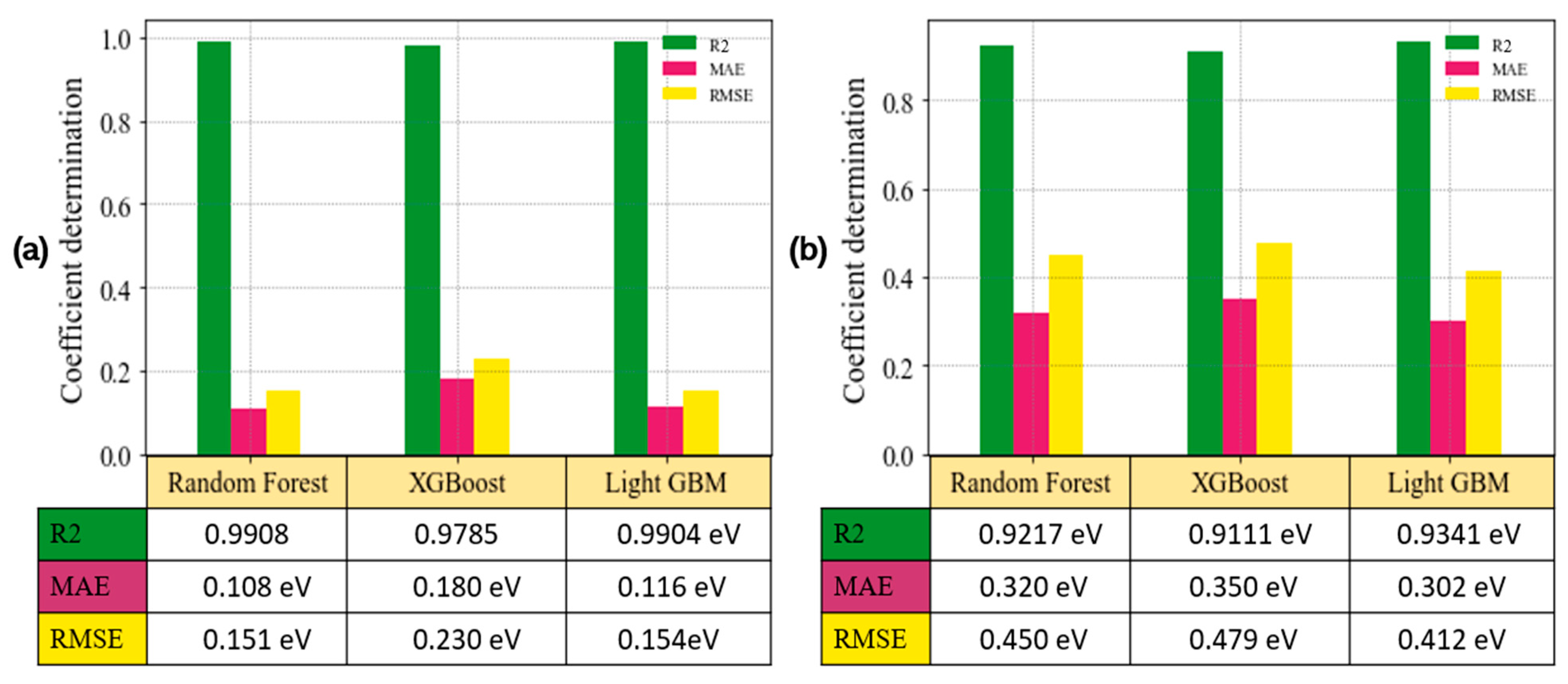
3.5. Model Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tao, Q.; Xu, P.; Li, M.; Lu, W. Machine learning for perovskite materials design and discovery. npj Comput. Mater. 2021, 7, 23. [Google Scholar] [CrossRef]
- Zhang, L.; He, M.; Shao, S. Machine learning for halide perovskite materials. Nano Energy 2020, 78, 105380. [Google Scholar] [CrossRef]
- Anand, D.V.; Xu, Q.; Wee, J.; Xia, K.; Sum, T.C. Topological feature engineering for machine learning based halide perovskite materials design. npj Comput. Mater. 2022, 8, 203. [Google Scholar] [CrossRef]
- Yılmaz, B.; Yıldırım, R. Critical review of machine learning applications in perovskite solar research. Nano Energy 2021, 80, 105546. [Google Scholar] [CrossRef]
- Travis, W.; Glover, E.N.K.; Bronstein, H.; Scanlon, D.O.; Palgrave, R.G. On the application of the tolerance factor to inorganic and hybrid halide perovskites: A revised system. Chem. Sci. 2016, 7, 4548–4556. [Google Scholar] [CrossRef]
- Saha-Dasgupta, T. Magnetism in Double Perovskites. J. Supercond. Nov. Magn. 2013, 26, 1991–1995. [Google Scholar] [CrossRef]
- Azam, S.; Khan, S.A.; Goumri-Said, S.; Kanoun, M.B. Predicted Thermoelectric Properties of the Layered XBi4S7 (X = Mn, Fe) Based Materials: First Principles Calculations. J. Electron. Mater. 2017, 46, 23–29. [Google Scholar] [CrossRef]
- Alhashmi, A.; Kanoun, M.B.; Goumri-Said, S. Machine Learning for Halide Perovskite Materials ABX3 (B = Pb, X = I, Br, Cl) Assessment of Structural Properties and Band Gap Engineering for Solar Energy. Materials 2023, 16, 2657. [Google Scholar] [CrossRef]
- Kanoun, M.B.; Goumri-Said, S. Insights into the impact of Mn-doped inorganic CsPbBr3 perovskite on electronic structures and magnetism for photovoltaic application. Mater. Today Energy 2021, 21, 100796. [Google Scholar] [CrossRef]
- Fadla, M.A.; Bentria, B.; Benghia, A.; Dahame, T.; Goumri-Said, S. Insights on the opto-electronic structure of the inorganic mixed halide perovskites γ-CsPb(I1-xBrx)3 with low symmetry black phase. J. Alloys Compd. 2020, 832, 154847. [Google Scholar] [CrossRef]
- Gladkikh, V.; Kim, D.Y.; Hajibabaei, A.; Jana, A.; Myung, C.W.; Kim, K.S. Machine Learning for Predicting the Band Gaps of ABX3 Perovskites from Elemental Properties. J. Phys. Chem. C 2020, 124, 8905–8918. [Google Scholar] [CrossRef]
- Pilania, G.; Mannodi-Kanakkithodi, A.; Uberuaga, B.P.; Ramprasad, R.; Gubernatis, J.E.; Lookman, T. Machine learning bandgaps of double perovskites. Sci. Rep. 2016, 6, 19375. [Google Scholar] [CrossRef]
- Chen, C.; Zuo, Y.; Ye, W.; Li, X.; Deng, Z.; Ong, S.P. A Critical Review of Machine Learning of Energy Materials. Adv. Energy Mater. 2020, 10, 1903242. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Esfarjani, K.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G. Perspectives on thermoelectrics: From fundamentals to device applications. Energy Environ. Sci. 2011, 5, 5147–5162. [Google Scholar] [CrossRef]
- Curtarolo, S.; Hart, G.L.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computa-tional materials design. Nat. Mater. 2013, 12, 191. [Google Scholar] [CrossRef] [PubMed]
- Mounet, N.; Gibertini, M.; Schwaller, P.; Campi, D.; Merkys, A.; Marrazzo, A.; Sohier, T.; Castelli, I.E.; Cepellotti, A.; Pizzi, G.; et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotechnol. 2018, 13, 246–252. [Google Scholar] [CrossRef] [PubMed]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The open quantum materials database (oqmd): Assessing the accuracy of dft formation energies. npj Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Khan, W.; Goumri-Said, S. Exploring the optoelectronic structure and thermoelectricity of recent photoconductive chalcogenides compounds, CsCdInQ3 (Q = Se, Te). RSC Adv. 2015, 5, 9455–9461. [Google Scholar] [CrossRef]
- Azam, S.; Khan, S.A.; Goumri-Said, S. Optoelectronic and Thermoelectric Properties of Bi2OX2 (X = S, Se, Te) for Solar Cells and Thermoelectric Devices. J. Electron. Mater. 2018, 47, 2513–2518. [Google Scholar] [CrossRef]
- Azam, S.; Goumri-Said, S.; Khan, S.A.; Ozisik, H.; Deligoz, E.; Kanoun, M.B.; Khan, W. Electronic structure and related optical, thermoelectric and dynamical properties of Lilianite-type Pb7Bi4Se13: Ab-initio and Boltzmann transport theory. Materialia 2020, 10, 100658. [Google Scholar] [CrossRef]
- Goumri-Said, S. Probing Optoelectronic and Thermoelectric Properties of Lead-Free Perovskite SnTiO3: HSE06 and Boltzmann Transport Calculations. Crystals 2022, 12, 1317. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, M.; Xie, X.; Yu, C.; Jiang, Q.; Huang, M.; Algadi, H.; Guo, Z.; Zhang, H. Applications of machine learning in perovskite materials. Adv. Compos. Hybrid Mater. 2022, 5, 2700–2720. [Google Scholar] [CrossRef]
- Talapatra, A.; Uberuaga, B.P.; Stanek, C.R.; Pilania, G. A Machine Learning Approach for the Prediction of Formability and Thermodynamic Stability of Single and Double Perovskite Oxides. Chem. Mater. 2021, 33, 845–858. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, D.; Niu, M.; Zhong, Y.; Ding, H.; Hu, Y.; Wu, X.-F.; Yuan, Z.-Y. Recent progress in metal halide perovskite-based photocatalysts: Physicochemical properties, synthetic strategies, and solar-driven applications. J. Mater. Chem. A 2023, 11, 22058–22086. [Google Scholar] [CrossRef]
- Zhang, L.; Mei, L.; Wang, K.; Lv, Y.; Zhang, S.; Lian, Y.; Liu, X.; Ma, Z.; Xiao, G.; Liu, Q.; et al. Advances in the Application of Perovskite Materials. Nano-Micro Lett. 2023, 15, 177. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Amit, Y.; Geman, D. Shape Quantization and Recognition with Randomized Trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Asselman, A.; Khaldi, M.; Aammou, S. Enhancing the prediction of student performance based on the machine learning XGBoost algorithm. Interact. Learn. Environ. 2021, 31, 3360–3379. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning, 2nd ed.; Zhang, C., Ma, Y.Q., Eds.; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting. Package Version-0.4-1.4. 2015. Available online: https://xgboost.ai/ (accessed on 15 May 2023).
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, C. Machine Learning in Rock Facies Classification: An Application of XGBoost. In Proceedings of the International Geophysical Conference, Qingdao, China, 17–20 April 2017; Society of Exploration Geophysicists: Qingdao, China, 2017; pp. 1371–1374. [Google Scholar] [CrossRef]
- Xgboost Developers. XGboost Parameter Documentation. 2023. Available online: https://xgboost.readthedocs.io/en/stable/parameter.html (accessed on 9 April 2023).
- Song, J.; Liu, G.; Jiang, J.; Zhang, P.; Liang, Y. Prediction of Protein–ATP Binding Residues Based on Ensemble of Deep Convolutional Neural Networks and LightGBM Algorithm. Int. J. Mol. Sci. 2021, 22, 939. [Google Scholar] [CrossRef] [PubMed]
- Gritsenko, O.; van Leeuwen, R.; van Lenthe, E.; Baerends, E.J. Self-consistent approximation to the Kohn-Sham exchange potential. Phys. Rev. A 1995, 51, 1944–1954. [Google Scholar] [CrossRef] [PubMed]
- Falkowski, A.R.; Kauwe, S.K.; Sparks, T.D. Optimizing Fractional Compositions to Achieve Extraordinary Properties. Integrating Mater. Manuf. Innov. 2021, 10, 689–695. [Google Scholar] [CrossRef]
- Murdock, R.J.; Kauwe, S.K.; Wang, A.Y.-T.; Sparks, T.D. Is Domain Knowledge Necessary for Machine Learning Materials Properties? Integr. Mater. Manuf. Innov. 2020, 9, 221–227. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Tavazza, F. Machine learning with force-field-inspired descriptors for materials: Fast screening and mapping energy landscape. Phys. Rev. Mater. 2018, 2, 083801. [Google Scholar] [CrossRef] [PubMed]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef]
- Oliynyk, A.O.; Antono, E.; Sparks, T.D.; Ghadbeigi, L.; Gaultois, M.W.; Meredig, B.; Mar, A. High-Throughput Machine-Learning-Driven Synthesis of Full-Heusler Compounds. Chem. Mater. 2016, 28, 7324–7331. [Google Scholar] [CrossRef]
- Kauwe, S.K.; Welker, T.; Sparks, T.D. Extracting Knowledge from DFT: Experimental Band Gap Predictions Through Ensemble Learning. Integrating Mater. Manuf. Innov. 2020, 9, 213–220. [Google Scholar] [CrossRef]
- Graser, J.; Kauwe, S.K.; Sparks, T.D. Machine Learning and Energy Minimization Approaches for Crystal Structure Predictions: A Review and New Horizons. Chem. Mater. 2018, 30, 3601–3612. [Google Scholar] [CrossRef]
- Im, J.; Lee, S.; Ko, T.-W.; Kim, H.W.; Hyon, Y.; Chang, H. Identifying Pb-free perovskites for solar cells by machine learning. npj Comput. Mater. 2019, 5, 37. [Google Scholar] [CrossRef]


| A-Site Cations | B-Site Cations | A- & B-Site Cations |
|---|---|---|
| Ag, Ba, Ca, Cs, K, La, Li, Mg, Na, Pb, Rb, Sr, Tl, Y | Al, Hf, Nb, Sb, Sc, Si, Ta, Ti, V, Zr | Ga, Ge, In, Sn |
| Models | Random Forest | XGBoost | Light GBM |
|---|---|---|---|
| Hyperparameters |
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djeradi, S.; Dahame, T.; Fadla, M.A.; Bentria, B.; Kanoun, M.B.; Goumri-Said, S. High-Throughput Ensemble-Learning-Driven Band Gap Prediction of Double Perovskites Solar Cells Absorber. Mach. Learn. Knowl. Extr. 2024, 6, 435-447. https://doi.org/10.3390/make6010022
Djeradi S, Dahame T, Fadla MA, Bentria B, Kanoun MB, Goumri-Said S. High-Throughput Ensemble-Learning-Driven Band Gap Prediction of Double Perovskites Solar Cells Absorber. Machine Learning and Knowledge Extraction. 2024; 6(1):435-447. https://doi.org/10.3390/make6010022
Chicago/Turabian StyleDjeradi, Sabrina, Tahar Dahame, Mohamed Abdelilah Fadla, Bachir Bentria, Mohammed Benali Kanoun, and Souraya Goumri-Said. 2024. "High-Throughput Ensemble-Learning-Driven Band Gap Prediction of Double Perovskites Solar Cells Absorber" Machine Learning and Knowledge Extraction 6, no. 1: 435-447. https://doi.org/10.3390/make6010022
APA StyleDjeradi, S., Dahame, T., Fadla, M. A., Bentria, B., Kanoun, M. B., & Goumri-Said, S. (2024). High-Throughput Ensemble-Learning-Driven Band Gap Prediction of Double Perovskites Solar Cells Absorber. Machine Learning and Knowledge Extraction, 6(1), 435-447. https://doi.org/10.3390/make6010022






