Ionic Strength Effect in the Equilibrium and Rheological Behavior of an Amphiphilic Triblock Copolymer at the Air/Solution Interface
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Experimental Methods
2.2.1. Equilibrium Interfacial Tension Measurements
- Surface force tensiometer: A surface force tensiometer, specifically a K10T Digital Tensiometer (KRÜSS GmbH, Hamburg, Germany), fitted with a platinum Wilhelmy plate contact probe of 40.5 mm in perimeter. Between each measurement, the platinum plate was cleansed using ethanol and Milli-Q water and then burnt with an ethanol torch to eliminate any remaining residue of organic matter. For the measurements, the samples were poured into a glass cell, previously cleaned with ethanol and Milli-Q water.
- 2.
- Shape profile analysis tensiometer: The interfacial tension of the air/solution interface was also measured by a drop profile analysis tensiometer designed and fabricated at the University of Granada. This device was based on the Axisymmetric Drop Shape Analysis (ADSA) method, which is described in detail elsewhere [43]. The setup, including the image capturing, the microinjector, the ADSA algorithm, and the fuzzy pressure control, was managed by a Windows-integrated program (DINATEN(R)) [44]. For the experiments, a solution microdroplet (15 μL) was formed at the tip of a PTFE capillary (0.2 cm) introduced in a thermostatized glass cuvette (Hellma GmbH & Co. KG, Müllheim, Germany). This led to experiments characterized by a Worthington number, Wo, above 0.4, which guaranteed good precision of the experimental results [45].
2.2.2. Interfacial Dilational Rheology Measurements
2.2.3. Bulk Viscosity Measurements
3. Results and Discussion
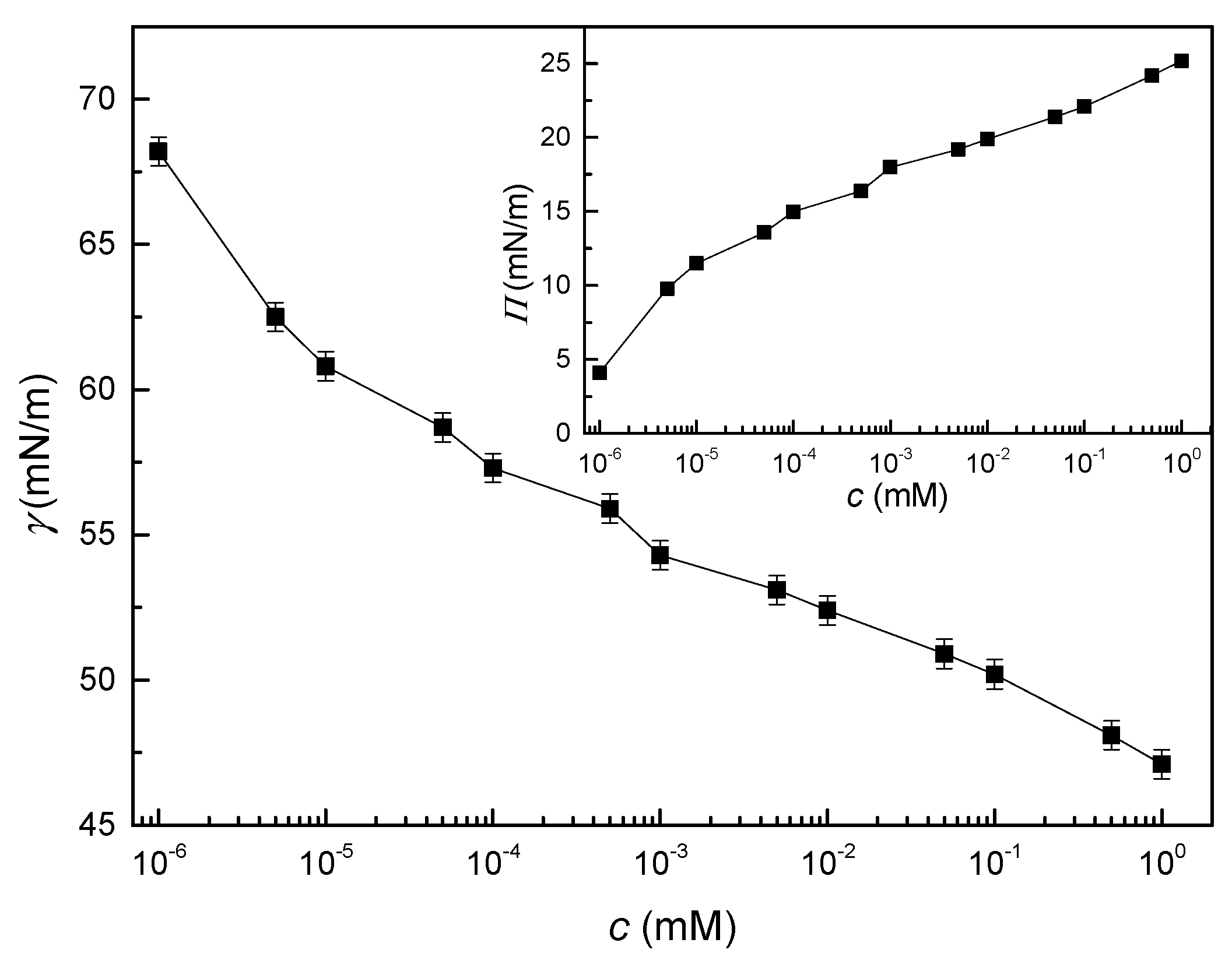
3.1. Interfacial Tension Isotherm
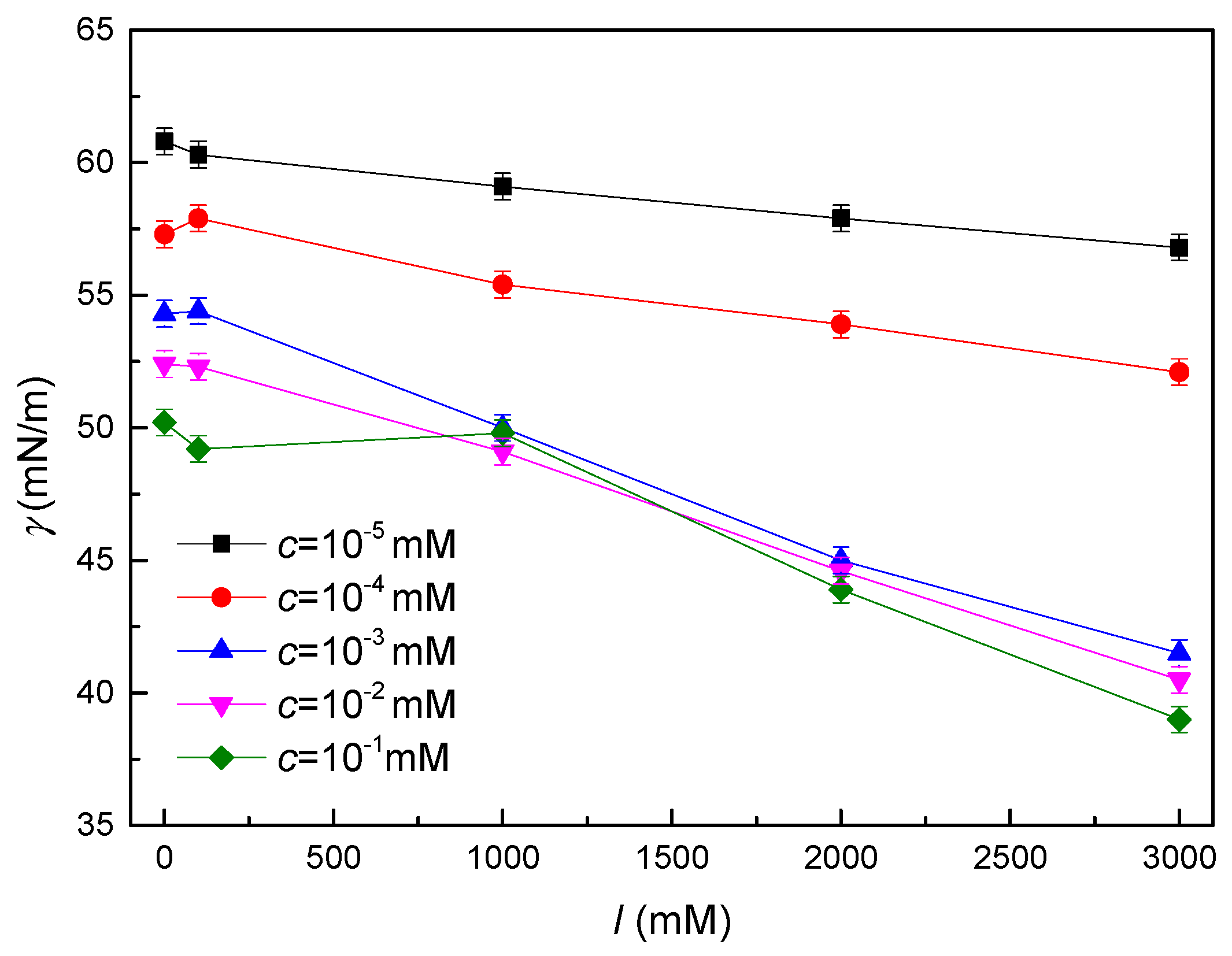
3.2. Low-Frequency Dilational Rheology
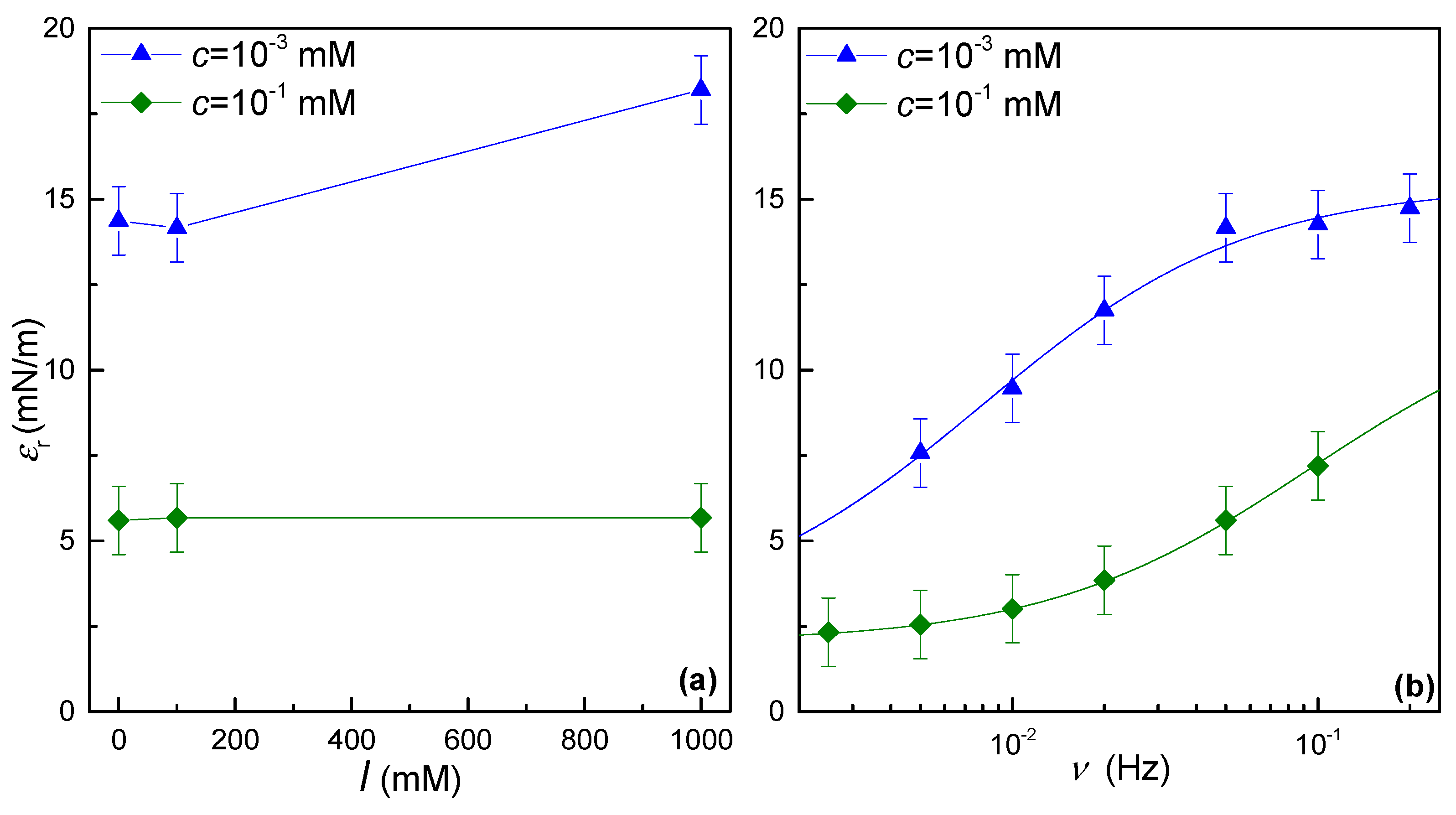
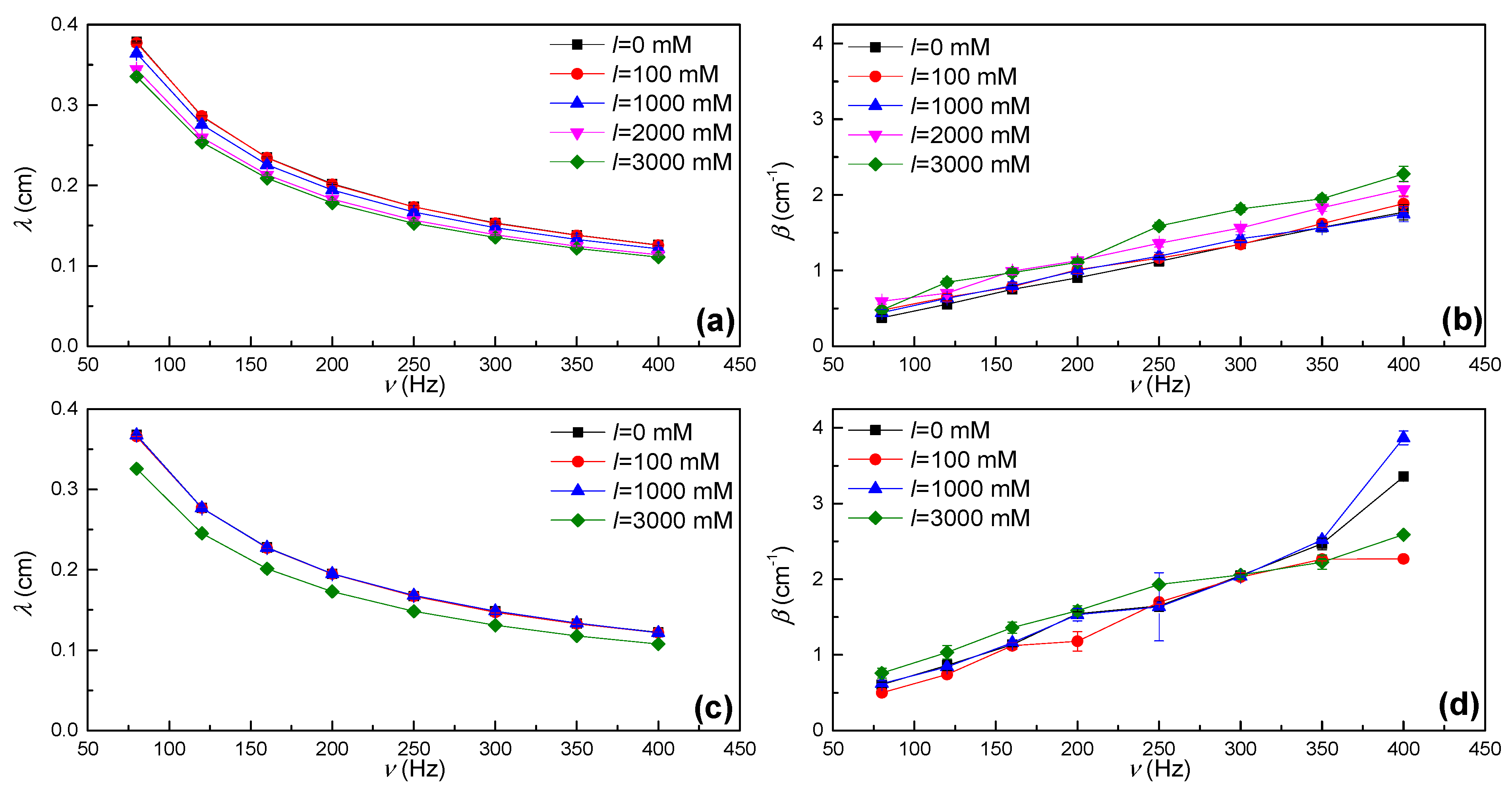
3.3. High-Frequency Dilational Rheology: Electrocapillary Wave Damping Measurements
3.3.1. Study of Propagation of Capillary Waves as Pluronic F-68-Laden Interfaces
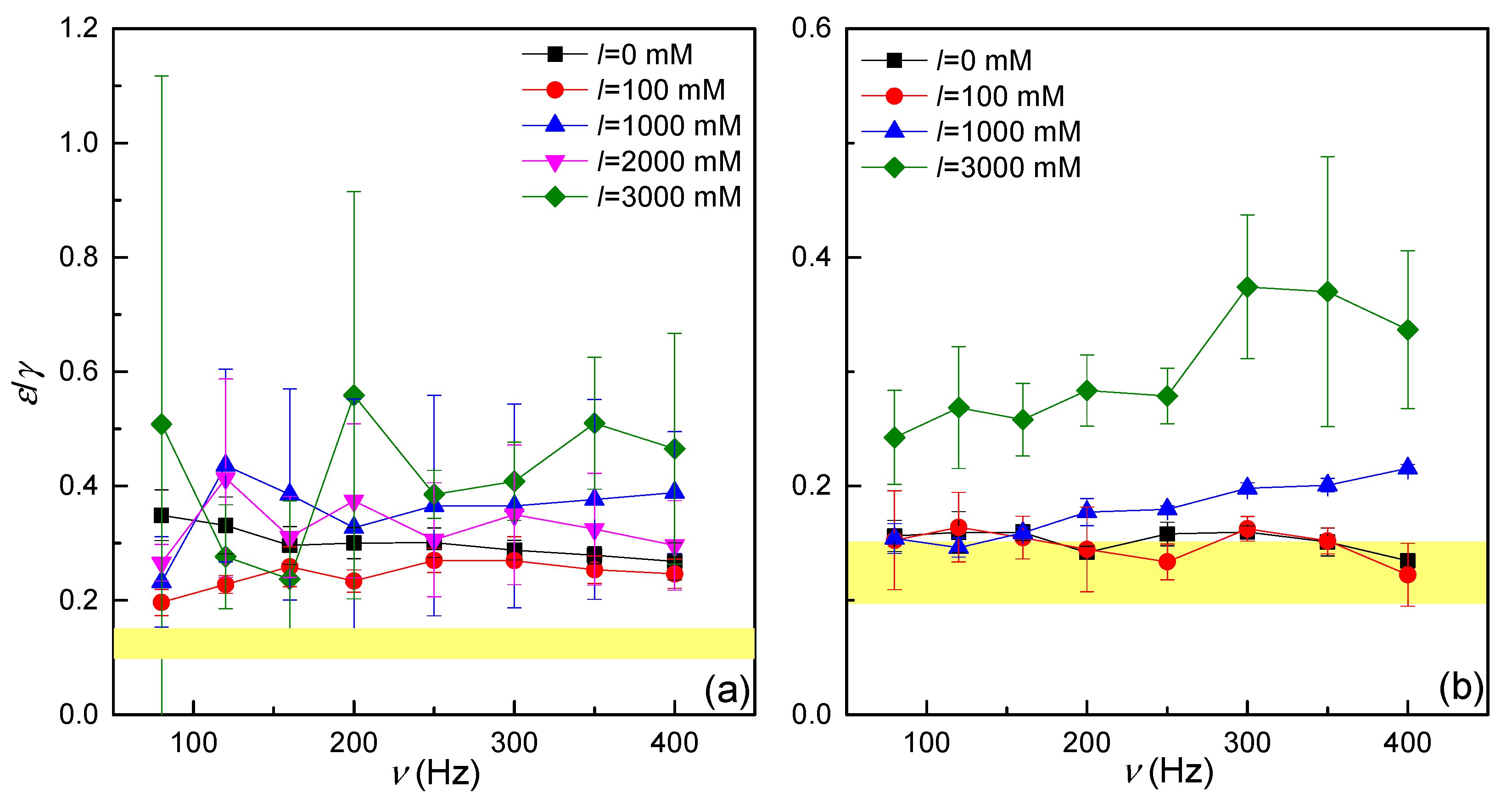
3.3.2. Accuracy of the Characterization of the Dilational Rheology by Electrocapillary Wave Measurements: The Resonance Condition
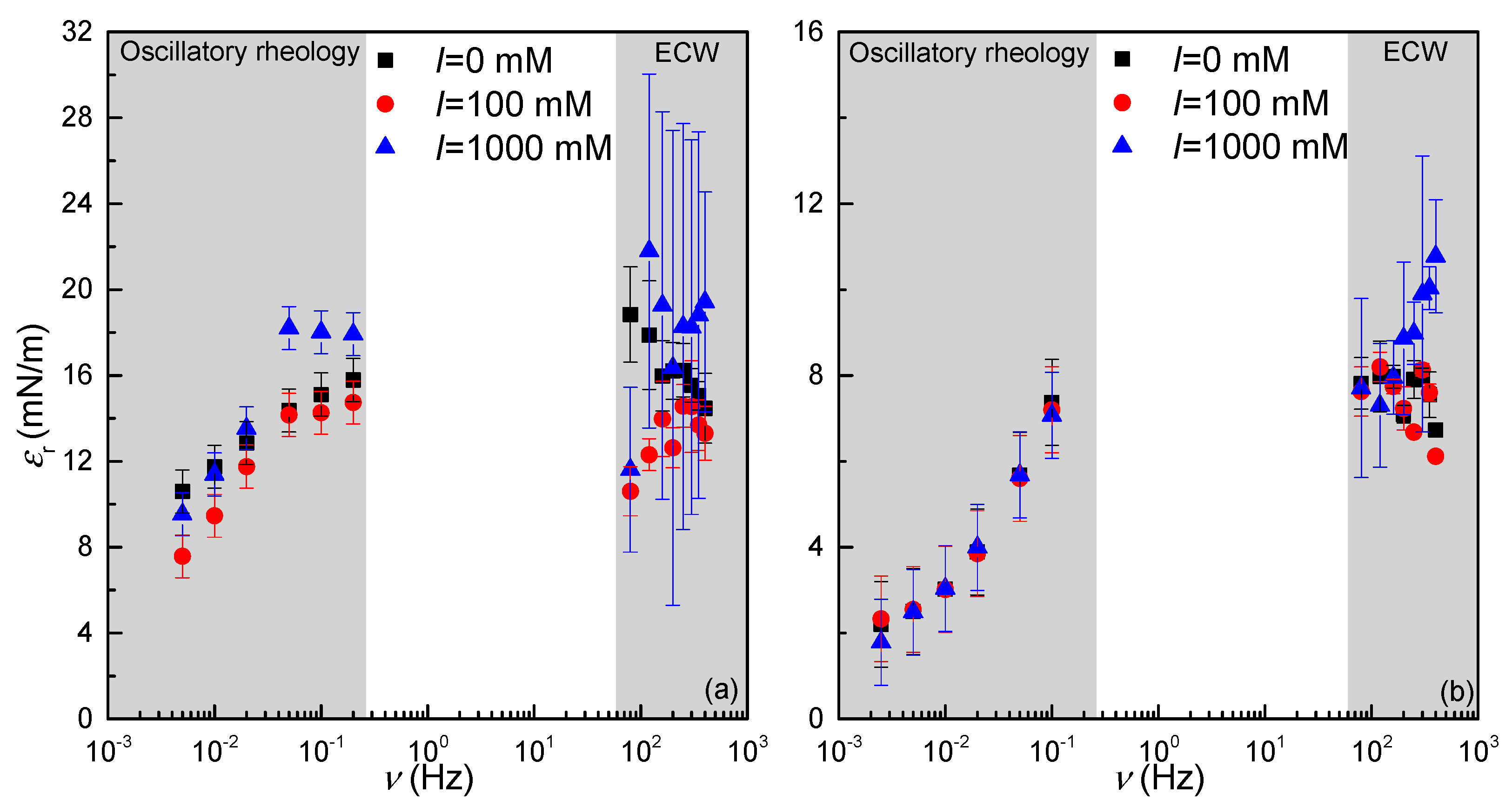
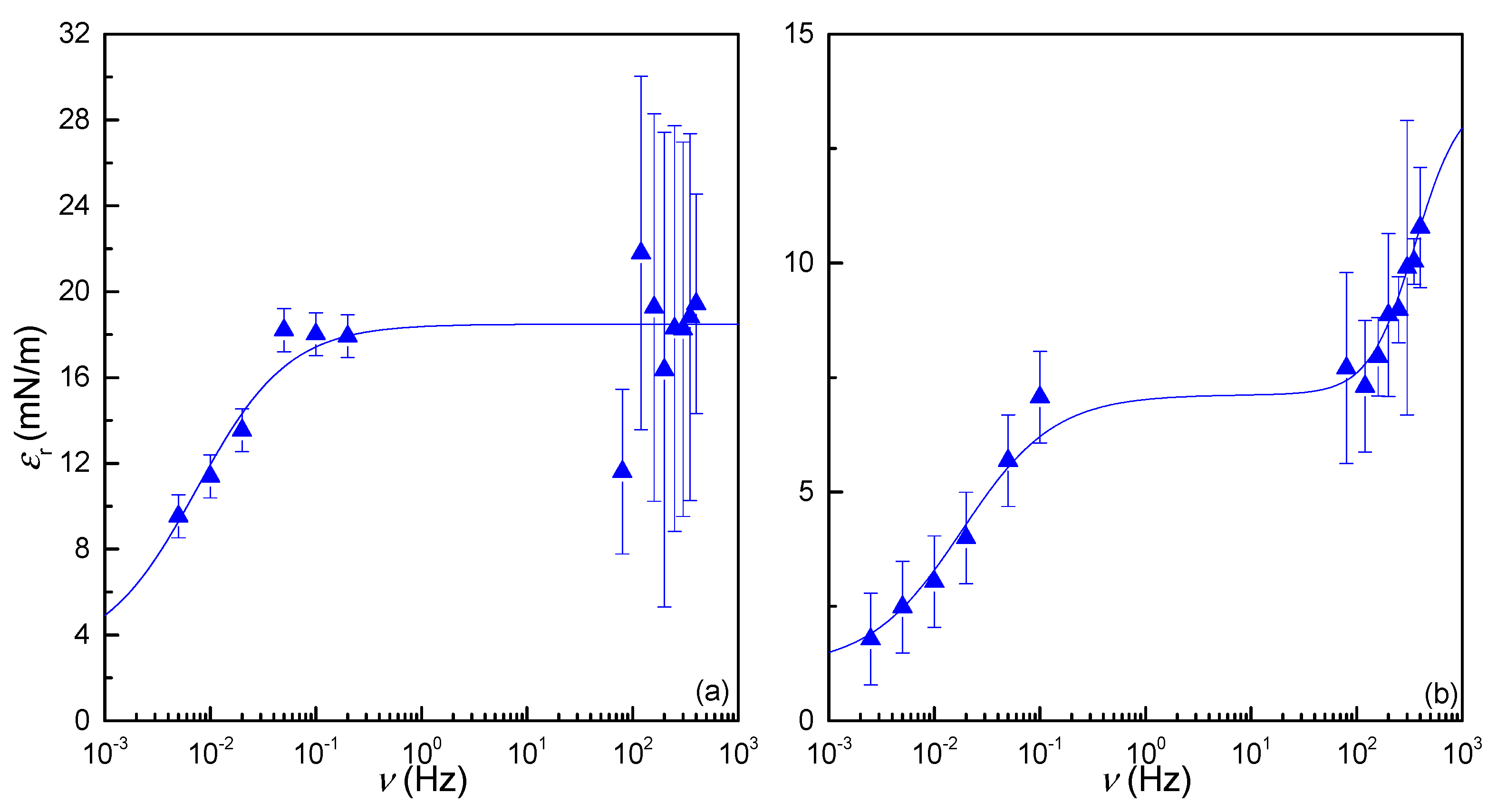
3.3.3. Dilational Spectrum: Combination of Oscillatory Rheology and Electrocapillary Wave Measurements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Bulk Viscosity, Density, and Interfacial Tension
| NaCl [mM] | η (mPa⋅s) | ρ (g/cm3) 1 | γ (mN/m) 2 |
|---|---|---|---|
| 0 | 0.90 ± 0.03 | 0.998 | 72.72 |
| 100 | 0.91 ± 0.03 | 1.002 | - |
| 1000 | 1.05 ± 0.03 | 1.038 | 73.77 |
| 2000 | 1.15 ± 0.03 | 1.075 | 74.94 |
| 3000 | 1.30 ± 0.03 | 1.111 | 76.61 |
References
- Jarak, I.; Varela, C.L.; Tavares Da Silva, E.; Roleira, F.F.M.; Veiga, F.; Figueiras, A. Pluronic-Based Nanovehicles: Recent Advances in Anticancer Therapeutic Applications. Eur. J. Med. Chem. 2020, 206, 112526. [Google Scholar] [CrossRef]
- Shamma, R.N.; Sayed, R.H.; Madry, H.; El Sayed, N.S.; Cucchiarini, M. Triblock Copolymer Bioinks in Hydrogel Three-Dimensional Printing for Regenerative Medicine: A Focus on Pluronic F127. Tissue Eng. Part B Rev. 2022, 28, 451–463. [Google Scholar] [CrossRef]
- Ganguly, R.; Kumar, S.; Kunwar, A.; Nath, S.; Sarma, H.D.; Tripathi, A.; Verma, G.; Chaudhari, D.P.; Aswal, V.K.; Melo, J.S. Structural and Therapeutic Properties of Curcumin Solubilized Pluronic F127 Micellar Solutions and Hydrogels. J. Mol. Liq. 2020, 314, 113591. [Google Scholar] [CrossRef]
- Singla, P.; Garg, S.; McClements, J.; Jamieson, O.; Peeters, M.; Mahajan, R.K. Advances in the Therapeutic Delivery and Applications of Functionalized Pluronics: A Critical Review. Adv. Colloid Interface Sci. 2022, 299, 102563. [Google Scholar] [CrossRef] [PubMed]
- Lucia, A.; Girard, C.; Fanucce, M.; Coviella, C.; Rubio, R.G.; Ortega, F.; Guzmán, E. Development of an Environmentally Friendly Larvicidal Formulation Based on Essential Oil Compound Blend to Control Aedes aegypti Larvae: Correlations between Physicochemical Properties and Insecticidal Activity. ACS Sustain. Chem. Eng. 2020, 8, 10995–11006. [Google Scholar] [CrossRef]
- Kumar, S.S.; Harikrishnan, K.K.; Urmila, S.P.; Gauri, V.; Saritha, A.; Gangopadhyay, M. Comprehensive Review of Pluronic® Polymers of Different Shapes with Prominent Applications in Photodynamic Therapy. Eur. Polym. J. 2023, 200, 112534. [Google Scholar] [CrossRef]
- Alexandridis, P. Poly(Ethylene Oxide)/Poly(Propylene Oxide) Block Copolymer Surfactants. Curr. Opin. Colloid Interface Sci. 1997, 2, 478–489. [Google Scholar] [CrossRef]
- Li, Z.; Peng, S.; Chen, X.; Zhu, Y.; Zou, L.; Liu, W.; Liu, C. Pluronics Modified Liposomes for Curcumin Encapsulation: Sustained Release, Stability and Bioaccessibility. Food Res. Int. 2018, 108, 246–253. [Google Scholar] [CrossRef] [PubMed]
- Braga, G.; Campanholi, K.D.S.S.; Ferreira, S.B.D.S.; Calori, I.R.; De Oliveira, J.H.; Vanzin, D.; Bruschi, M.L.; Pontes, R.M.; Março, P.H.; Tessaro, A.L.; et al. Tautomeric and Aggregational Dynamics of Curcumin-Supersaturated Pluronic Nanocarriers. ACS Appl. Polym. Mater. 2020, 2, 4493–4511. [Google Scholar] [CrossRef]
- Shaker, M.A.; Elbadawy, H.M.; Shaker, M.A. Improved Solubility, Dissolution, and Oral Bioavailability for Atorvastatin-Pluronic® Solid Dispersions. Int. J. Pharm. 2020, 574, 118891. [Google Scholar] [CrossRef]
- Carbone, C.; Rubio-Bueno, A.; Ortega, F.; Rubio, R.G.; Guzmán, E. Adsorption of Mixed Dispersions of Silica Nanoparticles and an Amphiphilic Triblock Copolymer at the Water–Vapor Interface. Appl. Sci. 2023, 13, 10093. [Google Scholar] [CrossRef]
- Velasco-Rodriguez, B.; Soltero-Martínez, J.F.; Rosales-Rivera, L.C.; Macías-Balleza, E.R.; Landázuri, G.; Larios-Durán, E.R. Adsorption and Interaction of Bovine Serum Albumin and Pluronic P103 Triblock Copolymer on a Gold Electrode: Double-Layer Capacitance Measurements. ACS Omega 2020, 5, 17347–17355. [Google Scholar] [CrossRef]
- Yun, K.H.; Sharma, K.; Kim, H.U.; Bae, T.-H. Modification of a PES Microfiltration Membrane to Enhance Sterile Filtration by Inhibiting Protein Adsorption. J. Ind. Eng. Chem. 2023, 123, 311–319. [Google Scholar] [CrossRef]
- Pérez-Sánchez, G.; Vicente, F.A.; Schaeffer, N.; Cardoso, I.S.; Ventura, S.P.M.; Jorge, M.; Coutinho, J.A.P. Rationalizing the Phase Behavior of Triblock Copolymers through Experiments and Molecular Simulations. J. Phys. Chem. C 2019, 123, 21224–21236. [Google Scholar] [CrossRef]
- Hopkins, C.C.; De Bruyn, J.R. Gelation and Long-Time Relaxation of Aqueous Solutions of Pluronic F127. J. Rheol. 2019, 63, 191–201. [Google Scholar] [CrossRef]
- Patel, D.; Jana, R.; Lin, M.-H.; Kuperkar, K.; Seth, D.; Chen, L.-J.; Bahadur, P. Revisiting the Salt-Triggered Self-Assembly in Very Hydrophilic Triblock Copolymer Pluronic® F88 Using Multitechnique Approach. Colloid Polym. Sci. 2021, 299, 1113–1126. [Google Scholar] [CrossRef]
- Da Silva, L.H.M.; Loh, W. Calorimetric Investigation of the Formation of Aqueous Two-Phase Systems in Ternary Mixtures of Water, Poly(Ethylene Oxide) and Electrolytes (Or Dextran). J. Phys. Chem. B 2000, 104, 10069–10073. [Google Scholar] [CrossRef]
- Suman, K.; Sourav, S.; Joshi, Y.M. Rheological Signatures of Gel–Glass Transition and a Revised Phase Diagram of an Aqueous Triblock Copolymer Solution of Pluronic F127. Phys. Fluids 2021, 33, 073610. [Google Scholar] [CrossRef]
- Boonrat, O.; Tantishaiyakul, V.; Hirun, N.; Rugmai, S.; Soontaranon, S. Structural Characterization Using SAXS and Rheological Behaviors of Pluronic F127 and Methylcellulose Blends. Polym. Bull. 2021, 78, 1175–1187. [Google Scholar] [CrossRef]
- Zheng, L.; Minamikawa, H.; Harada, K.; Inoue, T.; Chernik, G.G. Effect of Inorganic Salts on the Phase Behavior of an Aqueous Mixture of Heptaethylene Glycol Dodecyl Ether. Langmuir 2003, 19, 10487–10494. [Google Scholar] [CrossRef]
- Pandit, N.; Trygstad, T.; Croy, S.; Bohorquez, M.; Koch, C. Effect of Salts on the Micellization, Clouding, and Solubilization Behavior of Pluronic F127 Solutions. J. Colloid Interface Sci. 2000, 222, 213–220. [Google Scholar] [CrossRef]
- Sheelarani, B.; Karunanithi, P.; Dash, S. Effect of Valency of Cation on Micellization Behaviour of Pluronic Mixed Micelle F127 and L64. Chem. Phys. Lett. 2020, 739, 136956. [Google Scholar] [CrossRef]
- Tripathi, N.; Ray, D.; Aswal, V.K.; Kuperkar, K.; Bahadur, P. Salt Induced Micellization Conduct in PEO–PPO–PEO-Based Block Copolymers: A Thermo-Responsive Approach. Soft Matter 2023, 19, 7227–7244. [Google Scholar] [CrossRef]
- Rudani, B.A.; Sarolia, J.; Rai, R.; Aswal, V.K.; Bahadur, P.; Tiwari, S. Comparative Effect of Physiological Salts upon Micellization of T1304 and T1307. Langmuir 2023, 39, 9060–9068. [Google Scholar] [CrossRef]
- Alexandridis, P.; Holzwarth, J.F. Differential Scanning Calorimetry Investigation of the Effect of Salts on Aqueous Solution Properties of an Amphiphilic Block Copolymer (Poloxamer). Langmuir 1997, 13, 6074–6082. [Google Scholar] [CrossRef]
- Ward, C.L.; Cornejo, M.A.; Peli Thanthri, S.H.; Linz, T.H. A Review of Electrophoretic Separations in Temperature-Responsive Pluronic Thermal Gels. Anal. Chim. Acta 2023, 1276, 341613. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Li, X.; Zhai, M.; Huang, L.; Peng, J.; Li, J.; Wei, G. Ion-Specific Swelling of Poly(Styrene Sulfonic Acid) Hydrogel. J. Phys. Chem. B 2007, 111, 3391–3397. [Google Scholar] [CrossRef] [PubMed]
- Loh, W.W.; Lin, Q.; Lim, C.C.; Guo, L.; Tang, Y.K.; Loh, X.J.; Lim, J.Y.C. Hofmeister Effects of Anions on Self-Assembled Thermogels. Mater. Today Chem. 2022, 23, 100674. [Google Scholar] [CrossRef]
- Smith, J.D.; Saykally, R.J.; Geissler, P.L. The Effects of Dissolved Halide Anions on Hydrogen Bonding in Liquid Water. J. Am. Chem. Soc. 2007, 129, 13847–13856. [Google Scholar] [CrossRef] [PubMed]
- Guàrdia, E.; Laria, D.; Martí, J. Hydrogen Bond Structure and Dynamics in Aqueous Electrolytes at Ambient and Supercritical Conditions. J. Phys. Chem. B 2006, 110, 6332–6338. [Google Scholar] [CrossRef]
- Chen, X.; Flores, S.C.; Lim, S.-M.; Zhang, Y.; Yang, T.; Kherb, J.; Cremer, P.S. Specific Anion Effects on Water Structure Adjacent to Protein Monolayers. Langmuir 2010, 26, 16447–16454. [Google Scholar] [CrossRef] [PubMed]
- Kontogiannis, O.; Selianitis, D.; Lagopati, N.; Pippa, N.; Pispas, S.; Gazouli, M. Surfactant and Block Copolymer Nanostructures: From Design and Development to Nanomedicine Preclinical Studies. Pharmaceutics 2023, 15, 501. [Google Scholar] [CrossRef]
- Li, Y.; Tian, Y.; Jia, X.; Zhang, Z.; Sun, D.; Xie, H.; Zang, D.; Liu, T. Effect of Pharmaceutical Excipients on Micellization of Pluronic and the Application as Drug Carrier to Reverse MDR. J. Mol. Liq. 2023, 383, 122182. [Google Scholar] [CrossRef]
- Deyerle, B.A.; Zhang, Y. Effects of Hofmeister Anions on the Aggregation Behavior of PEO–PPO–PEO Triblock Copolymers. Langmuir 2011, 27, 9203–9210. [Google Scholar] [CrossRef] [PubMed]
- Ren, C.; Tian, W.; Szleifer, I.; Ma, Y. Specific Salt Effects on Poly(Ethylene Oxide) Electrolyte Solutions. Macromolecules 2011, 44, 1719–1727. [Google Scholar] [CrossRef]
- Llamas, S.; Mendoza, A.J.; Guzmán, E.; Ortega, F.; Rubio, R.G. Salt Effects on the Air/Solution Interfacial Properties of PEO-Containing Copolymers: Equilibrium, Adsorption Kinetics and Surface Rheological Behavior. J. Colloid Interface Sci. 2013, 400, 49–58. [Google Scholar] [CrossRef]
- Noskov, B.A.; Lin, S.-Y.; Loglio, G.; Rubio, R.G.; Miller, R. Dilational Viscoelasticity of PEO–PPO–PEO Triblock Copolymer Films at the Air–Water Interface in the Range of High Surface Pressures. Langmuir 2006, 22, 2647–2652. [Google Scholar] [CrossRef]
- Rivillon, S.; Muñoz, M.G.; Monroy, F.; Ortega, F.; Rubio, R.G. Experimental Study of the Dynamic Properties of Monolayers of PS–PEO Block Copolymers: The Attractive Monomer Surface Case. Macromolecules 2003, 36, 4068–4077. [Google Scholar] [CrossRef]
- Brinkkötter, M.; Geisler, R.; Großkopf, S.; Hellweg, T.; Schönhoff, M. Influence of Li-Salt on the Mesophases of Pluronic Block Copolymers in Ionic Liquid. J. Phys. Chem. B 2020, 124, 9464–9474. [Google Scholar] [CrossRef]
- Kumar, Y.; Hashmi, S.A.; Pandey, G.P. Lithium Ion Transport and Ion–Polymer Interaction in PEO Based Polymer Electrolyte Plasticized with Ionic Liquid. Solid State Ion. 2011, 201, 73–80. [Google Scholar] [CrossRef]
- Li, X.; Huang, K.; Xu, Y.; Liu, H. Interaction of Sodium and Potassium Ions with PEO-PPO Copolymer Investigated by FTIR, Raman and NMR. Vib. Spectrosc. 2014, 75, 59–64. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M.; Monroy, F.; Ortega, F.; Rubio, R.G.; Miller, R.; Noskov, B.A. Adsorption of Water-Soluble Polymers with Surfactant Character. Dilational Viscoelasticity. Langmuir 2007, 23, 3802–3808. [Google Scholar] [CrossRef]
- Cabrerizo-Vílchez, M.A.; Wege, H.A.; Holgado-Terriza, J.A.; Neumann, A.W. Axisymmetric Drop Shape Analysis as Penetration Langmuir Balance. Rev. Sci. Instrum. 1999, 70, 2438–2444. [Google Scholar] [CrossRef]
- Torcello-Gómez, A.; Maldonado-Valderrama, J.; Gálvez-Ruiz, M.J.; Martín-Rodríguez, A.; Cabrerizo-Vílchez, M.A.; De Vicente, J. Surface Rheology of Sorbitan Tristearate and β-Lactoglobulin: Shear and Dilatational Behavior. J. Non-Newton. Fluid Mech. 2011, 166, 713–722. [Google Scholar] [CrossRef]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.C.; Tabor, R.F. Measurement of Surface and Interfacial Tension Using Pendant Drop Tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef]
- Liggieri, L.; Santini, E.; Guzmán, E.; Maestro, A.; Ravera, F. Wide-Frequency Dilational Rheology Investigation of Mixed Silica Nanoparticle–CTAB Interfacial Layers. Soft Matter 2011, 7, 7699. [Google Scholar] [CrossRef]
- Maestro, A.; Ortega, F.; Rubio, R.G.; Rubio, M.A.; Krägel, J.; Miller, R. Rheology of Poly(Methyl Methacrylate) Langmuir Monolayers: Percolation Transition to a Soft Glasslike System. J. Chem. Phys. 2011, 134, 104704. [Google Scholar] [CrossRef] [PubMed]
- Monroy, F.; Ortega, F.; Rubio, R.G.; Velarde, M.G. Surface Rheology, Equilibrium and Dynamic Features at Interfaces, with Emphasis on Efficient Tools for Probing Polymer Dynamics at Interfaces. Adv. Colloid Interface Sci. 2007, 134–135, 175–189. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, E.; Maestro, A.; Carbone, C.; Ortega, F.; Rubio, R.G. Dilational Rheology of Fluid/Fluid Interfaces: Foundations and Tools. Fluids 2022, 7, 335. [Google Scholar] [CrossRef]
- Ramírez, P.; Stocco, A.; Muñoz, J.; Miller, R. Interfacial Rheology and Conformations of Triblock Copolymers Adsorbed onto the Water–Oil Interface. J. Colloid Interface Sci. 2012, 378, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Torcello-Gómez, A.; Santander-Ortega, M.J.; Peula-García, J.M.; Maldonado-Valderrama, J.; Gálvez-Ruiz, M.J.; Ortega-Vinuesa, J.L.; Martín-Rodríguez, A. Adsorption of Antibody onto Pluronic F68-Covered Nanoparticles: Link with Surface Properties. Soft Matter 2011, 7, 8450–8461. [Google Scholar] [CrossRef]
- Alexandridis, P.; Athanassiou, V.; Fukuda, S.; Hatton, T.A. Surface Activity of Poly(Ethylene Oxide)-Block-Poly(Propylene Oxide)-Block-Poly(Ethylene Oxide) Copolymers. Langmuir 1994, 10, 2604–2612. [Google Scholar] [CrossRef]
- Alexandridis, P.; Holzwarth, J.F.; Hatton, T.A. Micellization of Poly(Ethylene Oxide)-Poly(Propylene Oxide)-Poly(Ethylene Oxide) Triblock Copolymers in Aqueous Solutions: Thermodynamics of Copolymer Association. Macromolecules 1994, 27, 2414–2425. [Google Scholar] [CrossRef]
- Muñoz, M.G.; Monroy, F.; Hernández, P.; Ortega, F.; Rubio, R.G.; Langevin, D. Anomalous Damping of the Capillary Waves at the Air–Water Interface of a Soluble Triblock Copolymer. Langmuir 2003, 19, 2147–2154. [Google Scholar] [CrossRef]
- Jeworrek, C.; Evers, F.; Howe, J.; Brandenburg, K.; Tolan, M.; Winter, R. Effects of Specific versus Nonspecific Ionic Interactions on the Structure and Lateral Organization of Lipopolysaccharides. Biophys. J. 2011, 100, 2169–2177. [Google Scholar] [CrossRef]
- Lucassen, J.; Van Den Tempel, M. Dynamic Measurements of Dilational Properties of a Liquid Interface. Chem. Eng. Sci. 1972, 27, 1283–1291. [Google Scholar] [CrossRef]
- Langevin, D. Light Scattering by Liquid Surfaces and Complementary Techniques; Surfactant Science Series; Marcel Dekker: New York, NY, USA, 1992; ISBN 978-0-8247-8607-6. [Google Scholar]
- Levich, V.G. Physicochemical Hydrodynamics, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1962; ISBN 978-0-13-674440-5. [Google Scholar]
- Lucassen-Reynders, E.H.; Lucassen, J. Properties of Capillary Waves. Adv. Colloid Interface Sci. 1970, 2, 347–395. [Google Scholar] [CrossRef]
- Ravera, F.; Ferrari, M.; Santini, E.; Liggieri, L. Influence of Surface Processes on the Dilational Visco-Elasticity of Surfactant Solutions. Adv. Colloid Interface Sci. 2005, 117, 75–100. [Google Scholar] [CrossRef] [PubMed]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, 79th ed.; CRC: Boca Raton, FL, USA, 1998; ISBN 978-0-8493-0479-8. [Google Scholar]
- Ozdemir, O.; Karakashev, S.I.; Nguyen, A.V.; Miller, J.D. Adsorption and Surface Tension Analysis of Concentrated Alkali Halide Brine Solutions. Miner. Eng. 2009, 22, 263–271. [Google Scholar] [CrossRef]


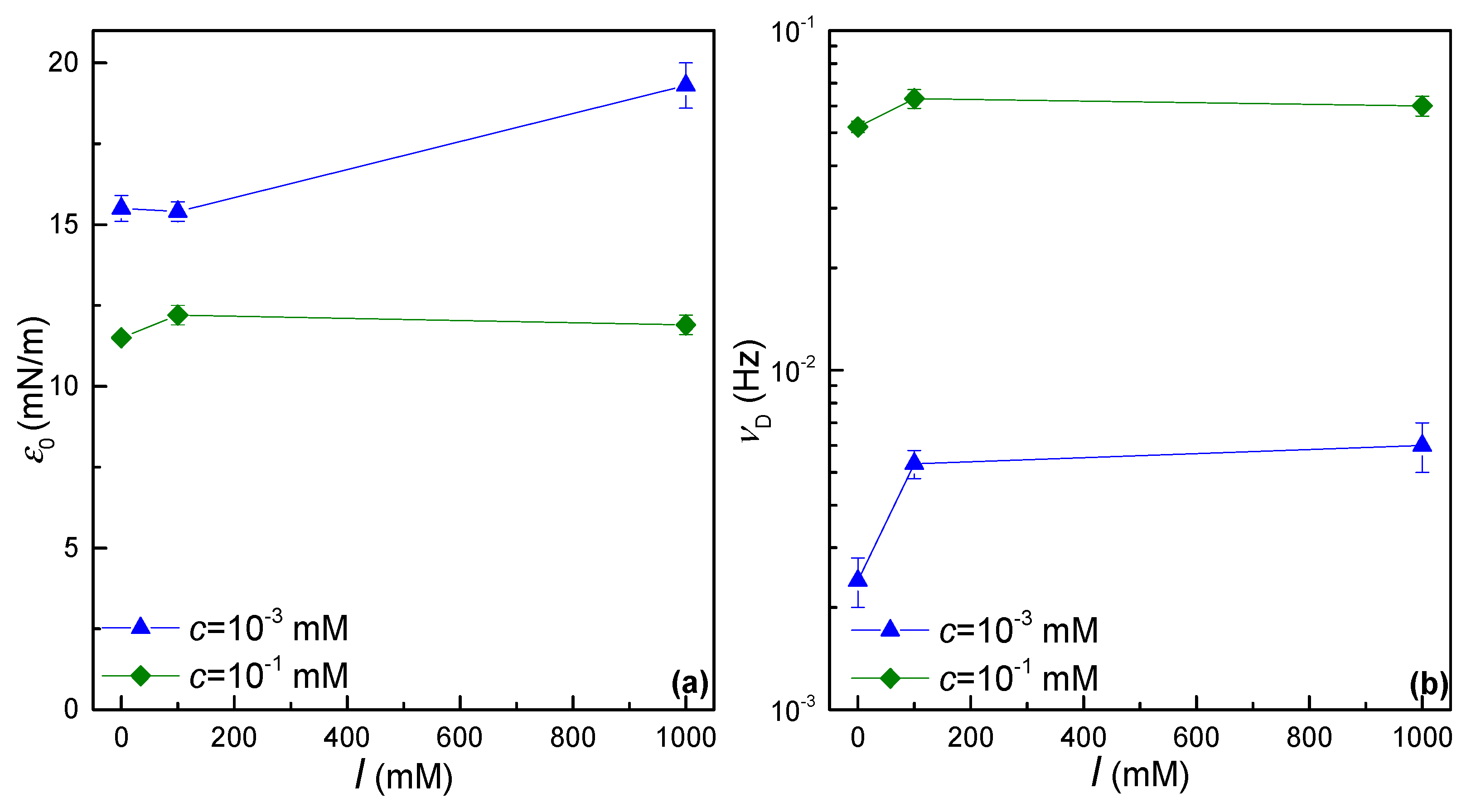

| c (mM) | 10−3 | 10−1 | ||||
|---|---|---|---|---|---|---|
| I (mM) | (mN/m) | (Hz) | (mN/m) | (Hz) | (mN/m) | (Hz) |
| 0 | 15.6 ± 0.2 | 2.5 ± 0.4 | 7.7 ± 0.1 | 1.5 ± 0.2 | - | - |
| 100 | 14.1 ± 0.2 | 3.7 ± 0.8 | 7.4 ± 0.2 | 1.3 ± 0.3 | - | - |
| 1000 | 18.5 ± 0.4 | 6 ± 1 | 7.1 ± 0.3 | 1.2 ± 0.3 | 14 ± 1 | 3.6 ± 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbone, C.; Guzmán, E.; Maldonado-Valderrama, J.; Rubio, R.G.; Ortega, F. Ionic Strength Effect in the Equilibrium and Rheological Behavior of an Amphiphilic Triblock Copolymer at the Air/Solution Interface. Colloids Interfaces 2024, 8, 16. https://doi.org/10.3390/colloids8020016
Carbone C, Guzmán E, Maldonado-Valderrama J, Rubio RG, Ortega F. Ionic Strength Effect in the Equilibrium and Rheological Behavior of an Amphiphilic Triblock Copolymer at the Air/Solution Interface. Colloids and Interfaces. 2024; 8(2):16. https://doi.org/10.3390/colloids8020016
Chicago/Turabian StyleCarbone, Carlo, Eduardo Guzmán, Julia Maldonado-Valderrama, Ramón G. Rubio, and Francisco Ortega. 2024. "Ionic Strength Effect in the Equilibrium and Rheological Behavior of an Amphiphilic Triblock Copolymer at the Air/Solution Interface" Colloids and Interfaces 8, no. 2: 16. https://doi.org/10.3390/colloids8020016
APA StyleCarbone, C., Guzmán, E., Maldonado-Valderrama, J., Rubio, R. G., & Ortega, F. (2024). Ionic Strength Effect in the Equilibrium and Rheological Behavior of an Amphiphilic Triblock Copolymer at the Air/Solution Interface. Colloids and Interfaces, 8(2), 16. https://doi.org/10.3390/colloids8020016










