Predictive Approach to the Phase Behavior of Polymer–Water–Surfactant–Electrolyte Systems Using a Pseudosolvent Concept
Abstract
:1. Introduction
2. Experimental Study of Phase Behavior
2.1. Materials
2.2. Phase Behavior Measurements
3. Development of a Pseudosolvent Model for Predicting Phase Behavior
3.1. The Pseudosolvent and Its Characteristic Energy
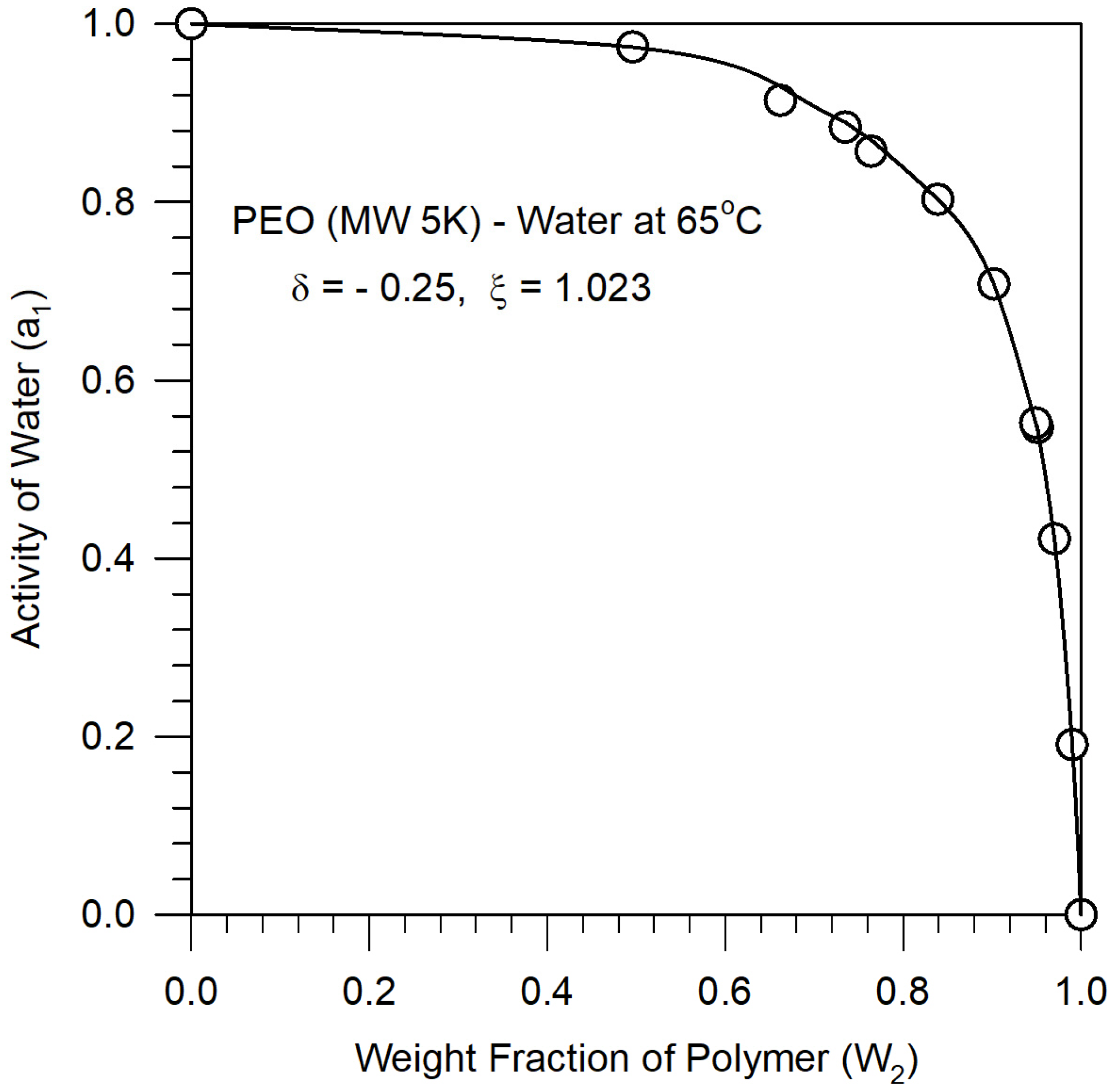
3.2. Polymer–Pseudosolvent Binary Parameters ξ and δ
3.3. Polymer–Pseudosolvent Phase Diagram in the Parametric Space of
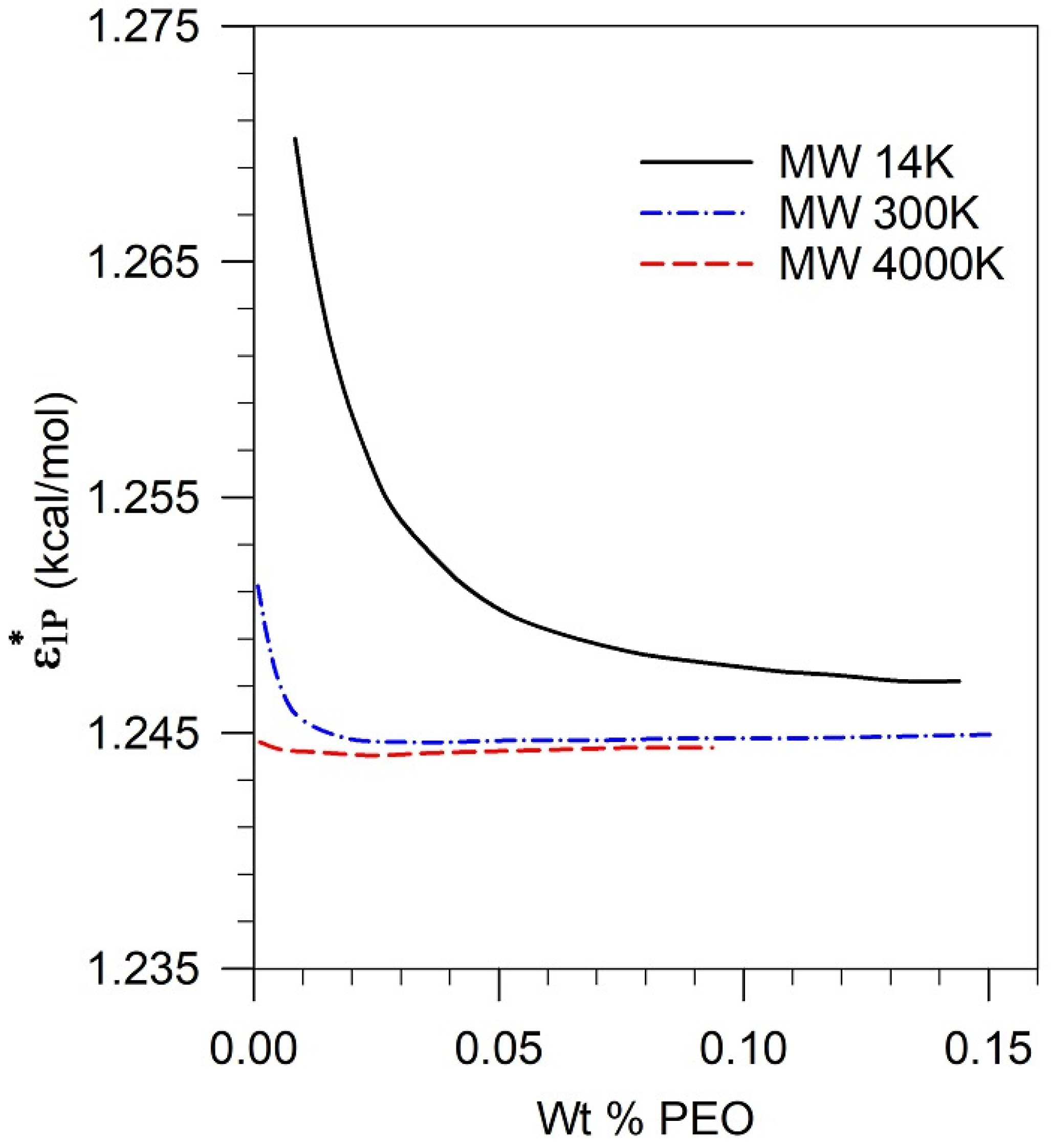
3.4. Mapping the Characteristic Energy of the Pseudosolvent to Its Composition
4. Calculation of ΔG from Thermodynamic Data on Surfactants and Electrolytes
4.1. Water + Electrolyte Systems
4.2. Water + Surfactant Systems
4.3. Water + Surfactant + Electrolyte Systems
4.4. Estimation of Thermodynamic Parameters from Literature
- (a)
- A and B in Equation (17) for the hydrophobic tail length-dependence of the CMC;
- (b)
- a in Equation (24) for the ionic strength-dependence of the CMC;
- (c)
- and α* in Equation (18) for counterion binding at the micellar surface;
- (d)
- in Equation (19) for the activity coefficient of the surfactant.
5. Phase Behavior Predictions and Construction of Phase Diagrams
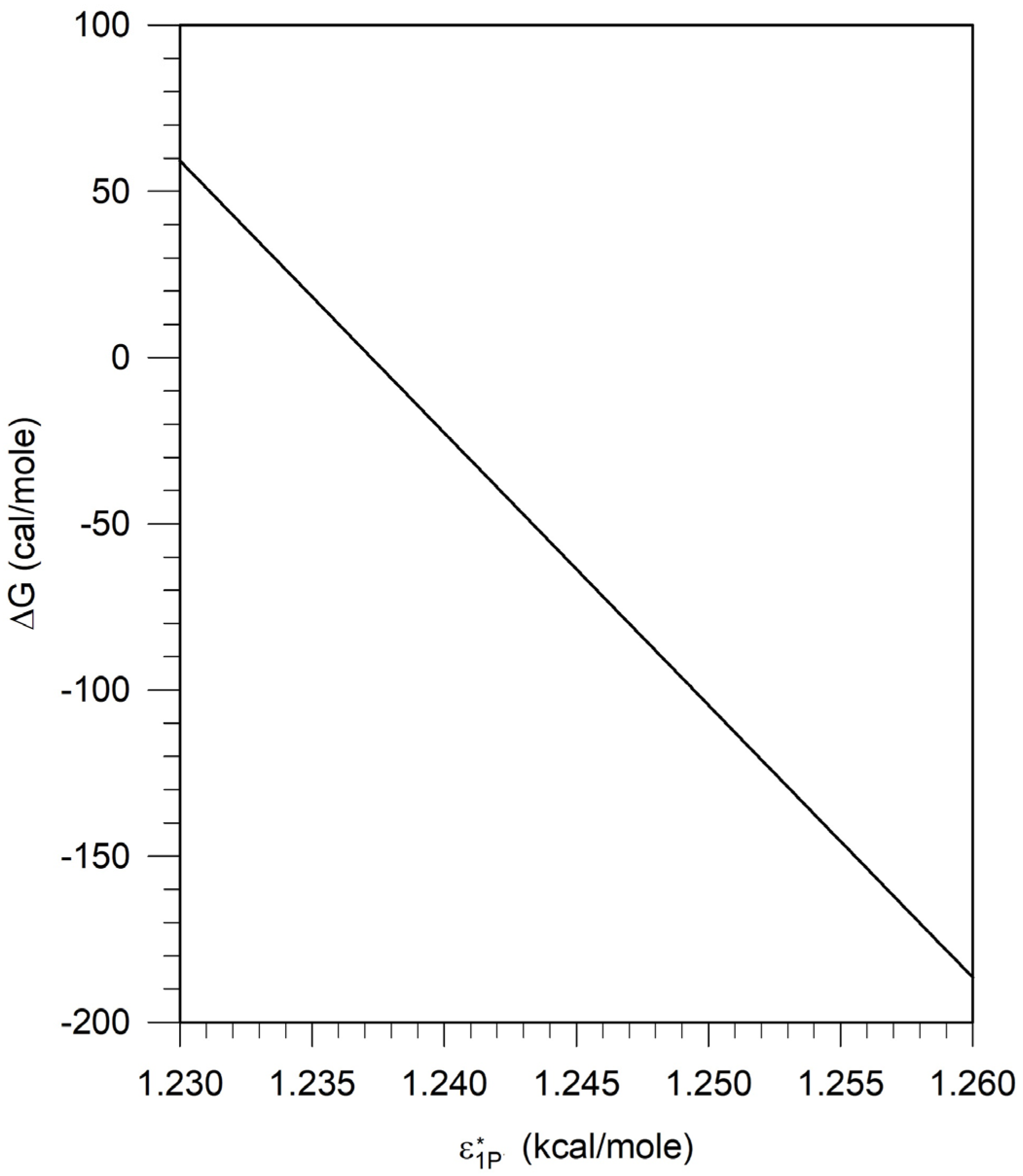
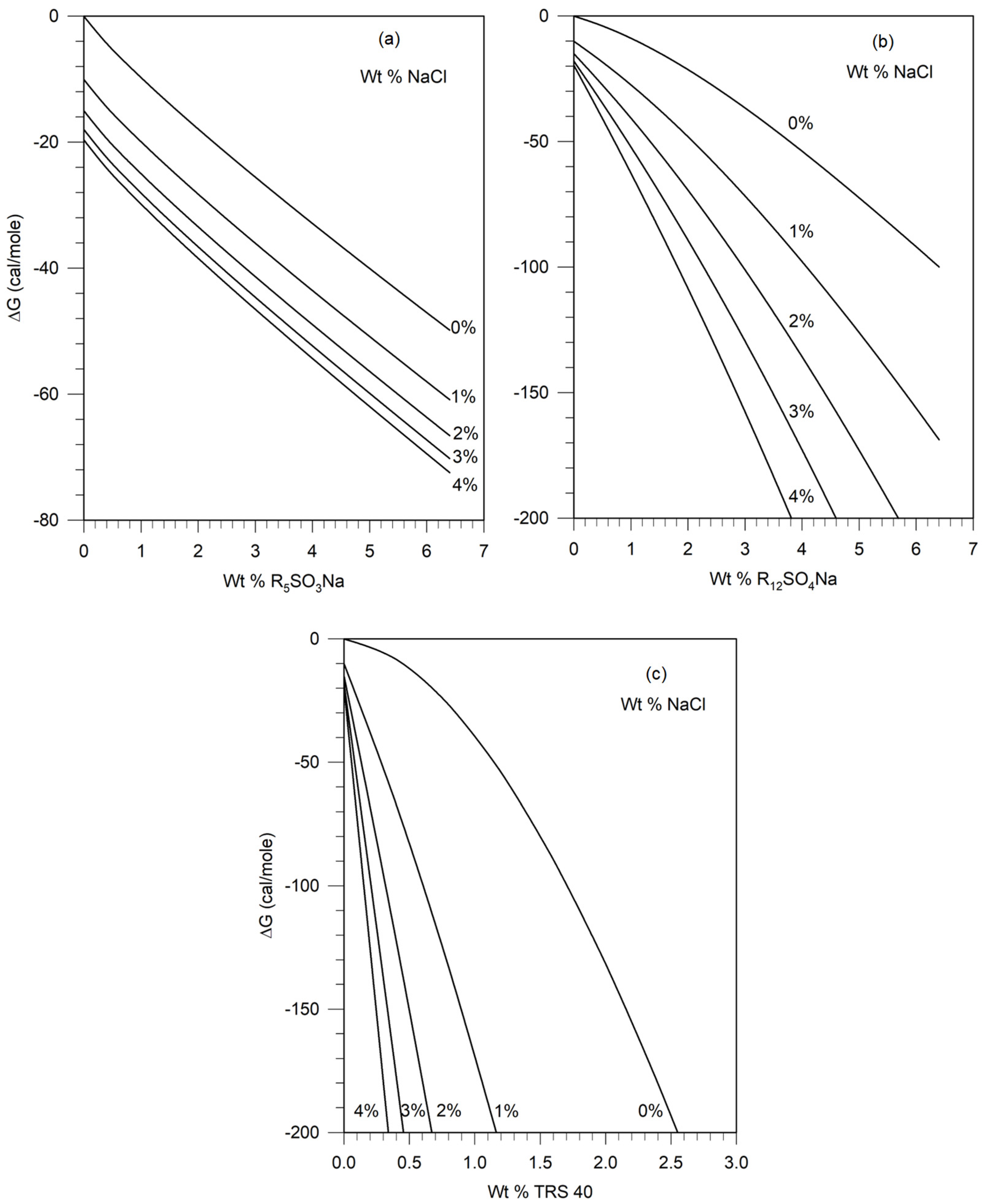
5.1. Calculation of the Free Energy Difference between the Pseudosolvent and Water
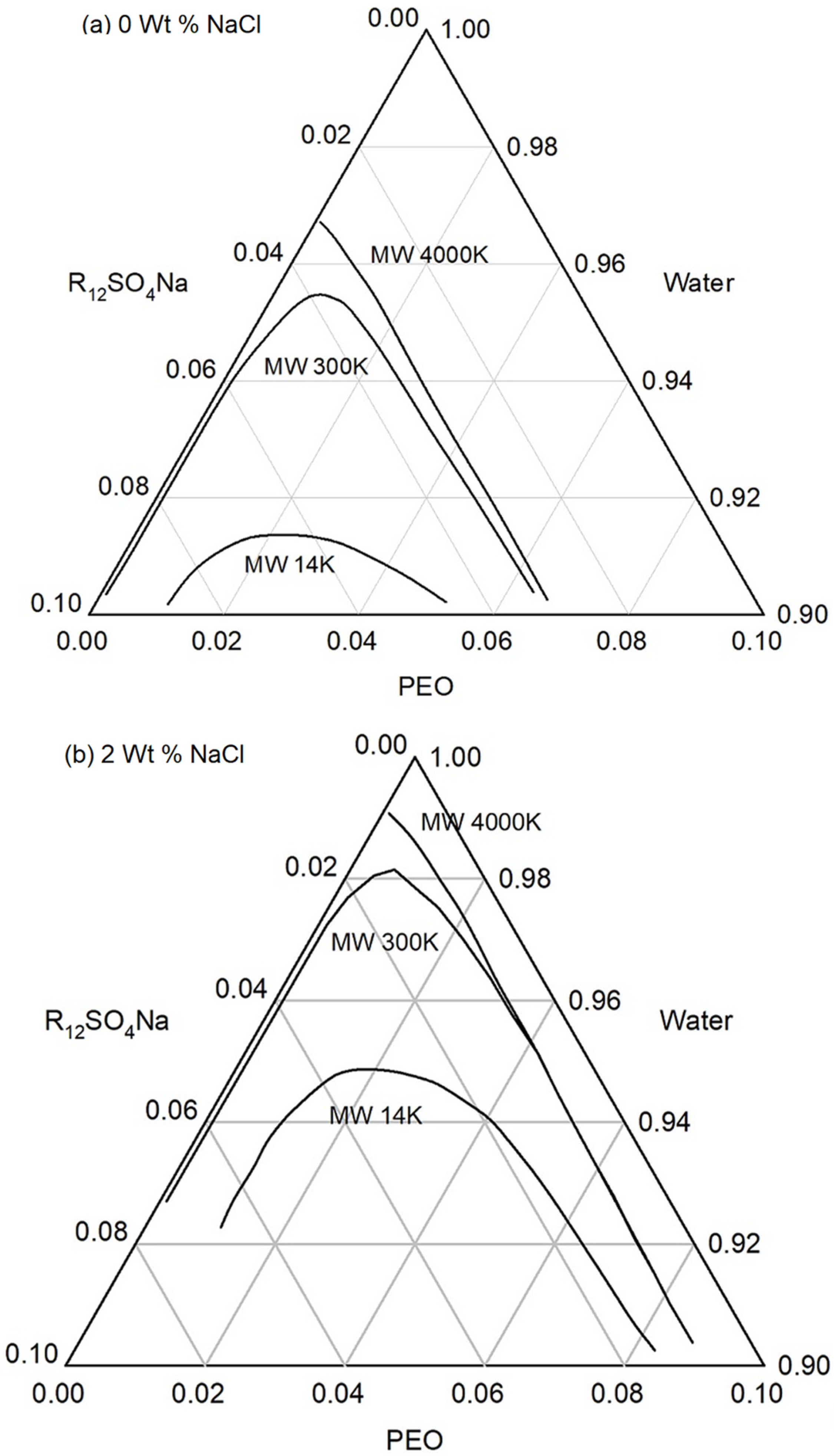
5.2. Construction of Ternary Phase Diagram from Theory Based on iso-ΔG Values
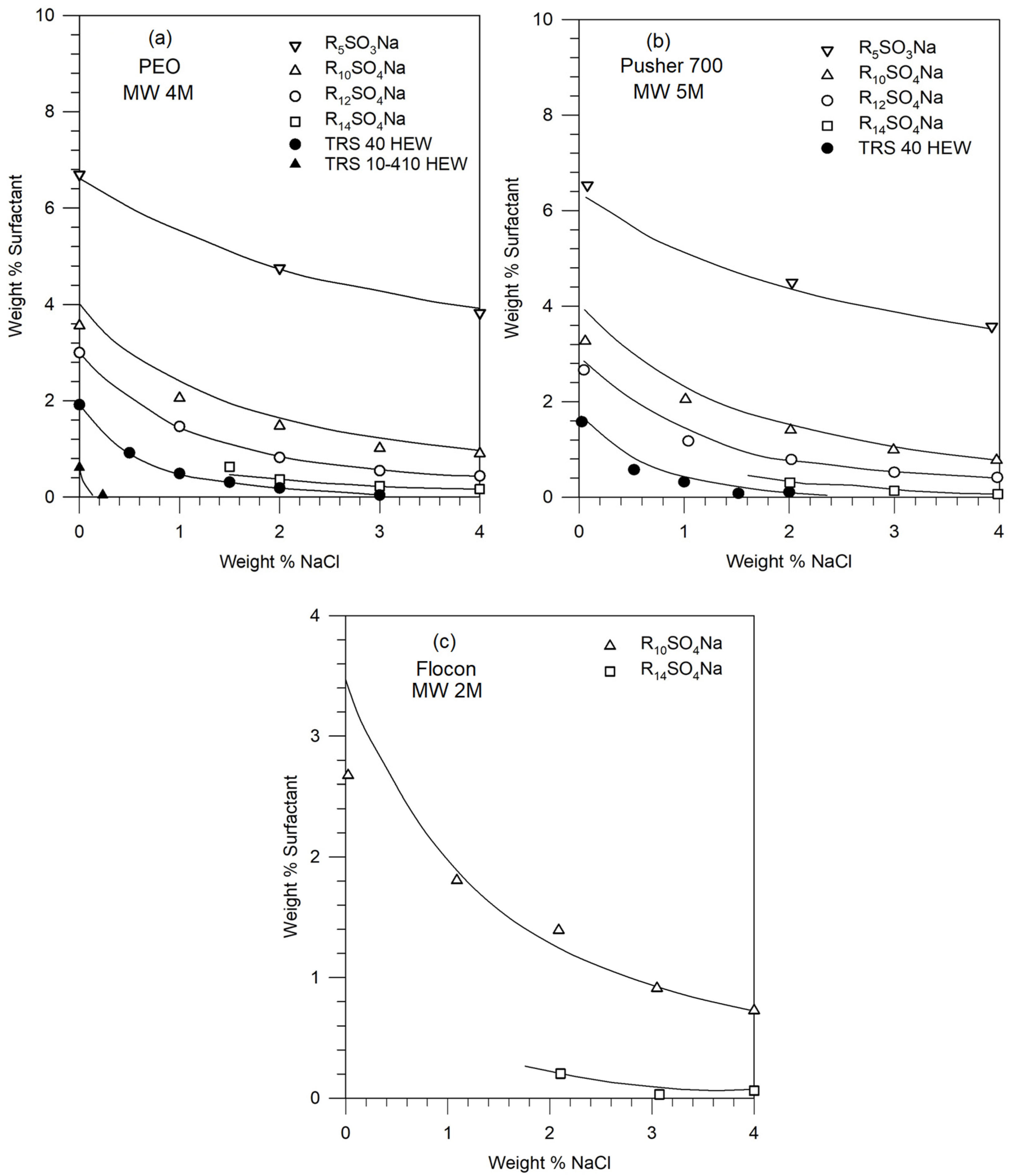
5.3. Construction of Phase Diagram Using a Single Experimental Phase Boundary Data
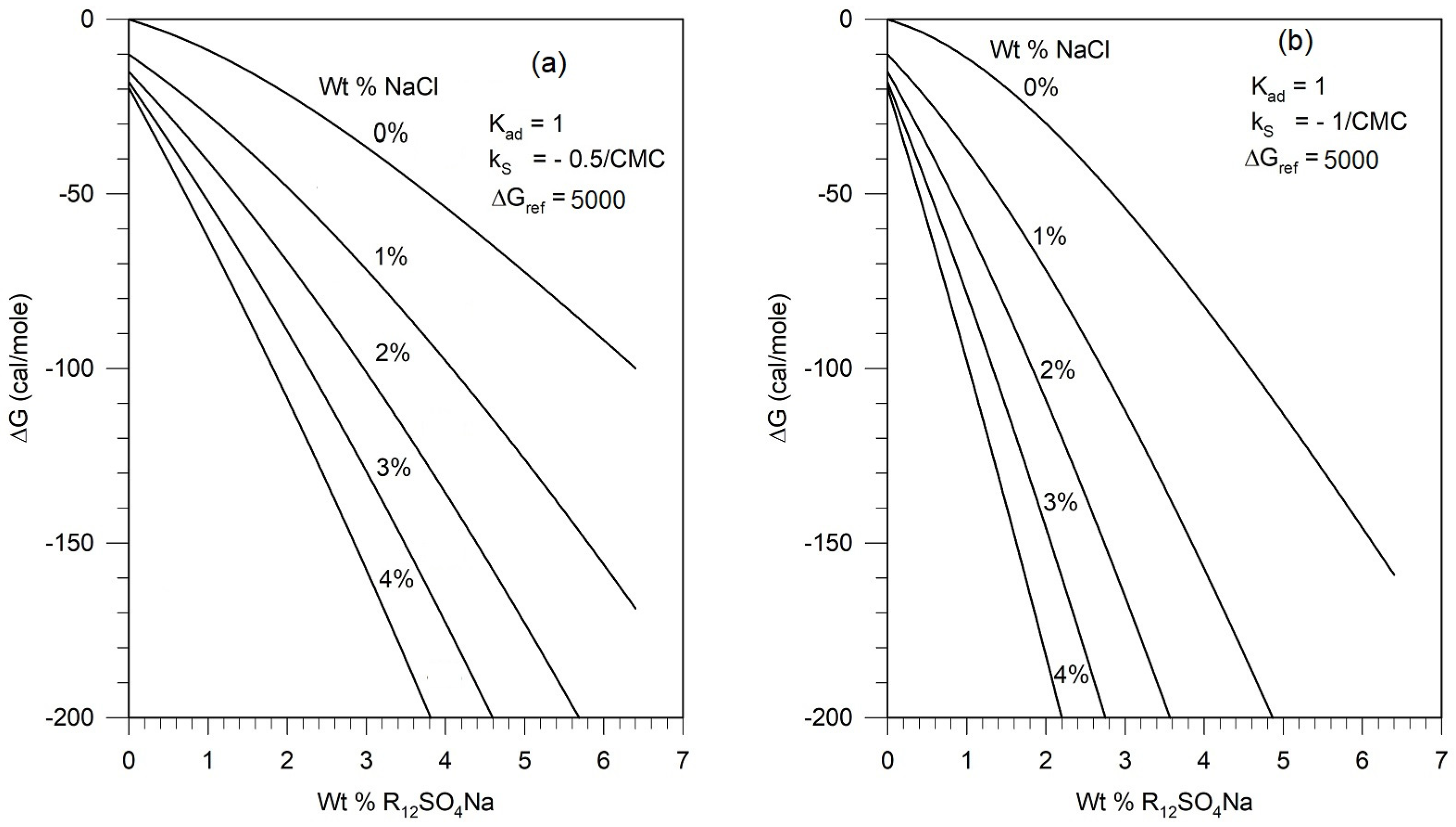
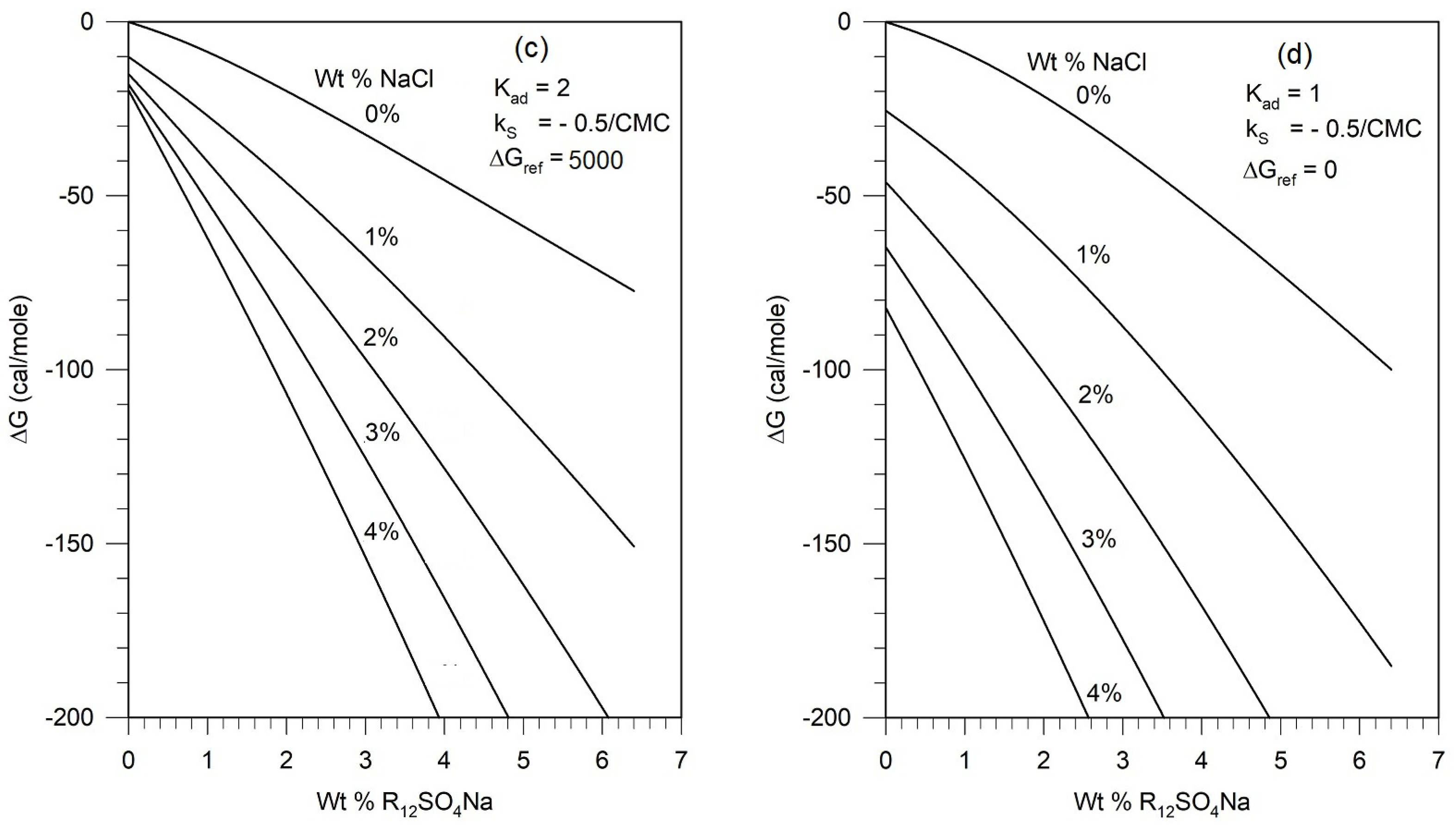
5.4. Assessment of Parametric Sensitivity to Predicted Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Parameter in the equation for the CMC dependence of on chain length |
| a | Parameter in the equation for the CMC dependence on salt concentration |
| a | Parameter defined in Equation (A16) |
| ai | Activity of component i |
| aOH/OH*, aOH*/OH | Wilson interaction parameters between hydrated water and free water |
| B | Parameter in the equation for the CMC dependence of on chain length |
| b | Parameter in the equation for the CMC dependence on salt concentration |
| b12 | Parameter defined in Equation (A17) |
| Ci | Molar concentration of component i |
| CMC | Critical micelle concentration, expressed as molar concentration |
| c12 | Parameter defined in Equation (A18) |
| e | Electronic charge (4.8 × 10−10 esu) |
| G | Free energy |
| Reduced free energy | |
| ΔG | Free energy difference between pseudosolvent and water |
| ΔGref | Correction to free energy change to account for the different reference states for electrolyte ions |
| I | Ionic strength of the solution |
| Kad | Adsorption equilibrium constant for counterion binding |
| k | Boltzmann constant |
| kS | Setschenow constant |
| M | Molecular weight |
| M | Micelle aggregation number |
| mi | Molarity of component i |
| N | Chain length of surfactant tail |
| N | Number of molecules |
| Ni | Number/cm3 concentration of ion i |
| No | Number of vacant lattice sites |
| NA | Avogadro number |
| n | Number of counterions bound to the micelle |
| nC | Hydration number of cation |
| nA | Hydration number of anion |
| ni | Number of moles of component i |
| P | Pressure of system |
| Reduced pressure | |
| Characteristic pressure parameter | |
| Characteristic pressure parameter of component i | |
| Group fraction of group k | |
| R | Universal gas constant |
| ro | Ion size parameter in Equation (9) |
| ri | Number of sites occupied by component i |
| T | Temperature of system |
| Reduced temperature | |
| Characteristic temperature parameter | |
| Characteristic temperature parameter of component i | |
| V | Volume of system |
| V* | Hard-core volume parameter |
| v | Volume per segment |
| Reduced volume | |
| Characteristic lattice site hard-core volume parameter for component i | |
| xi | Mole fraction of component i |
| Mole fraction of component i, including water of hydration | |
| X12 | Variable defined in Equation (A15) |
| Zi | Number of charges on species i |
| Greek Letters | |
| α | Thermal pressure coefficient of polymer |
| α | Degree of counterion dissociation on micelle surface |
| α* | Degree of counterion dissociation on micelle surface at infinite dilution |
| β | Isothermal compressibility of polymer |
| Activity coefficient of the interacting group k in the mixture | |
| Standard state activity coefficient of group k | |
| Activity coefficient of component i | |
| Activity coefficient of component i due to excess entropic contribution | |
| Activity coefficient of component i due to enthalpic contribution | |
| Activity coefficient contribution due to surfactant for component i | |
| Average activity coefficient of surfactant | |
| Total number of fundamental groups in species i | |
| δ | Polymer–solvent binary volume parameter correcting deviation from arithmetic mean |
| δ | Shielding parameter for micelle surface charge |
| Dielectric constant of water | |
| Characteristic energy parameter of solvent (water) | |
| Characteristic energy parameter of pseudosolvent | |
| Characteristic energy parameter of polymer | |
| κ | Inverse Debye length defined in Equation (9) |
| Chemical potential of component 1 | |
| ν | Ratio of characteristic hard-core volumes appearing in Equation (A16) |
| Number of atoms other than H in component i | |
| Number of interacting groups of kind k in component i | |
| ξ | Polymer–solvent binary energy parameter correcting deviation from geometric mean |
| ρ | Density |
| Reduced density | |
| Characteristic density parameter | |
| τ | Ratio of characteristic energies appearing in Equation (A16) |
| Volume fraction of component i | |
| Interaction parameter defined by Equation (A14) | |
| ψ | Parameter defined by Equation (A22) |
| ω | Molecular constant associated with molecular size and flexibility |
| Superscripts | |
| h | Hydration |
| ∞ | Infinite dilution |
| Subscripts | |
| 1 | Water |
| 2 | Polymer while discussing polymer–solvent systems |
| 2 | Counterion of electrolyte |
| 3 | Co-ion of electrolyte |
| 4 | Counterion of surfactant |
| 4S | Counterion of free (singly dispersed) surfactant |
| 5 | Co-ion of surfactant |
| 5S | Co-ion of free (singly dispersed) surfactant |
| A | Anion including associated hydrated water |
| C | Cation including associated hydrated water |
| i | Component i |
| mic | Micelle |
| w | Free water |
Appendix A. Lattice Fluid Theory
Appendix A.1. Equation of State for Pure Fluids
Appendix A.2. Estimation of Equation-of-State Parameters
Appendix A.3. Equation of State for Polymer Solution
Appendix A.4. Estimation of Binary Parameters by Fitting Water Activity
Appendix A.5. Criteria for Phase Stability
References
- Hansson, P.; Lindman, B. Surfactant-polymer interactions. Curr. Opin. Colloid Interface Sci. 1996, 1, 604–613. [Google Scholar] [CrossRef]
- Shah, D.O.; Schechter, R.S. (Eds.) Improved Oil Recovery by Surfactant and Polymer Flooding; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Druetta, P.; Picchioni, F. Surfactant–Polymer Flooding: Influence of the Injection Scheme. Energy Fuels 2018, 32, 12231–12246. [Google Scholar] [CrossRef]
- Druetta, P.; Picchioni, F. Surfactant-Polymer Interactions in a Combined Enhanced Oil Recovery Flooding. Energies 2020, 13, 6520. [Google Scholar] [CrossRef]
- Hamouma, M.; Delbos, A.; Dalmazzone, C.; Colin, A. Polymer Surfactant Interactions in Oil Enhanced Recovery Processes. Energy Fuels 2021, 35, 9312–9321. [Google Scholar] [CrossRef]
- Gradzielski, M. Polymer–surfactant interaction for controlling the rheological properties of aqueous surfactant solutions. Curr. Opin. Colloid Interface Sci. 2023, 63, 101662. [Google Scholar] [CrossRef]
- Trushenski, S.P.; Dauber, D.L.; Parris, D.R. Micellar Flooding—Fluid Propagation, Interaction, and Mobility. Soc. Pet. Eng. J. 1974, 14, 633–645. [Google Scholar] [CrossRef]
- Trushenski, S.P. Micellar Flooding: Sulfonate-Polymer Interaction. In Improved Oil Recovery by Surfactant and Polymer Flooding; Shah, D.O., Schechter, R.S., Eds.; Academic Press: New York, NY, USA, 1977; pp. 555–575. [Google Scholar]
- Szabo, M.T. The Effect of Sulfonate/Polymer Interaction on Mobility Buffer Design. Soc. Pet. Eng. J. 1979, 19, 5–14. [Google Scholar] [CrossRef]
- Pope, G.A.; Tsaur, K.; Schecter, R.S.; Wang, B. Effect of Several Polymers on the Phase Behavior of Micellar Fluids. Soc. Pet. Eng. J. 1982, 22, 816–830. [Google Scholar] [CrossRef]
- Gupta, S.P. Dispersive Mixing Effects on the Sloss Field Micellar System. SPE J. 1982, 22, 481–492. [Google Scholar] [CrossRef]
- Kalpakci, B. Flow Properties of Surfactant Solution in Porous Media and Surfactant-Polymer Interactions. Ph.D. Thesis, Department of Chemical Engineering, The Pennsylvania State University, University Park, PA, USA, 1981. [Google Scholar]
- Sheu, J.-Z. Thermodynamics of Phase Separation in Aqueous Polymer-Surfactant-Electrolyte Solution. Ph.D. Thesis, Department of Chemical Engineering, The Pennsylvania State University, University Park, PA, USA, 1983. [Google Scholar]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Dormidontova, E.E. Role of Competitive PEO-Water and Water-Water Hydrogen Bonding in Aqueous Solution PEO Behavior. Macromolecules 2002, 35, 987–1001. [Google Scholar] [CrossRef]
- Knychala, P.; Timachova, K.; Banaszak, M.; Balsara, N.P. 50th Anniversary Perspective: Phase Behavior of Polymer Solutions and Blends. Macromolecules 2017, 50, 3051–3065. [Google Scholar] [CrossRef]
- Mkandawire, W.D.; Milner, S.T. Simulated Osmotic Equation of State for Poly(ethylene Oxide) Solutions Predicts Tension—Induced Phase Separation. Macromolecules 2021, 54, 3613–3619. [Google Scholar] [CrossRef]
- Bekiranov, S.; Bruinsma, R.; Pincus, P. Solution behavior of polyethylene oxide in water as a function of temperature and pressure. Phys. Rev. E 1996, 55, 577–585. [Google Scholar] [CrossRef]
- Valsecchia, M.; Galindo, A.; Jackson, G. Modelling the thermodynamic properties of the mixture of water and polyethylene glycol (PEG) with the SAFT-γ Mie group-contribution approach. Fluid Phase Equilibria 2024, 577, 113952. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. An elementary molecular theory of classical fluids. Pure fluids. J. Phys. Chem. 1976, 80, 2352–2362. [Google Scholar] [CrossRef]
- Lacombe, R.H.; Sanchez, I.C. Statistical thermodynamics of fluid mixtures. J. Phys. Chem. 1976, 80, 2568–2580. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. An elementary equation of state for polymer liquids. J. Polym. Sci. Polym. Lett. Ed. 1977, 15, 71–75. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical thermodynamics of polymer solutions. Macromolecules 1978, 11, 1145–1156. [Google Scholar] [CrossRef]
- Sanchez, I.C. Statistical thermodynamics of bulk and surface properties of polymer mixtures. J. Macromol. Sci. Phys. 1980, 17 Pt B, 565–589. [Google Scholar] [CrossRef]
- Panayiotou, C.; Sanchez, I.C. Hydrogen Bonding in Fluids: An Equation-of-State Approach. J. Phys. Chem. 1991, 95, 10090–10097. [Google Scholar] [CrossRef]
- Malcolm, G.N.; Rowlinson, J.S. The thermodynamic properties of aqueous solutions of polyethylene glycol, polypropylene glycol and dioxane. Trans. Faraday Soc. 1957, 53, 921–931. [Google Scholar] [CrossRef]
- Kawaguchi, Y.; Kanai, H.; Kajiwara, H.; Arai, Y.J. Correlation for Activities of Water in Aqueous Electrolyte Solutions Using ASOG Model. J. Chem. Eng. Jpn. 1981, 14, 243–246. [Google Scholar] [CrossRef]
- Ronc, M.; Ratcliff, G.A. Prediction of excess free energies of liquid mixtures by an analytical group solution model. Can. J. Chem. Eng. 1971, 49, 825–830. [Google Scholar] [CrossRef]
- Wilson, G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Kojima, K.; Tochigi, K. Prediction of Vapor-Liquid Equilibria by the ASOG Method; Kodansha Ltd.: Tokyo, Japan, 1979. [Google Scholar]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd ed.; Butterworths: London, UK, 1965. [Google Scholar]
- Fowler, R.H.; Guggenheim, E.A. Statistical Thermodynamics; Cambridge University Press: Cambridge, UK, 1949; Chapter IX. [Google Scholar]
- Rosen, M.J. Surfactants and Interfacial Phenomena, 3rd ed.; Wiley-Interscience: New York, NY, USA, 2004. [Google Scholar]
- Burchfield, T.E.; Woolley, E.M. Model for Thermodynamics of Ionic Surfactant Solutions. 1. Osmotic and Activity Coefficients. J. Phys. Chem. 1984, 88, 2149–2155. [Google Scholar] [CrossRef]
- Dauheret, G.; Viallard, A. Activity Coefficients and Micellar Equilibria. I. The Mass Action Law Model Applied to Aqueous Solutions of Sodium Carboxylates at 298.15 K. Fluid Phase Equilibria 1982, 8, 233–250. [Google Scholar] [CrossRef]
- Long, F.A.; McDevit, W.F. Activity Coefficients of Nonelectrolyte Solutes in Aqueous Salt Solutions. Chem. Rev. 1952, 51, 119–169. [Google Scholar] [CrossRef]
- Setschenow, J. Über die Konstitution der Salzlösungen auf Grund ihres Verhaltens zu Kohlensäure. Z. Physik. Chem. 1889, 4, 117–125. [Google Scholar] [CrossRef]
- Deno, N.C.; Spink, C.H. The McDevit-Long equation for salt effects on non-electrolytes. J. Phys. Chem. 1963, 67, 1347–1349. [Google Scholar] [CrossRef]
- Mukerjee, P. Salt Effects on Nonionic Association Colloids. J. Phys. Chem. 1965, 69, 4038–4040. [Google Scholar] [CrossRef]
- Hall, D.G.; Tiddy, G.J.T. Surfactant Solutions: Dilute and Concentrated. In Anionic Surfactants. Physical Chemistry of Surfactant Action; Lucassen-Reynders, E.H., Ed.; Marcel Dekker: New York, NY, USA, 1981; Chapter 2. [Google Scholar]
- Corrin, M.L.; Harkins, W.D. The effect of salts on the critical concentration for the formation of micelles in colloidal electrolytes. J. Am. Chem. Soc. 1947, 69, 683–688. [Google Scholar] [CrossRef] [PubMed]
- Rosenholm, J.B. Critical evaluation of models for self-assembly of short and medium chain-length surfactants in aqueous solutions. Adv. Colloid Interface Sci. 2020, 276, 102047. [Google Scholar] [CrossRef] [PubMed]
- MacNeil, J.A.; Ray, G.B.; Sharma, P.; Leaist, D.G. Activity Coefficients of Aqueous Mixed Ionic Surfactant Solutions from Osmometry. J. Solut. Chem. 2014, 43, 93–108. [Google Scholar] [CrossRef]

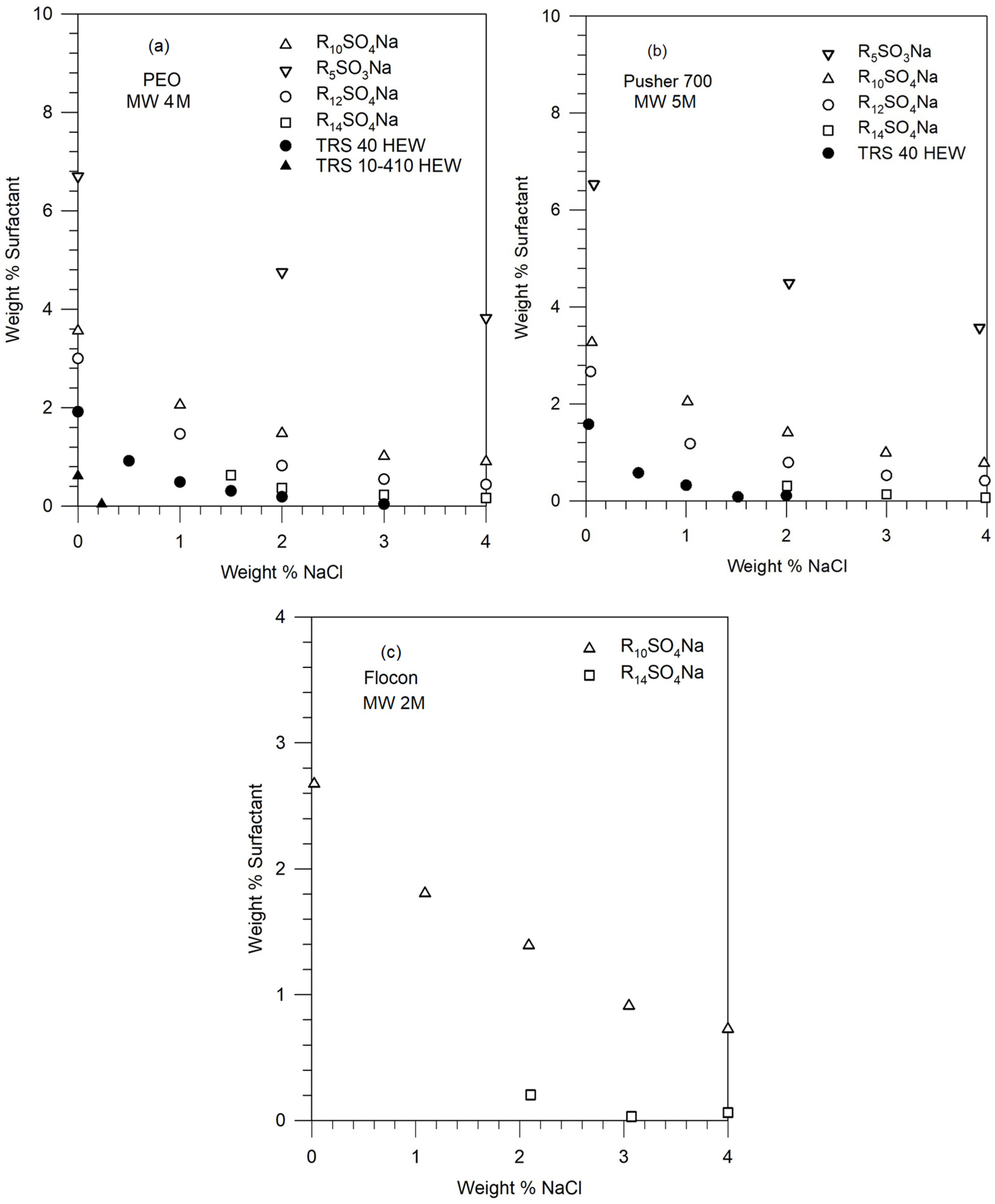
| Polymer | MW | Commercial Name | Supplier |
|---|---|---|---|
| Partially hydrolyzed Polyacrylamide | 5 × 106 | Pusher 700 | Dow Chemical Co. |
| Polyethylene oxide | 4 × 106 | PEO | BDH Chemical Ltd. |
| Biopolymer Xanthan | 2 × 106 | Flocon | Pfizer Chemical |
| Surfactant | Structure | EqWt | Supplier |
|---|---|---|---|
| Sodium pentylsulfonate | CH3(CH2)4SO3Na | 174 | Fisher Scientific |
| Sodium decyl sulfate | CH3(CH2)9SO4Na | 260 | Pfaltz & Bauer |
| Sodium dodecylsulfate | CH3(CH2)11SO4Na | 288 | BDH Chemical |
| Sodium tetradecylsulfate | CH3(CH2)13SO4Na | 316 | Pfaltz & Bauer |
| TRS 40 HEW | CH3(CH2)10C6H4SO3Na | 334 | Witco Chemical |
| TRS 10-410 HEW | CH3(CH2)17C6H4SO3Na | 436 | Witco Chemical |
| Ion | Hydration Number |
|---|---|
| Li+ | 1.8 |
| Na+ | 1.0 |
| K+ | 0.4 |
| Mg2+ | 3.6 |
| Ba2+ | 1.9 |
| Ca2+ | 3.1 |
| Ni2+ | 3.2 |
| Fe2+ | 3.1 |
| I− | 1.0 |
| Br− | 0.8 |
| Cl− | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheu, J.-Z.; Nagarajan, R. Predictive Approach to the Phase Behavior of Polymer–Water–Surfactant–Electrolyte Systems Using a Pseudosolvent Concept. Colloids Interfaces 2024, 8, 40. https://doi.org/10.3390/colloids8040040
Sheu J-Z, Nagarajan R. Predictive Approach to the Phase Behavior of Polymer–Water–Surfactant–Electrolyte Systems Using a Pseudosolvent Concept. Colloids and Interfaces. 2024; 8(4):40. https://doi.org/10.3390/colloids8040040
Chicago/Turabian StyleSheu, Ji-Zen, and Ramanathan Nagarajan. 2024. "Predictive Approach to the Phase Behavior of Polymer–Water–Surfactant–Electrolyte Systems Using a Pseudosolvent Concept" Colloids and Interfaces 8, no. 4: 40. https://doi.org/10.3390/colloids8040040
APA StyleSheu, J.-Z., & Nagarajan, R. (2024). Predictive Approach to the Phase Behavior of Polymer–Water–Surfactant–Electrolyte Systems Using a Pseudosolvent Concept. Colloids and Interfaces, 8(4), 40. https://doi.org/10.3390/colloids8040040





