Nanosized Being of Ionic Surfactant Micelles: An Advanced View on Micellization Process

Abstract

An advanced model of ionic surfactant micellization has been developed. The structural and kinetic properties of micelles were analyzed in parallel from a universally accepted point of view and taking into account the principles of quantum mechanics, the phenomenon of ion pairing in the Stern layer, the symmetry considerations, and the chaos theory. It was shown that a micelle can be considered as a layered fullerene-like structure with a cavity in its center, possessing the solid-like properties of micelles in radial directions and the liquid-like properties in the perpendicular ones, allowing for water penetration between the surfactant head group and nearby methylene groups. The dimensions of the minimal fullerene-like structure formed by the terminal hydrogen atoms of surfactant methyl groups around the central cavity, unable to be occupied by surfactant tail fragments, were estimated. It was indicated that permanently occurring surfactant self-organization/disintegration needs a probabilistic description and revision of processes occurring in micellar systems built by ionic surfactants. It was noted that the probabilistic approach alters the mechanism of colloidal dissolution of hydrocarbon compounds and their solubilization by micelles. The advanced model proposes the same macroscopic properties of micelles as the classical one but modifies the structural characteristics of micelles on the nanoscale.

1. Introduction

Despite the long, more than centennial, history of colloid science, it is actively developing at present [1,2]. Many of the available practical applications of surfactants are developed and operated well within the classical framework of surfactant micellization. However, over the past century, there have been fundamental renovations in many scientific fields, particularly related to the use of nanosized ideology in the self-organization processes, which are not limited only by the systems containing nanoparticles. Self-organization is naturally inherent to many biological systems built from amphiphilic molecules. The most convenient system to model and study different aspects of molecular self-assembly is the water solution of ionic surfactants, joining the amphiphilic and charge states of interacting molecules. Information about the driving forces, the mechanisms causing the emergence of ordered nanostructures at the molecular level, and the phenomena occurring inside and near such systems is still very incomplete. The existing micellization models are based on a quasi-chemical approximation, in which the process of surfactant self-association is considered as a reversible chemical reaction, or on the principles of nucleation theory. However, such empirical backgrounds are not complete and often bring unexplained contradictions between different experimental data.

Micelles arising in ionic surfactant solutions are nanosized supramolecular objects [3] that have no classical analogues. Historically, the term “micelle” itself has proven to be ambiguous. This term, introduced to describe an electrically neutral particle consisting of self-organized surfactant ions surrounded by counterions distributed in the diffuse layer bulk, is often used in relation to the micellar core (micellar particle). Taking this circumstance into account, we will also use the designation “micelle” for the central part of the micellar structure. Additional confusion is caused by the tendency to generalize processes occurring with ionic and nonionic surfactants, despite the fundamental differences between them, and to refer to associates of nonionic surfactants (which are not considered further) by the same term, “micelle”. Despite the existence of common properties in ionic micelles and nonionic associates at the macroscale, at the nanoscale, there is a sharp difference in the properties of ionic micelles compared with conventional conceptions, which is manifested in the discrepancy between the sizes, driving forces, electric fields, and types of kinetic units. The presence of ions stipulating the existence of ionic processes leads to the difference in kinetic processes occurring in solutions.

The ambiguity of micelles is also manifested by their properties. In particular, micelles cannot be attributed to either solid or liquid particles [4]. Moreover, they cannot even be assigned a single specific size since one cannot unambiguously determine the position of the micelle/water interface. Some counterions, rigidly bound to the micelle core, also take part in forming a united micellar aggregate. Other counterions are located in the micelle aqueous shell, which moves with the micelle as an indivisible hydrodynamic object of its own size. Some experimental techniques in addition to these parameters use another micelle dimension, namely the size of the micelle hydrocarbon core.

It is known that upon an increase in surfactant concentrations above the critical micelle concentration (CMC), ionic micelles permanently disintegrate and rehabilitate again, with their lifetime known as 10⁻⁴–1 s [5,6]. Despite the permanent counter processes of the disintegration and formation of micelles, their average number in a unit of time remains approximately constant. Thus, micellar solutions are microheterogeneous, two-phase, and nonequilibrium at the nanoscale due to the permanent processes of self-assembly and the disintegration of micelles. At the same time, micellar solutions are homogeneous, single-phase, and thermodynamically stable systems at the macroscale [7].

This is probably the reason that the long-term course of colloid chemistry, formulated on the basis of classical concepts, did not result in new ideas on the micelle dynamical structure. Only recently [8], researchers settled that “quantum mechanics and quantum coherence play a central role in chemistry,” and play an important role in the functioning of biological structures [9,10]. Investigations of the quantum properties of water and aqueous environment of micelles [11,12,13] led to the opinion that nanosized micelles should be described as quantum nanoparticles. Therefore, we are interested in why a system consisting of micellar nanoparticles with no classical analogues is still described only from classical positions. Do we lose sight of any features inherent in such systems at the nanoscale or at the femtosecond time scale corresponding to quantum coherence [14,15,16]? Perhaps now is the time to reconsider and to complement some existing concepts of self-organization processes, taking into account processes that are ignored by conventional approaches. The cooperative self-assembly of ionic surfactants in micellar solutions, when highly symmetric linear alkane hydrocarbon chains are synchronously combined into a spherical ionic micelle, indicates that micelles have the quantum coherence properties that are displayed in the coordination of ion movements. This process can be compared with characteristic coherence times (~10⁻¹³ s) [14,15,16]. From a classical point of view, such a time scale allows one to consider it as occurring almost instantly.

In this work, we attempted to discuss an advanced phenomenological model of ionic surfactant micellization, in which some structural and kinetic aspects are analyzed qualitatively, based not only on the well-known micellization concepts but also using the trends of modern science. Analyzing new aspects of the micelle structure, we used the following assumptions: (1) a micellar particle exists in a highly concentrated ionic environment formed by dissociated surfactant ions and counterions, which are partially free or bound into ion pairs; (2) the micellization of ionic surfactants should not contradict the principles of quantum mechanics; (3) micellar surfactant solutions are nonequilibrium at the nanoscale and, therefore, the theory of self-organization in nonequilibrium processes (chaos theory) can be applied to their description. The need for a probabilistic description of processes in surfactant micellar solutions, which is required by both these theories, and the symmetry considerations also make their own adjustments to the description of ionic surfactant micellization.

The obtained results exceeded all our expectations, giving fundamental explanations for many of the previously known experimental facts, and led to an unexpected consequence: the fullerene-like structure of spherical micelles can explain the existence of a cavity in the micelle center. In addition, the quantum properties and nonequilibrium of micellar systems on the nanoscale indicated the need to reconsider many processes occurring in micellar systems.

It should be noted that the accuracy of the obtained results is primarily determined by the correctness of the initial assumptions. Assumption 1 has long ceased to be exotic. Aqueous solutions of electrolytes are characterized by permanent processes of dissociation, association, and hydration of ions, as a result of which various ionic complexes are formed and disintegrated [17]. Similarly, Assumption 3, that “micelles themselves are continuously disintegrating and reforming” and have a lifetime comparable to part of a second, was not only confirmed experimentally but is also an important technological property of surfactants that determines foaming [5,6]. Note that only Assumption 2 is new. It actually postulates the existence of quantum properties in micelles, which seems intuitively correct, but there is no direct evidence for this, since no one knows how to calculate the possible states of micelles due to the large number of atoms involved in their structure. However, experimental evidence indicating the presence of quantum properties in massive symmetrical nanosized objects of another class, comparable in mass and number of atoms, was demonstrated in [18,19].

2. Conventional Model of Ionic Micelle Structure

To understand the preference of proposed principal modifications, it is necessary to consider the conventional model of the ionic micelle structure, which is the averaged version of its different variants. Unfortunately, the existing definitions and designations of the micelle basic structural components are confusing in many models, terms, and scales. It concerns the existence of different structural definitions [20,21,22] and conflicting experimental data on the size (morphology) of micelles, clearly seen in the case of mostly representative ionic surfactant sodium dodecyl sulfate (SDS) [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. For example, the definition of the radius of the micelle core (micellar particle) is still not completely determined.

The current classical concept of the micelle structure, containing the long-chain hydrophobic alkyl groups (with 8–18 C atoms) and charged head groups, can be formulated as follows. When the concentration of an ionic surfactant increases to some special value named CMC, the definite number of surfactant molecules (usually 50–100), called N_agg, self-associates into nearly spheroidal aggregates with radius R_agg. The inner part of the aggregate with radius R_hc is formed by the hydrophobic hydrocarbon radicals of surfactant ions (Figure 1). The structure of the hydrocarbon core is the same for anionic and cationic surfactants. The polar head groups of ionic surfactants form a charged shell, containing a certain number of bound water molecules, faced to the bulk aqueous medium [40,41,42,43,44]. Despite the fact that the micelle hydrocarbon core is almost completely free of water molecules, each hydrocarbon chain segment spends time near the micelle surface, contacting with the outer hydrophilic part of the micelle [40].

The maximal charge of the micellar aggregate q_ag = ±eN_agg (positive for cationic surfactants and negative for anionic ones) determines its surface potential Ψ(R_agg). However, some counterions adsorb onto a boundary of the shell with surfactant head groups, forming the Helmholtz layer. The adsorption of counterions results in the partial compensation of the micelle aggregate charge, up to the value of the micellar particle charge q_mic = ±αeN_agg, where α is the degree of the micelle ionization and e is the elementary electric charge. It should be noted that, in the classical model, the counterions of the Helmholtz layer do not bind directly to surfactant head groups. They are adsorbed onto the inner boundary of the Helmholtz layer. The adsorbed ions are allowed to move along the Helmholtz layer, participating in processes of surface diffusion.

The Helmholtz ionic monolayer is separated from the subsequent diffuse layer by another hypothetical boundary called the Stern plane [43,45]. The shell, restricted by the Stern plane, contains the surfactant head groups, adsorbed counterions, and bound water. It was noted [46] that a significant number of counterions are associated with the micelle surface and constitute an integral part of the micelle as the kinetic unit. The Helmholtz layer is often called the Helmholtz–Stern layer or sometimes simply as the Stern layer. The aggregate of surfactant ions with adsorbed counterions forms a micelle particle with radius R_mic (Figure 1), which is known as the solid-like micelle core [4,47,48]. The electric charge of micellar particle ±αeN_agg stipulates its Stern electric potential Ψ(R_mic). Actually, the R_mic value is determined by the length of surfactant ions, to which the size of adsorbed counterions must be added. It should be underlined that the composition of solid-like particles of the dispersed phase in the liquid dispersion medium must include the adsorbed counterions rigidly bound to this particle; i.e., the adsorbed counterions are also part of the dispersed phase. Therefore, the notions of the micelle particle and micelle core should be identical. The remaining counterions are distributed in the bulk aqueous phase, comprising the so-called diffuse part of the double layer or the micelle ionic atmosphere. As a whole, the ionic micelles are electrically neutral.

In addition to the considered conventional conceptions of the ionic micelle structure, there are also the modified models of the micelle morphology, e.g., the Stern–Graham model [49], with two separated adsorption layers: (1) the next after the micelle aggregate is the Helmholtz ionic monolayer with rigidly adsorbed dehydrated counterions, and (2) the subsequent layer with hydrated counterions, bound to the micelle core and occupying several interatomic distances. In this case, the layer with hydrated counterions is called the Stern layer, and its boundaries are named the inner and outer Stern planes (Figure 1).

The diffuse part of the double ionic layer is formed due to the thermal motion of counterions in the attractive electrostatic field of charged micellar particles, which aims to equalize the counterion concentration in bulk solution [43,50]. The water stratum, located immediately after the Helmholtz layer, is bound rather rigidly to the micelle core and has increased local viscosity. As a result of the hindered orientation mobility of water, the permittivity of this aqueous domain is sufficiently small.

Under the impact of some external physical forces (e.g., of electric, magnetic, acoustic nature) or under the ordinary thermal Brownian motion, the micelle double ionic layer can be broken. The interface, which separates the mobile fluid from its fraction, bound to the micelle surface, is called the slipping (shear) plane. Its radius determines another characteristic dimension of micelles, named the micelle hydrodynamic radius R_ζ, which is often rated as the micelle size (Figure 1). In [22], regarding the example of sodium dodecyl sulfite (SDS), we calculated the electric potential decay of dispersed-phase particles and determined the dimension parameter, which corresponds approximately to the micelle hydrodynamic radius. The results of these theoretical calculations were compared with our previous experimental data on the thickness of the SDS micelle hydrophilic layer obtained by SAXS [39]. It was found that the slipping plane, located near the outer Stern plane, is separated from it by only a few molecular layers of water. The results of this work show that a micelle is not something soft and watery but a more solid-like particle than was traditionally considered.

3. Advanced Model of Ionic Micelle Structure

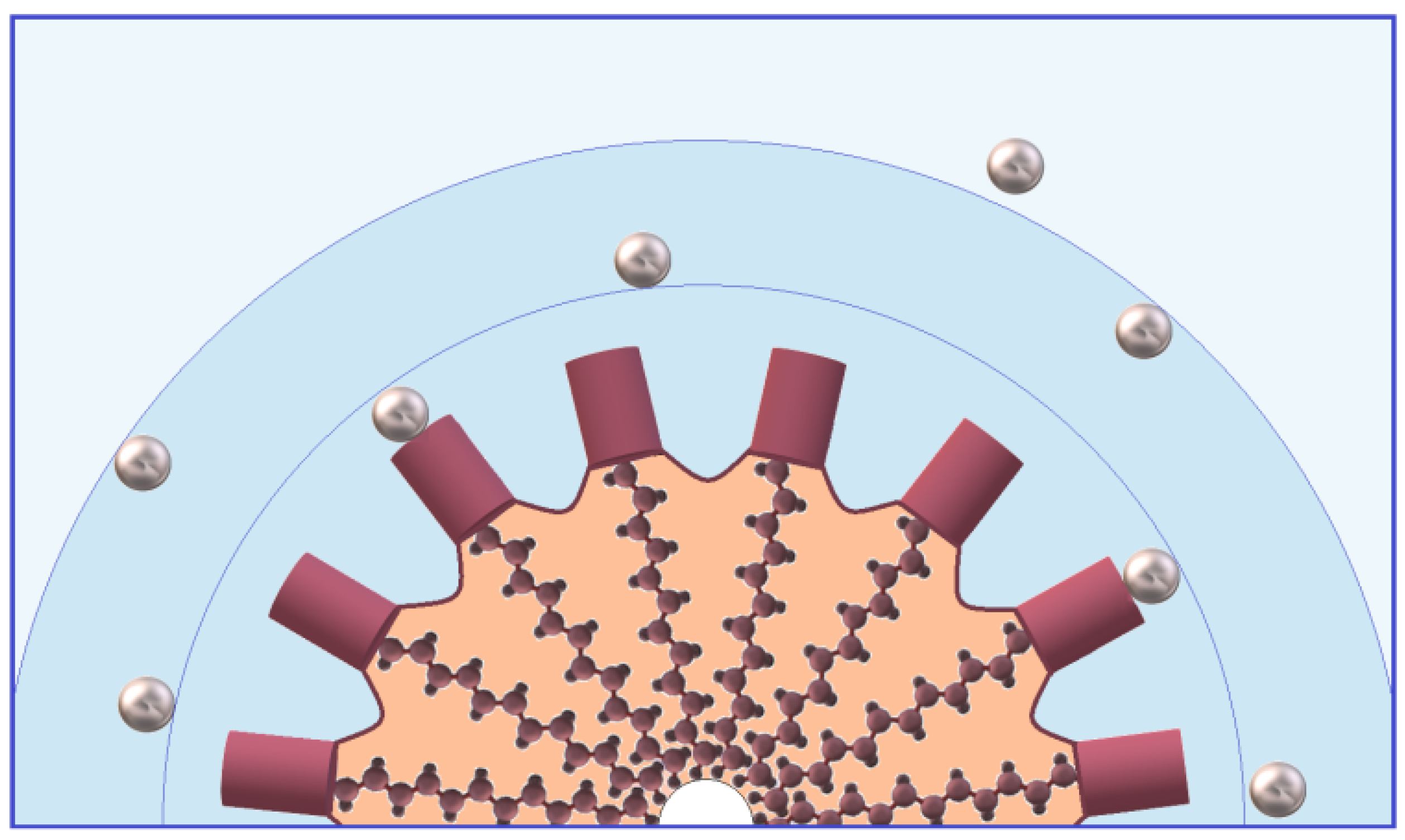
3.1. Hydrocarbon Core–Water Interface in Micelle

The surfactant micelle is a typical nano-structural particle [3,51]. The micelle core is always surrounded by highly concentrated ionic solution formed by dissociated counterions. This phenomenon is not taken into account by conventional models of micelles. The basic ionic processes taking place in the Stern layer at the interface between the micelle core and water medium are ion dissociation, association, and hydration, resulting in the formation and disintegration of various ionic complexes. Examples of ion association are contact ion pairs, solvent-shared ion pairs, and solvent-separated ion pairs, when ions retain their hydration shells [18]. Ion pairing, which occurs due to Coulomb attraction without covalent bonding, is found to occur for many solutions of inorganic and organic salts [52,53,54,55,56,57], interfaces of micelles [58,59], and biomolecular systems [60,61].

In conventional micellar models, the presence of ions and the existence of ion association of various degrees were addressed in [62]. To some extent, these facts were taken into account in a slightly modified model of the micelle structure [63], in which a decrease in the total charge of the micelle was described as the consequence of incomplete dissociation or ion pair formation. The close hypothesis was proposed by other authors [64], which showed that charged head groups and counterions, located in the Stern layer, form solvent-shared ion pairs, somewhat discriminating and overlapping their hydration shells.

The possible complexation of ions requires the modification of the structural model for surfactant micelles. In our advanced model, along with dissociated surfactant ions, their associates with ions should also be considered as constituent units forming the micelle core. Associates are the complexes of surfactant ions and counterions, bound both in contact ion pairs and in solvent-shared or solvent-separated ion pairs. The composition of micelles can also include complexes in which a surfactant ion, depending on the sign of its charge, binds to H⁺, H₃O⁺, OH⁻, etc. [65]. These complexes are disintegrating and restoring again with different surfactant ions in the micelle. The lifetime of these complexes is short. It is known that in solutions of inorganic salts, three relaxation times are observed, corresponding to three types of ion pairing. All of them are found in the picosecond range [54]. For bioorganic molecules, the transitions between states occur on a pico-to-nanosecond timescale [61]. In micellar solutions, at least one relaxation process with relaxation time about 10⁻¹⁰ s was detected [59]. The averaging of fast processes leads to inalterability in the micelle charge. The inclusion of dynamic exchange processes is the main difference in the proposed model.

The structure shown in Figure 2 can be used as a convenient 3D model, which assists in the visualization of the aggregation of surfactant ions into spherical micellar particles above CMC. Such fullerene-like structures with protruding fragments are quite popular now to explain the structure of viruses, including COVID-19 [66]. To visualize micelle layers in contact with aqueous pseudophase, the protruding parts are shown, symbolizing the head groups of surfactant. The real shape of head groups is determined by their chemical nature and can differ.

Thus, the spherical region in Figure 2 corresponds to the micelle hydrocarbon core with radius R_hc. Protruding parts, exserted from the micelle hydrocarbon core, show surfactant head groups. The micellar particle is surrounded by a water shell up to the hydrocarbon surface. The corresponding calculations are given in Section 3.5.

Grey balls coupled with protruding parts symbolize counterions and charged groups of various natures (H⁺, H₃O⁺, OH⁻, etc.) bound to surfactant head groups in the form of contact ion pairs. The real arrangement of counterions is determined by the chemical nature of the surfactant head groups, their possible orientation in space, and the quantum nature of chemical bonds, allowing for the existence of several most probable positions for counterions. The maximum radius of the micelle that includes contact ion pairs defines the geometric boundary R_mic of the dispersed-phase particle, which can also be called a micellar particle or micelle core (Figure 2). Ion pairing can occur in both radial and various lateral directions, leading to variations in the size of micellar particles depending on external conditions.

This proposed model presumes the possibility of counterion exchange between the micellar particle and solution, during which the contact ion pairs can be destroyed or created again in the dissociation/association processes. In the Stern layer, which occupies several molecular layers outside the dispersed-phase particle, the hydrated counterions are localized, bound both in contact ion pairs and in solvent-shared or solvent-separated ion pairs. Due to the exchange of a counterion with the bulk of the solution, the thickness of the shell of bound counterions, the degree of counterion binding to the micelle, and its charge can alter depending on the surfactant concentration, added electrolyte and temperature, resulting in processes observed in experiments. The untied hydrated counterions are located outside the outer Stern plane, forming an ionic micelle atmosphere.

The incomplete correspondence of classical theoretical concepts to the known experimental data has resulted in attempts to separate the micelle adsorption layer into two parts: the Helmholtz monolayer with dehydrated counterions and the Stern layer, enriched by hydrated counterions and propagating into several molecular layers (Stern–Graham model [46]). In the proposed model, such details are not necessary to introduce artificially [67,68]. In micellar particles, the surfactant ions, bound as contact ion pairs, determine the inner Stern plane (surface) and the radius of the micellar particle R_mic (Figure 2). In the advanced model, the radius of the ionic micellar particle is a natural concept, as can be seen from Figure 2.

The outer boundary of the Stern layer is determined by surfactant ions coupled to solvent-separated ion pairs. The orientation of molecules in this surficial layer, including water, is strictly limited by the micelle environment [11,12,13]. The quantum nature of ion complexation suggests the existence of cooperative phenomena, leading to the formation of an aqueous “pseudophase”, in which special conditions for various chemical processes are created. According to [13,65,69,70,71], the “pseudophase” is a concentrated mixture of hydrocarbons, electrolytes, and water, with unique structural and chemical properties that differ from the bulk properties of solvents. Analyzing Figure 2, we can conclude that the aqueous pseudophase captures not only the Helmholtz–Stern layer but a significant part of the shell layer containing surfactant head groups and also some regions geometrically corresponding to the hydrocarbon core. Figure 3 shows a comparative view of the pseudophase region for traditional (A) and advanced (B) models. These models will be discussed in detail in the next section. Note that the conception of head groups for traditional model corresponds to [40,42], while for our advanced one, another representation was chosen only for reasons of simplicity and clarity.

Taking into account that the relaxation times of ion dissociation/association processes are located in the pico- and nanosecond range, during the micelle lifetime (10^–4–1 s [5,6]), each surfactant head group can be found many times, both in compositions of various complexes and in completely dissociated states. The averaging over a time comparable to the micelle lifetime corresponds to a state with a high degree of symmetry. In fact, a micellar particle of radius R_mic, having a charge q_mic = ±αeN_agg, distributed over its surface (inner Stern surface), determines the Stern electric potential Ψ(R_mic) of this particle. Substantially, Figure 2 correlates with Figure 1, providing an instantaneous 3D micelle image, while Figure 1 corresponds to the time-averaged micelle structure. Thus, the accounting of possible dynamic processes leads to the greater specification of observed micellization, rather than the replacement of representations.

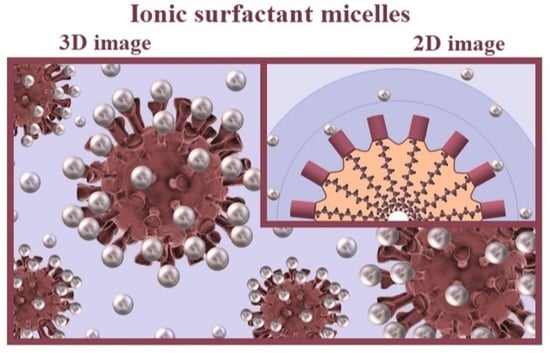
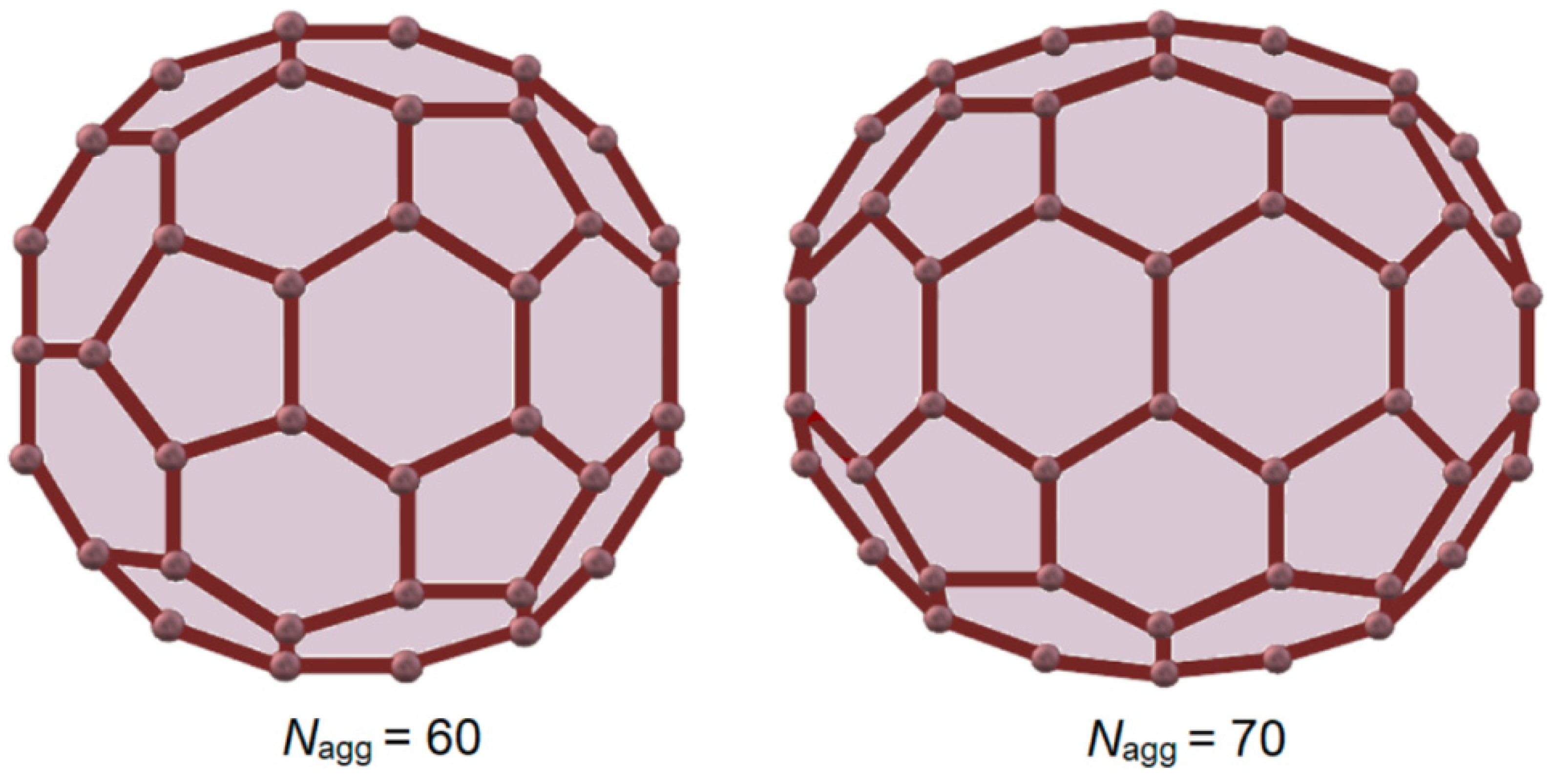
3.2. Fullerene-like Micelle

The typical aggregation number of surfactant ions in surfactant micelles of various surfactants (at concentrations slightly exceeding CMC) is close to 60 [40]. This means that 60 charged head groups of surfactant ions and at least 60 carbon atoms neighboring to head groups must be in appropriately equivalent positions at the same distance from their nearest selfsame neighbors. This principle is realized in the well-studied symmetry of a truncated icosahedron (C₆₀ fullerene symmetry). This symmetry makes it possible to visualize the micelle hydrocarbon core geometry (Figure 4). Carbon atoms, neighboring surfactant head groups, in micelles with aggregation number N_agg = 60 can form a fullerene-like structure, in which there are 32 faces (20 hexagons and 12 pentagons) per 60 absolutely equivalent vertices. This fact also allows us to draw certain conclusions. For example, the number of molecules of short-chain alcohols that can incorporate into micelles as small cosurfactants was roughly estimated as one alcohol molecule per one surfactant ion [72,73]. At the same time, the fullerene geometric model suggests that only face centers of the fullerene-like structure may be the sites of optimal binding. The symmetric arrangement of introduced cosurfactant molecules is a result of the symmetric compensation of intermolecular interactions in the systems formed from identical molecules, even though these molecules are of two different types (surfactant and cosurfactant). As a result, cosurfactant molecules occupy a place that is maximally distant from all nearest neighbors. Taking into account the symmetry considerations, this arrangement corresponds to the face centers of the formed spatial structure. Therefore, the micelles with N_agg = 60 have only 32 optimal sites for the incorporation of alcohol or cosurfactant molecules into the micelle structure, i.e., almost two-times less than the previously assumed amount.

Similar considerations allow us to assume the presence of at least 32 water molecules in the surface layer containing head groups. A more accurate calculation, which takes into account the size of the water molecule (2.8 Å), gives a three-fold greater value for one water layer. Depending on the size of the head group, there may be two or even more layers. The possible deflection of face surfaces of fullerene-like structure with radially rigid (will be explained in Section 3.6.4) diverging hydrocarbon chains, between which the regions with a reduced density are formed, also allows us to assume the penetration of water into the upper hydrocarbon layers under external water pressure (Figure 3). Thus, surfactant head groups are surrounded on almost all sides by water belonging to the Helmholtz–Stern pseudophase layer. Moreover, when averaging over fast-rate processes, it seems that the upper hydrocarbon layer, indicated in yellow in Figure 3B, contains water. This feature of our model is in agreement with the data from [67], in which an analysis of water dielectric relaxation processes showed that water molecules are found in the upper layers of micelles. It should be noted that assumptions about the possibility of water penetration into the hydrocarbon core have been made earlier [74,75], forming a basis of the “fjord model”, in which water penetrates up to the micelle center.

Figure 3 shows a schematic arrangement of the micelle zones near the hydrocarbon core/shell/water interface, allowing one to evaluate the features and similarities of both models. Note that the shape of head groups is determined by the surfactant chemical nature. In the region near the hydrocarbon core/shell/water interface, the main differences between models are due to the following factors:

(1)

The traditional model is static in nature. The advanced model introduces the association–dissociation processes of head groups with times comparable to 10⁻¹⁰ s.

(2)

In the classical model, the adsorbed ions are allowed to move along the Helmholtz layer, participating in the processes of surface diffusion. In the advanced model, this process is also possible but most likely indirect. The above estimations of the distance between adjacent head groups indicate the existence of water-filled space between head groups. The discontinuity of contact ion pairs, even if located on the lateral side of the head group surface, will not lead to the creation of a similar pair on an adjacent head group due to the large distance and presence of water molecules. However, a similar process involving solvent-shared ion pairs may well take place.

(3)

The possible deflection of faces of the fullerene-like structure (Figure 3B) leads to the intricate shape of the hydrocarbon core surface and increased pseudophase volume and allows us to explain the penetration of water into the upper hydrocarbon layers.

3.3. Aggregation Number of Surfactant Ions in Micelle

As noted above, many surfactant solutions near CMC are characterized by the presence of micelles, with an aggregation number close to 60. Therefore, to model the micelle structure, formed by 60 surfactant ions, the mathematical principles of truncated icosahedron symmetry (symmetry of fullerene C₆₀) can be applied. So far, as truncated icosahedron symmetry is the characteristic of carbon clusters of fullerene C₆₀, some additional conclusions can be drawn from the study of these clusters. In particular, since the most stable, widespread, and easily synthesized fullerene molecule is C₆₀, one can assume that a micelle formed by 60 surfactant ions is the most stable and widespread for surfactant self-organization near CMC. This assumption is based on the commonality of symmetry properties in space. Note that the probability of polydispersity in the micelle aggregation number is not rejected. However, it is believed that of all the micelles formed, the micelles with an aggregation number of 60 are the most stable and, accordingly, the most long-living. The variability in the aggregation number is inherent in the mechanism of the micelle formation.

The ionic surfactant solution above CMC is characterized by permanent ongoing processes of the self-association of surfactant ions into micelles and their disintegration [5]. Classical theory cannot describe the corresponding processes associated with quantum coherence. Micellar solution at the nanoscale can be considered a nonequilibrium system, to which the theory of self-organization in nonequilibrium systems (the chaos theory) can be applied [76,77,78]. A characteristic feature of the chaos theory is the exponential sensitivity of systems to small perturbations [79], the consequence of which should be the simultaneity of processes of the micelle disintegration/self-association at times ~10⁻¹³ s, which is much shorter than the micelle lifetime. Therefore, we can assume the following mechanism of processes occurring in surfactant solution. The internal thermal fluctuations or appearance of individual surfactant ions near micelle can break the symmetry of the micellar particle or its environment and lead to micelle disintegration. It should be noted that a charged particle built of ionic surfactant (unlike the nonionic one), in principle, cannot be incorporated into the structure of charged micelle having the same sign, since its penetration into the micelle requires overcoming the Coulomb repulsive forces, which create a huge potential barrier. In addition, the exchange of amphiphilic ion to/from micelles is also impossible because it violates the micelle symmetry.

During micelle disintegration, an excess concentration of surfactant ions in solution stimulates the formation of new micelles. In the presence of such processes, the lifetime of surfactant ions in micelles cannot differ from the micelle lifetime. The theory of self-organization in nonequilibrium systems rejects the possibility of the quasi-chemical approach to the micellization of ionic surfactants, which requires the stepwise addition of surfactant ions to the micelle. Really, the alteration in the micelle structural organization (change in aggregation number) can occur only due to their disintegration/self-organization, which means that the micellization process cannot be considered an ordinary chemical reaction.

Another consequence of the chaos theory [76,77,78] is the appearance of long-range correlations in systems characterized by nonequilibrium and self-organization. The particles located at macroscopic distances from one another cease to be independent. The existence of correlations leads to the appearance of “quasi-crystalline” micellar structures [39]. In addition, the permanently occurring processes of self-organization of surfactant ions into micelles and their disintegration require a probabilistic description.

In the micellization process, micelle self-assembly with different aggregation numbers can occur, but the probabilities of certain structures and their lifetime will be different. Accordingly, the average (observed) aggregation number depends on the relative contributions of all emerging structures. Since micelles are very symmetrical structures, obeying quantum mechanical principles, one should propose their formation in the same structural forms as fullerenes. To date, fullerene-like structures with an even number of atoms (20, 28, 42, 52, 58, 60, 70, 76, 78, 80, 82, 84, 90, 92, 94, 96, 98, 100...) have been experimentally discovered [80]. States with an odd number of constituent units apparently contradict the system symmetry and, therefore, cannot be realized, being an additional argument explaining the impossibility of the quasi-chemical approach, which considers the one-by-one addition of surfactant ions to micelles. The most stable and frequently observable fullerene-like structures are the structures of C₆₀ and C₇₀ types. The C₇₀ structure (Figure 4) differs from the C₆₀ one by five additional hexagons in the equatorial plane with a slight change in the micelle shape towards ellipsoidal due to the elongation of one symmetry axis. These two structures will make the main contribution to the micelle composition near CMC, where micelles remain almost spherical. However, the probabilities of their appearance for different surfactants will differ, as well as the radii of micelles, which will depend, first of all, on the length of their hydrocarbon chains.

An increase in the surfactant concentration leads either to growth in the concentration of spherical micelles or to a change in the micelle shape to ellipsoidal, and then to spherocylindrical and cylindrical, and the increment in micelle length is not accompanied by a variation in its transverse size [81,82,83,84]. In the described model, such transformations, which also depend on the external electrolyte concentration and temperature, can be explained by the possible appearance of micelles with elongated fullerene-like structures with additional inserts in the equatorial plane, each of which adds another 5 hexagons and 10 vertices. Thus, along with the C₆₀ and C₇₀ structures, more and more elongated fullerene structures appear, such as C₈₀, C₉₀, C₁₀₀, etc., with the same transverse dimension. Experiments showed that all alterations in micelle sizes were associated only with a change in major semi-axis length, while the minor semi-axes remained constant, indicating the transition of micelles from a spherical to rod shape [81,82,83,84]. The appearance of cylindrical micelles results in an energetically favorable decrease in the particle number in solution and increase in the average distance between them.

In particular, in [82], the micelle dimensions in 0.3 M SDS solutions were studied using the small-angle neutron scattering method. Analysis of the obtained data indicates that in such SDS solutions, the micelles are ellipsoidal with dimensions b = c = 1.7 nm and a = 3.58 nm. The axis ratio is a/b = 2.11. The aggregation number of the formed micelles N_agg = 106 indicates that this solution mainly contains micelles of C₁₀₀ and C₁₁₀ types. The specified aggregation number N_agg = 106 most closely corresponds to the fullerene-like structure C₁₁₀, i.e., a fullerene with an additional insertion of 25 hexagons and 50 vertices. We estimated the axis ratio of C₁₁₀ based on geometric considerations. It turned out that for C₁₁₀, the axis ratio a/b = 2.1. This fact may be an indirect confirmation of the fullerene-like structure of SDS micelles.

3.4. Time Characteristics of Ionic Surfactant Solutions

The results of earlier experiments on relaxation in ionic surfactant solutions showed the presence of two processes, characterized by different relaxation times [85,86,87]. The slow process with relaxation times ranging from 10⁻⁴ to 1 s [5,6] was unanimously attributed to the micelle lifetime. Authors first studied the fast relaxation process with an exchange rate 10⁻⁷ to 10⁻⁶ s, and they assigned it with the association/dissociation of counterions to/from micelles [85,86]. Later, this relaxation process was correlated to the association–dissociation (exchange) equilibrium of amphiphilic ions to/from micelles [5,87,88,89,90]. Note that for nonionic micelles (which are really not micelles but associates of surfactant molecules), the incorporation/detachment of molecules into/from associates is the main kinetic process. For ionic surfactants, such an exchange is associated with the convergence of charges with the same sign to extremely small distances, which is energetically impossible. This rapid relaxation process may correspond to diffusion of the monomer around the micelle and/or rotational diffusion of the micelle [42]. Moreover, for ionic surfactants, when a solution contains three types of kinetic units (micelles, surfactant ions, and counterions), the main kinetic process involves faster units presented at higher concentrations, namely the counterion/surfactant ion association/dissociation process, accompanied by ion pairing and counterion exchange between the internal and diffuse parts of solution. The relaxation times of these processes, as already noted, correspond to the pico- and nanosecond range [59,61].

Solutions of ionic surfactants, being nonequilibrium on the nanoscale, are also characterized by almost instantaneous self-assembly/disintegration related to quantum coherence. The classical micellization theory does not have a way to describe them. The frequencies of thermal oscillations in the temperature range of the micelle existence, i.e., from the Kraft point to the boiling point of water (~10 °C ÷ 100 °C), which almost corresponds to the region of physiologically significant temperatures for bioorganic molecules, can be found from the following relation:

hν_therm~kT

(1)

The calculated oscillation frequencies correspond to ν_therm~10¹² ÷ 10¹³ s⁻¹. Their characteristic time is in the range 10⁻¹³–10⁻¹² s. Thus, the estimation of quantum coherence times [8,9,10] makes it possible to introduce one more specific time connected with the micelle self-assembly/disintegration process (10⁻¹³–10⁻¹² s). A comparison with the micelle lifetime (10^–4–1 s) provides ground to consider these processes at the macroscale as practically instantaneous.

Historically, kinetic theories have been developed mainly for nonionic surfactants. They were created on the basis of quasi-chemical approximation using the mass action law, in which micellization was considered a reversible chemical reaction [91,92,93], or on the principles of nucleation theory [94,95,96], generalized afterwards for the case of ionic surfactants. The stepwise association of unimers or the destruction of existing micelles by the stepwise dissociation was considered the main mechanism of micellization. The desire to build a general theory of micellization for ionic and nonionic surfactants, in our opinion, was a big mistake. Despite the existence of common properties at the macroscale, at the nanoscale, there is a sharp difference in the properties of ionic micelles and nonionic associates, which manifests itself in a discrepancy in sizes, driving forces, electric fields, and types of kinetic units. The different temperature dependences of occurring processes also indicate different mechanisms for their implementation. Additional restrictions may be imposed by the symmetry of quantum mechanical systems. In contrast to micelles of ionic surfactants, which are much more monodisperse near CMC [97], nonionic surfactants can simultaneously exist in solution in various associative forms [98,99]. This observation results in the need to revise kinetic processes occurring in ionic surfactant solutions, while the description of nonionic surfactant behavior does not require any changes.

Thus, the consideration of dynamic processes, along with an expansion in their range, is the main distinguishing feature of the proposed model. The description of the occurring processes needs to emphasize two key points: (a) the enormous role of self-assembly/disintegration of micelles, which are almost ignored by the classical description and which control the processes of reciprocity with the environment (alterations in temperature, surfactant concentration, addition of electrolytes, etc.); (b) the necessity to add and revise the main kinetic processes taking place in ionic surfactant solutions.

Despite the fact that this study only considers the surfactant micellar state in aqueous solutions, some conclusions about association/dissociation processes can also be made based on the non-classical behavior of micellar solutions near the Kraft point. In [100], it is noted that the Kraft point, which characterizes the transition temperature from surfactant solution to the onset of micellization and vice versa, differs significantly depending on the temperature change direction. In particular, in SDS solutions, the micellization starts after an increase in temperature to 18 °C. Nevertheless, under a decrease in temperature, surfactant molecules retain the micellar state down to 10 °C. This discrepancy can be explained by micelle disintegration not to a monomolecular state but, to a significant extent, to dimers, which can more easily reunite in association/dissociation processes.

3.5. Structure of the Micelle Hydrocarbon Core

For further details on the structure of the micelle formed by 60 surfactant ions (fullerene-like micelle), it is necessary to take into account the quantum organization of the micelle components together with the mathematical principles inherent in the symmetry of truncated icosahedron (C₆₀ fullerene symmetry). In particular, the micelle aggregate can be considered as a quantum system of identical particles (surfactant ions). The principle of the identity of indiscernibles permits a very high degree of symmetry for spherical micelles and the identity of the spatial arrangement of hydrocarbon chains in such micelles, which can be realized only in the case of their radial arrangement without any bending of hydrocarbon chains. So, inside the core, the identical surfactant hydrocarbon chains are located radially. Outside the hydrocarbon core, the surfactant ions can differ in the size and charge of head groups due to an association with counterions or its absence. Since the association/dissociation processes are fast-flowing, upon averaging, micelles become symmetrical.

The initial concept of the micelle as a monomolecular layer of surfactant ions closed on itself corresponds to the radial arrangement of hydrocarbon chains [46]. Then, the radial arrangement of alkyl chains was turned down for a very simple reason—all the terminal methyl groups of hydrocarbon chains cannot fit the space in one point. The proposed attempts to consider a cavity inside a micelle [42,101,102,103,104] were rejected as contradicting the common sense and classical conceptions. In those years, the existence of a cavity inside some molecules was not yet known, since the fullerene molecule was discovered only in 1985. Now, it is no longer surprising that this emptiness can be a constituent part of molecules, as is observed for fullerenes and some other molecules. For example, the diameter of fullerene C₆₀ is 0.71 nm, and the diameter of its inner cavity is about 0.5 nm. A spontaneously created emptiness corresponds to the configuration of atoms disposed in a certain stable state, satisfying the energy minimum. The fullerene structure represents very rigid construction, conforming to these principles. Thus, the principle of the identity of indiscernibles forces us to return to the initial concept of the existence of a cavity inside micelles.

Ionic surfactants, in particular SDS with the chemical formula CH₃(CH₂)₁₁OSO₃Na, have the molecular configuration shown in Figure 5. Surfactants, combined into the fullerene-like structure due to the hydrophobic interaction of symmetrically located hydrocarbon chains and the Coulomb repulsion between charged head groups, should be arranged radially, forming a rigid structure in the radial direction. This design is confirmed by the solid-like micelle properties in the radial direction [4,47,48]. Previously, Dill and Flory [105] also concluded, for spherical aggregates, that the micelle center should exhibit a “degree of order approaching that in a crystal”. In addition, the radial arrangement of surfactant ions provides greater freedom for their outer parts to vibrate in perpendicular directions. The listed results made it possible to state that micelles are solid-like particles in the radial direction and liquid-like ones in two other directions [4,44].

Surfactant ions, which form micelles, are either in a dissociated state or bound to counterions in contact ion pairs. Regardless of this circumstance, the surfactant head groups constitute the first layer of a fullerene-like structure. All 12 subsequent layers, corresponding to SDS carbon atoms in respective sites, have the same type of symmetry. Therefore, hydrogen atoms are also found in sites of similar structures. The terminal hydrogen atoms of the hydrocarbon tail do not touch but are located at some distance from each other and, therefore, also form a fullerene-like structure with a cavity, which is quite natural for fullerene-type structures.

To estimate the size of this cavity inside the SDS micelle, one can use the size of the fullerene molecule (diameter 0.71 nm, radius 0.35 nm) and comparative size of carbon and hydrogen atoms. Based on the quantum mechanical wave functions, the calculated values of atomic radii (in picometers) are 53 pm for hydrogen and 67 pm for carbon [106]. Using these values, the fullerene-like structure built by the terminal hydrogen atoms of methyl groups within micelles should have a radius of about 0.28 nm (diameter 0.56 nm). The environment of the hydrogen-built fullerene structure can make additional corrections to its size, but it will only be an improvement in the initial estimation. This structure has a cavity with an approximate radius 0.2 nm (diameter 0.4 nm). Thus, the size of the cavity inside the micelle aggregate, consisting of 2520 atoms, is 1.25-times smaller than that of the C₆₀ fullerene molecule. So, the structure of the micelle hydrocarbon core can be described as the hydrogen-built fullerene in its center, with chemically adsorbed alkane chains around it. It should be noted that this is precisely the cavity size that was suggested in [44] to explain the obtained micelle aggregation numbers.

The obtained cavity size suggests the possibility to intercalate some of the simplest molecules into this cavity (H₂, N₂, O₂, H₂O …). Interestingly, the only hydrocarbon that can theoretically fit into this cavity is a methane molecule with a radius of 0.19 nm [107]. Examples of molecules intercalated inside the cavity of carbon fullerenes were obtained experimentally, and their properties were investigated [108]. This revealed that the invasion of additional molecules into the fullerene cavity does not lead to an improvement in the structural and strength properties of the host molecule. Accordingly, the most symmetrical and stable configuration should be the usual fullerene-like structure of hydrogen atoms with an intrinsic structural cavity in the micelle center.

To find the sizes of the hydrocarbon core and micellar particle, it is necessary to take into account the presence of a cavity, which is a distinctive feature of the advanced model. In particular, for SDS (Figure 5), one must consider the hydrogen-built fullerene (radius 0.28 nm) in the micelle center, then six double-carbon units, each having a size of 0.254 nm [109] (1.524 nm). Since the core size obtained in this calculation includes the C–O bond of the first carbon atom with the head group, which has approximately the same dimensions and spatial location as the C–C bond, half of this bond should be attributed to the hydrocarbon core and the other half to the head group. Accordingly, the hydrocarbon core size should be estimated as 1.74 nm. The size of the head group (sulfate ion SO₄) is estimated as a particle with a diameter of 0.506 nm [110], 0.46 nm [37], 0.44 nm [111], or 0.38 nm [100]. Since the size of the micellar particle is determined by associated surfactant ions, depending on the geometric characteristics of bonding with counterions, the Na⁺ counterion with 0.2 nm diameter can also be added to the total micellar core size [112]. On the whole, the radius of micellar particles is approximately equal to 2.3–2.4 nm, in which 1.74 nm falls on the hydrocarbon core with a cavity. The micellar aggregate has a size of 2.2–2.25 nm.

Similar considerations allow us to calculate the size of the micellar particle of a cationic surfactant, cetriltrimethylammonium bromide (CTAB), which has the chemical formula CH₃(CH₂)₁₅N(CH₃)₃Br. Taking into account the cavity of the same value, the radius of the hydrocarbon core is equal to 2.24 nm. To estimate the size of the CTAB head group, we can use the data from [26], which indicate its volume as 0.1023 nm³. Assuming a spheroidal shape for the head group, the corresponding calculations let us estimate the diameter of the CTAB head group as 0.58 nm. Thus, the radius of the CTAB micelle can be estimated as 2.82 nm. Unfortunately, the experimental data on the size of CTAB micelles, for example [82,113], are no less contradictory than the data on SDS, primarily due to some nonsphericity of micelles in the range of the concentrations studied.

In Figure 5, head groups are shown as cylinders instead of spheres, which are usually applied for the schematic representation of ionic surfactants of an arbitrary nature. Thus, we emphasize the existence of the comparable transverse dimensions of alkane chains and head groups, which is important when analyzing their arrangement in micelles. In particular, it is known that n-alkanes can be in several crystalline states with different symmetries, in which the cross-section of the methylene groups is approximately equal to S_cryst ≈ 0.188 nm²; in a semi-solid gel phase with hexagonal symmetry, when S_gel ≈ 0.20 nm²; in a liquid phase, when S_liq ≈ 0.23 nm². Accordingly, the transverse size (diameter) of hydrocarbon chains in these states can be estimated as d_cryst ≈ 0.489 nm, d_gel ≈ 0.504 nm, d_liq ≈ 0.541 nm. A comparison of these values with the experimentally determined sizes of head groups indicates complete correspondence between the sizes of hydrocarbon tails and head groups. A flat version of the schematic representation of the micelle with a cavity is shown in Figure 6. Unfortunately, the flat version does not convey all the features of the fullerene structure, which is arranged so optimally that no cross-section will contain more than two pairs of hydrocarbon chains.

The experimentally determined radius of the hydrocarbon core for SDS micelles varies mainly from 1.67 to 1.84 nm [25,26,27,28,29,103], and the radius of the micellar core is known to be in the range 2.2–2.5 nm [27,33,34,35,36,37,38], being quite consistent with our estimations. This fact is an indirect confirmation of the cavity inside micelles formed by the hydrogen-built fullerene structure.

3.6. Features of Structure and Properties of Surfactant Micelles

3.6.1. Penetration of Water Molecules up to Hydrocarbon Core

Fullerene symmetry has remarkable geometric properties (Figure 4). The positions of all head groups located in the first fullerene-like structure layer are absolutely identical. Each head group is located at the junction of two hexagons and one pentagon. In the cross-section passing through the two nearest surfactant ions, the angle between the chain directions is approximately 23.28°. The edge length a (distance between nearest atoms) and radius R of the almost spherical fullerene-like structure are related by an approximate ratio [114].

$$4\pi R^2\approx \left(20\cdot {\displaystyle \frac{3}{2}}\sqrt{3}+12\cdot {\displaystyle \frac{5}{4}}\sqrt{1+{\displaystyle \frac{2}{\sqrt{5}}}}\right)a^2=72.607a^2$$

(2)

This allows us to estimate the relationship between these dimensions as a = 0.42 R. Taking this ratio into account, it is possible to calculate the distance between head groups on the hydrocarbon core surface and at the middle level of the head group, i.e., at the distances from the micelle center, approximately equal to R_hc = 1.8 nm and R_1/2 = 1.8 + 0.25 = 2.05 nm. The calculated distances between radial directions in these places are a_hc = 0.76 nm and a_1/2 = 0.86 nm. Considering that head groups can have spherical (cylindrical) shapes and cross sizes of up to 0.5 nm, the distance between the nearest points of neighboring head groups turned out to be equal to 0.26 nm on the core surface and 0.36 nm or even more at the level of the midpoint of head groups. This confirms the considerations previously expressed in the analysis of Figure 3: (a) the penetration of water molecules to the hydrocarbon core; (b) the indirect character of surface diffusion (counterion exchange can only occur with the participation of solvent-separated ion pairs).

3.6.2. Gel-like Properties of Hydrocarbon Core

The widely accepted idea that the micelle core can be considered a droplet of hydrocarbon liquid does not correspond to the structure of advanced micelles. However, there are no sufficient grounds to consider it as a solid particle, except for the fact that the length of hydrocarbon chains is subject to some change, i.e., they can be considered rigid body. Thus, micellar particles demonstrate quasi-solid behavior only along the hydrocarbon chains, i.e., in the radial direction. The divergent arrangement of alkyl chains in each cross-section of the fullerene-like structure (fan-shaped on its flat analog) suggests the presence of crater-shaped (V-shaped) weakly structured domains under the central part of each face (between surfactant ions). Such a structure suggests a deflection of each face and water penetration to the depth of several upper methylene groups under hydrostatic forces (Figure 6). The deflection of the core surface indicates the contacts of the upper parts of chains with an aqueous environment and liquid-like properties of core contents. Liquid-like properties may also be indicated by the possible participation of the upper part of midpoint chains in oscillatory movements in perpendicular directions.

Additional structural features of ionic micelle hydrocarbon cores are determined by nature and the unique structural properties of hydrocarbon chains. It is known that n-alkane chains, due to their structural features, in addition to liquid and crystalline states, can be in intermediate phase states, characterized by different symmetries and different distances between chains [109]. The high-temperature semi-solid phase, usually called the “α-phase”, “gel phase”, “plastic phase” or “hexagonal phase”, is characterized by hexagonal symmetry. Molecules of n-alkanes in the gel phase are structurally and thermodynamically much closer to the ordered crystalline state. However, in this state, the occupied volume is 5–6% larger, which leads to less dense hydrocarbon chains packing and additional possibilities for chain rotation. The temperature range of this phenomenon for pure alkanes is small. However, a limitation of the sizes of alkane systems is in the form of thin layers on micro- and nanocrystal surfaces, their retention in pores, or in droplets of micro- and nanoemulsions, which increases the temperature ranges in which gel phases are formed. The confirmation of the gel structural state of alkane chains in micelles is their hexagonal symmetry, close to fullerene symmetry. Thus, it can be assumed that micelle hydrocarbon cores are characterized by a gel-like state, in which the properties of solids and liquids are simultaneously manifested. The presence of internal structural bonds gives gels the mechanical properties of solids: lack of fluidity, ability to retain shape, strength and ability to deform (plasticity and elasticity).

3.6.3. Surface Roughness of the Micelle Hydrocarbon Core

The existence of roughness has been discussed in many studies [44,115,116]. It was believed that roughness is caused by the non-identity of the head group arrangement, which appears due to a small temporary extrusion of individual chains above the surface level of the hydrocarbon droplet. In the advanced model, the micelle surface is also characterized by roughness. However, in this case, ordered roughness is observed, i.e., caused precisely by the symmetry of the system. The rigidity of hydrocarbon chains and plasticity of their environment (Figure 6) affect the surface roughness.

3.6.4. Increased Pseudophase Volume and Semi-Closed Hydrocarbon Surface Regions with Enhanced Hydrophobic Properties

When analyzing Figure 3, it was already noted that in the advanced micelle model, the pseudophase has a larger volume due to water penetration, not only up to the hydrocarbon core surface but also due to the filling of resulting crater-shaped (V-shaped) depressions in hydrocarbon surface faces (Figure 6). It should be noted that the crater-shaped regions can be considered semi-closed regions of the hydrocarbon surface with enhanced hydrophobic properties. The presence of special “hydrophobic spots” on the surface of the hydrocarbon core was discussed in [48,115], where it was noted that many water-insoluble compounds (for example, benzophenone, bromobenzene, butyronitrile) “prefer the highly aqueous micelle surface to the organic interior”. In the advanced model, molecules of specified compounds can penetrate into the crater-shaped regions with enhanced hydrophobic properties, displacing water molecules from there. In fact, the surface solubilization (binding) of specific compounds by near-surface pseudophase regions occurs.

3.6.5. Solubilization of Organic Compounds in Micellar Core

The solubilization of organic substances by micelles is the most important technological property of micellar solutions. In particular, the removal of organic pollutants is of great importance in environmental research [117]. For micellar solutions of ionic surfactants, the solubilization in the micellar core is more typical than the surface solubilization, during which a colloidal process of spontaneous and reversible penetration of low-polarity organic compounds into micelles occurs. It is believed that the process of colloidal dissolution in surfactant micelles occurs due to the penetration of diffusing organic molecules from an aqueous solution into the micellar core [118].

It should be noted that the process of penetration of individual molecules into the core of ionic surfactant micelles contradicts quantum principles and symmetry considerations. This means that the previously proposed solubilization mechanism should be revised. As already noted, at the nanoscale, a micellar solution should be considered as a nonequilibrium system, in which the processes of association/disintegration of micelles are permanent, and micelles are characterized by a certain lifetime. The theory of self-organization in nonequilibrium systems (chaos theory) is applicable to such systems [76,77,78]. The penetration of a hydrocarbon molecule into the core is associated with the violation of original micelle symmetry. Nonequilibrium systems are extremely sensitive to violations of their symmetry. Moreover, since the characteristic feature of chaos theory is the exponential sensitivity of systems to small disturbances, even the approaching of the guest to a micelle and the violation of its outer shell will cause micelle disintegration. These considerations force us to put forward another version of this process.

In our opinion, the appearance of free hydrocarbon molecules in aqueous solution stimulates two processes that occur together and lead to the same result: (1) the appearance of single hydrocarbon molecules in solution and their possible association with each other due to the hydrophobic effect; (2) the disintegration of the micelle due to internal reasons or due to the appearance of a molecule or associate of several combined hydrocarbon molecules near the micelle. Micelle disintegration leads to the emergence of an excess concentration of free surfactants. In turn, the presence of an excess surfactant concentration promotes the appearance of a new micelle. In this case, hydrocarbon molecules, as a result of hydrophobic interactions, will turn up in the center of newly formed micelles. The appearance of another molecule or associate of hydrocarbons near the enlarged micelle will stimulate the disintegration of the formed micelle. The absence of a shell of surfactant ions and the existence of hydrophobic interactions will lead to the association of closely located hydrocarbons, around which a new micelle with an enlarged hydrocarbon core will be formed. Thus, the nonequilibrium of micellar solutions at the nanoscale leads to the conclusion that the process of colloidal dissolution must occur through the disintegration and self-assembly of micelles.

4. Conclusions

This study presents an improved phenomenological model of ionic surfactant micellization based on well-known data with the involvement of additional assumptions reflecting the trends of modern scientific achievements, namely: (1) a micellar particle exists in a highly concentrated ionic medium formed by dissociated surfactant ions and counterions, which can be partially free or bound into ion pairs, and the change in these states is characterized by relaxation in the pico- and nanosecond range; (2) the micellization of ionic surfactants does not contradict the principles of quantum mechanics; (3) micellar solutions of surfactants are nonequilibrium at the nanoscale, and, therefore, the theory of self-organization in nonequilibrium processes (chaos theory) can be used to describe them. The need for a probabilistic description of processes in micellar solutions of ionic surfactants, which is required by both of these theories, and the symmetry considerations are also taken into account.

The above considerations provide a basis for an alternative model of ionic micelles, which assumes the same macroscopic properties of surfactant solutions at the macroscale but modified structural characteristics of micelles at the nanoscale. The proposed model led to greater detailing of the observed picture and entailed additional unexpected consequences: the existence of fullerene-like spherical micelles with an internal cavity and greater structuring of the hydrocarbon core surface and increased size of the near-surface pseudophase.

The nonequilibrium of micellar solutions at the nanoscale, their exponential sensitivity to small perturbations, and the quantum nature of nanosized micelles require a probabilistic description of micellar solutions of ionic surfactants, which leads to a revision of the processes occurring in micellar systems of ionic surfactants. In particular, the probabilistic approach leads to a change in the mechanisms of the colloidal dissolution of hydrocarbon compounds and their solubilization by micelles.

The employment of principles operating at the nanoscale helps to explain the micelle structure and diversity of micelle properties (solid in the radial direction and liquid-like in the perpendicular ones), which cannot be explained using classical models. Moreover, only within the framework of new conceptions can one understand why a kinetically nonequilibrium system at the nanoscale is thermodynamically balanced at the macroscale. Thus, the existing experimental data can be interpreted from the standpoint of both models, considering them as the experimental confirmation of our reasoning.

The area of micellar systems is at the intersection of different sciences, closely related to practice. Therefore, a correct understanding of the structure of micellar systems and solubilization mechanisms at the nanoscale will allow one to better understand the nature of the double layer, evaluate the functions of micellar structures in biological systems, the solubilization of drugs by micelles, etc., as well as to study the factors influencing the rates and mechanisms of micellar catalysis and propose new approaches to improve their efficiency.