Molecular Dynamics Study on the Lubrication Mechanism of the Phytic Acid/Copper Interface Under Loading Condition
Abstract
1. Introduction
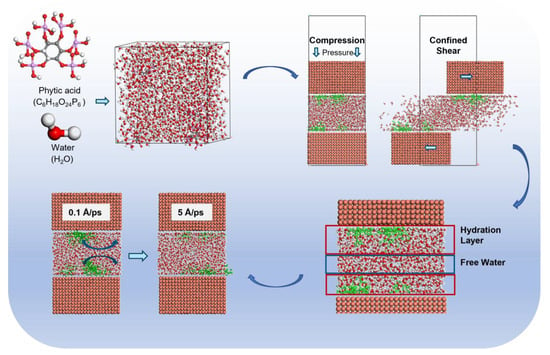
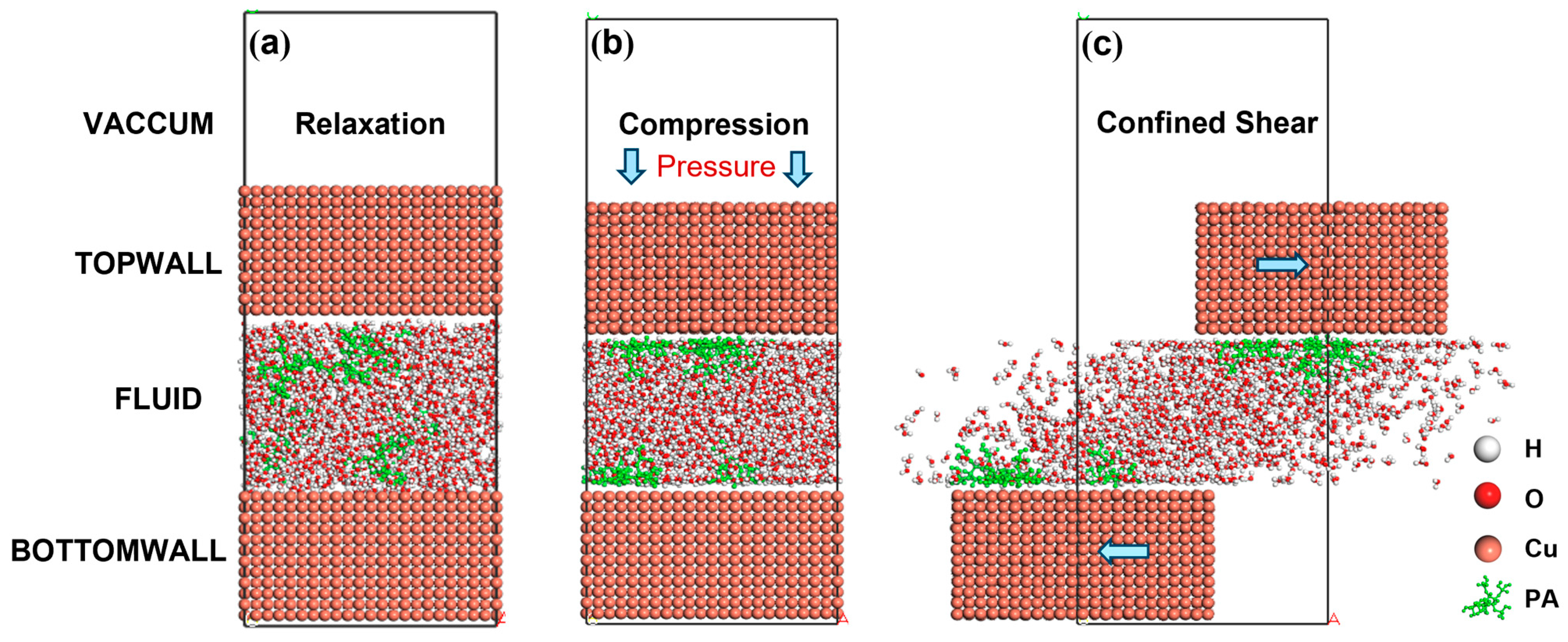
2. Model Establishment and Simulation Details
3. Results and Discussion
3.1. Bearing Mechanism of PA Solution Under Different Normal Loads
3.1.1. Alteration in Compressibility
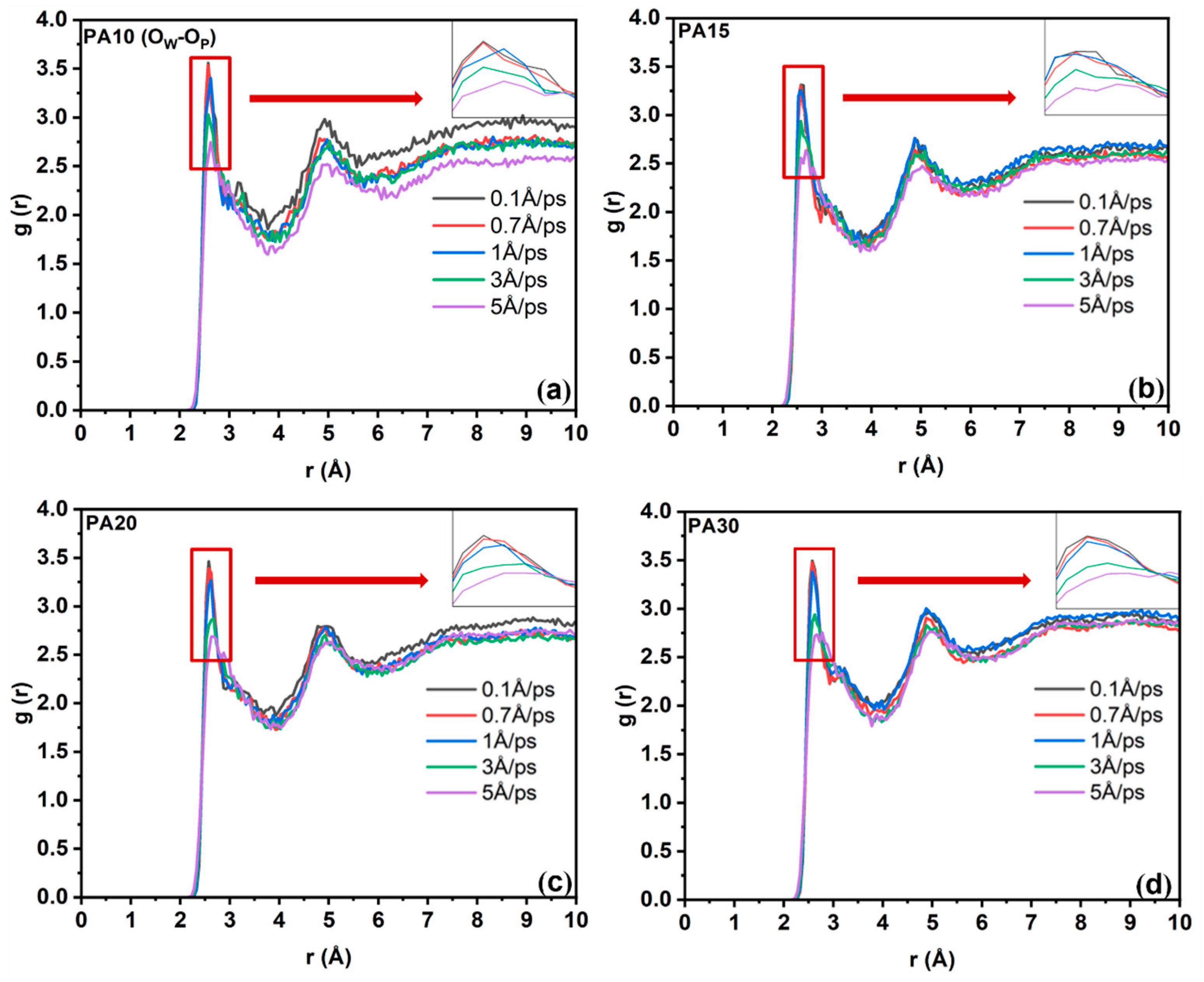
3.1.2. Formation of Hydrated Molecules
3.1.3. Spatial Distribution of PA Molecules in Solution
3.2. Lubrication Mechanism of Phytic Acid Solution at Different Shear Rates
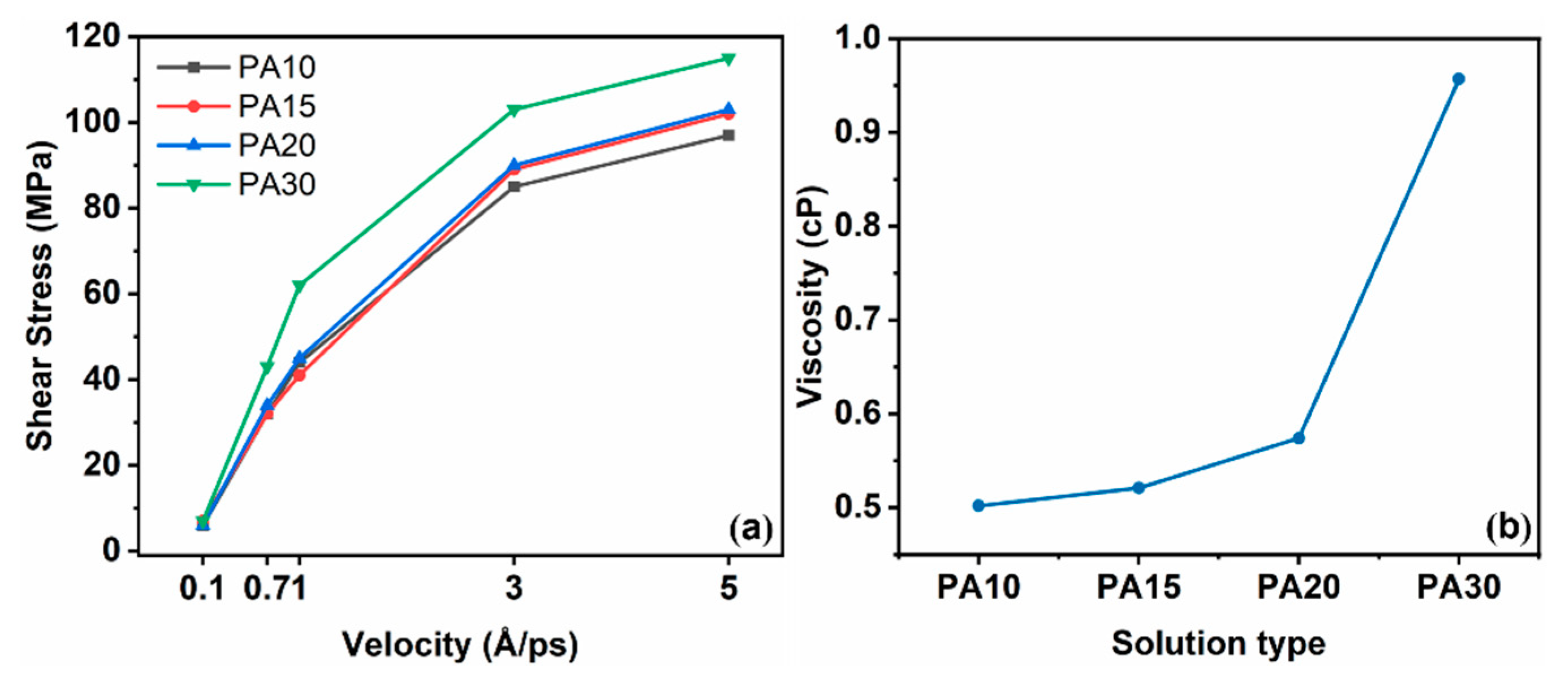
3.2.1. Relationship Between Shear Stress and Shear Rate
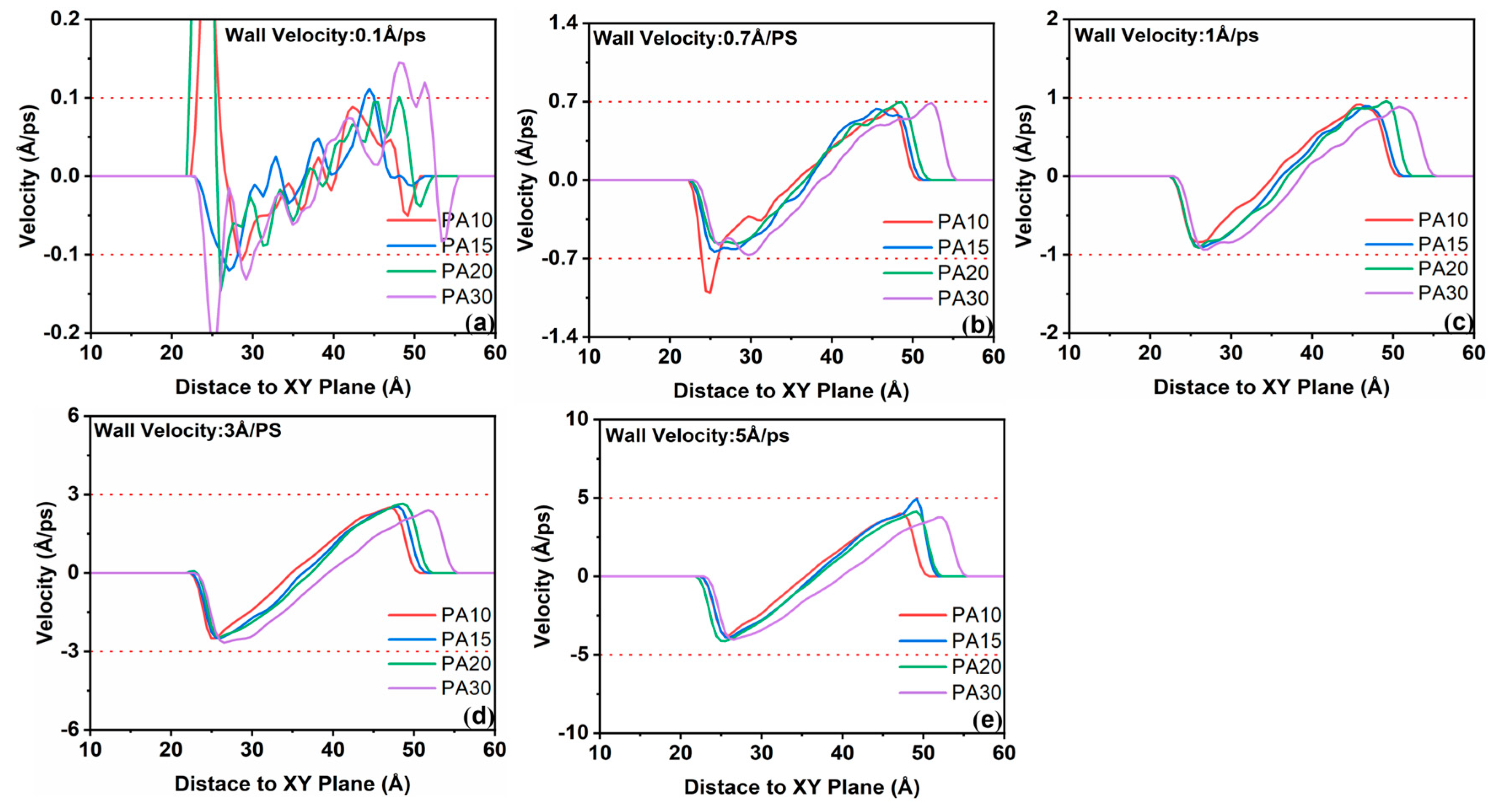
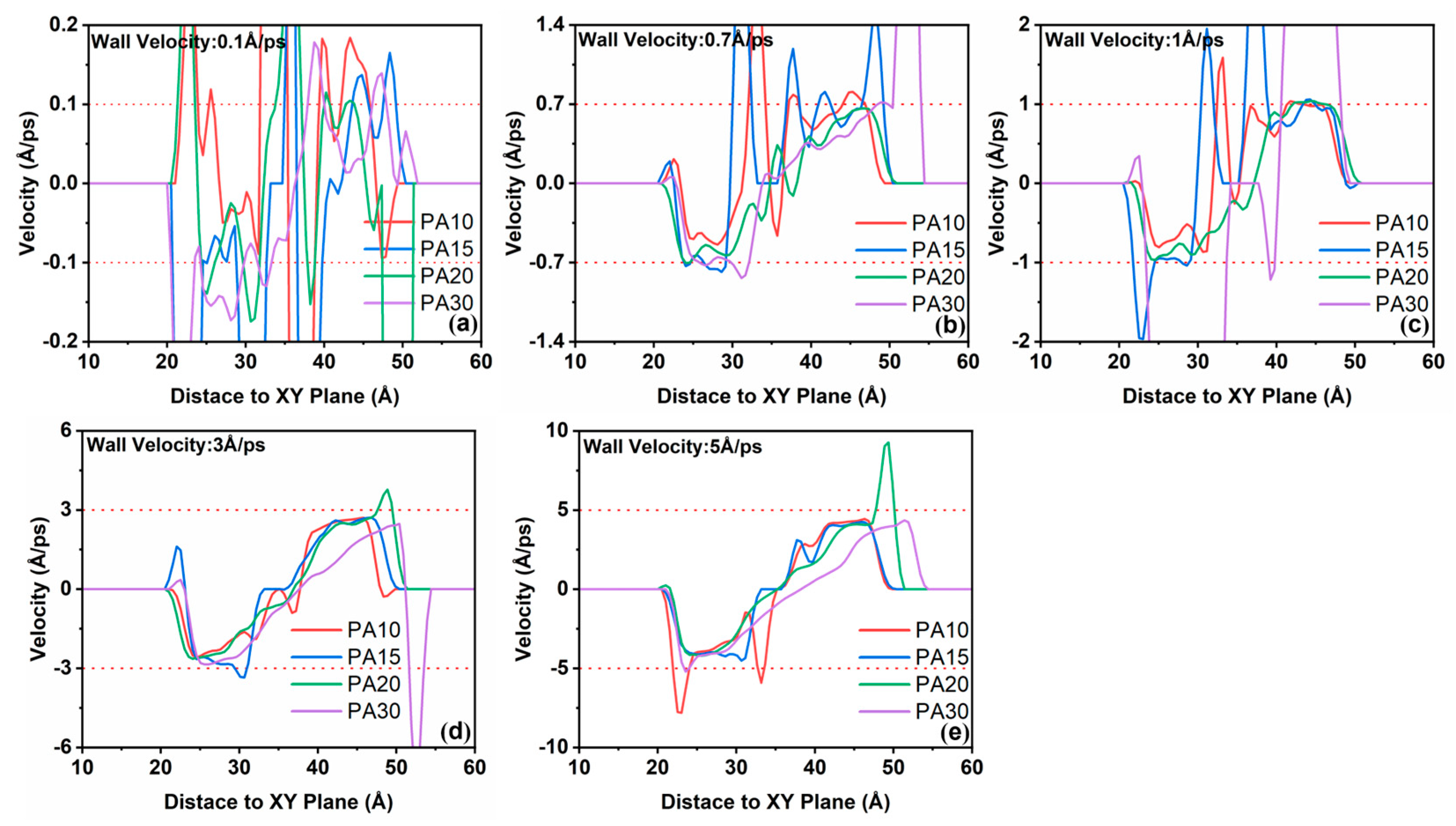
3.2.2. Influence of Velocity Difference Between Water and PA Molecules on Shear Stress
3.2.3. Influence of Confined Shear on Intermolecular Interactions Within the Liquid Layer
4. Conclusions
- (1)
- In PA solution, the compressibility of the liquid layer is negatively correlated with the number of PA molecules. This phenomenon occurs because PA molecules can adsorb tightly onto the surface of the copper atomic layer, forming a stable hydration layer through hydrogen bonding with water molecules. Consequently, in the liquid phase layer, a distribution pattern of PA hydration layer-free water–PA hydration layer emerges. In the compression simulation process, the layer of free water molecules is compressed due to the stable interaction between PA molecules and water molecules. An increase in the number of PA molecules results in a thicker hydration layer within the liquid phase, making it more resistant to compression. Consequently, the compression rate is reduced;
- (2)
- Due to the unique molecular structure of PA molecules (each molecule contains six phosphate groups and twelve hydroxyl groups), the PA molecule chelates with the metal to form an insoluble complex that replaces the water molecule in its original place. This effectively prevents water-induced corrosion on the copper surface;
- (3)
- In the confined shear simulation process, with the increase in shear velocity, a pronounced velocity discrepancy emerges between PA molecules and water molecules, leading to an elevation in interfacial shear stress. the strength of hydrogen bonds formed between PA and water molecules diminishes as the shear rate increases, leading to a shear-thinning effect in the PA solution, which compromises the load-bearing capacity of the liquid layer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sotres, J.; Arnebrant, T. Experimental Investigations of Biological Lubrication at the Nanoscale: The Cases of Synovial Joints and the Oral Cavity. Lubricants 2013, 1, 102–131. [Google Scholar] [CrossRef]
- Holmberg, K.; Erdemir, A. The impact of tribology on energy use and CO2 emission globally and in combustion engine and electric cars. Tribol. Int. 2019, 135, 389–396. [Google Scholar] [CrossRef]
- de Paula, F.H.M.; de Freitas, F.A.; Nunes, D.G.; Iglauer, S.; Gramatges, A.P.; Nascimento, R.S.V.; Lachter, E.R. Alkyl glyceryl ethers as water-based lubricant additives in mixtures with xanthan gum. Colloids Surf. A Physicochem. Eng. Asp. 2022, 634, 127881. [Google Scholar] [CrossRef]
- Holmberg, K.; Erdemir, A. Influence of tribology on global energy consumption, costs and emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Wood, R.J.K. Marine wear and tribocorrosion. Wear 2017, 376, 893–910. [Google Scholar] [CrossRef]
- Fu, Y.Q.; Bachelor, A.W.; Loh, N.L.; Tan, K.W. Effect of lubrication by mineral and synthetic oils on the sliding wear of plasma nitrided AISI 410 stainless steel. Wear 1998, 219, 169–176. [Google Scholar] [CrossRef]
- Wu, H.; Jia, F.; Li, Z.; Lin, F.; Huo, M.; Huang, S.; Sayyar, S.; Jiao, S.; Huang, H.; Jiang, Z. Novel water-based nanolubricant with superior tribological performance in hot steel rolling. Int. J. Extrem. Manuf. 2020, 2, 025002. [Google Scholar] [CrossRef]
- Li, W.; Kumara, C.; Luo, H.; Meyer, H.M., III; He, X.; Ngo, D.; Kim, S.H.; Qu, J. Ultralow Boundary Lubrication Friction by Three-Way Synergistic Interactions among Ionic Liquid, Friction Modifier, and Dispersant. Acs Appl. Mater. Interfaces 2020, 12, 17077–17090. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, G.; Xie, G. Ultralow concentration of graphene oxide nanosheets as oil-based lubricant additives. Appl. Surf. Sci. 2019, 498, 143683. [Google Scholar] [CrossRef]
- Haus, F.; German, J.; Junter, G.A. Primary biodegradability of mineral base oils in relation to their chemical and physical characteristics. Chemosphere 2001, 45, 983–990. [Google Scholar] [CrossRef]
- Delgado, M.A.; Quinchia, L.A.; Spikes, H.A.; Gallegos, C. Suitability of ethyl cellulose as multifunctional additive for blends of vegetable oil-based lubricants. J. Clean. Prod. 2017, 151, 1–9. [Google Scholar] [CrossRef]
- Rahman, M.H.; Warneke, H.; Webbert, H.; Rodriguez, J.; Austin, E.; Tokunaga, K.; Rajak, D.K.; Menezes, P.L. Water-Based Lubricants: Development, Properties, and Performances. Lubricants 2021, 9, 73. [Google Scholar] [CrossRef]
- Deng, M.; Li, J.; Zhang, C.; Ren, J.; Zhou, N.; Luo, J. Investigation of running-in process in water-based lubrication aimed at achieving super-low friction. Tribol. Int. 2016, 102, 257–264. [Google Scholar] [CrossRef]
- Ren, H.; Zeng, H.; Sun, C.; Yang, J.; Luo, X.; Li, J.; Li, B.; Sheng, W. Polymer Brush-Functionalized MoS2 as a Water-Based Lubricant Additive. Macromol. Rapid Commun. 2024, 46, e2400793. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Yang, X.; Xu, L.; Li, M.; Li, S.; Zhang, S.; Xia, J. Analysis and comparison of tribological performance of fatty acid-based lubricant additives with phosphorus and sulfur. J. Bioresour. Bioprod. 2020, 5, 134–142. [Google Scholar]
- Liu, M.; Yao, Y.; Tian, B.; Cui, K.; Wen, P.; Dong, R.; Fan, M. Robust lubricity and multifunctional water-based lubrication system induced by ionic liquids with its interfacial self-assembly behavior and unique hydration structure. Chem. Eng. J. 2025, 509, 161216. [Google Scholar] [CrossRef]
- Kreivaitis, R.; Gumbyte, M.; Kupcinskas, A.; Treinyte, J.; Kazancev, K.; Sendzikiene, E. Studying the Tribological Properties of Coffee Oil-Loaded Water-Based Green Lubricant. Appl. Sci. 2023, 13, 6336. [Google Scholar] [CrossRef]
- Chen, W.; Fu, X.; Cao, L.; Gao, S.; Wan, Y. Ultralow friction of copper by a green water-based lubricant containing phytic acid. J. Mol. Liq. 2021, 338, 116704. [Google Scholar] [CrossRef]
- Xiong, L.; He, Z.; Han, S.; Tang, J.; Wu, Y.; Zeng, X. Tribological properties study of N-containing heterocyclic imidazoline derivatives as lubricant additives in water-glycol. Tribol. Int. 2016, 104, 98–108. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Q.; Cai, M.; Shi, L.; Zhou, F.; Liu, W. Synergy of lithium salt and non-ionic surfactant for significantly improved tribological properties of water-based fluids. Tribol. Int. 2017, 113, 58–64. [Google Scholar] [CrossRef]
- Chen, W.; Amann, T.; Kailer, A.; Ruehe, J. Macroscopic Friction Studies of Alkylglucopyranosides as Additives for Water-Based Lubricants. Lubricants 2020, 8, 11. [Google Scholar] [CrossRef]
- Wan, Y.; Yu, Y.; Gao, S.; Gao, J. Low friction of phytic acid as a water-based lubricant additive. Ind. Lubr. Tribol. 2017, 69, 1085–1090. [Google Scholar] [CrossRef]
- Chen, A.; Arai, Y. Functional Group Specific Phytic Acid Adsorption at the Ferrihydrite-Water Interface. Environ. Sci. Technol. 2019, 53, 8205–8215. [Google Scholar] [CrossRef]
- Li, C.-C.; Guo, X.-Y.; Shen, S.; Song, P.; Xu, T.; Wen, Y.; Yang, H.-F. Adsorption and corrosion inhibition of phytic acid calcium on the copper surface in 3wt% NaCl solution. Corros. Sci. 2014, 83, 147–154. [Google Scholar] [CrossRef]
- Shi, H.; Han, E.-H.; Liu, F.; Kallip, S. Protection of 2024-T3 aluminium alloy by corrosion resistant phytic acid conversion coating. Appl. Surf. Sci. 2013, 280, 325–331. [Google Scholar] [CrossRef]
- Yang, H.F.; Feng, J.; Liu, Y.L.; Yang, Y.; Zhang, Z.R.; Shen, G.L.; Yu, R.Q. Electrochemical and surface enhanced Raman scattering spectroelectrochemical study of phytic acid on the silver electrode. J. Phys. Chem. B 2004, 108, 17412–17417. [Google Scholar] [CrossRef]
- El-Lateef, H.M.A.; El-Sayed, A.-R.; Mohran, H.S.; Shilkamy, H.A.S. Corrosion inhibition and adsorption behavior of phytic acid on Pb and Pb–In alloy surfaces in acidic chloride solution. Int. J. Ind. Chem. 2019, 10, 31–47. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, C.; Lu, H.; Gao, F.; Ma, H. Influence of phytic acid on the corrosion behavior of iron under acidic and neutral conditions. Electrochim. Acta 2014, 150, 188–196. [Google Scholar] [CrossRef]
- Zhao, P.; Zhou, X.; Yang, Y.; Wang, C.; Wang, C.; Liang, H.; Li, C.; Ren, H. Molecular dynamics simulation study of the effect of molecular structure of warm mix additive on lubricating properties. Constr. Build. Mater. 2023, 407, 133529. [Google Scholar] [CrossRef]
- Ma, Q.; Qi, P.; Dong, G. An experimental and molecular dynamics study of the superlubricity enabled by hydration lubrication. Appl. Surf. Sci. 2021, 553, 149590. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Jiang, Y.; Wang, X.; Luo, Y.; Zhu, X. Probing tribological properties of DLC film deposited on plunger surface of sucker-rod pump based on molecular dynamics simulation. Appl. Phys. A 2023, 129, 599. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Ma, L.; Li, Y.; Le, J.; Fu, Z.; Lu, L.; Zhang, D. Understanding the adsorption of imidazole corrosion inhibitor at the copper/water interface by ab initio molecular dynamics. Corros. Sci. 2024, 236, 112237. [Google Scholar] [CrossRef]
- Ma, L.; Lian, J.; Ma, X.; Bai, S.; Ma, L.; Zhao, J. A study on the tribological behavior of water-based nanolubricant during corrugated rolling of copper plates. Int. J. Adv. Manuf. Technol. 2023, 129, 1513–1526. [Google Scholar] [CrossRef]
- Xu, Z.; Xiong, Z.; Gong, M.; Zeng, Q.; Hong, J.; Fan, J. Molecular dynamics-based study of the modification mechanism of asphalt by graphene oxide. J. Mol. Model. 2023, 29, 368. [Google Scholar] [CrossRef]
- Luo, L.; Chu, L.; Fwa, T.F. Molecular dynamics analysis of moisture effect on asphalt-aggregate adhesion considering anisotropic mineral surfaces. Appl. Surf. Sci. 2020, 527, 146830. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applications-Overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Y.; Cui, J.; Li, Y.; Liang, Y.; Cao, G. Molecular dynamics simulation and DFT calculation of “green” scale and corrosion inhibitor. Comput. Mater. Sci. 2021, 188, 110229. [Google Scholar] [CrossRef]
- Honorio, T.; Masara, F.; Benboudjema, F. Heat capacity, isothermal compressibility, isosteric heat of adsorption and thermal expansion of water confined in C-S-H. Cement 2021, 6, 100015. [Google Scholar] [CrossRef]
- Boster, K.A.S.; Cai, S.; Ladrón-de-Guevara, A.; Sun, J.; Zheng, X.; Du, T.; Thomas, J.H.; Nedergaard, M.; Karniadakis, G.E.; Kelley, D.H. Artificial intelligence velocimetry reveals in vivo flow rates, pressure gradients, and shear stresses in murine perivascular flows. Proc. Natl. Acad. Sci. USA 2023, 120, e2217744120. [Google Scholar] [CrossRef]
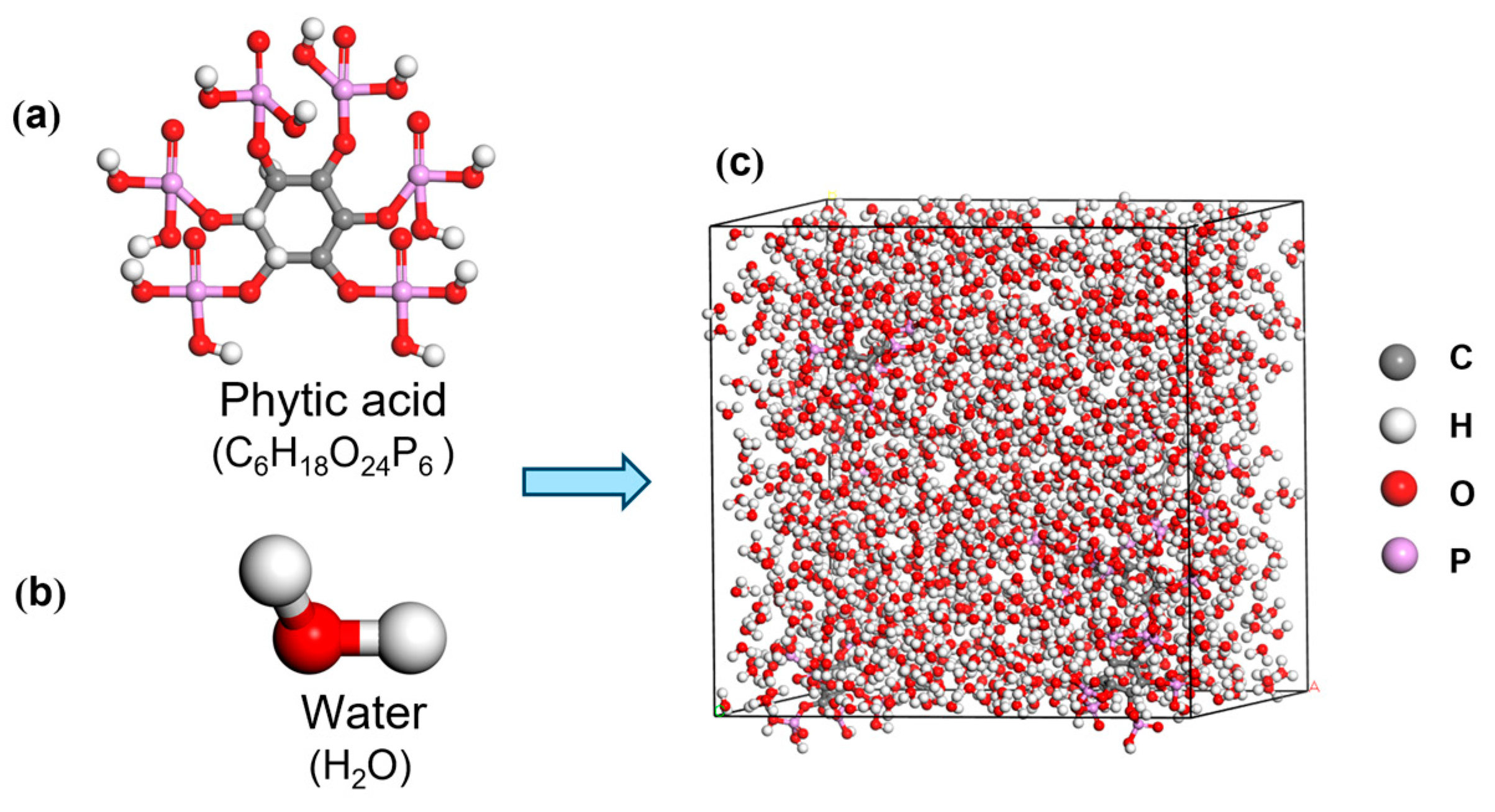




| Solution Type | Wt% (PA) | Density ρ (g/cm3) | Model Size (Å3) | Num. of Water Molecules (nw) | Num. of PA Molecules (nPA) |
|---|---|---|---|---|---|
| PA10 | 10 | 1.0210 | 35.7 × 35.7 × 35.7 | 1400 | 4 |
| PA15 | 15 | 1.0561 | 36.1 × 36.1 × 36.1 | 1400 | 7 |
| PA20 | 20 | 1.1005 | 36.3 × 36.3 × 36.3 | 1400 | 10 |
| PA30 | 30 | 1.1735 | 37.0 × 37.0 × 37.0 | 1400 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, M.; Xie, D.; Wang, X.; Jing, F.; Wen, F.; Leng, Y. Molecular Dynamics Study on the Lubrication Mechanism of the Phytic Acid/Copper Interface Under Loading Condition. Colloids Interfaces 2025, 9, 18. https://doi.org/10.3390/colloids9020018
Guan M, Xie D, Wang X, Jing F, Wen F, Leng Y. Molecular Dynamics Study on the Lubrication Mechanism of the Phytic Acid/Copper Interface Under Loading Condition. Colloids and Interfaces. 2025; 9(2):18. https://doi.org/10.3390/colloids9020018
Chicago/Turabian StyleGuan, Min, Dong Xie, Xiaoting Wang, Fengjuan Jing, Feng Wen, and Yongxiang Leng. 2025. "Molecular Dynamics Study on the Lubrication Mechanism of the Phytic Acid/Copper Interface Under Loading Condition" Colloids and Interfaces 9, no. 2: 18. https://doi.org/10.3390/colloids9020018
APA StyleGuan, M., Xie, D., Wang, X., Jing, F., Wen, F., & Leng, Y. (2025). Molecular Dynamics Study on the Lubrication Mechanism of the Phytic Acid/Copper Interface Under Loading Condition. Colloids and Interfaces, 9(2), 18. https://doi.org/10.3390/colloids9020018