Surfactants Adsorption onto Algerian Rock Reservoir for Enhanced Oil Recovery Applications: Prediction and Optimization Using Design of Experiments, Artificial Neural Networks, and Genetic Algorithm (GA)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Surfactants
2.2. Sample Preparation and Batch Adsorption
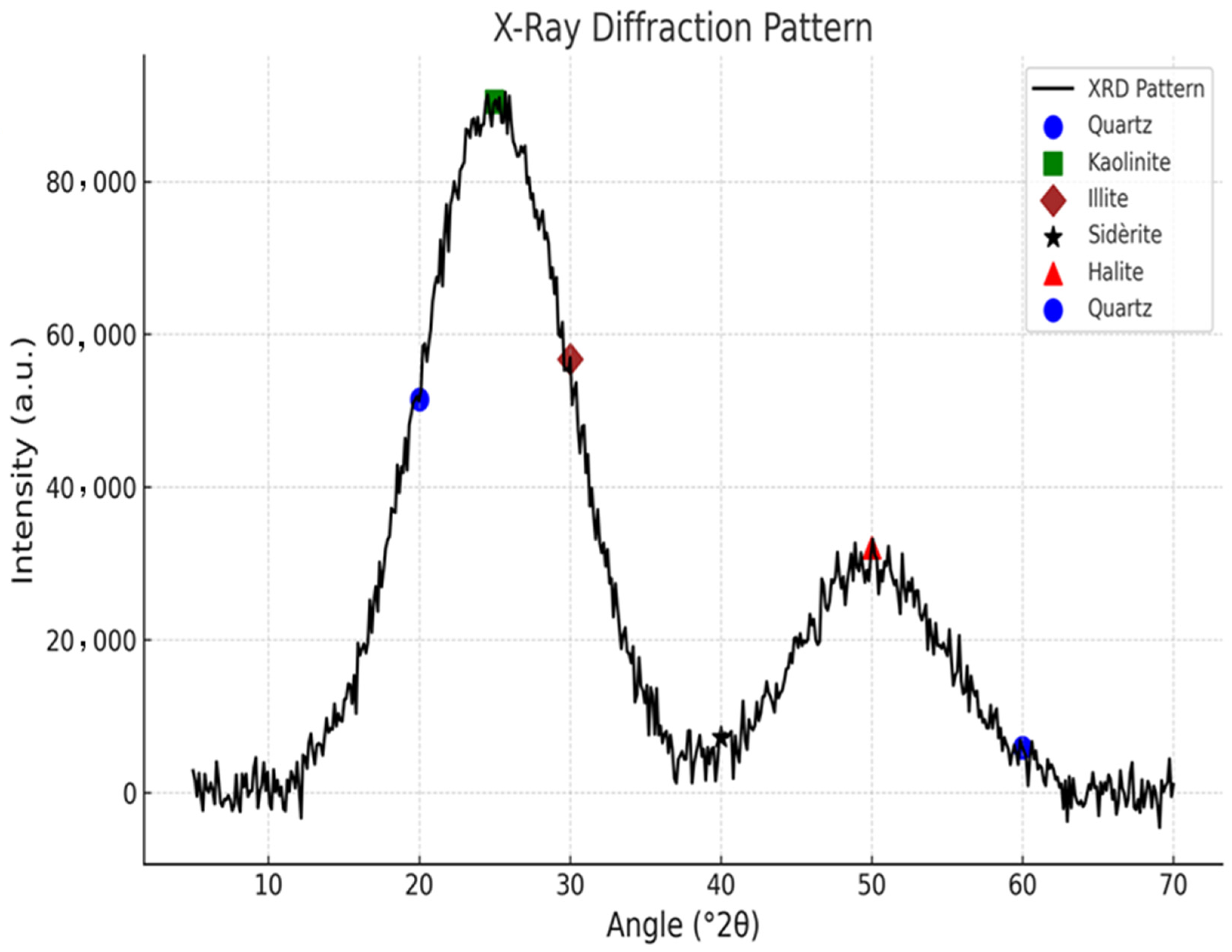
2.3. XRD and BET Analysis
2.4. Modeling Methods
2.4.1. Full Factorial Design (DOE) Modeling
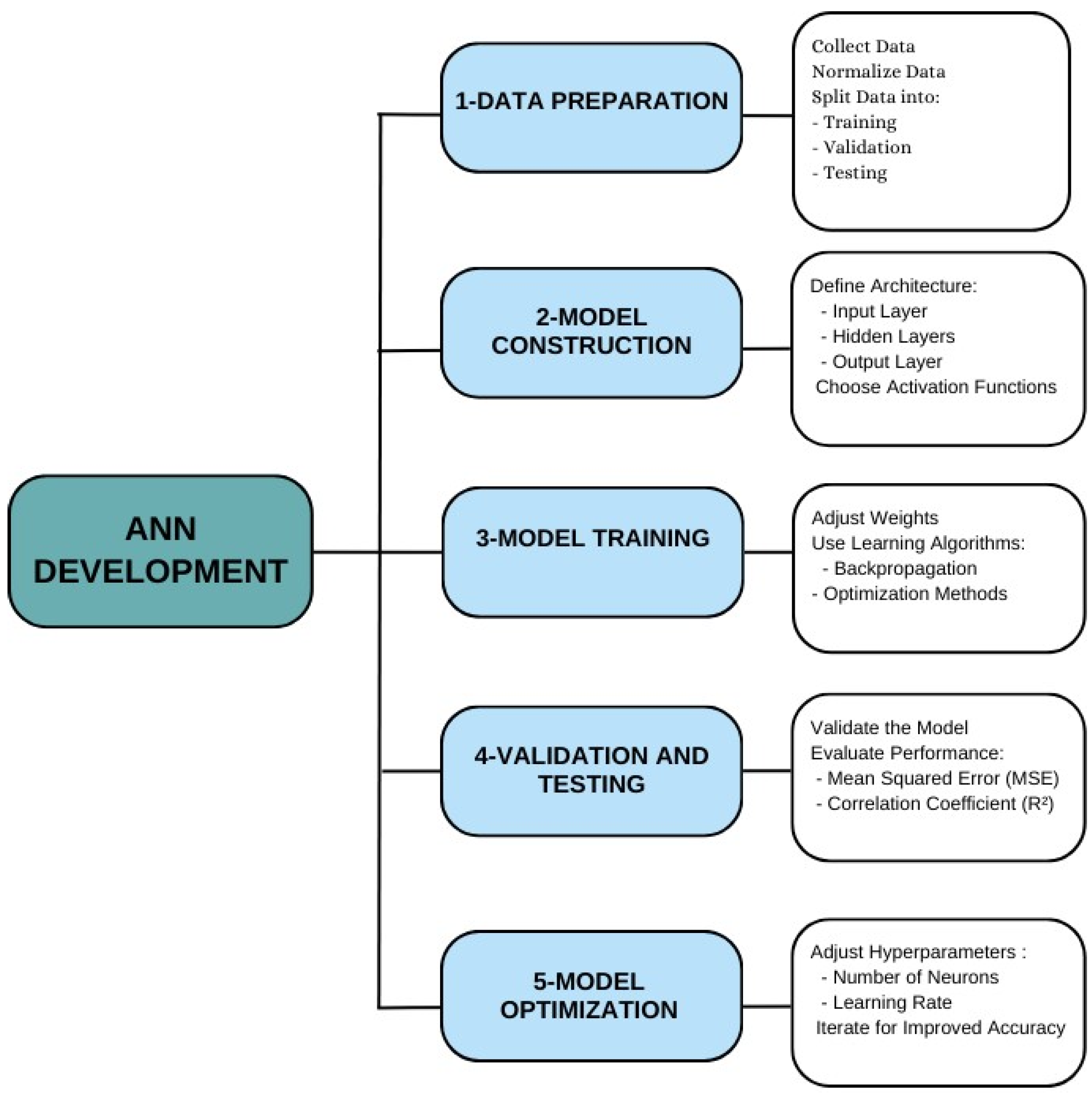
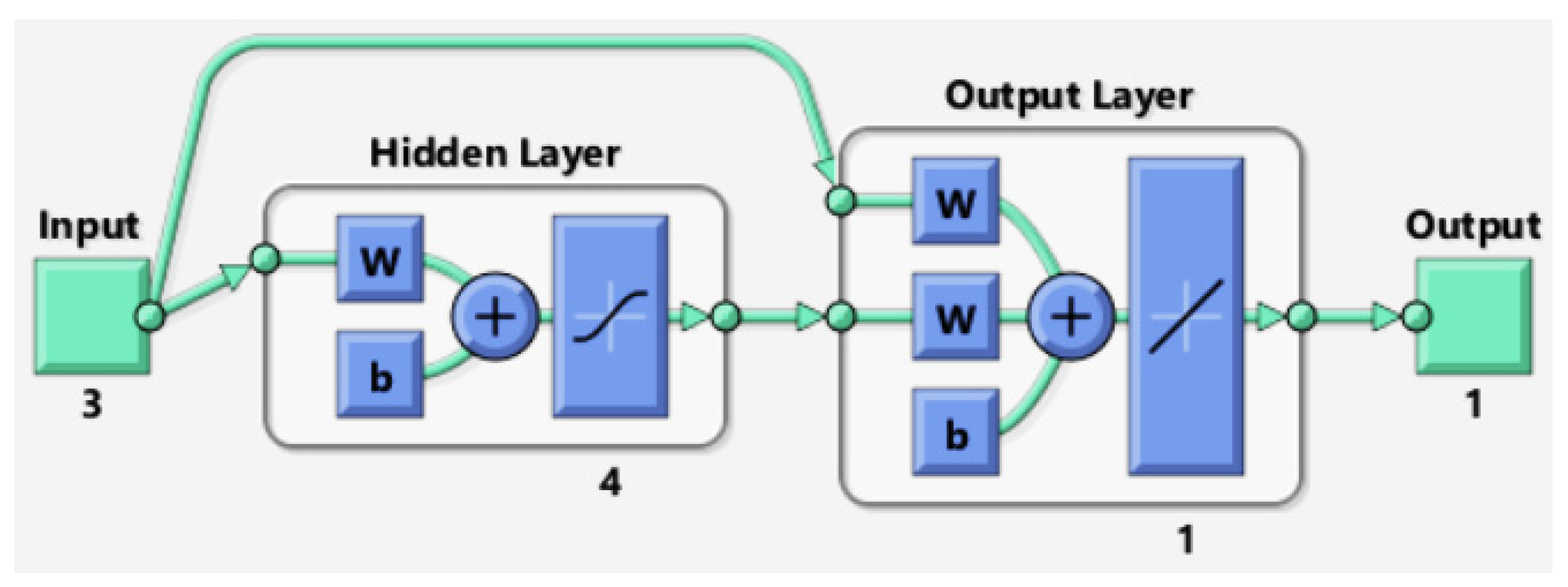
2.4.2. ANN Modeling Development
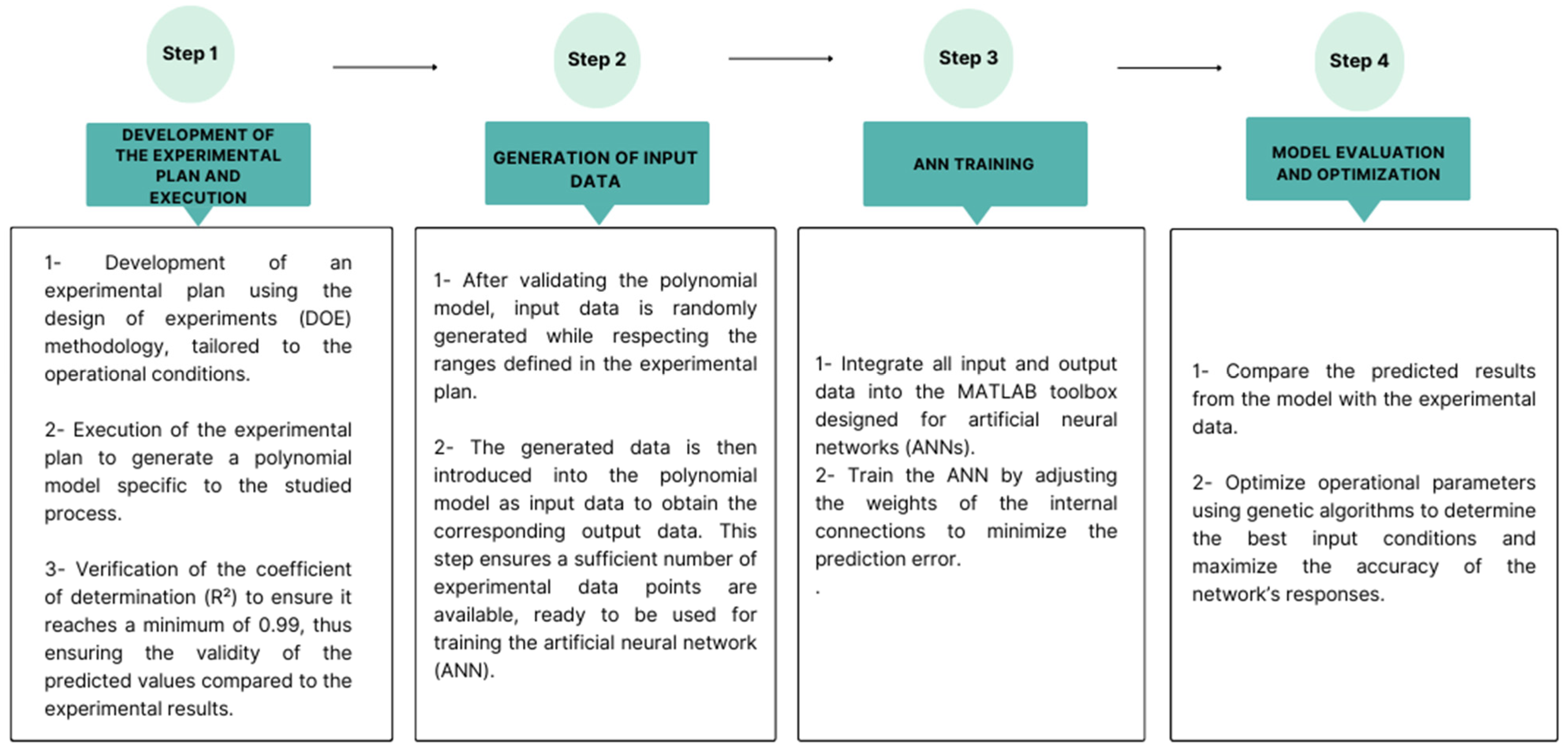
2.5. Data Generation for Network Training
2.6. GA Optimization
3. Results and Discussion
3.1. Characterization Analysis
3.2. Prediction with Factorial Design of Experiments
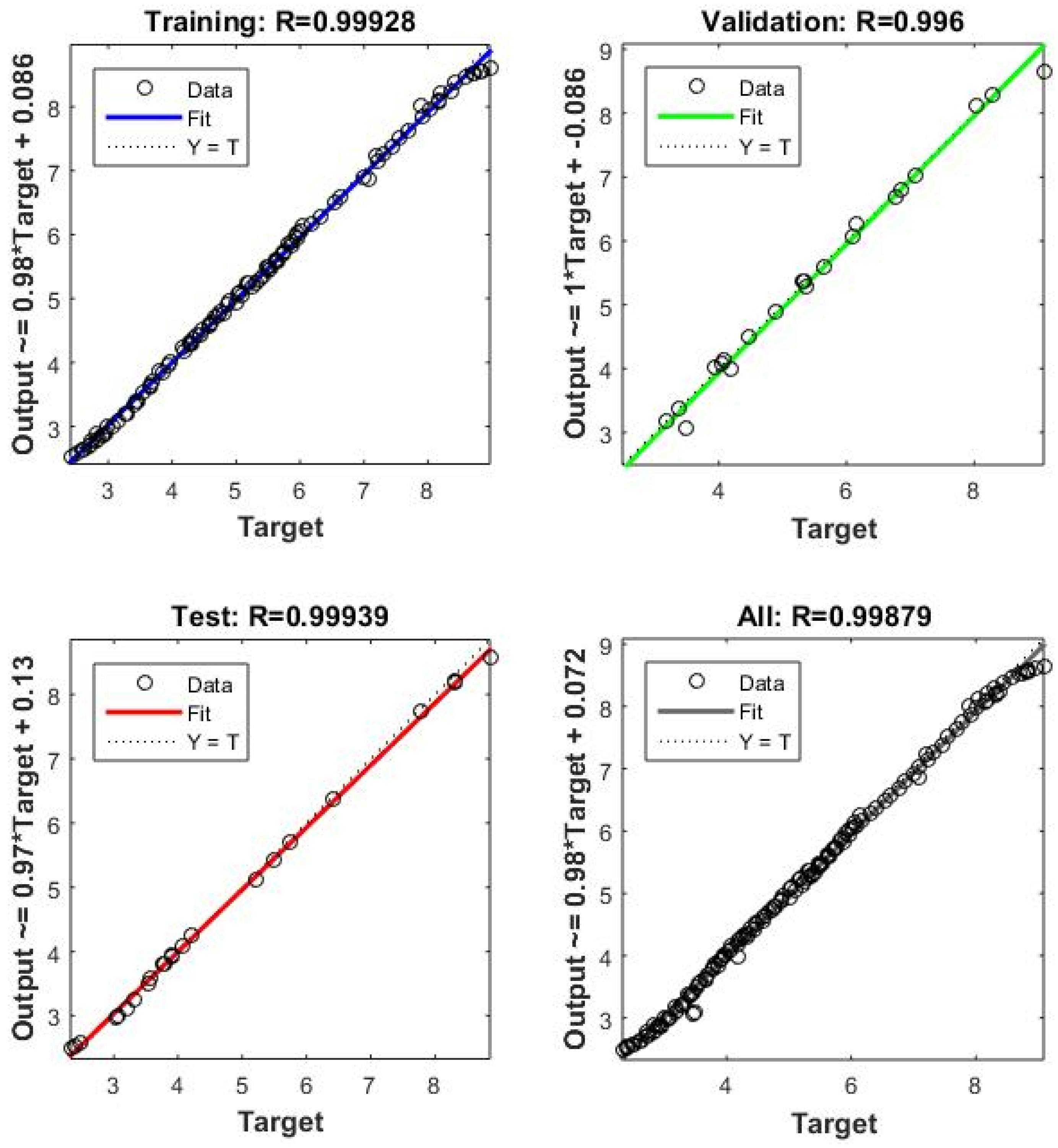
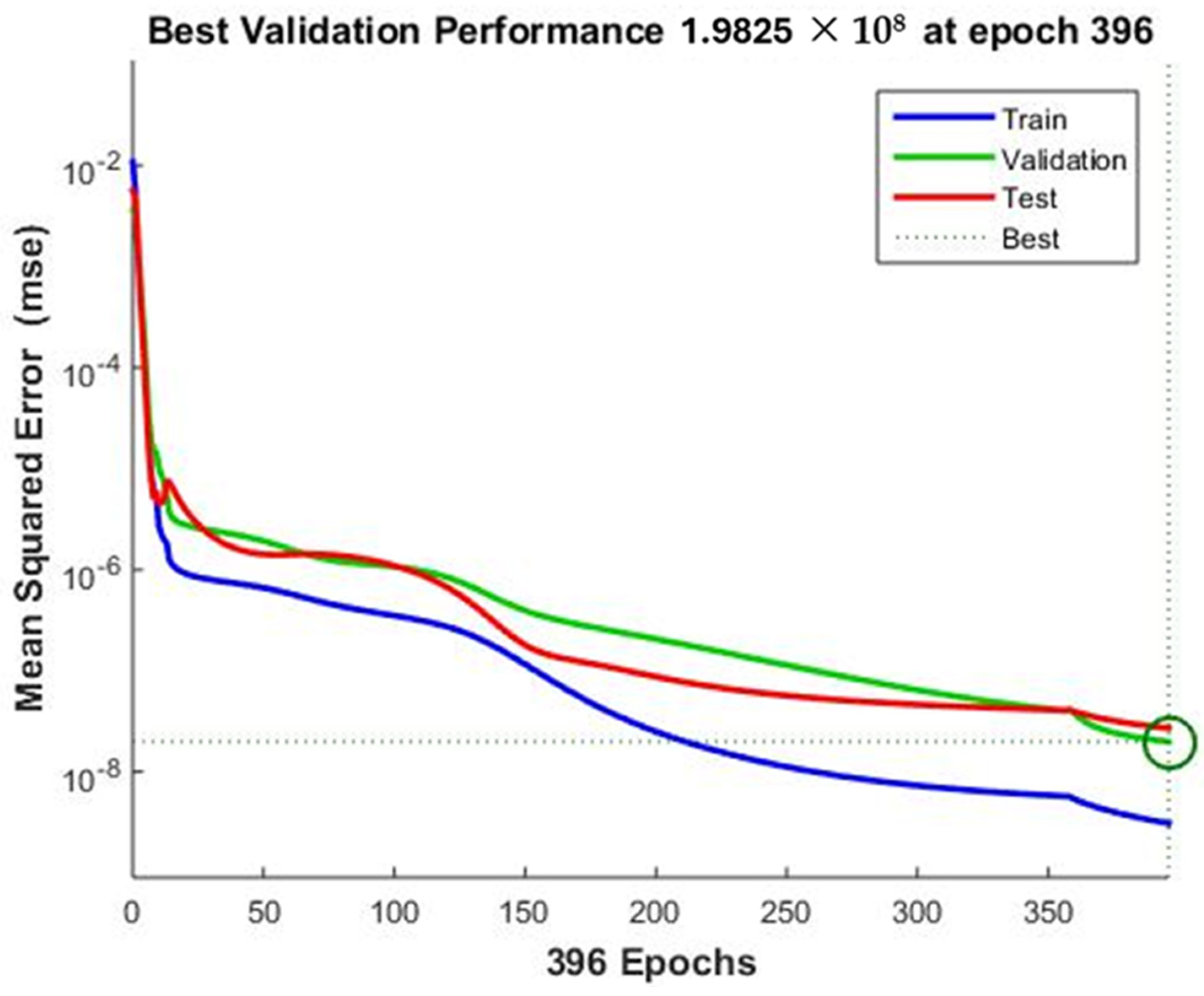
3.3. ANN Modeling
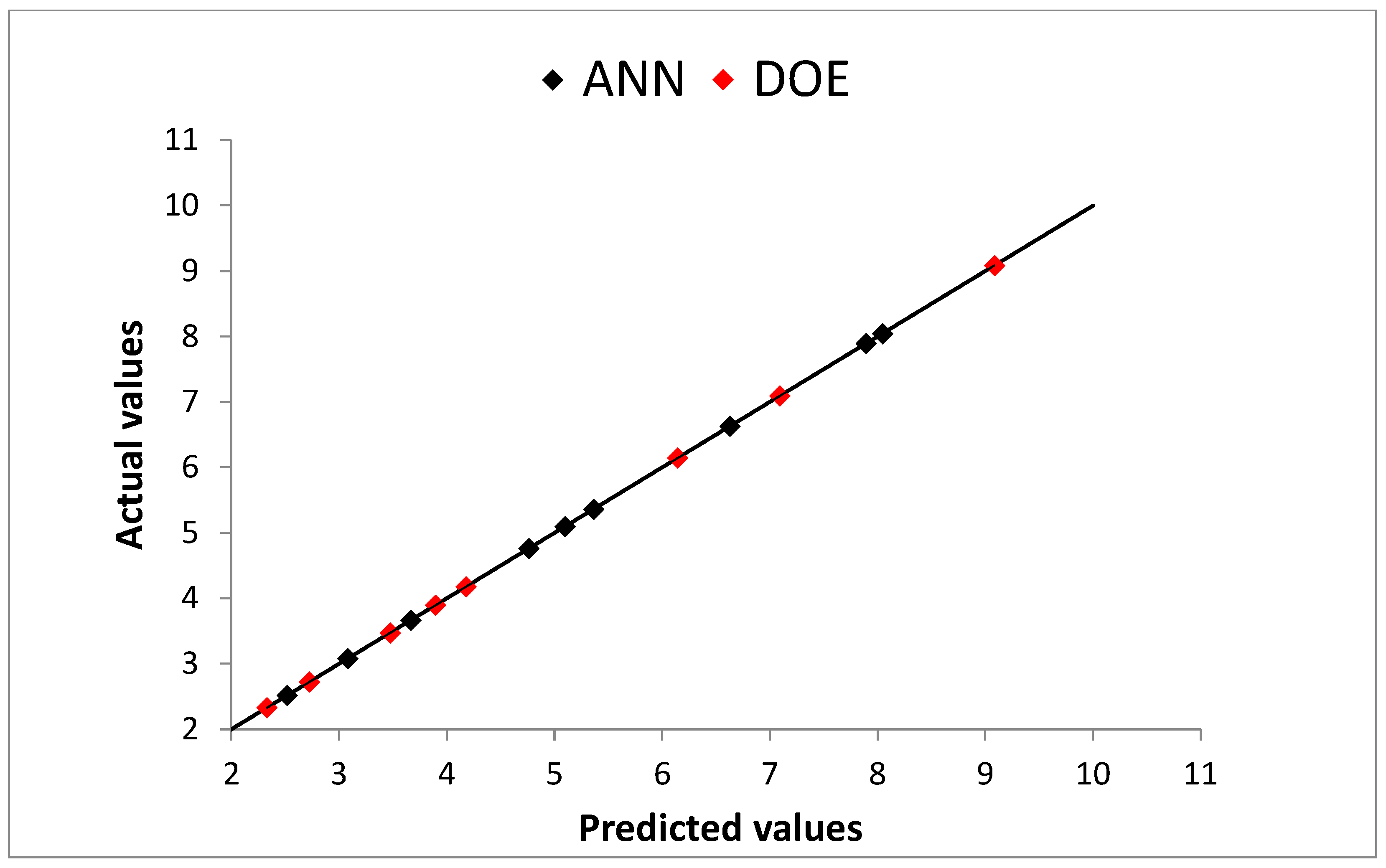
- Comparison of the developed DOE and ANN models
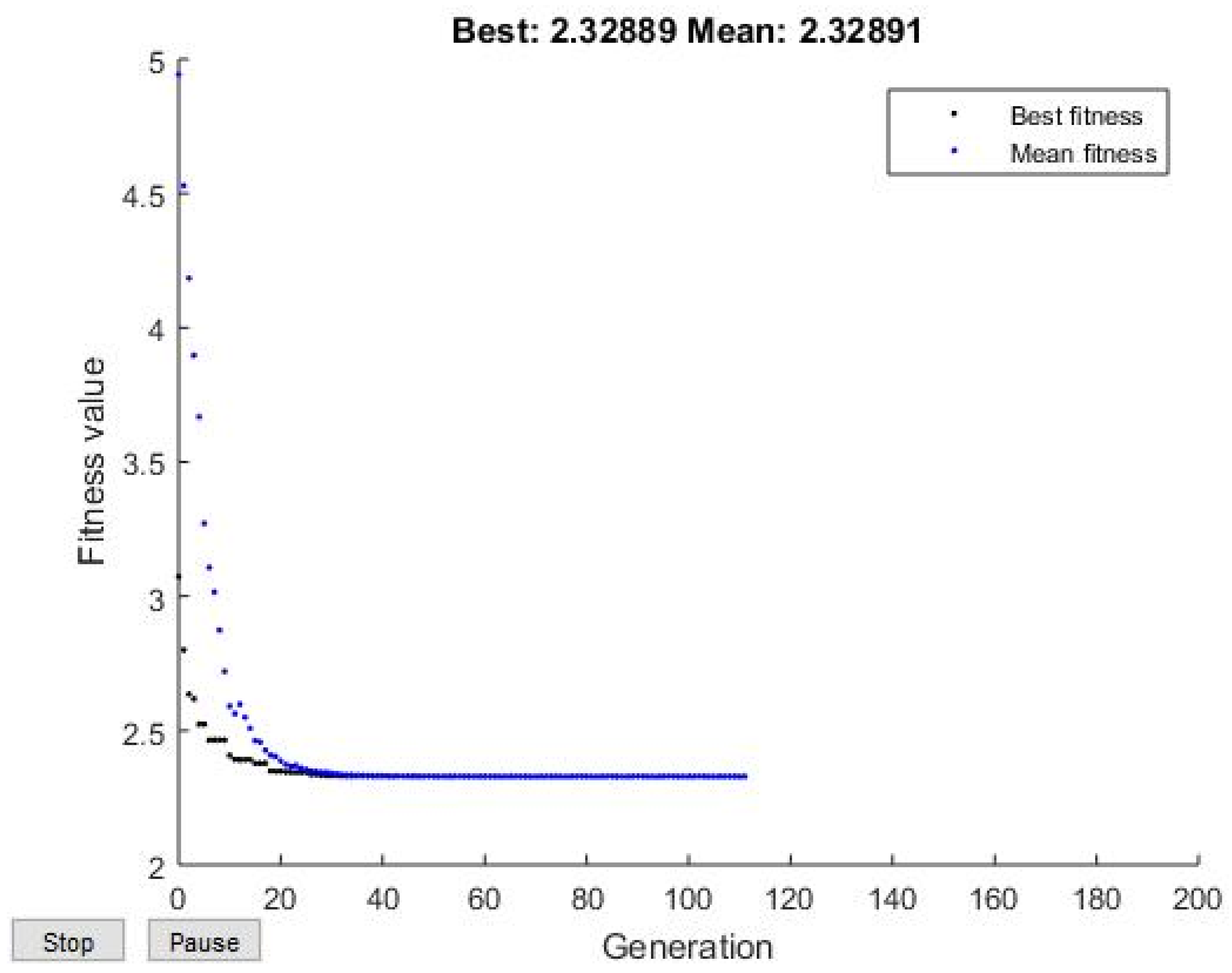
3.4. GA Optimization
- Comparison between DOE-GA, ANN-GA, and DOE-DF
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bauer, N.; Calvin, K.; Emmerling, J.; Fricko, O.; Fujimori, S.; Hilaire, J.; Eom, J.; Krey, V.; Kriegler, E.; Mouratiadou, I.; et al. Shared Socio-Economic Pathways of the Energy Sector–Quantifying the Narratives. Glob. Environ. Chang. 2017, 42, 316–330. [Google Scholar] [CrossRef]
- Bridge, G.; Özkaynak, B.; Turhan, E. Energy Infrastructure and the Fate of the Nation: Introduction to Special Issue. Energy Res. Soc. Sci. 2018, 41, 1–11. [Google Scholar] [CrossRef]
- Muggeridge, A.; Cockin, A.; Webb, K.; Frampton, H.; Collins, I.; Moulds, T.; Salino, P. Recovery Rates, Enhanced Oil Recovery and Technological Limits. Phil. Trans. R. Soc. A 2014, 372, 20120320. [Google Scholar] [CrossRef] [PubMed]
- Leach, A.; Mason, C.F.; van‘t Veld, K. Co-Optimization of Enhanced Oil Recovery and Carbon Sequestration. Resour. Energy Econ. 2011, 33, 893–912. [Google Scholar] [CrossRef]
- Tiong, A.C.Y.; Tan, I.S.; Foo, H.C.Y.; Lam, M.K.; Ben Mahmud, H.; Lee, K.T. A Mini-Investigation on Enhanced Oil Recovery Evolution (2007–2020). MATEC Web Conf. 2023, 377, 01015. [Google Scholar] [CrossRef]
- Vasilenko, V.A.; Vasilenko, V.A.; Skichko, E.A.; Sakharov, D.A.; Safarov, R.R.; Gordienko, M.G.; Oleinik, A.V. An Analysis of the Intellectual Property Market in the Field of Enhanced Oil Recovery Methods. Designs 2021, 5, 1. [Google Scholar] [CrossRef]
- Nikolova, C.; Gutierrez, T. Use of Microorganisms in the Recovery of Oil from Recalcitrant Oil Reservoirs: Current State of Knowledge, Technological Advances and Future Perspectives. Front. Microbiol. 2020, 10, 2996. [Google Scholar] [CrossRef]
- Lebouachera, S.E.I.; Balamane-Zizi, O.; Boublia, A.; Ghriga, M.A.; Hasanzadeh, M.; Hadri, H.E.; Tassalit, D.; Khodja, M.; Grassl, B.; Drouiche, N. Understanding the Factors Affecting the Adsorption of Surface-Active Agents onto Reservoir Rock in Chemical Enhanced Oil Recovery Applications: A Comprehensive Review. Chem. Afr. 2024, 7, 2283–2306. [Google Scholar] [CrossRef]
- Nazar, M.F.; Shah, S.S.; Khosa, M.A. Microemulsions in Enhanced Oil Recovery: A Review. Pet. Sci. Technol. 2011, 29, 1353–1365. [Google Scholar] [CrossRef]
- Negin, C.; Ali, S.; Xie, Q. Most Common Surfactants Employed in Chemical Enhanced Oil Recovery. Petroleum 2017, 3, 197–211. [Google Scholar] [CrossRef]
- Hosseini-Nasab, S.M.; Zitha, P.L.J.; Mirhaj, S.A.; Simjoo, M. A New Chemical-Enhanced Oil Recovery Method? Colloids Surf. A Physicochem. Eng. Asp. 2016, 507, 89–95. [Google Scholar] [CrossRef]
- Ar-Raihan, M.H.; Salsabila, R.; Adharis, A.; Ratri, P.J.; Mayangsari, T.R. Analysis of Surfactant and Polymer Behavior on Water/Oil Systems as Additives in Enhanced Oil Recovery (EOR) Technology through Molecular Dynamics Simulation: A Preliminary Study. J. Earth Energy Eng. 2023, 12, 27–39. [Google Scholar] [CrossRef]
- Sampora, Y.; Juwono, A.L.; Haryono, A.; Irawan, Y. Study of Synthesis Polyethylene Glycol Oleate Sulfonated as an Anionic Surfactant for Enhanced Oil Recovery (EOR). J. Phys. Conf. Ser. 2017, 909, 012078. [Google Scholar] [CrossRef]
- Koreh, P.; Lashkarbolooki, M.; Peyravi, M.; Al-Saedi, H. Applying membrane technology for preparing low salinity for hybrid nanofluid, surfactant, and alkaline enhanced oil recovery process. J. Fuel 2025, 390, 134713. [Google Scholar] [CrossRef]
- Maia, K.C.B.; Densy dos Santos Francisco, A.; Moreira, M.P.; Nascimento, R.S.V.; Grasseschi, D. Advancements in Surfactant Carriers for Enhanced Oil Recovery: Mechanisms, Challenges, and Opportunities. ACS Omega 2024, 9, 36874–36903. [Google Scholar] [CrossRef]
- Gbadamosi, A.; Patil, S.; Al Shehri, D.; Kamal, M.S.; Hussain, S.M.S.; Al-Shalabi, E.W.; Hassan, A.M. Recent Advances on the Application of Low Salinity Water flooding and Chemical Enhanced Oil Recovery. Energy Rep. 2022, 8, 9969–9996. [Google Scholar] [CrossRef]
- Thakur, G. Enhanced Recovery Technologies for Unconventional Oil Reservoirs. J. Pet. Technol. 2019, 71, 66–69. [Google Scholar] [CrossRef]
- Massarweh, O.; Abushaikha, A.S. A Review of Recent Developments in CO2 Mobility Control in Enhanced Oil Recovery. Petroleum 2022, 8, 291–317. [Google Scholar] [CrossRef]
- Lebouachera, S.E.I.; Chemini, R.; Khodja, M.; Grassl, B.; Tassalit, D.; Drouiche, N. Experimental Investigations of SDS Adsorption on the Algerian Rock Reservoir: Chemical Enhanced Oil Recovery Case. Res. Chem. Intermed. 2018, 44, 7665–7690. [Google Scholar] [CrossRef]
- Alhassawi, H.; Romero-Zerón, L. Novel Surfactant Delivery System for Controlling Surfactant Adsorption onto Solid Surfaces. Part II: Dynamic adsorption tests. Can. J. Chem. Eng. 2015, 93, 1371–1379. [Google Scholar] [CrossRef]
- Lebouachera, S.; Boublia, A.; Hadji, M.; Ghriga, M.A.; Tassalit, D.; Khodja, M.; Grassi, B.; Drouiche, N. Mini-review on the evaluation of thermodynamic parameters for surfactants adsorption onto rock reservoirs: cEOR applications. J. Chem. Pap. 2025, 79, 655–666. [Google Scholar] [CrossRef]
- Al-Azani, K.; Abu-Khamsin, S.; Kamal, M.S.; Shirish, P.; Shakil Hussain, S.M.; Norrman, K. Enhanced Oil Recovery in Heterogeneous Carbonate Rocks Using a Gemini Surfactant under Harsh Conditions. J. Energy Fuels 2025, 39, 3433–3445. [Google Scholar] [CrossRef]
- Belhaj, A.F.; Elraies, K.A.; Mahmood, S.M.; Zulkifli, N.N.; Akbari, S.; Hussien, O.S. The effect of surfactant concentration, salinity, temperature, and pH on surfactant adsorption for chemical enhanced oil recovery: A review. J. Petrol. Explor. Prod. Technol. 2020, 10, 125–137. [Google Scholar] [CrossRef]
- Bhui, U.K.; Sanyal, S.; Saha, R.; Rakshit, S.; Pal, S.K. Steady-State and Time-Resolved Fluorescence Spectroscopic Study of Petroleum Crudes in Aqueous-Surfactant Solutions: Its Implications for Enhanced Oil Recovery (EOR) during Surfactant Flooding. Fuel 2018, 234, 1081–1088. [Google Scholar] [CrossRef]
- Ma, L.; Xu, P.; Wang, L.; Xia, K.; Du, H.; Gao, R.; Chen, Z. Study on Anionic–Nonionic Mixed Surfactant for Enhanced Oil Recovery in a Hypersaline Reservoir. RSC Adv. 2024, 14, 552–559. [Google Scholar] [CrossRef]
- Prasad, T.; Raj, S.; Kundu, D. Artificial Neural Network Framework for the Selection of Deep Eutectic Solvents Promoted Enhanced Oil Recovery by Interfacial Tension Reduction Mechanism. Energy 2024, 307, 132602. [Google Scholar] [CrossRef]
- Javadi, A.; Moslemizadeh, A.; SheikholMoluki, V.; Fathianpour, N.; Mohammadzadeh, O.; Zendehboudi, S. A Combination of Artificial Neural Network and Genetic Algorithm to Optimize Gas Injection: A Case Study for EOR Applications. J. Mol. Liq. 2021, 339, 116654. [Google Scholar] [CrossRef]
- Chen, G.; Fu, K.; Liang, Z.; Sema, T.; Li, C.; Tontiwachwuthikul, P.; Idem, R. The Genetic Algorithm Based Back Propagation Neural Network for MMP Prediction in CO2-EOR Process. Fuel 2014, 126, 202–212. [Google Scholar] [CrossRef]
- Weile, D.S.; Michielssen, E. Genetic Algorithm Optimization Applied to Electromagnetics: A Review. IEEE Trans. Antennas Propagat. 1997, 45, 343–353. [Google Scholar] [CrossRef]
- Sangwan, K.S.; Saxena, S.; Kant, G. Optimization of Machining Parameters to Minimize Surface Roughness Using Integrated ANN-GA Approach. Procedia CIRP 2015, 29, 305–310. [Google Scholar] [CrossRef]
- Belhaj, A.F.; Elraies, K.A.; Alnarabiji, M.S.; Abdul Kareem, F.A.; Shuhli, J.A.; Mahmood, S.M.; Belhaj, H. Experimental Investigation, Binary Modelling and Artificial Neural Network Prediction of Surfactant Adsorption for Enhanced Oil Recovery Application. Chem. Eng. J. 2021, 406, 127081. [Google Scholar] [CrossRef] [PubMed]
- Moosavi, S.R.; Wood, D.A.; Ahmadi, M.A.; Choubineh, A. ANN-Based Prediction of Laboratory-Scale Performance of CO2-Foam Flooding for Improving Oil Recovery. Nat. Resour. Res. 2019, 28, 1619–1637. [Google Scholar] [CrossRef]
- Sun, Q.; Ertekin, T. Screening and Optimization of Polymer Flooding Projects Using Artificial-Neural-Network (ANN) Based Proxies. J. Pet. Sci. Eng. 2020, 185, 106617. [Google Scholar] [CrossRef]
- Le Van, S.; Chon, B. Artificial Neural Network Model for Alkali-Surfactant-Polymer Flooding in Viscous Oil Reservoirs: Generation and Application. Energies 2016, 9, 1081. [Google Scholar] [CrossRef]
- Lebouachera, S.E.I.; Chemini, R.; Khodja, M.; Grassl, B.; AbdelfetahGhriga, M.; Tassalit, D.; Drouiche, N. Experimental Design Methodology as a Tool to Optimize the Adsorption of New Surfactant on the Algerian Rock Reservoir: cEOR Applications. Eur. Phys. J. Plus 2019, 134, 436. [Google Scholar] [CrossRef]
- Barati, A.; Najafi, A.; Daryasafar, A.; Nadali, P.; Moslehi, H. Adsorption of a New Nonionic Surfactant on Carbonate Minerals in Enhanced Oil Recovery: Experimental and Modeling Study. Chem. Eng. Res. Des. 2016, 105, 55–63. [Google Scholar] [CrossRef]
- Yuan, N.; Wang, S.; Yu, Y.; Chen, C.; Shiau, B.-J.; Harwell, J.H. Expanded Salinity Window of Middle-Phase Microemulsions and Reduced Surfactant Adsorption by Hydrotrope. Langmuir 2023, 39, 17175–17189. [Google Scholar] [CrossRef]
- Mohd Musa, M.S.; Gopalan, P.Y.; Yekeen, N.; Al-Yaseri, A. Influence of Henna Extracts on Static and Dynamic Adsorption of Sodium Dodecyl Sulfate and Residual Oil Recovery from Quartz Sand. ACS Omega 2023, 8, 13118–13130. [Google Scholar] [CrossRef]
- Goupy, J.; Creighton, L. Introduction to Design of Experiments with JMP Examples, 3rd ed.; SAS Institute: Cary, NC, USA, 2007. [Google Scholar]
- Jha, A.K.; Sit, N. Comparison of Response Surface Methodology (RSM) and Artificial Neural Network (ANN) Modelling for Supercritical Fluid Extraction of Phytochemicals from Terminalia Chebula Pulp and Optimization Using RSM Coupled with Desirability Function (DF) and Genetic Algorithm (GA) and ANN with GA. Ind. Crops Prod. 2021, 170, 113769. [Google Scholar] [CrossRef]
- Kumar, S.S.; Prasad, C.D.; Hanumanthappa, H.; Choudhary, R.K.; Sollapur, S.B. Numerical analysis of thermal spray coatings using artificial neural networks (ANN) overview. Int. J. Interact. Des. Manuf. 2025, 19, 1533–1548. [Google Scholar] [CrossRef]
- Tabatabaei, S.M.; Attari, N.; Panahi, S.A.; Asadian-Pakfar, M.; Sedaee, B. EOR Screening Using Optimized Artificial Neural Network by Sparrow Search Algorithm. Geoenergy Sci. Eng. 2023, 229, 212023. [Google Scholar] [CrossRef]
- Jani, D.B.; Mishra, M.; Sahoo, P.K. Application of Artificial Neural Network for Predicting Performance of Solid Desiccant Cooling Systems–A Review. Renew. Sustain. Energy Rev. 2017, 80, 352–366. [Google Scholar] [CrossRef]
- Kalam, S.; Yousuf, U.; Abu-Khamsin, S.A.; Waheed, U.B.; Khan, R.A. An ANN Model to Predict Oil Recovery from a 5-Spot Waterflood of a Heterogeneous Reservoir. J. Pet. Sci. Eng. 2022, 210, 110012. [Google Scholar] [CrossRef]
- Ahmadi, M.A. Developing a Robust Surrogate Model of Chemical Flooding Based on the Artificial Neural Network for Enhanced Oil Recovery Implications. Math. Probl. Eng. 2015, 2015, 706897. [Google Scholar] [CrossRef]
- Benramdane, I.K.; Nasrallah, N.; Amrane, A.; Kebir, M.; Trari, M.; Fourcade, F.; Assadi, A.A.; Maachi, R. Optimization of the Artificial Neuronal Network for the Degradation and Mineralization of Amoxicillin Photoinduced by the Complex Ferrioxalate with a Gradual and Progressive Approach of the Ligand. J. Photochem. Photobiol. A Chem. 2021, 406, 112982. [Google Scholar] [CrossRef]
- Moradi, M.J.; Khaleghi, M.; Salimi, J.; Farhangi, V.; Ramezanianpour, A.M. Predicting the Compressive Strength of Concrete Containing Metakaolin with Different Properties Using ANN. Measurement 2021, 183, 109790. [Google Scholar] [CrossRef]
- Abbasi, M.; Soleymani, A.R.; Parsa, J.B. Degradation of Rhodamine B by an Electrochemical Ozone Generating System Consist of a Ti Anode Coated with Nanocomposite of Sn–Sb–Ni Oxide. Process Saf. Environ. Prot. 2015, 94, 140–148. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Abdalla, A.A.; Mohammed, A.S.; Mohammed, A.A. Mathematical Modeling Techniques to Predict the Compressive Strength of High-Strength Concrete Incorporated Metakaolin with Multiple Mix Proportions. Clean. Mater. 2022, 5, 100132. [Google Scholar] [CrossRef]
- Khataee, A.R.; Kasiri, M.B. Artificial Neural Networks Modeling of Contaminated Water Treatment Processes by Homogeneous and Heterogeneous Nanocatalysis. J. Mol. Catal. A Chem. 2010, 331, 86–100. [Google Scholar] [CrossRef]
- Asteris, P.G.; Lemonis, M.E.; Le, T.-T.; Tsavdaridis, K.D. Evaluation of the Ultimate Eccentric Load of Rectangular CFSTs Using Advanced Neural Network Modeling. Eng. Struct. 2021, 248, 113297. [Google Scholar] [CrossRef]
- Amar, M.N.; Zeraibi, N.; Ghahfarokhi, A.J. Applying Hybrid Support Vector Regression and Genetic Algorithm to Water Alternating CO2 Gas EOR. Greenh. Gases Sci. Technol. 2020, 10, 613–630. [Google Scholar] [CrossRef]
- Emera, M.K.; Sarma, H.K. Use of Genetic Algorithm to Estimate CO2–Oil Minimum Miscibility Pressure—A Key Parameter in Design of CO2 Miscible Flood. J. Pet. Sci. Eng. 2005, 46, 37–52. [Google Scholar] [CrossRef]
- Liu, D.; Agarwal, R.; Li, Y. Numerical Simulation and Optimization of CO2 Enhanced Shale Gas Recovery Using a Genetic Algorithm. J. Clean. Prod. 2017, 164, 1093–1104. [Google Scholar] [CrossRef]
- Shende, A.S.; Joshi, T.J.; Rao, P.S. Process Optimization of Microwave-Assisted Aqueous Extraction of Tannins and Saponins from Malabar Spinach (Basella alba) Leaves Using ANN-GA and RSM Methodology. Meas. Food 2024, 13, 100117. [Google Scholar] [CrossRef]
- HemmatEsfe, M.; Alidoust, S. Modeling and Precise Prediction of Thermophysical Attributes of Water/EG Blend-Based CNT Nanofluids by NSGA-II Using ANN and RSM. Arab. J. Sci. Eng. 2021, 46, 6423–6437. [Google Scholar] [CrossRef]
- HemmatEsfe, M.; Saedodin, S.; Bahiraei, M.; Esfandeh, S. Preliminary Feasibility Study on Using a Nano-Composition in Enhanced Oil Recovery Process: Neural Network Modeling. Neural Comput. Appl. 2021, 33, 10111–10127. [Google Scholar] [CrossRef]
- Halima, D.; Djelloul, B.; Mehdi, G.; Camel, T.; Ali, B.; Bouchra, B. Solar Radiation Estimation Based on a New Combined Approach of Artificial Neural Networks (ANN) and Genetic Algorithms (GA) in South Algeria. CMC 2024, 79, 4725–4740. [Google Scholar] [CrossRef]
- NabizadehChianeh, F.; Basiri Parsa, J.; RezaeiVahidian, H. Artificial Neural Network Modeling for Removal of Azo Dye from Aqueous Solutions by Ti Anode Coated with Multiwall Carbon Nanotubes. Environ. Prog. Sustain. Energy 2017, 36, 1778–1784. [Google Scholar] [CrossRef]
- KiannejadAmiri, M.; GhorbanzadeZaferani, S.P.; SarmastiEmami, M.R.; Zahmatkesh, S.; Pourhanasa, R.; SadeghiNamaghi, S.; Klemeš, J.J.; Bokhari, A.; Hajiaghaei-Keshteli, M. Multi-Objective Optimization of Thermophysical Properties GO Powders-DW/EG Nf by RSM, NSGA-II, ANN, MLP and ML. Energy 2023, 280, 128176. [Google Scholar] [CrossRef]
- Onu, C.E.; Nwabanne, J.T.; Ohale, P.E.; Asadu, C.O. Comparative Analysis of RSM, ANN and ANFIS and the Mechanistic Modeling in Eriochrome Black-T Dye Adsorption Using Modified Clay. S. Afr. J. Chem. Eng. 2021, 36, 24–42. [Google Scholar] [CrossRef]
- Igwegbe, C.A.; Mohmmadi, L.; Ahmadi, S.; Rahdar, A.; Khadkhodaiy, D.; Dehghani, R.; Rahdar, S. Modeling of Adsorption of Methylene Blue Dye on Ho-CaWO4 Nanoparticles Using Response Surface Methodology (RSM) and Artificial Neural Network (ANN) Techniques. MethodsX 2019, 6, 1779–1797. [Google Scholar] [CrossRef] [PubMed]
- Gomez, C.; Ruiz, D.; Cely, M. Specialist System in Flow Pattern Identification Using Artificial Neural Networks. J. Appl. Eng. Sci. 2023, 21, 285–299. [Google Scholar] [CrossRef]
- Hasanzadeh, M.; Farahani, M.D.; Far, H.S.; Lebouachera, S.E.I. Modeling of Textile Dye Removal from Aqueous Solution with a Zr-MOF Framework: Design of Experiments and Artificial Neural Network Approaches. Emergent Mater. 2024, 7, 2583–2593. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous Optimization of Several Response Variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]




| Factors | Low level (−1) | Highlevel (+1) |
|---|---|---|
| X1 (Surfactant choice) | SDS | EOR ASP 5100 |
| X2 (Concentration of surfactant) | 200 | 800 |
| X3 (Temperature in °C) | 25 | 80 |
| Network Types | Feed Forward Backpropagation |
|---|---|
| Cascade Forward Backpropagation | |
| Training function | Trainscg |
| TrainLM | |
| Adaptation learning function | learngd |
| learngdm | |
| Transfer function for Hiden | tansig |
| logsig | |
| Transfer function for output layer | tansig |
| purelin | |
| Number of neurons in the hidden layer | 12 |
| Population size | 50 |
| Number of generation | 200 |
| Crossover fraction | 0.8 |
| Mutation rate | 0.01 |
| N | Input | Output | |||||
|---|---|---|---|---|---|---|---|
| 1 | Surfactant | Concentration of surfactant | Temperature | Qe | |||
| 2 | uncoded value | coded value | uncoded value | coded value | uncoded value | coded value | |
| 3 | SDS | −1 | 200 | −1 | 25 | −1 | 2.3288125 |
| 4 | EOR ASP 5100 | 1 | 200 | −1 | 25 | −1 | 2.7228875 |
| 5 | SDS | −1 | 800 | 1 | 25 | −1 | 4.1765875 |
| 6 | EOR ASP 5100 | 1 | 800 | 1 | 25 | −1 | 7.0920125 |
| 7 | SDS | −1 | 200 | −1 | 80 | 1 | 3.4739875 |
| 8 | EOR ASP 5100 | 1 | 200 | −1 | 80 | 1 | 3.8946125 |
| 9 | SDS | −1 | 800 | 1 | 80 | 1 | 6.1436125 |
| 10 | EOR ASP 5100 | 1 | 800 | 1 | 80 | 1 | 9.0855875 |
| 11 | SDS | −1 | 220 | −0.93333333 | 26 | −0.96363636 | 2.41172445 |
| 12 | EOR ASP 5100 | 1 | 220 | −0.93333333 | 26 | −0.96363636 | 2.89032718 |
| 13 | SDS | −1 | 240 | −0.86666667 | 28 | −0.89090909 | 2.51745014 |
| 14 | EOR ASP 5100 | 1 | 240 | −0.86666667 | 28 | −0.89090909 | 3.08106332 |
| 15 | SDS | −1 | 260 | −0.8 | 30 | −0.81818182 | 2.62516818 |
| 16 | EOR ASP 5100 | 1 | 260 | −0.8 | 30 | −0.81818182 | 3.27379182 |
| 17 | SDS | −1 | 280 | −0.73333333 | 32 | −0.74545455 | 2.73487859 |
| 18 | EOR ASP 5100 | 1 | 280 | −0.73333333 | 32 | −0.74545455 | 3.46851268 |
| 19 | SDS | −1 | 300 | −0.66666667 | 34 | −0.67272727 | 2.84658136 |
| 20 | EOR ASP 5100 | 1 | 300 | −0.66666667 | 34 | −0.67272727 | 3.66522591 |
| 21 | SDS | −1 | 320 | −0.6 | 36 | −0.6 | 2.9602765 |
| 22 | EOR ASP 5100 | 1 | 320 | −0.6 | 36 | −0.6 | 3.8639315 |
| 23 | SDS | −1 | 340 | −0.53333333 | 38 | −0.52727273 | 3.075964 |
| 24 | EOR ASP 5100 | 1 | 340 | −0.53333333 | 38 | −0.52727273 | 4.06462945 |
| 25 | SDS | −1 | 360 | −0.46666667 | 40 | −0.45454546 | 3.19364386 |
| 26 | EOR ASP 5100 | 1 | 400 | −0.33333333 | 44 | −0.30909091 | 4.6786775 |
| 27 | SDS | −1 | 420 | −0.26666667 | 46 | −0.23636364 | 3.55863764 |
| 38 | EOR ASP 5100 | 1 | 420 | −0.26666667 | 46 | −0.23636364 | 4.88734491 |
 |  |  |  |  |  |  |  |
| 69 | EOR ASP 5100 | 1 | 760 | 0.86666667 | 67 | 0.52727273 | 8.28126423 |
| 70 | SDS | −1 | 770 | 0.9 | 69 | 0.6 | 5.62494475 |
| 71 | EOR ASP 5100 | 1 | 770 | 0.9 | 69 | 0.6 | 8.43554225 |
| 72 | SDS | −1 | 780 | 0.93333333 | 71 | 0.67272727 | 5.737231 |
| 73 | EOR ASP 5100 | 1 | 780 | 0.93333333 | 71 | 0.67272727 | 8.59081645 |
| 74 | SDS | −1 | 785 | 0.95 | 73 | 0.74545455 | 5.82913822 |
| 75 | EOR ASP 5100 | 1 | 785 | 0.95 | 73 | 0.74545455 | 8.70470038 |
| 76 | SDS | −1 | 790 | 0.96666667 | 75 | 0.81818182 | 5.92154352 |
| Network No. | Network Type | Training Function | Adaptation Learning Function | Transfer Function | Output (Qe) | ||
|---|---|---|---|---|---|---|---|
| Hidden Layer | Output Layer | MSE | R2 | ||||
| 1 | Feed Forward Backpropagation | trainlm | learngd | tansig | purelin | 0.00192256 | 0.999718645 |
| 2 | tansig | 0.049768699 | 0.992988724 | ||||
| 3 | logsig | purelin | 0.000654851 | 0.996762602 | |||
| 4 | tansig | 0.000104353 | 0.999984644 | ||||
| 5 | learngdm | tansig | purelin | 0.013302013 | 0.998028686 | ||
| 6 | tansig | 0.001047364 | 0.999845396 | ||||
| 7 | logsig | purelin | 0.020678007 | 0.997024576 | |||
| 8 | tansig | 0.01179353 | 0.998244096 | ||||
| 9 | trainscg | learngd | tansig | purelin | 0.010965378 | 0.998402231 | |
| 10 | tansig | 0.02787814 | 0.995591963 | ||||
| 11 | logsig | purelin | 0.059602925 | 0.991226048 | |||
| 12 | tansig | 0.031101368 | 0.995437096 | ||||
| 13 | learngdm | tansig | purelin | 0.001270703 | 0.999812559 | ||
| 14 | tansig | 0.014380639 | 0.997867883 | ||||
| 15 | logsig | purelin | 0.014368615 | 0.997889598 | |||
| 16 | tansig | 0.083067505 | 0.987482642 | ||||
| 17 | Cascade Forward Back propagation | trainlm | learngd | tansig | purelin | 0.000309774 | 0.999954487 |
| 18 | tansig | 0.032258779 | 0.995362984 | ||||
| 19 | logsig | purelin | 0.004887721 | 0.99927919 | |||
| 20 | tansig | 9.10106 × 10−6 | 0.999998662 | ||||
| 21 | learngdm | tansig | purelin | 8.90312×10−7 | 0.999999869 | ||
| 22 | tansig | 0.000254115 | 0.9999626 | ||||
| 23 | logsig | purelin | 0.001304255 | 0.999809106 | |||
| 24 | tansig | 0.000634489 | 0.99990587 | ||||
| 25 | trainscg | learngd | tansig | purelin | 0.004647879 | 0.999318984 | |
| 26 | tansig | 0.025080224 | 0.996315409 | ||||
| 27 | logsig | purelin | 0.004459436 | 0.99934599 | |||
| 28 | tansig | 0.015544225 | 0.997674503 | ||||
| 29 | learngdm | tansig | purelin | 0.191194234 | 0.970380954 | ||
| 30 | tansig | 0.00494906 | 0.999252877 | ||||
| 31 | logsig | purelin | 0.042068385 | 0.993766037 | |||
| 32 | tansig | 0.009195451 | 0.998631633 | ||||
| Number of Neurons | MSE | R2 |
|---|---|---|
| 1 | 0.009853974956 | 0.998539413722 |
| 2 | 0.005177182735 | 0.999239763890 |
| 3 | 0.000036998429 | 0.999994569068 |
| 4 | 0.000000006840 | 0.999999998995 |
| 5 | 0.000000008452 | 0.999999999611 |
| 6 | 0.000000087957 | 0.999999987078 |
| 7 | 0.000003739225 | 0.999999450701 |
| 8 | 0.000000668454 | 0.999999901797 |
| 9 | 0.000000171151 | 0.999999974857 |
| 10 | 0.000000890312 | 0.999999869212 |
| 11 | 0.283142838389 | 0.958860619811 |
| 12 | 0.061986921414 | 0.990618200261 |
| DOE | ANN | |
|---|---|---|
| 1.00014 | 1.000016 | |
| CV | 0.010022 | 0.00165 |
| VAB | 0.000132 | 0.000015 |
| PF/3 | 0.01212 | 0.00157 |
| Coefficient of determination (R2) | 0.99 | 0.99 |
| Relative error (%) | 9.10927 × 10−5 | 1.87966 × 10−4 |
| MSE | 2.37656 × 10−7 | 6.84028 × 10−9 |
| Optimization Methods | DOE-GA | ANN-GA | DOE-DF |
|---|---|---|---|
| Optimum conditions | SDS, 200 ppm, and 25 °C | ||
| Predicted response | 2.32889 | 2.3247 | 2.3289 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benramdane, K.I.; Hadji, M.E.M.; Khodja, M.; Drouiche, N.; Grassl, B.; Lebouachera, S.E.I. Surfactants Adsorption onto Algerian Rock Reservoir for Enhanced Oil Recovery Applications: Prediction and Optimization Using Design of Experiments, Artificial Neural Networks, and Genetic Algorithm (GA). Colloids Interfaces 2025, 9, 19. https://doi.org/10.3390/colloids9020019
Benramdane KI, Hadji MEM, Khodja M, Drouiche N, Grassl B, Lebouachera SEI. Surfactants Adsorption onto Algerian Rock Reservoir for Enhanced Oil Recovery Applications: Prediction and Optimization Using Design of Experiments, Artificial Neural Networks, and Genetic Algorithm (GA). Colloids and Interfaces. 2025; 9(2):19. https://doi.org/10.3390/colloids9020019
Chicago/Turabian StyleBenramdane, Kahina Imene, Mohamed El Moundhir Hadji, Mohamed Khodja, Nadjib Drouiche, Bruno Grassl, and Seif El Islam Lebouachera. 2025. "Surfactants Adsorption onto Algerian Rock Reservoir for Enhanced Oil Recovery Applications: Prediction and Optimization Using Design of Experiments, Artificial Neural Networks, and Genetic Algorithm (GA)" Colloids and Interfaces 9, no. 2: 19. https://doi.org/10.3390/colloids9020019
APA StyleBenramdane, K. I., Hadji, M. E. M., Khodja, M., Drouiche, N., Grassl, B., & Lebouachera, S. E. I. (2025). Surfactants Adsorption onto Algerian Rock Reservoir for Enhanced Oil Recovery Applications: Prediction and Optimization Using Design of Experiments, Artificial Neural Networks, and Genetic Algorithm (GA). Colloids and Interfaces, 9(2), 19. https://doi.org/10.3390/colloids9020019










