Efficient Resource Management for Sum Capacity Maximization in 5G NOMA Systems

Abstract

The modern cellular technologies are expected to provide high data rates and massive connectivity in fifth generation (5G) systems; however, this may be impossible through traditional radio access techniques. Recently, non-orthogonal multiple access (NOMA) has emerged as one of the promising cellular techniques for modern cellular communications with its ability to provide access for multiple users to the network over the same system resources. This paper studies resource management problem for downlink transmission of multiuser NOMA system. Our objective is to optimize both frequency and power resources for sum capacity maximization while taking into account each user minimum capacity requirement. Firstly, the problem of resource management decouples into two subproblems, that is, efficient sub-channel assignment and optimal power allocation, respectively. Secondly, for given power at base station, we design two sub-optimal algorithms for sub-channel assignment based on user channel condition and user minimum capacity requirement, respectively. Lastly, for any given sub-channel assignment, the problem first transforms into standard convex optimization problem and then we employ duality theory. To evaluate our proposed NOMA scheme, the enhanced version of existing NOMA optimization scheme is also presented as a benchmark. Results demonstrate that the proposed NOMA resource management scheme outperforms the benchmark NOMA optimization scheme in terms of sum capacity.

1. Introduction

The existing generations of communication networks like third generation (3G) and fourth generation (4G), orthogonal multiple access (OMA) technologies such as code-division multiple access (CDMA) and orthogonal frequency division multiple access (OFDMA) have been widely adopted by academia and industry. Although these technologies can significantly reduce the inter-user interference, the objective of high spectral efficiency and massive connectivity is a far cry and need to be further improved [1]. The next generations such as fifth generation (5G) and beyond 5G (5GB) mobile networks are expected to provide ultra-high data rates and meet with the explosive growth of wireless connections [2]. In order to fulfill these demands, new radio access techniques are actively pursued and explored. Recently, non-orthogonal multiple access (NOMA) has been emerged as one of the best candidates for 5G and B5G cellular networks and received tremendous interest from research community due to its potential of connecting more users on the same system resources [3,4]. In the downlink wireless transmission, with the help of superposition coding at the base station (BS), NOMA can multiplex multiple users at the same resource and time [5]. The BS assigns low transmit power to the user with better channel and high transmit power to the one with weaker channel to facilitate successive interference cancellation (SIC) process at the receivers [6]. After receiving the signals from BS, the strong user applies SIC technique to remove the signal of weak user before decoding its own signal. However, weak user can not apply SIC and receives the signal with the interference of a strong user [7].

Besides the advantages of high spectral efficiency and massive connectivity, NOMA faces a number of challenges for successful implementation. The users are required to satisfy the minimum gap among their transmission powers to guarantee the successful process of SIC [8]. The high number of users sharing the same system resources can significantly increase the complexity of SIC at the receivers [9]. Furthermore, different users sharing the same system resources can cause inter-user interference [10]. To overcome these limitations, the network resources need to be efficiently utilized—the process is called optimal resource allocation [11].

1.1. Related Work

Optimization of resource management for NOMA transmission has been studied extensively in literature. For instance, the authors of Reference [12] formulated a resource management problem to enhance the sum capacity of two-user NOMA system. The proposed framework first guarantees the minimum quality of service (QoS) of one mobile user and then allocate the remaining power to other mobile user to maximize the overall system capacity. A price based power optimization scheme was presented in downlink wireless network [13]. The objective was to maximize the revenues and average achievable rate of the proposed network by adopting game theoretic approach. To deal with non-convex optimization, they decouple the problem and use alternating optimization algorithm to obtain the efficient solution. The research in Reference [14] provided a low complexity power allocation to enhance the weighted sum capacity in downlink NOMA systems. They considered two cases, namely a two-use case and a multi-user case and exploited low complex and closed form solutions to solve the non-convex optimization. Yang et al. in Reference [15] proposed a Karush–Kuhn–Tucker (KKT) based solution for power management to enhance the sum capacity of the network subject to a minimum user rate. Ding et al. in Reference [16] investigated the outage performance and ergodic capacity for downlink NOMA network. Under the constraint of interference threshold from the secondary system to the primary system, the power management problem for capacity enhancement and outage probability in two-user cognitive radio NOMA network was proposed in Reference [17]. A proportional fairness scheduling approach was considered for fair power allocation to maximize the sum rate and maximize the minimum of normalized rate in a two-user network [18]. Tan et al. proposed the channel estimation and power management problem for two-user system to maximize the average effective signal to interference plus noise ratio (SINR) of the strong user with bounded average effective SINR of the weak user [19]. To maximize the effective sum capacity with delay QoS constraint, Choi et al. provided a sub-optimal solution based on truncated channel inversion power control in a two-user downlink system [20].

In addition, resource optimization techniques for NOMA in multi-cell communications networks have also been investigated [3,21,22,23,24,25,26]. In Reference [21], a KKT-based efficient power management technique was presented by Khan et al. to enhance the sum capacity of multi-cell multi-user NOMA network. In similar study, a KKT-based closed form solution for power optimization was provided by Yang et al. in multi-cell network to minimize the total system power and maximize the system sum capacity [22]. The study in Reference [23] considered a downlink heterogeneous network (HetNet) based on power multiplexing. The authors formulated a non-convex optimization problem to improve the network capacity and outage probability. They provided sub-optimal algorithm for user scheduling and power allocation. A problem for optimal power allocation was investigated in HetNet based on power multiplexing [24]. The objective of the research was to increase to the network throughput subject to users QoS requirements. They adopted a distributed power approach based on Stackelberg equilibrium. To improve the fairness among different users and enhance the sum rate of the system, Zhao et al. provided an efficient resource management scheme in HetNet [25]. They exploited matching theory for sub-channel assignments to different small-cell BSs and sequential convex programming based on KKT conditions for power allocation at different BSs. Fang et al. in [3] provided energy efficient resource management in NOMA HetNet. They first transformed non-convex optimization to a convex problem and then employed dual method for sub-channel and power allocation. In another study, Song et al. in Reference [26] investigated an optimization problem to reduce total power consumptions in HetNet based on NOMA exploiting power multiplexing. They used a relaxation method to transform the non-convex power allocation problem to a convex problem and derived a closed form solution based on Lagrange method.

Besides the aforementioned advances, a joint power and code multiplexing scheme was presented in 5G and 5GB networks to improve the symbol error rate and sum rate of the system [27]. The proposed framework was compared with the conventional power multiplexing and code multiplexing. Their simulation results shown better performance compared to the baseline schemes. Moreover, the authors of References [28,29] have also provided the rate and power allocation optimization for downlink and uplink transmission in rate splitting multiple access (RSMA) based wireless networks.

1.2. Motivation and Contributions

In this paper, we consider sub-channel assignment and power management problem in multi-user NOMA system to maximize the sum capacity. The main motivation of this work is to enhance the previous work as presented in Reference [12]. Note that the work provided in Reference [12] only consider power allocation for two user network to enhance the sum capacity. Their approach was to satisfy the minimum capacity of first user and then allocate the remaining power to the second user to maximize its capacity. Different from Reference [12], our technique first allocate power to both users to satisfy their minimum capacity requirements and then optimize the remaining power for them to maximize the sum capacity. In addition, we apply two novel algorithms of sub-channel allocation to our proposed power management scheme and to the one in Reference [12]. These algorithms are based on user channel condition and user minimum capacity requirement. Thus, we use Reference [12] as a benchmark scheme in our work.

• Consider a NOMA network using power multiplexing, where a BS intends to communicates with K users through M sub-channels. We formulate a resource management problem for sub-channel assignment and power allocation. Our objective is to maximize the sum capacity of the system subject to the user minimum capacity requirement.
• The problem of resource management decouples into two sub-problems where we fist provide two sub-optimal algorithms for sub-channel assignment under the fixed power of BS. We design these algorithms based on user channel condition and user minimum capacity requirement, respectively. For efficient power allocation, we then transform the optimization problem into standard convex optimization and for any given sub-channel allocation, we exploit dual theory to obtain the optimal solution.
• For a fair comparison, we also consider the work in Reference [12] as a benchmark for power allocation. Reference [12] first satisfy the minimum QoS of one user and then allocates the remaining power to another user to maximize its capacity. Different from the work in Reference [12], we first satisfy the minimum capacity requirements of both users and then optimize the remaining power among these users.
• For simulation results, we apply the sub-channel assignment algorithms to the proposed power allocation scheme and the one in Reference [12]. We also provide the results of the proposed power management technique and the power management technique of Reference [12] for random sub-channel assignment. Results demonstrate that our NOMA technique provides a higher capacity than that in Reference [12].

The reminder of this paper is organized as follows: We discuss the downlink NOMA model and various formulation steps for resource management in Section 2. Section 3 provides resource management with fixed power control while Section 4 presents resource management with optimal power control, respectively. We evaluate and discuss our results in Section 5. Finally, we conclude our paper in Section 4. Table 1 provides the definition of different abbreviations and notations used in this paper.

Table 1. Definition of different abbreviations and notations used in this paper.

Abbreviation	Definition
NOMA	Non-orthogonal multiple access.
3G	Third generation.
4G	Fourth generation.
CDMA	Code-division multiple access.
5G	Fifth generation.
HetNet	Heterogeneous network.
5GB	Beyond 5G.
SC	Sub-channel.
OMA	Orthogonal multiple access.
BS	Base station.
SIC	Successive interference cancellation.
CU	Cellular user.
AWGN	Additive white Gaussian noise.
SINR	Signal-to-noise-plus-interference ratio.
KKT	Karush–Kuhn–Tucker.
RSMA	Rate splitting multiple access.
OFDMA	Orthogonal frequency division multiple access.
Notation	Definition
$\mathcal{K}$	The set of cellular users in the proposed NOMA network.
$\mathcal{M}$	The set of sub-channels in the system.
$U_m$	The set of cellular users on a sub-channel at one time.
$U_{\max }$	The maximum number of cellular users on a sub-channel at one time.
$C{U}_j$	Represents the cellular user j.
$S{C}_j$	Represents the sub-channel m.
$p_{j,m}$	The transmit power of BS for $C{U}_j$ over $S{C}_m$.
$h_{j,m}$	The channel gain of $C{U}_j$ over $S{C}_m$.
$P_{BS}$	The total power of BS.
$y_{j,m}$	The received signal of $C{U}_j$ over $S{C}_m$.
${\omega }_{i,m}$	The data symbol of $C{U}_i$ over $S{C}_m$.
$x_{j,m}$	The AWGN of $C{U}_j$ over $S{C}_m$.
$n_0$	The noise variance of AWGN.
$C_{j,m}$	The capacity of $C{U}_j$ over $S{C}_m$.
${{\rm Y}}_{j,m}$	The SINR of $C{U}_j$ over $S{C}_m$.
${\beta }_{j,m}$	The binary variable for sub-channel allocation.
$S_{\mathrm{sum}}$	The sum capacity of the system.
${\overline{C}}_{\min }$	The minimum user capacity to achieve the QoS requirements.
$\alpha$	The power allocation factor.
$P_m$	The total transmit power on $S{C}_m$.
H	The channel matrix.
R	The matrix of user minimum capacity for QoS requirements.
$P_r$	The remaining power after capacity requirements.
$\mathcal{L}$	The Lagrangian function.
$\lambda ,\eta$	The non-negative Lagrangian multipliers.
$\varphi$	The iteration index.
$\delta$	The non-negative step size.

2. System Model and Problem Formulation

As depicted in Figure 1, a NOMA network exploiting power multiplexing in downlink transmission is considered, where a single BS which is located at the center of the cell and communicates with K different users using NOMA protocol. The K is an even integer and we assume that $\mathcal{K}=\{1,2,3,\cdots ,K\}$ denotes the set of K cellular users. We divide the total spectrum of the system into M sub-channels uniformly, where $\mathcal{M}=\{1,2,3,\cdots ,M\}$ denotes the set of M sub-channels. This network considers single antenna configuration for all its associated nodes. The information of all users is assumed to be available at the source. In addition, we consider independent and identically distributed (i.i.d) Rayleigh fading channels between BS and users. According to the NOMA protocol, we assume that a sub-channel can accommodate more than one user at one time. However, to reduce the SIC complexity at the users, we restrict a sub-channel to accommodate no more than $U_{\max }$ users at one time. This condition also helps to minimize the interference among NOMA users which operate on the same sub-channel. We denote the transmit power of cellular user $C{U}_j\in \mathcal{K}$ on sub-channel $S{C}_m\in \mathcal{M}$ by $p_{j,m}$ while the channel gain between BS and $C{U}_j$ by $h_{j,m}$, respectively. The transmit power should satisfy ${\displaystyle \sum _{j=1}^K}{p}_{j,m}\le P_{BS}$, where $P_{BS}$ is the total power of BS. If $U_m$ denotes the set of users on $S{C}_m$ and ${\omega }_{i,m}$ denotes the signal of $C{U}_i\in U_m$ on $S{C}_m$. Then, the received signal at $C{U}_j$ on $S{C}_m$ can be given by

$$\begin{array}{cc}\hfill y_{j,m}& =h_{j,m}\sum _{i\in U_m}\sqrt{p_{i,m}}{\omega }_{i,m}+x_{j,m},\hfill \end{array}$$

(1)

where $x_{j,m}$ in (1) is the additive white Gaussian noise of $C{U}_j$ on $S{C}_m$ with zero mean and variance $n_0$. As the $S{C}_m$ can accommodate $U_m$ users, the $C{U}_j$ in $U_m$ can receives interference from any other $C{U}_i$ if $h_{j,m}/n_0<h_{i,m}/n_0$. However, $U_j$ will apply SIC to the users in $U_m$ which have weak channel gains. The achievable capacity of $C{U}_j$ on $S{C}_m$ can be given as

$$\begin{array}{c}\hfill C_{j,m}={log}_2\left(1+{{\rm Y}}_{j,m}\right),\end{array}$$

(2)

where ${{\rm Y}}_{j,m}$ in (2) is the SINR of $C{U}_j$ on $S{C}_m$ and can be defined as

$$\begin{array}{c}\hfill {{\rm Y}}_{j,m}=\frac{p_{j,m}{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2{\displaystyle \sum _{i=j+1}}{p}_{i,m}+n_0}.\end{array}$$

(3)

where the denominator term $|h_{j,m}{|}^2{\displaystyle \sum _{i=j+1}}{p}_{i,m}$ in (3) denotes the interference of other users in $U_m$ which have strong channel gains than $U_j$. On the account of sub-channel allocation to the users, we define a $M\times K$ sub-channel matrix H, where ${\beta }_{j,m}\in \{0,1\}$ denotes whether $S{C}_m$ is assigned to $C{U}_j$. In this paper, we evaluate the network performance by sum capacity of the users which is given by

$$\begin{array}{c}\hfill C_{\mathrm{sum}}=\sum _{j=1}^K\sum _{m=1}^M{\beta }_{j,m}{C}_{j,m}.\end{array}$$

(4)

Figure 1. Downlink non-orthogonal multiple access (NOMA) system.

Our objective is to optimize $\{{\beta }_{j,m},p_{j,m}\}$ in each time slot to enhance the sum capacity of the NOMA network subject to guarantee the minimum user capacity. To do so, we need to investigate the resource optimization problem which can be formated as:

$$\begin{array}{cc}\hfill \left(\mathrm{P}1\right)& \underset{{\beta }_{j,m}{p}_{j,m}}{\mathrm{maximize}}\left\{C_{\mathrm{sum}}=\sum _{j=1}^K\sum _{m=1}^M{\beta }_{j,m}{C}_{j,m}\right\}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \sum _{m=1}^M{\beta }_{j,m}\le 1,\forall j,\hfill \end{array}$$

(6)

$$\begin{array}{c}\sum _{j=1}^K{\beta }_{j,m}\le U_{\max },\forall m,\hfill \end{array}$$

(7)

$$\begin{array}{c}{C}_{j,m}\ge {\overline{C}}_{\min },\forall j,\forall m,\hfill \end{array}$$

(8)

$$\begin{array}{c}\sum _{j=1}^K\sum _{m=1}^M{\beta }_{j,m}{p}_{j,m}\le P_{BS},\hfill \end{array}$$

(9)

$$\begin{array}{c}{p}_{j,m}\ge 0,\forall j,\forall m.\hfill \end{array}$$

(10)

where (5) denotes the objective function for sum capacity maximization. Constraint in (6) ensures that $C{U}_j$ has access to no more than one sub-channel at one time. Constraint in (7) shows that a sub-channel can accommodates no more than $U_{\max }$ users at one time. Constraint in (8) guarantees the minimum capacity of each user, where ${\overline{C}}_{\min }$ is the threshold of minimum user capacity. In addition, the maximum and minimum power limits are defined in constraints (9) and (10), respectively.

Due to binary variable for sub-channel allocation and interference terms in (5) and (8), the problem (P1) is a non-convex optimization problem which is difficult to handle. Therefore we employ sub-optimal techniques to obtain the efficient solutions.

3. Resource Management With Fixed Power Control

We can see in (5) of the optimization problem (P1) that the sub-channel allocation and power management are coupled with each other in terms of system sum capacity. We fist decouple the sub-channel assignment and power allocation and then employ the sub-optimal approaches to obtain the efficient solutions. In this section, we provide efficient sub-channel assignment under fixed power allocation. To reduce the SIC complexity and interference among NOMA users, we assume that a sub-channel can accommodate no more than two users. With that, the constraint (7) can be rewritten as ${\displaystyle \sum _{j=1}^K}{\beta }_{j,m}\le 2,\forall m$. Further, we consider that the total number of sub-channel as $M=K/2$. For the given power of BS, the problem of efficient sub-channel allocation can be then simplified as:

$$\begin{array}{cc}\hfill \left(\mathrm{P}2\right)& \underset{{\beta }_{j,m}}{\mathrm{maximize}}\left\{C_{\mathrm{sum}}=\sum _{j=1}^K\sum _{m=1}^M{\beta }_{j,m}{C}_{j,m}\right\}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \sum _{m=1}^M{\beta }_{j,m}\le 1,\forall j,\hfill \end{array}$$

(12)

$$\begin{array}{c}\sum _{j=1}^K{\beta }_{j,m}\le 2,\forall m,\hfill \end{array}$$

(13)

$$\begin{array}{c}{C}_{j,m}\ge {\overline{C}}_{\min },\forall j,\forall m.\hfill \end{array}$$

(14)

where constraint in (13) shows that a sub-channel can be assigned to no more than two users. Now we propose two algorithms for sub-channel allocation based on user channel condition and user minimum capacity requirement.

3.1. User Channel Condition Based Sub-Channel Assignment Algorithm

Here we design an efficient algorithm (represented as Algorithm 1) for sub-channel allocation to the users based on user channel condition under fixed transmit power at BS.

Algorithm 1 Sub-channel Assignment Based on User Channel Condition

1.   Initialize K, M, $H_{K\times M}$, $P_m=P_{BS}/M$, ${\beta }_{j,m}$, ${\mathcal{S}}_{\max }$ and $R_{K\times 1}$.

2.   For $m=1:M$ do

3.   Divide matrix H into two matrices $H1$ and $H1$.

4.   $H1=H(1:M,1:K/2)$.

5.   $H2=H(1:M,(K/2)+1:K)$.

6.   For $u=1:K/2$ do

7.   $B\left(H1\right(u),H2((K/2)+1-u\left)\right)=1$.

8.   For $i=1:K$ do

9.   For $j=1:K$ do

10.   If $B(i,j)==1$ do

11.   Compute the sum capacity using ${\beta }_{j,m}$.

12.   For $P_m=5:1:P_{BS}$ do

13.   Compute $C_{i,m}={log}_2(1+\frac{\alpha P_m{\left|h_{i,m}\right|}^2}{n_0})$.

14.   Compute $C_{j,m}={log}_2(1+\frac{(1-\alpha )P_m{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2{p}_{i,m}+n_0})$.

15.   Compute $C_{\mathrm{sum}}=C_{i,m}+C_{j,m}$ on $S{C}_m$.

16.   End For $P_m$.

17.   End For j.

18.   End For i.

19.   End For u.

20.   At each index of m, assign a sub-channel to any two users with high sum capacity.

21.   End For m.

22.   Plot the sum capacity of the system

In this algorithm, we first initialize K and M, where $M=K/2$. Then we allocate the transmit power for sub-channels as $P_m=P_{BS}/M$. For each value of $P_m$, the power of $C{U}_j$ and $C{U}_i$ must satisfy as $p_{i,m}+p_{j,m}\le P_m$, where $p_{i,m}=\alpha P_m$ and $p_{j,m}=(1-\alpha )P_m$, respectively. Note that $\alpha$ is the fraction of power allocation which is lies between 0 and 1. Since we assume that the BS has perfect information of all its users, we generate a channel matrix H which is $M\times K$ and sort its columns in decreasing order. In addition, we initialize the matrix R for user minimum capacity which is $K\times 1$. Next, we divide matrix H into two matrices $H1$ and $H2$, where $H1$ and $H2$ are matrices of dimensions $M\times K/2$. Now select a user from $H1$ which has strongest channel gain and a user from $H2$ which has weakest channel gain. If $C{U}_i\in H1$ with strongest channel gain and $C{U}_j\in H2$ with weakest channel gain, then allocate a sub-channel m which provide high sum capacity. This process will continue until all sub-channels are assigned to the users. At the end of said process, we compute the sum capacity of the system. The detail steps of this process are provided in Algorithm 1.

3.2. User Minimum Capacity Requirement Based Sub-Channel Algorithm

In this subsection, we design a novel algorithm for sub-channel allocation to the users based on user minimum capacity requirement as shown in Algorithm 2.

Algorithm 2 Sub-channel Assignment Based on User Minimum Capacity Requirement

1.  Initialize K, M, $H_{K\times M}$, $P_m=P_{BS}/M$, ${\beta }_{j,m}$, ${\mathcal{S}}_{\max }$ and $R_{K\times 1}$.

2.  For $m=1:M$ do

3.  For $i=1:K$ do

4.  For $j=1:K$ do

5.  $B(i,j)=1$, when $C{U}_i=\max$ and $C{U}_j=\min$.

6.  If $B(i,j)==1$ do

7.  Compute the sum capacity using ${\beta }_{j,m}$.

8.  For $P_m=5:1:P_{BS}$ do

9.  Compute $C_{i,m}={log}_2(1+\frac{\alpha P_m{\left|h_{i,m}\right|}^2}{n_0})$.

10.  Compute $C_{j,m}={log}_2(1+\frac{(1-\alpha )P_m{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2{p}_{i,m}+n_0})$.

11.  Compute $C_{\mathrm{sum}}=C_{i,m}+C_{j,m}$ on $S{C}_m$.

12.  End For $P_m$.

13.  End For j.

14.  End For i.

15.  At each index of m, assign a sub-channel to any two users with high sum capacity

16.  End For m.

17.  Plot the sum capacity of the system.

According to the algorithm, we first initialize K and M, where $M=K/2$. Then, we allocate the transmit power for sub-channels as $P_m=P_{BS}/M$. For each value of $P_m$, the power of $C{U}_j$ and $C{U}_i$ must satisfy as $p_{i,m}+p_{j,m}\le P_m$, where $p_{i,m}=\alpha P_m$ and $p_{j,m}=(1-\alpha )P_m$. Since we assume that the BS has perfect information of all its users, we generate a channel matrix H which is $M\times K$ and sort its columns in descending order. In addition, we initialize the matrix R for user minimum capacity which is $K\times 1$. Now we select two users from H, one with highest capacity requirement (represented as ‘max’) and one with lowest capacity requirement (represented as ‘min’). Let us assume that $C{U}_i\in H$ has highest capacity requirement and $C{U}_j\in H$ has the lowest capacity requirement. Assign a sub-channel m to $C{U}_i$ and $C{U}_j$ which provide high sum capacity. The process will continue until all sub-channels assign to the users. In the end, we calculate the sum capacity of the system.

4. Resource Management with Optimal Power Control

This section provides efficient power allocation for any given sub-channel assignment. Specifically, we first transform the power allocation problem into standard convex optimization problem and then exploit dual methods to obtain the efficient solution. As presented in Section 3, we perform the sub-channel assignment for fixed transmit power at BS, which can be obtained through problem (P2) using Algorithms 1 and 2. Then, under a given sub-channel assignment $\left\{{\beta }_{i,m}\right\}$, the problem for $C{U}_i$ and $C{U}_j$ on $S{C}_m$ can be simplified as (P3):

$$\begin{array}{cc}\hfill \left(\mathrm{P}3\right)& \underset{p_{i,m},p_{j,m}}{\mathrm{maximize}}\left\{{log}_2\left(1+\frac{p_{i,m}{\left|h_{i,m}\right|}^2}{n_0}\right)+{log}_2\left(1+\frac{p_{j,m}{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2{p}_{i,m}+n_0}\right)\right\}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& {log}_2\left(1+\frac{p_{i,m}{\left|h_{i,m}\right|}^2}{n_0}\right)\ge {\overline{C}}_{i,m}^{\min },\hfill \end{array}$$

(16)

$$\begin{array}{c}{log}_2\left(1+\frac{p_{j,m}{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2{p}_{i,m}+n_0}\right)\ge {\overline{C}}_{j,m}^{\min },\hfill \end{array}$$

(17)

$$\begin{array}{c}{p}_{i,m}+p_{j,m}\le P_m,\hfill \end{array}$$

(18)

$$\begin{array}{c}{p}_{i,m}<p_{j,m},\hfill \end{array}$$

(19)

$$\begin{array}{c}{p}_{i,m}\ge 0,p_{j,m}\ge 0.\hfill \end{array}$$

(20)

where (15) denotes the objective function for sum capacity maximization on $S{C}_m$. Constraints in (16) and (17) guarantee the minimum required capacity of $C{U}_i$ and $C{U}_j$ over $S{C}_m$, in which ${\overline{C}}_{i,\min }$ and ${\overline{C}}_{j,\min }$ are the minimum capacity thresholds of $C{U}_i$ and $C{U}_j$ over $S{C}_m$, respectively. In addition, constraints in (18) limits the transmit power of $C{U}_i$ and $C{U}_j$ on $S{C}_m$ while constraint in (19) makes the SIC technique successful. The last constraint in (20) shows the non-negative power of $C{U}_i$ and $C{U}_j$ on $S{C}_m$.

We first calculate the minimum transmit power to satisfy the minimum capacity requirement of $C{U}_i$ and $C{U}_j$ on $S{C}_m$, which can be derived as:

$$p_{i,m}^{*}=\frac{(2^{{\overline{C}}_{i,m}^{\min }}-1)n_0}{|h_{i,m}{|}^2},$$

(21)

$$p_{j,m}^{*}=\frac{(2^{{\overline{C}}_{j,m}^{\min }}-1)(p_{i,m}^{*}|h_{j,m}{|}^2+n_0)}{|h_{j,m}{|}^2}.$$

(22)

The remaining power after capacity requirements of $C{U}_i$ and $C{U}_j$ on $S{C}_m$ which is denoted as $P_r$ and can be given by

$$\begin{array}{c}\hfill P_r=P_m-(p_{i,m}^{*}+p_{j,m}^{*}),\end{array}$$

(23)

In this article, our aim is to optimize the remaining power $P_r$ among $C{U}_i$ and $C{U}_j$ on $S{C}_m$. With $p_{i,m}^{*}$ and $p_{j,m}^{*}$, the sum capacity problem (P3) can be modified as:

$$\begin{array}{cc}\hfill \left(\mathrm{P}4\right)& \underset{p_{i,m},p_{j,m}}{\mathrm{maximize}}\left\{{log}_2\left(1+\frac{(p_{i,m}+p_{i,m}^{*}){\left|h_{i,m}\right|}^2}{n_0}\right)+{log}_2\left(1+\frac{(p_{j,m}^{*}+p_{j,m}){\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2(p_{i,m}^{*}+p_{i,m})+n_0}\right)\right\}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& p_{i,m}+p_{j,m}\le P_r,\hfill \end{array}$$

(25)

$$\begin{array}{c}{p}_{i,m}^{*}+p_{i,m}<p_{j,m}^{*}+p_{j,m},\hfill \end{array}$$

(26)

$$\begin{array}{c}{p}_{i,m}\ge 0,p_{j,m}\ge 0.\hfill \end{array}$$

(27)

where (25) in (P4) can be satisfied with equality by utilizing the NOMA downlink framework [10]. Now let $\alpha$ be the fraction of power allocation to $C{U}_i$ over sub-channel m, then the transmit power of $C{U}_i$ and $C{U}_j$ on $S{C}_m$ can be respectively expressed as $p_{i,m}=\alpha P_r$ and $P_{j,m}=(1-\alpha )P_r$. Note that the value of $\alpha$ lies between 0 and 1. By introducing $\alpha$, the optimization problem (P4) can be further simplified as (P5):

$$\begin{array}{cc}\hfill \left(\mathrm{P}5\right)& \underset{\alpha }{\mathrm{maximize}}\left\{{log}_2\left(1+\frac{(\alpha P_r+p_{i,m}^{*}){\left|h_{i,m}\right|}^2}{n_0}\right)+{log}_2\left(1+\frac{((1-\alpha )P_r+p_{j,m}^{*}){\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2(\alpha P_r+p_{i,m}^{*})+n_0}\right)\right\}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& p_{i,m}^{*}+\alpha P_r<p_{j,m}^{*}+(1-\alpha )P_r,\hfill \end{array}$$

(29)

$$\begin{array}{c}\alpha \le 0.5.\hfill \end{array}$$

(30)

where the last constraint in (30) ensures that the fraction power of $C{U}_i$ on $S{C}_m$ should be less than or equal to 0.5. The problem (P5) is a standard convex optimization problem and dual method can be employed to obtain the efficient solution [11]. The corresponding dual problem is

$$\underset{\lambda ,\eta }{\mathrm{minimize}}D(\lambda ,\eta ),$$

(31)

where $D(\lambda ,\eta )$ is called the dual function and can be given by

$$D(\lambda ,\eta )=\underset{\alpha }{\mathrm{maximize}}\mathcal{L}(\alpha ,\lambda ,\eta ).$$

(32)

The Lagrangian function of optimization problem (P5) can be defined as:

$$\begin{array}{cc}\hfill \mathcal{L}(\alpha ,\lambda ,\eta )=& {log}_2\left(1+\frac{(\alpha P_r+p_{i,m}^{*}){\left|h_{i,m}\right|}^2}{n_0}\right)+{log}_2\left(1+\frac{((1-\alpha )P_r+p_{j,m}^{*}){\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2(\alpha P_r+p_{i,m}^{*})+n_0}\right)\hfill \\ & -\lambda (2\alpha P_r+p_{i,m}^{*}-P_r-p_{j,m}^{*})-\eta (\alpha -0.5),\hfill \end{array}$$

(33)

Under high signal to noise ratio (SNR) approximation, from the properties of log, we obtain

$$\begin{array}{cc}\hfill \mathcal{L}(\alpha ,\lambda ,\eta )=& {log}_2((\alpha P_r+p_{i,m}^{*})|h_{i,m}{|}^2)-{log}_2(n_0)+{log}_2(|h_{j,m}{|}^2((1-\alpha )P_r+p_{j,m}^{*}))\hfill \\ & -{log}_2(|h_{j,m}{|}^2(\alpha P_r+p_{i,m}^{*})+n_0)-\lambda (2\alpha P_r+p_{i,m}^{*}-P_r-p_{j,m}^{*})-\eta (\alpha -0.5).\hfill \end{array}$$

(34)

Now differentiating by $\alpha$ as $\frac{\partial \mathcal{L}(\alpha ,\lambda ,\eta )}{\partial \alpha }$, we obtain

$$\begin{array}{cc}\hfill \frac{\partial \mathcal{L}(\alpha ,\lambda ,\eta )}{\partial \alpha }=& \frac{1}{{ln}_2}\left(\frac{P_r{\left|h_{i,m}\right|}^2}{|h_{i,m}{|}^2(\alpha P_r+p_{i,m}^{*})}\right)+\frac{1}{{ln}_2}\left(\frac{-P_r{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2((1-\alpha )P_r+p_{j,m}^{*})}\right)\hfill \\ & -\frac{1}{{ln}_2}\left(\frac{P_r{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2(\alpha P_r+p_{i,m}^{*})+n_0}\right)-2\lambda P_r-\eta ,\hfill \end{array}$$

(35)

By setting $\frac{\partial \mathcal{L}(\alpha ,\lambda ,\eta )}{\partial \alpha }=0$, we get

$$\begin{array}{c}\frac{1}{{ln}_2}\left(\frac{P_r{\left|h_{i,m}\right|}^2}{|h_{i,m}{|}^2(\alpha P_r+p_{i,m}^{*})}-\frac{P_r{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2((1-\alpha )P_r+p_{j,m}^{*})}-\frac{P_r{\left|h_{j,m}\right|}^2}{|h_{j,m}{|}^2(\alpha P_r+p_{i,m}^{*})+n_0}\right)-2\lambda P_r-\eta =0,\hfill \end{array}$$

(36)

After some straightforward simplification, we obtain

$$\begin{array}{c}{P}_r|h_{i,m}{|}^2(((1-\alpha )P_r+p_{j,m}^{*})|h_{j,m}{|}^2)\times ((\alpha P_r+p_{i,m}^{*})|h_{j,m}{|}^2+n_0)-P_r|h_{j,m}{|}^2((\alpha P_r+p_{i,m}^{*})|h_{i,m}{|}^2)\hfill \\ \times ((\alpha P_r+p_{i,m}^{*})|h_{j,m}{|}^2+n_0)-P_r|h_{j,m}{|}^2((\alpha P_r+p_{i,m}^{*})|h_{i,m}{|}^2)(((1-\alpha )P_r+p_{j,m}^{*})|h_{j,m}{|}^2)\hfill \\ =(2\lambda P_r{ln}_2+\eta {ln}_2)((\alpha P_r+p_{i,m}^{*})|h_{i,m}{|}^2)(((1-\alpha )P_r+p_{j,m}^{*})|h_{j,m}{|}^2)((\alpha P_r+p_{i,m}^{*})|h_{j,m}{|}^2+n_0).\hfill \end{array}$$

(37)

Finally, the $\alpha$ is obtained from solution of (37). To get the optimal value of Lagrangian multipliers $\lambda$ and $\eta$, we employ sub-gradient method which can be iteratively updated as [30]:

$$\lambda (\varphi +1)=\lambda \left(\varphi \right)+\delta \left(\varphi \right)\left(2\alpha P_r+p_{i,m}^{*}-P_r-p_{j,m}^{*}\right),$$

(38)

$$\eta (\varphi +1)=\eta \left(\varphi \right)+\delta \left(\varphi \right)(\alpha -0.5).$$

(39)

where $\varphi$ denotes the iteration index and $\delta$ is the non-negative step size. In each iteration, the multipliers $\lambda$ and $\eta$ are updated using the calculated values of $\alpha$. Then, in the next iteration, these updated values of $\lambda$ and $\eta$ are used to calculate the optimal $\alpha$. Note that the said process will repeat until convergence.

5. Results and Analysis

This section presents our simulation results based on the provided schemes discussed in Section 3 and Section 4. We evaluate the following NOMA schemes:

• Prop-Sch1: It is the proposed power optimization technique as presented in Section 4.
• Sch2: This is the solution for power allocation scheme presented in Reference [12]. According to this scheme, the minimum capacity of one user satisfies first and then allocate all the remaining power to another user.
• Prop1: This denotes the user minimum capacity requirement based sub-channel assignment using proposed power allocation scheme.
• Prop2: This is the user channel condition based sub-channel allocation using proposed power technique.
• Enh1 [12]: This corresponds to the user minimum capacity requirement based sub-channel allocation using power optimization technique given in paper [12].
• Enh2 [12]: It is the user channel condition based sub-channel allocation using power optimization technique provided in Reference [12].
• SProp: This is the random sub-channel assignment using proposed power allocation scheme.
• SEnh [12]: This denotes the random sub-channel assignment using power allocation scheme given in Reference [12].

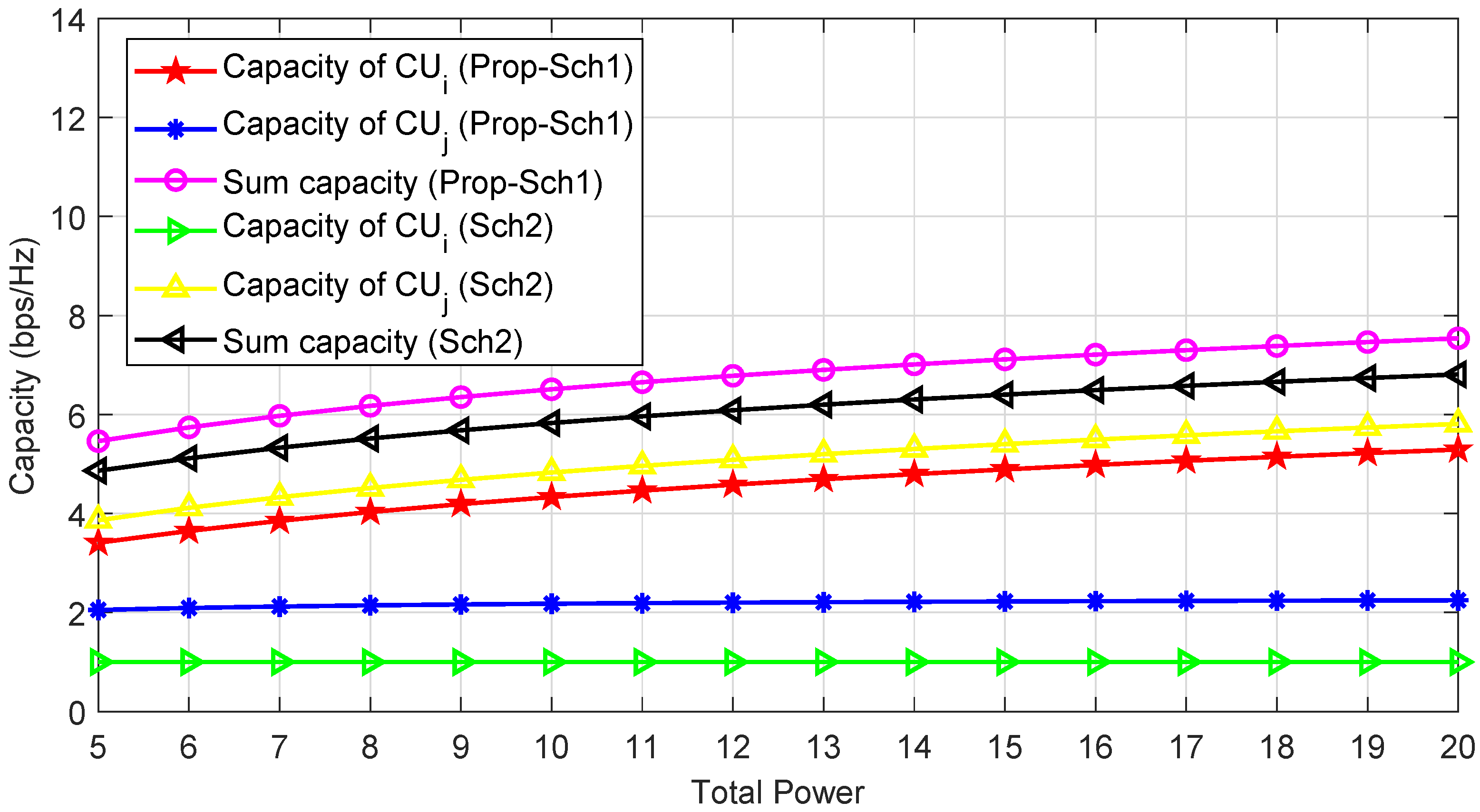
In Figure 2, we plot the capacity of the Prob-Sch1 and Sch2 against the total power of BS. We show the individual capacity of $C{U}_i$ and $C{U}_j$ on $S{C}_m$ as well as the sum capacity of both users over $S{C}_m$ for both Prob-Sch1 and Sch2, respectively. As is expected, the sum capacity of Prop-Sch1 significantly outperforms the Sch2. More specifically, for fixed transmit power of BS, ie, 10, the sum capacity of the Prop-Sch1 is 6.7 bps/Hz while for the same value of transmit power, the sum capacity of the Sch2 is 5.8 bps/Hz. This is because the Prop-Sch1 is better than Sch2. Moreover, the gap between $C{U}_i$ and $C{U}_j$ using Prop-Sch1 is far less than the one in Sch2. It is because in the Prop-Sch1, we first satisfy the minimum capacity requirement of both users and then optimize the remaining power among $C{U}_i$ and $C{U}_j$. However, in Sch2, the minimum capacity requirement of one user is satisfied first and then allocate all the remaining power to the other user.

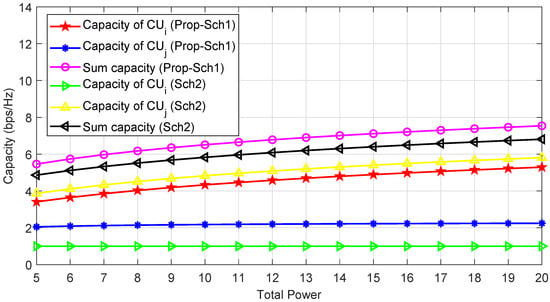
Figure 2. Capacity versus total power of the BS for Prop-Sch1 and Sch2.

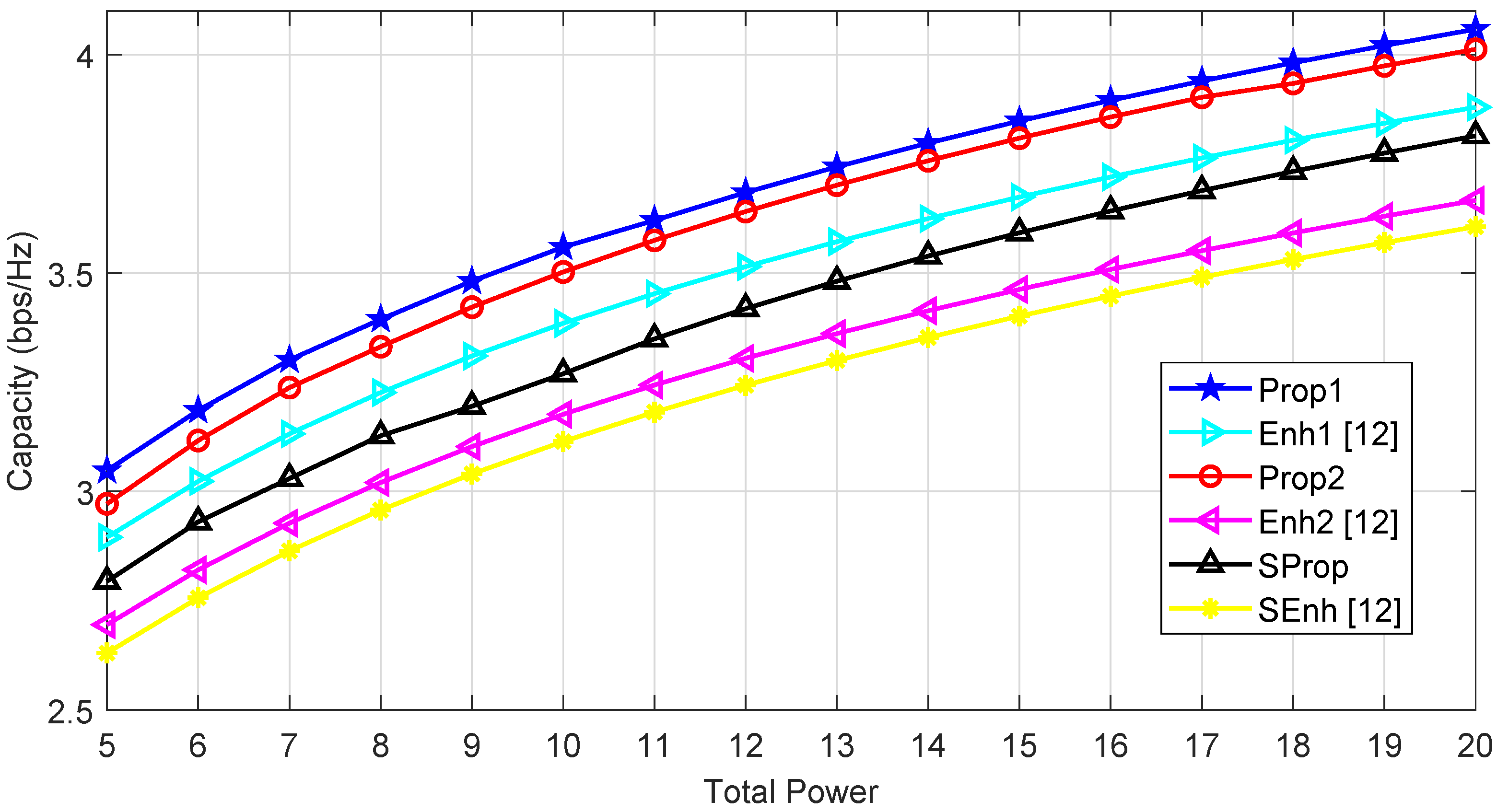
Figure 3 depicts the sum capacity of different NOMA schemes versus total power of BS. We compare Prop1 with Enh1 [12], Prop2 with Enh2 [12] and Sprop with SEnh [12], respectively. We can see that our proposed techniques significantly outperforms the benchmark schemes. In addition, we can also observe that the schemes using Algorithm 2 for sub-channel assignment achieve high capacity from those using Algorithm 1. For instance, the capacity of Prop1 using Algorithm 2 is 4.1 bps/Hz when transmit power is 20, while it is 4 bps/Hz for Prop2 which using Algorithm 1. It shows that user minimum capacity requirement based sub-channel assignment as discussed in Algorithm 2 is more efficient than the user channel condition based sub-channel assignment presented in Algorithm 1.

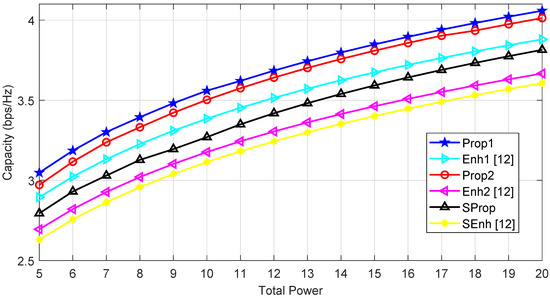
Figure 3. Capacity versus total transmit power of the base station (BS) for all schemes.

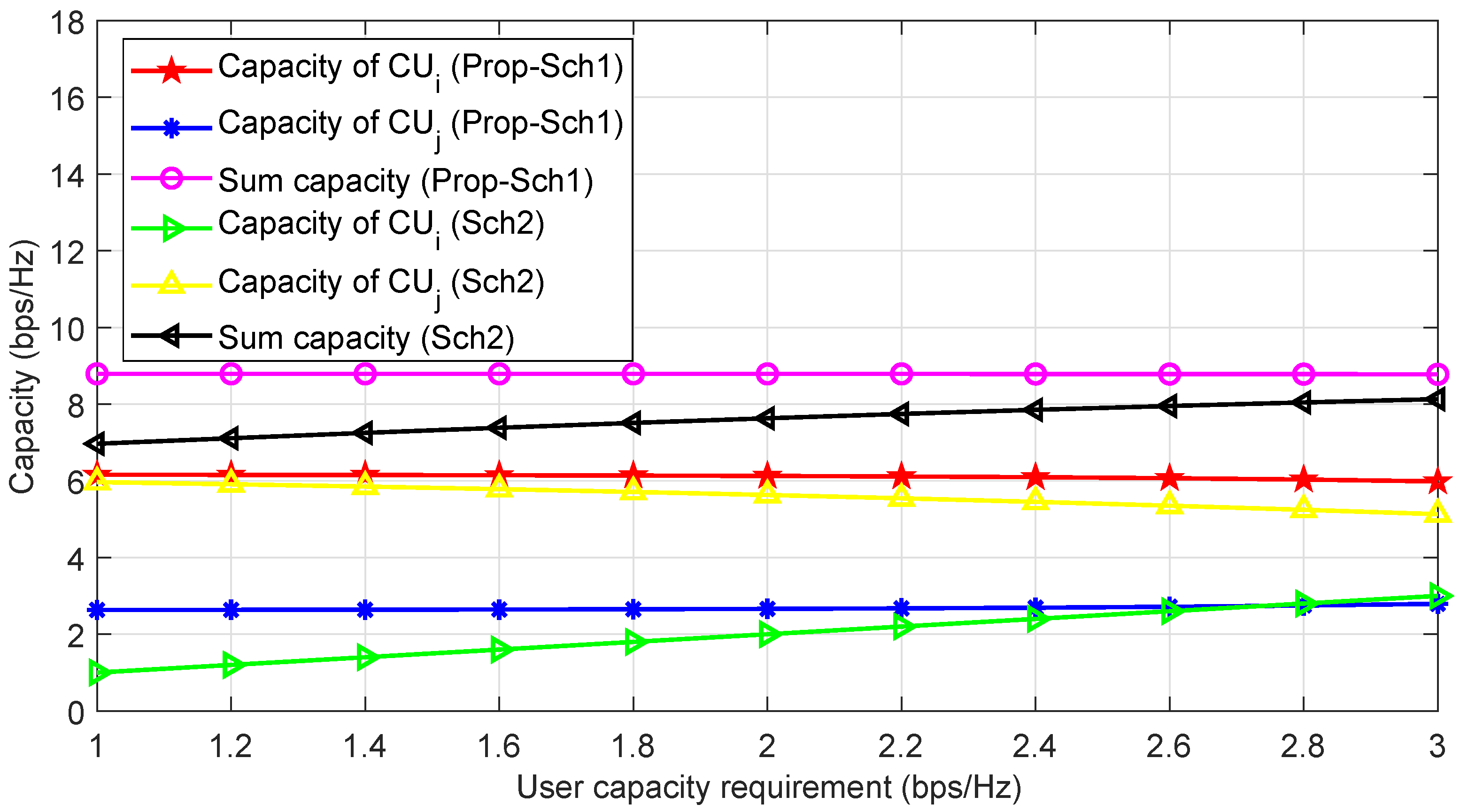
In Figure 4, we provide the capacity of Prop-Sch1 and Sch2 against the user minimum capacity requirement. Here we can observe that for increasing values of minimum capacity requirement, the Prop-Sch1 achieves high capacity compared to Sch2. Moreover, we can see that $C{U}_i$ using Sch2 closely follows the minimum capacity requirement and also see the decrease in the capacity of $C{U}_j$ for high values of minimum capacity. It is because the transmit power of $C{U}_j$ may reduce when $C{U}_i$ unable to achieve the minimum capacity with its available transmit power. However, the capacity of $C{U}_i$ and $C{U}_j$ using Prop-Sch1 remains unchanged for increasing values of user minimum capacity which shows the effectiveness of Prop-Sch1 over Sch2.

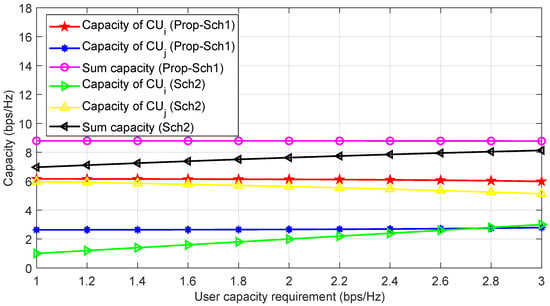
Figure 4. Capacity of Prop-Sch1 and Sch2 versus user minimum capacity requirement when $P_{BS}=20$.

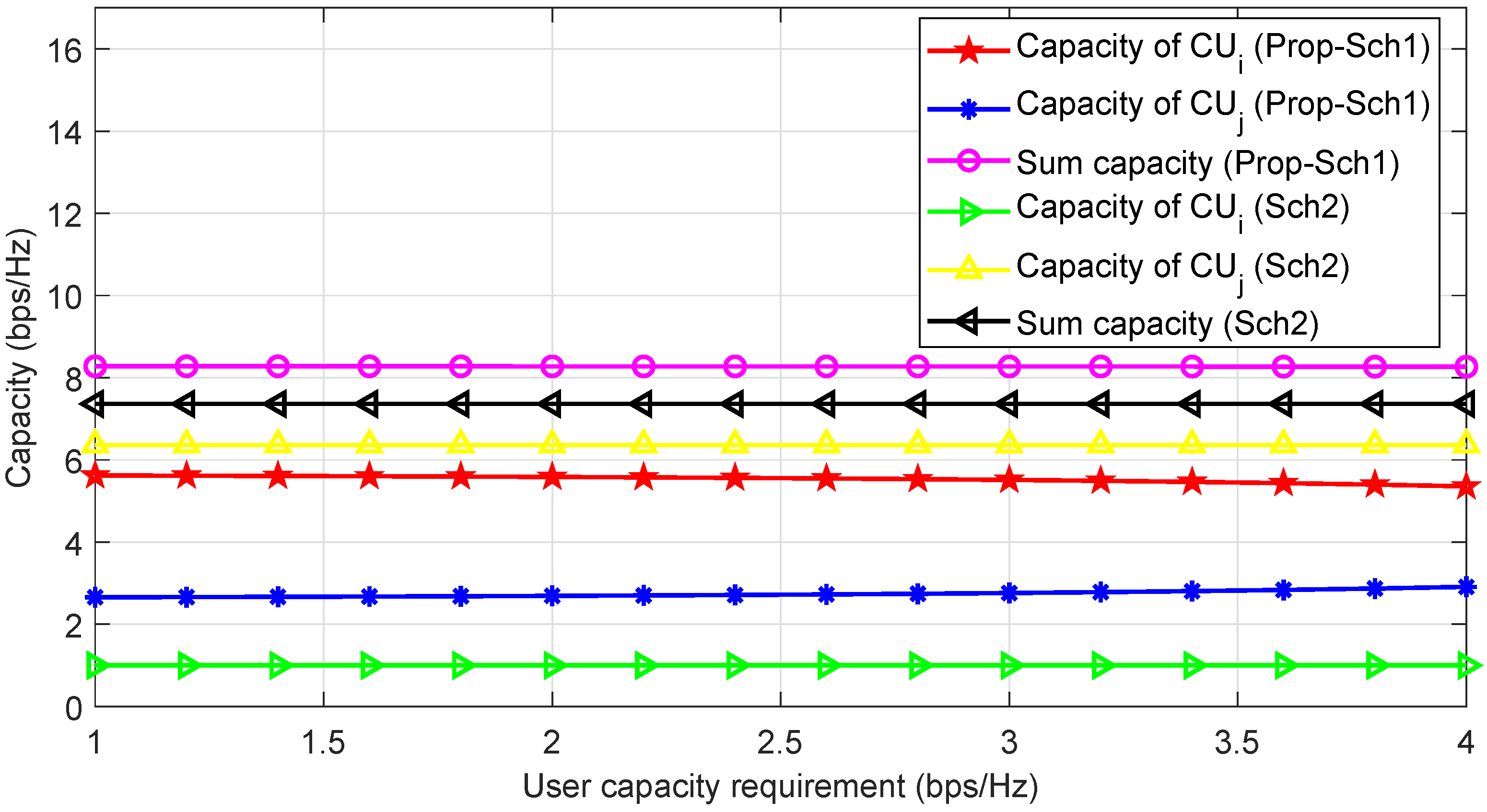
In Figure 5, we plot the capacity for Prop-Sch1 and Sch2 by setting the minimum capacity of $C{U}_i$ on $S{C}_m$ as ${\overline{C}}_{i,m}^{\min }=1$ bps/Hz and increasing the capacity of other users. The results dhow that Prop-Sch1 achieves high sum capacity compared to the Sch2. More specifically, for all values of minimum capacity, the sum capacity of $C{U}_i$ and $C{U}_j$ over $S{C}_m$ is 8.2 bps/Hz while it is 7.2 bps/Hz for the benchmark Sch2. This is because our proposed NOMA optimization technique is more efficient than the one in benchmark.

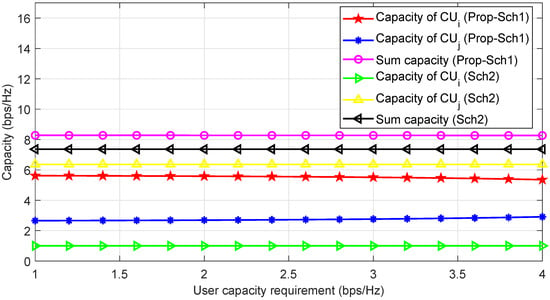
Figure 5. Comparison of Prop-Sch1 and Sch2 when setting the $C_1=1$ bps/Hz and increasing the Rate requirement of other users.

6. Conclusions

NOMA technology is going to be key candidate to fulfill the high spectral demands of next generation networks. This paper has provided a new resource management scheme for sum capacity maximization under the minimum capacity constraint. First, we have formulated a non-convex resource management problem for sub-channel assignment and power allocation. Second, we have provided two sub-optimal algorithms for sub-channel assignment under fixed transmit power of BS. These algorithms have designed based on user channel condition and user minimum capacity requirement. Third, for any given sub-channel assignment, we have exploited duality theory to calculate the optimal power allocation. Finally, we have provided and compared the results of different proposed NOMA schemes with the benchmark NOMA schemes. It has shown from the results that our NOMA technique is more efficient than the benchmark NOMA scheme.

Although, the results in this paper consider two users, in the future, our objective is to consider multiuser for evaluation. We also aim to extend our work to multi-cell scenario.