Adaptive Active Disturbance Rejection Control for Vehicle Steer-by-Wire under Communication Time Delays
Abstract
:1. Introduction
- Large time delays in a communication channel that the second-order SBW suffers are considered, therein a first-order Taylor series expansion is introduced to address the time delays. However, the order of SBW becomes three; thus, the increase in system order makes the control tasks more complicated. To solve the complexity arising from the Taylor approximation, we propose a novel active disturbance rejection control (AADRC) for the time-delayed SBW subject to system uncertainties and disturbances from external factors.
- Because of consideration and approximation of the time delays, the overall disturbances acting on the SBW become very large. To overcome this issue, we lump the nonlinearities, uncertainties, and external disturbances of the SBW that are separated from the total disturbances. Such separation of disturbances makes the feasibility of application of the novel AADRC which is a combination of AESO and AFSEFBC.
- A novel AESO is proposed to estimate unmeasured velocity and acceleration, as well as the lumped disturbance with better estimation precision, low computation cost, and minimum peak phenomenon. Adaptive gains of the AESO are updated online based on a position estimation error to improve estimation performance.
- A novel AFSEFBC is improved to enhance the trajectory tracking efficiency of the angular steering position of the front wheel, in which its gains are adjusted online according to the position tracking error, and thus the angular steering position is improved in terms of lesser overshoot and better steady state.
- The boundedness of the estimation and the tracking error of the closed-loop stability of the AESO and AFSEFBC, respectively, is rigorously analyzed.
2. SBW Plant Dynamical Modeling
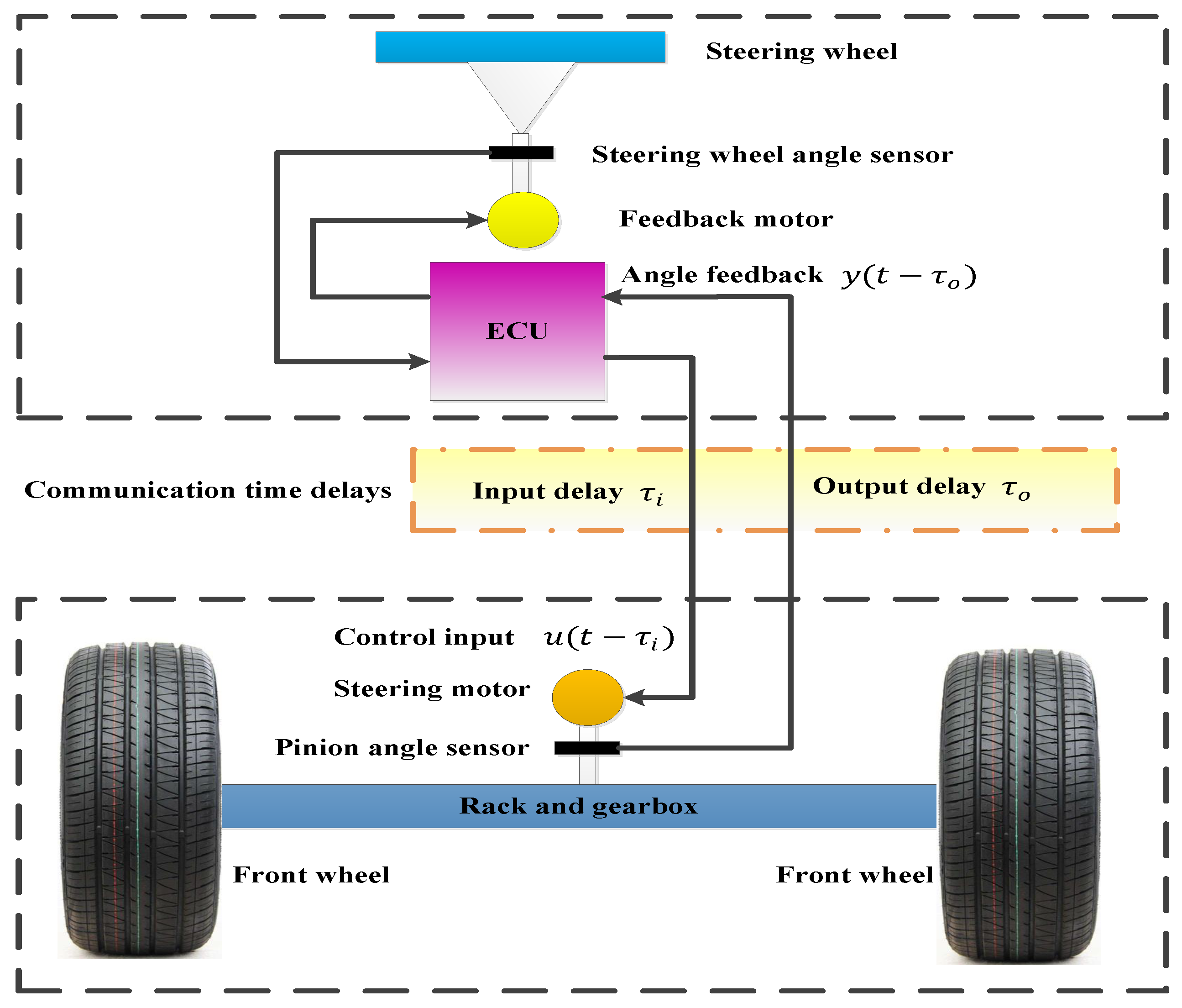
2.1. Structure of the SBW Plant
2.2. Dynamical Modeling of the Nominal SBW Plant with Uncertainties
2.3. Dynamical Modeling of the Time-Delayed SBW Plant with Uncertainties
2.4. Time-Delay Approximation by Taylor Series
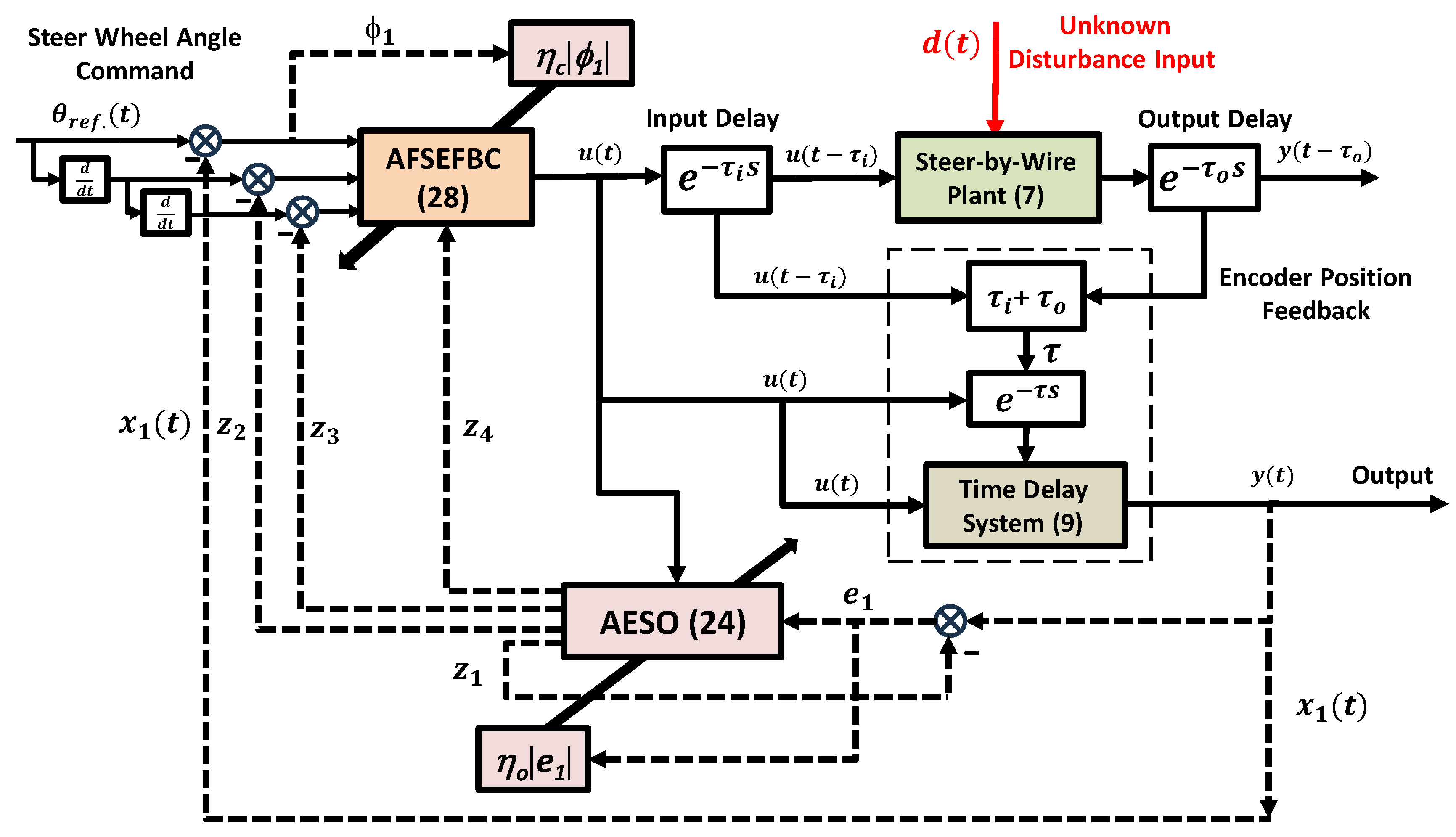
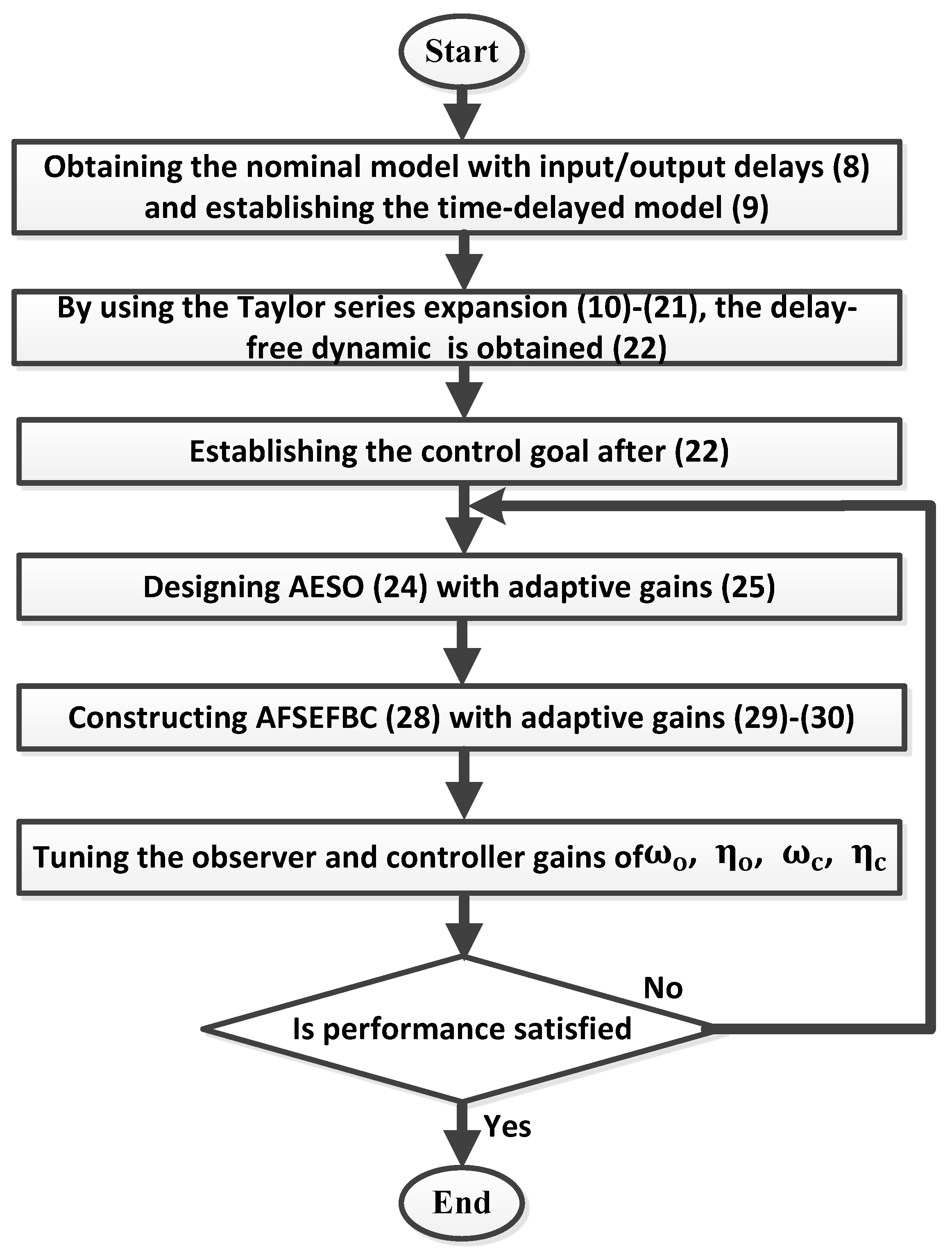
3. Proposed Controller Design and Stability Analysis
3.1. Construction of the AESO Estimator
3.2. Construction of AFSEFBC
3.3. Stability Proof
3.3.1. Convergence of the AESO
3.3.2. Convergence of the AFSEFBC
4. Simulation Design and Analysis
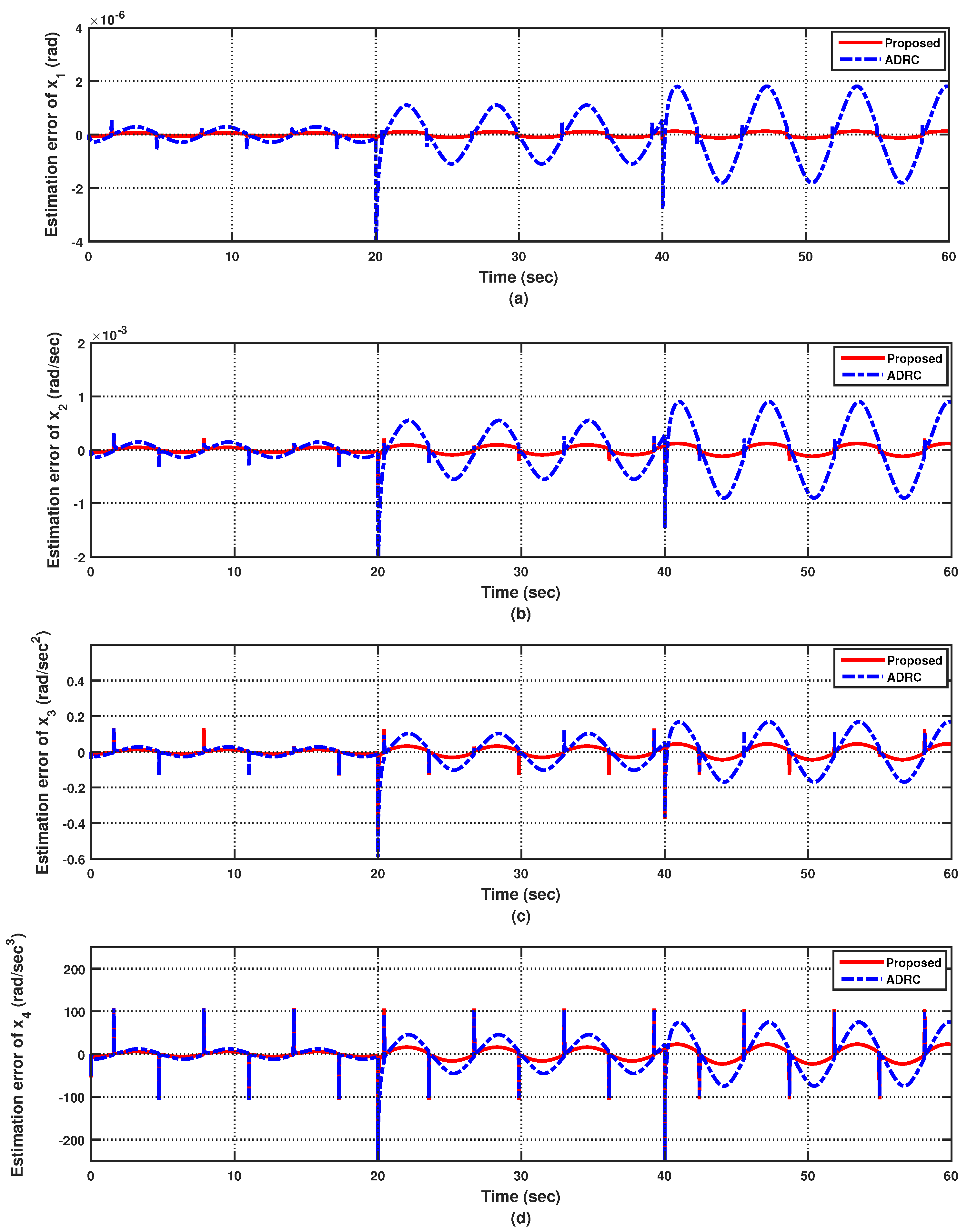
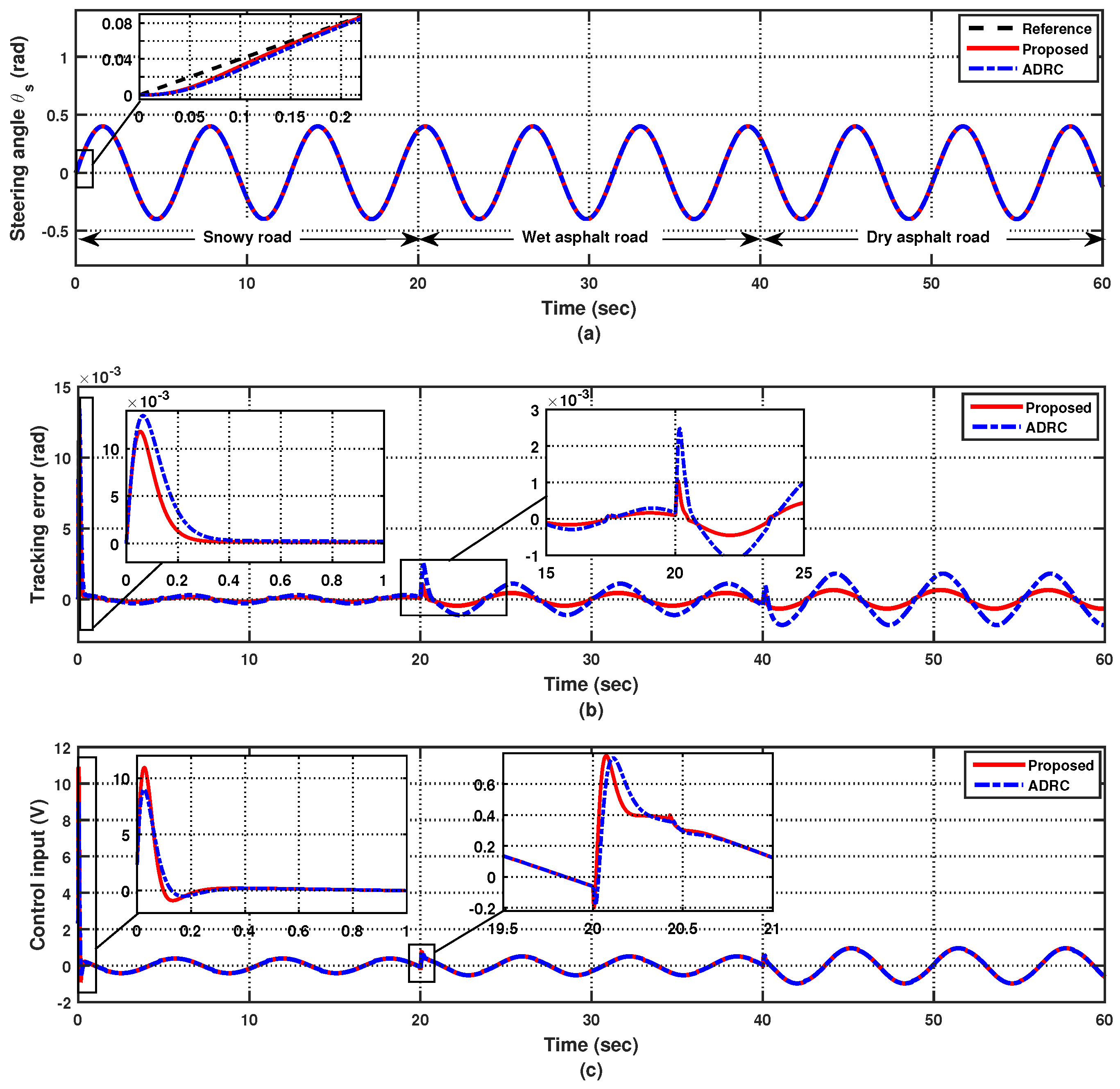
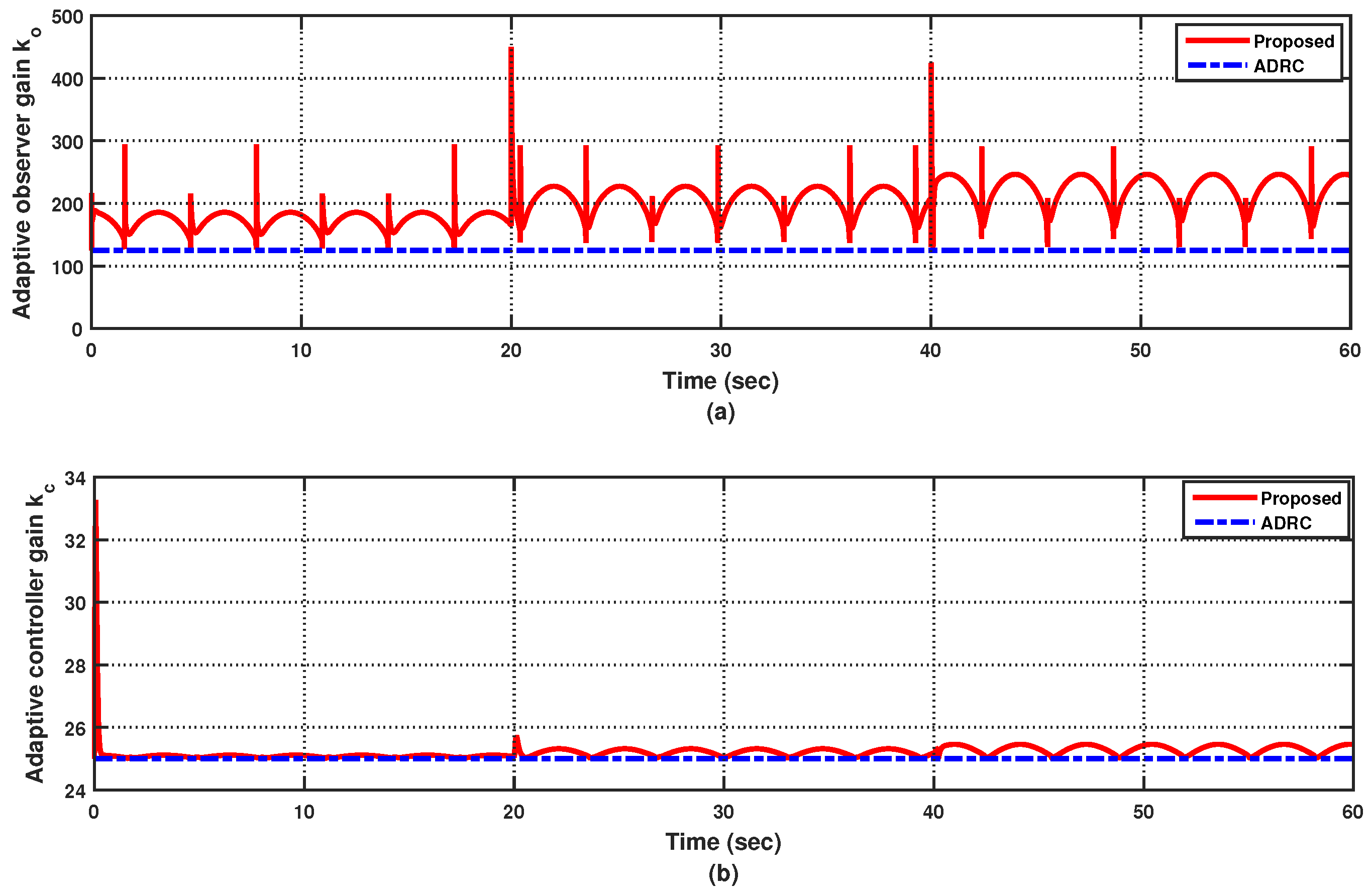
4.1. Case 1: Nominal SBW System with Nonlinearity under the Fixed Input and Output Time Delay
4.2. Case 2: Uncertain SBW System with Nonlinearity under Input and Output Time-Varying Delay
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Man, Z.; Shen, W.; Cao, Z.; Zheng, J.; Jin, J.; Tuan, D. Robust Control for Steer-by-Wire Systems With Partially Known Dynamics. IEEE Trans. Ind. Inform. 2014, 10, 2003–2015. [Google Scholar] [CrossRef]
- Sun, Z.; Zheng, J.; Man, Z.; Wang, H. Robust control of a vehicle steer-by-wire system using adaptive sliding mode. IEEE Trans. Ind. Electron. 2015, 63, 2251–2262. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, X.; Li, L.; Shao, W. Design and applications of steering angle tracking control with robust compensator for steer-by-wire system of intelligent vehicle. IFAC-PapersOnLine 2021, 54, 221–227. [Google Scholar] [CrossRef]
- Shi, Q.; He, S.; Wang, H.; Stojanovic, V.; Shi, K.; Lv, W. Extended state observer based fractional order sliding mode control for steer-by-wire systems. IET Control Theory Appl. 2023. [Google Scholar] [CrossRef]
- Ye, Q.; Wang, R.; Cai, Y.; Chadli, M. The stability and accuracy analysis of automatic steering system with time delay. ISA Trans. 2020, 104, 278–286. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives—A Survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef]
- Xiong, L.; Jiang, Y.; Fu, Z. Steering Angle Control of Autonomous Vehicles Based on Active Disturbance Rejection Control. IFAC-PapersOnLine 2018, 51, 796–800. [Google Scholar] [CrossRef]
- Sun, Z.; Zheng, J.; Man, Z.; Wang, H.; Lu, R. Sliding mode-based active disturbance rejection control for vehicle steer-by-wire systems. IET Cyber-Phys. Syst. Theory Appl. 2018, 3, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Z.; Do, M.; Zheng, J.; Cao, Z.; Xie, L. Neural-network-based robust control for steer-by-wire systems with uncertain dynamics. Neural Comput. Appl. 2015, 26, 1575–1586. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Ma, M.; Yu, M.; Yazdani, A.; Chen, L. Active front steering-based electronic stability control for steer-by-wire vehicles via terminal sliding mode and extreme learning machine. IEEE Trans. Veh. Technol. 2020, 69, 14713–14726. [Google Scholar] [CrossRef]
- Benosman, M. Model-based vs data-driven adaptive control: An overview. Int. J. Adapt. Control Signal Process. 2018, 32, 753–776. [Google Scholar] [CrossRef]
- Sun, Z.; Zheng, J.; Wang, H.; Man, Z. Adaptive fast non-singular terminal sliding mode control for a vehicle steer-by-wire system. IET Control Theory Appl. 2017, 11, 1245–1254. [Google Scholar] [CrossRef]
- Ye, M.; Wang, H. Robust adaptive integral terminal sliding mode control for steer-by-wire systems based on extreme learning machine. Comput. Electr. Eng. 2020, 86, 106756. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, J.; Nie, B.; Liu, Y.; He, X. Adaptive Control of PMSM Servo System for Steering-by-Wire System With Disturbances Observation. IEEE Trans. Transp. Electrif. 2022, 8, 2015–2028. [Google Scholar] [CrossRef]
- Iqbal, J.; Zuhaib, K.; Han, C.; Khan, A.; Ali, M. Adaptive Global Fast Sliding Mode Control for Steer-by-Wire System Road Vehicles. Appl. Sci. 2017, 7, 738. [Google Scholar] [CrossRef]
- Yang, H.; Liu, W.; Li, C.; Fan, Y. An adaptive hierarchical control approach of vehicle handling stability improvement based on Steer-by-Wire Systems. Mechatronics 2021, 77, 102583. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, G.; Wang, D. Observer-based fixed-time adaptive fuzzy control for SbW systems with prescribed performance. Eng. Appl. Artif. Intell. 2022, 114, 105026. [Google Scholar] [CrossRef]
- Shukla, H.; Roy, S.; Gupta, S. Robust Adaptive Control of Steer-by-wire Systems under Unknown State-dependent Uncertainties. Int. J. Adapt. Control Signal Process. 2022, 36, 198. [Google Scholar] [CrossRef]
- Wang, H.; Man, Z.; Kong, H.; Zhao, Y.; Yu, M.; Cao, Z.; Zheng, J.; Do, M.T. Design and implementation of adaptive terminal sliding-mode control on a steer-by-wire equipped road vehicle. IEEE Trans. Ind. Electron. 2016, 63, 5774–5785. [Google Scholar] [CrossRef]
- Shah, M.B.N.; Husain, A.R.; Aysan, H.; Punnekkat, S.; Dobrin, R.; Bender, F.A. Error handling algorithm and probabilistic analysis under fault for CAN-based steer-by-wire system. IEEE Trans. Ind. Inform. 2016, 12, 1017–1034. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, W.; Wang, C.; Lian, Y. Layered Time-delay Robust Control Strategy for Yaw Stability of SBW Vehicles. IEEE Trans. Intell. Veh. 2023; early access. [Google Scholar]
- Chuei, R.; Zheng, Y.; Cao, Z.; Man, Z. Improved sliding mode observer based repetitive control for linear systems with time-varying input and state delays. Int. J. Adapt. Control. Signal Process. 2023; early access. [Google Scholar]
- Lu, Y.; Liang, J.; Wang, F.; Yin, G.; Pi, D.; Feng, J.; Liu, H. An active front steering system design considering the CAN network delay. IEEE Trans. Transp. Electrif. 2023, 9, 5244–5256. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Y.; Xu, X. Fractional order adaptive fast super-twisting sliding mode control for steer-by-wire vehicles with time-delay estimation. Electronics 2021, 10, 2024. [Google Scholar] [CrossRef]
- Chakirov, R.; Vagapov, Y.; Gaede, A. Active sidestick for steer-by-wire systems. J. Electr. Electron. Eng. 2010, 3, 43–46. [Google Scholar]
- Paolo, P.; Peter, M.; Norah, N. Fluid Interface Concept for Automated Driving. HCI Mobil. Transp. Automot. Syst. Autom. Driv. In-Veh. Exp. Des. 2020, 12212, 114–115. [Google Scholar]
- Mortazavizadeh, S.; Ghaderi, A.; Ebrahimi, M.; Hajian, M. Recent Developments in the Vehicle Steer-by-Wire System. IEEE Trans. Transp. Electrif. 2020, 6, 1226–1235. [Google Scholar] [CrossRef]
- Chen, B.M.; Lee, T.H.; Peng, K.; Venkataramanan, V. Composite nonlinear feedback control for linear systems with input saturation: Theory and an application. IEEE Trans. Autom. Control 2003, 48, 427–439. [Google Scholar] [CrossRef]
- Yih, P.; Gerdes, J.C. Modification of vehicle handling characteristics via steer-by-wire. IEEE Trans. Control Syst. Technol. 2005, 13, 965–976. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wang, H.; Kong, H.; Man, Z.; Cao, Z.; Shen, W. Sliding mode control for steer-by-wire systems with AC motors in road vehicles. IEEE Trans. Ind. Electron. 2013, 61, 1596–1611. [Google Scholar] [CrossRef]
- Baviskar, A.; Wagner, J.R.; Dawson, D.M.; Braganza, D.; Setlur, P. An adjustable steer-by-wire haptic-interface tracking controller for ground vehicles. IEEE Trans. Veh. Technol. 2008, 58, 546–554. [Google Scholar] [CrossRef]
- Wu, Q.; Yu, L.; Wang, Y.W.; Zhang, W.A. LESO-based position synchronization control for networked multi-axis servo systems with time-varying delay. IEEE/CAA J. Autom. Sin. 2020, 7, 1116–1123. [Google Scholar] [CrossRef]
- Li, P.; Zhu, G.; Zhang, M. Linear Active Disturbance Rejection Control for Servo Motor Systems With Input Delay via Internal Model Control Rules. IEEE Trans. Ind. Electron. 2021, 68, 1077–1086. [Google Scholar] [CrossRef]
- Cao, W.; Wang, L.; Li, J.; Peng, C.; Zhou, J.; He, H. Analysis and Design of Drivetrain Control for the AEV With Network-Induced Compounding-Construction Loop Delays. IEEE Trans. Veh. Technol. 2021, 70, 5578–5591. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Jiang, C.; Huang, Z. A new uncertainty propagation method considering multimodal probability density functions. Struct. Multidiscip. Optim. 2019, 60, 1983–1999. [Google Scholar] [CrossRef]



| Symbols | Descriptions | Values | Units |
|---|---|---|---|
| Equivalent inertial moment of the SBW system | 85.5 | kgm2 | |
| Equivalent viscous damping friction of the SBW system | 218.8 | Nms/rad | |
| Coulomb friction constant | 4.2 | Nm | |
| Scale factor to account for transmitting from the linear motion of the rack to the steering angle of front wheels | 6.0 | - | |
| Gear ratio between the pinion and rack system | 3.0 | - | |
| Gear ratio of the gear head | 8.5 | - | |
| Scale factor accounting for converting from the input voltage of steering motor to the output torque of the steering motor | 1.8 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rsetam, K.; Zheng, Y.; Cao, Z.; Man, Z. Adaptive Active Disturbance Rejection Control for Vehicle Steer-by-Wire under Communication Time Delays. Appl. Syst. Innov. 2024, 7, 22. https://doi.org/10.3390/asi7020022
Rsetam K, Zheng Y, Cao Z, Man Z. Adaptive Active Disturbance Rejection Control for Vehicle Steer-by-Wire under Communication Time Delays. Applied System Innovation. 2024; 7(2):22. https://doi.org/10.3390/asi7020022
Chicago/Turabian StyleRsetam, Kamal, Yusai Zheng, Zhenwei Cao, and Zhihong Man. 2024. "Adaptive Active Disturbance Rejection Control for Vehicle Steer-by-Wire under Communication Time Delays" Applied System Innovation 7, no. 2: 22. https://doi.org/10.3390/asi7020022
APA StyleRsetam, K., Zheng, Y., Cao, Z., & Man, Z. (2024). Adaptive Active Disturbance Rejection Control for Vehicle Steer-by-Wire under Communication Time Delays. Applied System Innovation, 7(2), 22. https://doi.org/10.3390/asi7020022






