Pedestrian Behavior in Static and Dynamic Virtual Road Crossing Experiments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
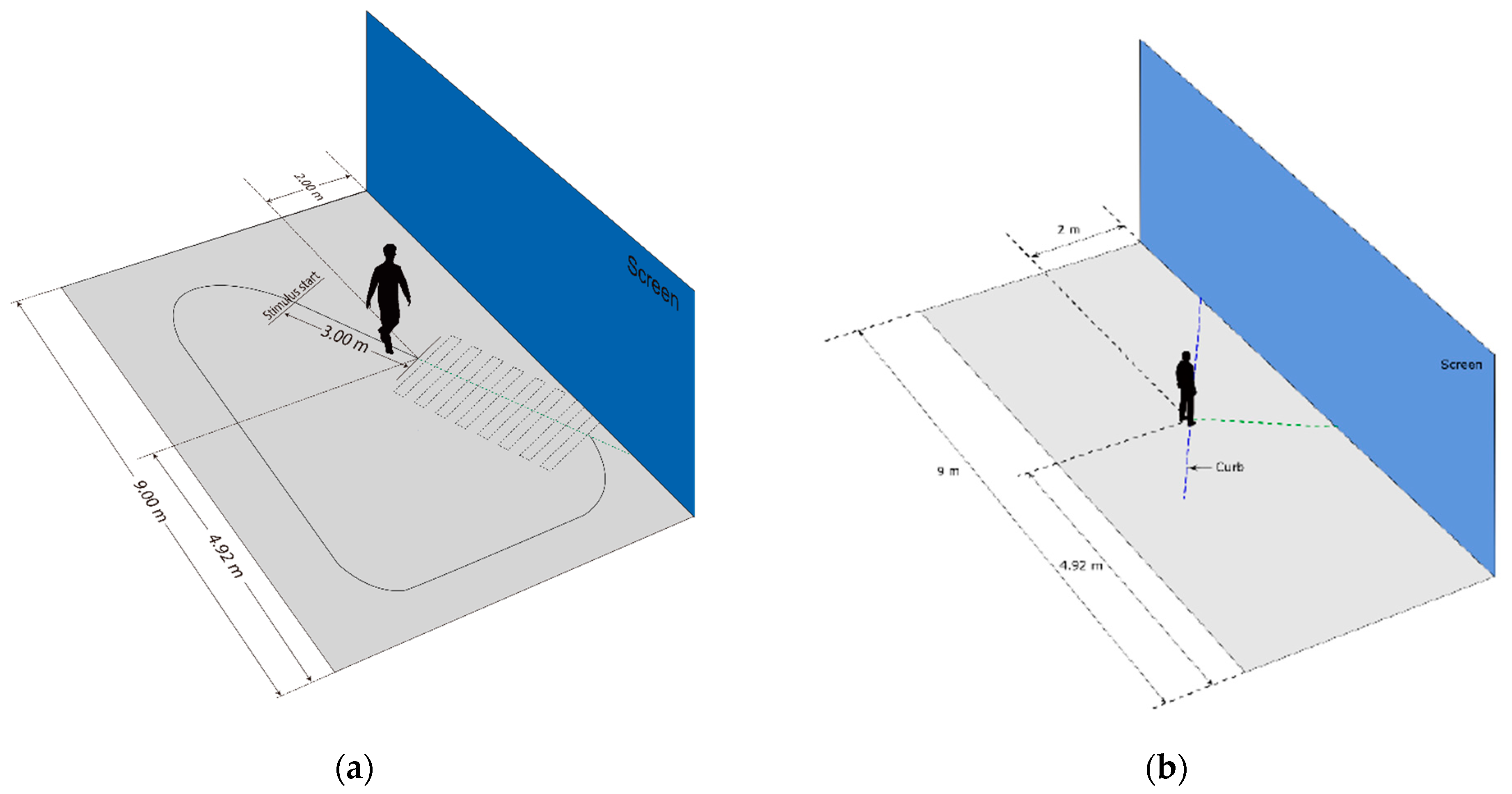
2.2. Virtual Environment
2.3. Stimuli
2.4. Instruments
2.5. Experimental Procedure
2.6. Analysis
3. Results
3.1. Constant Speed Patterns
3.1.1. Percentage of Crossings
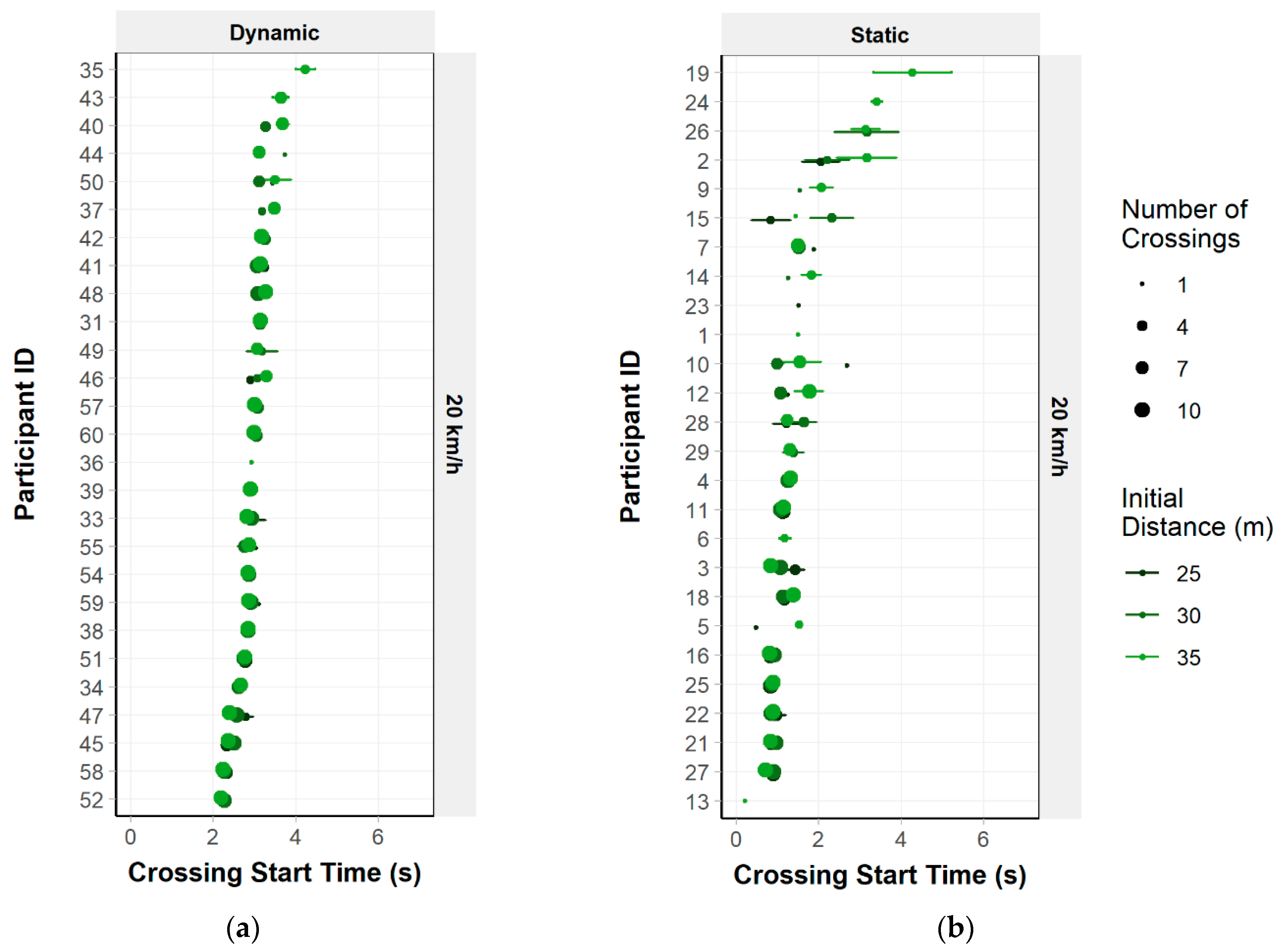
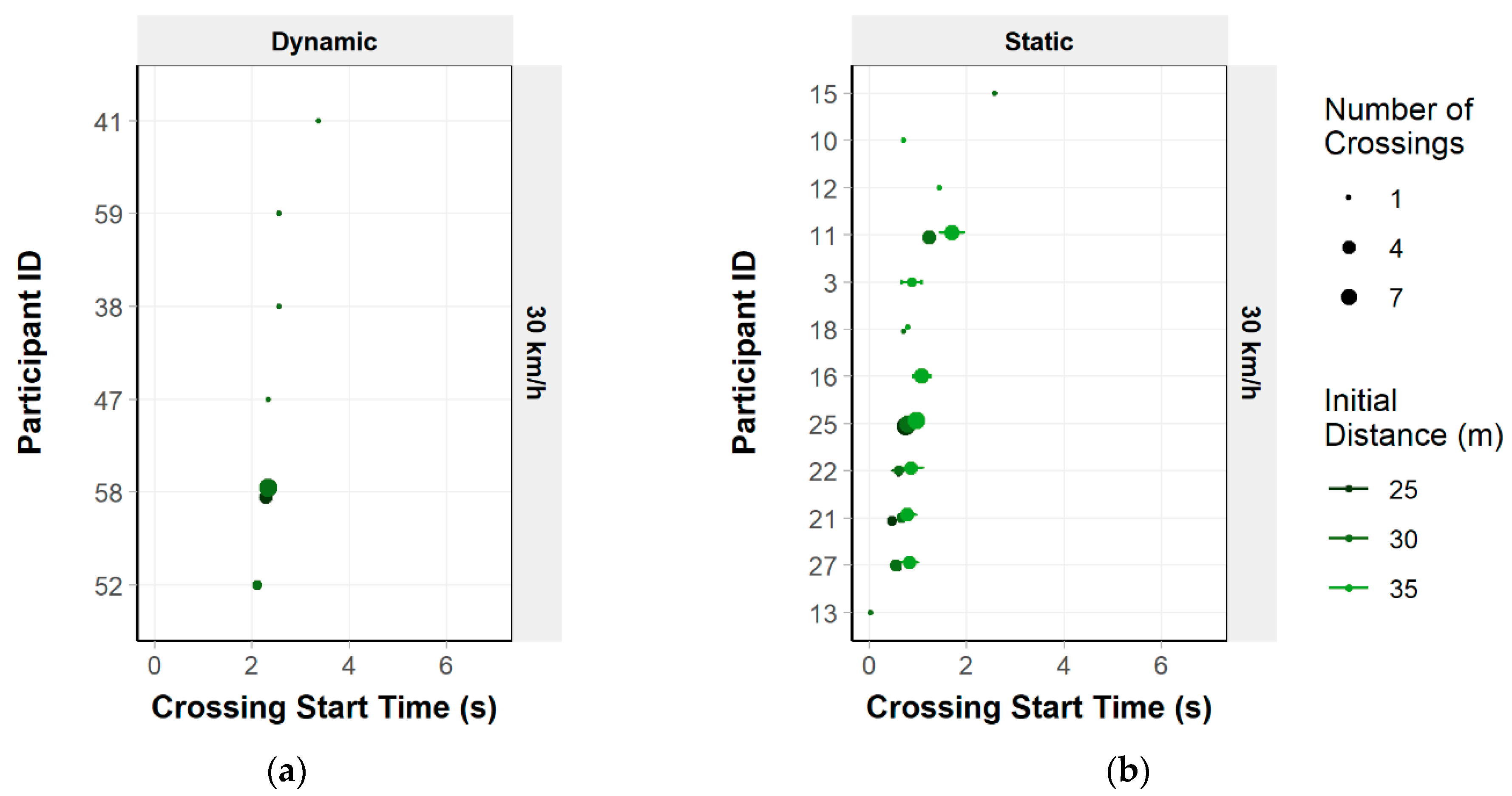
3.1.2. Crossing Start Time
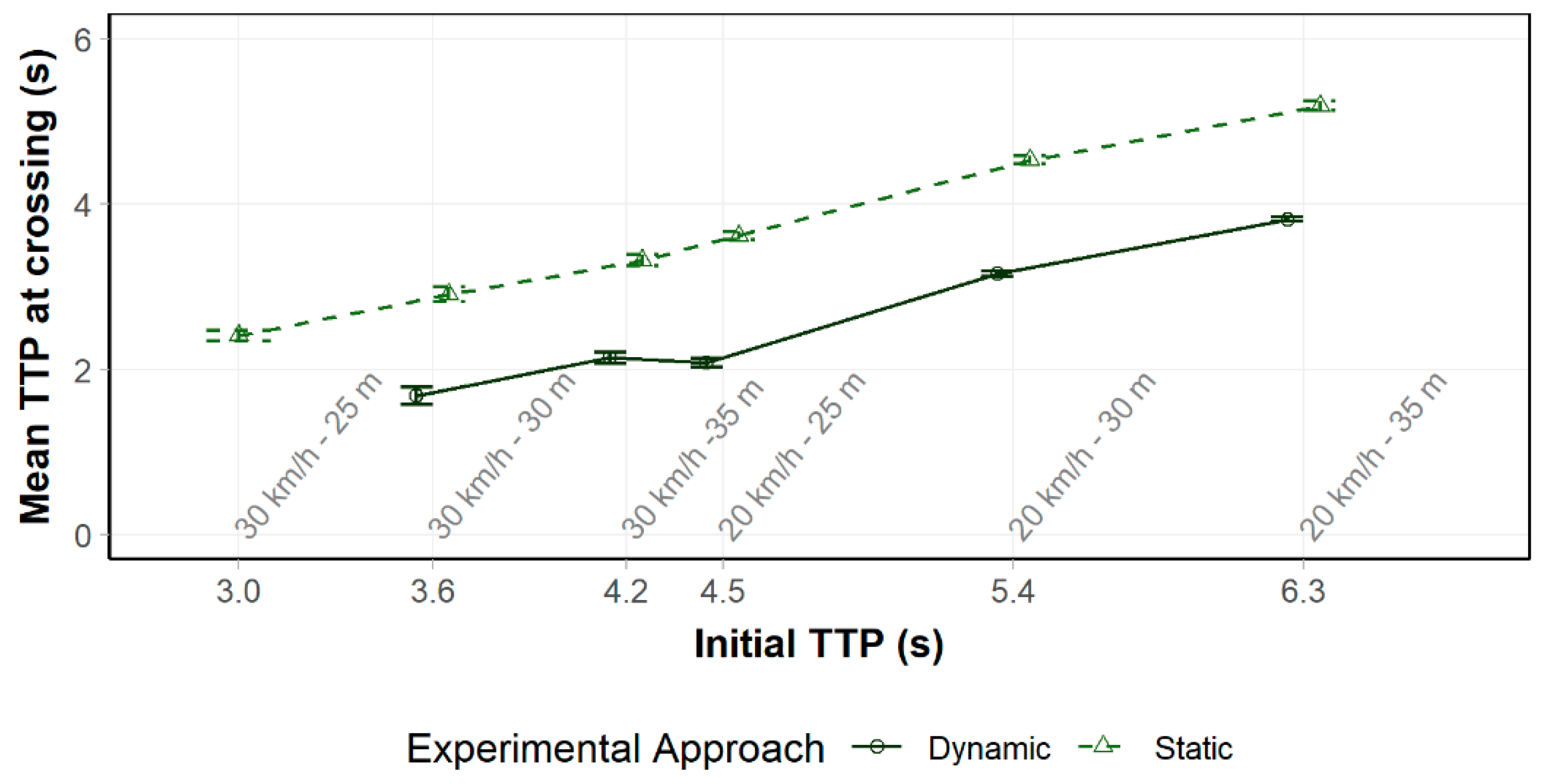
3.1.3. Time-to-Passage
3.2. Different Speed Patterns
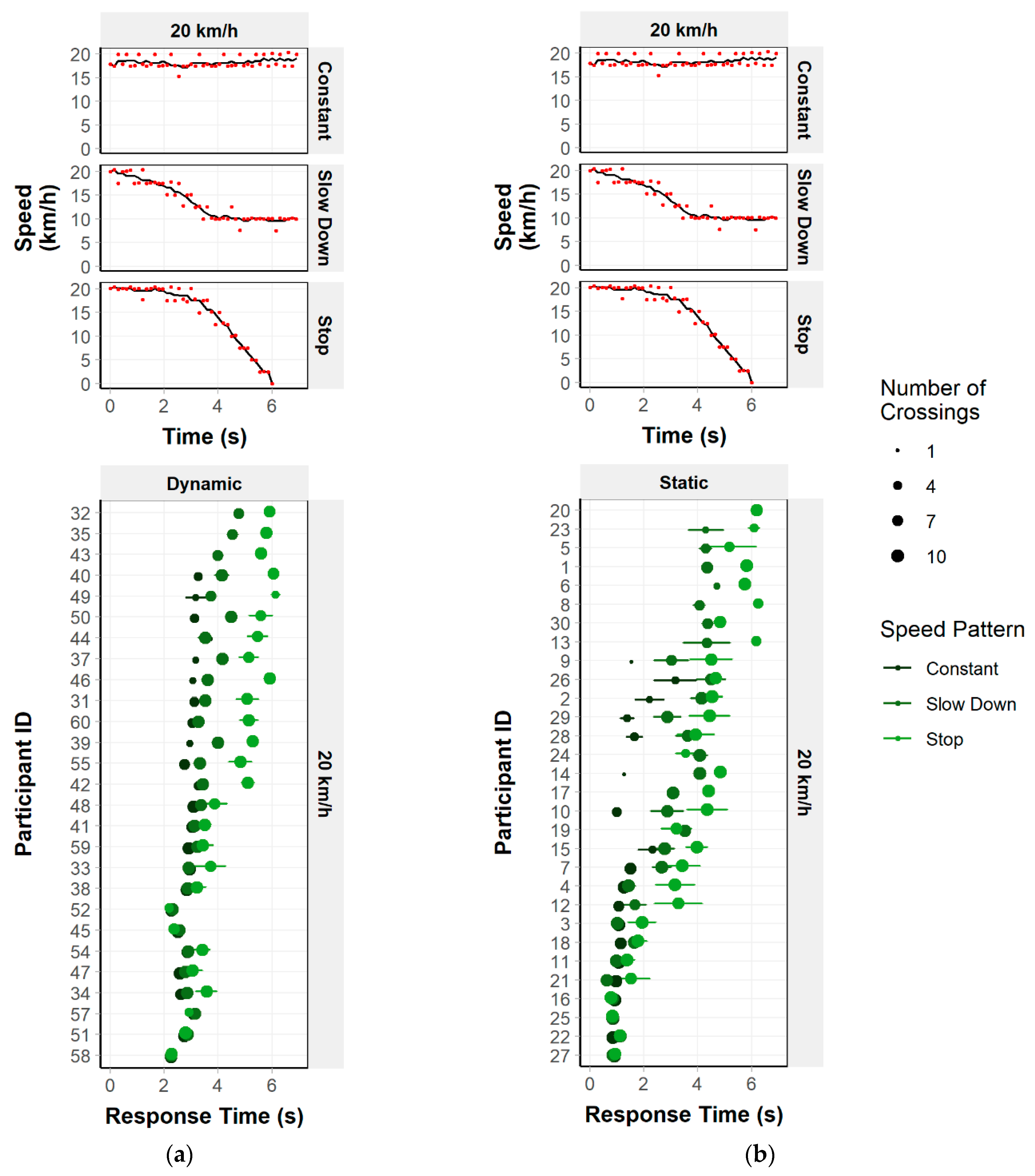
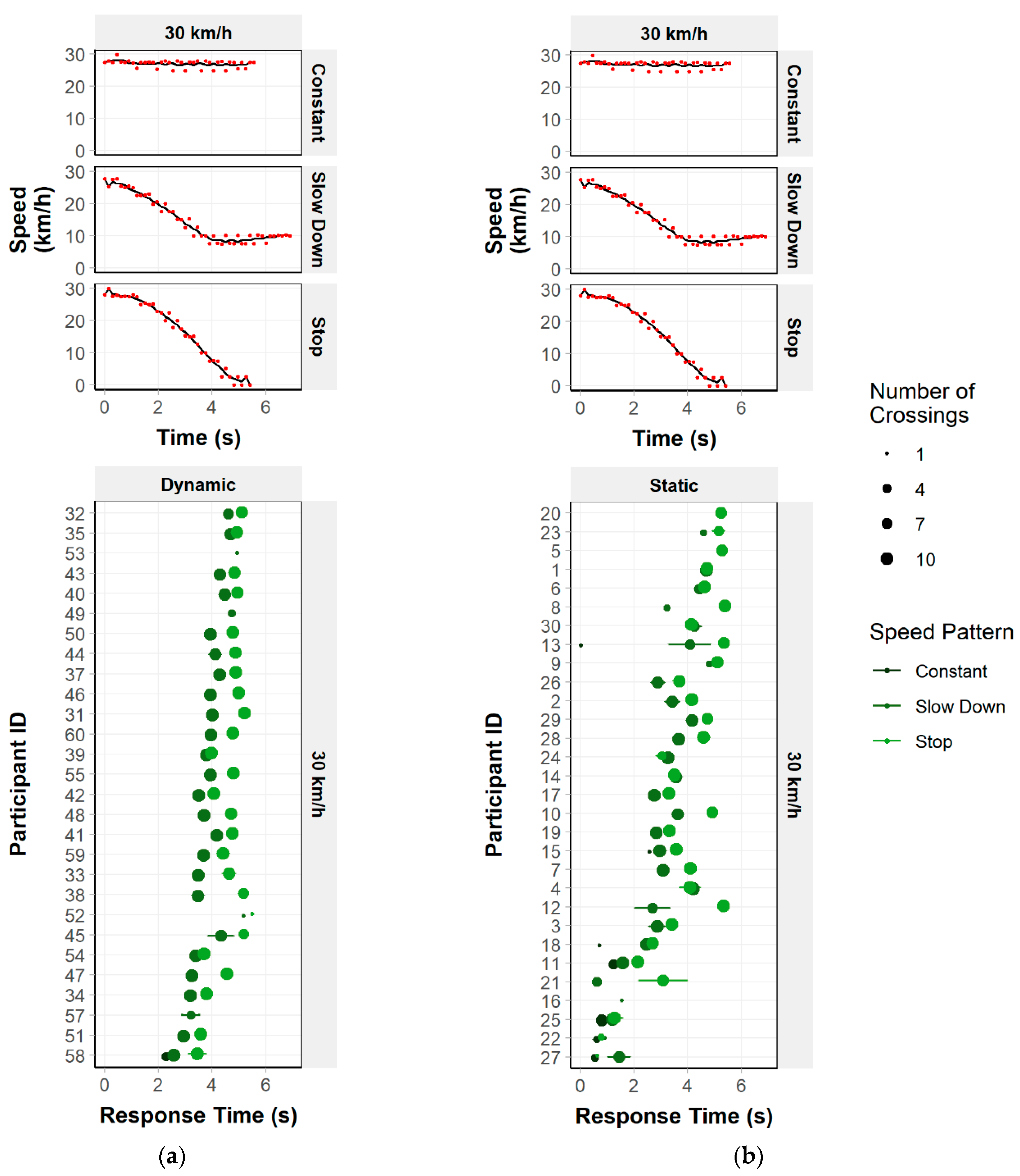
3.2.1. Percentage of Crossings
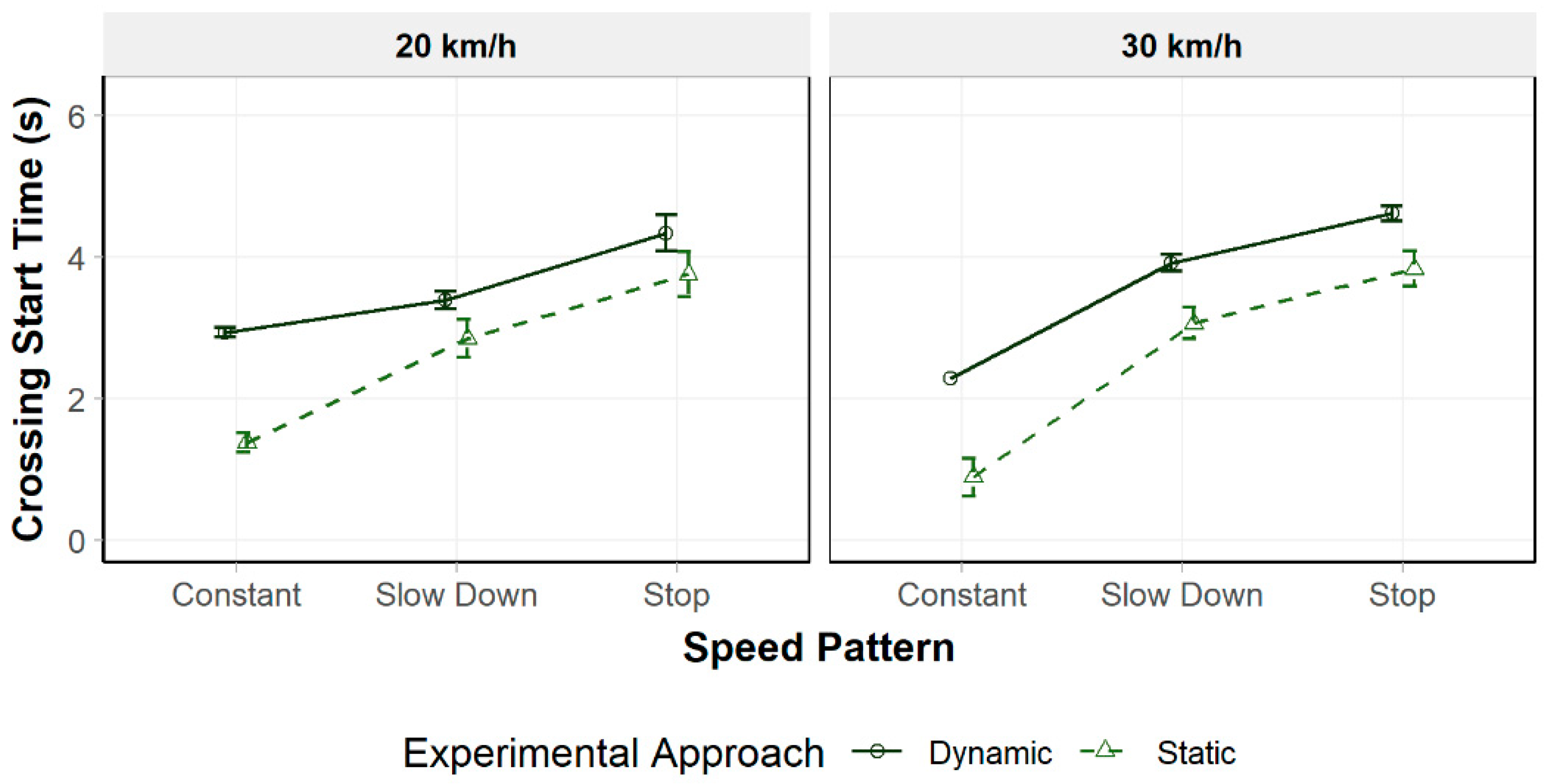
3.2.2. Crossing Start Time
3.2.3. Time-to-Passage
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bernhoft, I.M.; Carstensen, G. Preferences and Behaviour of Pedestrians and Cyclists by Age and Gender. Transp. Res. Part F Traffic Psychol. Behav. 2008, 11, 83–95. [Google Scholar] [CrossRef]
- Ewing, R.; Dumbaugh, E. The Built Environment and Traffic Safety: A Review of Empirical Evidence. J. Plan. Lit. 2009, 23, 347–367. [Google Scholar] [CrossRef]
- Ezzati Amini, R.; Katrakazas, C.; Antoniou, C. Negotiation and Decision-Making for a Pedestrian Roadway Crossing: A Literature Review. Sustainability 2019, 11, 6713. [Google Scholar] [CrossRef]
- Granié, M.A.; Brenac, T.; Montel, M.C.; Millot, M.; Coquelet, C. Influence of Built Environment on Pedestrian’s Crossing Decision. Accid. Anal. Prev. 2014, 67, 75–85. [Google Scholar] [CrossRef]
- Holland, C.; Hill, R. The Effect of Age, Gender and Driver Status on Pedestrians’ Intentions to Cross the Road in Risky Situations. Accid. Anal. Prev. 2007, 39, 224–237. [Google Scholar] [CrossRef]
- Ishaque, M.M.; Noland, R.B. Behavioural Issues in Pedestrian Speed Choice and Street Crossing Behaviour: A Review. Transp. Rev. 2008, 28, 61–85. [Google Scholar] [CrossRef]
- Johansson, C.; Gårder, P.; Leden, L. The Effect of Change of Code on Safety and Mobility for Children and Elderly as Pedestrians at Marked Crosswalks: A Case Study Comparing Sweden to Finland. In Proceedings of the Annual TRB Meeting, Washington, DC, USA, 11–15 January 2004. [Google Scholar]
- LaScala, E.A.; Gerber, D.; Gruenewald, P.J. Demographic and Environmental Correlates of Pedestrian Injury Collisions: A Spatial Analysis. Accid. Anal. Prev. 2000, 32, 651–658. [Google Scholar] [CrossRef] [PubMed]
- Leden, L. Pedestrian Risk Decrease with Pedestrian Flow. A Case Study Based on Data from Signalized Intersections in Hamilton, Ontario. Accid. Anal. Prev. 2002, 34, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.-S.; Kourtellis, A.; Wang, Z.; Guo, R. Understanding Interactions between Drivers and Pedestrian Features at Signalized Intersections; Florida Department of Transportation: Tallahassee, FL, USA, 2015. [Google Scholar]
- Moyano Díaz, E. Theory of Planned Behavior and Pedestrians’ Intentions to Violate Traffic Regulations. Transp. Res. Part F Traffic Psychol. Behav. 2002, 5, 169–175. [Google Scholar] [CrossRef]
- Oxley, J.A.; Ihsen, E.; Fildes, B.N.; Charlton, J.L.; Day, R.H. Crossing Roads Safely: An Experimental Study of Age Differences in Gap Selection by Pedestrians. Accid. Anal. Prev. 2005, 37, 962–971. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Lassarre, S.; Yannis, G. Introducing Human Factors in Pedestrian Crossing Behaviour Models. Transp. Res. Part F Traffic Psychol. Behav. 2016, 36, 69–82. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Lassarre, S.; Yannis, G. Pedestrian Risk Taking While Road Crossing: A Comparison of Observed and Declared Behaviour. Transp. Res. Procedia 2016, 14, 4354–4363. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Lassarre, S.; Yannis, G. Human Factors of Pedestrian Walking and Crossing Behaviour. Transp. Res. Procedia 2017, 25, 2002–2015. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Yannis, G.; Golias, J. Analysis of Pedestrian Exposure to Risk in Relation to Crossing Behavior. Transp. Res. Rec. 2012, 2299, 79–90. [Google Scholar] [CrossRef]
- Rosenbloom, T.; Ben-Eliyahu, A.; Nemrodov, D. Children’s Crossing Behavior with an Accompanying Adult. Saf. Sci. 2008, 46, 1248–1254. [Google Scholar] [CrossRef]
- Sucha, M.; Dostal, D.; Risser, R. Pedestrian-Driver Communication and Decision Strategies at Marked Crossings. Accid. Anal. Prev. 2017, 102, 41–50. [Google Scholar] [CrossRef]
- Sueur, C.; Class, B.; Hamm, C.; Meyer, X.; Pelé, M. Different Risk Thresholds in Pedestrian Road Crossing Behaviour: A Comparison of French and Japanese Approaches. Accid. Anal. Prev. 2013, 58, 59–63. [Google Scholar] [CrossRef]
- Turner, S.; Fitzpatrick, K.; Brewer, M.; Park, E.S. Motorist Yielding to Pedestrians at Unsignalized Intersections: Findings from a National Study on Improving Pedestrian Safety. Transp. Res. Rec. 2006, 1982, 1–12. [Google Scholar] [CrossRef]
- Zegeer, C.V.; Carter, D.L.; Hunter, W.W.; Stewart, J.R.; Huang, H.; Do, A.; Sandt, L. Index for Assessing Pedestrian Safety at Intersections. Transp. Res. Rec. 2006, 1982, 76–83. [Google Scholar] [CrossRef]
- Deb, S.; Strawderman, L.J.; Carruth, D.W. Investigating Pedestrian Suggestions for External Features on Fully Autonomous Vehicles: A Virtual Reality Experiment. Transp. Res. Part F Traffic Psychol. Behav. 2018, 59, 135–149. [Google Scholar] [CrossRef]
- Feng, Y.; Duives, D.; Daamen, W.; Hoogendoorn, S. Data Collection Methods for Studying Pedestrian Behaviour: A Systematic Review. Build. Environ. 2021, 187, 107329. [Google Scholar] [CrossRef]
- Lassarre, S.; Bonnet, E.; Bodin, F.; Papadimitriou, E.; Yannis, G.; Golias, J. A GIS-Based Methodology for Identifying Pedestrians’ Crossing Patterns. Comput. Environ. Urban Syst. 2012, 36, 321–330. [Google Scholar] [CrossRef]
- Deb, S.; Rahman, M.M.; Strawderman, L.J.; Garrison, T.M. Pedestrians’ Receptivity toward Fully Automated Vehicles: Research Review and Roadmap for Future Research. IEEE Trans. Hum.-Mach. Syst. 2018, 48, 279–290. [Google Scholar] [CrossRef]
- Cao, S.; Zhang, J.; Song, W.; Shi, C.; Zhang, R. The Stepping Behavior Analysis of Pedestrians from Different Age Groups via a Single-File Experiment. J. Stat. Mech. Theory Exp. 2018, 2018, 33402. [Google Scholar] [CrossRef]
- Fu, L.; Cao, S.; Shi, Y.; Chen, S.; Yang, P.; Fang, J. Walking Behavior of Pedestrian Social Groups on Stairs: A Field Study. Saf. Sci. 2019, 117, 447–457. [Google Scholar] [CrossRef]
- Wei, X.; Lv, W.; Song, W.; Li, X. Survey Study and Experimental Investigation on the Local Behavior of Pedestrian Groups. Complexity 2015, 20, 87–97. [Google Scholar] [CrossRef]
- Charron, C.; Festoc, A.; Guéguen, N. Do Child Pedestrians Deliberately Take Risks When They Are in a Hurry? An Experimental Study on a Simulator. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 635–643. [Google Scholar] [CrossRef]
- Meir, A.; Oron-Gilad, T.; Parmet, Y. Can Child-Pedestrians’ Hazard Perception Skills Be Enhanced? Accid. Anal. Prev. 2015, 83, 101–110. [Google Scholar] [CrossRef]
- Schwebel, D.C.; Gaines, J.; Severson, J. Validation of Virtual Reality as a Tool to Understand and Prevent Child Pedestrian Injury. Accid. Anal. Prev. 2008, 40, 1394–1400. [Google Scholar] [CrossRef] [PubMed]
- Thomson, J.A.; Tolmie, A.K.; Foot, H.C.; Whelan, K.M.; Sarvary, P.; Morrison, S. Influence of Virtual Reality Training on the Roadside Crossing Judgments of Child Pedestrians. J. Exp. Psychol. Appl. 2005, 11, 175–186. [Google Scholar] [CrossRef] [PubMed]
- Zito, G.A.; Cazzoli, D.; Scheffler, L.; Jäger, M.; Müri, R.M.; Mosimann, U.P.; Nyffeler, T.; Mast, F.W.; Nef, T. Street Crossing Behavior in Younger and Older Pedestrians: An Eye- and Head-Tracking Study. BMC Geriatr. 2015, 15, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Cavallo, V.; Dommes, A.; Dang, N.T.; Vienne, F. A Street-Crossing Simulator for Studying and Training Pedestrians. Transp. Res. Part F Traffic Psychol. Behav. 2019, 61, 217–228. [Google Scholar] [CrossRef]
- Feldstein, I.; Dietrich, A.; Milinkovic, S.; Bengler, K. A Pedestrian Simulator for Urban Crossing Scenarios. IFAC-PapersOnLine 2016, 49, 239–244. [Google Scholar] [CrossRef]
- Morrongiello, B.A.; Corbett, M.; Milanovic, M.; Pyne, S.; Vierich, R. Innovations in Using Virtual Reality to Study How Children Cross Streets in Traffic: Evidence for Evasive Action Skills. Inj. Prev. 2015, 21, 266–270. [Google Scholar] [CrossRef] [PubMed]
- Simpson, G.; Johnston, L.; Richardson, M. An Investigation of Road Crossing in a Virtual Environment. Accid. Anal. Prev. 2003, 35, 787–796. [Google Scholar] [CrossRef]
- Sween, R.; Deb, S.; Carruth, D.W.; Waddell, D.; Furuichi, M. Development of an Effective Pedestrian Simulator for Research. In Advances in Human Aspects of Transportation; Stanton, N.A., Landry, S., Di Bucchianico, G., Vallicelli, A., Eds.; Springer: Cham, Switzerland, 2017; pp. 183–191. ISBN 978-3-319-41682-3. [Google Scholar]
- Deb, S.; Carruth, D.W.; Sween, R.; Strawderman, L.; Garrison, T.M. Efficacy of Virtual Reality in Pedestrian Safety Research. Appl. Ergon. 2017, 65, 449–460. [Google Scholar] [CrossRef]
- Fu, Q.-W.; Liu, Q.-H.; Hu, T. Multi-objective optimization research on VR task scenario design based on cognitive load. Facta Univ. Ser. Mech. Eng. 2024, 22, 293–313. [Google Scholar] [CrossRef]
- Soares, F.; Silva, E.; Pereira, F.; Silva, C.; Sousa, E.; Freitas, E. To Cross or Not to Cross: Impact of Visual and Auditory Cues on Pedestrians’ Crossing Decision-Making. Transp. Res. Part F Traffic Psychol. Behav. 2021, 82, 202–220. [Google Scholar] [CrossRef]
- Blender Foundation. (n.d.). 2.79—Blender.org. Available online: https://www.blender.org/download/releases/2-79/ (accessed on 28 May 2024).
- Soares, F.; Silva, E.; Pereira, F.; Silva, C.; Sousa, E.; Freitas, E. The Influence of Noise Emitted by Vehicles on Pedestrian Crossing Decision-Making: A Study in a Virtual Environment. Appl. Sci. 2020, 10, 2913. [Google Scholar] [CrossRef]
- EN ISO 11819-2; Acoustics—Measurement of the Influence of Road Surfaces on Traffic Noise—Part 2: The Close-Proximity Method. ISO: London, UK, 2017.
- Pereira, F.; Soares, F.; Silva, C.; Sousa, E.; Freitas, E. CPX Based Synthesis for Binaural Auralization of Vehicle Rolling Noise to an Arbitrary Positioned Stander-by Receiver. Appl. Acoust. 2021, 182, 108211. [Google Scholar] [CrossRef]
- Feldstein, I.; Dyszak, G. Road Crossing Decisions in Real and Virtual Environments: A Comparative Study on Simulator Validity. Accid. Anal. Prev. 2020, 137, 105356. [Google Scholar] [CrossRef] [PubMed]
- Lobjois, R.; Cavallo, V. The Effects of Aging on Street-Crossing Behavior: From Estimation to Actual Crossing. Accid. Anal. Prev. 2009, 41, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Johnsson, C.; Laureshyn, A.; De Ceunynck, T. In Search of Surrogate Safety Indicators for Vulnerable Road Users: A Review of Surrogate Safety Indicators. Transp. Rev. 2018, 38, 765–785. [Google Scholar] [CrossRef]







| Experimental Approach | Total | ||
|---|---|---|---|
| Static | Dynamic | ||
| Age | 24–60 years (M = 39.70; SD = 12.11) | 23–57 years (M = 39.17; SD = 10.44) | 23–60 years (M = 39.88; SD = 11.20) |
| Sex | 46% Male; 54% Female | 57% Male; 43% Female | 52% Male; 48% Female |
| Condition | Vi (km/h) | Vf (km/h) | Di.mov (m) | Di (m) | Df (m) |
|---|---|---|---|---|---|
| 1 | 20 | 20 | 35 | - | - |
| 2 | 30 | 30 | 35 | - | - |
| 3 | 20 | 20 | 30 | - | - |
| 4 | 30 | 30 | 30 | - | - |
| 5 | 20 | 20 | 25 | - | - |
| 6 | 30 | 30 | 25 | - | - |
| 7 | 30 | 10 | 30 | 25 | 5 |
| 8 | 20 | 10 | 30 | 15 | 10 |
| 9 | 20 | 0 | 30 | 15 | 5.50 |
| 10 | 30 | 0 | 30 | 20 | 5.50 |
| Indicator 1 | Condition | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| LAeq (dB(A)) | 66.22 | 65.67 | 65.23 | 71.09 | 70.58 | 70.19 | 58.59 | 60.04 | 58.90 | 61.04 |
| LAmax (dB(A)) | 72.81 | 72.81 | 72.81 | 77.49 | 77.49 | 77.49 | 61.12 | 64.28 | 63.93 | 66.15 |
| L5 (dB(A)) | 72.27 | 72.08 | 71.85 | 76.88 | 76.83 | 76.77 | 60.70 | 63.74 | 63.40 | 65.46 |
| L10 (dB(A)) | 71.09 | 70.68 | 70.28 | 76.19 | 75.75 | 75.31 | 60.43 | 63.45 | 62.75 | 63.93 |
| L50 (dB(A)) | 62.72 | 61.89 | 60.98 | 67.67 | 66.93 | 65.85 | 58.17 | 57.34 | 57.89 | 60.52 |
| L90 (dB(A)) | 57.81 | 57.32 | 56.12 | 60.09 | 60.28 | 59.97 | 56.42 | 56.06 | 52.80 | 52.65 |
| Measurement time (s) | 6.45 | 7.50 | 8.40 | 4.80 | 5.55 | 6.15 | 7.50 | 7.05 | 10.20 | 9.30 |
| Dynamic range (dB(A)) | 28.15 | 28.15 | 28.15 | 32.83 | 32.83 | 32.83 | 16.46 | 19.62 | 19.27 | 21.50 |
| Indicator 1 | Condition | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| LAeq (dB(A)) | 66.35 | 65.75 | 65.32 | 71.07 | 70.49 | 70.10 | 58.80 | 61.64 | 59.15 | 62.49 |
| LAmax (dB(A)) | 72.70 | 72.67 | 72.89 | 78.16 | 78.03 | 77.71 | 62.03 | 65.83 | 63.32 | 66.34 |
| L5 (dB(A)) | 71.68 | 71.81 | 71.77 | 77.16 | 76.93 | 76.60 | 61.65 | 65.17 | 62.91 | 65.65 |
| L10 (dB(A)) | 70.56 | 70.74 | 70.33 | 75.83 | 75.38 | 75.05 | 61.26 | 64.95 | 62.15 | 65.48 |
| L50 (dB(A)) | 62.54 | 62.65 | 61.39 | 67.82 | 66.61 | 66.03 | 58.90 | 61.71 | 58.75 | 62.13 |
| L90 (dB(A)) | 57.27 | 56.98 | 55.65 | 61.15 | 60.96 | 60.76 | 51.37 | 50.47 | 55.21 | 55.73 |
| Measurement time (s) | 6.45 | 7.50 | 8.40 | 4.80 | 5.55 | 6.15 | 7.5 | 7.05 | 10.20 | 9.30 |
| Dynamic range (dB(A)) | 25.47 | 25.44 | 25.66 | 30.93 | 30.80 | 30.48 | 14.80 | 18.60 | 16.09 | 19.11 |
| Experimental Approach | Vi (km/h) | Di.mov (m) | Crossings | Crashes | ||
|---|---|---|---|---|---|---|
| Mean (%) | SD (%) | SE (%) | (%) | |||
| Static | 20 | 25 | 23.00 | 31.90 | 5.82 | |
| 30 | 41.30 | 42.30 | 7.73 | |||
| 35 | 49.30 | 40.70 | 7.43 | |||
| 30 | 25 | 4.33 | 16.80 | 3.06 | ||
| 30 | 7.67 | 17.70 | 3.24 | |||
| 35 | 12.70 | 22.90 | 4.18 | |||
| Dynamic | 20 | 25 | 12.30 | 19.80 | 3.61 | 59.50 |
| 30 | 54.30 | 39.90 | 7.28 | 0.61 | ||
| 35 | 74.00 | 35.00 | 6.39 | 0.90 | ||
| 30 | 25 | 0 | 0 | 0 | 0 | |
| 30 | 1.33 | 7.30 | 1.33 | 75.00 | ||
| 35 | 5.00 | 16.80 | 3.06 | 20.00 | ||
| Experimental Approach | Vi (km/h) | Di.mov (m) | Crossing Start Time | TTP | ||||
|---|---|---|---|---|---|---|---|---|
| Mean (s) | SD (s) | SE (s) | Mean (s) | SD (s) | SE (s) | |||
| Static | 20 | 25 | 1.07 | 0.45 | 0.05 | 3.62 | 0.41 | 0.05 |
| 30 | 1.18 | 0.58 | 0.05 | 4.53 | 0.52 | 0.05 | ||
| 35 | 1.31 | 0.82 | 0.07 | 5.22 | 0.75 | 0.06 | ||
| 30 | 25 | 0.69 | 0.19 | 0.05 | 2.41 | 0.23 | 0.06 | |
| 30 | 0.87 | 0.49 | 0.10 | 2.91 | 0.43 | 0.09 | ||
| 35 | 1.05 | 0.50 | 0.08 | 3.32 | 0.43 | 0.07 | ||
| Dynamic | 20 | 25 | 2.74 | 0.35 | 0.06 | 2.08 | 0.34 | 0.06 |
| 30 | 2.83 | 0.37 | 0.03 | 3.16 | 0.37 | 0.03 | ||
| 35 | 2.93 | 0.46 | 0.03 | 3.81 | 0.39 | 0.03 | ||
| 30 | 25 | - | - | - | - | - | - | |
| 30 | 2.28 | 0.15 | 0.08 | 1.68 | 0.21 | 0.10 | ||
| 35 | 2.41 | 0.30 | 0.08 | 2.14 | 0.25 | 0.06 | ||
| Experimental Approach | Vi (km/h) | Speed Pattern | Crossings | Crashes | ||
|---|---|---|---|---|---|---|
| Mean (%) | SD (%) | SE (%) | (%) | |||
| Static | 20 | Constant | 41.30 | 42.30 | 7.73 | |
| Slow Down | 80.30 | 27.10 | 4.95 | |||
| Stop | 87.70 | 17.90 | 3.28 | |||
| 30 | Constant | 7.67 | 17.70 | 3.24 | ||
| Slow Down | 69.30 | 35.80 | 6.54 | |||
| Stop | 82.70 | 28.40 | 5.18 | |||
| Dynamic | 20 | Constant | 54.30 | 39.90 | 7.28 | 0.61 |
| Slow Down | 85.00 | 30.60 | 5.59 | 0 | ||
| Stop | 79.00 | 32.70 | 5.98 | 0 | ||
| 30 | Constant | 1.33 | 7.30 | 1.33 | 75.00 | |
| Slow Down | 79.30 | 34.20 | 6.25 | 3.36 | ||
| Stop | 75.70 | 38.70 | 7.07 | 0 | ||
| Experimental Approach | Vi (km/h) | Speed Pattern | Crossing Start Time | TTP | ||||
|---|---|---|---|---|---|---|---|---|
| Mean (s) | SD (s) | SE (s) | Mean (s) | SD (s) | SE (s) | |||
| Static | 20 | Constant | 1.18 | 0.58 | 0.05 | 4.53 | 0.52 | 0.05 |
| Slow Down | 2.63 | 1.63 | 0.11 | 4.12 | 0.58 | 0.04 | ||
| Stop | 3.64 | 2.19 | 0.14 | 4.68 | 6.07 | 0.37 | ||
| 30 | Constant | 0.87 | 0.49 | 0.10 | 2.91 | 0.43 | 0.09 | |
| Slow Down | 3.10 | 1.24 | 0.09 | 3.06 | 0.33 | 0.02 | ||
| Stop | 4.01 | 1.30 | 0.08 | 6.83 | 10.50 | 0.67 | ||
| Dynamic | 20 | Constant | 2.83 | 0.37 | 0.03 | 3.16 | 0.37 | 0.03 |
| Slow Down | 3.36 | 0.79 | 0.05 | 3.80 | 0.35 | 0.02 | ||
| Stop | 4.34 | 1.51 | 0.10 | 3.86 | 4.96 | 0.32 | ||
| 30 | Constant | 2.28 | 0.15 | 0.08 | 1.68 | 0.21 | 0.10 | |
| Slow Down | 3.81 | 0.71 | 0.05 | 3.08 | 0.34 | 0.02 | ||
| Stop | 4.56 | 0.67 | 0.04 | 7.34 | 11.50 | 0.77 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soares, F.; Pereira, F.; Faria, S.; Sousa, E.; Almeida, R.; Freitas, E.F. Pedestrian Behavior in Static and Dynamic Virtual Road Crossing Experiments. Appl. Syst. Innov. 2024, 7, 94. https://doi.org/10.3390/asi7050094
Soares F, Pereira F, Faria S, Sousa E, Almeida R, Freitas EF. Pedestrian Behavior in Static and Dynamic Virtual Road Crossing Experiments. Applied System Innovation. 2024; 7(5):94. https://doi.org/10.3390/asi7050094
Chicago/Turabian StyleSoares, Francisco, Frederico Pereira, Susana Faria, Emanuel Sousa, Raul Almeida, and Elisabete F. Freitas. 2024. "Pedestrian Behavior in Static and Dynamic Virtual Road Crossing Experiments" Applied System Innovation 7, no. 5: 94. https://doi.org/10.3390/asi7050094
APA StyleSoares, F., Pereira, F., Faria, S., Sousa, E., Almeida, R., & Freitas, E. F. (2024). Pedestrian Behavior in Static and Dynamic Virtual Road Crossing Experiments. Applied System Innovation, 7(5), 94. https://doi.org/10.3390/asi7050094









