Study of Systems of Active Vibration Protection of Navigation Instrument Equipment
Abstract
:1. Introduction
2. Materials and Methods
3. The Mathematical Model
- Setting independent parameters ξ, ζa, ζo, ζv, kc and β.
- Cycle:
- 2.1.
- Setting variable parameters and .
- 2.2.
- Determination by Formula (3) η and ζc.
- 2.3.
- Calculation of the coefficients of the Rausch matrix for the defined , χ, η and ζc and checking their compliance with the sustainability criterion.
- 2.4.
- Formation of a “stability” matrix for given values of variables and χ.
4. Building the Boundaries of Sustainability
4.1. Custom Frequencies
4.2. Vibration Isolation Efficiency
| (χ >> ξ) | (ξ >> χ) | |||
| 0.346 | 0.346 | 0.244 | 0.233 | |
5. Numerical Analysis
β = ωv/ωo = 3; kc = 0.5; δ = ωc/ωo = 0.24; η = Tf/To = 1.19; ζc = 1.13;
Δ = 2(ςc + ςo + ςv) + η(1 − kc) = 2.97.
β = ωv/ωo = 3; kc = 0.5; δ = ωc/ωo = 0.18; η = Tf/To = 1.35; ζc = 1.52;
Δ = 2(ςc + ςo + ςv) + η(1 − kc) = 3.83.
- (a)
- vibration protection against micro-vibration in the low-frequency range;
- (b)
- vibration protection against intense vibration in a wide frequency range.
6. Conclusions
- -
- the effect of the vibration isolator parameters on its efficiency, its own dynamics, and the possibility of reducing the lower limit of the vibration isolation frequency range has been clarified;
- -
- a linear mathematical model of an active vibration isolator was developed, taking into account the dynamics of sensitive elements and the executive mechanism;
- -
- analytical relations were obtained for an approximate estimation of the zeros and poles of the transfer function of the active vibration isolator and the results of the analysis based on these relations;
- -
- a well-founded schematic implementation was developed of the navigation equipment vibration isolation system using an elastic suspension on vertically arranged flat springs according to the scheme of the inverted pendulum. This makes it possible to achieve low natural frequencies of the vibration isolator in the horizontal plane (0.5–1 Hz), and also ensures the practical absence of angular rotation of the navigation equipment relative to the Earth.
- -
- the main requirements for the technical means of implementing an active vibration isolator are determined, when justifying the need for a coordinated selection of gain coefficients and time constants of individual feedback elements of an active vibration isolator of navigation equipment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Odintsov, A.A. Theory and Calculation of Gyroscopic Devices; Vyshcha Shkola: Kiev, Ukraine, 1985; 392p. [Google Scholar]
- Akande, I.G.; Fajobi, M.A.; Odunlami, O.A.; Oluwole, O.O. Exploitation of composite materials as vibration isolator and damper in machine tools and other mechanical systems: A review. Mater. Today Proc. 2020, 43, 1465–1470. [Google Scholar] [CrossRef]
- Yao, J.; Wu, K.; Guo, M.; Wang, G.; Wang, L. An Ultralow-Frequency Active Vertical Vibration Isolator with Geometric Antispring Structure for Absolute Gravimetry. IEEE Trans. Instrum. Meas. 2020, 69, 8758149. [Google Scholar] [CrossRef]
- Korobiichuk, I. Mathematical model of precision sensor for an automatic weapons stabilizer system. Measurement 2016, 89, 151–158. [Google Scholar] [CrossRef]
- Yao, J.-M.; Zhuang, W.; Feng, J.-Y.; Wang, Q.-Y.; Zhao, Y.; Wang, S.-K.; Wu, S.-Q.; Li, T.-C. Effect of vibration noise with fixed phase on absolute gravimetry applying vibration isolator. Wuli Xuebao/Acta Phys. Sin. 2021, 70, 219101. [Google Scholar] [CrossRef]
- Li, S.; Feng, G.; Zhao, Q. Design and Research of Semiactive Quasi-Zero Stiffness Vibration Isolation System for Vehicles. Shock. Vib. 2021, 2021, 5529509. [Google Scholar] [CrossRef]
- Kim, J.; Jeon, Y.; Um, S.; Park, U.; Kim, K.-S.; Kim, S. A Novel Passive Quasi-Zero Stiffness Isolator for Ultra-Precision Measurement Systems. Int. J. Precis. Eng. Manuf. 2019, 20, 1573–1580. [Google Scholar] [CrossRef]
- Doan, N.V.; Goo, N.S.; Ko, Y.; Seo, S.; Chung, M. Design and Analysis of Micro-Vibration Isolation System for Digital Image Correlation System-Based Structural Health Monitoring. Int. J. Aeronaut. Space Sci. 2022, 23, 711–722. [Google Scholar] [CrossRef]
- Li, Z.; Wu, K.; Guo, M.; Chen, Y.; Wen, Y.; Wang, L. Constrained Model Predictive Control for Six-DOF Vibration Isolator of the Absolute Marine Gravimeter. In Proceedings of the Conference Record—IEEE Instrumentation and Measurement Technology Conference, Glasgow, Scotland, 17–20 May 2021; p. 9459933. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Lai, J.; Zhong, C.; Dai, Z.; Yu, M. Robustness analysis of magnetorheological elastomer-based vibration isolation system with optimal fuzzy controller. Smart Mater. Struct. 2023, 32, 035018. [Google Scholar] [CrossRef]
- Pavić, G. Application of energy criteria to vibration isolation. J. Sound Vib. 2022, 520, 116619. [Google Scholar] [CrossRef]
- Zeng, R.; Wen, G.; Zhou, J.; Zhao, G. Limb-inspired bionic quasi-zero stiffness vibration isolator. Acta Mech. Sin./Lixue Xuebao 2021, 37, 1152–1167. [Google Scholar] [CrossRef]
- Han, W.-J.; Lu, Z.-Q.; Niu, M.-Q.; Chen, L.-Q. Analytical and experimental investigation on a NiTiNOL circular ring-type vibration isolator with both stiffness and damping nonlinearities. J. Sound Vib. 2023, 547, 117543. [Google Scholar] [CrossRef]
- Tao, Y.; Rui, X.; Zhang, J.; Yang, F. Simulation of vibration characteristics of IMU with controllable magnetorheological isolation system. Multibody Syst. Dyn. 2023, 59, 293–312. [Google Scholar] [CrossRef]
- Yilmaz, C.; Kikuchi, N. Analysis and design of passive band-stop filter-type vibration isolators for low-frequency applications. J. Sound Vib. 2006, 291, 1004–1028. [Google Scholar] [CrossRef]
- Lanets, O.; Kachur, O.; Korendiy, V. Derivation of analytical dependencies for determining stiffness parameters of vibration isolators of vibratory machine. Ukr. J. Mech. Eng. Mater. Sci. 2020, 6, 3–4. [Google Scholar] [CrossRef]
- Ferdek, U.; Dukała, M. Experimental analysis of nonlinear characteristics of absorbers with wire rope isolators. Open Eng. 2021, 11, 1170–1179. [Google Scholar] [CrossRef]
- Dylejko, P.G.; MacGillivray, I.R. On the concept of a transmission absorber to suppress internal resonance. J. Sound Vib. 2014, 333, 2719–2734. [Google Scholar] [CrossRef]
- Yilmaz, C.; Hulbert, G. Theory of phononic gaps induced by inertial amplification in finite structures. Phys. Lett. A 2010, 374, 3576–3584. [Google Scholar] [CrossRef]
- Acar, G.; Yilmaz, C. Experimental and numerical evidence for the existence of wide and deep phononic gaps induced by inertial amplification in two-dimensional solid structures. J. Sound Vib. 2013, 332, 6389–6404. [Google Scholar] [CrossRef]
- Dylejko, P.G.; Kessissoglou, N.J.; Tso, Y.; Norwood, C.J. Optimisation of a resonance changer to minimise the vibration transmission in marine vessels. J. Sound Vib. 2007, 300, 101–116. [Google Scholar] [CrossRef]
- Snowdon, J.C. Mechanical four-pole parameters and their application. J. Sound Vib. 1971, 15, 307–323. [Google Scholar] [CrossRef]
- Sun, L.L.; Hansen, C.H.; Doolan, C. Evaluation of the performance of a passive–active vibration isolation system. Mech. Syst. Signal Process. 2015, 50-51, 480–497. [Google Scholar] [CrossRef]
- Goyder, H.G.; White, R.G. Vibrational power flow from machines into built-up structures. II. Wave propagation and power flow in beam-stiffened plates. J. Sound Vib. 1980, 68, 77–96. [Google Scholar] [CrossRef]
- Pinnington, R.J. Vibration power flow transmission to a seating of vibration isolated motor. J. Sound Vib. 1987, 118, 515–530. [Google Scholar] [CrossRef]
- Jenkins, M.D.; Nelson, P.A.; Pinnington, R.J.; Elliott, S.J. Active isolation of periodic machinery vibrations. J. Sound Vib. 1993, 166, 117–140. [Google Scholar] [CrossRef]
- Redman-White, W.; Nelson, P.A.; Curtia, A.R.D. Experiments on the active control of flexural wave power flow. J. Sound Vib. 1987, 112, 187–191. [Google Scholar] [CrossRef]
- Gardonio, P.; Elliott, S.J.; Pinnington, R.J. Active isolation of structural vibration on a multiple-degree-of-freedom system. Part I: The dynamics of the system. J. Sound Vib. 1997, 207, 61–93. [Google Scholar] [CrossRef]
- Qiu, X.; Hansen, C. Applying effort constraints on adaptive feedforward control using the active set method. J. Sound Vib. 2003, 260, 757–762. [Google Scholar] [CrossRef]
- Sun, L.; Leung, A.Y.T.; Lee, Y.Y.; Song, K. Vibrational power-flow analysis of a MIMO system using the transmission matrix approach. Mech. Syst. Signal Process. 2007, 21, 365–388. [Google Scholar] [CrossRef]
- Du, Y.; Burdisso, R.A.; Nikolaidis, E.; Tiwari, D. Effects of isolators internal resonances on force transmissibility and radiated noise. J. Sound Vib. 2003, 268, 751–778. [Google Scholar] [CrossRef]
- Mead, D.J.; White, R.; Zhang, X.M. Power Transmission in a Periodically Supported Infinite Beam Excited at a Single Point. J. Sound Vib. 1994, 169, 558–561. [Google Scholar] [CrossRef]
- Cuschieri, J.M. Vibration transmission through periodic structures using a mobility power flow approach. J. Sound Vib. 1990, 143, 65–74. [Google Scholar] [CrossRef]
- Balaji, P.S.; Moussa, L.; Rahaman, M.E.; Tiong, P.L.Y.; Ho, L.H.; Adnan, A. Performance study of wire rope isolators for vibration isolation equipment and structures. J. Eng. Appl. Sci. 2016, 11, 11036–11042. [Google Scholar]
- Zou, L.; Zheng, C.; Zheng, Z.; Hu, F.; Shao, Y.; Xue, X. Comparison of Dynamic Performance of an All-Metallic Vibration Isolator by Elliptic Method and Frequency Sweeping Method. Symmetry 2022, 14, 2017. [Google Scholar] [CrossRef]
- He, X.; Ou, H.; He, X. Optimization of Vibration Isolation Parameters of Electromagnetic Vibration Feeder and Design of Vibration Isolator. J. Phys. Conf. Ser. 2022, 2383, 012021. [Google Scholar] [CrossRef]
- Lu, Z.; Tiejun, Y.; Brennan, M.J.; Liu, Z.; Chen, L.-Q. Experimental Investigation of a Two-Stage Nonlinear Vibration Isolation System with HighStatic-Low-Dynamic Stiffness. J. Appl. Mech. Trans. ASME 2017, 84, 021001. [Google Scholar] [CrossRef]
- Lu, Z.; Brennan, M.J.; Chen, L.-Q. On the transmissibilities of nonlinear vibration isolation system. J. Sound Vib. 2016, 375, 28–37. [Google Scholar] [CrossRef]
- Lu, Z.-Q.; Gu, D.-H.; Ding, H.; Lacarbonara, W.; Chen, L.-Q. Nonlinear vibration isolation via a circular ring. Mech. Syst. Signal Process. 2020, 136, 106490. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Brennan, M.; Ding, H.; Chen, L.Q. High-static-low-dynamic-stiffness vibration isolation enhanced by damping nonlinearity. Sci. China Technol. Sci. 2019, 62, 1103–1110. [Google Scholar] [CrossRef]
- Cheng, X.; Lu, H.; McFarland, D.M. Reconstruction of waves traveling in a nonlinear granular chain from acoustic measurements. Mech. Syst. Signal Process. 2021, 161, 107988. [Google Scholar] [CrossRef]
- Chou, J.-Y.; Chang, C.-M. Image motion extraction of structures using computer vision techniques: A comparative study. Sensors 2021, 21, 6248. [Google Scholar] [CrossRef]
- Kapasakalis, K.A.; Alamir, C.-H.T.; Antoniadis, I.A.; Sapountzakis, E.J. Frequency-based design of the Kdamper concept for seismic isolation of bridges. Lect. Notes Mech. Eng. 2021, 58, 169–191. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, J.; Zhao, J.; Bian, X.; Zou, L. Improving low frequency isolation performance of optical platforms using electromagnetic active-negative-stiffness method. Appl. Sci. 2020, 10, 7342. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, L.; Hu, Y.; Yang, F. Vibration characteristics analysis of convalescent-wheelchair robots equipped with dynamic absorbers. Shock Vib. 2018, 2018, 5393051. [Google Scholar] [CrossRef]
- Lu, R.; Borghesani, P.; Randall, R.B.; Smith, W.A.; Peng, Z. Removal of transfer function effects from gear vibration signals under constant and variable speed conditions. Mech. Syst. Signal Process. 2023, 184, 109714. [Google Scholar] [CrossRef]
- Brennan, M.J.; Tang, B. Virtual experiments in mechanical vibrations: Structural dynamics and signal processing. In Virtual Experiments in Mechanical Vibrations: Structural Dynamics and Signal Processing; Wiley: Hoboken, NJ, USA, 2019; pp. 1–336. [Google Scholar]
- Qiu, Y.; Hong, D.; Kim, B. Location optimization standard of passive–active vibration isolation element for plate structures in next generation mobilities. JVC J. Vib. Control. 2024, 30, 2742–2758. [Google Scholar] [CrossRef]
- Jauregui-Correa, J.C. The design of vibration absorbers using the rheological properties of viscoelastic materials. In Advances in Rheology Research; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2017; pp. 347–380. [Google Scholar]
- Krzyzynski, T.; Maciejewski, I.; Meyer, L.; Meyer, H. Modelling and Control Design of Vibration Reduction Systems: Methods and Procedures of Selecting Vibro-Isolation Properties; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–184. [Google Scholar] [CrossRef]
- Mendis, P.; Ngo, T. Vibration and shock problems of civil engineering structures. In Vibration and Shock Handbook; Taylor & Francis Ltd.: London, UK, 2015; p. 13. [Google Scholar]
- Ouyang, X.; Cao, S.; Hou, Y.; Li, G.; Huang, X. Nonlinear dynamics of a dual-rotor system with active elastic support/dry friction dampers based on complex nonlinear modes. Int. J. Non-Linear Mech. 2024, 166, 104856. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, A.; Li, Q.; Zhu, J.; Hou, L.; Zhao, J.; Yi, J.; Pu, H.; Luo, J. Semi-active control of the electromagnetic negative stiffness mechanism in a double-layer vibration isolator. Nonlinear Dyn. 2024, 112, 13951–13969. [Google Scholar] [CrossRef]
- Von Wysocki, T.; Leupolz, M.; Gauterin, F. Metamodels Resulting from Two Different Geometry Morphing Approaches Are Suitable to Direct the Modification of Structure-Born Noise Transfer in the Digital Design Phase. Appl. Syst. Innov. 2020, 3, 47. [Google Scholar] [CrossRef]
- Hu, A.; Paoletti, P. Analytical exploration of generic undamped mass–spring chains: A comprehensive study. Syst. Signal Process. 2024, 212, 111277. [Google Scholar] [CrossRef]
- Frolov, K.V. Reducing the amplitude of oscillations of resonant systems by controlled parameter changes. Machinology 1965, 3, 38–42. [Google Scholar]
- Korobiichuk, I.; Mel’nick, V.; Karachun, V. Hypersonic Technologies for Launching and Problems of Inertial Navigation; Monografie, Studia, Rozprawy; Oficyna Wydawnicza Sieć Badawcza Łukasiewicz—Przemysłowy Instytut Automatyki i Pomiarów PIAP: Warsaw, Poland, 2022; p. 308. [Google Scholar]
- Bhardwaj, R.; Mishra, J.; Narayan, S.; Suseendran, G. Mathematics in Computational Science and Engineering; Scrivener Publishing LLC.: Beverly, MA, USA, 2022; pp. 1–448. [Google Scholar] [CrossRef]
- Derbel, N.; Derbel, F.; Kanoun, O. Systems, Automation, and Control. Systems, Automation, and Control; De Gruyter: Vienna, Austria, 2019; pp. 1–319. [Google Scholar] [CrossRef]
- Palani, S. Automatic Control Systems: With MATLAB, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–98. [Google Scholar] [CrossRef]
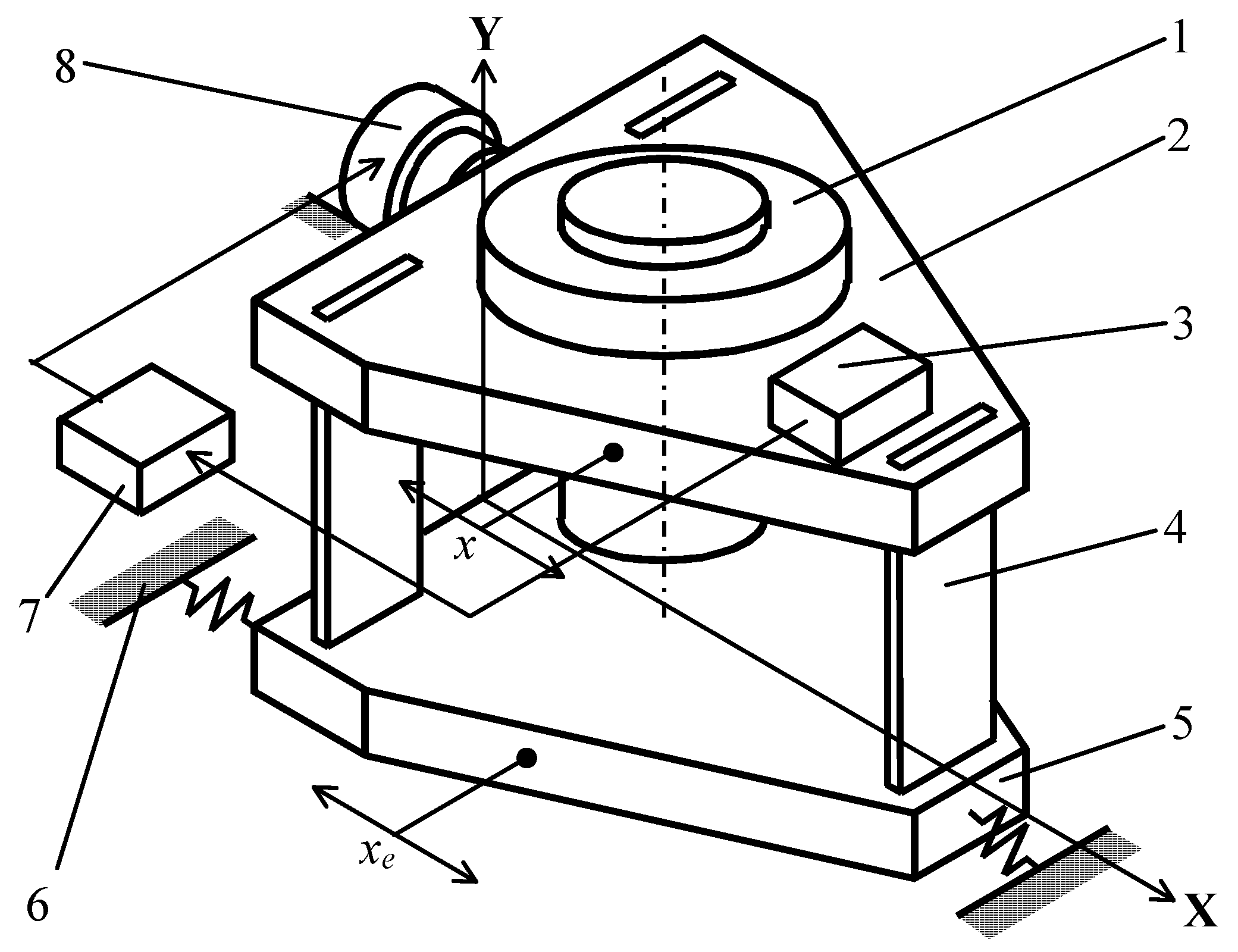
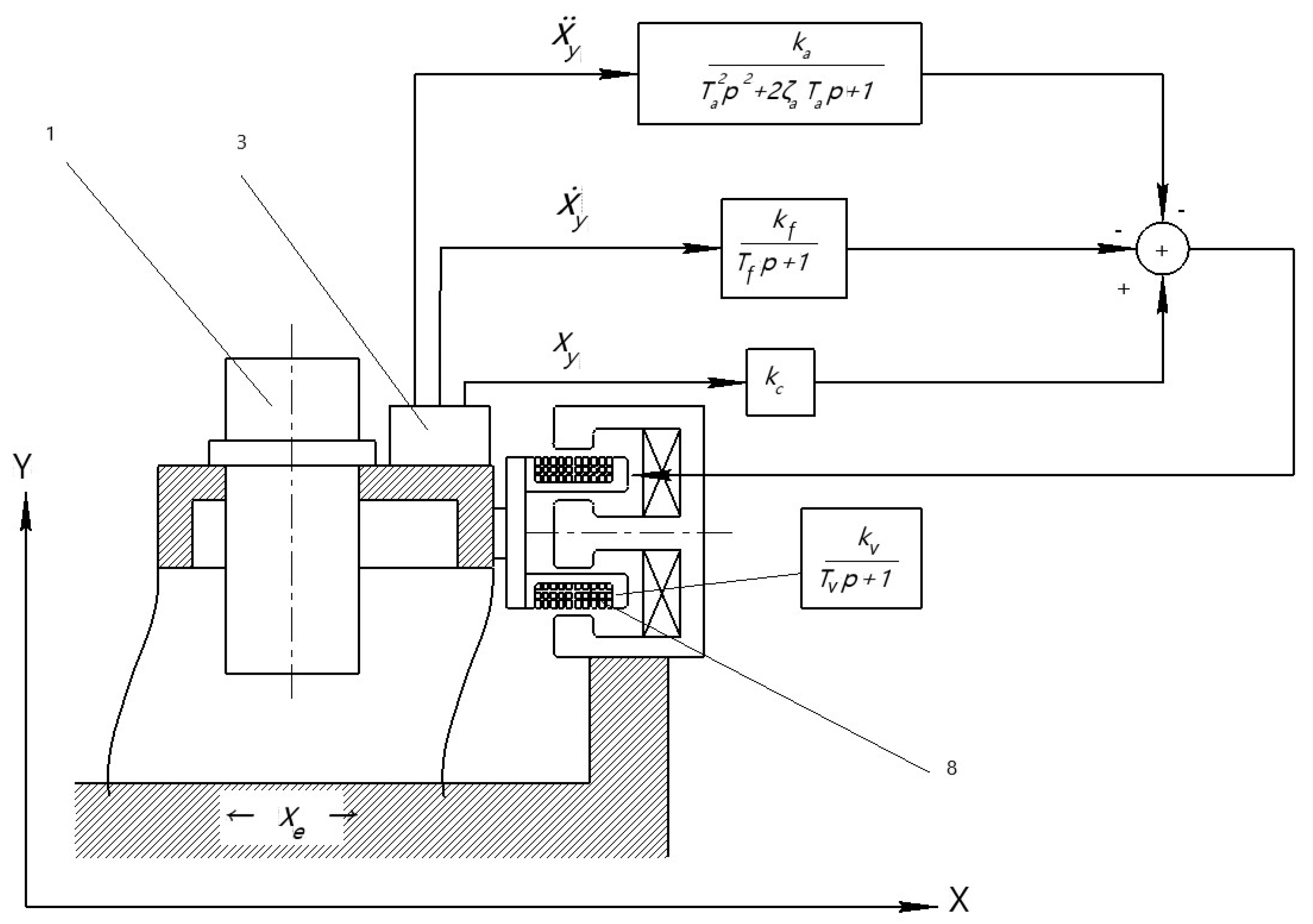
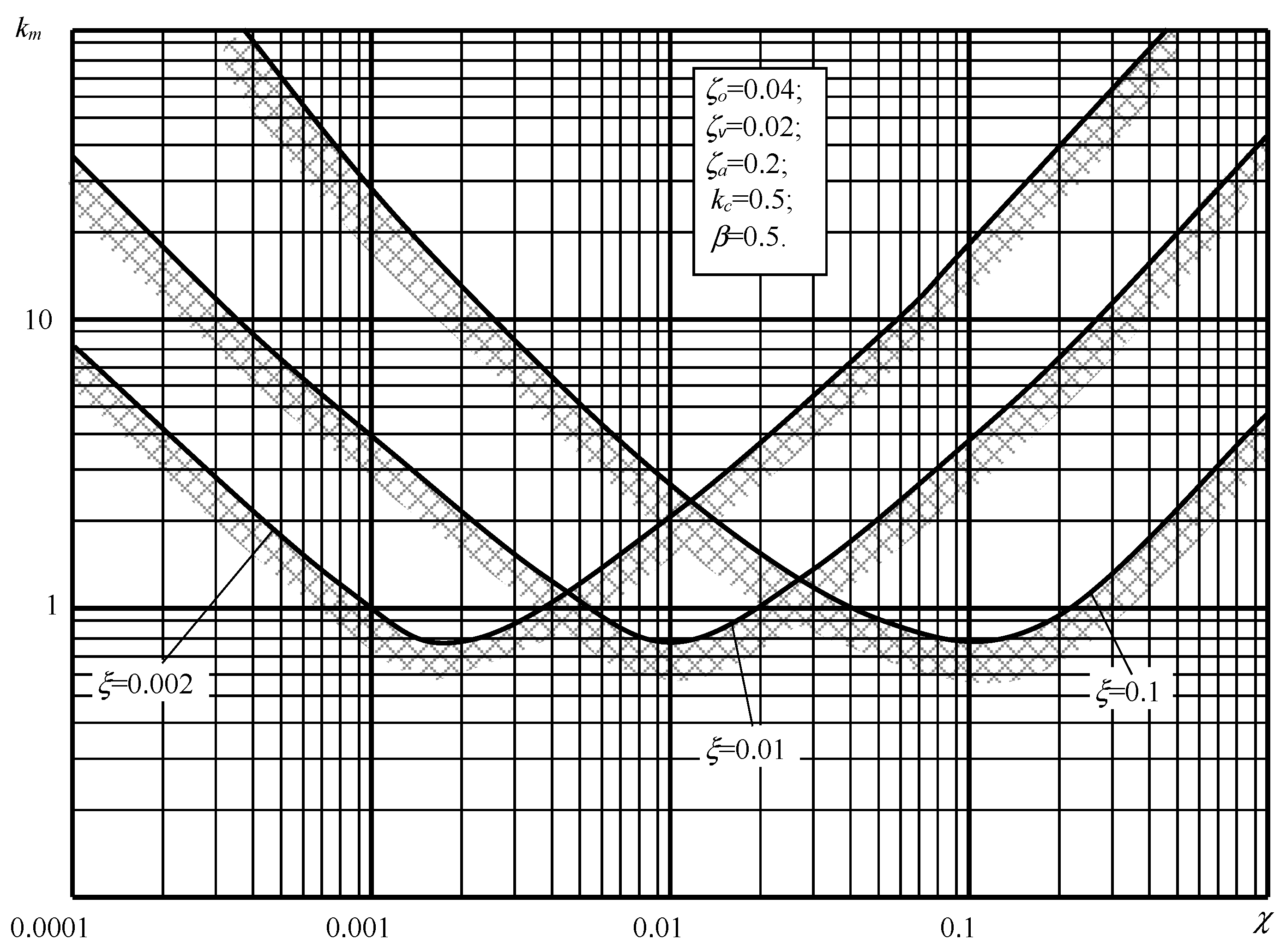
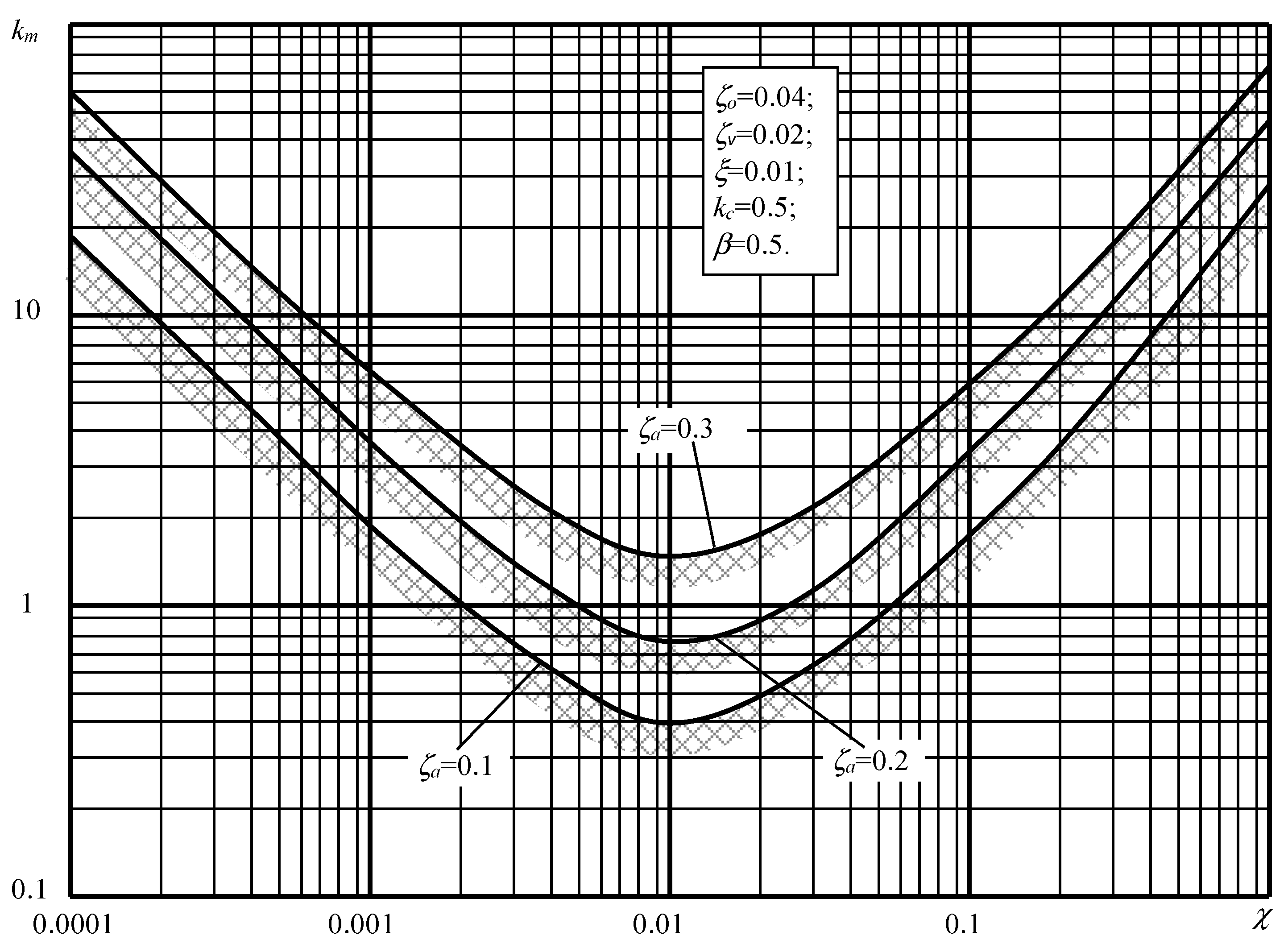

| Name | Values, Units of Measurement |
|---|---|
| Gyroscope kinetic moment | H = 0. 4 Nms |
| Mass of the sensing element | m = 1 kg |
| Distance from the suspension point to the center of mass | l = 0.1 m |
| The moment of the SE inertia relative to the X-axis | kg/m2 |
| The moment of the SE inertia relative to the Y-axis | kg/m2 |
| The moment of the SE inertia relative to the Z-axis | kg/m2 |
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Re3 | 0.3467768 | 0.256749317 | 0.117519317 | −0.1128104 | −0.4650924 | −1.02941 | −1.9377 |
| Im3 | 0.36524514 | 0.445138778 | 0.528962868 | 0.608364352 | 0.64599082 | 0.576247 | 0.245708 |
| M3 | 0.50364491 | 0.513876195 | 0.541860227 | 0.6187353 | 0.79599945 | 1.179723 | 1.953217 |
| AFR | 1.24856133 | 1.349432397 | 1.4448686 | 1.473692407 | 1.35620841 | 1.105217 | 0.81908 |
| № | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Re3 | −3.341773 | −5.5901633 | −9.157163183 | −14.754527 | −23.65425 | −37.5 | −59.403 |
| Im3 | −0.62738654 | −2.67948542 | −7.157731842 | −16.4854 | −35.8159026 | −74.7 | −153.5 |
| M3 | 3.40015612 | 6.199158595 | 11.62268311 | 22.12384415 | 42.92205078 | 83.55 | 164.592 |
| AFR | 0.57973902 | 0.395232371 | 0.26303725 | 0.172436993 | 0.111088793 | 0.071 | 0.0448 |
| № | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Re3 | −93.32 | −146 | −226 | −341 | −503 | −701.141 | −873.8 |
| Im3 | −310.85 | −626 | −1259 | −2497 | −4954 | −9765.024 | −18,956.4 |
| M3 | 324.552 | 643 | 1279 | 2521 | 4979 | 9790.1632 | 18,976.57 |
| AFR | 0.02799 | 0.02 | 0.01 | 0.006 | 0.003 | 0.0015868 | 0.000872 |
| № | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| Re3 | −813.7 | 41.7202 | 3050.48 | 10,784 | 26,118.8993 | 40,284.7 | −33,862.97 |
| Im3 | −36,350 | −67,275 | −118,566 | −186,292 | −213,646.734 | 78,757.48 | 1,733,191.7 |
| M3 | 36,359.1 | 67,275 | 118,605 | 186,604 | 215,237.3664 | 88,462.41 | 1,733,522.5 |
| AFR | 0.00116 | 0.00177 | 0.00258 | 0.00402 | 0.008446198 | 0.050161 | 0.0062181 |
| № | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| Re3 | −679,340.2 | −4,177,154 | −20,303,229.5 | −91,018,634 | −383,737,459.7 | −1,594,343,217 | −6,480,670,727 |
| Im3 | 8,490,859.2 | 32,961,875 | 115,645,385.6 | 391,191,215.9 | 1,275,274,890 | 4,136,250,339 | 13,227,130,761 |
| M3 | 8,517,992.3 | 33,225,500 | 117,414,123.3 | 401,640,335.5 | 1,331,758,418 | 4,432,888,129 | 14,729,429,087 |
| AFR | 0.0031207 | 0.00199 | 0.001400288 | 0.001030313 | 0.000779086 | 0.000594806 | 0.000456499 |
| № | 36 | 37 | 38 | 39 | 40 | 41 | |
| Re3 | −26,202,029,354 | −1.06402 × 1011 | −4.22651 × 1011 | −1.69342 × 1012 | −6.78923 × 1012 | −2.69315 × 1013 | |
| Im3 | 42,210,027,687 | 1.35384 × 1011 | 4.26707 × 1011 | 1.35535 × 1012 | 4.30869 × 1012 | 1.35796 × 1013 | |
| M3 | 49,681,312,177 | 1.72192 × 1011 | 6.00594 × 1011 | 2.16902 × 1012 | 8.04104 × 1012 | 3.01615 × 1013 | |
| AFR | 0.000349713 | 0.000266346 | 0.000202738 | 0.00015367 | 0.000116616 | 8.91301 × 10−5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korobiichuk, I.; Mel’nick, V.; Kosova, V.; Pavlenko, V.; Bursacov, K. Study of Systems of Active Vibration Protection of Navigation Instrument Equipment. Appl. Syst. Innov. 2024, 7, 95. https://doi.org/10.3390/asi7050095
Korobiichuk I, Mel’nick V, Kosova V, Pavlenko V, Bursacov K. Study of Systems of Active Vibration Protection of Navigation Instrument Equipment. Applied System Innovation. 2024; 7(5):95. https://doi.org/10.3390/asi7050095
Chicago/Turabian StyleKorobiichuk, Igor, Viktorij Mel’nick, Vera Kosova, Viktoriia Pavlenko, and Kirilo Bursacov. 2024. "Study of Systems of Active Vibration Protection of Navigation Instrument Equipment" Applied System Innovation 7, no. 5: 95. https://doi.org/10.3390/asi7050095
APA StyleKorobiichuk, I., Mel’nick, V., Kosova, V., Pavlenko, V., & Bursacov, K. (2024). Study of Systems of Active Vibration Protection of Navigation Instrument Equipment. Applied System Innovation, 7(5), 95. https://doi.org/10.3390/asi7050095






